Structural Studies of Aluminated form of Zeolites—EXAFS and XRD Experiment, STEM Micrography, and DFT Modelling
Abstract
1. Introduction
1.1. Importance of Zeolites
1.2. Zeolite Structure
1.3. Localisation of Aluminium Centres in Zeolite Structures
1.4. Extraframework Cations
1.5. EXAFS
2. Experimental Part
2.1. Materials
2.2. Computational Models
2.3. X-ray Spectroscopy
2.4. XRD
2.5. TEM Microscopic Studies
2.6. Computational Details
3. Results
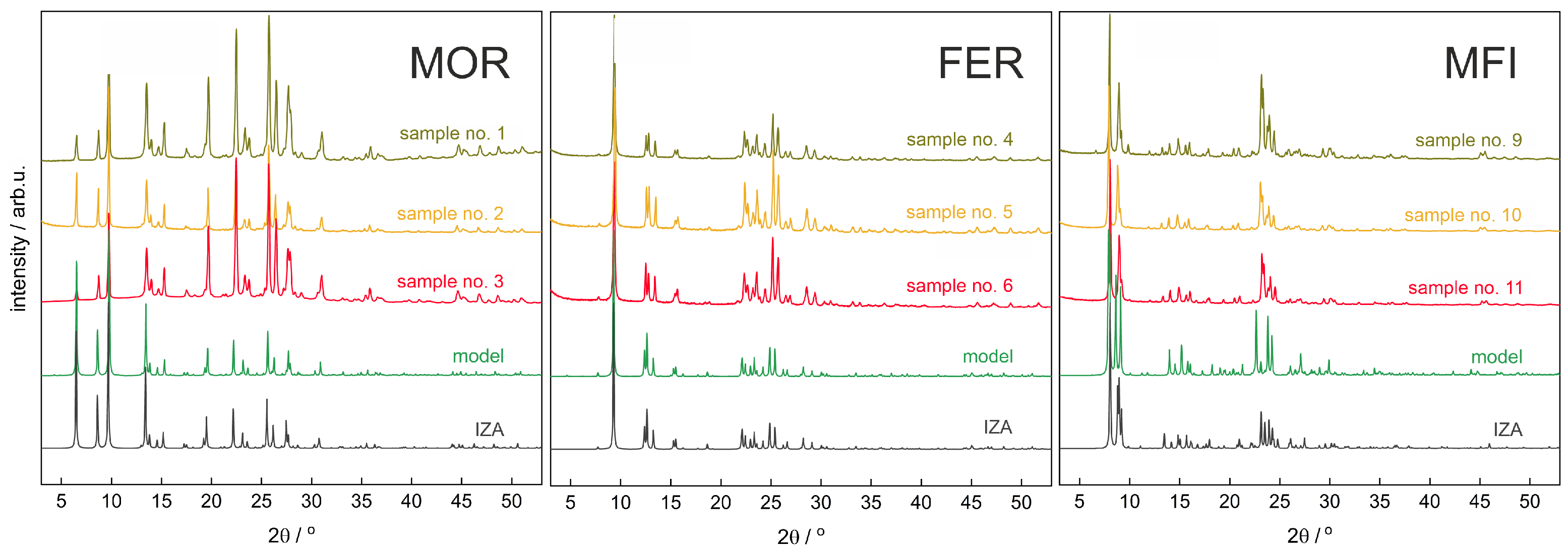
3.1. XRD
3.2. Pre-Screening of the Potential Zeolite Structures via RDF
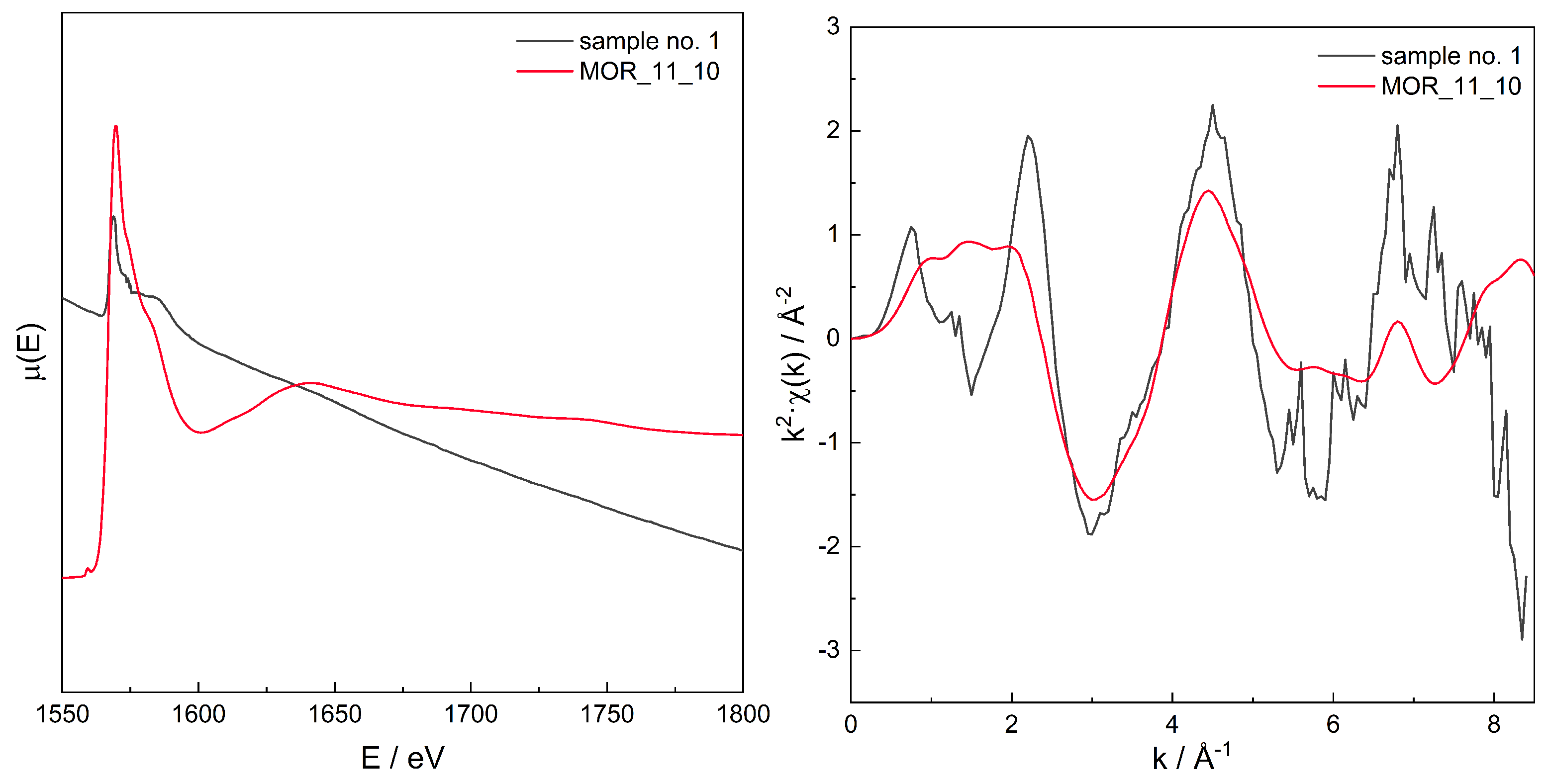
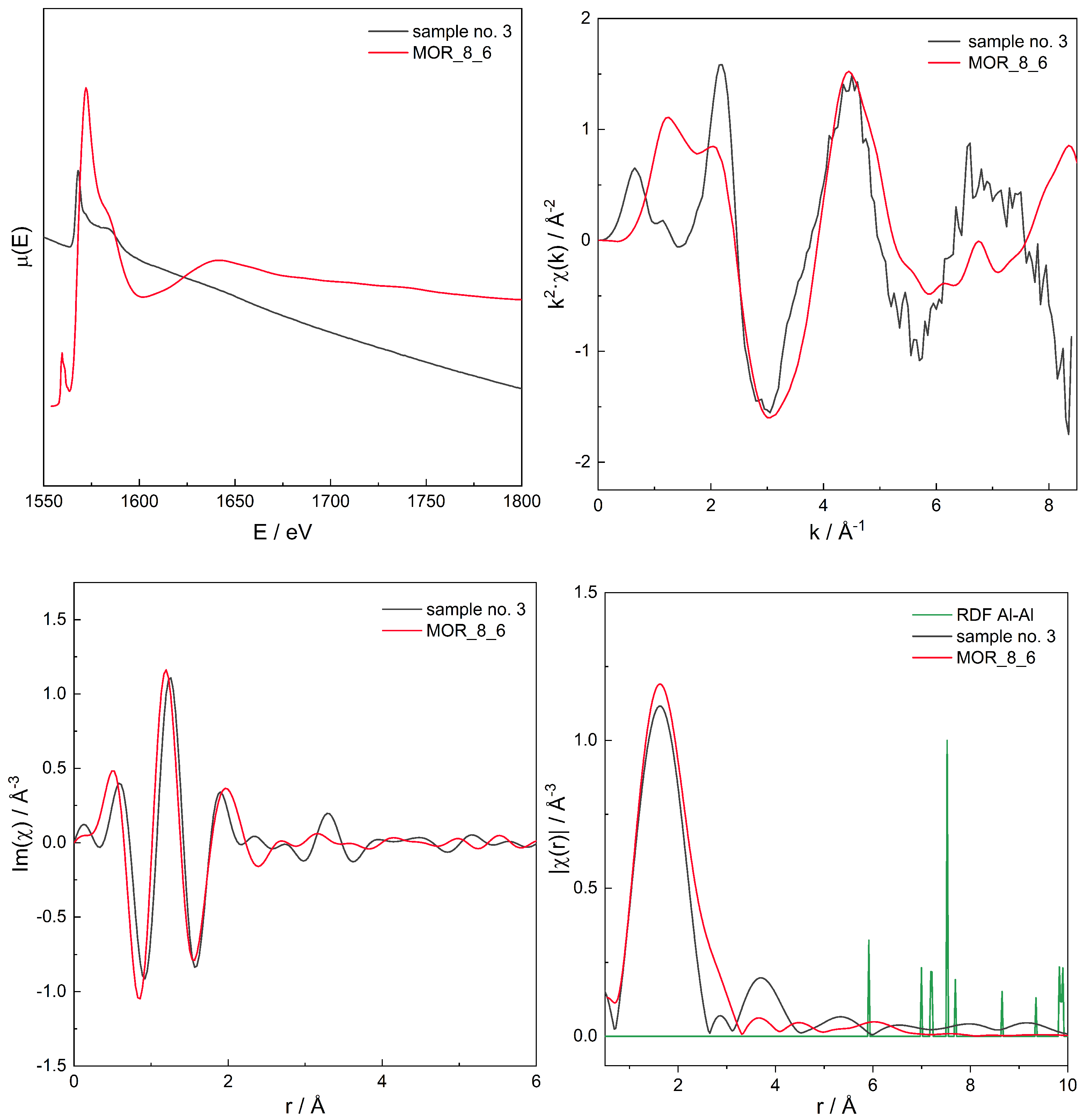
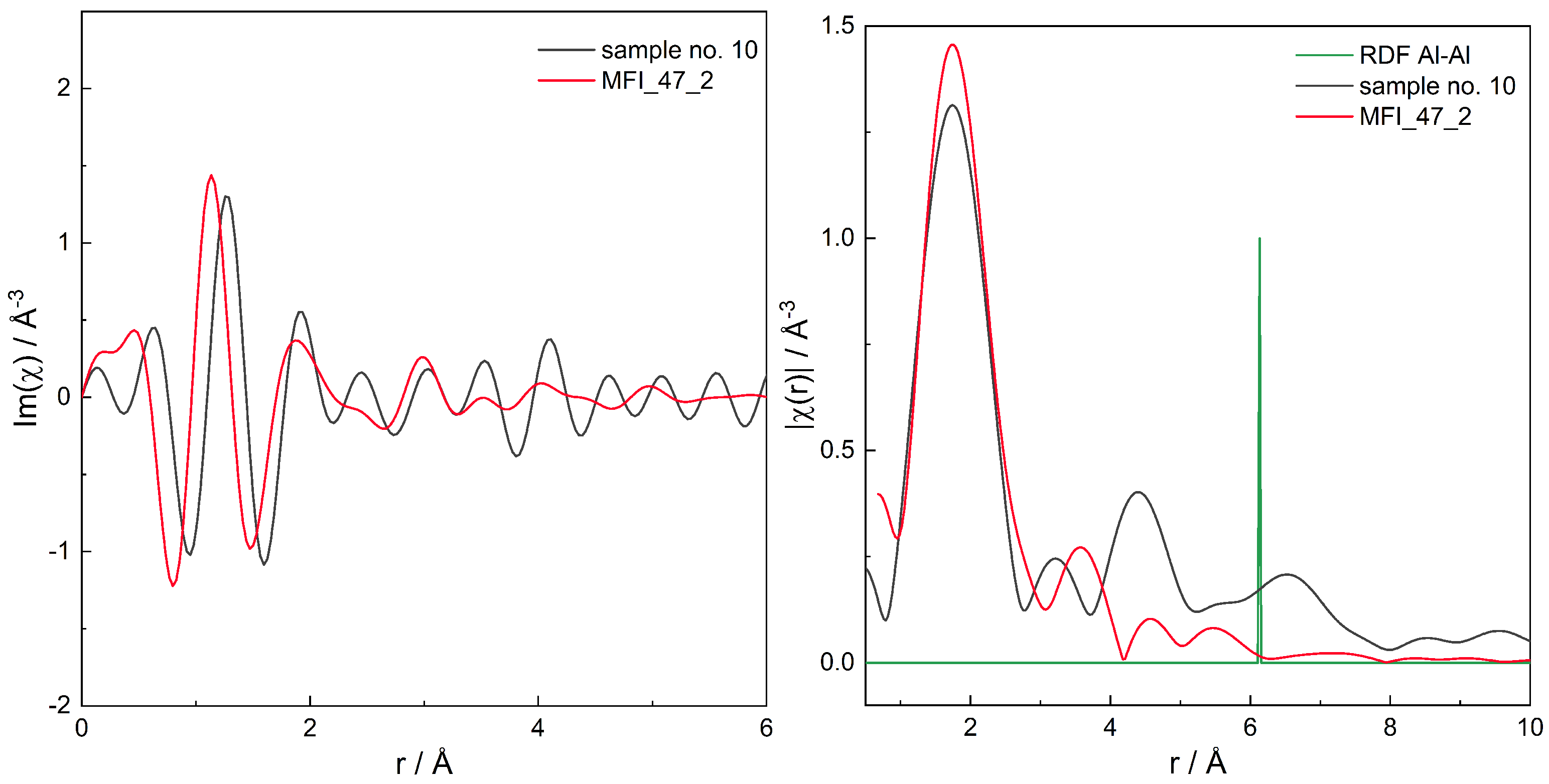
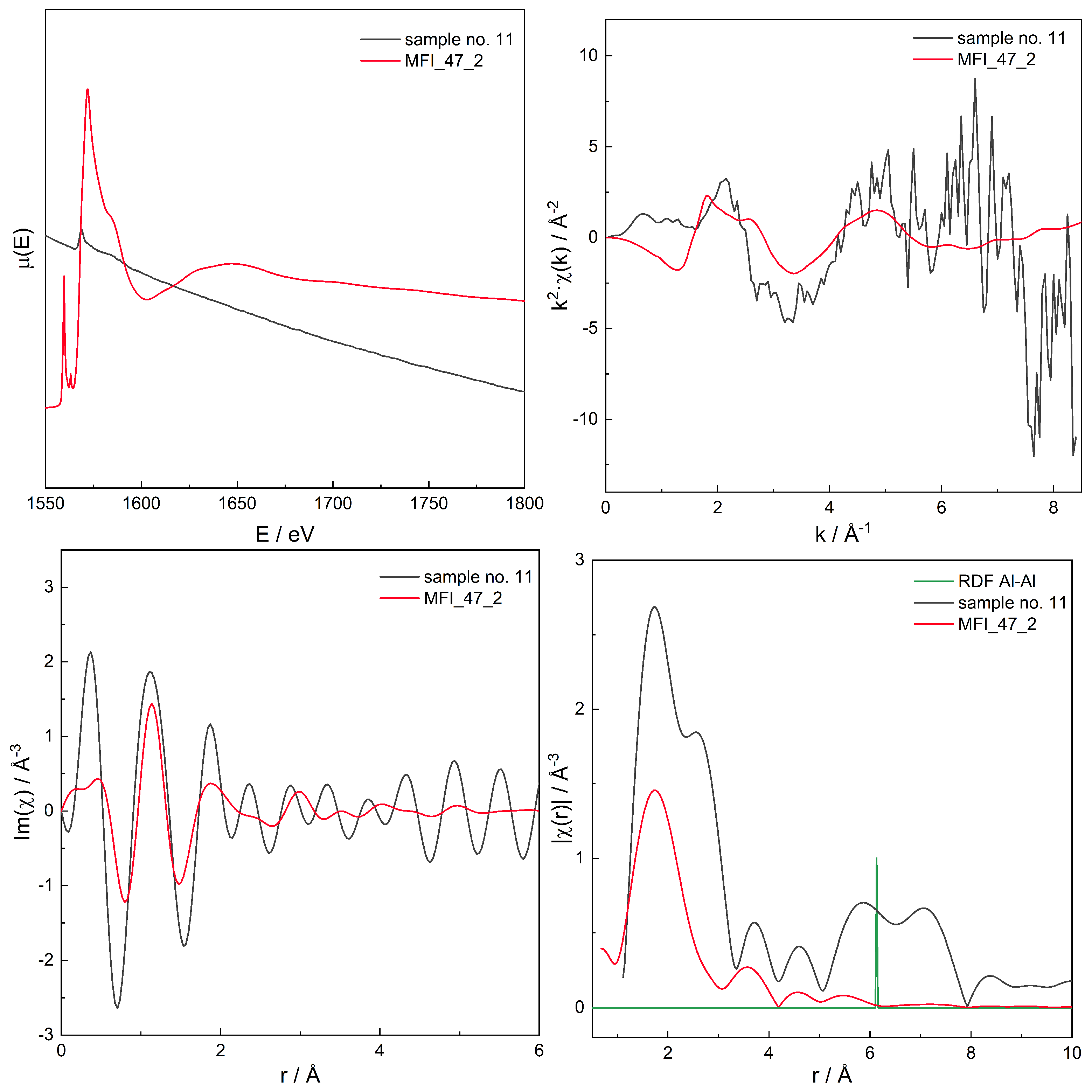
3.3. EXAFS
Additivity of EXAFS Spectra
3.4. STEM
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Strzempek, M.; Tarach, K.A.; Góra-Marek, K.; Rey, F.; Palomino, M.; Valencia, S.; Piskorz, W. Multiscale exploration of hydrocarbon adsorption and hopping through ZSM-5 channels—From Monte Carlo modelling to experiment. Phys. Chem. Chem. Phys. 2021, 23, 2981–2990. [Google Scholar] [CrossRef] [PubMed]
- Vermeiren, W.; Gilson, J.P. Impact of Zeolites on the Petroleum and Petrochemical Industry. Top. Catal. 2009, 52, 1131–1161. [Google Scholar] [CrossRef]
- Guisnet, M.; Gilson, J.P. Zeolites for Cleaner Technologies; Catalytic Science Series; Imperial College Press: London, UK, 2002; Volume 3. [Google Scholar] [CrossRef]
- Corma, A.; Martínez, A. Zeolites in refining and petrochemistry. In Zeolites and Ordered Mesoporous Materials: Progress and Prospects; Čejka, J., van Bekkum, H., Eds.; Elsevier: Amsterdam, The Netherlands, 2005; pp. 337–366. [Google Scholar] [CrossRef]
- Olsbye, U.; Svelle, S.; Bjørgen, M.; Beato, P.; Janssens, T.V.W.; Joensen, F.; Bordiga, S.; Lillerud, K.P. Conversion of methanol to hydrocarbons: How zeolite cavity and pore size controls product selectivity. Angew. Chem. Int. Ed. 2012, 51, 5810–5831. [Google Scholar] [CrossRef] [PubMed]
- Olah, G.A. Towards Oil Independence Through Renewable Methanol Chemistry. Angew. Chem. Int. Ed. 2013, 52, 104–107. [Google Scholar] [CrossRef]
- Liebau, F.; Gies, H.; Gunawardane, R.P.; Marler, B. Classification of tectosilicates and systematic nomenclature of clathrate type tectosilicates: A proposal. Zeolites 1986, 6, 373–377. [Google Scholar] [CrossRef]
- Loewenstein, W. The distribution of aluminum in the tetrahedra of silicates and aluminates. Am. Mineral. 1954, 39, 92–96. [Google Scholar]
- Dempsey, E.; Kuehl, G.H.; Olson, D.H. Variation of the lattice parameter with aluminum content in synthetic sodium faujasites. Evidence for ordering of the framework ions. J. Phys. Chem. 1969, 73, 387–390. [Google Scholar] [CrossRef]
- Tielens, F.; Langenaeker, W.; Geerlings, P. Ab initio study of the bridging hydroxyl acidity and stability in the 12-membered ring of zeolites. J. Mol. Struct. THEOCHEM 2000, 496, 153–162. [Google Scholar] [CrossRef]
- Piskorz, W.; Zasada, F. Catalytic Properties of Selected Transition Metal Oxides-Computational Studies. In Transition Metals in Coordination Environments. Computational Chemistry and Catalysis Viewpoints; Broclawik, E., Borowski, T., Radoń, M., Eds.; Springer Nature Switzerland AG: Berlin/Heidelberg, Germany, 2019; pp. 345–408. [Google Scholar] [CrossRef]
- Kornatowski, J.; Sychev, M.; Kuzenkov, S.; Strnadová, K.; Pilz, W.; Kassner, D.; Pieper, G.; Baur, W.H. V-Ti and V-Al silicate molecular sieves of MFI topology: Synthesis and characteristics. J. Chem. Soc. Faraday Trans. 1995, 91, 2217. [Google Scholar] [CrossRef]
- Kowalak, S.; Stawiński, K.; Makowiak, A. Incorporation of zinc into silica mesoporous molecular sieves. Microporous Mesoporous Mater. 2001, 44–45, 283–293. [Google Scholar] [CrossRef]
- Nogier, J.P.; Millot, Y.; Man, P.P.; Shishido, T.; Che, M.; Dzwigaj, S. Probing the incorporation of Ti(IV) into the BEA zeolite framework by XRD, FTIR, NMR, and DR UV-jp810722bis. J. Phys. Chem. C 2009, 113, 4885–4889. [Google Scholar] [CrossRef]
- Trejda, M.; Ziolek, M.; Millot, Y.; Chalupka, K.; Che, M.; Dzwigaj, S. Methanol oxidation on VSiBEA zeolites: Influence of V content on the catalytic properties. J. Catal. 2011, 281, 169–176. [Google Scholar] [CrossRef]
- Xu, R.; Pang, W.; Yu, J.; Huo, Q.; Chen, J. Chemistry of Zeolites and Related Porous Materials Synthesis and Structure; John Wiley and Sons: Hoboken, NJ, USA, 2007; p. 679. [Google Scholar] [CrossRef]
- Meeprasert, J.; Kungwan, N.; Jungsuttiwong, S.; Namuangruk, S. Location and reactivity of extra-framework cation in the alkali exchanged LTL zeolites: A periodic density functional study. Microporous Mesoporous Mater. 2014, 195, 227–239. [Google Scholar] [CrossRef]
- Tielens, F.; Dzwigaj, S. Group V metal substitution in silicate model zeolites: In search for the active site. Chem. Phys. Lett. 2010, 501, 59–63. [Google Scholar] [CrossRef]
- Kozyra, P.; Piskorz, W. A comparative computational study on hydrogen adsorption on the Ag+, Cu+, Mg2+, Cd2+, and Zn2+ cationic sites in zeolites. Phys. Chem. Chem. Phys. 2016, 18, 12592–12603. [Google Scholar] [CrossRef]
- Woertink, J.S.; Smeets, P.J.; Groothaert, M.H.; Vance, M.A.; Sels, B.F.; Schoonheydt, R.A.; Solomon, E.I. A [Cu2O]2+ core in Cu-ZSM-5, the active site in the oxidation of methane to methanol. Proc. Natl. Acad. Sci. USA 2009, 106, 18908–18913. [Google Scholar] [CrossRef] [PubMed]
- Selvaraj, T.; Rajalingam, R.; Balasubramanian, V. Impact of zeolite-Y framework on the geometry and reactivity of Ru (III) benzimidazole complexes—A DFT study. Appl. Surf. Sci. 2018, 434, 781–786. [Google Scholar] [CrossRef]
- IZA-SC. Database of Zeolite Structures. Zeolite Framework Types. Available online: https://europe.iza-structure.org/IZA-SC/ftc_table.php (accessed on 1 January 2021).
- Bhan, A.; Iglesia, E. A Link between Reactivity and Local Structure in Acid Catalysis on Zeolites. Accounts Chem. Res. 2008, 41, 559–567. [Google Scholar] [CrossRef] [PubMed]
- Mlekodaj, K.; Dedecek, J.; Pashkova, V.; Tabor, E.; Klein, P.; Urbanova, M.; Karcz, R.; Sazama, P.; Whittleton, S.R.; Thomas, H.M.; et al. Al organization in the SSZ-13 Zeolite. Al distribution and extraframework sites of divalent cations. J. Phys. Chem. C 2018, 123, 7968–7987. [Google Scholar] [CrossRef]
- Akporiaye, D.E.; Dahl, I.M.; Mostad, H.B.; Wendelbo, R. Aluminum distribution in chabazite: An experimental and computational study. J. Phys. Chem. 1996, 100, 4148–4153. [Google Scholar] [CrossRef]
- Benco, L.; Bucko, T.; Hafner, J.; Toulhoat, H. Periodic DFT calculations of the stability of Al/Si substitutions and extraframework Zn2+ cations in mordenite and reaction pathway for the dissociation of H2 and CH4. J. Phys. Chem. B 2005, 109, 20361–20369. [Google Scholar] [CrossRef] [PubMed]
- García-Pérez, E.; Dubbeldam, D.; Liu, B.; Smit, B.; Calero, S. A computational method to characterize framework aluminum in aluminosilicates. Angew. Chem. Int. Ed. 2007, 46, 276–278. [Google Scholar] [CrossRef] [PubMed]
- Olson, D.H.; Khosrovani, N.; Peters, A.W.; Toby, B.H. Crystal structure of dehydrated CsZSM-5 (5.8Al): Evidence for nonrandom aluminum distribution. J. Phys. Chem. B 2000, 104, 4844–4848. [Google Scholar] [CrossRef]
- Lu, B.; Kanai, T.; Oumi, Y.; Sano, T. Aluminum distribution in high-silica mordenite. J. Porous Mater. 2007, 14, 89–96. [Google Scholar] [CrossRef]
- Sazama, P.; Tabor, E.; Klein, P.; Wichterlova, B.; Sklenak, S.; Mokrzycki, L.; Pashkova, V.; Ogura, M.; Dedecek, J. Al-rich beta zeolites. Distribution of Al atoms in the framework and related protonic and metal-ion species. J. Catal. 2016, 333, 102–114. [Google Scholar] [CrossRef]
- Di Iorio, J.R.; Gounder, R. Controlling the Isolation and Pairing of Aluminum in Chabazite Zeolites Using Mixtures of Organic and Inorganic Structure-Directing Agents. Chem. Mater. 2016, 28, 2236–2247. [Google Scholar] [CrossRef]
- Klinowski, J. Nuclear magnetic resonance studies of zeolites. Prog. Nucl. Magn. Reson. Spectrosc. 1984, 16, 237–309. [Google Scholar] [CrossRef]
- Majda, D.; Paz, F.A.; Friedrichs, D.; Foster, M.D.; Simperler, A.; Bell, R.G.; Klinowski, J. Hypothetical zeolitic frameworks: In search of potential heterogeneous catalysts. J. Phys. Chem. C 2008, 112, 1040–1047. [Google Scholar] [CrossRef]
- Porcher, F.F.; Souhassou, M.; Lecomte, C.E.P. Experimental determination of electrostatic properties of Na-X zeolite from high resolution X-ray diffraction. Phys. Chem. Chem. Phys. 2014, 16, 12228–12236. [Google Scholar] [CrossRef] [PubMed]
- Lesthaeghe, D.; Horré, A.; Waroquier, M.; Marin, G.B.; Van Speybroeck, V. Theoretical Insights on Methylbenzene Side-Chain Growth in ZSM-5 Zeolites for Methanol-to-Olefin Conversion. Chem. A Eur. J. 2009, 15, 10803–10808. [Google Scholar] [CrossRef]
- Joyner, R.W.; Smith, A.D.; Stockenhuber, M.; van den Berg, M.W.E. The local structure of aluminium sites in zeolites. Phys. Chem. Chem. Phys. 2004, 6, 5435. [Google Scholar] [CrossRef]
- Joyner, R.W.; Smith, A.D.; Stockenhuber, M.; van den Berg, M.W.E. A soft X-ray exafs study of the local structure of tetrahedral aluminium in zeolites. Stud. Surf. Sci. Catal. 2004, 154, 1406–1410. [Google Scholar] [CrossRef]
- Kulkarni, A.R.; Zhao, Z.J.; Siahrostami, S.; Nørskov, J.K.; Studt, F. Cation-exchanged zeolites for the selective oxidation of methane to methanol. Catal. Sci. Technol. 2018, 8, 114–123. [Google Scholar] [CrossRef]
- Iwamoto, M.; Yokoo, S.; Sakai, K.; Kagawa, S. Catalytic decomposition of nitric oxide over copper(II)-exchanged, Y-type zeolites. J. Chem. Soc. Faraday Trans. 1 1981, 77, 1629. [Google Scholar] [CrossRef]
- Iwamoto, M.; Furukawa, H.; Mine, Y.; Uemura, F.; Mikuriya, S.i.; Kagawa, S. Copper(II) ion-exchanged ZSM-5 zeolites as highly active catalysts for direct and continuous decomposition of nitrogen monoxide. J. Chem. Soc. Chem. Commun. 1986, 16, 1272. [Google Scholar] [CrossRef]
- Oda, A.; Torigoe, H.; Itadani, A.; Ohkubo, T.; Yumura, T.; Kobayashi, H.; Kuroda, Y. Unprecedented reversible redox process in the ZnMFI-H2 system involving formation of stable atomic Zn0. Angew. Chem. Int. Ed. 2012, 51, 7719–7723. [Google Scholar] [CrossRef]
- Dubkov, K.; Ovanesyan, N.; Shteinman, A.; Starokon, E.; Panov, G. Evolution of Iron States and Formation of α-Sites upon Activation of FeZSM-5 Zeolites. J. Catal. 2002, 207, 341–352. [Google Scholar] [CrossRef]
- Starokon, E.V.; Parfenov, M.V.; Arzumanov, S.S.; Pirutko, L.V.; Stepanov, A.G.; Panov, G.I. Oxidation of methane to methanol on the surface of FeZSM-5 zeolite. J. Catal. 2013, 300, 47–54. [Google Scholar] [CrossRef]
- Xu, J.; Armstrong, R.D.; Shaw, G.; Dummer, N.F.; Freakley, S.J.; Taylor, S.H.; Hutchings, G.J. Continuous selective oxidation of methane to methanol over Cu- and Fe-modified ZSM-5 catalysts in a flow reactor. Catal. Today 2016, 270, 93–100. [Google Scholar] [CrossRef]
- Park, K.S.; Kim, J.H.; Park, S.H.; Moon, D.J.; Roh, H.S.; Chung, C.H.; Um, S.H.; Choi, J.H.; Bae, J.W. Direct activation of CH4 to oxygenates and unsaturated hydrocarbons using N2O on Fe-modified zeolites. J. Mol. Catal. A Chem. 2017, 426, 130–140. [Google Scholar] [CrossRef]
- Stepanov, A.G.; Arzumanov, S.S.; Gabrienko, A.A.; Parmon, V.N.; Ivanova, I.I.; Freude, D. Significant influence of Zn on activation of the C-H bonds of small alkanes by brønsted acid sites of zeolite. ChemPhysChem 2008, 9, 2559–2563. [Google Scholar] [CrossRef] [PubMed]
- Biscardi, J.A.; Meitzner, G.D.; Iglesia, E. Structure and density of active Zn species in Zn/H-ZSM5 propane aromatization catalysts. J. Catal. 1998, 179, 192–202. [Google Scholar] [CrossRef]
- Niu, X.; Gao, J.; Miao, Q.; Dong, M.; Wang, G.; Fan, W.; Qin, Z.; Wang, J. Influence of preparation method on the performance of Zn-containing HZSM-5 catalysts in methanol-to-aromatics. Microporous Mesoporous Mater. 2014, 197, 252–261. [Google Scholar] [CrossRef]
- Wang, X.; Xu, J.; Qi, G.; Li, B.; Wang, C.; Deng, F. Alkylation of benzene with methane over ZnZSM-5 zeolites studied with solid-state NMR spectroscopy. J. Phys. Chem. C 2013, 117, 4018–4023. [Google Scholar] [CrossRef]
- Smeets, P.J.; Woertink, J.S.; Sels, B.F.; Solomon, E.I.; Schoonheydt, R.A. Transition-metal ions in zeolites: Coordination and activation of oxygen. Inorg. Chem. 2010, 49, 3573–3583. [Google Scholar] [CrossRef] [PubMed]
- Pietrzyk, P.; Piskorz, W.; Sojka, Z.; Broclawik, E. Molecular structure, spin density distribution, and hyperfine coupling constants of the η1{CuNO}11 adduct in the ZSM-5 zeolite: DFT calculations and comparison with EPR data. J. Phys. Chem. B 2003, 107, 6105–6113. [Google Scholar] [CrossRef]
- Uzunova, E.L.; Göltl, F.; Kresse, G.; Hafner, J. Application of hybrid functionals to the modeling of NO adsorption on Cu-SAPO-34 and Co-SAPO-34: A periodic DFT study. J. Phys. Chem. C 2009, 113, 5274–5291. [Google Scholar] [CrossRef]
- Davidová, M.; Nachtigallová, D.; Nachtigall, P.; Sauer, J. Nature of the Cu+-NO bond in the gas phase and at different types of Cu+ sites in zeolite catalysts. J. Phys. Chem. B 2004, 108, 13674–13682. [Google Scholar] [CrossRef]
- Izquierdo, R.; Rodríguez, L.J.; Añez, R.; Sierraalta, A. Direct catalytic decomposition of NO with Cu-ZSM-5: A DFT-ONIOM study. J. Mol. Catal. A Chem. 2011, 348, 55–62. [Google Scholar] [CrossRef]
- Göltl, F.; Hafner, J. Structure and properties of metal-exchanged zeolites studied using gradient-corrected and hybrid functionals. III. Energetics and vibrational spectroscopy of adsorbates. J. Chem. Phys. 2012, 136, 64501. [Google Scholar] [CrossRef]
- Heyden, A.; Peters, B.; Bell, A.T.; Keil, F.J. Comprehensive DFT study of nitrous oxide decomposition over Fe-ZSM-5. J. Phys. Chem. B 2005, 109, 1857–1873. [Google Scholar] [CrossRef]
- Pietrzyk, P.; Sojka, Z.; Dzwigaj, S.; Che, M. Generation, identification, and reactivity of paramagnetic VO2 centers in zeolite BEA for model studies of processes involving spin pairing, electron transfer, and oxygen transfer. J. Am. Chem. Soc. 2007, 129, 14174–14175. [Google Scholar] [CrossRef]
- Behrens, P. XANES, EXAFS and Related Techniques. In Molecular Sieves—Science and Technology. Characterization I; Karge, H.G., Weitkamp, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; Chapter 4; pp. 427–466. [Google Scholar] [CrossRef]
- Van Bokhoven, J.A.; van der Eerden, A.M.J.; Koningsberger, D.C. Three-Coordinate Aluminum in Zeolites Observed with In situ X-ray Absorption Near-Edge Spectroscopy at the Al K-Edge: Flexibility of Aluminum Coordinations in Zeolites. J. Am. Chem. Soc. 2003, 125, 7435–7442. [Google Scholar] [CrossRef]
- Bianconi, A. One-Electron Transitions in the XANES of Condensed Systems. In Core-Level Spectroscopy in Condensed Systems; Springer Series in Solid-State Sciences; Kanamori, J., Kotani, A., Eds.; Springer: Berlin/Heidelberg, Germany, 1988; Volume 81, pp. 14–32. [Google Scholar] [CrossRef]
- Newville, M. EXAFS analysis using FEFF and FEFFIT. J. Synchrotron Radiat. 2001, 8, 96–100. [Google Scholar] [CrossRef]
- Bugaev, L.A.; van Bokhoven, J.A.; Sokolenko, A.P.; Latokha, Y.V.; Avakyan, L.A. Local Structure of Aluminum in Zeolite Mordenite as Affected by Temperature. J. Phys. Chem. B 2005, 109, 10771–10778. [Google Scholar] [CrossRef]
- Zaja̧c, M.; Giela, T.; Freindl, K.; Kollbek, K.; Korecki, J.; Madej, E.; Pitala, K.; Kozioł-Rachwał, A.; Sikora, M.; Spiridis, N.; et al. The first experimental results from the 04BM (PEEM/XAS) beamline at Solaris. Nucl. Instruments Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2021, 492, 43–48. [Google Scholar] [CrossRef]
- Lutterotti, L.; Bortolotti, M.; Ischia, G.; Lonardelli, I.; Wenk, H.R. Rietveld texture analysis from diffraction images. Z. Krist. Suppl. 2007, 2007, 125–130. [Google Scholar] [CrossRef]
- Lutterotti, L.; Pillière, H.; Fontugne, C.; Boullay, P.; Chateigner, D. Full-profile search–match by the Rietveld method. J. Appl. Crystallogr. 2019, 52, 587–598. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for open-shell transition metals. Phys. Rev. B 1993, 48, 13115–13118. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Methfessel, M.S.; Paxton, A.T. High-precision sampling for Brillouin-zone integration in metals. Phys. Rev. B 1989, 40, 3616–3621. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Erratum to Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1997, 78, 1396. [Google Scholar] [CrossRef]
- Grimme, S. Accurate description of van der Waals complexes by density functional theory including empirical corrections. J. Comput. Chem. 2004, 25, 1463–1473. [Google Scholar] [CrossRef] [PubMed]
- Murnaghan, F.D. The compressibility of media under extreme pressures. Proc. Natl. Acad. Sci. USA 1944, 30, 244–247. [Google Scholar] [CrossRef] [PubMed]
- Cabaret, D.; Sainctavit, P.; Ildefonse, P.; Flank, A.M. Full multiple-scattering calculations on silicates and oxides at the Al K edge. J. Phys. Condens. Matter 1996, 8, 3691–3704. [Google Scholar] [CrossRef]
- Van Bokhoven, J.A.; Nabi, T.; Sambe, H.; Ramaker, D.E.; Koningsberger, D.C. Interpretation of the Al K- and L II/III -edges of aluminium oxides: Differences between tetrahedral and octahedral Al explained by different local symmetries. J. Phys. Condens. Matter 2001, 13, 10247–10260. [Google Scholar] [CrossRef]
- Joly, Y. X-ray absorption near-edge structure calculations beyond the muffin-tin approximation. Phys. Rev. B 2001, 63, 125120. [Google Scholar] [CrossRef]
- Guda, S.A.; Guda, A.A.; Soldatov, M.A.; Lomachenko, K.A.; Bugaev, A.L.; Lamberti, C.; Gawelda, W.; Bressler, C.; Smolentsev, G.; Soldatov, A.V.; et al. Optimized Finite Difference Method for the Full-Potential XANES Simulations: Application to Molecular Adsorption Geometries in MOFs and Metal–Ligand Intersystem Crossing Transients. J. Chem. Theory Comput. 2015, 11, 4512–4521. [Google Scholar] [CrossRef] [PubMed]
- Bourke, J.D.; Chantler, C.T.; Joly, Y. FDMX: Extended X-ray absorption fine structure calculations using the finite difference method. J. Synchrotron Radiat. 2016, 23, 551–559. [Google Scholar] [CrossRef]
- Ravel, B.; Newville, M. ATHENA, ARTEMIS, HEPHAESTUS: Data analysis for X-ray absorption spectroscopy using IFEFFIT. J. Synchrotron Radiat. 2005, 12, 537–541. [Google Scholar] [CrossRef] [PubMed]
- Ravel, B. Demeter: XAS Data Processing and Analysis. 2018. Available online: https://bruceravel.github.io/demeter/ (accessed on 10 October 2020).
- Mote, V.D.; Purushotham, Y.; Dole, B.N. Williamson-Hall analysis in estimation of lattice strain in nanometer-sized ZnO particles. J. Theor. Appl. Phys. 2012, 6, 6. [Google Scholar] [CrossRef]
- Dubbeldam, D.; Torres-Knoop, A.; Walton, K.S. On the inner workings of Monte Carlo codes. Mol. Simul. 2013, 39, 1253–1292. [Google Scholar] [CrossRef]
- Dubbeldam, D.; Calero, S.; Ellis, D.E.; Snurr, R.Q. RASPA: Molecular simulation software for adsorption and diffusion in flexible nanoporous materials. Mol. Simul. 2016, 42, 81–101. [Google Scholar] [CrossRef]
- Pellicer-Porres, J.; Segura, A.; Martínez-Criado, G.; Rodríguez-Mendoza, U.R.; Lavín, V. Formation of nanostructures in Eu3+ doped glass–ceramics: An XAS study. J. Phys. Condens. Matter 2013, 25, 025303. [Google Scholar] [CrossRef]










| Sample No. | Framework | Si/Al | Product ID | mfr. | B.a.s | L.a.s | (B + L) a.s. | (NH3) | /cm−1 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | MOR | 15 | 660-HOA | Tosoh | 1231 | 20 | 1251 | 313 | |
| 2 | MOR | 10 | CBV-21A | Tosoh | 1635 | 5 | 1640 | 310 | |
| 3 | MOR | 8 | 620-HOA | Tosoh | 1790 | 10 | 1800 | 309 | |
| 4 | FER | 9 | — (own synthesis) | 1100 | 0 | 1100 | 309 | ||
| 5 | FER | 9 | — (own synthesis) | 1363 | 51 | 1414 | 308 | ||
| 6 | FER | 9 | — (own synthesis) | 612 | 0 | 612 | 303 | ||
| 9 | MFI | CBV-2314 | Zeolyst | ||||||
| 10 | MFI | 25 | CBV-5524G | Zeolyst | |||||
| 11 | MFI | 40 | CBV-8014 | Zeolyst | |||||
| 12 | MFI | 140 | CBV-28014 | Zeolyst | |||||
| 13 | MFI | 750 | HSZ-890HOA | Tosoh | |||||
| Model Label | Framework | Si/Al | T Sites Substitutions |
|---|---|---|---|
| FER_8_1 | FER | 8 | T1g, T3e, T4c, T4d |
| MFI_11_1 | MFI | 11.5 | T7b, T7c, T7g, T10c, T10f, T10h, T12c, T12f |
| MFI_11_2 | MFI | 11.5 | T1f, T6c, T7b, T7c, T7g, T10c, T10h, T12f |
| MFI_15_1 | MFI | 15 | T8c, T9c, T10e, T12a, T12d, T12f |
| MFI_15_2 | MFI | 15 | T8c, T9c, T10e, T11h, T12a, T12e |
| MFI_15_3 | MFI | 15 | T8c, T9c, T10g, T11h, T12a, T12e |
| MFI_15_4 | MFI | 15 | T6g, T9c, T10g, T11h, T12a, T12e |
| MFI_15_5 | MFI | 15 | T8d, T9c, T9g, T11h, T12a, T12e |
| MFI_15_6 | MFI | 15 | T9c, T9g, T11h, T12a, T12d, T12f |
| MFI_15_7 | MFI | 15 | T3b, T9c, T9g, T11h, T12a, T12d |
| MFI_15_8 | MFI | 15 | T6c, T6g, T9g, T11h, T12a, T12d |
| MFI_15_9 | MFI | 15 | T3a, T6c, T6e, T6g, T9g, T11h |
| MFI_15_10 | MFI | 15 | T3a, T3e, T6g, T8d, T9c, T9g |
| MFI_23_1 | MFI | 23 | T10c, T10f, T12c, T12f |
| MFI_23_2 | MFI | 23 | T1e, T10c, T12c, T12f |
| MFI_47_1 | MFI | 47 | T12c, T12f |
| MFI_47_2 | MFI | 47 | T3d, T12c |
| MOR_8_5 | MOR | 8.6 | T2e, T3a, T3h, T4e, T4g |
| MOR_8_6 | MOR | 8.6 | T2e, T4a, T4e, T4g, T4h |
| MOR_11_1 | MOR | 11 | T2e, T3a, T3e, T3g |
| MOR_11_6 | MOR | 11 | T2p, T3b, T3e, T3g |
| MOR_11_8 | MOR | 11 | T2p, T3a, T3f, T3g |
| MOR_11_10 | MOR | 11 | T2e, T3b, T3e, T4g |
| MOR_11_11 | MOR | 11 | T1m, T2p, T3a, T4f |
| MOR_11_12 | MOR | 11 | T1m, T2p, T4b, T4f |
| MOR_11_13 | MOR | 11 | T1m, T1p, T2k, T2p |
| MOR_11_14 | MOR | 11 | T2d, T2f, T3b, T4a |
| MOR_11_15 | MOR | 11 | T1d, T2d, T2f, T3c |
| MOR_11_16 | MOR | 11 | T1m, T2k, T2p, T3h |
| MOR_11_17 | MOR | 11 | T2d, T2f, T3b, T3c |
| MOR_11_18 | MOR | 11 | T2d, T2f, T2l, T3b |
| MOR_15_1 | MOR | 15 | T2e, T3e, T3g |
| MOR_15_9 | MOR | 15 | T2m, T3e, T3g |
| Sample No. | Framework | Si/Al | /nm | == |
|---|---|---|---|---|
| 1 | MOR | 15 | ||
| 2 | MOR | 10 | ||
| 3 | MOR | 8 | ||
| 6 | FER | 9 | ||
| 9 | MFI | 11.5 | ||
| 10 | MFI | 25 | ||
| 11 | MFI | 40 |
| Sample No. | Framework | Si/Al | T-Al Structure Contribution/% | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | MOR | 15 | 0 ± 0.40 (0) | 0 ± 0.43 (0) | 1.15 ± 0.67 (1.70) | 0 ± 0.69 (0) | ||||||||
| 2 | MOR | 10 | 0 ± 0.44 (0) | 0 ± 0.48 (0) | 0.84 ± 0.74 (1.13) | 0 ± 0.78 (0) | ||||||||
| 3 | MOR | 8 | 0 ± 0.60 (0) | 0 ± 0.64 (0) | 1.91 ± 1.00 (1.83) | 0 ± 1.04 (0) | ||||||||
| 4 | FER | 9 | 0.14 ± 0.63 (0) | 0 ± 0.65 (0) | 0.55 ± 0.40 (1.38) | 0 ± 0.79 (0) | ||||||||
| 5 | FER | 9 | 0 ± 0.76 (0) | 0 ± 0.79 (0) | 0.59 ± 0.48 (1.20) | 0 ± 0.96 (0) | ||||||||
| 6 | FER | 9 | 0.24 ± 0.97 (0.24) | 0 ± 1.02 (0) | 0.87 ± 0.62 (1.41) | 0 ± 1.22 (0) | ||||||||
| 9 | MFI | 2.35 ± 3.17 (0.74) | 0 ± 6.18 (0) | 0 ± 5.81 (0) | 0 ± 6.24 (0) | 0 ± 6.69 (0) | 0 ± 6.22 (0) | 0 ± 5.64 (0) | 0 ± 5.64 (0) | 0 ± 7.13 (0) | 0 ± 4.92 (0) | 0 ± 9.84 (0) | 0 ± 6.84 (0) | |
| 10 | MFI | 25 | 0.54 ± 1.03 (0.53) | 0 ± 2.00 (0) | 0 ± 1.88 (0) | 0 ± 2.02 (0) | 0 ± 2.16 (0) | 0 ± 2.01 (0) | 0 ± 1.82 (0) | 0 ± 1.82 (0) | 0 ± 2.31 (0) | 0 ± 1.59 (0) | 0 ± 3.18 (0) | 0 ± 2.21 (0) |
| 11 | MFI | 40 | 2.00 ± 1.38 (1.45) | 0 ± 2.69 (0) | 0 ± 2.53 (0) | 0 ± 2.72 (0) | 0.07 ± 2.91 (0.02) | 0 ± 2.71 (0) | 0 ± 2.46 (0) | 0 ± 2.46 (0) | 0 ± 3.11 (0) | 0 ± 2.15 (0) | 0 ± 4.29 (0) | 0 ± 2.98 (0) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jajko, G.; Kozyra, P.; Strzempek, M.; Indyka, P.; Zając, M.; Witkowski, S.; Piskorz, W. Structural Studies of Aluminated form of Zeolites—EXAFS and XRD Experiment, STEM Micrography, and DFT Modelling. Molecules 2021, 26, 3566. https://doi.org/10.3390/molecules26123566
Jajko G, Kozyra P, Strzempek M, Indyka P, Zając M, Witkowski S, Piskorz W. Structural Studies of Aluminated form of Zeolites—EXAFS and XRD Experiment, STEM Micrography, and DFT Modelling. Molecules. 2021; 26(12):3566. https://doi.org/10.3390/molecules26123566
Chicago/Turabian StyleJajko, Gabriela, Paweł Kozyra, Maciej Strzempek, Paulina Indyka, Marcin Zając, Stefan Witkowski, and Witold Piskorz. 2021. "Structural Studies of Aluminated form of Zeolites—EXAFS and XRD Experiment, STEM Micrography, and DFT Modelling" Molecules 26, no. 12: 3566. https://doi.org/10.3390/molecules26123566
APA StyleJajko, G., Kozyra, P., Strzempek, M., Indyka, P., Zając, M., Witkowski, S., & Piskorz, W. (2021). Structural Studies of Aluminated form of Zeolites—EXAFS and XRD Experiment, STEM Micrography, and DFT Modelling. Molecules, 26(12), 3566. https://doi.org/10.3390/molecules26123566