Incorporation of Molecular Reorientation into Modeling Surface Pressure-Area Isotherms of Langmuir Monolayers
Abstract
1. Introduction
2. Theory
2.1. Lattice–Sublattice Model
2.2. Free Energy and Lateral Pressure
2.3. The Limiting Case
3. Results and Discussion
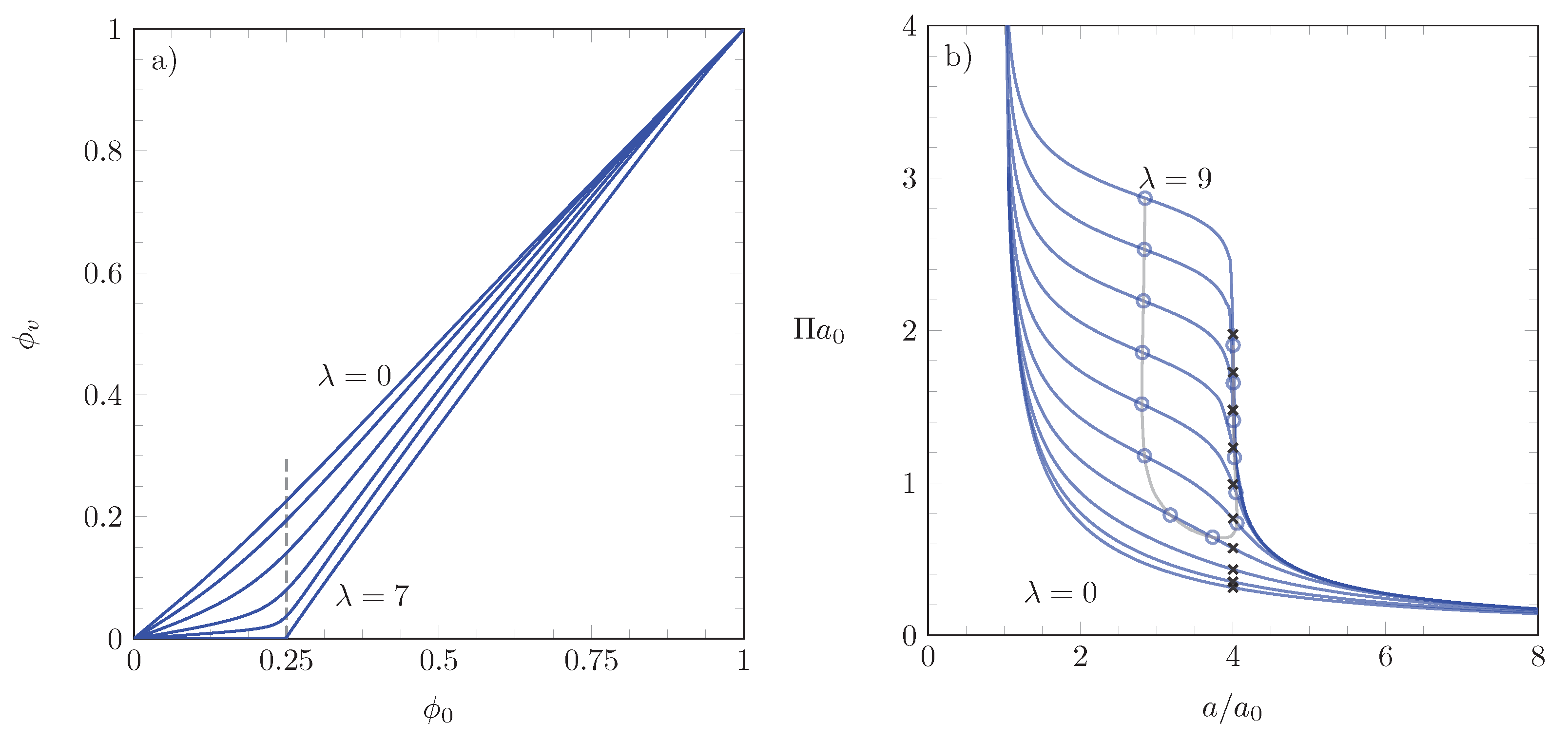
3.1. Numerical Results
3.2. Points of Inflection
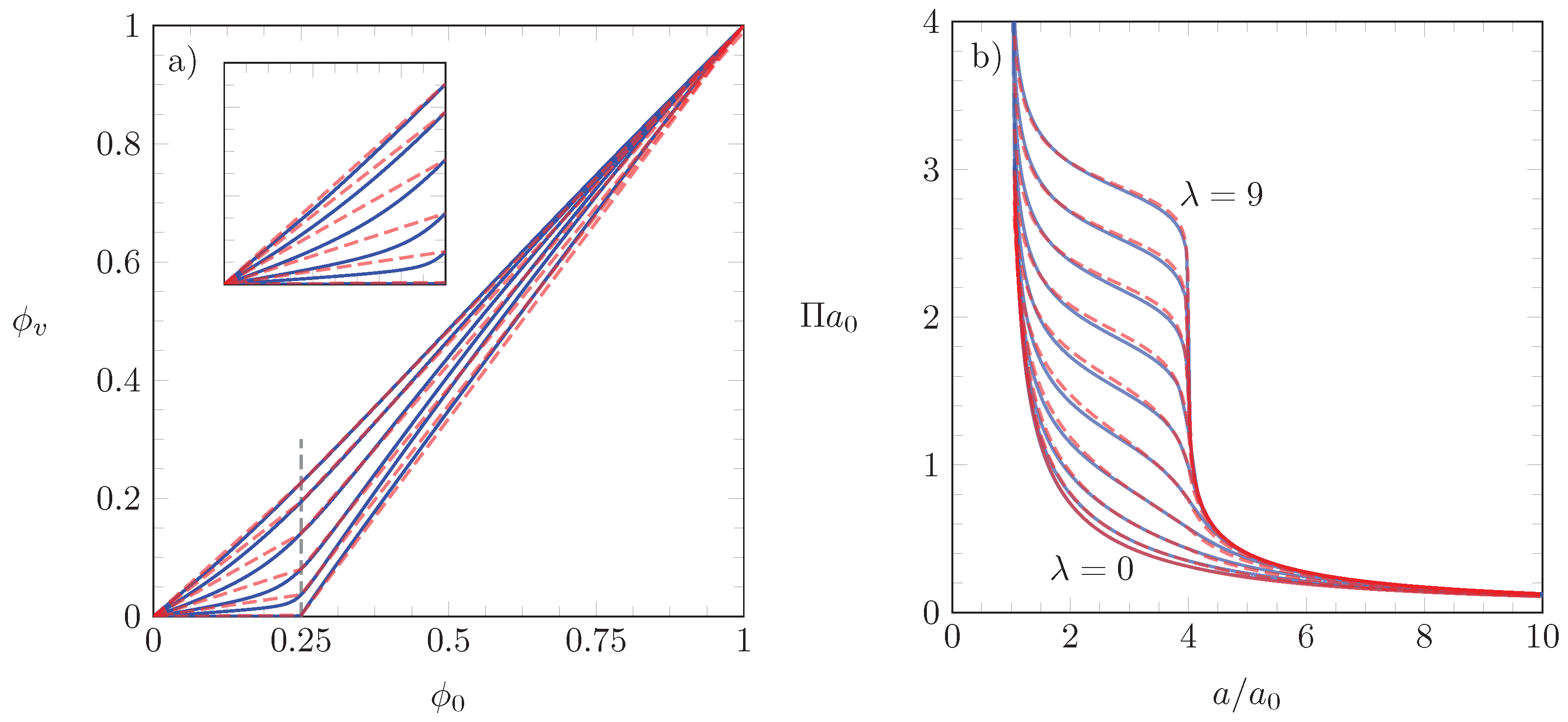
3.3. Analytic Solution for
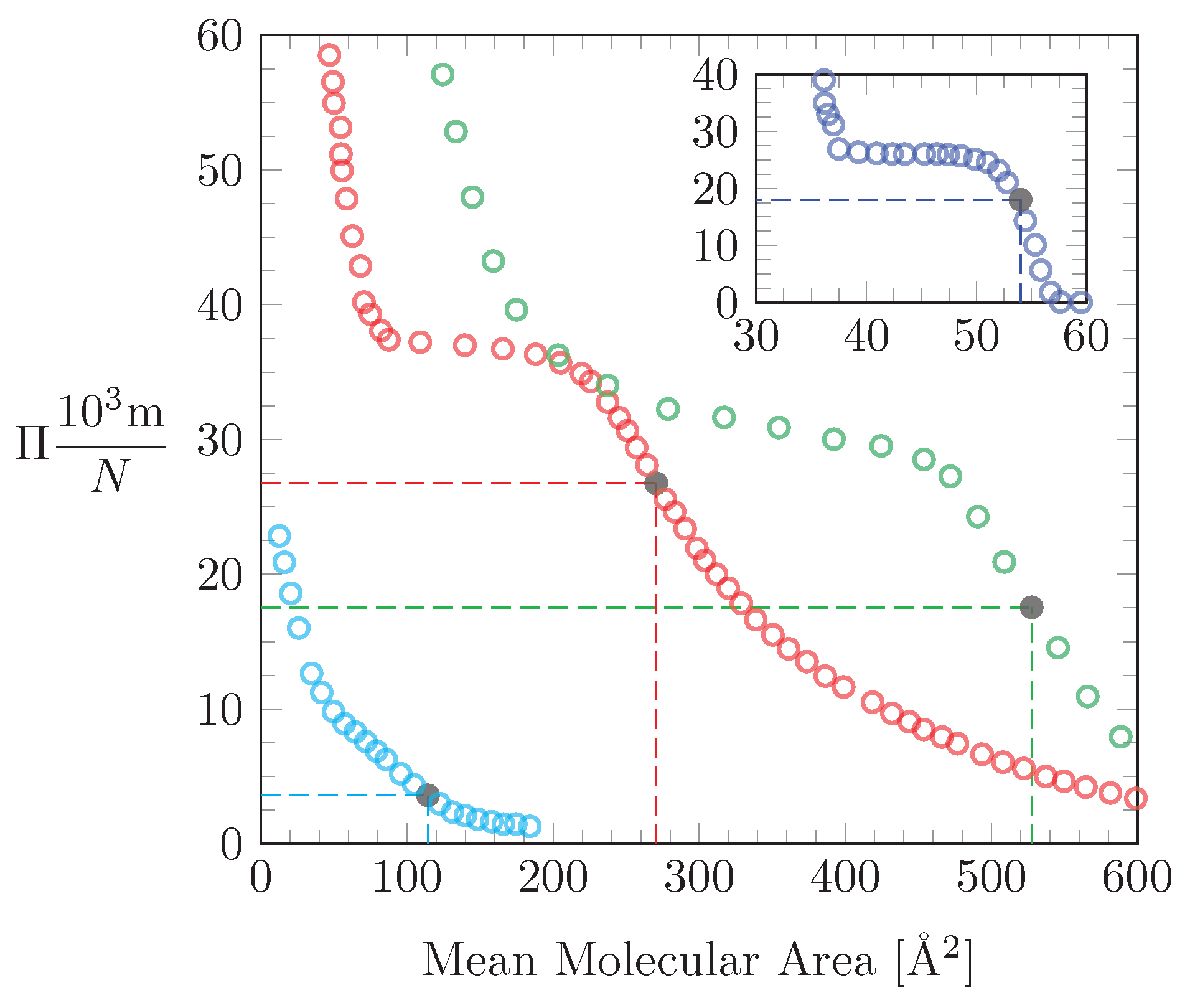
3.4. Application of our Theoretical Model to Experimental Isotherms
4. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Knobler, C.M.; Desai, R.C. Phase transitions in monolayers. Annu. Rev. Phys. Chem. 1992, 43, 207–236. [Google Scholar] [CrossRef]
- Kaganer, V.M.; Möhwald, H.; Dutta, P. Structure and phase transitions in Langmuir monolayers. Rev. Mod. Phys. 1999, 71, 779. [Google Scholar] [CrossRef]
- Vollhardt, D.; Fainerman, V. Progress in characterization of Langmuir monolayers by consideration of compressibility. Adv. Colloid Interface Sci. 2006, 127, 83–97. [Google Scholar] [CrossRef]
- Giner-Casares, J.J.; Brezesinski, G.; Möhwald, H. Langmuir monolayers as unique physical models. Curr. Opin. Colloid Interface Sci. 2014, 19, 176–182. [Google Scholar] [CrossRef]
- Blume, A. A comparative study of the phase transitions of phospholipid bilayers and monolayers. Biochim. Biophys. Acta Biomembr. 1979, 557, 32–44. [Google Scholar] [CrossRef]
- McConnell, H.M. Structures and transitions in lipid monolayers at the air-water interface. Annu. Rev. Phys. Chem. 1991, 42, 171–195. [Google Scholar] [CrossRef]
- Brezesinski, G.; Möhwald, H. Langmuir monolayers to study interactions at model membrane surfaces. Adv. Colloid Interface Sci. 2003, 100, 563–584. [Google Scholar] [CrossRef]
- McConnell, H.M.; Radhakrishnan, A. Condensed complexes of cholesterol and phospholipids. Biochim. Biophys. Acta Biomembr. 2003, 1610, 159–173. [Google Scholar] [CrossRef]
- Mudgil, P.; Torres, M.; Millar, T.J. Adsorption of lysozyme to phospholipid and meibomian lipid monolayer films. Colloids Surf. B 2006, 48, 128–137. [Google Scholar] [CrossRef]
- Janich, C.; Hädicke, A.; Bakowsky, U.; Brezesinski, G.; Wölk, C. Interaction of DNA with Cationic Lipid Mixtures: Investigation at Langmuir Lipid Monolayers. Langmuir 2017, 33, 10172–10183. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Meleson, K.; Israelachvili, J. Thermodynamic equilibrium of domains in a two-component Langmuir monolayer. Biophys. J. 2006, 91, 444–453. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.W.; Min, Y.; Dhar, P.; Ramachandran, A.; Israelachvili, J.N.; Zasadzinski, J.A. Relating domain size distribution to line tension and molecular dipole density in model cytoplasmic myelin lipid monolayers. Proc. Natl. Acad. Sci. USA 2011, 108, 9425–9430. [Google Scholar] [CrossRef] [PubMed]
- Rufeil-Fiori, E.; Wilke, N.; Banchio, A.J. Dipolar interactions between domains in lipid monolayers at the air-water interface. Soft Matter 2016, 12, 4769–4777. [Google Scholar] [CrossRef] [PubMed]
- Ruckenstein, E.; Li, B. Phase transition from a liquid expanded to a liquid condensed surfactant monolayer. J. Phys. Chem. 1996, 100, 3108–3114. [Google Scholar] [CrossRef]
- Jiang, M.; Zhong, F.; Xing, D.; Dong, J. Coupling of phase transitions in Langmuir monolayers. J. Chem. Phys. 1999, 110, 2660–2663. [Google Scholar] [CrossRef]
- Netz, R.R.; Andelman, D.; Orland, H. Protein adsorption on lipid monolayers at their coexistence region. J. Phys. II 1996, 6, 1023–1047. [Google Scholar] [CrossRef][Green Version]
- Mengistu, D.H.; Bohinc, K.; May, S. Binding of DNA to zwitterionic lipid layers mediated by divalent cations. J. Phys. Chem. B 2009, 113, 12277–12282. [Google Scholar] [CrossRef]
- Bohinc, K.; Brezesinski, G.; May, S. Modeling the influence of adsorbed DNA on the lateral pressure and tilt transition of a zwitterionic lipid monolayer. Phys. Chem. Chem. Phys. 2012, 14, 10613–10621. [Google Scholar] [CrossRef]
- Levental, I.; Janmey, P.; Cēbers, A. Electrostatic contribution to the surface pressure of charged monolayers containing polyphosphoinositides. Biophys. J. 2008, 95, 1199–1205. [Google Scholar] [CrossRef]
- Baoukina, S.; Monticelli, L.; Marrink, S.J.; Tieleman, D.P. Pressure- area isotherm of a lipid monolayer from molecular dynamics simulations. Langmuir 2007, 23, 12617–12623. [Google Scholar] [CrossRef]
- Miñones, J.; Yebra-Pimentel, E.; Iribarnegaray, E.; Conde, O.; Casas, M. Compression—Expansion curves of cyclosporin A monolayers on substrates of various ionic strengths. Colloids Surf. A 1993, 76, 227–232. [Google Scholar] [CrossRef]
- Seoane, J.; Romeu, N.V.; Minones, J.; Conde, O.; Dynarowicz, P.; Casas, M. The behavior of amphotericin B monolayers at the air/water interface. Trends Colloid Interface Sci. XI 1997, 173–179. [Google Scholar] [CrossRef]
- Minones, J.; Carrera, C.; Dynarowicz-atka, P.; Minones, J.; Conde, O.; Seoane, R.; Rodriguez Patino, J. Orientational changes of amphotericin B in Langmuir monolayers observed by Brewster angle microscopy. Langmuir 2001, 17, 1477–1482. [Google Scholar] [CrossRef]
- Hąc-Wydro, K.; Dynarowicz-ątka, P. Nystatin in Langmuir monolayers at the air/water interface. Colloids Surf. B 2006, 53, 64–71. [Google Scholar] [CrossRef] [PubMed]
- Kim, V.; Ermakov, A.; Glukhovskoy, E.; Rakhnyanskaya, A.; Gulyaev, Y.V.; Cherepenin, V.; Taranov, I.; Kormakova, P.; Potapenkov, K.; Usmanov, N.; et al. Planar nanosystems on the basis of complexes formed by amphiphilic polyamine, magnetite nanoparticles, and DNA molecules. Nanotechnol. Russ. 2014, 9, 280–287. [Google Scholar] [CrossRef]
- Vico, R.V.; Silva, O.F.; de Rossi, R.H.; Maggio, B. Molecular Organization, Structural Orientation, and Surface Topography of Monoacylated β-Cyclodextrins in Monolayers at the Air-Aqueous Interface. Langmuir 2008, 24, 7867–7874. [Google Scholar] [CrossRef] [PubMed]
- Wnętrzak, A.; Chachaj-Brekiesz, A.; Janikowska-Sagan, M.; Rodriguez, J.L.F.; Conde, J.M.; Dynarowicz-atka, P. Crucial role of the hydroxyl group orientation in Langmuir monolayers organization—The case of 7-hydroxycholesterol epimers. Colloids Surf. A 2019, 563, 330–339. [Google Scholar] [CrossRef]
- Targosz-Korecka, M.; Wnętrzak, A.; Chachaj-Brekiesz, A.; Gonet-Surówka, A.; Kubisiak, A.; Filiczkowska, A.; Szymoński, M.; Dynarowicz-Latka, P. Effect of selected B-ring-substituted oxysterols on artificial model erythrocyte membrane and isolated red blood cells. Biochim. Biophys. Acta Biomembr. 2020, 1862, 183067. [Google Scholar] [CrossRef] [PubMed]
- Chachaj-Brekiesz, A.; Wnętrzak, A.; Włodarska, S.; Lipiec, E.; Dynarowicz-Latka, P. Molecular insight into neurodegeneration–Langmuir monolayer study on the influence of oxysterols on model myelin sheath. J. Steroid Biochem. Mol. Biol. 2020, 202, 105727. [Google Scholar] [CrossRef] [PubMed]
- Dynarowicz-atka, P.; Dhanabalan, A.; Oliveira, O.N. A study on two-dimensional phase transitions in langmuir monolayers of a carboxylic acid with a symmetrical triphenylbenzene ring system. J. Phys. Chem. B 1999, 103, 5992–6000. [Google Scholar] [CrossRef]
- Lee, I.C.; Frank, C.W.; Yamamoto, T.; Tseng, H.R.; Flood, A.H.; Stoddart, J.F.; Jeppesen, J.O. Langmuir and Langmuir-Blodgett Films of Amphiphilic Bistable Rotaxanes. Langmuir 2004, 20, 5809–5828. [Google Scholar] [CrossRef]
- Misdrahi, M.F.; Wang, M.; Pradeep, C.P.; Li, F.Y.; Lydon, C.; Xu, L.; Cronin, L.; Liu, T. Amphiphilic properties of dumbbell-shaped inorganic–organic–inorganic molecular hybrid materials in solution and at an interface. Langmuir 2011, 27, 9193–9202. [Google Scholar] [CrossRef]
- Hupfer, M.; Kaufmann, M.; May, S.; Preiß, J.; Weiß, D.; Dietzek, B.; Beckert, R.; Presselt, M. Enhancing the supramolecular stability of monolayers by combining dipolar with amphiphilic motifs: A case of amphiphilic push–pull-thiazole. Phys. Chem. Chem. Phys. 2019, 21, 13241–13247. [Google Scholar] [CrossRef]
- Taylor, S.E.; Schwarz, G. The molecular area characteristics of the HIV-1 gp41-fusion peptide at the air/water interface. Effect of pH. Biochim. Biophys. Acta Biomembr. 1997, 1326, 257–264. [Google Scholar] [CrossRef][Green Version]
- Strzalka, J.; Chen, X.; Moser, C.C.; Dutton, P.L.; Ocko, B.M.; Blasie, J.K. X-ray scattering studies of maquette peptide monolayers. 1. Reflectivity and grazing incidence diffraction at the air/water interface. Langmuir 2000, 16, 10404–10418. [Google Scholar] [CrossRef]
- Tronin, A.; Strzalka, J.; Chen, X.; Dutton, P.; Ocko, B.; Blasie, J. Orientational distributions of the di-α-helical synthetic peptide ZnPPIX-BBC16 in Langmuir monolayers by x-ray reflectivity and polarized epifluorescence. Langmuir 2001, 17, 3061–3066. [Google Scholar] [CrossRef]
- Paczesny, J.; Binkiewicz, I.; Janczuk, M.; Wybrannska, K.; Richter, Ł.; Hołyst, R. Langmuir and Langmuir–Blodgett films of unsymmetrical and fully condensed polyhedral oligomeric silsesquioxanes (POSS). J. Phys. Chem. C 2015, 119, 27007–27017. [Google Scholar] [CrossRef]
- Ariga, K.; Tanaka, K.; Katagiri, K.; Kikuchi, J.I.; Shimakoshi, H.; Ohshima, E.; Hisaeda, Y. Langmuir monolayer of organoalkoxysilane for vitamin B 12-modified electrode. Phys. Chem. Chem. Phys. 2001, 3, 3442–3446. [Google Scholar] [CrossRef]
- Jiang, M.; Zhai, X.; Liu, M. Hybrid molecular films of gemini amphiphiles and Keggin-type polyoxometalates: Effect of the spacer length on the electrochemical properties. J. Mater. Chem. 2007, 17, 193–200. [Google Scholar] [CrossRef]
- Han, Y.; Huang, S.; Yan, T. A mean-field theory on the differential capacitance of asymmetric ionic liquid electrolytes. J. Phys. Condens. Matter 2014, 26, 284103. [Google Scholar] [CrossRef] [PubMed]
- McEldrew, M.; Goodwin, Z.A.; Kornyshev, A.A.; Bazant, M.Z. Theory of the double layer in water-in-salt electrolytes. J. Phys. Chem. Lett. 2018, 9, 5840–5846. [Google Scholar] [CrossRef] [PubMed]
- Bossa, G.V.; Berntson, B.K.; May, S. Curvature elasticity of the electric double layer. Phys. Rev. Lett. 2018, 120, 215502. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Huang, J. Treatment of ion-size asymmetry in lattice-gas models for electrical double layer. J. Phys. Chem. C 2018, 122, 28652–28664. [Google Scholar] [CrossRef]
- Davis, H.T.; Davis, H.T. Statistical Mechanics of Phases, Interfaces and Thin Films; VCH Publishers: New York, NY, USA, 1996. [Google Scholar]
- Jiang, M.; Zhong, F.; Xing, D.; Wang, Z.; Dong, J. Orientational phase transition in molecular monolayer on an air–water interface. J. Chem. Phys. 1997, 106, 6171–6175. [Google Scholar] [CrossRef][Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agudelo, J.; Bossa, G.V.; May, S. Incorporation of Molecular Reorientation into Modeling Surface Pressure-Area Isotherms of Langmuir Monolayers. Molecules 2021, 26, 4372. https://doi.org/10.3390/molecules26144372
Agudelo J, Bossa GV, May S. Incorporation of Molecular Reorientation into Modeling Surface Pressure-Area Isotherms of Langmuir Monolayers. Molecules. 2021; 26(14):4372. https://doi.org/10.3390/molecules26144372
Chicago/Turabian StyleAgudelo, José, Guilherme Volpe Bossa, and Sylvio May. 2021. "Incorporation of Molecular Reorientation into Modeling Surface Pressure-Area Isotherms of Langmuir Monolayers" Molecules 26, no. 14: 4372. https://doi.org/10.3390/molecules26144372
APA StyleAgudelo, J., Bossa, G. V., & May, S. (2021). Incorporation of Molecular Reorientation into Modeling Surface Pressure-Area Isotherms of Langmuir Monolayers. Molecules, 26(14), 4372. https://doi.org/10.3390/molecules26144372





