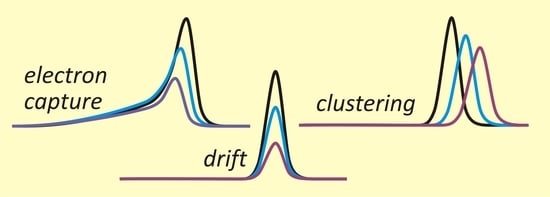
Studies on the Processes of Electron Capture and Clustering of Benzyl Chloride by Ion Mobility Spectrometry
Abstract
:1. Introduction
2. Materials and Methods
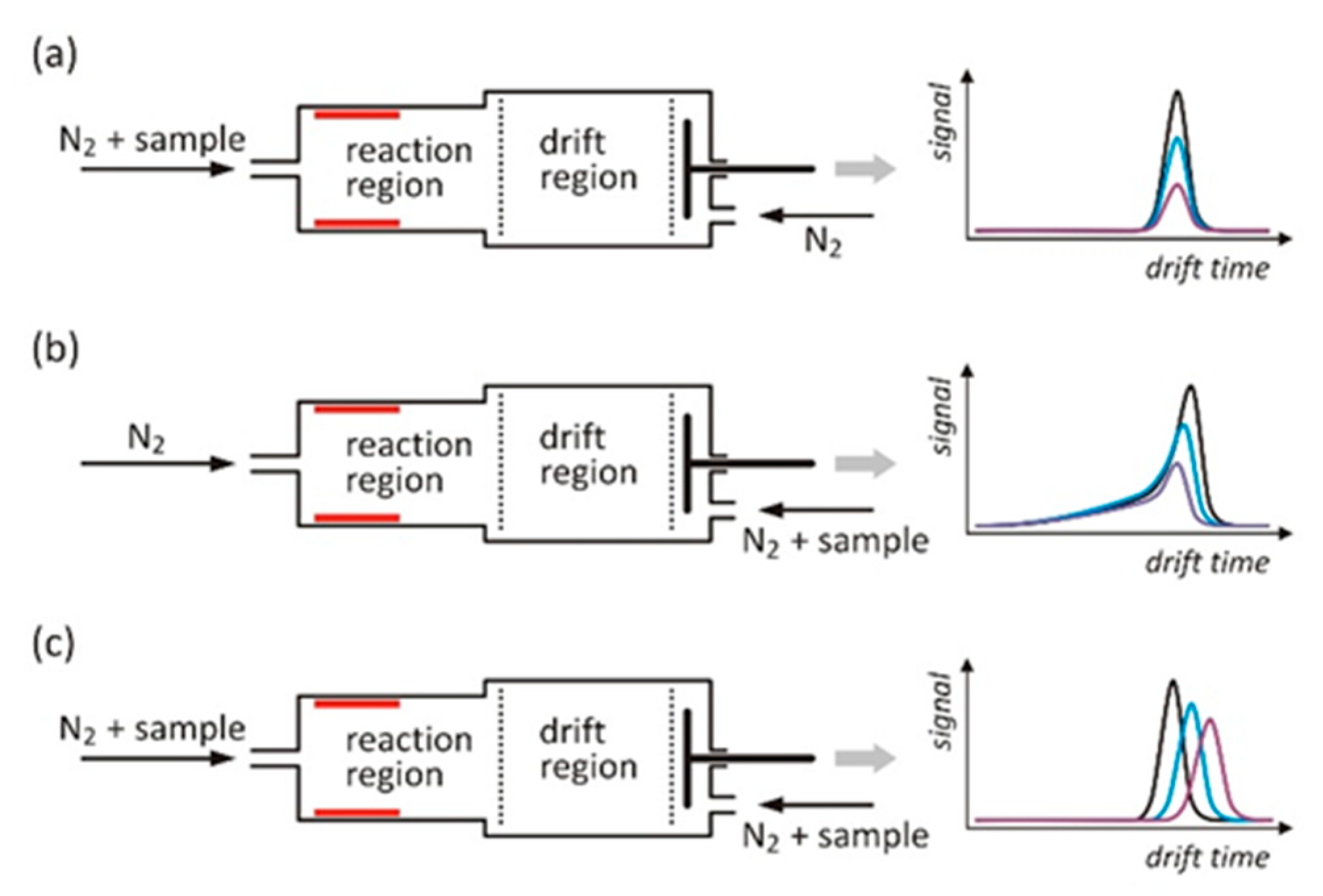
2.1. The Theory of Charge Transport in the Drift Section of IMS Detectors
2.1.1. A Simple Model Used to Determine the Electron Attachment Rate
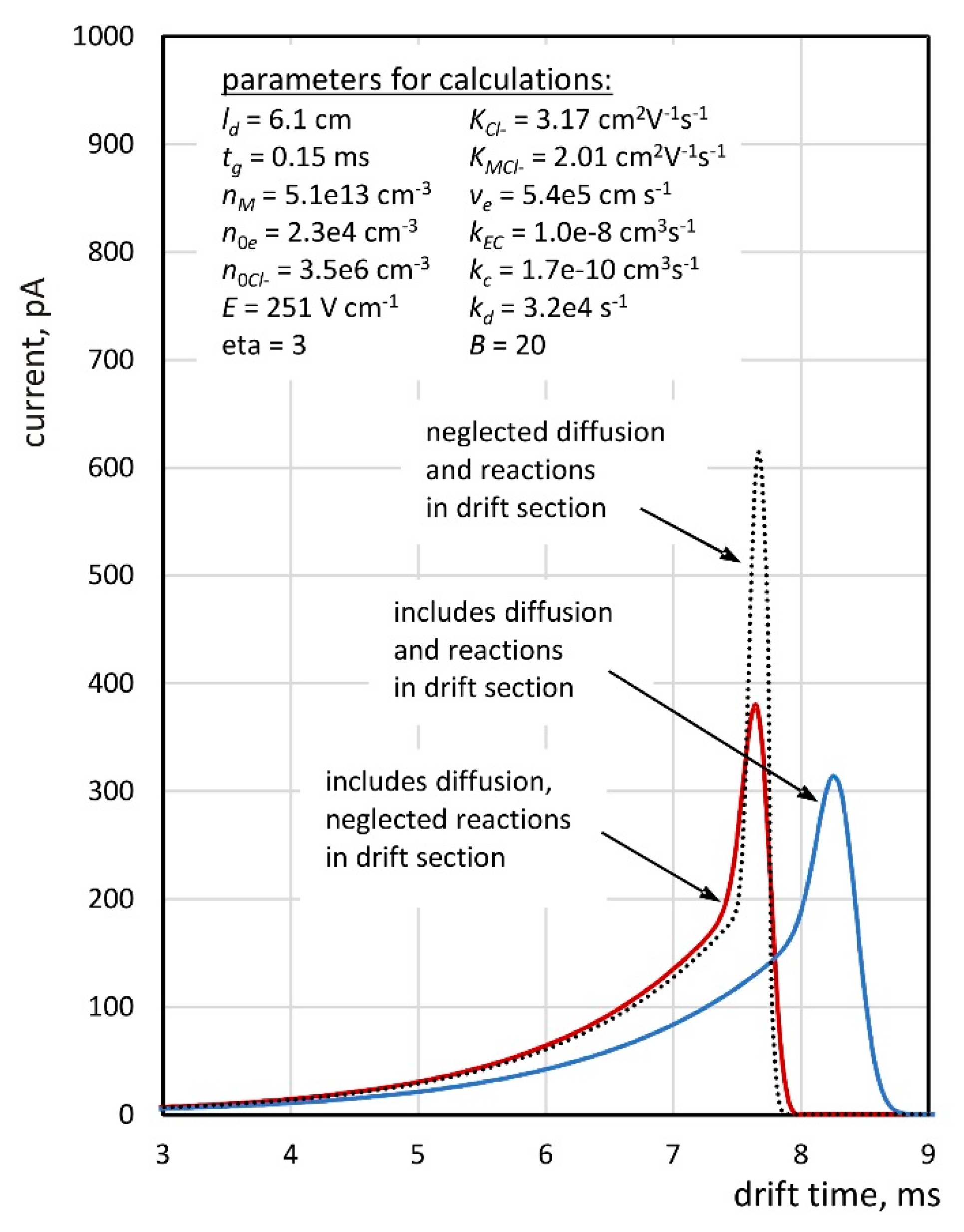
2.1.2. Description of the Ions’ Movement in the Drift Section, Including Diffusion and Ion–Molecule Reactions
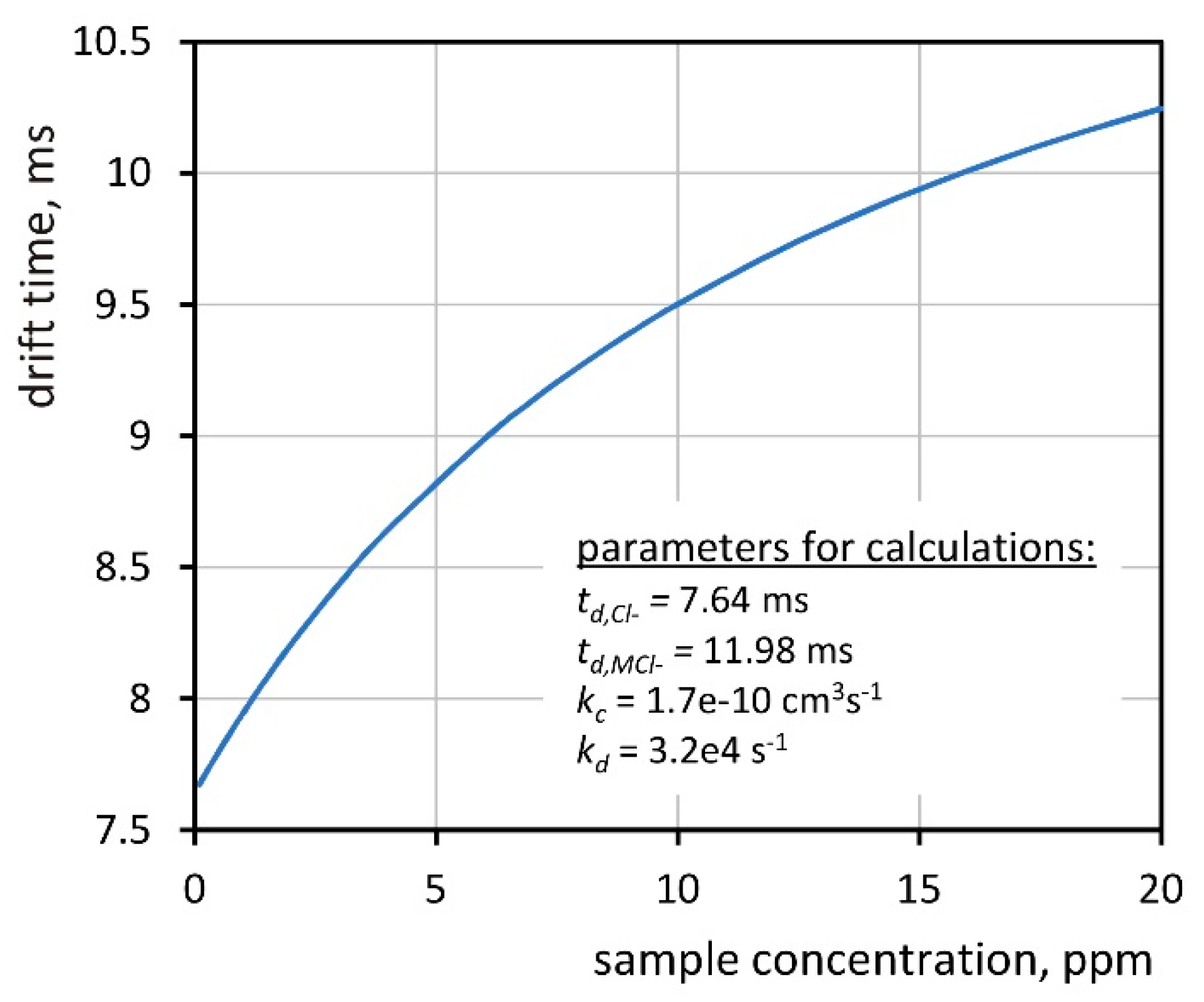
2.1.3. Shift of the Peaks Caused by Ion–Molecule Reactions
3. Results
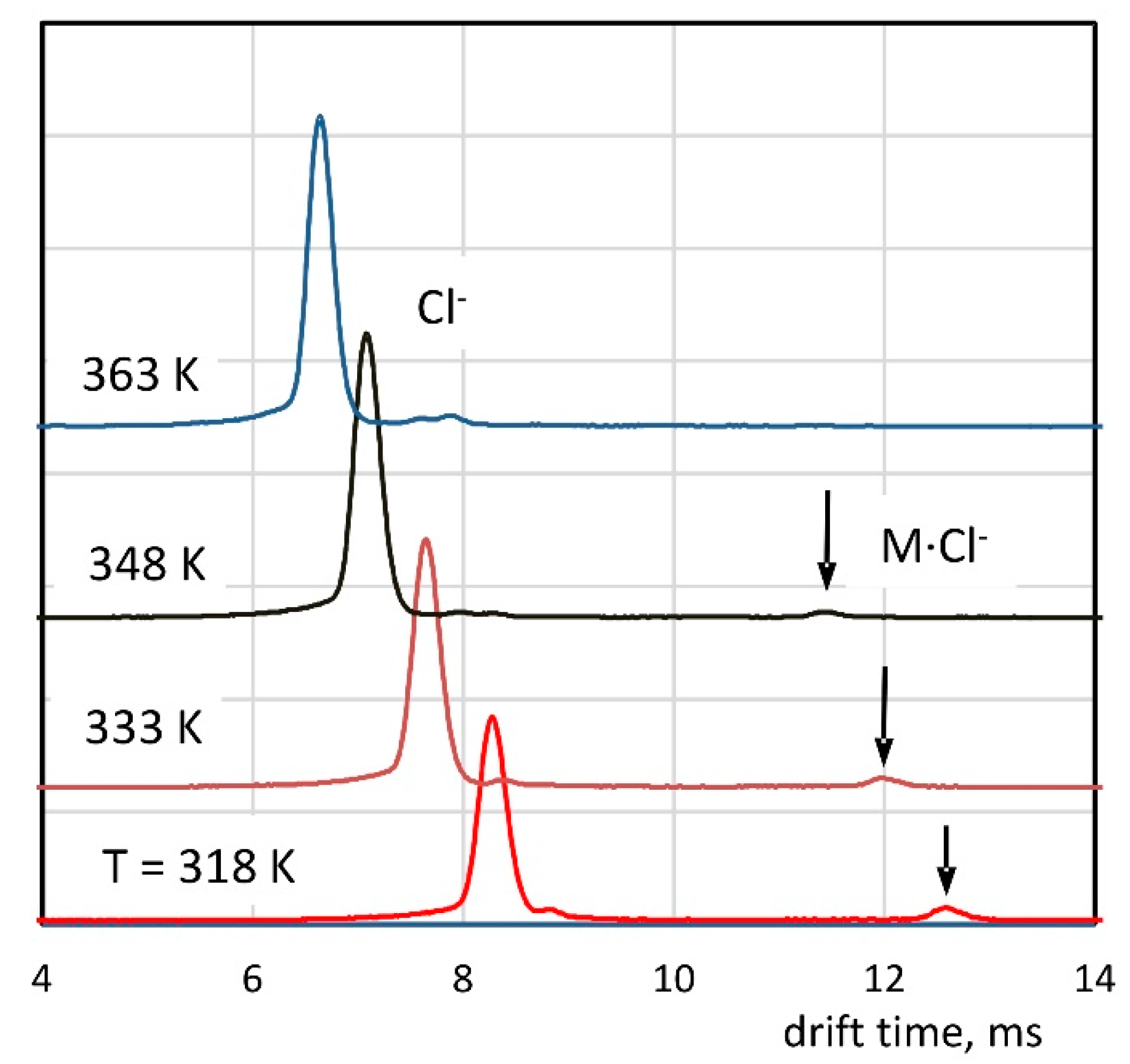
3.1. Drift Times and Reduced Mobilities
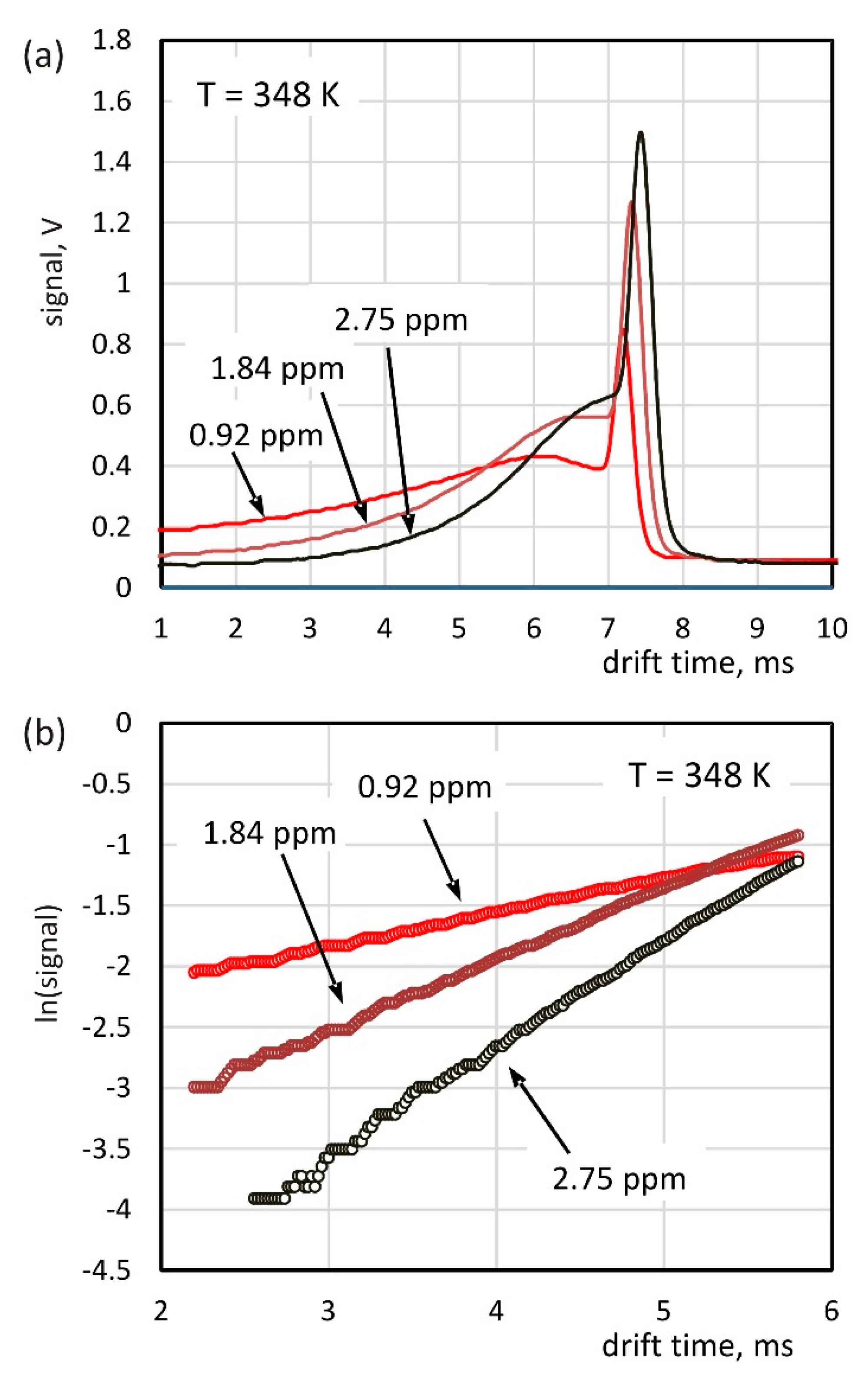
3.2. Electron Attachment Rates
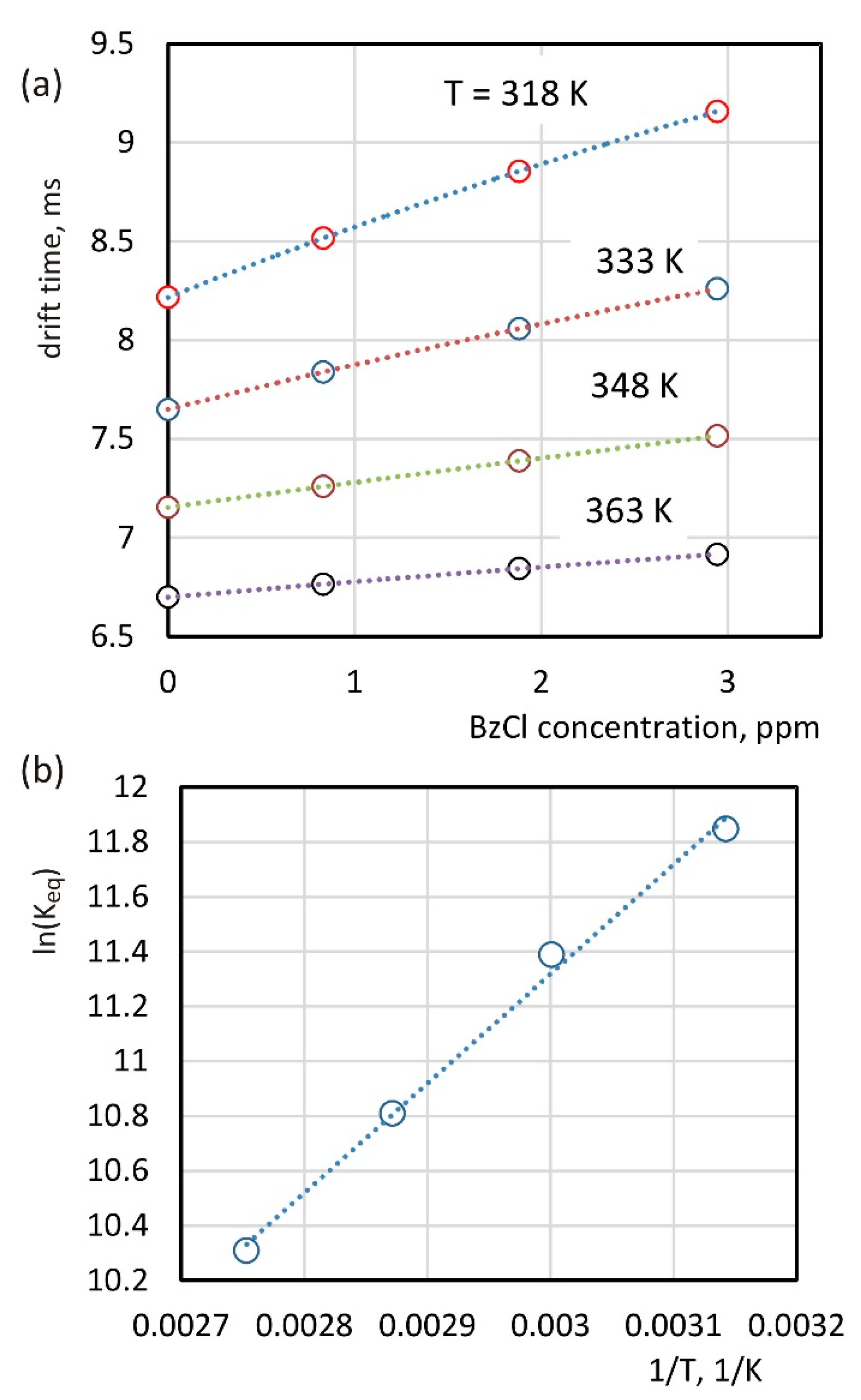
3.3. Equilibrium Constants for Ion Clustering Processes
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Eiceman, G.A.; Karpas, Z.; Hill, H.H. Ion Mobility Spectrometry, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Ewing, R.G.; Atkinson, D.A.; Eiceman, G.A.; Ewing, G.J. A critical review of ion mobility spectrometry for the detection of explosives and explosive related compounds. Talanta 2001, 54, 515–529. [Google Scholar] [CrossRef]
- Buryakov, I.A. Detection of explosives by ion mobility spectrometry. J. Anal. Chem. 2011, 66, 674–694. [Google Scholar] [CrossRef]
- Puton, J.; Namieśnik, J. Ion mobility spectrometry: Current status and application for chemical warfare agents detection. Trends Anal. Chem. 2016, 85, 10–20. [Google Scholar] [CrossRef]
- Jazan, E.; Tabrizchi, M. Kinetic study of proton-bound dimer formation using ion mobility spectrometry. Chem. Phys. 2009, 355, 37–42. [Google Scholar] [CrossRef]
- Ewing, R.G.; Eiceman, G.A.; Stone, J.A. Proton-bound cluster ions in ion mobility spectrometry. Int. J. Mass Spectrom. 1999, 193, 57–68. [Google Scholar] [CrossRef]
- Tabrizchi, M.; Shooshtari, S. Proton affinity measurements using ion mobility spectrometry. J. Chem. Thermodyn. 2003, 35, 863–870. [Google Scholar] [CrossRef]
- Ewing, R.G.; Eiceman, G.A.; Harden, C.S.; Stone, J.A. The kinetics of the decompositions of the proton bound dimers of 1,4-dimethylpyridine and dimethyl methylphosphonate from atmospheric pressure ion mobility spectra. Int. J. Mass Spectrom. 2006, 255–256, 76–85. [Google Scholar] [CrossRef]
- Valadbeigi, Y.; Farrokhpour, H.; Rouholahnejad, F.; Tabrizchi, M. Experimental and theoretical study of the kinetic of proton transfer reaction by ion mobility spectrometry. Int. J. Mass Spectrom. 2014, 369, 105–111. [Google Scholar] [CrossRef]
- Valadbeigi, Y.; Farrokhpour, H.; Tabrizchi, M. Effect of hydration on the kinetics of proton-bound dimer formation: Experimental and theoretical study. J. Phys. Chem. A 2014, 118, 7663–7671. [Google Scholar] [CrossRef]
- Tabrizchi, M.; Khezri, E. The effect of ion molecule reactions on peaks in ion mobility spectrometry. Int. J. Ion Mobility Spectrom. 2008, 11, 19–25. [Google Scholar] [CrossRef]
- Izadi, Z.; Tabrizchi, M.; Farrokhpour, H. Average drift time and average mobility in ion mobility spectrometry. Int. J. Mass Spectrom. 2017, 412, 20–25. [Google Scholar] [CrossRef]
- Liu, D.; Min, S. Rapid analysis of organochlorine and pyrethroid pesticides in tea samples by directly suspended droplet microextraction using a gas chromatography– electron capture detector. J. Chrom. A 2012, 1235, 166–173. [Google Scholar] [CrossRef] [PubMed]
- Fabrikant, I.I.; Eden, S.; Mason, N.J.; Fedor, J. Recent Progress in Dissociative Electron Attachment: From Diatomics to Biomolecules. Adv. At. Mol. Opt. Phys. 2017, 66, 545–656. [Google Scholar]
- Tabrizchi, M.; Abedi, A. A novel use of negative Ion mobility spectrometry for measuring electron attachment rates. J. Phys. Chem. A 2004, 108, 6319–6324. [Google Scholar] [CrossRef]
- Feng, H.; Niu, W.; Han, H.; Huang, C.; Wang, H.; Matuska, J.; Sabo, M.; Matejcik, S.; Jianga, H.; Chua, Y. Rate constants of electron attachment to chlorobenzenes measured by atmospheric pressure nitrogen corona discharge electron attachment ion mobility spectrometry. Int. J. Mass Spectrom. 2011, 305, 30–34. [Google Scholar] [CrossRef]
- Huang, C.; Xu, B.; Niu, W.; Gao, H.; Hong, Y.; Yan, L.; Xia, L.; Shen, C.; Chu, Y. An experimental study of low energy electrons attachment to CH2ClBr using ion mobility spectrometry. Int. J. Mass Spectrom. 2016, 402, 29–35. [Google Scholar] [CrossRef]
- Kučera, M.; Stano, M.; Wnorowska, J.; Barszczewska, W.; Loffhagen, D.; Matejčík, S. Electron attachment to oxygen in nitrogen buffer gas at atmospheric pressure. Eur. Phys. J. D 2013, 67, 11. [Google Scholar] [CrossRef]
- Waraksa, E.; Perycz, U.; Namieśnik, J.; Sillanpää, M.; Dymerski, T.; Wójtowicz, M.; Puton, J. Dopants and gas modifiers in ion mobility spectrometry. Trends Anal. Chem. 2016, 82, 237–249. [Google Scholar] [CrossRef]
- González-Méndez, R.; Watts, P.; Howse, D.C.; Procino, I.; McIntyre, H.; Mayhew, C.A. Ion Mobility Studies on the Negative Ion-Molecule Chemistry of Isoflurane and Enflurane. J. Am. Soc. Mass Spectrom. 2017, 98, 939–946. [Google Scholar] [CrossRef] [Green Version]
- Gaik, U.; Sillanpää, M.; Witkiewicz, Z.; Puton, J. Nitrogen oxides as dopants for the detection of aromatic compounds with ion mobility spectrometry. Anal. Bioanal. Chem. 2017, 409, 3223–3231. [Google Scholar] [CrossRef] [Green Version]
- Spangler, G.E.; Collins, C.I. Peak shape analysis and plate theory for plasma chromatography. Anal. Chem. 1975, 47, 403–407. [Google Scholar] [CrossRef]
- Bordorf, H.; Mayer, T. Temperature dependence of ion mobility signals of halogenated compounds. Talanta 2012, 101, 17–23. [Google Scholar] [CrossRef]
- Daum, K.A.; Atkinson, D.A.; Ewing, R.G. The role of oxygen in the formation of TNT product ions in ion mobility spectrometry. Int. J. Mass Spectrom. 2002, 214, 257–267. [Google Scholar] [CrossRef]
- Nakamura, Y. Drift velocity and longitudinal diffusion coefficient of electrons in nitrogen and carbon monoxide. J. Phys. D Appl. Phys. 1987, 20, 933. [Google Scholar] [CrossRef]
- Jarvis, G.K.; Kennedy, R.A.; Mayhew, C.A. Investigations of low energy attachment to ground state group 6B hexafluorides (SF6, SeF6, and TeF6) using an electron swarm mass spectrometric technique. Int. J. Mass Spectrom. 2001, 25, 253–270. [Google Scholar] [CrossRef]
- Warman, J.M.; Sauer, M.C., Jr.; Johnson, G.R.A. Competitive Electron Attachment in Gaseous Halobenzene–Benzyl Chloride Mixtures. Evidence for Electron Transfer from the Chlorobenzene Anion to Benzyl Chloride. J. Chem. Phys. 1969, 51, 3477–3484. [Google Scholar] [CrossRef]
- Warman, J.M.; Sauer, M.C. The temperature dependence of electron attachment to CCl4, CHCl3 and C6H5CH2Cl. Int. J. Radiat. Phys. Chem. 1971, 3, 273–282. [Google Scholar] [CrossRef]
- Hotop, H.; Ruf, M.-W.; Kopyra, J.; Miller, T.M.; Fabrikant, I.I. On the relation between the activation energy for electron attachment reactions and the size of their thermal rate coefficients. J. Chem. Phys. 2011, 134, 064303. [Google Scholar] [CrossRef] [Green Version]
- Aflatooni, K.; Gallup, G.A.; Burrow, P.D. Dissociative electron attachment in nonplanar chlorocarbons with π */σ *-coupled molecular orbitals. J. Chem. Phys. 2010, 132, 9. [Google Scholar] [CrossRef] [Green Version]
- Nag, P.; Tarana, M.; Fedor, J. Effects of π *-σ * coupling on dissociative-electron-attachment angular distributions in vinyl, allyl, and benzyl chloride and in chlorobenzene. Phys. Rev. A 2021, 103, 032830. [Google Scholar] [CrossRef]
- Hunter, S.R.; Carter, J.G.; Christophorou, L.G. Low energy attachment to SF6 in N2, Ar and Xe buffer gases. J. Chem. Phys. 1989, 90, 4879–4891. [Google Scholar] [CrossRef]

| Temperature | Cl− (Chlorine Ions) | M·Cl− (Cluster Ions) | ||
|---|---|---|---|---|
| td, ms | K0, cm2V−1s−1 | td, ms | K0, cm2V−1s−1 | |
| 318 K | 8.25 | 2.52 | 12.58 | 1.65 |
| 333 K | 7.64 | 2.60 | 11.98 | 1.65 |
| 348 K | 7.08 | 2.69 | 11.44 | 1.66 |
| 363 K | 6.64 | 2.75 | No peak | No peak |
| Temperature | kEC, 10−9 cm3s−1 | ||
|---|---|---|---|
| CBzCl = 0.92 ppm | CBzCl = 1.84 ppm | CBzCl = 2.75 ppm | |
| 318 K | 8.09 | 8.71 | 9.08 |
| 333 K | 8.72 | 9.48 | 10.20 |
| 348 K | 9.77 | 10.50 | 10.40 |
| 363 K | 10.80 | 11.50 | 11.50 |
| Temperature | Keq(2) | ||
|---|---|---|---|
| CBzCl = 0.83 ppm | CBzCl = 1.88 ppm | CBzCl = 2.94 ppm | |
| 318 K | 13,630 | 13,930 | 14,300 |
| 333 K | 8780 | 8790 | 8880 |
| 348 K | 4880 | 4930 | 5020 |
| 363 K | 3000 | 3030 | 2950 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wolańska, I.; Budzyńska, E.; Puton, J. Studies on the Processes of Electron Capture and Clustering of Benzyl Chloride by Ion Mobility Spectrometry. Molecules 2021, 26, 4562. https://doi.org/10.3390/molecules26154562
Wolańska I, Budzyńska E, Puton J. Studies on the Processes of Electron Capture and Clustering of Benzyl Chloride by Ion Mobility Spectrometry. Molecules. 2021; 26(15):4562. https://doi.org/10.3390/molecules26154562
Chicago/Turabian StyleWolańska, Izabela, Edyta Budzyńska, and Jarosław Puton. 2021. "Studies on the Processes of Electron Capture and Clustering of Benzyl Chloride by Ion Mobility Spectrometry" Molecules 26, no. 15: 4562. https://doi.org/10.3390/molecules26154562
APA StyleWolańska, I., Budzyńska, E., & Puton, J. (2021). Studies on the Processes of Electron Capture and Clustering of Benzyl Chloride by Ion Mobility Spectrometry. Molecules, 26(15), 4562. https://doi.org/10.3390/molecules26154562