Mechanisms of Tebuconazole Adsorption in Profiles of Mineral Soils
Abstract
:1. Introduction
2. Results
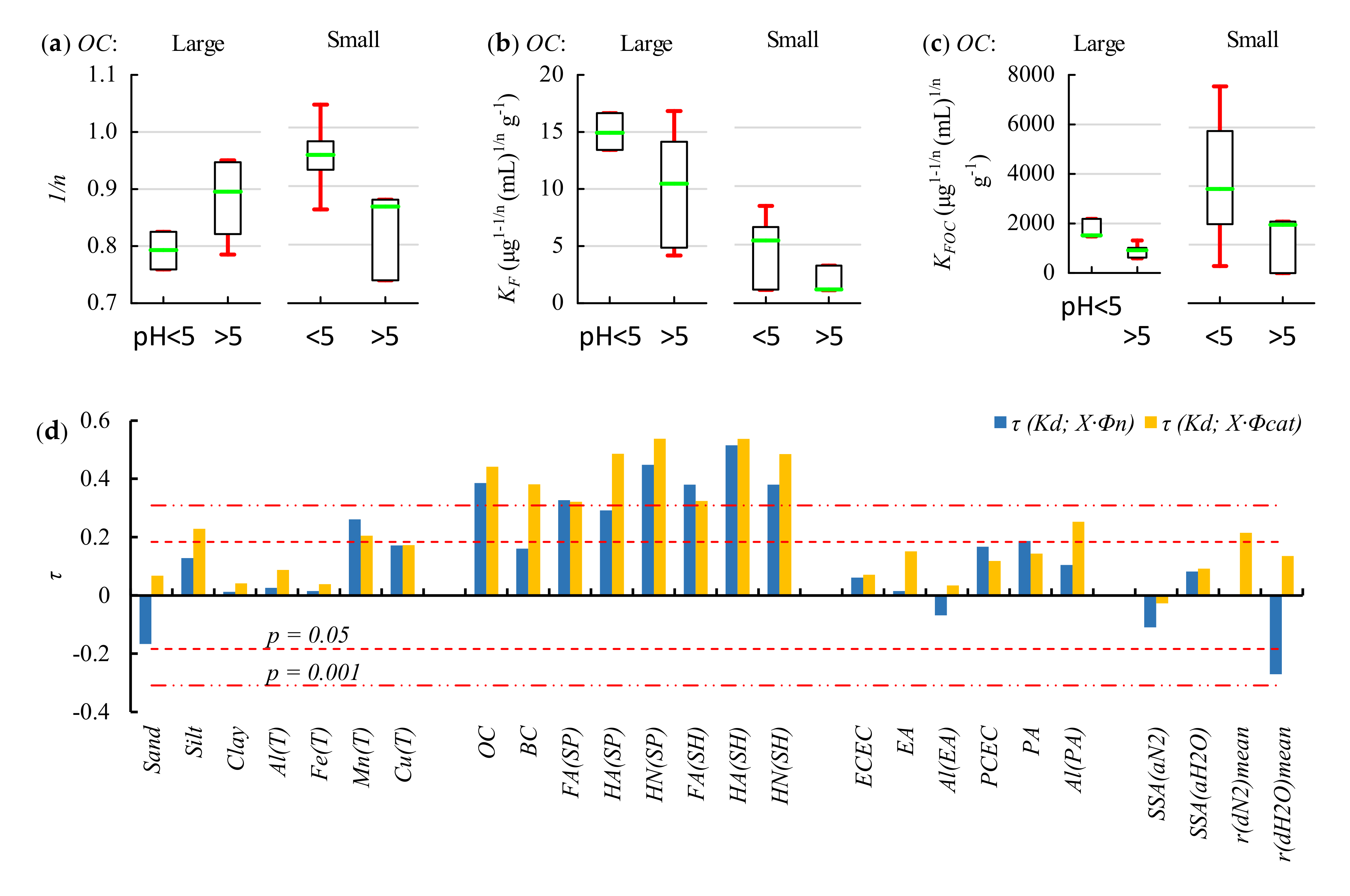
2.1. Preliminary Analysis—Adsorption Isotherms
2.2. Soil Properties Affecting Adsorption—Results of pH-Dependent Adsorption Analyses
2.2.1. pH-Dependent Adsorption Model
2.2.2. Correlation Analysis
2.2.3. Regression Analyses
2.3. Relationship between FT-IR Characteristics of SOM and Adsorption of TB
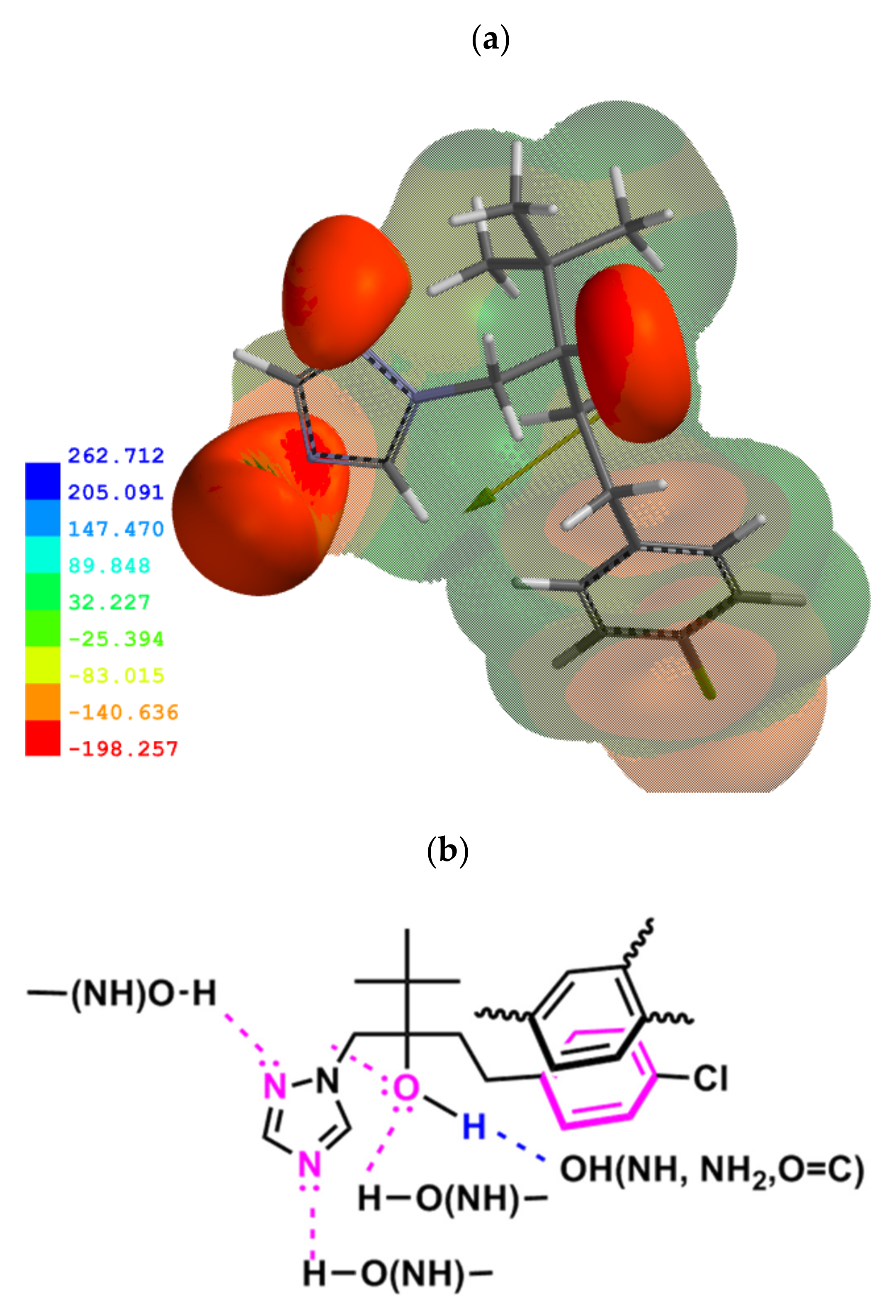
2.4. Mechanisms of TB Adsorption on SOM and Clay Minerals
3. Materials and Methods
3.1. Soils
3.2. Sample Preparation and FT-IR Analysis
3.3. Batch Adsorption Experiments
3.4. Molecular Modeling and Statistical Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Škulcová, L.; Neuwirthová, N.; Šimek, Z.; Trojan, M.; Bielská, L. Enantioselective behavior of the fungicide tebuconazole in soil. Environ. Process. 2020, 7, 173–188. [Google Scholar] [CrossRef]
- Mosquera-Vivas, C.S.; Martinez, M.J.; García-Santos, G.; Guerrero-Dallos, J.A. Adsorption-desorption and hysteresis phenomenon of tebuconazole in Colombian agricultural soils: Experimental assays and mathematical approaches. Chemosphere 2018, 190, 393–404. [Google Scholar] [CrossRef]
- Lewis, K.A.; Tzilivakis, J.; Warner, D.J.; Green, A. An international database for pesticide risk assessments and management. Hum. Ecol. Risk Assess. 2016, 22, 1050–1064. [Google Scholar] [CrossRef] [Green Version]
- EFSA. Conclusion on the peer review of the pesticide risk assessment of the active substance tebuconazole. EFSA J. 2014, 12, 3485. [Google Scholar] [CrossRef]
- Bošković, N.; Brandstätter-Scherr, K.; Sedláček, P.; Bílková, Z.; Bielská, L.; Hofman, J. Adsorption of epoxiconazole and tebuconazole in twenty different agricultural soils in relation to their properties. Chemosphere 2020, 261, 127637. [Google Scholar] [CrossRef] [PubMed]
- European Commision. Ad-Hoc Study to Support the Initial Establishment of the List of Candidates for Substitution as Required in Article 80(7) of Regulation (EC) No 1107/2009. 2013. Available online: https://ec.europa.eu/food/system/files/2016-10/pesticides_ppp_app-proc_cfs_report-201307.pdf (accessed on 14 April 2021).
- Berenzen, N.; Lentzen-Godding, A.; Probst, M.; Schulz, H.; Schulz, R.; Liess, M. A comparison of predicted and measured levels of runoff-related pesticide concentrations in small lowland streams on a landscape level. Chemosphere 2005, 58, 683–691. [Google Scholar] [CrossRef]
- Siek, M.; Paszko, T. Factors affecting coupled degradation and time-dependent sorption processes of tebuconazole in mineral soil profiles. Sci. Total Environ. 2019, 690, 1035–1047. [Google Scholar] [CrossRef]
- Silva, V.; Mol, H.G.J.; Zomer, P.; Tienstra, M.; Ritsema, C.; Geissena, V. Pesticide residues in European agricultural soils—A hidden reality unfolded. Sci. Total Environ. 2019, 653, 1532–1545. [Google Scholar] [CrossRef]
- Vallée, R.; Dousset, S.; Billet, D.; Benoit, M. Sorption of selected pesticides on soils, sediment and straw from a constructed agricultural drainage ditch or pond. Environ. Sci. Pollut. R. 2014, 21, 4895–4905. [Google Scholar] [CrossRef]
- Gámiz, B.; López-Cabeza, R.; Facenda, G.; Velarde, P.; Hermosín, M.C.; Cox, L.; Celis, R. Effect of synthetic clay and biochar addition on dissipation and enantioselectivity of tebuconazole and metalaxyl in an agricultural soil: Laboratory and field experiments. Agr. Ecosyst. Environ. 2016, 230, 32–41. [Google Scholar] [CrossRef] [Green Version]
- Čadková, E.; Komárek, M.; Kaliszová, R.; Koudelková, V.; Dvořák, J.; Vaněk, A. Sorption of tebuconazole onto selected soil minerals and humic acids. J. Environ. Sci. Health B 2012, 47, 336–342. [Google Scholar] [CrossRef]
- Čadková, E.; Komárek, M.; Kaliszová, R.; Száková, J.; Vaněk, A.; Bordas, F.; Bollinger, J.C. The influence of copper on tebuconazole sorption onto soils, humic substances, and ferrihydrite. Environ. Sci. Pollut. Res. 2013, 20, 4205–4215. [Google Scholar] [CrossRef] [PubMed]
- Badawi, N.; Rosenbom, A.E.; Jensen, A.M.D.; Sorensen, S.R. Degradation and sorption of the fungicide tebuconazole in soils from golf greens. Environ. Pollut. 2016, 219, 368–378. [Google Scholar] [CrossRef]
- Arias, M.; Paradelo, M.; Lopez, E.; Simal-Gandara, J. Influence of pH and soil copper on adsorption of metalaxyl and penconazole by the surface layer of vineyard soils. J. Agric. Food Chem. 2006, 54, 8155–8162. [Google Scholar] [CrossRef]
- Mal’tseva, E.V.; Yudina, N.V.; Chaikovskaya, O.N.; Nechaev, L.V. Association constants of modified humic acids with biocides of the triazole series: Cyproconazole and tebuconazole. Russ. J. Phys. Chem. A 2011, 85, 1558–1561. [Google Scholar] [CrossRef]
- Tchaikovskaya, O.N.; Yudina, N.V.; Maltseva, E.V.; Nechaev, L.V.; Svetlichnyi, V.A. Interaction of humic acids with organic toxicants. Russ. Phys. J. 2016, 59, 597–603. [Google Scholar] [CrossRef]
- Jarvis, N. Meta-analysis of pesticide sorption in subsoil. Environ. Toxicol. Chem. 2018, 37, 755–761. [Google Scholar] [CrossRef]
- Jarvis, N. Extended sorption partitioning models for pesticide leaching risk assessments: Can we improve upon the koc concept? Sci. Total Environ. 2016, 539, 294–303. [Google Scholar] [CrossRef] [PubMed]
- Parolo, M.E.; Savini, M.C.; Loewy, R.M. Characterization of soil organic matter by FT-IR spectroscopy and its relationship with chlorpyrifos sorption. J. Environ. Manag. 2017, 196, 316–322. [Google Scholar] [CrossRef] [PubMed]
- Singh, N. Sorption behavior of triazole fungicides in Indian soils and its correlation with soil properties. J. Agric. Food Chem. 2002, 50, 6434–6439. [Google Scholar] [CrossRef]
- IUSS Working Group WRB. World reference base for soil resources 2014, update 2015. In International Soil Classification System for Naming Soils and Creating Legends for Soil Maps; World soil Resources Reports No. 106; FAO: Roma, Italy, 2015; p. 192. [Google Scholar]
- Tόth, G.; Montanarella, L.; Stolbovoy, V.; Máté, F.; Bόdis, K.; Jones, A.; Paganos, P.; Van Liedekere, M. Soils of the European Union; European Comission, Joint Research Centre, Institute for Environment and Sustainability: Ispra, Italy, 2008; p. 85. [Google Scholar]
- Bieganowski, A.; Witkowska-Walczak, B.; Gliński, J.; Sokołowska, Z.; Sławiński, C.; Brzezińska, M.; Włodarczyk, T. Database of Polish arable mineral soils: A review. Int. Agrophys. 2013, 27, 335–350. [Google Scholar] [CrossRef] [Green Version]
- OECD. OECD Guideline for Testing of Chemicals. Method 106. Adsorption-Desorption Using Batch Equilibrium Method; OECD: Paris, France, 2020. [Google Scholar]
- Giles, C.H.; MacEwan, T.H.; Nakhwa, S.N.; Smith, D. Studies in adsorption. Part XI. A system of classification of solution adsorption isotherms, and its use in diagnosis of adsorption mechanisms and in measurement of specific surface areas of solids. J. Chem. Soc. 1960, 111, 3973–3993. [Google Scholar] [CrossRef]
- Pignatello, J.J. Soil organic matter as a nanoporous sorbent of organic pollutants. Interf. Sci. Adv. Colloid 1998, 76–77, 445–467. [Google Scholar] [CrossRef]
- Álvarez-Martín, A.; Rodríguez-Cruz, M.S.; Andrades, M.S.; Sánchez-Martín, M.J. Application of a biosorbent to soil: A potential method for controlling water pollution by pesticides. Environ. Sci. Pollut. Res. 2016, 23, 9192–9203. [Google Scholar] [CrossRef]
- Ni, Y.; Liang, X.; Chen, J.; Zhang, Q.; Ma, L.; Wu, W.; Kettrup, A. Investigation on the influence of methanol on adsorption and leaching of pesticides with soil column liquid chromatography. Chemosphere 2004, 56, 1137–1142. [Google Scholar] [CrossRef] [PubMed]
- Papadopoulou, E.S.; Karas, P.A.; Nikolaki, S.; Storck, V.; Ferrari, F.; Trevisan, M.; Tsiamis, G.; Martin-Laurent, F.; Karpouzas, D.G. Dissipation and adsorption of isoproturon, tebuconazole, chlorpyrifos and their main transformation products under laboratory and field conditions. Sci. Total Environ. 2016, 569–570, 86–96. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Lee, L.S.; Fabrega, J.R.; Jafvert, C.T. Role of pH in partitioning and cation exchange of aromatic amines on water-saturated soils. Chemosphere 2001, 44, 627–635. [Google Scholar] [CrossRef]
- Paszko, T. Adsorption, degradation and mobility of carbendazim in profiles of Polish mineral soils. Geoderma 2014, 226, 160–169. [Google Scholar] [CrossRef]
- McLaren, R.G.; Crawford, D.V. Studies on soil copper I. The fractionation of copper in soils. Soil Sci. 1973, 24, 172–181. [Google Scholar] [CrossRef]
- Abdi, H. Partial least squares regression and projection on latent structure regression (PLS Regression). WIREs Comp. Stat. 2010, 2, 97–106. [Google Scholar] [CrossRef]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemometr. Intell. Lab. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Paszko, T.; Matysiak, J.; Kaminski, D.; Pasieczna-Patkowska, S.; Huber, M.; Król, B. Adsorption of bentazone in the profiles of mineral soils with low organic matter content. PLoS ONE 2020, 15, e0242980. [Google Scholar] [CrossRef] [PubMed]
- Ukalska-Jaruga, A.; Smreczak, B.; Klimkowicz-Pawlas, A. Soil organic matter composition as a factor affecting the accumulation of polycyclic aromatic hydrocarbon. J. Soils Sediments 2019, 19, 1890–1900. [Google Scholar] [CrossRef] [Green Version]
- Lian, F.; Xing, B. Black carbon (biochar) in water/soil environments: Molecular structure, sorption, stability, and potential risk. Environ. Sci. Technol. 2017, 51, 13517–13532. [Google Scholar] [CrossRef] [PubMed]
- Pignatello, J.J. Interactions of anthropogenic organic chemicals with natural organic matter and black carbon in environmental particles. In Biophysico-Chemical Processes of Anthropogenic Organic Compounds in Environmental Systems; Xing, B., Senesi, N., Huang, P.M., Eds.; John Wiley & Sons, Inc.: Hoboken, NY, USA, 2011; pp. 3–50. [Google Scholar] [CrossRef]
- Oades, J.M. An introduction to organic matter in mineral soils. In Minerals in Soil Environments, 2nd ed.; Dixon, J.B., Weed, S.B., Eds.; Soil Science Society of America, Inc.: Madison, WI, USA, 1989; Volume 1, pp. 89–159. [Google Scholar] [CrossRef]
- Seifferlein, E.R.; Jones, P.; Ferguson, R.; Burt, R.; Mays, D. Extractable acidity by a centrifuge method. Commun. Soil Sci. Plan. 2005, 36, 2067–2083. [Google Scholar] [CrossRef]
- Curtin, D.; Rostad, H.P.W. Cation exchange and buffer potential of Saskatchewan soils estimated from texture, organic matter and pH. Can. J. Soil Sci. 1997, 77, 621–626. [Google Scholar] [CrossRef]
- Rumpel, C.; Rabia, N.; Derenne, S.; Quenea, K.; Eusterhues, K.; Kögel-Knabner, I.; Mariotti, A. Alteration of soil organic matter following treatment with hydrofluoric acid (HF). Org. Geochem. 2006, 37, 1437–1451. [Google Scholar] [CrossRef]
- Chukanov, N.V. Infrared Spectra of Mineral Species; Extended Library; Springer: Dordrecht, The Netherlands, 2014; Volume 1, p. 1726. [Google Scholar]
- Müller, C.M.; Pejcic, B.; Esteban, L.; Delle Piane, C.; Raven, M.; Mizaikoff, B. Infrared attenuated total reflectance spectroscopy: An innovative strategy for analyzing mineral components in energy relevant systems. Sci. Rep. 2014, 4, 6764. [Google Scholar] [CrossRef] [Green Version]
- Silverstein, R.M.; Webster, F.X.; Kiemle, D.J. Spectrometric Identification of Organic Compounds, 7th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005; p. 502. [Google Scholar]
- Tatzber, M.; Stemmer, M.; Spiegel, H.; Katzlberger, C.; Haberhauer, G.; Mentler, A.; Gerzabek, M.H. FTIR-spectroscopic characterization of humic acids and humin fractions obtained by advanced NaOH, Na4P2O7, and Na2CO3 extraction procedures. J. Plant Nutr. Soil Sc. 2007, 170, 522–529. [Google Scholar] [CrossRef]
- Plaza, C.; Senesi, N.; Polo, A.; Brunetti, G. Acid-base properties of humic and fulvic acids formed during composting. Environ. Sci. Technol. 2005, 39, 7141–7146. [Google Scholar] [CrossRef]
- Krivoshein, P.K.; Volkov, D.S.; Rogova, O.B.; Proskurnin, M.A. FTIR photoacoustic spectroscopy for identification and assessment of soil components: Chernozems and their size fractions. Photoacoustics 2020, 18, 100162. [Google Scholar] [CrossRef]
- Snelders, E.; Camps, S.M.; Karawajczyk, A.; Schaftenaar, G.; Kema, G.H.; van der Lee, H.A.; Klaassen, C.H.; Melchers, W.J.; Verweij, P.E. Triazole fungicides can induce cross-resistance to medical triazoles in Aspergillus fumigatus. PLoS ONE 2012, 7, e31801. [Google Scholar] [CrossRef] [Green Version]
- Želonková, K.; Havadej, S.; Verebová, V.; Holečková, B.; Uličný, J.; Staničová, J. Fungicide tebuconazole influences the structure of human serum albumin molecule. Molecules 2019, 24, 3190. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vidali, R.; Remoundaki, E.; Tsezos, M. An experimental and modeling study of humic acid concentration effect on H(+) binding: Application of the NICA-Donnan model. J. Colloid Interface Sci. 2009, 339, 330–335. [Google Scholar] [CrossRef] [PubMed]
- Weber, J.B. Mineral structure and pH effects on the adsorption of 13 s-triazine compounds on the montmorillonite clay. Am. Miner. 1966, 51, 1657–1670. [Google Scholar]
- Weber, J.B.; Weed, S.B.; Ward, T.M. Adsorption of s-triazines by soil organic matter. Weed Sci. 1969, 17, 417–421. [Google Scholar] [CrossRef]
- Helal, A.A.; Imam, D.M.; Khalifa, S.M.; Aly, H.F. Interaction of pesticides with humic compounds and their metal complexes. Radiochemistry 2006, 48, 419–425. [Google Scholar] [CrossRef]
- ISO 11277. Soil Quality—Determination of Particle Size Distribution in Mineral Soil Material—Method by Sieving and Sedimentation; ISO: Geneva, Switzerland, 2020.
- Cave, M.R.; Harmon, K. Determination of trace metal distributions in the iron oxide phases of red bed sandstones by chemometric analysis of whole rock and selective leachate data. Analyst 1997, 122, 501–512. [Google Scholar] [CrossRef]
- Ramnarine, R.; Voroney, R.P.; Wagner-Riddle, C.; Dunfield, K.E. Carbonate removal by acid fumigation for measuring the δ 13C of soil organic carbon. Can. J. Soil Sci. 2011, 91, 247–250. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, M.W.I.; Skjemstad, J.O.; Czimczik, C.I.; Glaser, B.; Prentice, K.M.; Gelinas, Y.; Kuhlbusch, A.J. Comparative analysis of black carbon in soils. Glob. Biogeochem. Cycles 2001, 15, 163–167. [Google Scholar] [CrossRef] [Green Version]
- ISO 12782-4. Soil Quality—Parameters for Geochemical Modelling of Leaching and Speciation of Constituents in Soils and Materials—Part 4: Extraction of Humic Substances from Solid Samples; ISO: Geneva, Switzerland, 2012.
- Fox, P.M.; Nico, P.S.; Tfaily, M.M.; Heckman, K.; Davis, J. Characterization of natural organic matter in low-carbon sediments: Extraction and analytical approaches. Org. Geochem. 2017, 114, 12–22. [Google Scholar] [CrossRef] [Green Version]
- ISO 11260. Soil Quality—Determination of Effective Cation Exchange Capacity and Base Saturation Level Using Barium Chloride Solution; ISO: Geneva, Switzerland, 2018.
- ISO 14254. Soil Quality—Determination of Exchangeable Acidity Using Barium Chloride Solution as Extractant; ISO: Geneva, Switzerland, 2018.
- Shokrollahi, A.; Ghaedi, M.; Niband, M.S.; Rajabi, H.R. Selective and sensitive spectrophotometric method for determination of sub-micro-molar amounts of aluminium ion. J. Hazard. Mater. 2008, 151, 642–648. [Google Scholar] [CrossRef]
- ISO 13536. Soil Quality—Determination of the Potential Cation Exchange Capacity and Exchangeable Cations Using Barium Chloride Solution Buffered at pH = 8.1; ISO: Geneva, Switzerland, 1995.
- Wavefunction Spartan′10 for Windows, Macintosh and Linux. Available online: http://downloads.wavefun.com/Spartan10Manual.pdf (accessed on 14 April 2021).
- Reyes, A.; Moncada, F.; Charry, J. The any particle molecular orbital approach: A short review of the theory and applications. Int. J. Quantum Chem. 2018, 119, e25705. [Google Scholar] [CrossRef] [Green Version]
- Singh, U.C.; Kollman, P.A. An approach to computing electrostatic charges for molecules. J. Comput. Chem. 1984, 5, 129–145. [Google Scholar] [CrossRef]
- Addinsoft XLSTAT Statistical and Data Analysis Solution. Boston, USA. Available online: https://www.xlstat.com (accessed on 14 April 2021).

| No. | Equation Standardized Regression Coefficient; VIP | R2/LV a |
|---|---|---|
| (4) | Kd = 1.69 + 7.49∙(OC-BC)Φn+ 4.84∙BCΦn + 20.52∙(OC-BC)Φcat+ 51.23∙BCΦcat 0.56; 1.08 0.10; 0.63 0.74; 1.26 0.08; 0.91 | 0.903/3 |
| (5) | Kd = 1.74 + 8.79∙(OC-BC)Φn+ 20.89∙(OC-BC)Φcat 0.66; 0.93 0.76; 1.07 | 0.902/1 |
| (6) | Kd = 1.24 + 27.64∙FA(SP)Φn + 5.44∙HA(SP)Φn + 3.96∙HN(SP)Φn + 36.78∙FA(SP)Φcat + 43.68∙HA(SP)Φcat + 12.75∙HN(SP)Φcat 0.24; 0.94 0.14; 0.55 0.26; 1.03 0.25; 1.00 0.28; 1.11 0.31; 1.23 | 0.867/1 |
| (7) | Kd = 1.67 + 10.86∙HN(SP)Φn + 47.43∙FA(SP)Φcat + 19.08∙HN(SP)Φcat 0.70; 1.01 0.32; 0.90 0.46; 1.08 | 0.931/2 |
| (8) | Kd = 1.68 + 13.20∙FA(SH)Φn + 10.25∙HA(SH)Φn + 6.72∙HN(SH)Φn + 34.46∙FA(SH)Φcat + 24.58∙HA(SH)Φcat + 13.40∙HN(SH)Φcat 0.11; 0.94 0.07; 1.03 0.59; 1.03 0.27; 0.94 0.21; 1.01 0.28; 1.04 | 0.894/3 |
| (9) | Kd = 1.74 + 6.86∙HN(SH)Φn + 41.68∙HN(SH)Φcat 0.60; 0.80 0.88; 1.17 | 0.895/1 |
| (10) | Kd = 0.39 + 10.08∙(OC-BC)Φn+ 18.60∙(OC-BC)Φcat + 0.54∙PAΦcat 0.76; 1.11 0.67; 1.25 0.21; 0.46 | 0.955/2 |
| (11) | Kd = 0.38 + 12.16∙HN(SP)Φn + 25.32∙HN(SP)Φcat + 0.85∙PAΦcat 0.79; 1.08 0.61; 1.28 0.34; 0.46 | 0.982/3 |
| (12) | Kd = 0.01 + 35.45∙HA(SH)Φn + 8.33∙HN(SH)Φn + 24.48∙HN(SH)Φcat + 0.84∙PAΦcat 0.25; 1.18 0.73; 0.97 0.51; 1.18 0.33; 0.52 | 0.956/3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siek, M.; Paszko, T.; Jerzykiewicz, M.; Matysiak, J.; Wojcieszek, U. Mechanisms of Tebuconazole Adsorption in Profiles of Mineral Soils. Molecules 2021, 26, 4728. https://doi.org/10.3390/molecules26164728
Siek M, Paszko T, Jerzykiewicz M, Matysiak J, Wojcieszek U. Mechanisms of Tebuconazole Adsorption in Profiles of Mineral Soils. Molecules. 2021; 26(16):4728. https://doi.org/10.3390/molecules26164728
Chicago/Turabian StyleSiek, Marcin, Tadeusz Paszko, Maria Jerzykiewicz, Joanna Matysiak, and Urszula Wojcieszek. 2021. "Mechanisms of Tebuconazole Adsorption in Profiles of Mineral Soils" Molecules 26, no. 16: 4728. https://doi.org/10.3390/molecules26164728
APA StyleSiek, M., Paszko, T., Jerzykiewicz, M., Matysiak, J., & Wojcieszek, U. (2021). Mechanisms of Tebuconazole Adsorption in Profiles of Mineral Soils. Molecules, 26(16), 4728. https://doi.org/10.3390/molecules26164728







