A Surfactant Concentration Model for the Systematic Determination of the Critical Micellar Concentration and the Transition Width
Abstract
:1. Introduction
2. The Surfactant Concentration Model
3. Application to Different Techniques
3.1. Electrical Conductivity of Ionic Surfactant Solutions
3.1.1. Comparison to the Carpena Model
- (i)
- Both methods are based on empirical models. The concentration model relies on the Phillips condition for the cmc and on the description of the degree of micellization as a continuous normal distribution function, derived from a probabilistic description of the distribution of free and micellized surfactants. The Carpena method starts with the Boltzmann function for the description of the differential conductivity. Other conditions or sigmoidal functions would lead to other models with similar results. However, the concentration model is derived from more general assumptions that make it applicable to any property-concentration relationship.
- (ii)
- The value of the transition width Δ[S]0 of the Carpena method, has no direct relation to that of the transition width σ = r·cmc of the concentration model, which stems from the width of the Gaussian function of Equation (2). Both widths define the slopes of the corresponding sigmoidal functions at the inflection point [S]0 = cmc:
- (iii)
- The values of the cmc determined by the two methods are in practice identical. The sigmoidal Boltzmann function of Equation (14) is not identical to the sigmoidal error function of Equation (9), but very similar. The fit of the SDS conductivity data of our original paper (Figure 2 in [9]) with Equation (15) yields cmcCarpena = 8.096 ± 0.005 mM, identical to cmc = 8.099 ± 0.005 mM obtained with Equation (12). The same is true for the slopes a and b. The reduced χ2 values are very similar with χ2 = 0.436 and χ2 = 0.427 for Equations (12) and (15), respectively. The transition width is Δ[S]0 = 0.519 mM. Compared to the transition width from the concentration model σ = r·cmc = 0.112 × 8.099 mM = 0.907 mM, the ratio σ/Δ[S]0 = 1.75 falls within the expected interval indicated above.
3.1.2. Example of the Use for Surfactant Mixtures
3.1.3. Global Fit of Conductivity Data. Application to Weakly Surface-Active Drugs
3.2. Surface Tension
3.3. NMR-Chemical Shift
3.4. Fluorescence of a Dye Probe Molecule
3.4.1. Steady-State and Time Resolved Fluorescence of Pyrene
3.5. UV-Vis Absorbance
3.6. Fluorescence Correlation Spectroscopy
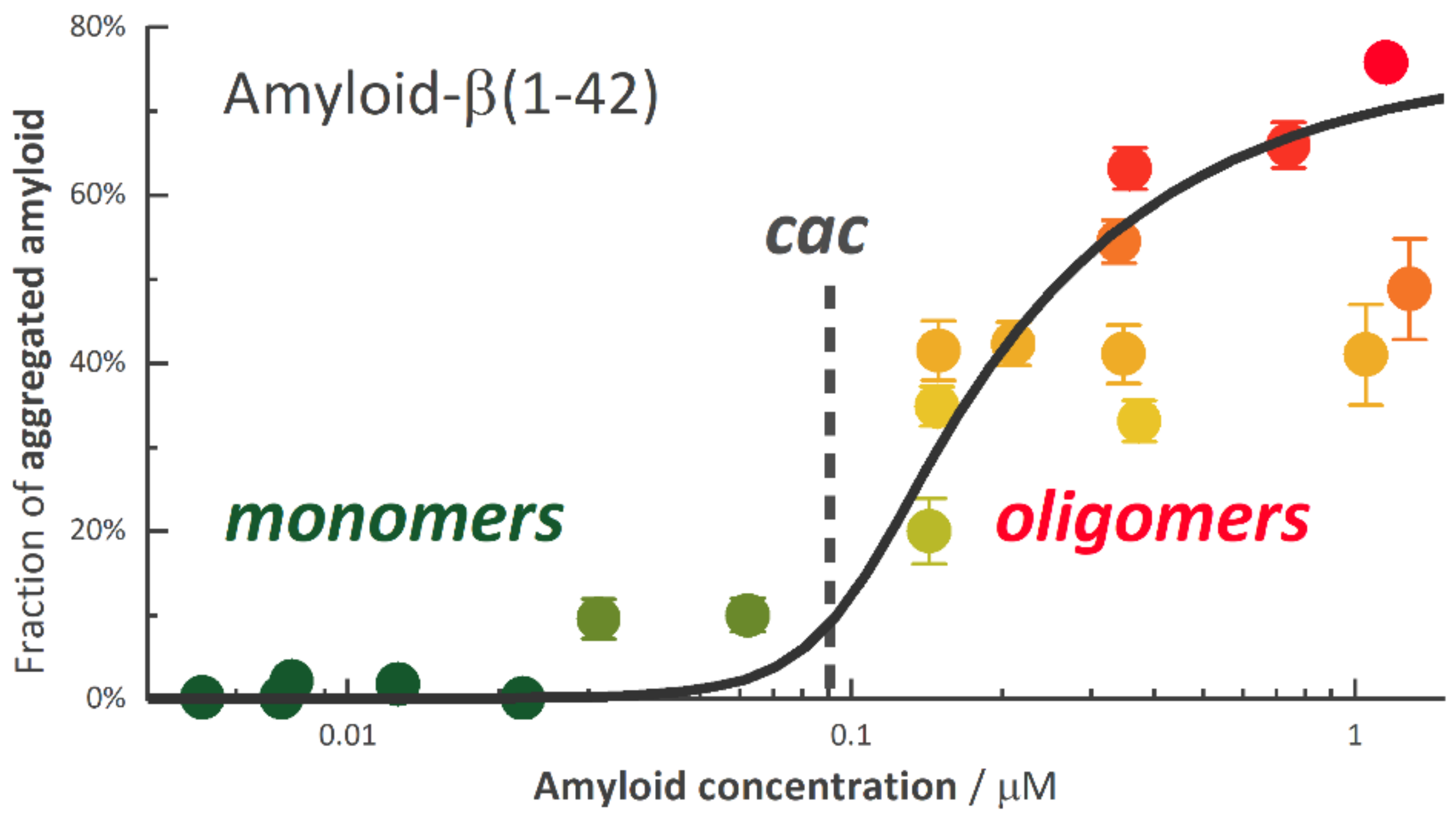
3.7. Aggregation of Non-Surfactant Systems
3.8. Water-Micelle Partitioning Coefficients from Conductivity and UV-Vis Spectra
4. Influence of Nonlinear Property-Concentration Relationships on the cmc Value
5. Analysis with Sparse Data Points
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A

| cmc/mol kg−1 | a/mol kg−1 | b/mol kg−1 K−1 | c/mol kg−1 K−2 |
|---|---|---|---|
| ClMP | 0.30 ± 0.04 | (−2.2 ± 0.2) × 10−3 | (4.3 ± 0.4) × 10−6 |
| IMP | 0.29 ± 0.03 | (−2.1 ± 0.2) × 10−3 | (4.2 ± 0.4) × 10−6 |

References
- Phillips, J. The energetics of micelle formation. Trans. Faraday Soc. 1955, 51, 561–569. [Google Scholar] [CrossRef]
- Mukerjee, P.; Mysels, K.J. Critical Micelle Concentrations of Aqueous Surfactant Systems; NIST National Institute of Standards and Technology: Washington, DC, USA, 1971; Volume NSRDS-NBS 36.
- García-Mateos, I.; Mercedes Velázquez, M.; Rodríguez, L.J. Critical micelle concentration determination in binary mixtures of ionic surfactants by deconvolution of conductivity/concentration curves. Langmuir 1990, 6, 1078–1083. [Google Scholar] [CrossRef]
- Shanks, P.C.; Franses, E.I. Estimation of Micellization Parameters of Aqueous Sodium Dodecyl-Sulfate from Conductivity Data. J. Phys. Chem. 1992, 96, 1794–1805. [Google Scholar] [CrossRef]
- Pérez-Rodríguez, M.; Prieto, G.; Rega, C.; Varela, L.M.; Sarmiento, F.; Mosquera, V. A comparative study of the determination of the critical micelle concentration by conductivity and dielectric constant measurements. Langmuir 1998, 14, 4422–4426. [Google Scholar] [CrossRef]
- Carpena, P.; Aguiar, J.; Bernaola-Galván, P.; Ruiz, C.C. Problems associated with the treatment of conductivity-concentration data in surfactant solutions: Simulations and experiments. Langmuir 2002, 18, 6054–6058. [Google Scholar] [CrossRef]
- Patist, A. Determining critical micelle concentration. In Handbook of Applied Surface and Colloid Chemistry; Holmberg, K., Ed.; John Wiley & Sons: New York, NY, USA, 2001; Volume 2, p. 239. [Google Scholar]
- López Fontán, J.L.; Costa, J.; Ruso, J.; Prieto, G.; Sarmiento, F. A nonparametric approach to calculate critical micelle concentrations: The local polynomial regression method. Eur. Phys. J. E Soft Matter Biol. Phys. 2004, 13, 133–140. [Google Scholar] [CrossRef]
- Al-Soufi, W.; Piñeiro, L.; Novo, M. A model for monomer and micellar concentrations in surfactant solutions: Application to conductivity, NMR, diffusion, and surface tension data. J. Colloid Interface Sci. 2012, 370, 102–110. [Google Scholar] [CrossRef]
- Scholz, N.; Behnke, T.; Resch-Genger, U. Determination of the Critical Micelle Concentration of Neutral and Ionic Surfactants with Fluorometry, Conductometry, and Surface Tension—A Method Comparison. J. Fluoresc. 2018, 28, 465–476. [Google Scholar] [CrossRef] [PubMed]
- Perinelli, D.R.; Cespi, M.; Lorusso, N.; Palmieri, G.F.; Bonacucina, G.; Blasi, P. Surfactant Self-Assembling and Critical Micelle Concentration: One Approach Fits All? Langmuir 2020, 36, 5745–5753. [Google Scholar] [CrossRef]
- Moulik, S.P.; Rakshit, A.K.; Naskar, B. Evaluation of Non-Ambiguous Critical Micelle Concentration of Surfactants in Relation to Solution Behaviors of Pure and Mixed Surfactant Systems: A Physicochemical Documentary and Analysis. J. Surfactants Deterg. 2021, 24. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Intermolecular and Surface Forces; Academic Press: New York, NY, USA, 2010. [Google Scholar]
- Zana, R. Dynamics of Surfactant Self-Assemblies: Micelles, Microemulsions, Vesicles, and Lyotropic Phases; Taylor & Francis/CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Blankschtein, D.; Shiloach, A.; Zoeller, N. Thermodynamic theories of micellar and vesicular systems. Curr. Opin. Colloid Interface Sci. 1997, 2, 294–300. [Google Scholar] [CrossRef]
- Goldsipe, A.; Blankschtein, D. Molecular-Thermodynamic Theory of Micellization of Multicomponent Surfactant Mixtures: 2. pH-Sensitive Surfactants. Langmuir 2007, 23, 5953–5962. [Google Scholar] [CrossRef] [PubMed]
- Iyer, J.; Mendenhall, J.D.; Blankschtein, D. Computer Simulation–Molecular-Thermodynamic Framework to Predict the Micellization Behavior of Mixtures of Surfactants: Application to Binary Surfactant Mixtures. J. Phys. Chem. B 2013, 117, 6430–6442. [Google Scholar] [CrossRef] [PubMed]
- Puvvada, S.; Blankschtein, D. Molecular-thermodynamic approach used to predict micellization, phase behavior, and phase separation of micellar solutions. Langmuir 1990, 6, 894–895. [Google Scholar] [CrossRef]
- Stephenson, B.C.; Beers, K.; Blankschtein, D. Complementary use of simulations and molecular-thermodynamic theory to model micellization. Langmuir 2006, 22, 1500–1513. [Google Scholar] [CrossRef]
- Hadgiivanova, R.; Diamant, H. Premicellar aggregation of amphiphilic molecules. J. Phys. Chem. B 2007, 111, 8854–8859. [Google Scholar] [CrossRef]
- Sammalkorpi, M.; Sanders, S.; Panagiotopoulos, A.; Karttunen, M.; Haataja, M. Simulations of Micellization of Sodium Hexyl Sulfate. J. Phys. Chem. B 2011, 115, 1403–1410. [Google Scholar] [CrossRef]
- Gezae Daful, A.; Baulin, V.; Avalos, J.; Mackie, A. Accurate Critical Micelle Concentrations from a Microscopic Surfactant Model. J. Phys. Chem. B 2011, 115, 3434–3443. [Google Scholar] [CrossRef] [PubMed]
- Diamant, H.; Andelman, D. Free energy approach to micellization and aggregation: Equilibrium, metastability, and kinetics. Curr. Opin. Colloid Interface Sci. 2016, 22, 94–98. [Google Scholar] [CrossRef] [Green Version]
- Piñeiro, L.; Freire, S.; Bordello, J.; Novo, M.; Al-Soufi, W. Dye exchange in micellar solutions. Quantitative analysis of bulk and single molecule fluorescence titrations. Soft Matter 2013, 9, 10779–10790. [Google Scholar] [CrossRef]
- Piñeiro, L.; Novo, M.; Al-Soufi, W. Fluorescence emission of pyrene in surfactant solutions. Adv. Colloid Interface Sci. 2015, 215, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Hadgiivanova, R.; Diamant, H. Premicellar aggregation of amphiphilic molecules: Aggregate lifetime and polydispersity. J. Chem. Phys. 2009, 130, 114901. [Google Scholar] [CrossRef] [Green Version]
- Zettl, H.; Portnoy, Y.; Gottlieb, M.; Krausch, G. Investigation of Micelle Formation by Fluorescence Correlation Spectroscopy. J. Phys. Chem. B 2005, 109, 13397–13401. [Google Scholar] [CrossRef]
- Rusanov, A.I. The mass action law theory of micellar solutions. Adv. Colloid Interface Sci. 1993, 45, 1–78. [Google Scholar] [CrossRef]
- Morisada, S.; Shinto, H. Implicit Solvent Model Simulations of Surfactant Self-Assembly in Aqueous Solutions. J. Phys. Chem. B 2010, 114, 6337–6343. [Google Scholar] [CrossRef]
- Hunter, R.J. Foundations of Colloid Science; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Pereyra, R.B.; Fernández Leyes, M.D.; Silbestri, G.F.; Durand, G.A.; Schulz, P.C.; Ritacco, H.A.; Schulz, E.P. Experimental and thermodynamic analysis of mixed micelles formed by dodecylethylmethacrylatedimethylammonium bromide and tetradecyltrimethylammonium bromide. Colloids Surf. Physicochem. Eng. Asp. 2021, 614, 126118. [Google Scholar] [CrossRef]
- Beechem, J.M.; Gratton, E.; Ameloot, M.; Knutson, J.R.; Brand, L. The Global Analysis of Fluorescence Intensity and Anisotropy Decay Data: Second-Generation Theory and Programs; Lakowicz, J.R., Ed.; Topics in Fluorescence Spectroscopy; Plenum Press: New York, NY, USA, 1991; pp. 241–306. [Google Scholar]
- Knutson, J.R.; Beechem, J.M.; Brand, L. Simultaneous Analysis of Multiple Fluorescence Decay Curves: A Global Approach. Chem. Phys. Lett. 1983, 102, 501–507. [Google Scholar] [CrossRef]
- Dommelen, L.V.; Boens, N.; Ameloot, M.; De Schryver, F.C.; Kowalczyk, A. Species-Associated Spectra and Upper and Lower Bounds on the Rate Constants of Reversible Intramolecular Two-State Excited-State Processes with Added Quencher. Global Compartmental Analysis of the Fluorescence Decay Surface. J. Phys. Chem. 1993, 97, 11738–11753. [Google Scholar] [CrossRef]
- Van Stokkum, I.H.M.; Larsen, D.S.; van Grondelle, R. Global and target analysis of time-resolved spectra. Biochim. Biophys. Acta (BBA) Bioenerg. 2004, 1657, 82–104. [Google Scholar] [CrossRef] [Green Version]
- Al-Soufi, W.; Novo, M.; Mosquera, M.; Rodríguez-Prieto, F. Principal Component Global Analysis of Series of Fluorescence Spectra. Rev. Fluoresc. 2009, 2011, 23–45. [Google Scholar]
- López Fontán, J.L.; Costa, J.; Ruso, J.M.; Prieto, G.; Sarmiento, F. Electrical Conductivities and Critical Micelle Concentrations (Determined by the Local Polynomial Regression Method) of Imipramine and Clomipramine Hydrochlorides from (283 to 313) K. J. Chem. Eng. Data 2004, 49, 1008–1012. [Google Scholar] [CrossRef]
- Szyszkowski, B. Experimental studies of the capillary properties of aqueous solutions of fatty acids. Z. Phys. Chem. 1908, 64, 385. [Google Scholar] [CrossRef] [Green Version]
- Mysels, K.J. Surface tension of solutions of pure sodium dodecyl sulfate. Langmuir 1986, 2, 423–428. [Google Scholar] [CrossRef]
- Fainerman, V.; Miller, R. Surface tension isotherms for surfactant adsorption layers including surface aggregation. Langmuir 1996, 12, 6011–6014. [Google Scholar] [CrossRef]
- Boussambe, G.N.M.; Guillet, P.; Mahler, F.; Marconnet, A.; Vargas, C.; Cornut, D.; Soulié, M.; Ebel, C.; Le Roy, A.; Jawhari, A.; et al. Fluorinated diglucose detergents for membrane-protein extraction. Methods 2018, 147, 84–94. [Google Scholar] [CrossRef]
- Guillet, P.; Mahler, F.; Garnier, K.; Nyame Mendendy Boussambe, G.; Igonet, S.; Vargas, C.; Ebel, C.; Soulié, M.; Keller, S.; Jawhari, A.; et al. Hydrogenated Diglucose Detergents for Membrane-Protein Extraction and Stabilization. Langmuir 2019, 35, 4287–4295. [Google Scholar] [CrossRef] [PubMed]
- Wehbie, M.; Onyia, K.K.; Mahler, F.; Le Roy, A.; Deletraz, A.; Bouchemal, I.; Vargas, C.; Babalola, J.O.; Breyton, C.; Ebel, C.; et al. Maltose-Based Fluorinated Surfactants for Membrane-Protein Extraction and Stabilization. Langmuir 2021, 37, 2111–2122. [Google Scholar] [CrossRef]
- Gahane, A.Y.; Ranjan, P.; Singh, V.; Sharma, R.K.; Sinha, N.; Sharma, M.; Chaudhry, R.; Thakur, A.K. Fmoc-phenylalanine displays antibacterial activity against Gram-positive bacteria in gel and solution phases. Soft Matter 2018, 14, 2234–2244. [Google Scholar] [CrossRef]
- Artykulnyi, O.P.; Petrenko, V.I.; Bulavin, L.A.; Ivankov, O.I.; Avdeev, M.V. Impact of poly (ethylene glycol) on the structure and interaction parameters of aqueous micellar solutions of anionic surfactants. J. Mol. Liq. 2019, 276, 806–811. [Google Scholar] [CrossRef]
- Amato, M.; Caponetti, E.; Martino, D.C.; Pedone, L. 1 H and 19F NMR Investigation on Mixed Hydrocarbon-Fluorocarbon Micelles. J. Phys. Chem. B 2003, 107, 10048–10056. [Google Scholar] [CrossRef]
- Yu, G.J.; Chen, X.Y.; Mao, S.Z.; Liu, M.L.; Du, Y.R. Hydrophobic terminal group of surfactant initiating micellization as revealed by 1H NMR spectroscopy. Chin. Chem. Lett. 2017, 28, 1413–1416. [Google Scholar] [CrossRef]
- Ananthapadmanabhan, K.P.; Goddard, E.D.; Turro, N.J.; Kuo, P.L. Fluorescence Probes for Critical Micelle Concentration. Langmuir 1985, 1, 352–355. [Google Scholar]
- Nakahara, Y.; Kida, T.; Nakatsuji, Y.; Akashi, M. New Fluorescence Method for the Determination of the Critical Micelle Concentration by Photosensitive Monoazacryptand Derivatives. Langmuir 2005, 21, 6688–6695. [Google Scholar] [CrossRef]
- Romani, A.P.; Machado, A.E.D.H.; Hioka, N.; Severino, D.; Baptista, M.S.; Codognoto, L.; Rodrigues, M.R.; De Oliveira, H.P.M. Spectrofluorimetric Determination of Second Critical Micellar Concentration of SDS and SDS/Brij 30 Systems. J. Fluoresc. 2009, 19, 327–332. [Google Scholar] [CrossRef]
- Thorsteinsson, M.V.; Richter, J.; Lee, A.L.; DePhillips, P. 5-Dodecanoylaminofluorescein as a probe for the determination of critical micelle concentration of detergents using fluorescence anisotropy. Anal. Biochem. 2005, 340, 220–225. [Google Scholar] [CrossRef]
- Förster, T.; Selinger, B. Der Konzentrationsumschlag der Fluoreszenz aromatischer Kohlenwasserstoffe in mizell-kolloidaler Lösung. Z. Nat. Teil A 1964, 19, 38. [Google Scholar] [CrossRef] [Green Version]
- Graetzel, M.; Thomas, J. The application of fluorescence techniques to the study of micellar systems. Mod. Fluoresc. Spectrosc. 1976, 2, 169–216. [Google Scholar]
- Kalyanasundaram, K.; Thomas, J.K. Environmental Effects on Vibronic Band Intensities in Pyrene Monomer Fluorescence and Their Application in Studies of Micellar Systems. J. Am. Chem. Soc. 1977, 99, 2039–2044. [Google Scholar] [CrossRef]
- De Schryver, F.; Croonen, Y.; Geladé, E.; Van der Auweraer, M.; Dederen, J.; Roelants, E.; Boens, N. Fluorescence Quenching in Micellar Systems. In Surfactants in Solution; Springer: Berlin/Heidelberg, Germany, 1984; pp. 663–672. [Google Scholar]
- Glushko, V.; Thaler, M.S.; Karp, C.D. Pyrene fluorescence fine structure as a polarity probe of hydrophobic regions: Behavior in model solvents. Arch. Biochem. Biophys. 1981, 210, 33–42. [Google Scholar] [CrossRef]
- Karpovich, D.S.; Blanchard, G.J. Relating the polarity-dependent fluorescence response of pyrene to vibronic coupling. Achieving a fundamental understanding of the py polarity scale. J. Phys. Chem. 1995, 99, 3951–3958. [Google Scholar] [CrossRef]
- Al-Soufi, W.; Reija, B.; Novo, M.; Felekyan, S.; Kühnemuth, R.; Seidel, C.A.M. Fluorescence Correlation Spectroscopy, a Tool to investigate Supramolecular Dynamics: Inclusion Complexes of Pyronines with Cyclodextrin. J. Am. Chem. Soc. 2005, 127, 8775–8784. [Google Scholar] [CrossRef]
- Novo, M.; Felekyan, S.; Seidel, C.A.M.; Al-Soufi, W. Dye-Exchange Dynamics in Micellar Solutions Studied by Fluorescence Correlation Spectroscopy. J. Phys. Chem. B 2007, 111, 3614–3624. [Google Scholar] [CrossRef]
- Al-Soufi, W.; Reija, B.; Felekyan, S.; Seidel, C.A.; Novo, M. Dynamics of supramolecular association monitored by fluorescence correlation spectroscopy. Chem. Phys. Chem. 2008, 9, 1819–1827. [Google Scholar] [CrossRef] [PubMed]
- Bordello, J.; Novo, M.; Al-Soufi, W. Exchange-Dynamics of a Neutral Hydrophobic Dye in Micellar Solutions Studied by Fluorescence Correlation Spectroscopy. J. Colloid Interface Sci. 2010, 345, 369–376. [Google Scholar] [CrossRef] [PubMed]
- Novo, M.; Freire, S.; Al-Soufi, W. Critical aggregation concentration for the formation of early Amyloid-β (1–42) oligomers. Sci. Rep. 2018, 8, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Lewandowski, A.; Szymczyk, K. Partitioning of Selected Anisole and Veratrole Derivatives between Water and Anionic Surfactant Micelles. Molecules 2020, 25, 5818. [Google Scholar] [CrossRef]
- Xu, H.; Li, P.X.; Ma, K.; Thomas, R.K.; Penfold, J.; Lu, J.R. Limitations in the Application of the Gibbs Equation to Anionic Surfactants at the Air/Water Surface: Sodium Dodecylsulfate and Sodium Dodecylmonooxyethylenesulfate above and Below the CMC. Langmuir 2013, 29, 9335–9351. [Google Scholar] [CrossRef] [PubMed]
- Dvorsky, R.; Praus, P.; Trojková, J. Model of synthesis of zns nanoparticles stabilized by cetyltrimethylammonium bromide. Chalcogenide Lett. 2013, 10, 385–392. [Google Scholar]
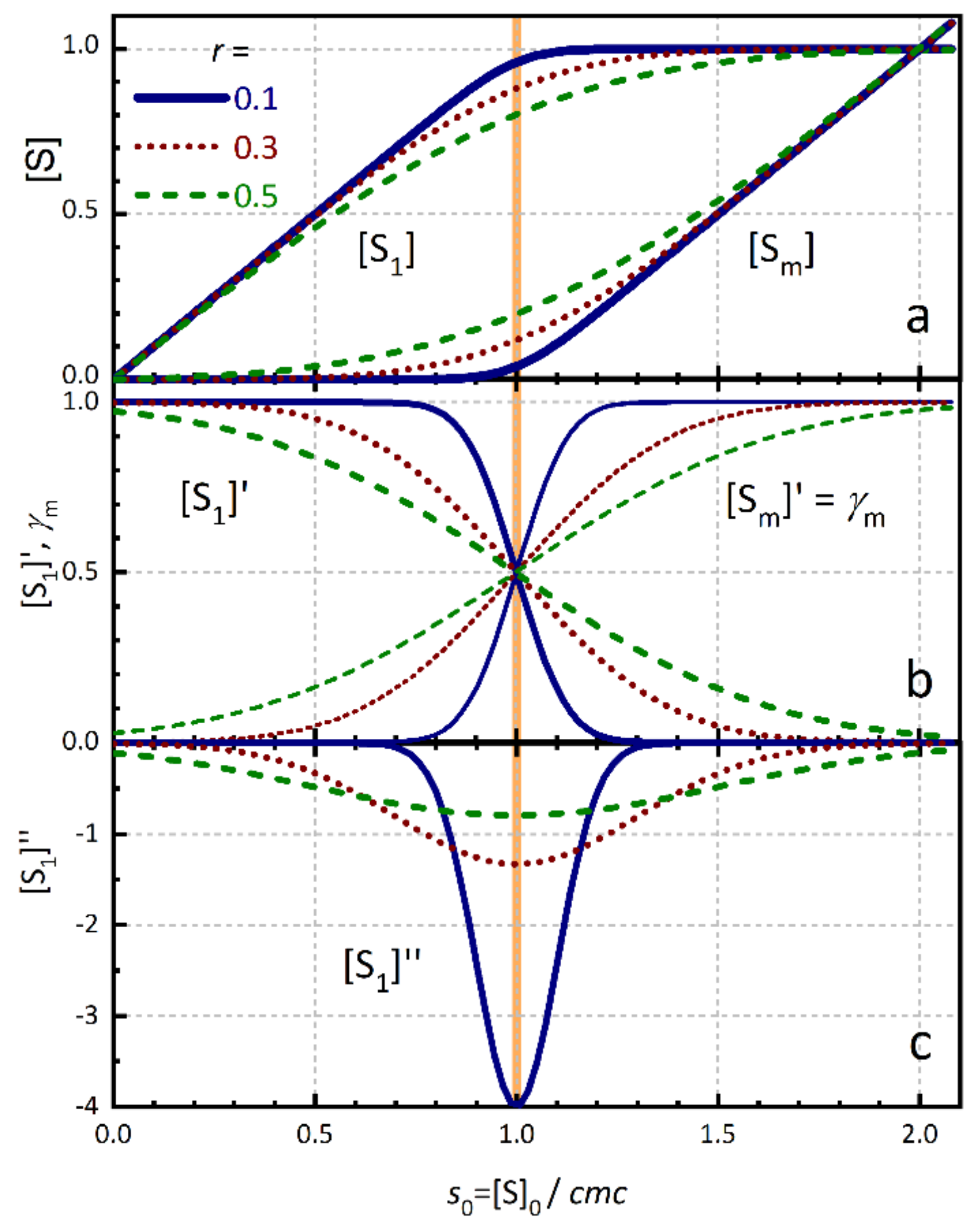





| TX100 | SDS | |
|---|---|---|
| cmc/10−3 mol L−1 | 0.275 ± 0.005 | 8.1 ± 0.1 |
| r | 0.16 ± 0.01 | 0.07 ± 0.03 |
| K/103 mol L−1 | 3300 ± 200 | 190 ± 40 |
| Kq/103 mol L−1 | 2.2 ± 0.2 | 0.23 ± 0.03 |
| // [a] | 0.45/0.98/1.5 | 0.44/0.91/1.4 |
| Data | cmc/mM | r | a(1) | b(1) |
|---|---|---|---|---|
| all points | 8.099 ± 0.005 | 0.112 ± 0.001 | 66.74 ± 0.03 | 26.43 ± 0.01 |
| 10 points | 8.12 ± 0.02 | 0.08 ± 0.03 | 66.6 ± 0.1 | 26.37 ± 0.08 |
| 10 points | 8.10 ± 0.02 | 0.1 fixed | 66.75 ± 0.09 | 26.35 ± 0.08 |
| 10 points | 8.12 ± 0.02 | 0.001 fixed | 66.60 ± 0.09 | 26.37 ± 0.07 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Soufi, W.; Novo, M. A Surfactant Concentration Model for the Systematic Determination of the Critical Micellar Concentration and the Transition Width. Molecules 2021, 26, 5339. https://doi.org/10.3390/molecules26175339
Al-Soufi W, Novo M. A Surfactant Concentration Model for the Systematic Determination of the Critical Micellar Concentration and the Transition Width. Molecules. 2021; 26(17):5339. https://doi.org/10.3390/molecules26175339
Chicago/Turabian StyleAl-Soufi, Wajih, and Mercedes Novo. 2021. "A Surfactant Concentration Model for the Systematic Determination of the Critical Micellar Concentration and the Transition Width" Molecules 26, no. 17: 5339. https://doi.org/10.3390/molecules26175339
APA StyleAl-Soufi, W., & Novo, M. (2021). A Surfactant Concentration Model for the Systematic Determination of the Critical Micellar Concentration and the Transition Width. Molecules, 26(17), 5339. https://doi.org/10.3390/molecules26175339






