Unravelling the Interactions of Magnetic Ionic Liquids by Energy Decomposition Schemes: Towards a Transferable Polarizable Force Field
Abstract
:1. Introduction
2. Computational Details
3. Results and Discussion
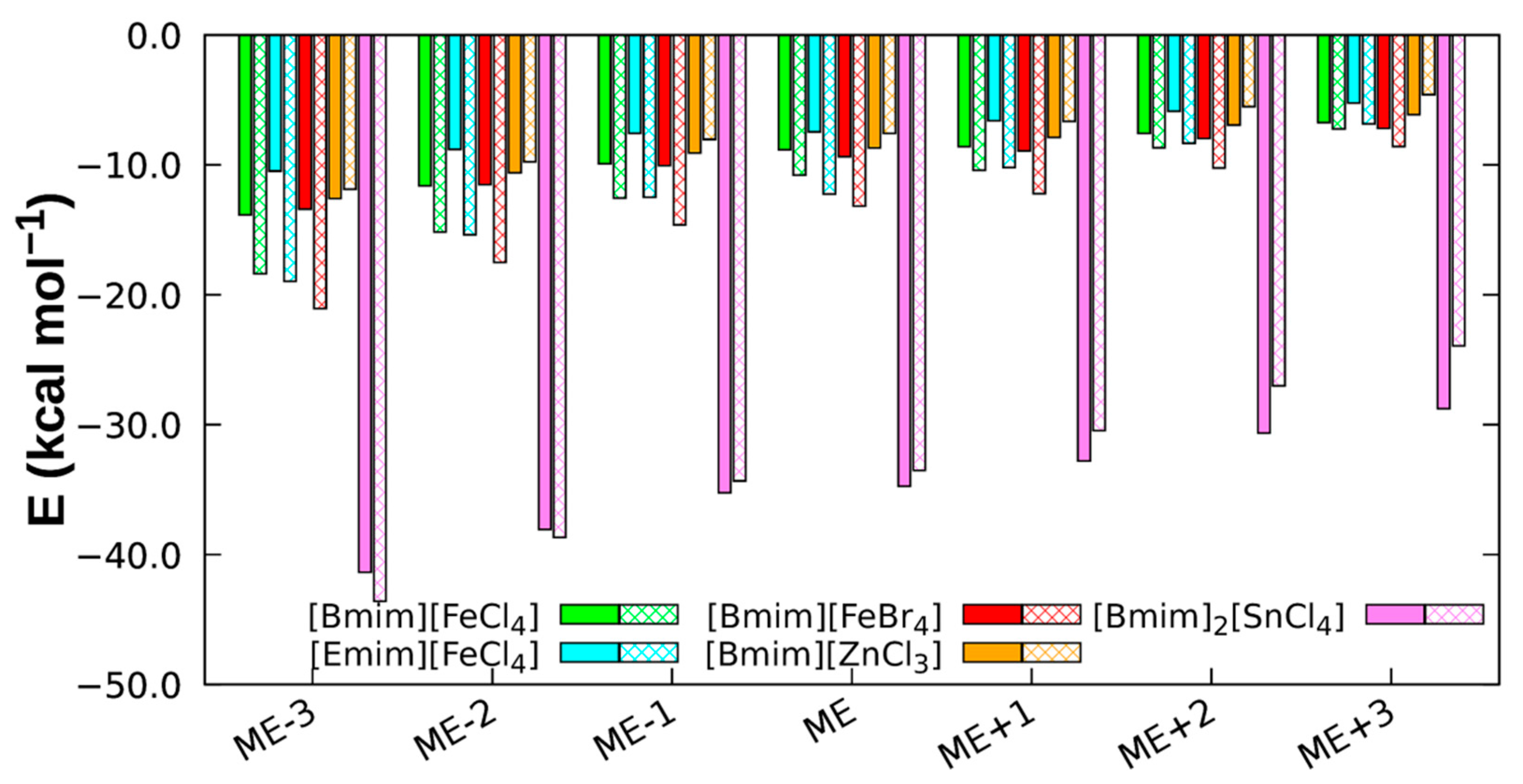
3.1. Structure and Stability of Ion Pairs
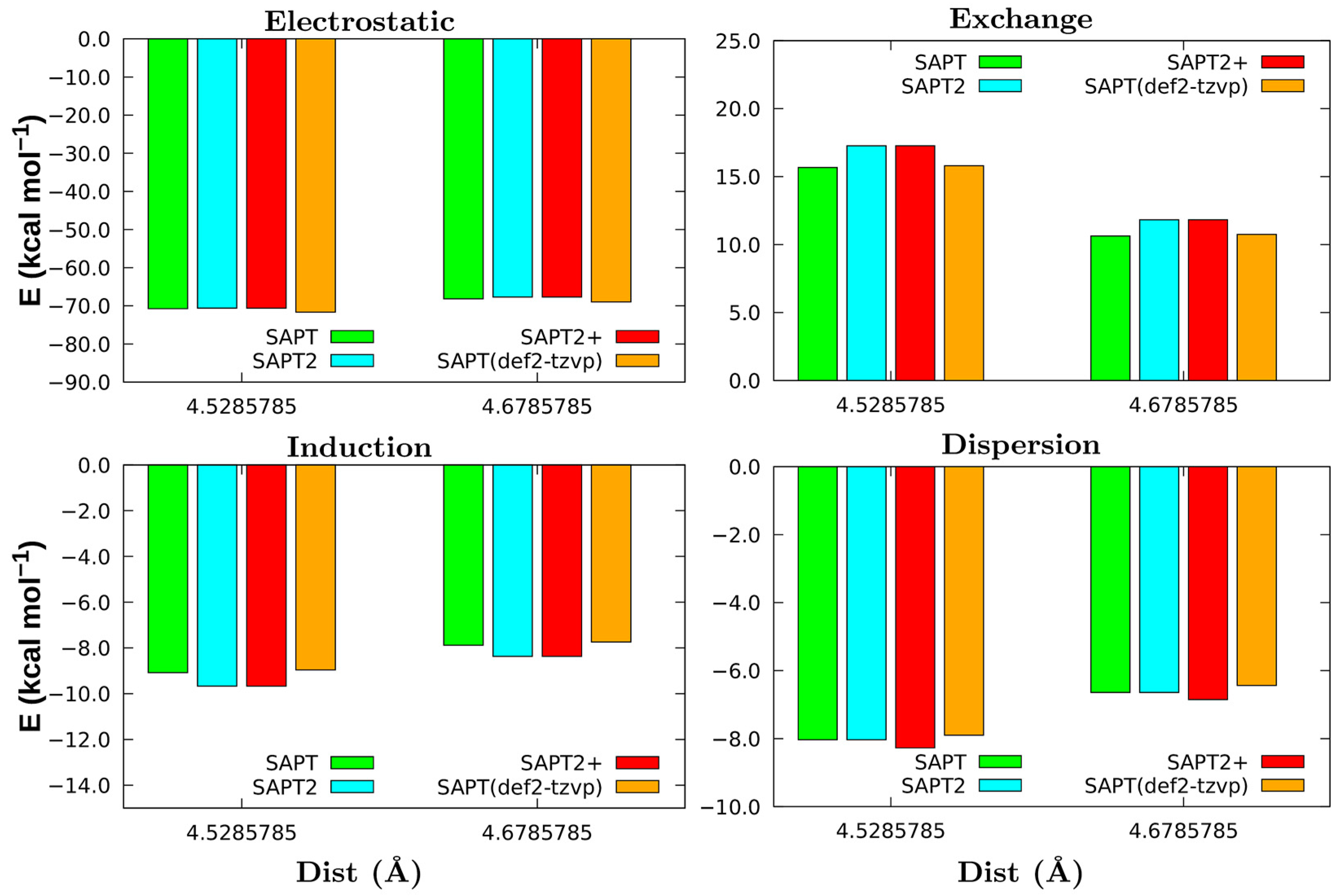
3.2. Non-Covalent Interactions of Ion Pairs from SAPT Level
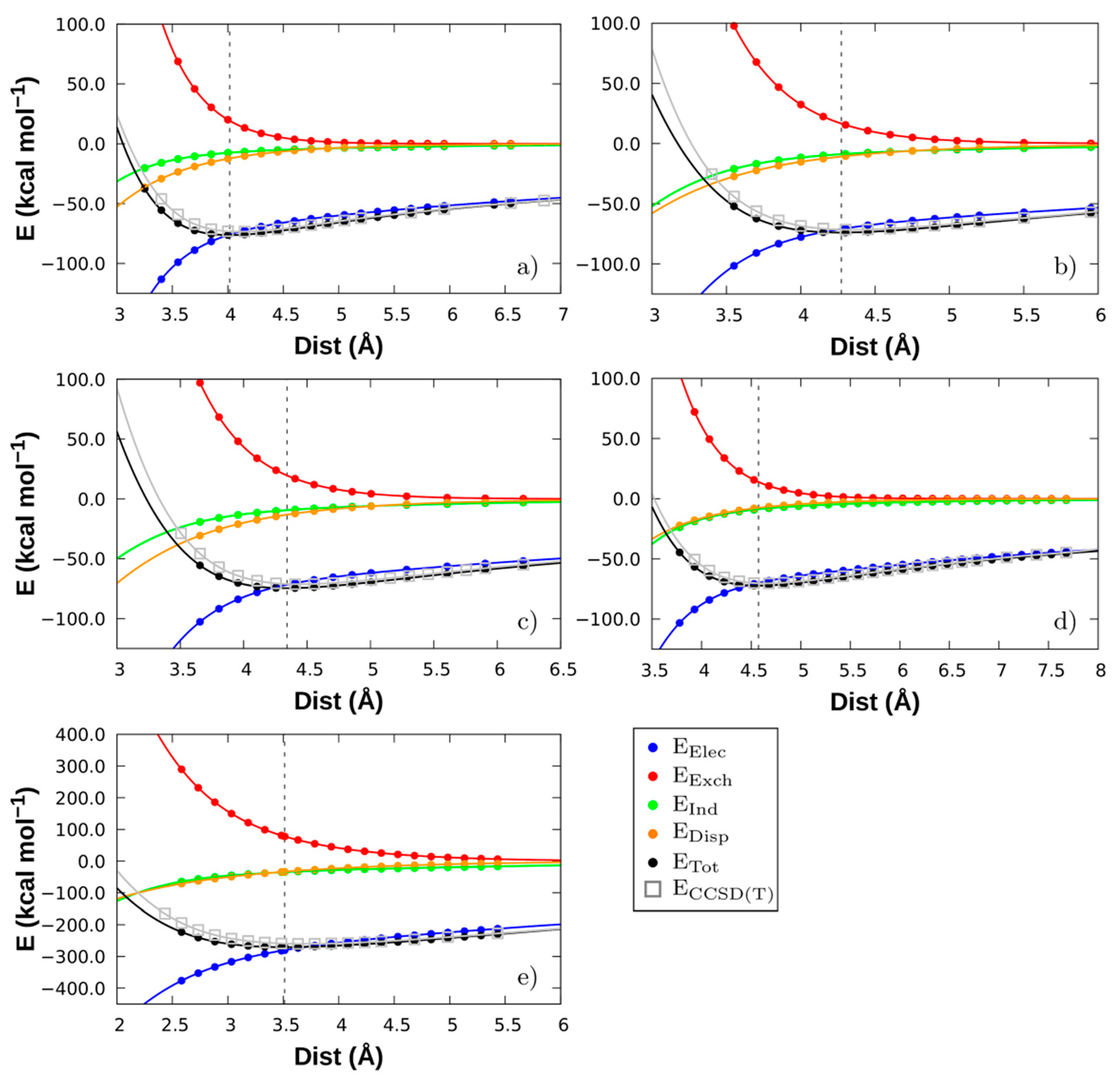
3.3. Comparison between LED DLPNO-CCSD(T) and SAPT
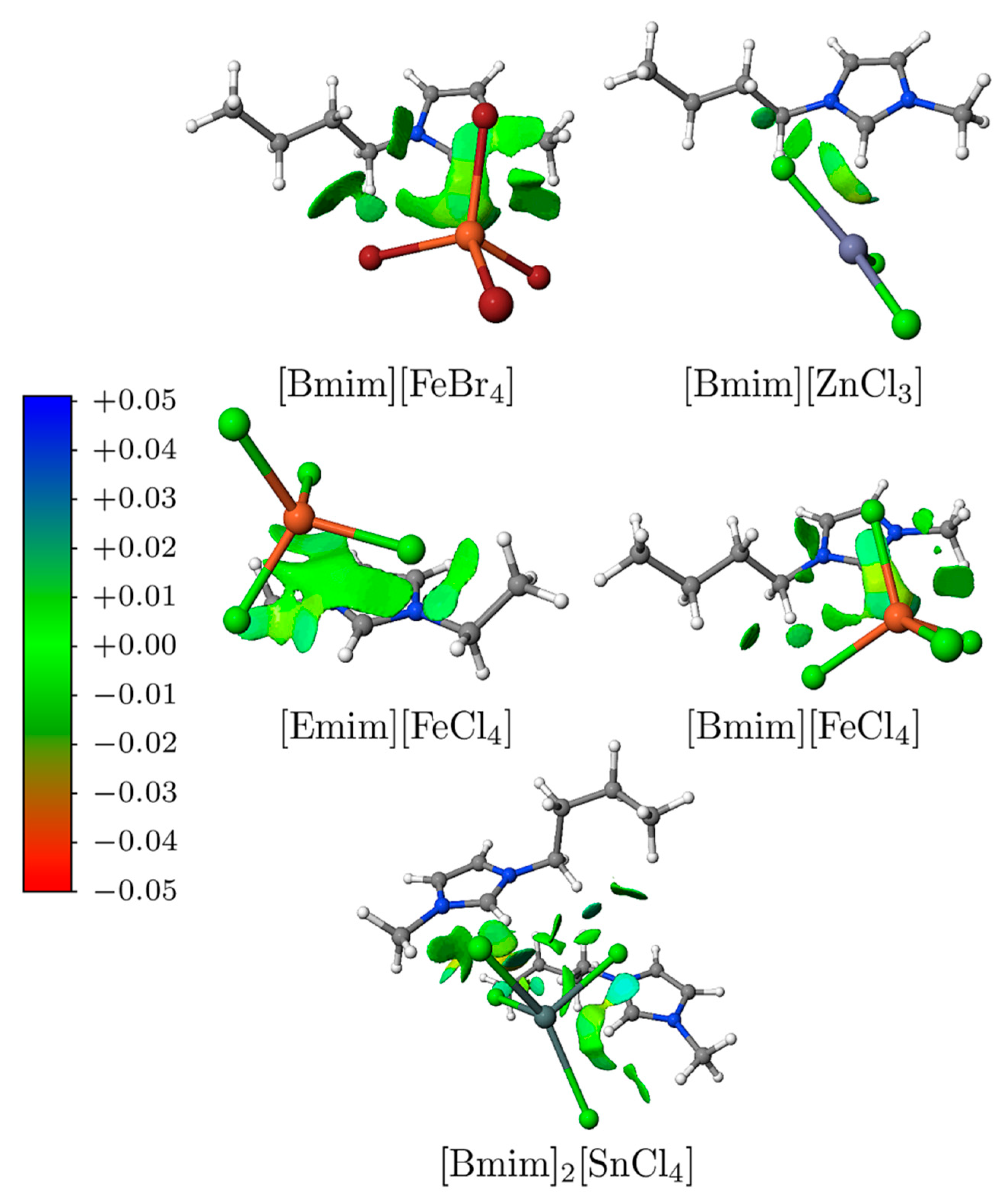
3.4. NCI Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Vekariya, R.L. A Review of Ionic Liquids: Applications towards Catalytic Organic Transformations. J. Mol. Liq. 2017, 227, 44. [Google Scholar] [CrossRef]
- Hallett, J.P.; Welton, T. Room-Temperature Ionic Liquids: Solvents for Synthesis and Catalysis. 2. Chem. Rev. 2011, 111, 3508–3576. [Google Scholar] [CrossRef]
- Zhao, Q.; Chu, H.; Zhao, B.; Liang, Z.; Zhang, L.; Zhang, Y. Advances of Ionic Liquids-Based Methods for Protein Analysis. Trends Anal. Chem. 2018, 108, 239–246. [Google Scholar] [CrossRef]
- Figueiredo, N.M.; Voroshylova, I.V.; Koverga, V.A.; Ferreira, E.S.C.; Cordeiro, M.N.D.S. Influence of Alcohols on the Inter-Ion Interactions in Ionic Liquids: A Molecular Dynamics Study. J. Mol. Liq. 2019, 294, 111538. [Google Scholar] [CrossRef]
- Bystrov, S.S.; Matveev, V.V.; Egorov, A.V.; Chernyshev, Y.S.; Konovalov, V.A.; Balevičius, V.; Chizhik, V.I. Translational Diffusion in a Set of Imidazolium-Based Ionic Liquids [Bmim]+A- and Their Mixtures with Water. J. Phys. Chem. B 2019, 123, 9187–9197. [Google Scholar] [CrossRef]
- Hayashi, S.; Hamaguchi, H.O. Discovery of a Magnetic Ionic Liquid [Bmim]FeCl4. Chem. Lett. 2004, 33, 1590–1591. [Google Scholar] [CrossRef]
- Clark, K.D.; Nacham, O.; Purslow, J.A.; Pierson, S.A.; Anderson, J.L. Magnetic Ionic Liquids in Analytical Chemistry: A Review. Anal. Chim. Acta 2016, 934, 9–21. [Google Scholar] [CrossRef] [PubMed]
- Zeng, S.; Liu, L.; Shang, D.; Feng, J.; Dong, H.; Xu, Q.; Zhang, X.; Zhang, S. Efficient and Reversible Absorption of Ammonia by Cobalt Ionic Liquids through Lewis Acid-Base and Cooperative Hydrogen Bond Interactions. Green Chem. 2018, 20, 2075–2083. [Google Scholar] [CrossRef]
- Panja, S.K.; Saha, S. Recyclable, Magnetic Ionic Liquid Bmim[FeCl4]-Catalyzed, Multicomponent, Solvent-Free, Green Synthesis of Quinazolines. RSC Adv. 2013, 3, 14495–14500. [Google Scholar] [CrossRef]
- Daniel, C.I.; Vaca Chávez, F.; Feio, G.; Portugal, C.A.M.; Crespo, J.G.; Sebastião, P.J. 1H NMR Relaxometry, Viscometry, and PFG NMR Studies of Magnetic and Nonmagnetic Ionic Liquids. J. Phys. Chem. B 2013, 117, 11877–11884. [Google Scholar] [CrossRef] [PubMed]
- Daniel, C.I.; Rubio, A.M.; Sebastião, P.J.; Afonso, C.A.M.; Storch, J.; Izák, P.; Portugal, C.A.M.; Crespo, J.G. Magnetic Modulation of the Transport of Organophilic Solutes through Supported Magnetic Ionic Liquid Membranes. J. Membr. Sci. 2016, 505, 36–43. [Google Scholar] [CrossRef]
- Santos, E.; Albo, J.; Irabien, A. Magnetic Ionic Liquids: Synthesis, Properties and Applications. RSC Adv. 2014, 4, 40008–40018. [Google Scholar] [CrossRef]
- Joseph, A.; Żyła, G.; Thomas, V.I.; Nair, P.R.; Padmanabhan, A.S.; Mathew, S. Paramagnetic Ionic Liquids for Advanced Applications: A Review. J. Mol. Liq. 2016, 218, 319–331. [Google Scholar] [CrossRef]
- Xun, S.; Zhu, W.; Zheng, D.; Zhang, L.; Liu, H.; Yin, S.; Zhang, M.; Li, H. Synthesis of Metal-Based Ionic Liquid Supported Catalyst and Its Application in Catalytic Oxidative Desulfurization of Fuels. Fuel 2014, 136, 358–365. [Google Scholar] [CrossRef]
- Ko, N.H.; Lee, J.S.; Huh, E.S.; Lee, H.; Jung, K.D.; Kim, H.S.; Cheong, M. Extractive Desulfurization Using Fe-Containing Ionic Liquids. Energy Fuels 2008, 22, 1687–1690. [Google Scholar] [CrossRef]
- Andevary, H.H.; Akbari, A.; Omidkhah, M. High Efficient and Selective Oxidative Desulfurization of Diesel Fuel Using Dual-Function [Omim]FeCl4 as Catalyst/Extractant. Fuel Process. Technol. 2019, 185, 8–17. [Google Scholar] [CrossRef]
- Yao, A.; Xiong, X.; Kang, M.; Guo, Y.; Chen, C.; Chu, T. Direct Dissolution of UO2 in Carboxyl-Functionalized Ionic Liquids in the Presence or Absence of Fe-Containing Ionic Liquids. Dalton Trans. 2020, 49, 14881–14890. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zeng, S.; Huo, F.; Shang, D.; He, H.; Bai, L.; Zhang, X.; Li, J. Metal Chloride Anion-Based Ionic Liquids for Efficient Separation of NH3. J. Clean. Prod. 2019, 206, 661–669. [Google Scholar] [CrossRef]
- Yue, Q.F.; Yang, H.G.; Zhang, M.L.; Bai, X.F. Metal-Containing Ionic Liquids: Highly Effective Catalysts for Degradation of Poly(Ethylene Terephthalate). Adv. Mater. Sci. Eng. 2014, 2014, e454756. [Google Scholar] [CrossRef] [Green Version]
- Clark, K.D.; Nacham, O.; Yu, H.; Li, T.; Yamsek, M.M.; Ronning, D.R.; Anderson, J.L. Extraction of DNA by Magnetic Ionic Liquids: Tunable Solvents for Rapid and Selective DNA Analysis. Anal. Chem. 2015, 87, 1552–1559. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.; Yu, J.; Qazi, A.B.; Zhang, L.; Liu, X. Metal-Based Ionic Liquids in Oxidative Desulfurization: A Critical Review. Environ. Sci. Technol. 2021, 55, 1419–1435. [Google Scholar] [CrossRef]
- Albo, J.; Santos, E.; Neves, L.A.; Simeonov, S.P.; Afonso, C.A.M.; Crespo, J.G.; Irabien, A. Separation Performance of CO 2 through Supported Magnetic Ionic Liquid Membranes (SMILMs). Sep. Purif. Technol. 2012, 97, 26–33. [Google Scholar] [CrossRef]
- He, X.; Qiang, W.; Wu, J.; Shao, Q.; Cao, P.; Cheng, L.; Zhang, X.; Deng, Y. Manipulation of Magnetic Ionic Liquid Droplets and Their Application in Energy Harvesting. J. Phys. Appl. Phys. 2017, 50, 465002. [Google Scholar] [CrossRef] [Green Version]
- Saha, A.; Payra, S.; Asatkar, A.; Patel, A.R.; Banerjee, S. [AcMIM]FeCl4: A Magnetically Separable Organocatalyst for the Clean Synthesis of Tetrahydrobenzo[b]Pyran Derivatives. Curr. Organocatalysis 2018, 6, 177–182. [Google Scholar] [CrossRef] [Green Version]
- Sadjadi, S. Magnetic (Poly) Ionic Liquids: A Promising Platform for Green Chemistry. J. Mol. Liq. 2021, 323, 114994. [Google Scholar] [CrossRef]
- Getsis, A.; Balke, B.; Felser, C.; Mudring, A.V. Dysprosium-Based Ionic Liquid Crystals: Thermal, Structural, Photo- and Magnetophysical Properties. Cryst. Growth Des. 2009, 9, 4429–4437. [Google Scholar] [CrossRef]
- Grimme, S. Improved Second-Order Møller-Plesset Perturbation Theory by Separate Scaling of Parallel- and Antiparallel-Spin Pair Correlation Energies. J. Chem. Phys. 2003, 118, 9095–9102. [Google Scholar] [CrossRef]
- Raghavachari, K.; Trucks, G.W.; Pople, J.A.; Head-Gordon, M. A Fifth-Order Perturbation Comparison of Electron Correlation Theories. Chem. Phys. Lett. 1989, 157, 479–483. [Google Scholar] [CrossRef]
- Bartlett, R.J.; Musiał, M. Coupled-Cluster Theory in Quantum Chemistry. Rev. Mod. Phys. 2007, 79, 291–352. [Google Scholar] [CrossRef] [Green Version]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef] [Green Version]
- Parker, T.M.; Burns, L.A.; Parrish, R.M.; Ryno, A.G.; Sherrill, C.D. Levels of Symmetry Adapted Perturbation Theory (SAPT). I. Efficiency and Performance for Interaction Energies. J. Chem. Phys. 2014, 140, 094106. [Google Scholar] [CrossRef]
- Gonthier, J.F.; Sherrill, C.D. Density-Fitted Open-Shell Symmetry-Adapted Perturbation Theory and Application to π-Stacking in Benzene Dimer Cation and Ionized DNA Base Pair Steps. J. Chem. Phys. 2016, 145, 134106. [Google Scholar] [CrossRef] [PubMed]
- Son, C.Y.; McDaniel, J.G.; Schmidt, J.R.; Cui, Q.; Yethiraj, A. First-Principles United Atom Force Field for the Ionic Liquid BMIM+BF4-: An Alternative to Charge Scaling. J. Phys. Chem. B 2016, 120, 3560–3568. [Google Scholar] [CrossRef]
- Pádua, A.A.H. Resolving Dispersion and Induction Components for Polarisable Molecular Simulations of Ionic Liquids. J. Chem. Phys. 2017, 146, 204501. [Google Scholar] [CrossRef] [Green Version]
- Grimme, S.; Hujo, W.; Kirchner, B. Performance of Dispersion-Corrected Density Functional Theory for the Interactions in Ionic Liquids. Phys. Chem. Chem. Phys. 2012, 14, 4875–4883. [Google Scholar] [CrossRef] [PubMed]
- Izgorodina, E.I.; Golze, D.; Maganti, R.; Armel, V.; Taige, M.; Schubert, T.J.S.; Macfarlane, D.R. Importance of Dispersion Forces for Prediction of Thermodynamic and Transport Properties of Some Common Ionic Liquids. Phys. Chem. Chem. Phys. 2014, 16, 7209–7221. [Google Scholar] [CrossRef] [PubMed]
- Goloviznina, K.; Canongia Lopes, J.N.; Costa Gomes, M.; Pádua, A.A.H. A Transferable, Polarisable Force Field for Ionic Liquids. J. Chem. Theory Comput. 2019, 15, 5858–5871. [Google Scholar] [CrossRef]
- Zuchowski, P.S.; Podeszwa, R.; Moszyński, R.; Jeziorski, B.; Szalewicz, K. Symmetry-Adapted Perturbation Theory Utilizing Density Functional Description of Monomers for High-Spin Open-Shell Complexes. J. Chem. Phys. 2008, 129, 084101. [Google Scholar] [CrossRef]
- Cybulski, H.; Zuchowski, P.S.; Fernández, B.; Sadlej, J. The Water-Nitric Oxide Intermolecular Potential-Energy Surface Revisited. J. Chem. Phys. 2009, 130, 104303. [Google Scholar] [CrossRef]
- Hapka, M.; Zuchowski, P.S.; Szczęśniak, M.M.; Chałasiński, G. Symmetry-Adapted Perturbation Theory Based on Unrestricted Kohn-Sham Orbitals for High-Spin Open-Shell van Der Waals Complexes. J. Chem. Phys. 2012, 137, 164104. [Google Scholar] [CrossRef]
- Stasyuk, O.A.; Sedlak, R.; Guerra, C.F.; Hobza, P. Comparison of the DFT-SAPT and Canonical EDA Schemes for the Energy Decomposition of Various Types of Noncovalent Interactions. J. Chem. Theory Comput. 2018, 14, 3440–3450. [Google Scholar] [CrossRef]
- Podeszwa, R.; Bukowski, R.; Rice, B.M.; Szalewicz, K. Potential Energy Surface for Cyclotrimethylene Trinitramine Dimer from Symmetry-Adapted Perturbation Theory. Phys. Chem. Chem. Phys. 2007, 9, 5561–5569. [Google Scholar] [CrossRef]
- Smith, D.G.A.; Burns, L.A.; Simmonett, A.C.; Parrish, R.M.; Schieber, M.C.; Galvelis, R.; Kraus, P.; Kruse, H.; Di Remigio, R.; Alenaizan, A.; et al. P SI4 1.4: Open-Source Software for High-Throughput Quantum Chemistry. J. Chem. Phys. 2020, 152, 184108. [Google Scholar] [CrossRef] [PubMed]
- Schneider, W.B.; Bistoni, G.; Sparta, M.; Saitow, M.; Riplinger, C.; Auer, A.A.; Neese, F. Decomposition of Intermolecular Interaction Energies within the Local Pair Natural Orbital Coupled Cluster Framework. J. Chem. Theory Comput. 2016, 12, 4778–4792. [Google Scholar] [CrossRef]
- Hansen, A.; Liakos, D.G.; Neese, F. Efficient and Accurate Local Single Reference Correlation Methods for High-Spin Open-Shell Molecules Using Pair Natural Orbitals. J. Chem. Phys. 2011, 135, 214102. [Google Scholar] [CrossRef] [PubMed]
- Neese, F. The ORCA Program System. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef] [PubMed]
- Tan, S.Y.S.; Izgorodina, E.I. Comparison of the Effective Fragment Potential Method with Symmetry-Adapted Perturbation Theory in the Calculation of Intermolecular Energies for Ionic Liquids. J. Chem. Theory Comput. 2016, 12, 2553–2568. [Google Scholar] [CrossRef] [PubMed]
- Riplinger, C.; Neese, F. An Efficient and near Linear Scaling Pair Natural Orbital Based Local Coupled Cluster Method. J. Chem. Phys. 2013, 138, 034106. [Google Scholar] [CrossRef] [PubMed]
- Riplinger, C.; Sandhoefer, B.; Hansen, A.; Neese, F. Natural Triple Excitations in Local Coupled Cluster Calculations with Pair Natural Orbitals. J. Chem. Phys. 2013, 139, 134101. [Google Scholar] [CrossRef] [PubMed]
- Altun, A.; Neese, F.; Bistoni, G. Local Energy Decomposition Analysis of Hydrogen-Bonded Dimers within a Domain-Based Pair Natural Orbital Coupled Cluster Study. Beilstein J. Org. Chem. 2018, 14, 919–929. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Contreras-García, J.; Johnson, E.R.; Keinan, S.; Chaudret, R.; Piquemal, J.P.; Beratan, D.N.; Yang, W. NCIPLOT: A Program for Plotting Noncovalent Interaction Regions. J. Chem. Theory Comput. 2011, 7, 625–632. [Google Scholar] [CrossRef] [PubMed]
- Laplaza, R.; Peccati, F.; Boto, R.A.; Quan, C.; Carbone, A.; Piquemal, J.P.; Maday, Y.; Contreras-García, J. NCIPLOT and the Analysis of Noncovalent Interactions Using the Reduced Density Gradient. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2021, 11, 1–18. [Google Scholar] [CrossRef]
- González-Veloso, I.; Rodríguez-Otero, J.; Cabaleiro-Lago, E.M. Endohedral Alkali Cations Promote Charge Transfer Transitions in Complexes of C60 with [10]Cycloparaphenylenes. Phys. Chem. Chem. Phys. 2019, 21, 16665–16675. [Google Scholar] [CrossRef] [PubMed]
- Jmol: An Open-Source Java Viewer for Chemical Structures in 3D. Available online: http://Www.Jmol.Org/ (accessed on 14 February 2021).
- Philippi, F.; Welton, T. Targeted Modifications in Ionic Liquids—From Understanding to Design. Phys. Chem. Chem. Phys. 2021, 23, 6993–7021. [Google Scholar] [CrossRef]
- Kirchner, B.; Malberg, F.; Firaha, D.S.; Hollóczki, O. Ion Pairing in Ionic Liquids. J. Phys. Condens. Matter 2015, 27, 463002. [Google Scholar] [CrossRef] [PubMed]
- Kirchner, B.; Hollóczki, O.; Canongia Lopes, J.N.; Pádua, A.A.H. Multiresolution Calculation of Ionic Liquids. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2015, 5, 202–214. [Google Scholar] [CrossRef]
- Rackers, J.A.; Ponder, J.W. Classical Pauli Repulsion: An Anisotropic, Atomic Multipole Model. J. Chem. Phys. 2019, 150, 1–22. [Google Scholar] [CrossRef]
- Zahn, S.; Bruns, G.; Thar, J.; Kirchner, B. What Keeps Ionic Liquids in Flow? Phys. Chem. Chem. Phys. 2008, 10, 6921–6924. [Google Scholar] [CrossRef]
- Pinter, B.; Fievez, T.; Bickelhaupt, F.M.; Geerlings, P.; De Proft, F. On the Origin of the Steric Effect. Phys. Chem. Chem. Phys. 2012, 14, 9846–9854. [Google Scholar] [CrossRef] [PubMed]
- Matthews, R.P.; Welton, T.; Hunt, P.A. Competitive Pi Interactions and Hydrogen Bonding within Imidazolium Ionic Liquids. Phys. Chem. Chem. Phys. 2014, 16, 3238–3253. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Qi, C.-S.; Wu, X.-M.; Rong, H.; Gong, L.-F. Relationship between Melting Point and the Interaction Energy of Alkyl Imidazolium Tetrafluoroborate Ionic Liquids. Acta Phys. Chim. Sin. 2011, 27, 2059–2064. [Google Scholar]
- Boto, R.A.; Peccati, F.; Laplaza, R.; Quan, C.; Carbone, A.; Piquemal, J.P.; Maday, Y.; Contreras-García, J. NCIPLOT4: Fast, Robust, and Quantitative Analysis of Noncovalent Interactions. J. Chem. Theory Comput. 2020, 16, 4150–4158. [Google Scholar] [CrossRef] [PubMed]

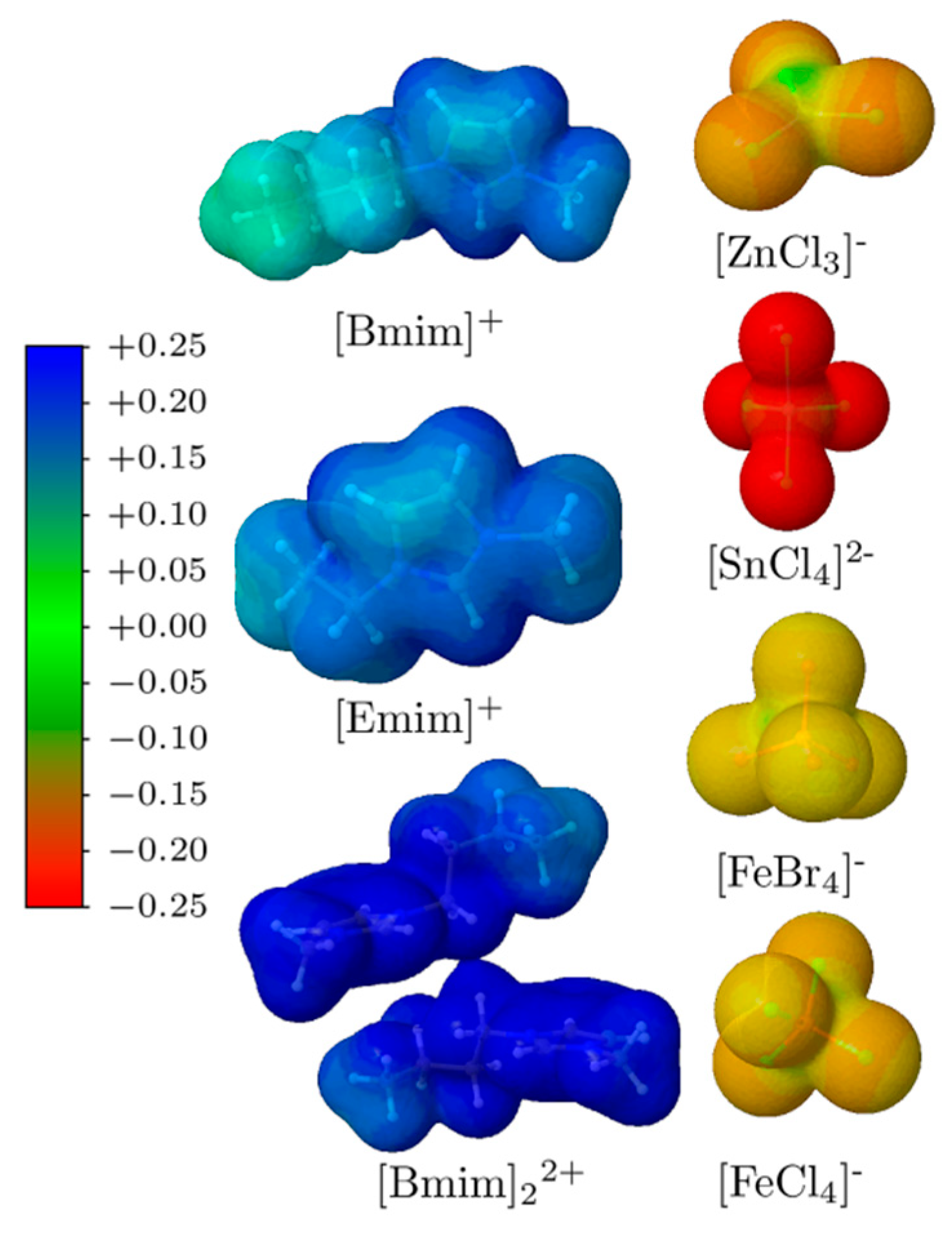
| System | Dist (Å) | Eelec | Eexch | Eind | Edisp | Etot | ECCSD(T) |
|---|---|---|---|---|---|---|---|
| [Emim][FeCl4] | 4.016 | −75.88 | +19.29 | −7.45 | −12.24 | −76.28 | −73.24 |
| [Bmim][FeCl4] | 4.273 | −70.97 | +16.63 | −8.83 | −10.79 | −73.95 | −71.52 |
| [Bmim][FeBr4] | 4.342 | −71.66 | +19.60 | −9.36 | −13.17 | −74.60 | −71.09 |
| [Bmim][ZnCl3] | 4.574 | −69.92 | +13.94 | −8.69 | −7.58 | −72.25 | −70.27 |
| [Bmim]2[SnCl4] | 3.513 | −280.07 | +77.82 | −34.73 | −33.52 | −270.50 | −259.30 |
| System | Dist (Å) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| [Emim][FeCl4] | 4.016 | −6.20 | −0.75 | −28.15 | −114.87 | −10.48 | −1.66 | +61.62 | +27.24 |
| [Bmim][FeCl4] | 4.273 | −5.45 | −0.81 | −31.21 | −111.63 | −9.77 | −1.51 | +58.61 | +30.26 |
| [Bmim][FeBr4] | 4.342 | −5.64 | −0.97 | −31.15 | −119.78 | −11.63 | −1.62 | +70.42 | +29.27 |
| [Bmim][ZnCl3] | 4.574 | −3.67 | −0.65 | −31.58 | −106.62 | −7.75 | −1.13 | +49.71 | +31.42 |
| [Bmim]2[SnCl4] | 3.513 | −15.06 | −1.73 | −102.20 | −426.83 | −35.73 | −4.96 | +225.63 | +101.57 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
González-Veloso, I.; Figueiredo, N.M.; Cordeiro, M.N.D.S. Unravelling the Interactions of Magnetic Ionic Liquids by Energy Decomposition Schemes: Towards a Transferable Polarizable Force Field. Molecules 2021, 26, 5526. https://doi.org/10.3390/molecules26185526
González-Veloso I, Figueiredo NM, Cordeiro MNDS. Unravelling the Interactions of Magnetic Ionic Liquids by Energy Decomposition Schemes: Towards a Transferable Polarizable Force Field. Molecules. 2021; 26(18):5526. https://doi.org/10.3390/molecules26185526
Chicago/Turabian StyleGonzález-Veloso, Iván, Nádia M. Figueiredo, and M. Natália D. S. Cordeiro. 2021. "Unravelling the Interactions of Magnetic Ionic Liquids by Energy Decomposition Schemes: Towards a Transferable Polarizable Force Field" Molecules 26, no. 18: 5526. https://doi.org/10.3390/molecules26185526
APA StyleGonzález-Veloso, I., Figueiredo, N. M., & Cordeiro, M. N. D. S. (2021). Unravelling the Interactions of Magnetic Ionic Liquids by Energy Decomposition Schemes: Towards a Transferable Polarizable Force Field. Molecules, 26(18), 5526. https://doi.org/10.3390/molecules26185526







