Molecular Recognition and Self-Organization in Life Phenomena Studied by a Statistical Mechanics of Molecular Liquids, the RISM/3D-RISM Theory
Abstract
1. Introduction
2. Brief Review of the 3D-RISM/RISM Theory
3. Molecular Recognition in Life Phenomena
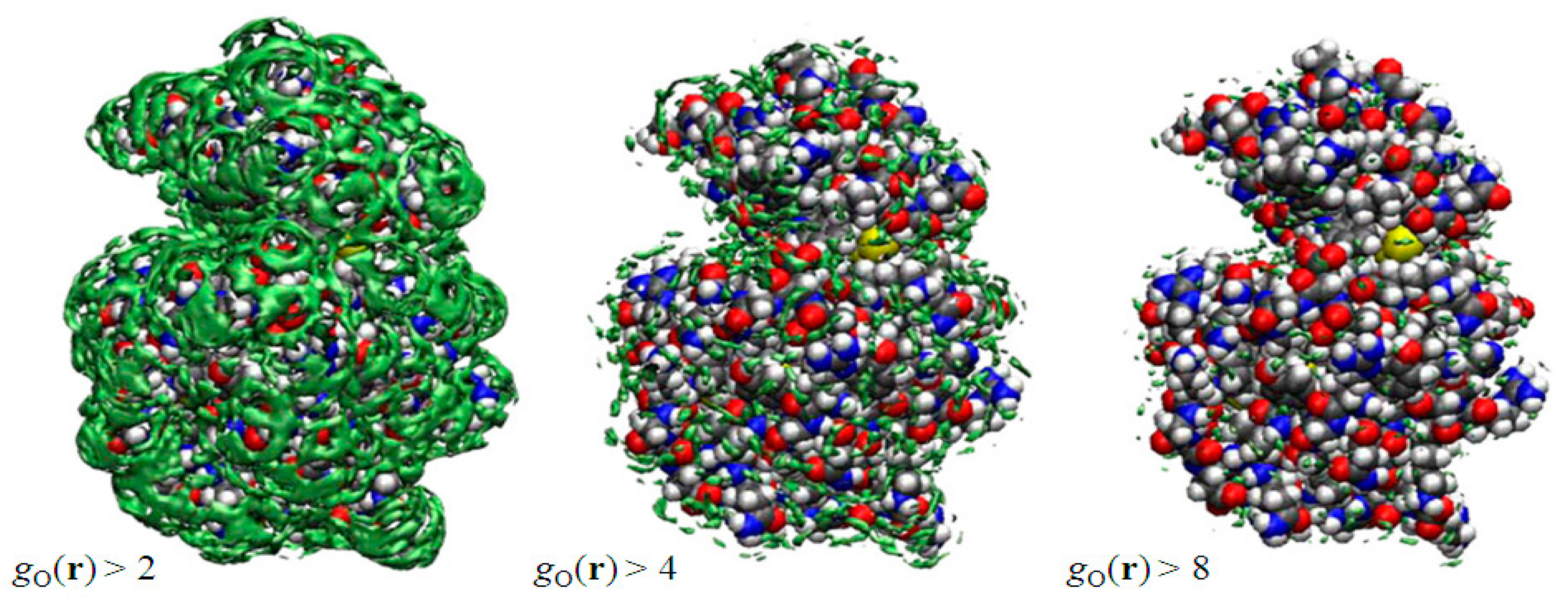
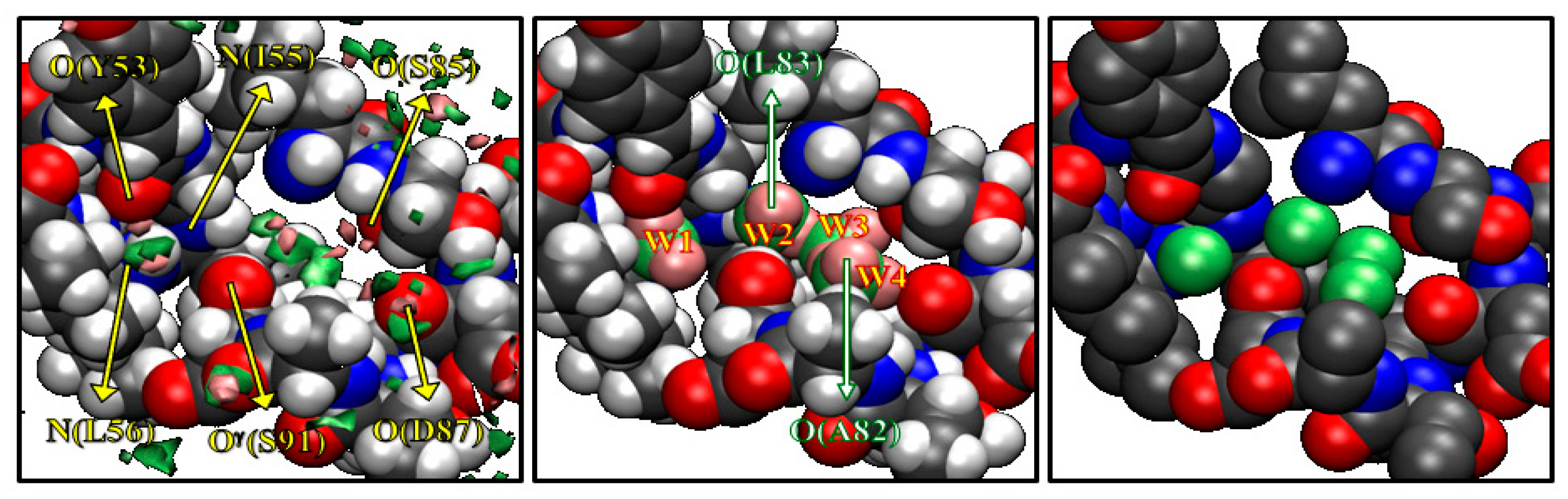
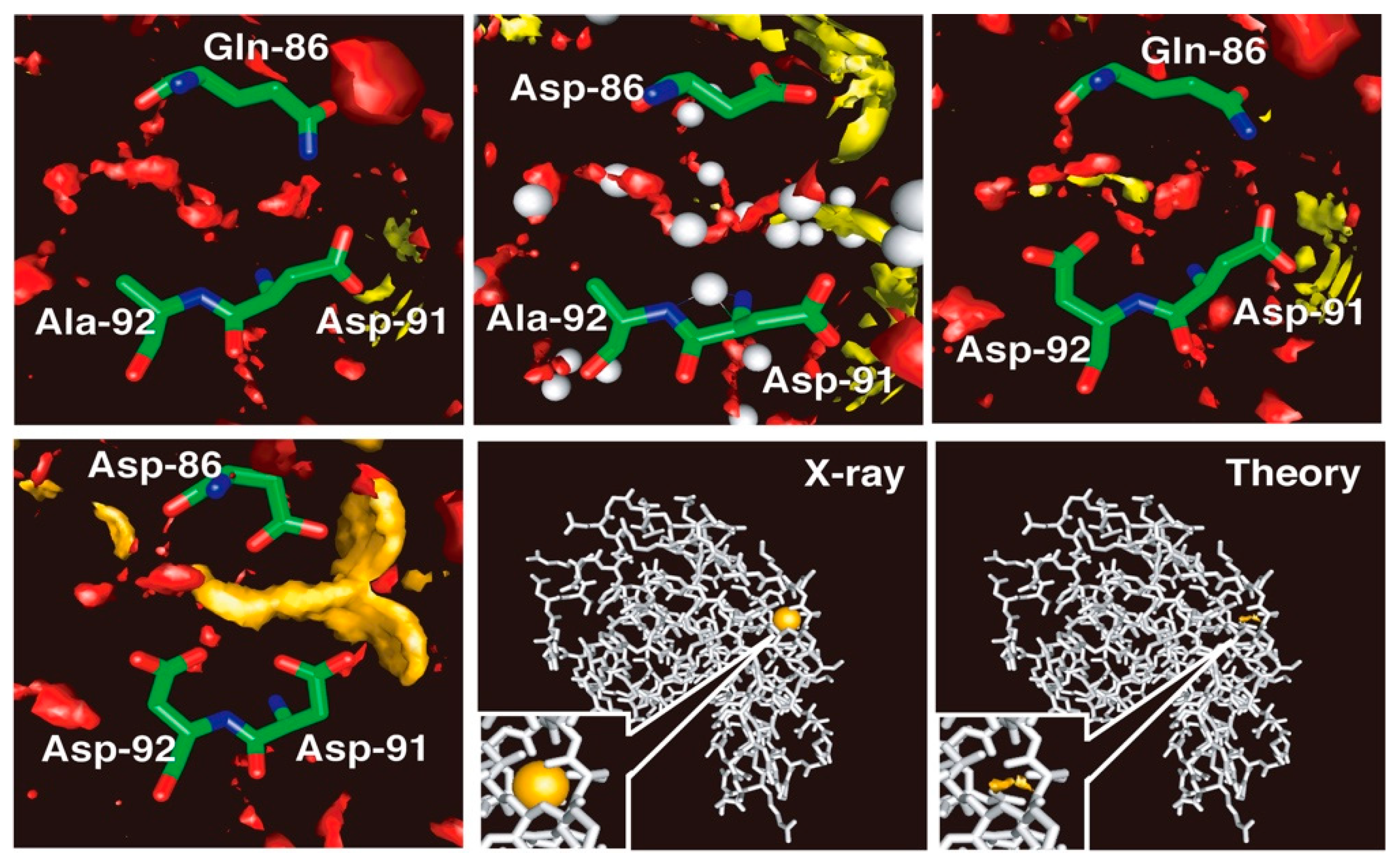
3.1. Recognition of Water Molecules by Protein
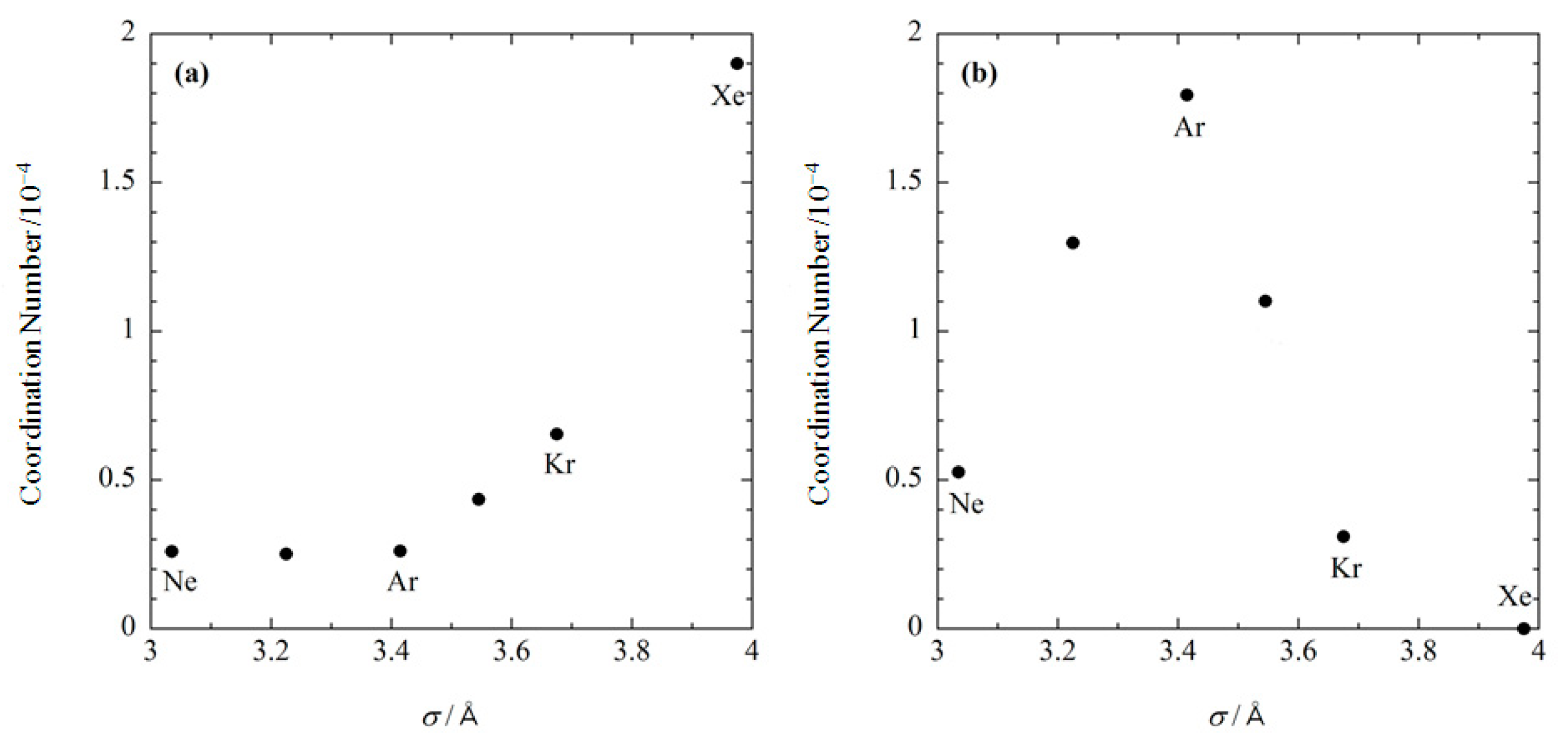
3.2. Noble Gas Recognized by Protein
3.3. Selective Ion-Binding by Protein
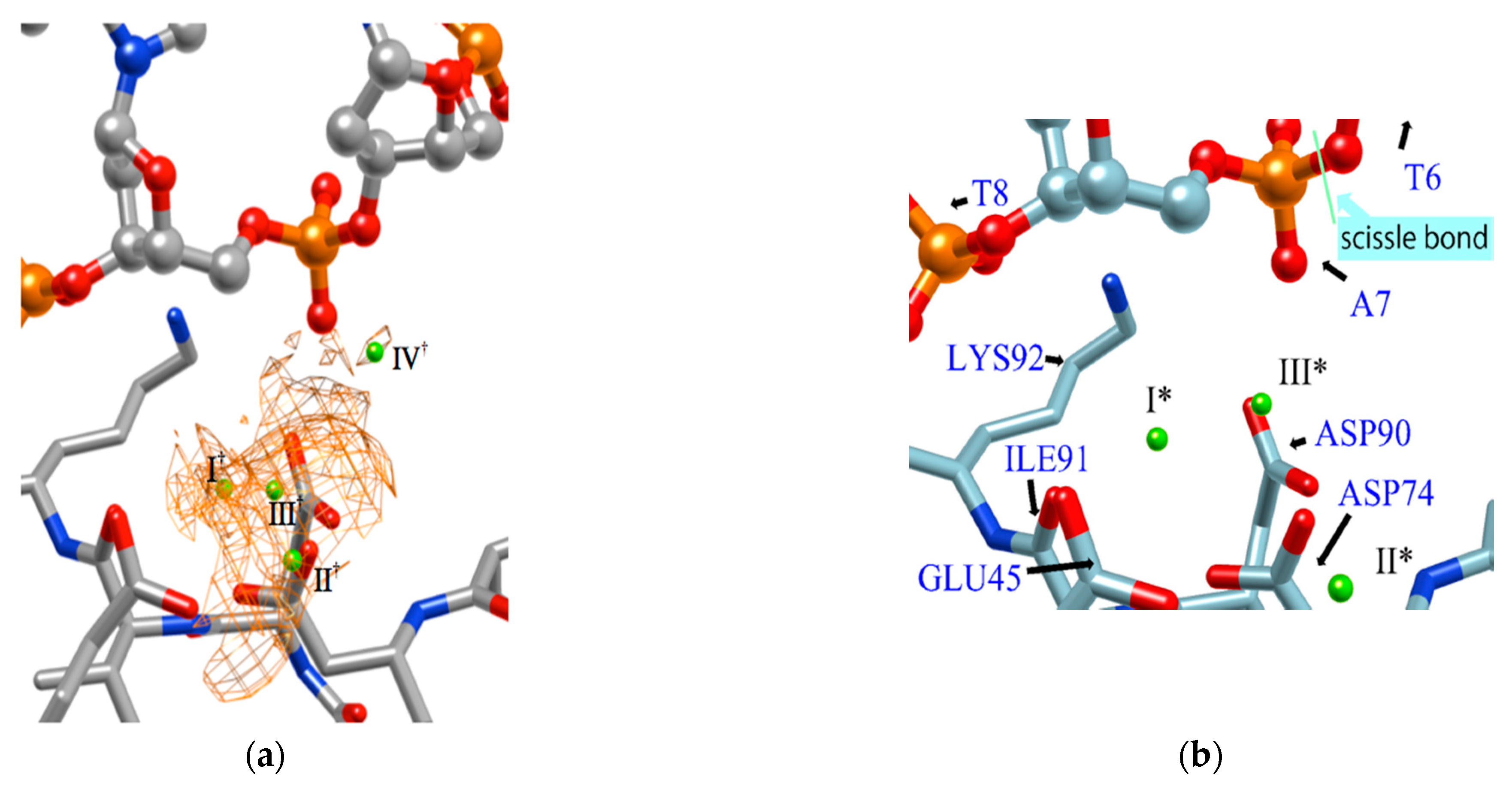
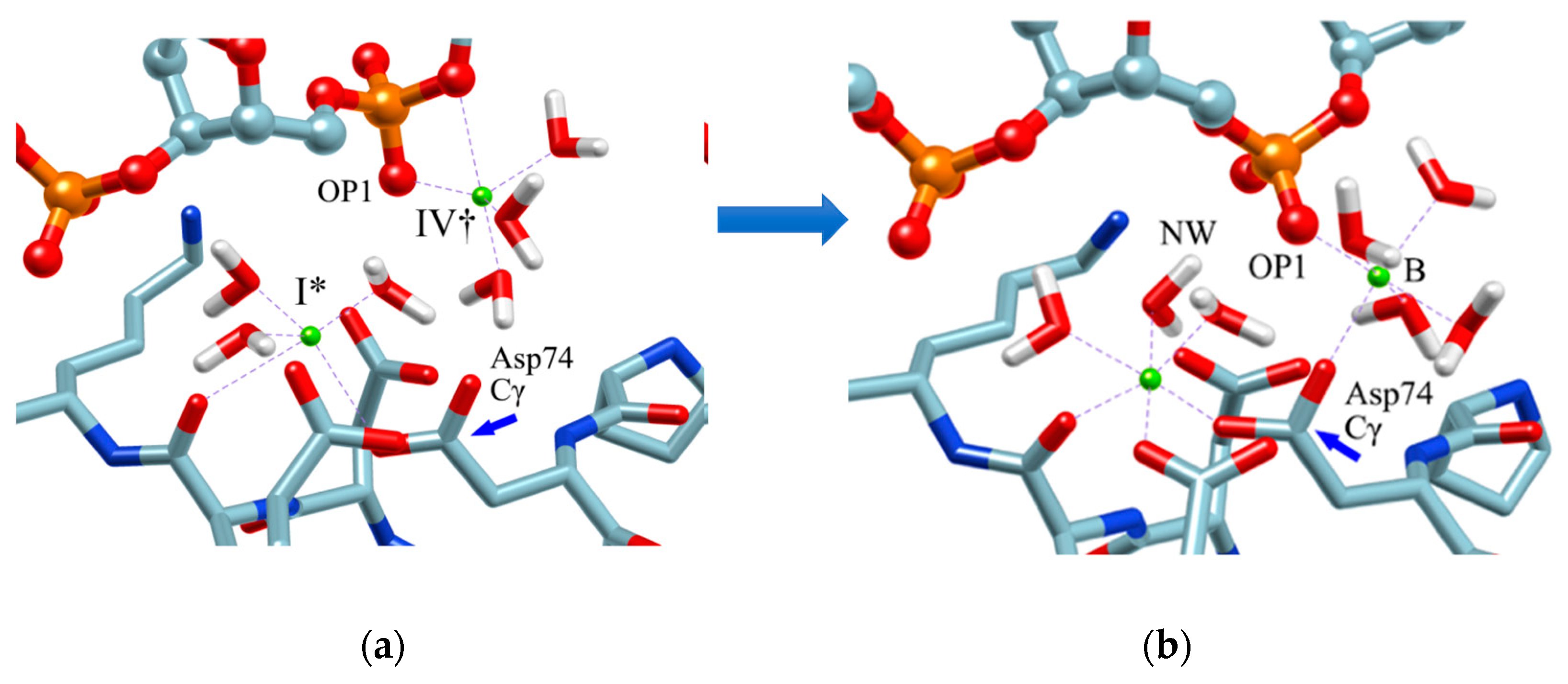
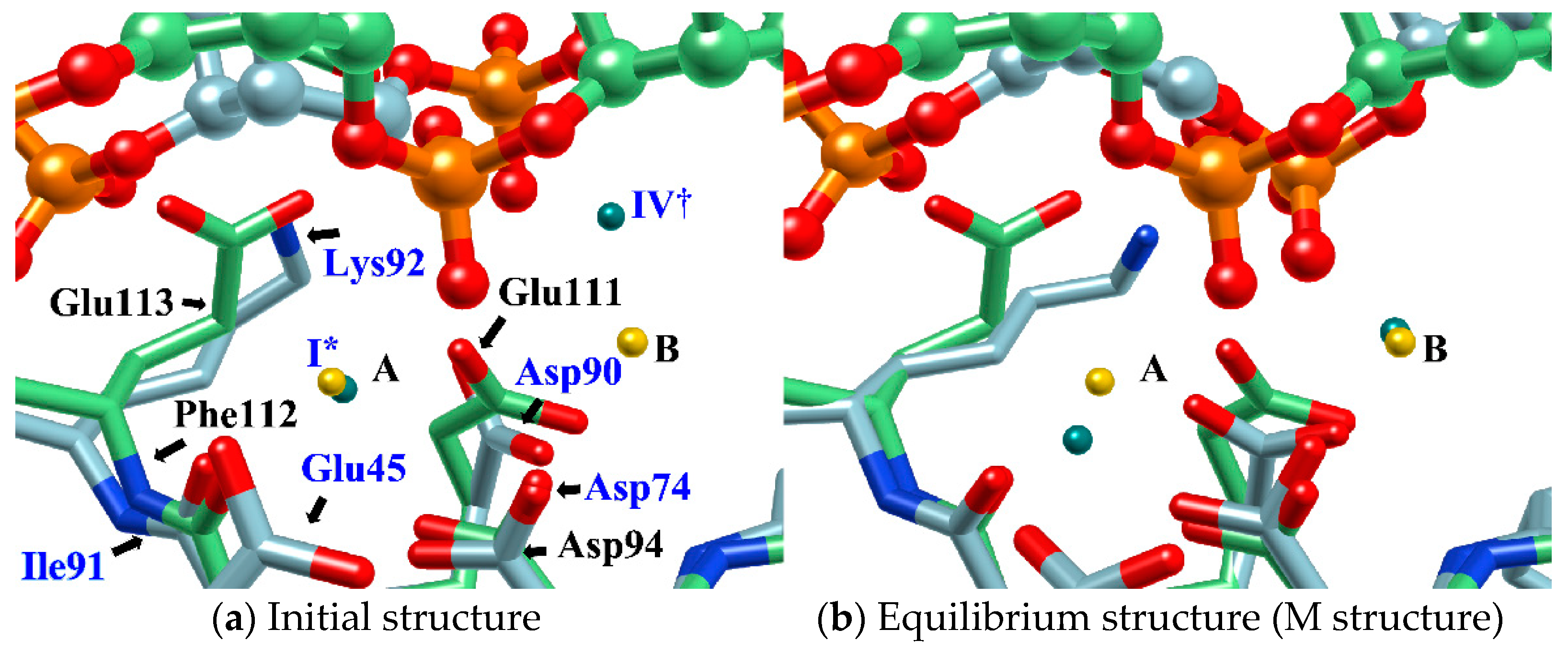
3.4. Molecular Recognition in an Enzymatic Reaction: Role of Mg2+ Ions in DNA Hydrolysis Reaction by Restriction Enzyme EcoRV
- The phosphate group (scissile phosphate group) involved in DNA cleavage was twisted, and moved to the position suitable for nucleophilic attack.
- The Mg2+ ion at the position IV† moved to position “B” in the figure, and a water molecule serving as the substrate was placed at the proper position in the reaction.
- The position and orientation of one water molecule changed, and it moved to the position where it could act as a nucleophile.
3.5. Molecular Recognition in Drug Screening
4. Structural Fluctuation and Reorganization of Protein in Water
4.1. The Theory of Structural Fluctuation of Protein
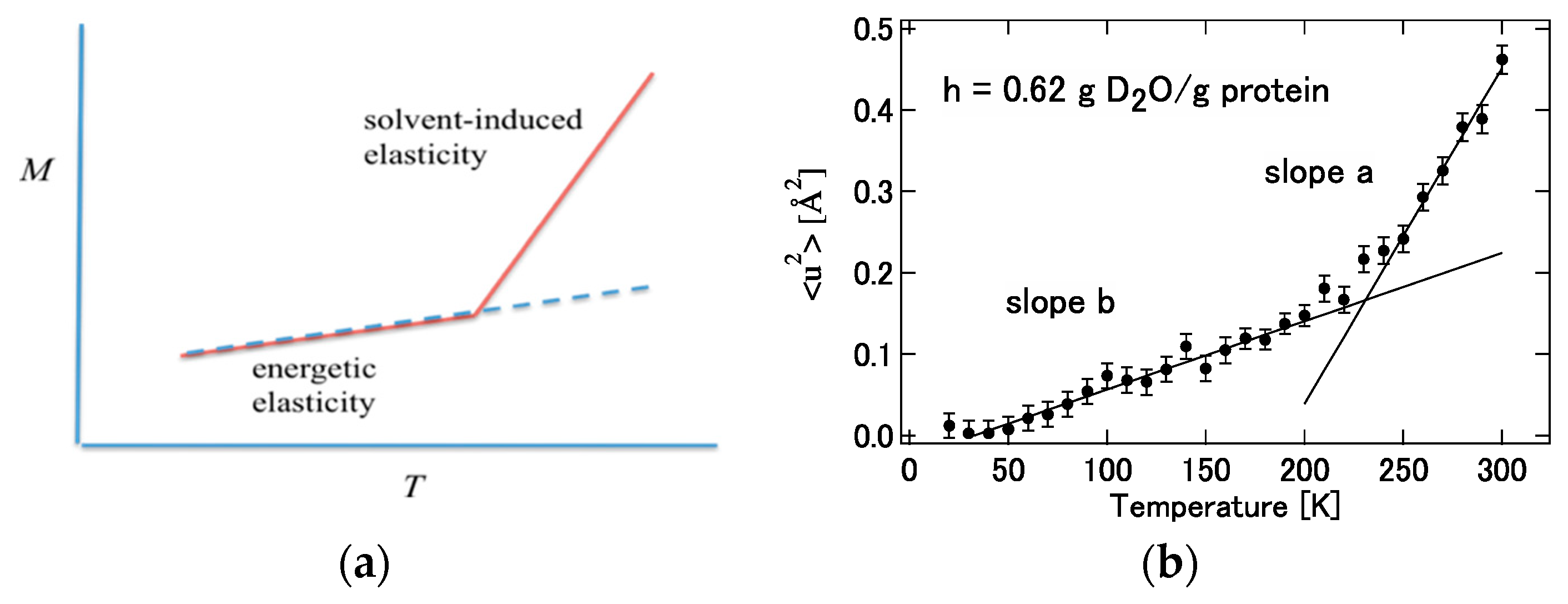
4.2. Incoherent Elastic Neutron Scattering
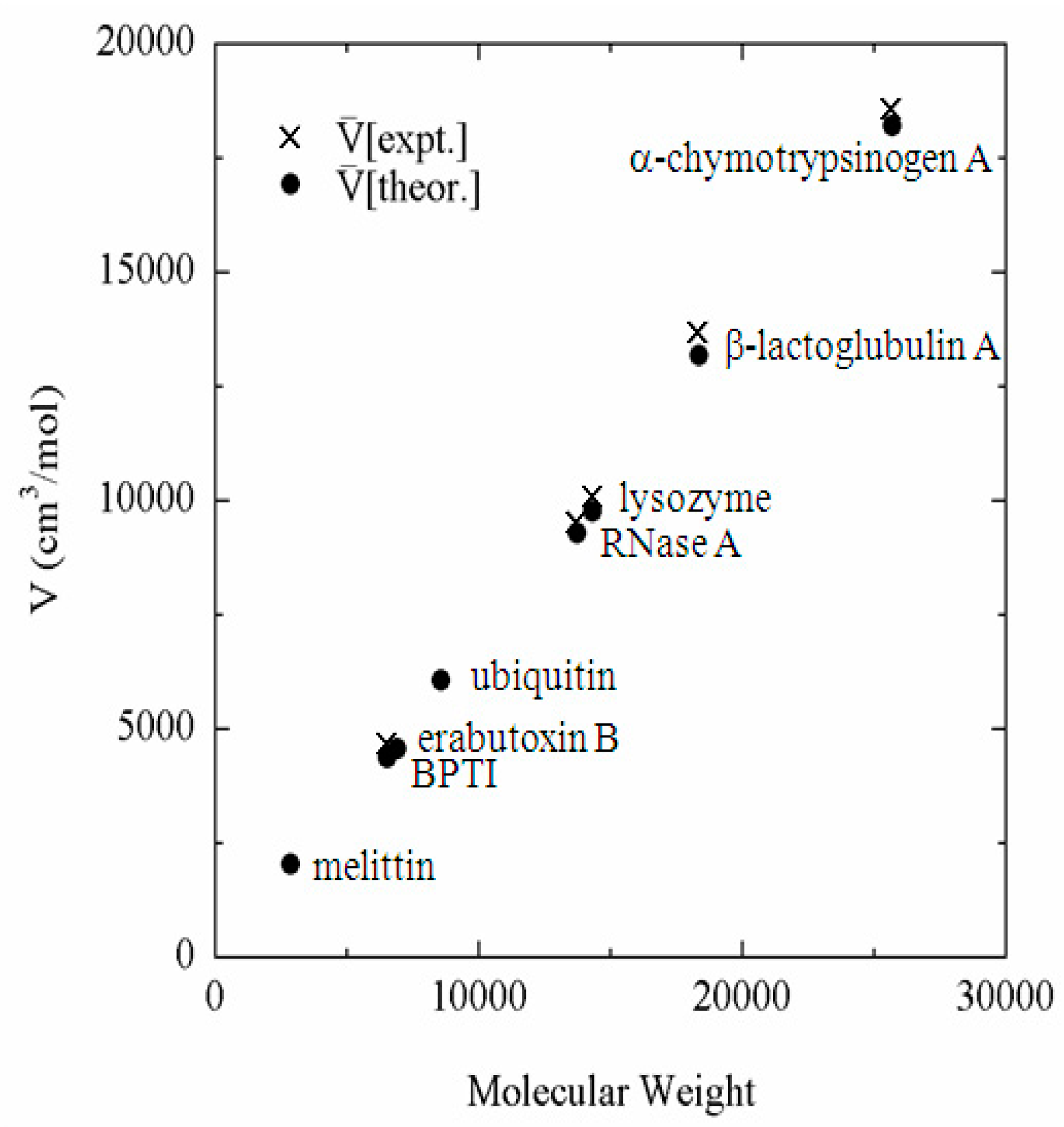
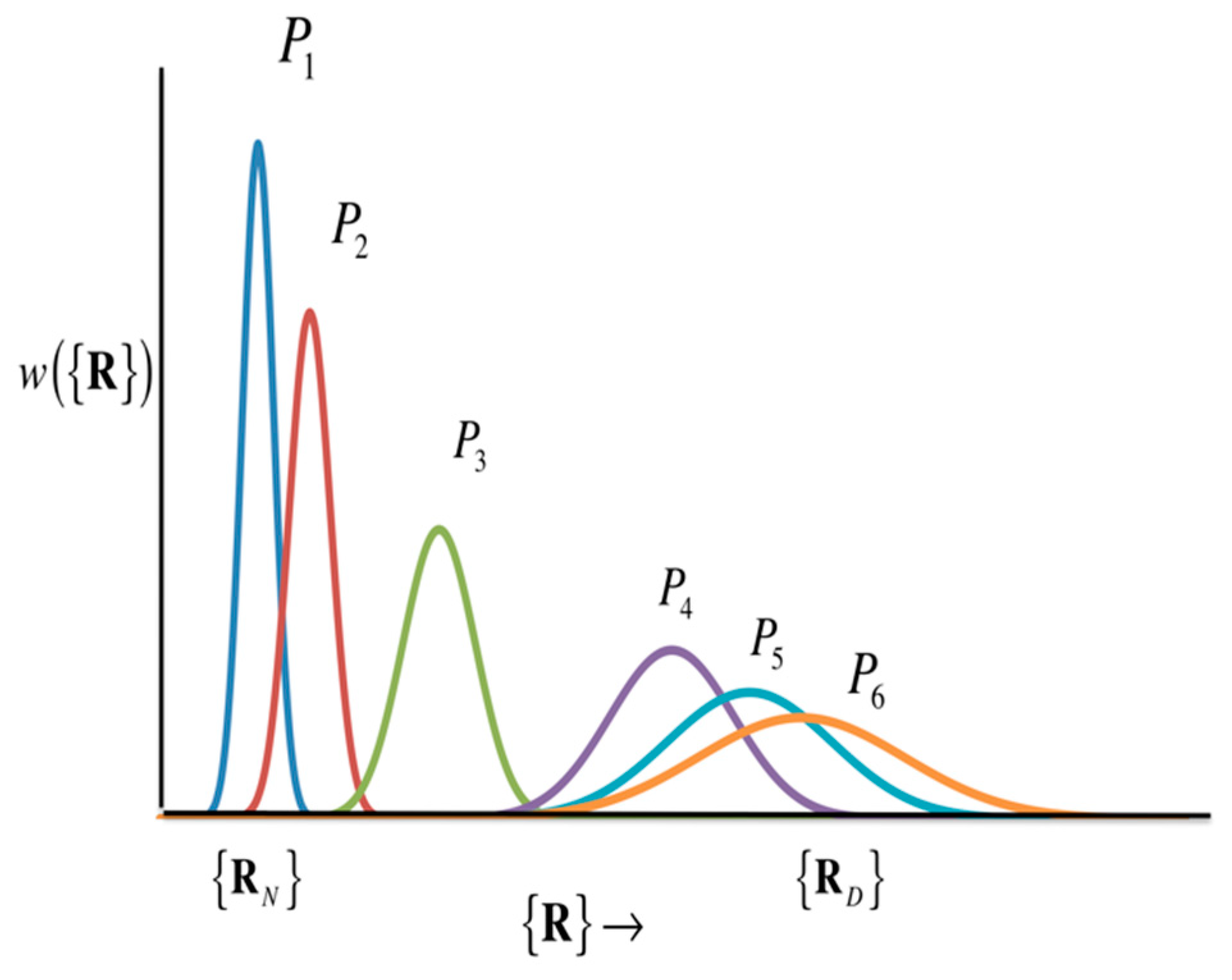
5. Protein Folding as an Example of Self-Organization Process
6. Summary and Perspective
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lehn, J.-M. From Molecular Recognition towards Molecular Information Processing and Self-Organization. Angewante Chem. 1990, 29, 1304–1319. [Google Scholar] [CrossRef]
- Hirata, F. Exploring Life Phenomena with Statistical Mechanics of Molecular Liquids; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Michaelis, L.; Menten, M. Die kinetik der invertinwirkung. Biochem. Z 1913, 49, 333–369. [Google Scholar]
- Preston, G.M.; Carroll, T.P.; Guggino, W.B.; Agre, P. Appearance of water channels in Xenopus oocytes expressing red cell CHIP28 protein. Science 1992, 256, 385–387. [Google Scholar] [CrossRef]
- Doyle, D.A.; Cabral, J.M.; Pfuetzner, R.A.; Kuo, A.; Gulbis, J.M.; Cohen, S.L.; Chait, B.T.; MacKinnon, R. The structure of the potassium channel: Molecular basis of K+ conduction and selectivity. Science 1998, 280, 69–77. [Google Scholar] [CrossRef]
- Phongphanphanee, S.; Yoshida, N.; Oiki, S.; Hirata, F. The ‘Ambivalent’ Snug-fit Sites in the KcsA Potassium Channel Probed by 3D-RISM Theory. Pure Appl. Chem. 2014, 86, 97–104. [Google Scholar] [CrossRef][Green Version]
- Phongphanphanee, S.; Yoshida, N.; Hirata, F. On the proton exclusion of aquaporins: A statistical mechanics study. J. Am. Chem. Soc. 2008, 130, 1540–1541. [Google Scholar] [CrossRef]
- Phongphanphanee, S.; Rungrotmongkol, T.; Yoshida, N.; Hannonbua, S.; Hirata, F. Proton transport through the influenza A M2 channel: Three-dimensional reference interaction site model study. J. Am. Chem. Soc. 2010, 132, 9782–9788. [Google Scholar] [CrossRef]
- Imai, T.; Oda, K.; Kovalenko, A.; Hirata, F.; Kidera, A. Ligand mapping on protein surfaces by the 3D-RISM theory: Toward Computational Fragment-based Drug Design. J. Am. Chem. Soc. 2009, 131, 12430–12440. [Google Scholar] [CrossRef] [PubMed]
- Imai, T.; Isogai, H.; Seto, T.; Kovalenko, A.; Hirata, F. Theoretical Study of Volume Changes Accompanying Xenon-Lysozyme Binding: Implications for the Molecular Mechanism of Pressure Reversal of Anesthesia. J. Phys. Chem. B 2006, 110, 12149–12154. [Google Scholar] [CrossRef] [PubMed]
- Kiyota, Y.; Yoshida, N.; Hirata, F. A New Approach for Investigating the Molecular Recognition of Protein: Toward Structural-Based Drug Design Based on the 3D-RISM Theory. J. Chem. Theor. Comp. 2011, 7, 3803–3815. [Google Scholar] [CrossRef] [PubMed]
- Phanich, J.; Rungrotmongkol, T.; Sindhikara, D.; Phongphanphanee, S.; Yoshida, N.; Hirata, F.; Kungwan, N.; Spot Hannongbua, S. A 3D-RISM/RISM Study of the Oseltamivir Binding Efficiency with the Wild-type and Resistance-Associated Mutant Forms of the Viral Influenza B Neuraminidase. Protein Sci. 2016, 25, 147–158. [Google Scholar] [CrossRef] [PubMed]
- Sugita, M.; Hamano, M.; Kasahara, K.; Kikuchi, T.; Hirata, F. New Protocol for Predicting the Ligand-Biding Site and Mode Based on the 3D-RISM/KH Theory. J. Chem. Theory Comput. 2020, 16, 2864–2876. [Google Scholar] [CrossRef] [PubMed]
- Sugita, M.; Hirata, F. Predicting the binding free energy of the inclusion process of 2-hydroxypropyl-b-cyclodextrin and small molecules by means of the MM/3D-RISM method. J. Phys. Condens. Matter 2016, 28, 384002–384013. [Google Scholar] [CrossRef] [PubMed]
- Hayashino, Y.; Sugita, M.; Arima, H.; Irie, T.; Kikuchi, T.; Hirata, F. Predicting the Binding Mode of 2-Hydroxypropyl-β-Cyclodextrin (HPβCD) to Cholesterol by Means of the MD Simulation and the 3D-RISM/KH Theory. J. Phys. Chem. B 2018, 122, 5716–5725. [Google Scholar] [CrossRef] [PubMed]
- Hasegawa, T.; Sugita, M.; Kikuchi, T.; Hirata, F. A Systematic Analysis of the Binding Affinity bewteen the Pim-1 Kinase and Its Inhibitors Based on the MM/3D-RISM/KH Method. J. Chem. Inf. Modeling 2017, 57, 2789–2798. [Google Scholar] [CrossRef] [PubMed]
- Sackmann, E. Physical Basis of Self-organization and function of membranes: Physics of vesicles. In Hand Book of Biological Physics; Lipowsky, R., Sackmann, E., Eds.; Elsevier Science B.V.: Amsterdam, The Netherlands, 1995; Chapter 5. [Google Scholar]
- Anfinsen, C.B. Principle that Govern the Folding of Protein Chain. Science 1973, 181, 223–230. [Google Scholar] [CrossRef]
- Arai, M.; Kuwajima, K. Role of the Molten Gloubule State in Protein Folding. Adv. Protein Chem. 2000, 53, 209–282. [Google Scholar]
- Bryngelson, J.D.; Onuchic, J.N.; Socci, N.D.; Wolynes, P.G. Funnels, Pathways, and the Energy Landscape of Protein Folding: A Synthesis. Proteins 1995, 21, 167–195. [Google Scholar] [CrossRef]
- Hirata, F. (Ed.) Molecular Theory of Solvation; Kluwer: Dordrecht, The Netherlands, 2003. [Google Scholar]
- Terazima, M.; Kataoka, M.; Ueoka, R.; Okamoto, Y. (Eds.) Molecular Science of Fluctuations toward Biological Functions; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Kim, B.; Hirata, F. Structural fluctuation of protein in water around its native state: A new statistical mechanics formulation. J. Chem. Phys. 2012, 138, 054108. [Google Scholar] [CrossRef]
- Hirata, F.; Akasaka, K. Structural fluctuation of proteins induced by thermodynamic perturbation. J. Chem. Phys. 2015, 142, 044110. [Google Scholar] [CrossRef]
- Hirata, F. On the interpretation of the temperature dependence of the mean sqaure of displacement (MSD) of protein, obtained from the incoherent neutron scattering. J. Mol. Liq. 2018, 270, 218–226. [Google Scholar] [CrossRef]
- Jonson, K. Role of Induced Fit in Enzyme Specificity: A Molecular Forward/Reverse Switch. J. Biol. Chem. 2008, 283, 26297–26301. [Google Scholar] [CrossRef] [PubMed]
- Hammes, G.G.; Chang, Y.-C.; Oas, T.G. Conformational selection or induced fit: A flux description of reaction mechanism. Proc. Natl. Acad. Sci. USA 2009, 106, 13737–13741. [Google Scholar] [CrossRef] [PubMed]
- Henzler-Widman, K.; Kern, D. Dynamic Personality of Protein. Nature 2007, 450, 964–972. [Google Scholar] [CrossRef]
- Yoshida, M.; Muneyuki, E.; Hisabori, T. ATP synthase—A marvellous rotray engine of the cell. Nat. Rev. Mol. Cell Biol. 2001, 2, 669–677. [Google Scholar] [CrossRef] [PubMed]
- Hirata, F.; Rossky, P.J. An Extended RISM Equation for Molecular Polar Liquids. Chem. Phys. Lett. 1981, 83, 329–334. [Google Scholar] [CrossRef]
- Hirata, F.; Pettitt, B.M.; Rossky, P.J. Application of an Extended RISM Equation to Dipolar and Quadrupolar Fluids. J. Chem. Phys. 1982, 77, 509–520. [Google Scholar] [CrossRef]
- Beglov, D.; Roux, B. An integral equation to describe the solvation of polar molecules in liquid water. J. Phys. Chem. B 1997, 101, 782–7826. [Google Scholar] [CrossRef]
- Kovalenko, A.; Hirata, F. Three-Dimensional Density Profiles of Water in Contact with a Solute of Arbitraly Shape: A RISM Approach. Chem. Phys. Lett. 1998, 290, 237–244. [Google Scholar] [CrossRef]
- Kovalenko, A.; Hirata, F. Self-Consistent Description of a Metal-Water Interface by the Kohn-Sham Density Functional Theory and the Three-Dimensional Reference Interaction Site Model. J. Chem. Phys. 1999, 110, 10095–10112. [Google Scholar] [CrossRef]
- Chandler, D.; Andersen, H.C. Optimized Cluster Expansions for Classical Fluids. 2. Theory of Molecular Liquids. J. Chem. Phys. 1972, 57, 1930–1931. [Google Scholar] [CrossRef]
- Hansen, J.P.; McDonald, I.R. Theory of Simple Liquids; Academic Press: London, UK, 1986. [Google Scholar]
- Singer, S.J.; Chandler, D. Free-energy Functions in the Extended RISM Approximation. Mol. Phys. 1985, 55, 621–625. [Google Scholar] [CrossRef]
- Imai, T.; Kinoshita, M.; Hirata, F. Theoretical Study for Partial Molar Volume of Amino Acids in Aqueous Solution: Implacation of Ideal Fluctuation Volume. J. Chem. Phys. 2000, 112, 9469–9478. [Google Scholar] [CrossRef]
- Imai, T.; Kovalenko, A.; Hirata, F. Solvation Thermodynamics of Protein Studied by the 3D-RISM Theory. Chem. Phys. Lett. 2004, 395, 1–6. [Google Scholar] [CrossRef]
- Imai, T.; Kovalenko, A.; Hirata, F. Partial Molar Volume of Proteins Studied by the Three-Dimensional Reference Interaction Site Model Theory. J. Phys. Chem. B 2005, 109, 6658–6665. [Google Scholar] [CrossRef]
- Franks, F. Water: Compehensive Treatise; Plenum: New York, NY, USA, 1972. [Google Scholar]
- Eisenberg, D.; Kauzman, W. The Structure and Properties of Water; Clarendon: Oxford, UK, 1969. [Google Scholar]
- Nakasako, M. Water-Protein interactions from high-resolution protein crystalography. Philos. Trans. Biol. Sci. 2004, 359, 1191–1206. [Google Scholar] [CrossRef]
- Arai, S.; Chatake, T.; Ohhara, T.; Kurihara, K.; Tanaka, I.; Suzuki, N.; Fujimoto, Z.; Mizuno, H.; Niimura, N. Complicated water orientation in the minor groove of the B-DNA decamer d(CCATTAATGG) observed by neutron diffraction measurement. Nucleic Acids Res. 2005, 33, 3017–3024. [Google Scholar] [CrossRef][Green Version]
- Niimura, N.; Arai, S.; Kurihara, K.; Chatake, T.; Tanaka, I.; Bau, R. Recent results on hydrogen and hydration in biology studied by neutron macromolecular crystallography. Cell. Mol. Life Sci. 2005, 62, 285–300. [Google Scholar] [CrossRef]
- Imai, T.; Hiraoka, R.; Kovalenko, A.; Hirata, F. Water molecules in protein cavity detected by a statistical-mechanical theory. J. Am.Chem. Soc. 2005, 127, 15334–15335. [Google Scholar] [CrossRef]
- Wilson, K.P.; Malcolm, B.A.; Matthews, B.W. Structural and thermodynamic analysis of compensating mutations within the core of chicken egg white lysozyme. J. Biol. Chem. 1992, 267, 10842. [Google Scholar] [CrossRef]
- Evans, J. Probing for Water in Protein Cavities; Royal Society of Chemistry: London, UK, 2005. [Google Scholar]
- Lazaridis, T. Inhomogeneous Fluid Approach to Solvation Thermodynamics, 1. Theory. J. Phys. Chem. B 1998, 102, 3531–3541. [Google Scholar] [CrossRef]
- Lazaridis, T. Inhomogeneous Fluid Approach to Solvation Thermodynamics, 2. Application to simple Fluids. J. Phys. Chem. B 1998, 102, 3542–3550. [Google Scholar] [CrossRef]
- Young, T.T.; Abel, R.R.; Kim, B.B.; Beme, B.J.B.; Friesner, R.A.R. Motifs for Molecular Recognition Exploiting Hydrophobic Enclosure in Protein-Ligad Binding. Proc. Natl. Acad. Sci. USA 2007, 104, 808–813. [Google Scholar] [CrossRef] [PubMed]
- Sindhikara, D.J.; Yoshida, N.; Hirata, F. Placevent: An Algorithm for Prediction of Explcit Solvent Atom Distribution–Application to HIV-1 Protease and F-ATP Synthase. J. Comput. Chem. 2012, 33, 1536–1543. [Google Scholar] [CrossRef]
- Sindhikara, D.J.; Hirata, F. Analysis of Biomolecular Solvation Site by 3D-RISM Theory. J. Phys. Chem. B 2013, 117, 6718–6723. [Google Scholar] [CrossRef]
- Imai, T.; Hiraoka, R.; Seto, T.; Kovalenko, A.; Hirata, F. Three-Dimensional Distribution Function Theory for the Prediction of Protein-Ligand Binding Sites and Affinities: Application to the Binding of Noble Gases to Hen Egg-White Lysozyme in Aqueous Solution. J. Phys. Chem. B 2007, 111, 11585–11591. [Google Scholar] [CrossRef]
- Prangé, T.; Schiltz, M.; Pernot, L.; Colloc’h, N.; Longhi, S.; Bourguet, W.; Fourme, R. Exploring hydrophobic sites in proteins wth xenon and krypton. Proteins Struct. Funct. Genet. 1998, 30, 6–73. [Google Scholar] [CrossRef]
- Herzberg, O.; James, M.N. Structure of the calcium regulatory muscle protein troponin-C at 2.8-A resolution. Nature 1985, 313, 653–659. [Google Scholar] [CrossRef]
- Ikura, M.; Clore, G.M.; Gronenborn, A.M.; Zhu, G.; Klee, C.B.; Bax, A. Solution structure of a calmodulin-target peptide complex by multidimensional NMR. Science 1992, 256, 632–638. [Google Scholar] [CrossRef]
- Hille, B. Ionic Channels of Excitable Membranes; Sinauer Associates: Shunderland, MA, USA, 2001. [Google Scholar]
- Tsuda, S.; Ogura, K.; Hasegawa, Y.; Yagi, K.; Hikichi, K. H-1-NMR study of rabbit skeltal-mascle troponin-C-NG2+-induced conformational change. Biochemistry 1990, 29, 4951–4958. [Google Scholar] [CrossRef]
- Yoshida, N.; Phongphanphanee, S.; Maruyama, Y.; Imai, T.; Hirata, F. Selective Ion-Binding by Protein Probed with the 3D-RISM Theory. J. Am. Chem. Soc. 2006, 128, 12042–12043. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, N.; Phongphanphanee, S.; Hirata, F. Selective Ion-Binding by Protein Probed with the Statistical Mechanical Integral Equation Theory. J. Phys. Chem. B 2007, 111, 4588–4595. [Google Scholar] [CrossRef]
- Kuroki, R.; Yutani, K. Structural and thermodynamic responses of mutations at a Ca2+ binding site engineered into human lysozyme. J. Biol. Chem. 1998, 273, 34310–34315. [Google Scholar] [CrossRef]
- Cowan, J.A. Structure and Catalytic Chemistry of Magnetisium-Dependent Enzymes. Biometals 2002, 15, 225–235. [Google Scholar] [CrossRef] [PubMed]
- Kostrewa, D.; Winkler, F.K. Mg2+ Binding to the Active Site of EcoRV Endonuclease Endonuclease: A Crystallographic Study of Complexes with Substrate and Product DNA at 2Å Resolution. Biochemistry 1995, 34, 683–696. [Google Scholar] [CrossRef] [PubMed]
- Vipond, I.B.; Baldwin, G.S.; Halford, S.E. Divalent Metal Ions at the Active Sites of the EcoRV and EcoRI Restriction Endonucleases. Biochemistry 1995, 34, 697–704. [Google Scholar] [CrossRef] [PubMed]
- Groll, D.H.; Jeltsch, A.; Selent, U.; Pingoud, A. Does the Restriction Endonuclease EcoRV Employ a Two-Metal-Ion Mechanism for DNA Cleavage? Biochemistry 1997, 36, 11389–11401. [Google Scholar] [CrossRef] [PubMed]
- Horton, N.C.; Perona, J.J. Making the Most of Metal Ions. Nat. Struct. Biol. 2001, 8, 290–293. [Google Scholar] [CrossRef]
- Horton, N.; Perona, J.J. DNA Cleavage by EcoRV Endonuclease: Two Metal Ions in Three Metal Ion Binding Sites. Biochemistry 2004, 8, 6841–6857. [Google Scholar] [CrossRef]
- Onishi, I.; Sunaba, S.; Yoshida, N.; Hirata, F. Role of Mg2+ Ions in DNA Hydrolysis by EcoRV, Studied by the 3D-Reference Interaction Site Model and Molecular Dynamics. J. Phys. Chem. B 2018, 122, 9061–9075. [Google Scholar] [CrossRef]
- Viadiu, H.; Aggarwal, A.K. The role of metals in catalysis by the restriction endonuclease BamHI. Nat. Struc. Biol. 1998, 5, 910–916. [Google Scholar] [CrossRef] [PubMed]
- Kitchen, B.D.; Decornez, H.; Furr, J.R.; Bajorath, J. Docking and scoring in virtual screening for drug discovery: Meyhods and applications. Nat. Rev. Drug Discov. 2004, 3, 935–949. [Google Scholar] [CrossRef] [PubMed]
- Klebe, G. Virtual ligand screening: Strategies, perspectives and limitations. Drug Discov. Today 2006, 11, 580–594. [Google Scholar] [CrossRef] [PubMed]
- Sotriffer, C.; Klebe, G. Identification and mappinf of small-molecule binding sites in proteins: Computational tools for structure-based drug design. Farmaco 2002, 57, 243–251. [Google Scholar] [CrossRef]
- Gohlke, H.; Klebe, G. Approaches to the description and prediction of the binding affinity of small- molecule ligands to macromolecular receptors. Angew. Chem. Int. Ed. 2002, 41, 2645–2676. [Google Scholar] [CrossRef]
- Halperin, I.; Ma, B.; Wolfson, H.; Nussinov, R. Principles of docking: An overview of search algorithms and a guide to scoring functions. Proteins Struct. Funct. Genet. 2002, 47, 409–443. [Google Scholar] [CrossRef]
- Brooijmans, N.; Kuntz, I.D. Molecular recofnition and docking algorithms. Annu. Rev. Biophys. Biomol. Struct. 2003, 32, 335–373. [Google Scholar] [CrossRef]
- Lichtarge, O.; Sowa, M.E. Evolutionary predictions of binding surfaces and interactions. Curr. Opin. Struct. Biol. 2002, 12, 21–27. [Google Scholar] [CrossRef]
- Sousa, S.F.; Fernandes, P.A.; Ramos, M.J. Protein-ligand docking: Current status and future challenges. Proteins: Struct. Funct. Genet. 2006, 65, 15–26. [Google Scholar] [CrossRef]
- Ladbury, J.E. Just add water! The effect of water on the specificity of protein-ligand binding sites and its potential application to drug design. Chem. Biol. 1996, 3, 973–980. [Google Scholar] [CrossRef]
- Bachmann, M.; Möröy, T. The Serine/Threonine Kinase Pim-1. Int. J. Biochem. Cell Biol. 2005, 37, 726–730. [Google Scholar] [CrossRef]
- Merkel, A.L.; Meggers, E.; Ocker, M. PIM1 Kinase as a Target for Cancer Therapy. Expert Opin. Investig. Drugs 2012, 21, 425–436. [Google Scholar] [CrossRef]
- Imai, T.; Miyashita, N.; Sugita, Y.; Kovalenko, A.; Hirata, F.; Kidera, A. Functionality Mapping on Internal Surfaces of Multidrug Transporter AcrB Based on Molecular Theory of Solvation: Implication for Drug Effux Ptahway. J. Phys. Chem.B. 2011, 115, 8288–8295. [Google Scholar] [CrossRef]
- Blinov, N.; Huang, W.; Nikolic, D.; Wishart, D. 3D-RISM-Docc: A New Fragment-Based Drug Design Protocol. J. Chem. Theor. Comp. 2012, 8, 3356–3372. [Google Scholar]
- Nikolic, D.; Blinov, N.; Nikolic, D. Biomolecular Recognition Based on 3D Molecular Theory of Solvation. Biophys. J. 2014, 106, 411A. [Google Scholar]
- Zhukova, Y.N.; Alekseeva, M.G.; Zakharevich, N.V.; Shtil, A.A.; Danilenko, V.N. Pim Family of Protein Kinases: Structure, Functions, and Roles in Hematopoietic Malignancies. Mol. Biol. 2011, 45, 695–703. [Google Scholar] [CrossRef]
- Liang, C.; Li, Y.-Y. Use of Regulators and Inhibitors of Pim-1, a Serine/Threonine Kinase, for Tumour Therapy (Review). Mol. Med. Rep. 2014, 9, 1–10. [Google Scholar] [CrossRef]
- Tursynbay, Y.; Zhang, J.; Li, Z.; Tokay, T.; Zhumadilov, Z.; Wu, D.; Xie, Y. Pim-1 Kinase as Cancer Drug Target: An Update (Review). Biomed. Rep. 2015, 4, 1–7. [Google Scholar] [CrossRef]
- Shah, N.; Pang, B.; Yeoh, K.-G.; Thorn, S.; Chen, C.S.; Lilly, M.B.; Salto-Tellez, M. Potential Roles for the PIM1 Kinase in Human Cancer—A Molecular and Therapeutic Appraisal. Eur. J. Cancer. 2008, 44, 2144–2151. [Google Scholar] [CrossRef]
- Valdman, A.; Fang, X.; Pang, S.-T.; Ekman, P.; Egevad, L. Pim-1 Expression in Prostatic Intraepithelial Neoplasia and Human Prostate Cancer. Prostate 2004, 60, 367–371. [Google Scholar] [CrossRef]
- Laird, P.W.; van der Lugt, N.M.T.; Clarke, A.; Domen, J.; Linders, K.; McWhir, J.; Berns, A.; Hooper, M. In Vivo Analysis of Pim-1 Deficiency. Neucleic Acids Res. 2003, 21, 4750–4755. [Google Scholar] [CrossRef] [PubMed]
- Domen, J.; van der Lugt, N.M.T.; Laird, P.W.; Saris, C.J.M.; Clarke, A.R.; Hooper, M.L.; Berns, A. Impaired Interleukin-3 Response in Pim-1-Deficient Bone Marrow-Derived Mast Cells. Blood 1993, 82, 1445–1452. [Google Scholar] [CrossRef] [PubMed]
- Burger, M.T.; Nishiguchi, G.; Han, W.; Lan, J.; Simmons, R.; Atallah, G.; Ding, Y.; Tamez, V.; Zhang, Y.; Mathur, M.; et al. Identification of N-(4-((1 R,3 S,5, S)-3-Amino-5-Methylcyclohexyl)Pyridin-3-Y1)-6-(2,6-Difluorophenyl)-5-Fluoropicolinamide(PIM447), a potent and selective proviral insertion site of moloney murine leukemia (PIM) 1, 2, and 3 kinase inhibitor in clinical trials for hematological malignancies. J. Med. Chem. 2015, 2, 8373–8386. [Google Scholar]
- Wan, X.; Zhang, W.; Li, L.; Xie, Y.; Li, W.; Huang, N. A New Target for an Old Drug: Identifying Mitoxantrone as a Nanomolar Inhibitor of PIM1 Kinase via Kinome-Wide Selectivity Modeling. J. Med. Chem. 2013, 56, 2619–2629. [Google Scholar] [CrossRef]
- Grey, R.; Pierce, A.C.; Bemis, G.W.; Jacobs, M.D.; Moody, C.S.; Jajoo, R.; Mohal, N.; Green, J. Structure-Based Design of 3-Aryl-6-Amino-Triazolo[4,3-B]Pyridazine Inhibitors of Pim-1 Kinase. Bioorg. Med. Chem. Lett. 2009, 19, 3019–3022. [Google Scholar] [CrossRef]
- Levinthal, C. Are there pathways for protein folding? J. Chim. Phys. 1968, 65, 44–45. [Google Scholar] [CrossRef]
- Mori, H. Transport, Collective Motion, and Brownian Motions. Prog. Theor. Phys. 1965, 33, 423–455. [Google Scholar] [CrossRef]
- Kataoka, M.; Nishi, I.; Fujisawa, T.; Ueki, T.; Tokunaga, F.; Goto, Y. Structural Characterization of the Moten Globule and Native States of Apomyoglobin by Solution X-ray Scattring. J. Mol. Biol. 1995, 249, 215–228. [Google Scholar] [CrossRef]
- Ikeguchi, M.; Ueno, J.; Sato, M.; Kidera, A. Protein Structural Change upon ligand binding. Phys. Rev. Lett. 2005, 94, 78102. [Google Scholar] [CrossRef]
- Doster, W.; Cusack, S.; Petry, W. Dynamical Transition of Myoglobin Revealed by Ineleastic Neutron Scattering. Nature 1989, 337, 754–756. [Google Scholar] [CrossRef]
- Nakagawa, H.; Joti, Y.; Kitao, A.; Kataoka, M. Hydration Affects Both Harmonic and Anharmonic Nature of Protein Dynamics. Biophys. J. 2008, 95, 2916–2923. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Fenimore, P.W.; Frauenfelder, H.; Mezai, F. Protein fluctuations explored by inelastic neutron scattering and dielectric relaxation spectroscopy. Philos. Mag. 2008, 88, 3877–3883. [Google Scholar] [CrossRef]
- Nakagawa, H.; Kataoka, M. Percolation of Hydration Water as a Control of Protein Dynamics. J. Phys. Soc. Jpn. 2010, 79, 083801–083805. [Google Scholar] [CrossRef]
- Hirata, F.; Sugita, M.; Yoshida, M.; Akasaka, K. Structural Fluctuation of Protein and Anfinsen’s Thermodynamic Hypothesis. J. Chem. Phys. 2018, 148, 20901–20909. [Google Scholar] [CrossRef] [PubMed]

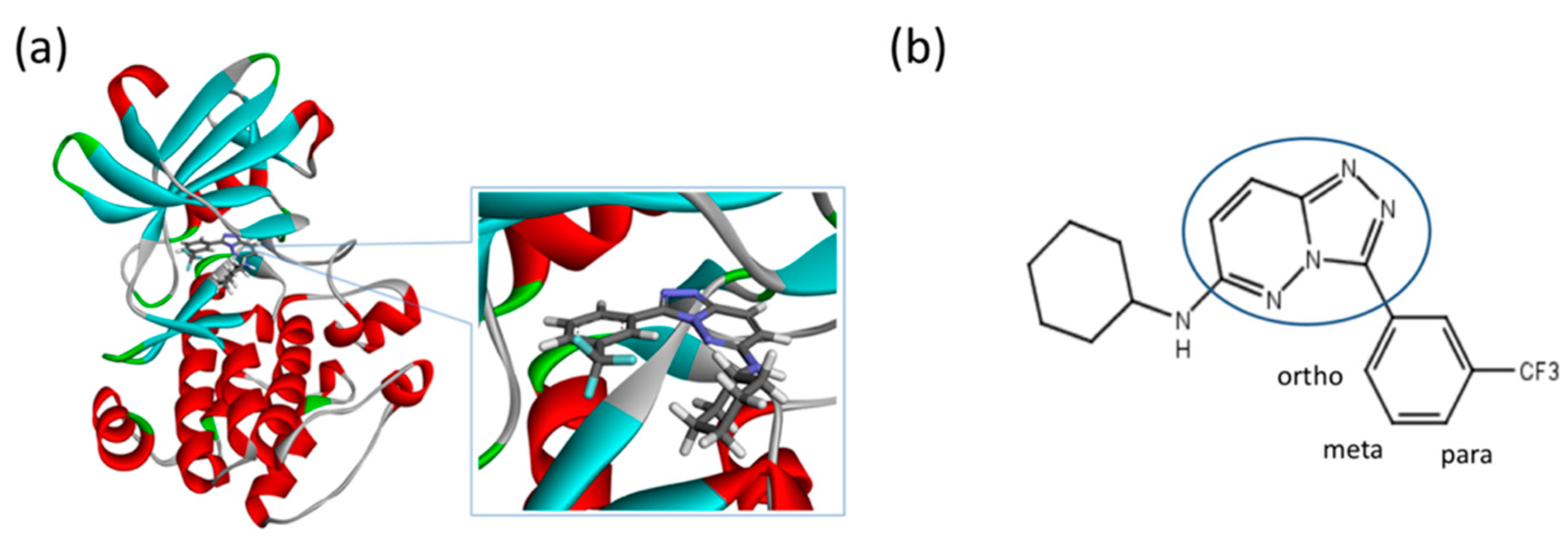
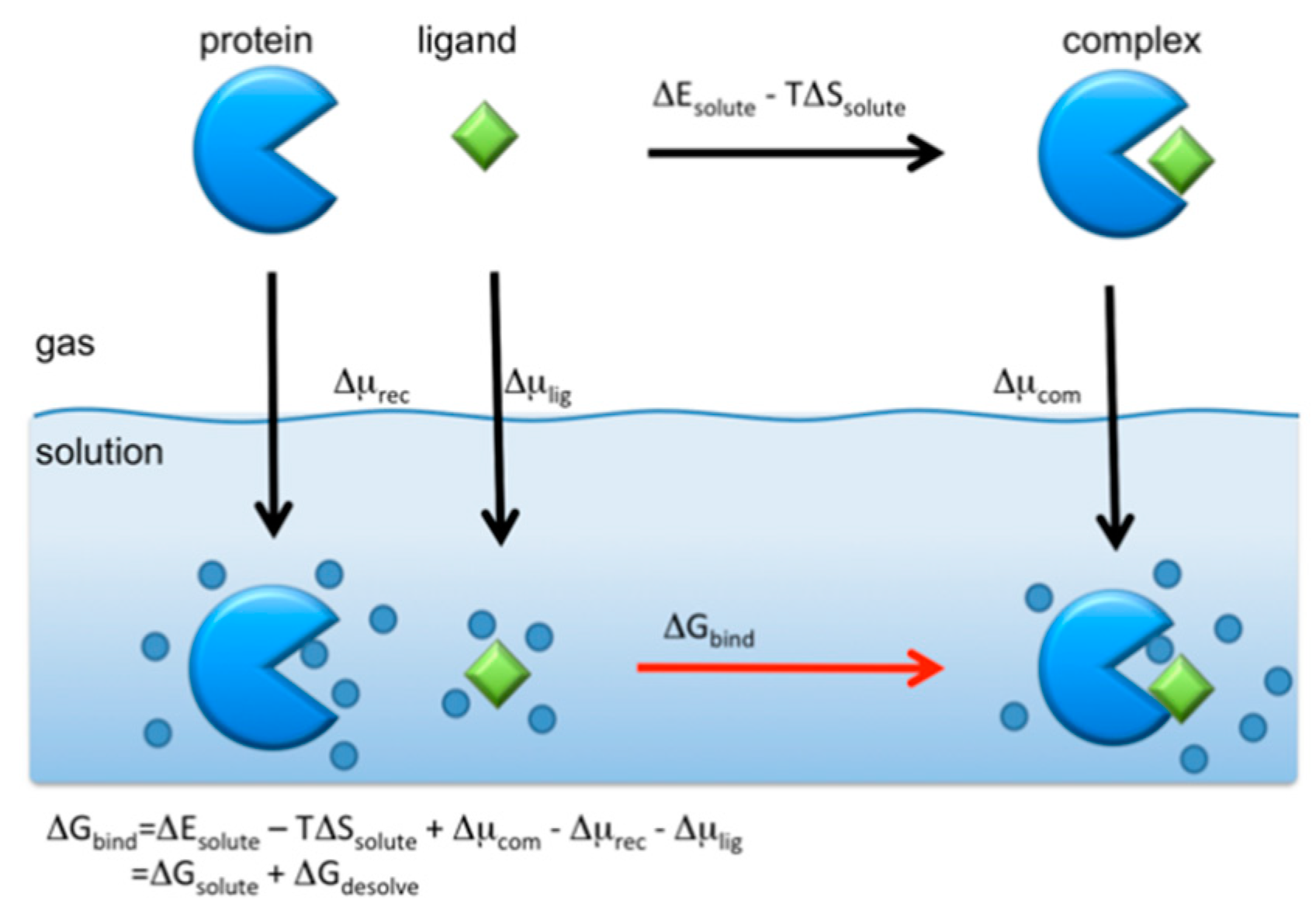
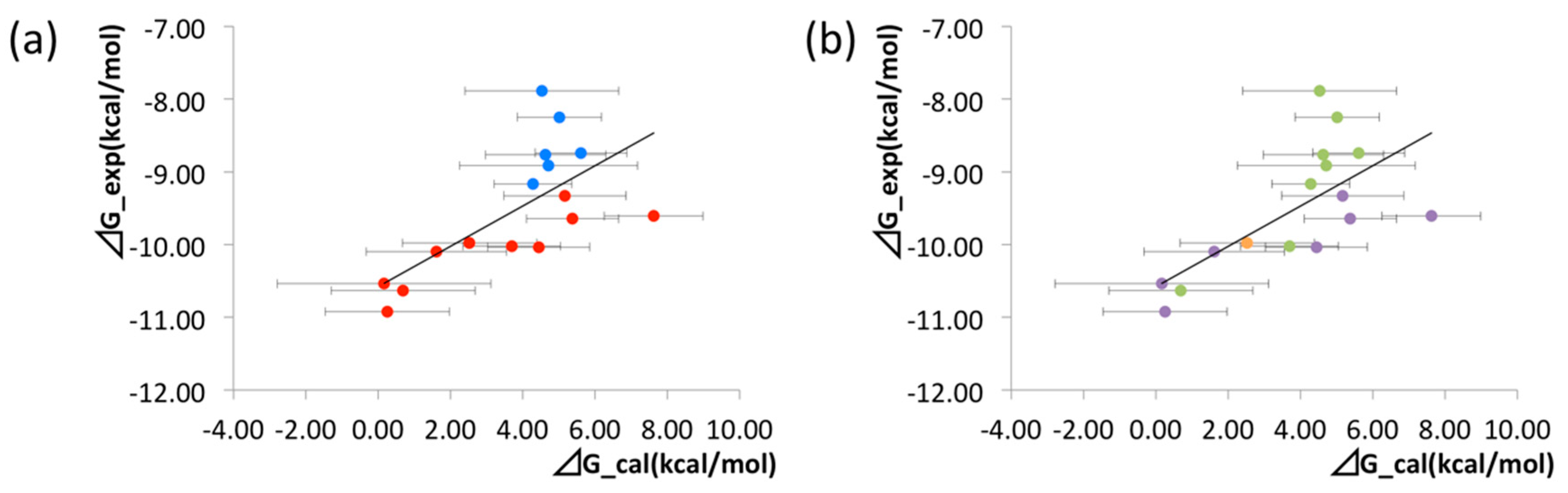

| No. | Structure | Ki (nM) | (kcal/mol) | (kcal/mol) | No. | Structure | Ki (nM) | (kcal/mol) | (kcal/mol) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 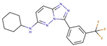 | 11 | −10.93 | 0.00 | 9 | 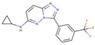 | 18 | −10.63 | 0.30 |
| 2 | 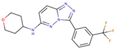 | 44 | −10.10 | 0.83 | 10 | 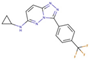 | 320 | −8.92 | 2.01 |
| 3 |  | 94 | −9.65 | 1.28 | 11 | 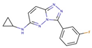 | 430 | −8.74 | 2.19 |
| 4 | 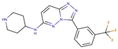 | 21 | −10.54 | 0.39 | 12 | 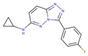 | 210 | −9.17 | 1.76 |
| 5 | 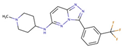 | 160 | −9.33 | 1.60 | 13 |  | 410 | −8.77 | 2.16 |
| 6 | 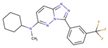 | 49 | −10.03 | 0.89 | 14 | 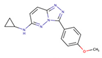 | 980 | −8.25 | 2.68 |
| 7 |  | 100 | −9.61 | 1.32 | 15 | 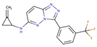 | 50 | −10.02 | 0.91 |
| 8 | 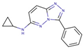 | 1800 | −7.89 | 3.04 | 16 | 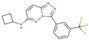 | 54 | −9.98 | 0.95 |
| No. | (kcal/mol) | (kcal/mol) | (kcal/mol) | (kcal/mol) | (kcal/mol) | |
|---|---|---|---|---|---|---|
| Ave. | Std. err. | |||||
| 1 | −56.18 | 8.06 | 48.02 | 0.26 | 1.33 | −10.93 |
| 2 | −51.81 | 8.05 | 45.39 | 1.62 | 1.94 | −10.10 |
| 3 | −42.22 | 12.85 | 34.76 | 5.38 | 1.27 | −9.65 |
| 4 | −50.34 | 7.95 | 42.56 | 0.17 | 2.96 | −10.54 |
| 5 | −57.74 | 12.83 | 50.09 | 5.17 | 1.69 | −9.33 |
| 6 | −60.98 | 12.57 | 52.86 | 4.45 | 1.41 | −10.03 |
| 7 | −60.04 | 15.29 | 52.37 | 7.62 | 1.37 | −9.61 |
| 8 | −44.7 | 9.96 | 39.27 | 4.53 | 2.13 | −7.89 |
| 9 | −42.49 | 6.54 | 36.64 | 0.69 | 1.99 | −10.63 |
| 10 | −54.48 | 11.11 | 48.08 | 4.71 | 2.46 | −8.92 |
| 11 | −43.69 | 9.79 | 39.51 | 5.61 | 1.27 | −8.74 |
| 12 | −44.39 | 8.87 | 39.81 | 4.29 | 1.07 | −9.17 |
| 13 | −55.57 | 9.6 | 0.61 | 4.63 | 1.67 | −8.77 |
| 14 | −52.04 | 10.11 | 46.95 | 5.02 | 1.16 | −8.25 |
| 15 | −59.06 | 13.3 | 49.45 | 3.7 | 1.35 | −10.02 |
| 16 | −53.51 | 9.88 | 46.16 | 2.53 | 1.86 | −9.98 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sugita, M.; Onishi, I.; Irisa, M.; Yoshida, N.; Hirata, F. Molecular Recognition and Self-Organization in Life Phenomena Studied by a Statistical Mechanics of Molecular Liquids, the RISM/3D-RISM Theory. Molecules 2021, 26, 271. https://doi.org/10.3390/molecules26020271
Sugita M, Onishi I, Irisa M, Yoshida N, Hirata F. Molecular Recognition and Self-Organization in Life Phenomena Studied by a Statistical Mechanics of Molecular Liquids, the RISM/3D-RISM Theory. Molecules. 2021; 26(2):271. https://doi.org/10.3390/molecules26020271
Chicago/Turabian StyleSugita, Masatake, Itaru Onishi, Masayuki Irisa, Norio Yoshida, and Fumio Hirata. 2021. "Molecular Recognition and Self-Organization in Life Phenomena Studied by a Statistical Mechanics of Molecular Liquids, the RISM/3D-RISM Theory" Molecules 26, no. 2: 271. https://doi.org/10.3390/molecules26020271
APA StyleSugita, M., Onishi, I., Irisa, M., Yoshida, N., & Hirata, F. (2021). Molecular Recognition and Self-Organization in Life Phenomena Studied by a Statistical Mechanics of Molecular Liquids, the RISM/3D-RISM Theory. Molecules, 26(2), 271. https://doi.org/10.3390/molecules26020271







