The Participation of 3,3,3-Trichloro-1-nitroprop-1-ene in the [3 + 2] Cycloaddition Reaction with Selected Nitrile N-Oxides in the Light of the Experimental and MEDT Quantum Chemical Study
Abstract
:1. Introduction
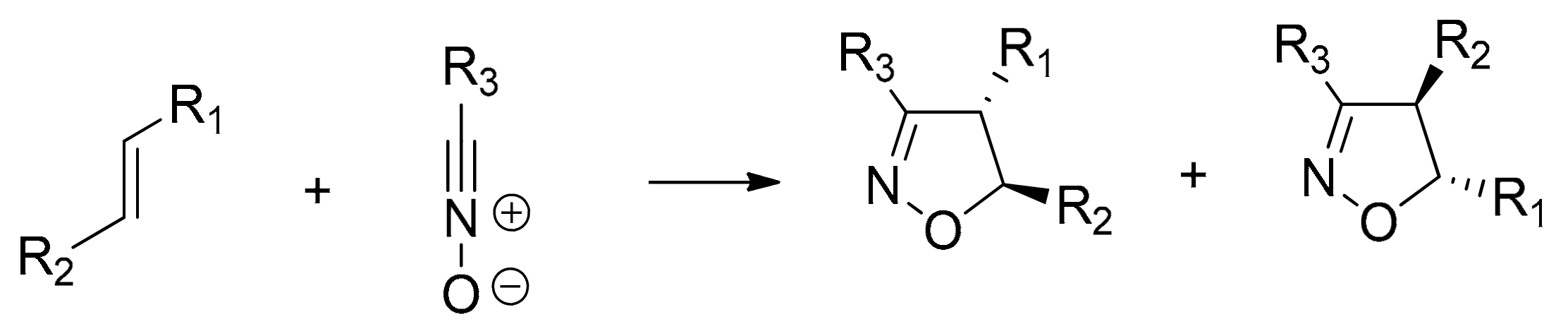
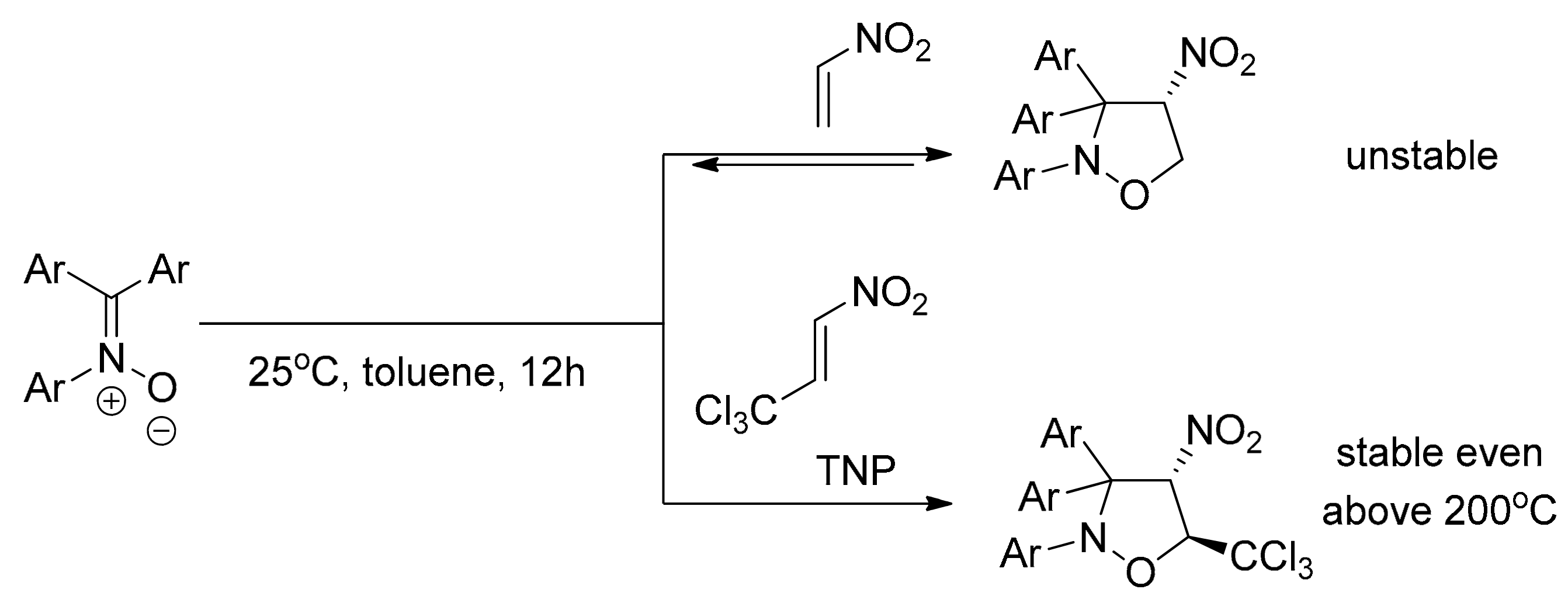
2. Results and Discussion
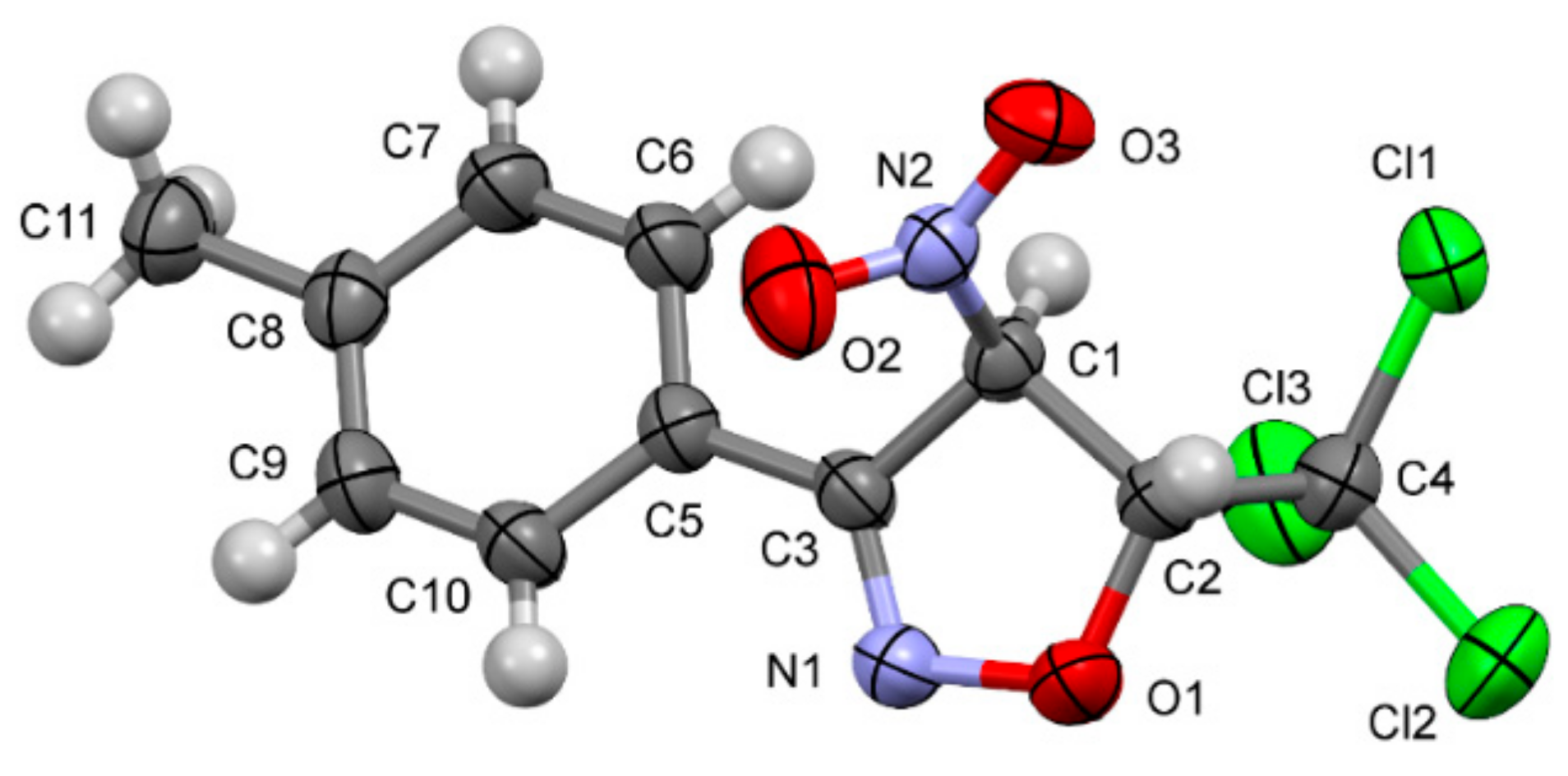
2.1. Experimental Study
2.2. Theoretical Study
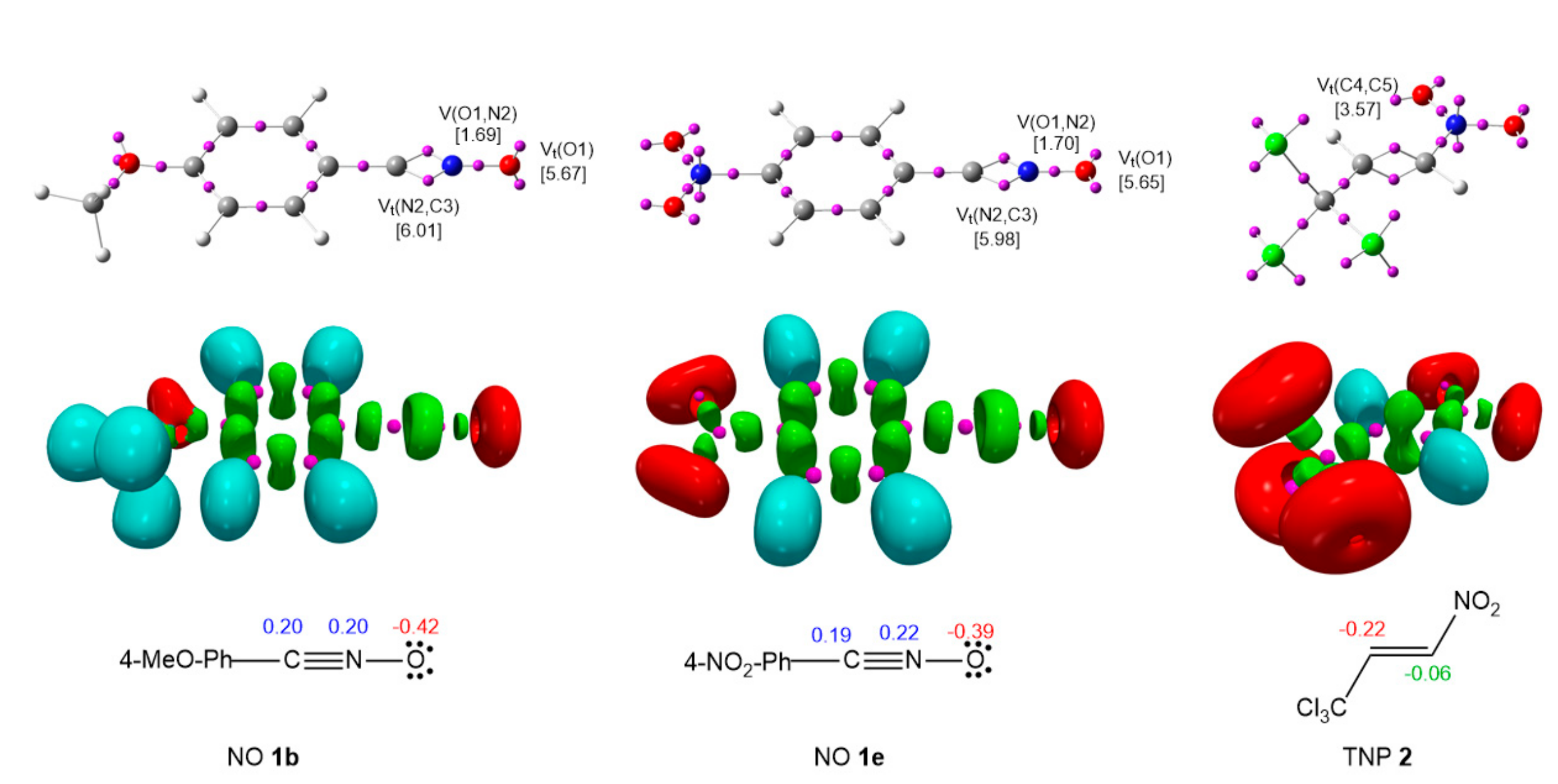
2.2.1. Analysis of the Electronic Structures of the Reagents
2.2.2. Analysis of the CDFT Reactivity Indices of the Reagents
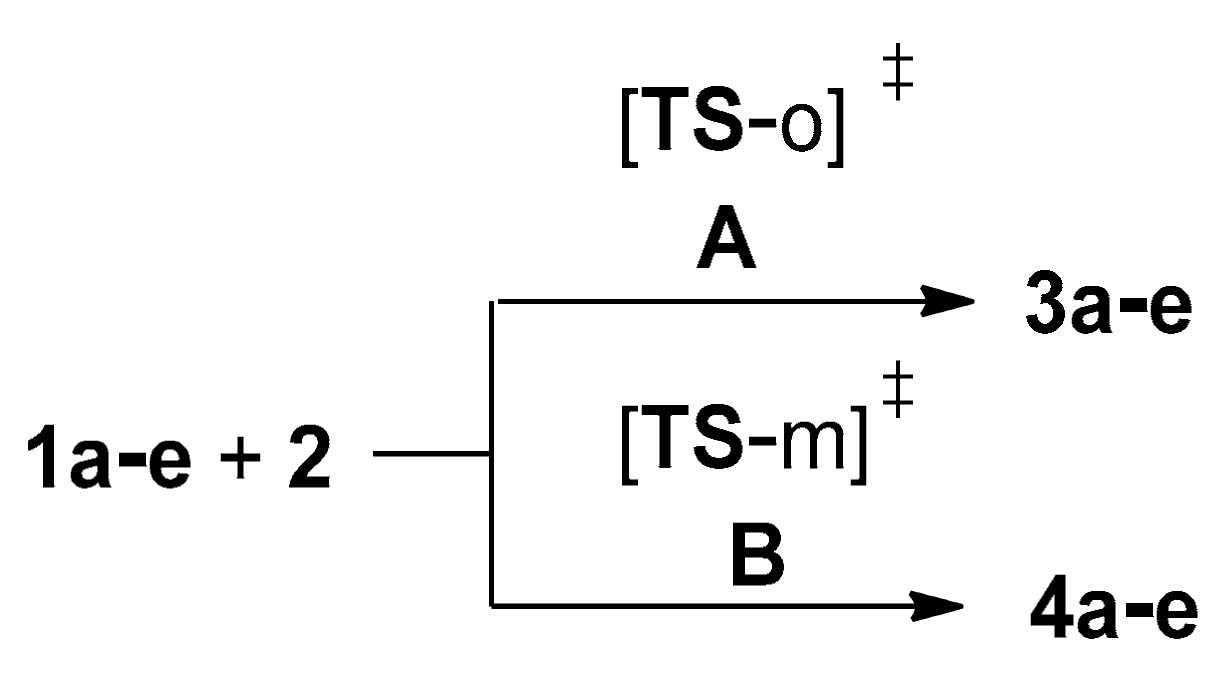
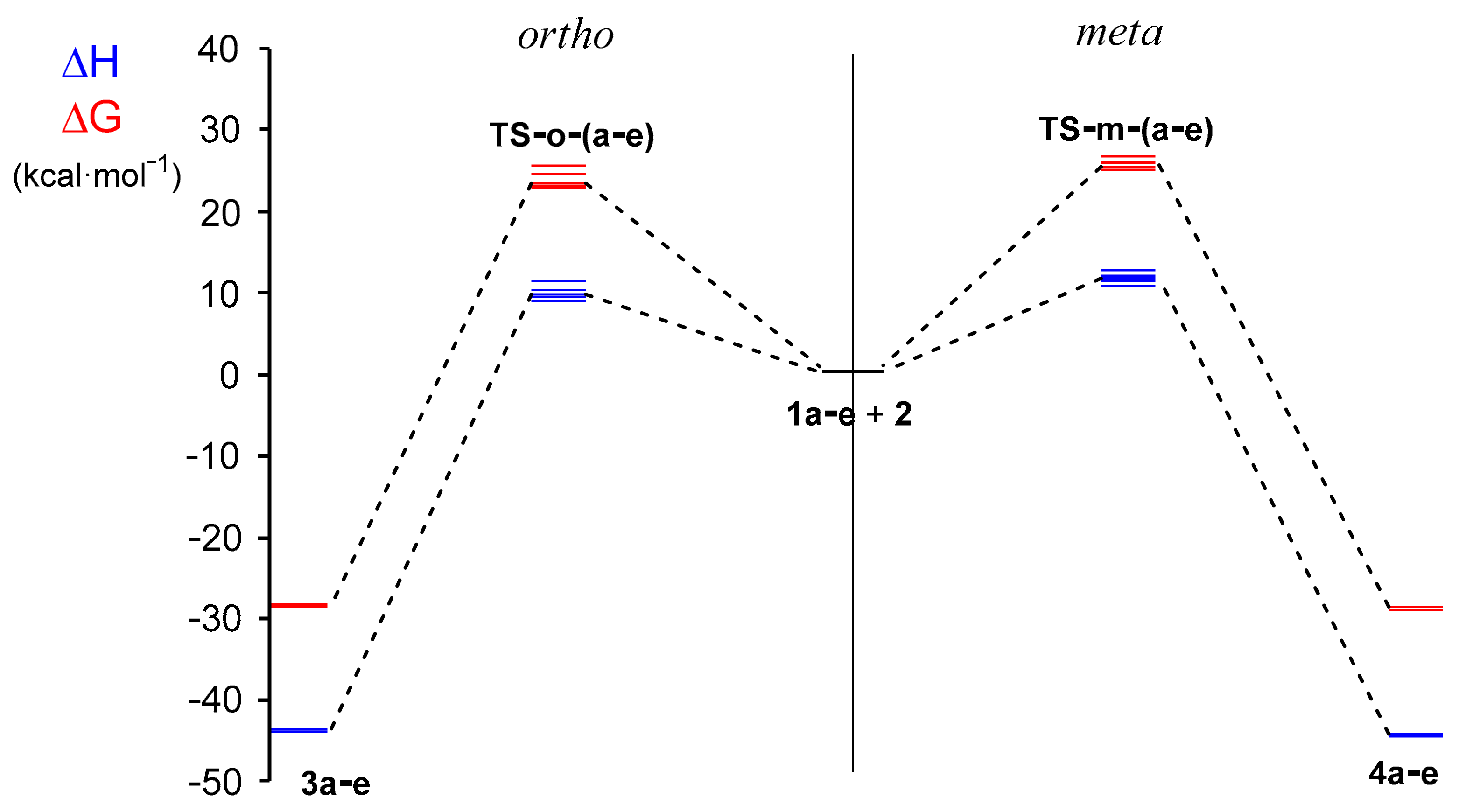
2.2.3. Study of the Potential Energy Surfaces Associated with the 32CA Reactions between NOs 1a–e and TNP 2
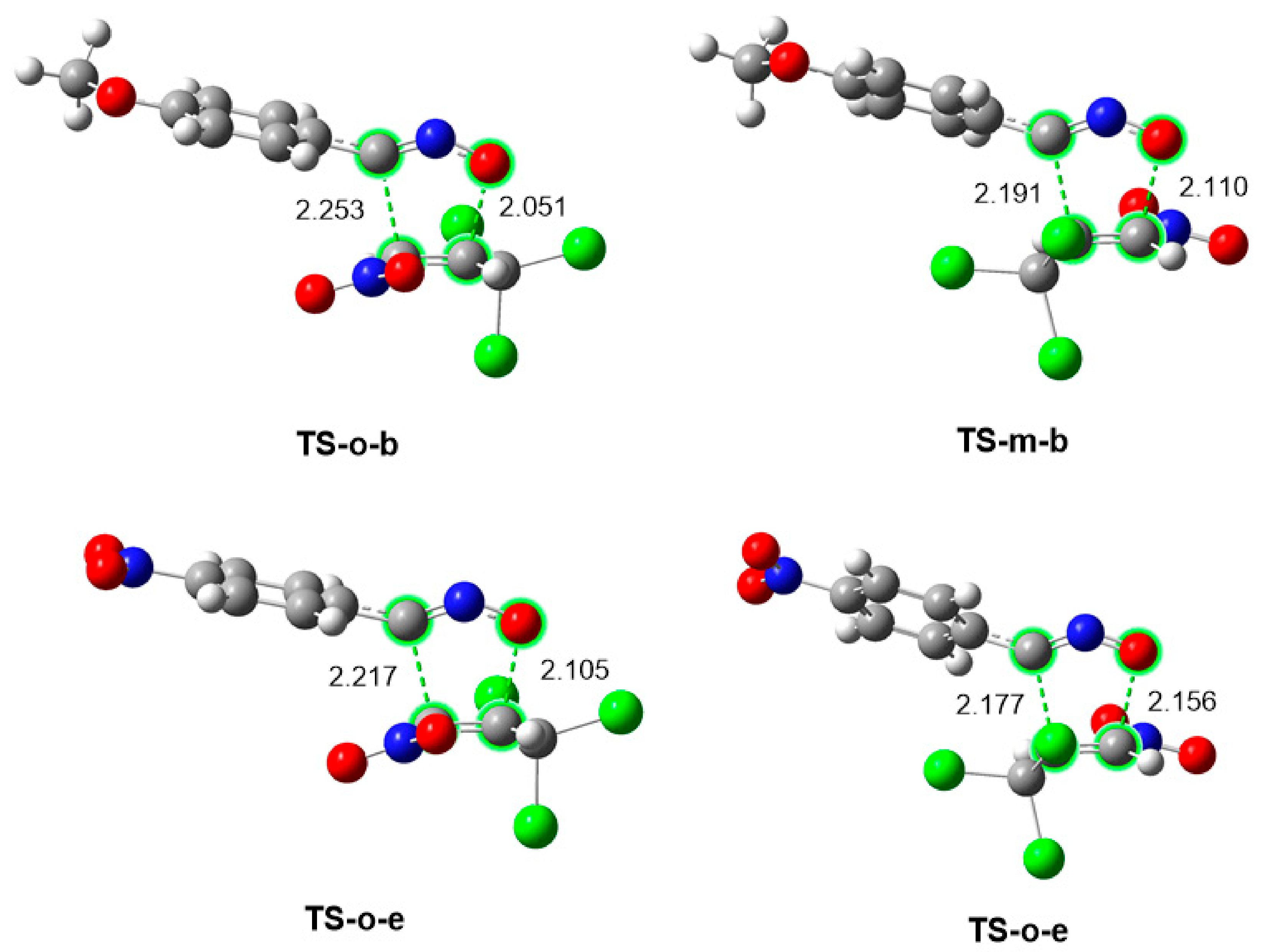
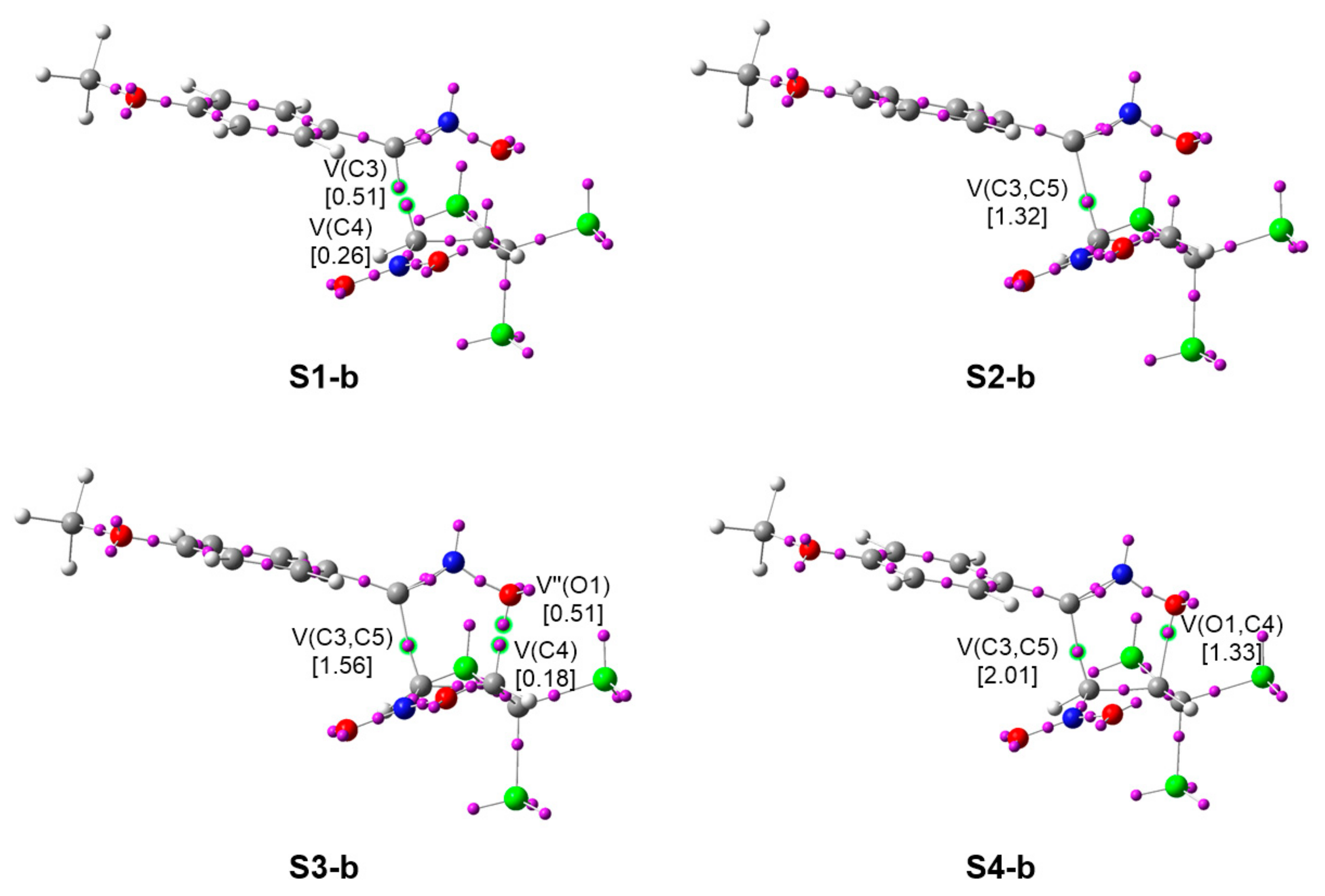
2.2.4. Characterization of the Bond Formation Process
3. Methods and Procedures
3.1. Experimental
3.1.1. Analytical Techniques
3.1.2. RTG Analysis
3.1.3. Materials
Cycloaddition between Nitrile N-Oxides and 3,3,3-Trichloro-1-nitroprop-1-ene—General Procedure
3.2. Computational
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Prajapti, S.K.; Shrivastava, S.; Bihade, U.; Gupta, A.K.; Naidu, V.G.M.; Banerjee, U.C.; Babu, B.N. Synthesis and biological evaluation of novel Δ2-isoxazoline fused cyclopentane derivatives as potential antimicrobial and anticancer agents. MedChemComm 2015, 6, 839–845. [Google Scholar] [CrossRef]
- Domingo, L.R.; Emamian, S.; Salami, M.; Ríos-Gutiérrez, M. Understanding the molecular mechanism of [3 + 2] cycloaddition reaction of benzonitrile oxide toward an N-vinylpyrrole derivative with the aid of ELF topological analysis. J. Phys. Org. Chem. 2016, 29, 368–376. [Google Scholar] [CrossRef]
- Ren, J.; Wang, S.; Ni, H.; Yao, R.; Liao, C.; Ruan, B. Synthesis, Characterization and Antitumor Activity of Novel Ferrocene-Based Amides Bearing Pyrazolyl Moiety. J. Inorg. Organomet. Polym. 2015, 25, 419–426. [Google Scholar] [CrossRef]
- Houk, K.N.; Sims, J.; Watts, C.R.; Luskus, L.J. Origin of reactivity, regioselectivity, and periselectivity in 1,3-dipolar cycloadditions. J. Am. Chem. Soc. 1973, 95, 7301–7315. [Google Scholar] [CrossRef]
- Rai, N.S.; Kalluraya, B.; Lingappa, B.; Shenoy, S.; Puranic, V.G. Convenient access to 1,3,4-trisubstituted pyrazoles carrying 5-nitrothiophene moiety via 1,3-dipolar cycloaddition of sydnones with acetylenic ketones and their antimicrobial evaluation. Eur. J. Med. Chem. 2008, 43, 1715–1720. [Google Scholar] [CrossRef] [PubMed]
- Ríos-Gutiérrez, M.; Domingo, L.R. Unravelling the Mysteries of the [3 + 2] Cycloaddition Reactions. Eur. J. Org. Chem. 2019, 267–282. [Google Scholar] [CrossRef]
- Ríos-Gutiérrez, M.; Domingo, L.R.; Ghodsi, F. Unveiling the Different Reactivity of Bent and Linear Three-Atom-Components Participating in [3 + 2] Cycloaddition Reactions. Organics 2021, 2, 274–286. [Google Scholar] [CrossRef]
- Ríos-Gutiérrez, M.; Chafaa, F.; Khorief Nacereddine, A.; Djerourou, A.; Domingo, L.R. A DFT study of [3 + 2] cycloaddition reactions of an azomethine imine with N-vinyl pyrrole and N-vinyl tetrahydroindole. J. Mol. Graph. Model. 2016, 70, 296–304. [Google Scholar] [CrossRef]
- Ríos-Gutiérrez, M.; Domingo, L.R.; Esseffar, M.; Oubella, A.; Ait Itto, M.Y. Unveiling the Different Chemical Reactivity of Diphenyl Nitrilimine and Phenyl Nitrile Oxide in [3 + 2] Cycloaddition Reactions with (R)-Carvone through the Molecular Electron Density Theory. Molecules 2020, 25, 1085. [Google Scholar] [CrossRef] [Green Version]
- Zeroual, A.; Ríos-Gutiérrez, M.; El Idrissi, M.; El Alaoui El Abdallaoui, H.; Domingo, L.R. An MEDT study of the mechanism and selectivities of the [3 + 2] cycloaddition reaction of tomentosin with benzonitrile oxide. Int. J. Quantum Chem. 2019, 119, e25980. [Google Scholar] [CrossRef]
- Mirosław, B.; Babyuk, D.; Łapczuk-Krygier, A.; Kącka-Zych, A.; Demchuk, O.M.; Jasiński, R. Regiospecific formation of the nitromethyl-substituted 3-phenyl-4,5-dihydroisoxazole via [3 + 2] cycloaddition. Monatsh. Chem. 2018, 149, 1877–1884. [Google Scholar] [CrossRef]
- Ndassa, I.M.; Adjieufack, A.I.; Mbadcam Ketcha, J.; Berski, S.; Ríos-Gutiérrez, M.; Domingo, L.R. Understanding the reactivity and regioselectivity of [3 + 2] cycloaddition reactions between substituted nitrile oxides and methyl acrylate. A molecular electron density theory study. Int. J. Quantum Chem. 2017, 117, e25451. [Google Scholar] [CrossRef]
- Yavari, I.; Malekafzali, A.; Eivazzadeh-Keihan, R.; Skoulika, S.; Alivaisi, R. A one-pot synthesis of trichloromethylated pyrimidines from trichloroacetimidamides and acetylenic esters. Tetrahedron Lett. 2016, 57, 1733–1735. [Google Scholar] [CrossRef]
- Furuya, T.; Kamlet, A.S.; Ritter, T. Catalysis for fluorination and trifluoromethylation. Nature 2011, 473, 470–477. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Purser, S.; Moore, P.R.; Swallow, S.; Gouverneur, V. Fluorine in medicinal chemistry. Chem. Soc. Rev. 2008, 37, 320–330. [Google Scholar] [CrossRef]
- Darko, L.L. Synthesis and biological properties of certain trichloromethyl compounds. J. Med. Chem. 1971, 14, 527–528. [Google Scholar] [CrossRef]
- Srivastav, M.K.; Shantakumar, S.M. Design and Synthesis of novel 2-trichloromethyl-4-substituted quinazoline derivatives as anti-tubercular agents. Chem. Sci. Trans. 2013, 2, 1056–1062. [Google Scholar]
- Boguszewska-Czubara, A.; Kula, K.; Wnorowski, A.; Biernasiuk, A.; Popiolek, Ł.; Miodowski, D.; Demchuk, O.M.; Jasiński, R. Novel functionalized β-nitrostyrenes: Promising candidates for new antibacterial drugs. Saudi Pharm. J. 2019, 27, 593–601. [Google Scholar] [CrossRef] [PubMed]
- Boguszewska-Czubara, A.; Łapczuk-Krygier, A.; Rykała, K.; Biernasiuk, A.; Wnorowski, A.; Popiolek, Ł.; Maziarka, A.; Hordyjewska, A.; Jasiński, R. Novel synthesis scheme and in vitro antimicrobial evaluation of a panel of (E)-2-aryl-1-cyano-1-nitroethenes. J. Enzym. Inhib. Med. Chem. 2016, 31, 900–907. [Google Scholar] [CrossRef] [Green Version]
- Ono, N. Conversion of Nitro Compounds into Other Compounds. In The Nitro Group in Organic Synthesis; Wiley: New York, NY, USA, 2001; pp. 159–182. [Google Scholar]
- Ballini, R.; Petrini, M. Recent synthetic developments in the nitro to carbonyl conversion (Nef reaction). Tetrahedron 2004, 60, 1017–1047. [Google Scholar] [CrossRef]
- Sibi, M.P.; Manyem, S. Enantioselective Conjugate Additions. Tetrahedron 2000, 56, 8033–8061. [Google Scholar] [CrossRef]
- Halimehjani, A.Z.; Namboothini, I.N.N.; Hooshmand, S.E. Nitroalkenes in the synthesis of carbocyclic compounds. RSC Adv. 2014, 4, 31261–31299. [Google Scholar] [CrossRef]
- Kula, K.; Dobosz, J.; Jasiński, R.; Kącka-Zych, A.; Łapczuk-Krygier, A.; Mirosław, B.; Demchuk, O.M. [3 + 2] Cycloaddition of diaryldiazomethanes with (E)-3,3,3-trichloro-1-nitroprop-1-ene: An experimental, theoretical and structural study. J. Mol. Struct. 2020, 1203, 127473. [Google Scholar] [CrossRef]
- Kula, K.; Kącka-Zych, A.; Łapczuk-Krygier, A.; Wzorek, Z.; Nowak, A.; Jasiński, R. Experimental and theoretical mechanistic study on the thermal decomposition of 3,3-diphenyl-4-(trichloromethyl)-5-nitropyrazoline. Molecules 2021, 26, 1364. [Google Scholar] [CrossRef]
- Jasiński, R. The question of the regiodirection of the [2 + 3] cycloaddition reaction of triphenylnitrone to nitroethene. Chem. Heterocycl. Compd. 2009, 45, 748. [Google Scholar] [CrossRef]
- Jasiński, R.; Mróz, K.; Kącka-Zych, A. Experimental and theoretical DFT study on synthesis of sterically crowded 2,3,3,(4)5- tetrasubstituted-4-nitroisoxazolidines via 1,3-dipolar cycloaddition reactions between ketonitrones and conjugated nitroalkenes. J. Heterocycl. Chem. 2016, 53, 1424–1429. [Google Scholar] [CrossRef]
- Jasiński, R.; Mróz, K. Kinetic aspects of [3 + 2] cycloaddition reactions between (E)-3,3,3-trichloro-1-nitroprop-1-ene and ketonitrones. React. Kinet. Mech. Catal. 2015, 116, 35–41. [Google Scholar] [CrossRef] [Green Version]
- Domingo, L.R. Molecular Electron Density Theory: A modern view of reactivity in organic chemistry. Molecules 2016, 21, 1319. [Google Scholar] [CrossRef]
- Kula, K.; Dresler, E.; Demchuk, O.M.; Jasiński, R. New aldimine N-oxides as precursors for preparation of heterocycles with potential biological activity. Przem. Chem. 2015, 94, 1385–1387. [Google Scholar]
- Liu, K.-C.; Shelton, B.R.; Howe, R.K. A particularly convenient preparation of benzohydroximinoyl chlorides (nitrile oxide precursors). J. Org. Chem. 1980, 45, 3916–3918. [Google Scholar] [CrossRef]
- Perekalin, W.; Lipina, E.S.; Berestovitskaya, V.M.; Efremov, D.A. The Nitro-Aldol (Henry) Reaction. In Nitroalkenes: Conjugated Nitrocompounds, 1st ed.; Wiley: New York, NY, USA, 1994; pp. 30–70. [Google Scholar]
- Kącka, A.B.; Jasiński, R.A. A density functional theory mechanistic study of thermal decomposition reactions of nitroethyl carboxylates: Undermine of “pericyclic” insight. Heteroat. Chem. 2016, 27, 279–289. [Google Scholar] [CrossRef]
- Barbaro, G.; Battaglia, A.; Dondoni, A. Kinetics and mechanism of dimerisation of benzonitrile N-oxides to furazan N-oxides. J. Chem. Soc. B 1970, 588–592. [Google Scholar] [CrossRef]
- Silverstein, R.M.; Webster, F.X.; Kiemle, D.J.; Bryce, D.L. Spectrometric Identification of Organic Compounds, 8th ed.; Wiley: New York, NY, USA, 2014. [Google Scholar]
- Fryźlewicz, A.; Łapczuk-Krygier, A.; Kula, K.; Demchuk, O.M.; Dresler, E.; Jasiński, R. Regio- and stereoselective synthesis of nitro-functionalized analogs of nicotine. Chem. Heterocycl. Compd. 2020, 56, 120–122. [Google Scholar] [CrossRef]
- Becke, A.D.; Edgecombe, K.E. A simple measure of electron localization in atomic and molecular systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
- Adjieufack, A.I.; Ndassa, I.M.; Ketcha Mbadcam, J.; Ríos-Gutiérrez, M.; Domingo, L.R. Steric interactions controlling the syn diastereofacial selectivity in the [3 + 2] cycloaddition reaction between acetonitrile oxide and 7-oxanorborn-5-en-2-ones: A molecular electron density theory study. J. Phys. Org. Chem. 2017, 30, e3710. [Google Scholar] [CrossRef]
- Domingo, L.R.; Aurell, M.J.; Pérez, P. A DFT analysis of the participation of zwitterionic TACs in polar [3 + 2] cycloaddition reactions. Tetrahedron 2014, 70, 4519–4525. [Google Scholar] [CrossRef]
- Huisgen, R. 1,3-dipolar cycloaddition. Proc. Chem. Soc. 1961, 357–396. [Google Scholar]
- Parr, R.G.; Yang, W. Density Functional Theory of Atoms and Molecules, 1st ed.; Oxford University Press: New York, NY, USA, 1989. [Google Scholar]
- Domingo, L.R.; Ríos-Gutiérrez, M.; Pérez, P. Applications of the Conceptual Density Functional Theory Indices to Organic Chemistry Reactivity. Molecules 2016, 21, 748. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Parr, R.G.; Pearson, R.G. Absolute Hardness: Companion Parameter to Absolute Electronegativity. J. Am. Chem. Soc. 1983, 105, 7512–7516. [Google Scholar] [CrossRef]
- Domingo, L.R.; Ríos-Gutiérrez, M.; Pérez, P. A molecular electron density theory study of the participation of tetrazines in aza-Diels–Alder reactions. RSC Adv. 2020, 10, 15394–15405. [Google Scholar] [CrossRef] [Green Version]
- Domingo, L.R.; Kula, K.; Ríos-Gutiérrez, M. Unveiling the reactivity of cyclic azomethine ylides in [3 + 2] cycloaddition reactions within the Molecular Electron Density Theory. Eur. J. Org. Chem. 2020, 2020, 5938–5948. [Google Scholar]
- Parr, R.G.; Szentpaly, L.V.; Liu, S. Electrophilicity Index. J. Am. Chem. Soc. 1999, 121, 1922–1924. [Google Scholar] [CrossRef]
- Domingo, L.R.; Aurell, M.J.; Pérez, P.; Contreras, R. Quantitative characterization of the global electrophilicity power of common diene/dienophile pairs in Diels–Alder reactions. Tetrahedron 2002, 58, 4417–4423. [Google Scholar] [CrossRef]
- Jaramillo, P.; Domingo, L.R.; Chamorro, E.; Pérez, P. A further exploration of a nucleophilicity index based on the gas-phase ionization potentials. J. Mol. Struct. THEOCHEM 2008, 865, 68–72. [Google Scholar] [CrossRef]
- Aurell, M.J.; Domingo, L.R.; Pérez, P.; Contreras, R. A theoretical study on the regioselectivity of 1,3-dipolar cycloadditions using DFT-based reactivity indexes. Tetrahedron 2004, 60, 11503–11509. [Google Scholar] [CrossRef]
- Domingo, L.R.; Pérez, P.; Sáez, J.A. Understanding the local reactivity in polar organic reactions through electrophilic and nucleophilic Parr functions. RSC Adv. 2013, 3, 1486–1494. [Google Scholar] [CrossRef]
- Evans, M.G.; Polanyi, M. Some applications of the transition state method to the calculation of reaction velocities, especially in solution. Trans. Faraday Soc. 1935, 31, 875–894. [Google Scholar] [CrossRef]
- Domingo, L.R. A new C–C bond formation model based on the quantum chemical topology of electron density. RSC Adv. 2014, 4, 32415–32428. [Google Scholar] [CrossRef] [Green Version]
- Zawadzińska, K.; Kula, K. Application of β-phosphorylated nitroethenes in [3 + 2] cycloaddition reactions involving benzonitrile N-oxide in the light of DFT computational study. Organics 2021, 2, 26–37. [Google Scholar] [CrossRef]
- Krokidis, X.; Noury, S.; Silvi, B. Characterization of elementary chemical processes by catastrophe theory. J. Phys. Chem. A 1997, 101, 7277–7283. [Google Scholar] [CrossRef]
- Berski, S.; Andrés, J.; Silvi, B.; Domingo, L.R. The Joint Use of Catastrophe Theory and Electron Localization Function to Characterize Molecular Mechanisms. A Density Functional Study of the Diels−Alder Reaction between Ethylene and 1,3-Butadiene. J. Phys. Chem. A 2003, 107, 6014–6024. [Google Scholar] [CrossRef]
- Polo, V.; Andrés, J.; Berski, S.; Domingo, L.R.; Silvi, B. Understanding reaction mechanisms in organic chemistry from catastrophe theory applied to the electron localization function topology. J. Phys. Chem. A 2008, 112, 7128–7136. [Google Scholar] [CrossRef]
- Domingo, L.R.; Picher, M.T.; Arroyo, P.; Sáez, J.A. 1,3-Dipolar Cycloadditions of Electrophilically Activated Benzonitrile N-Oxides. Polar Cycloaddition versus Oxime Formation. J. Org. Chem. 2006, 71, 9319–9330. [Google Scholar] [CrossRef]
- Kula, K.; Zawadzińska, K. Local nucleophile-electrophile interactions in [3 + 2] cycloaddition reactions between benzonitrile N-oxide and selected conjugated nitroalkenes in the light of MEDT computational study. Curr. Chem. Lett. 2021, 10, 9–16. [Google Scholar] [CrossRef]
- Jasiński, R.; Jasińska, E.; Dresler, E. A DFT computational study of the molecular mechanism of [3 + 2] cycloaddition reactions between nitroethene and benzonitrile N-oxides. J. Mol. Model. 2017, 23, 13. [Google Scholar] [CrossRef] [Green Version]
- Łapczuk-Krygier, A.; Kącka-Zych, A.; Kula, K. Recent progress in the field of cycloaddition reactions involving conjugated nitroalkenes. Curr. Chem. Lett. 2019, 8, 13–38. [Google Scholar] [CrossRef]
- Jasinski, R.; Dresler, E. On the Question of Zwitterionic Intermediates in the [3 + 2] Cycloaddition Reactions: A Critical Review. Organics 2020, 1, 49–69. [Google Scholar] [CrossRef]
- Domingo, L.R.; Sáez, J.A. Understanding the Electronic Reorganization along the Nonpolar [3 + 2] Cycloaddition Reactions of Carbonyl Ylides. J. Org. Chem. 2011, 76, 373–379. [Google Scholar] [CrossRef]
- Domingo, L.R.; Acharjee, N. Unveiling the Chemo- and Regioselectivity of the [3 + 2] Cycloaddition Reaction between 4-Chlorobenzonitrile Oxide and β-Aminocinnamonitrile with a MEDT Perspective. ChemistrySelect 2021, 6, 4521. [Google Scholar] [CrossRef]
- Domingo, L.R.; Sáez, J.A.; Zaragozá, R.J.; Arnó, M. Understanding the Participation of Quadricyclane as Nucleophile in Polar [2σ + 2σ + 2π] Cycloadditions toward Electrophilic π Molecules. J. Org. Chem. 2008, 73, 8791–8799. [Google Scholar] [CrossRef] [PubMed]
- Sheldrick, G.M. A short history of SHELX. Acta Crystallogr. Sect. A 2008, 64, 112–122. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. OLEX2: A complete structure solution, refinement and analysis program. J. Appl. Crystallogr. 2009, 42, 339–341. [Google Scholar] [CrossRef]
- Chai, J.-D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [Green Version]
- Hehre, W.J.; Radom, L.; Schleyer, P.v.R.; Pople, J.A. Ab Initio Molecular Orbital Theory; Wiley: New York, NY, USA, 1986. [Google Scholar]
- Schlegel, H.B. Optimization of equilibrium geometries and transition structures. J. Comput. Chem. 1982, 3, 214–218. [Google Scholar] [CrossRef]
- Schlegel, H.B. Geometry Optimization on Potential Energy Surfaces. In Modern Electronic Structure Theory; Yarkony, D.R., Ed.; World Scientific Publishing: Singapore, 1994; pp. 459–501. [Google Scholar]
- Kula, K.; Łapczuk-Krygier, A. A DFT computational study on the [3 + 2] cycloaddition between parent thionitrone and nitroethene. Curr. Chem. Lett. 2018, 7, 27–34. [Google Scholar] [CrossRef]
- Mlostoń, G.; Jasiński, R.; Kula, K.; Heimgartner, H. A DFT Study on the Barton-Kellogg Reaction—The molecular mechanism of the formation of thiiranes in the reaction between diphenyldiazomethane and diaryl thioketones. Eur. J. Org. Chem. 2020, 176–182. [Google Scholar] [CrossRef]
- Jasiński, R. On the Question of Stepwise [4 + 2] Cycloaddition Reactions and Their Stereochemical Aspects. Symmetry 2021, 13, 1911. [Google Scholar] [CrossRef]
- Domingo, L.R.; Kula, K.; Ríos-Gutiérrez, M.; Jasiński, R. Understanding the Participation of Fluorinated Azomethine Ylides in Carbenoid-Type [3 + 2] Cycloaddition Reactions with Ynal Systems: A Molecular Electron Density Theory Study. J. Org. Chem. 2021, 86, 12644–12653. [Google Scholar] [CrossRef]
- Jasiński, R. β-Trifluoromethylated nitroethenes in Diels-Alder reaction with cyclopentadiene: A DFT computational study. J. Fluor. Chem. 2018, 206, 1–7. [Google Scholar] [CrossRef]
- Fukui, K. Formulation of the reaction coordinate. J. Phys. Chem. 1970, 74, 4161–4163. [Google Scholar] [CrossRef]
- Gonzalez, C.; Schlegel, H.B. Reaction path following in mass-weighted internal coordinates. J. Phys. Chem. 1990, 94, 5523–5527. [Google Scholar] [CrossRef]
- Gonzalez, C.; Schlegel, H.B. Improved algorithms for reaction path following: Higher order implicit algorithms. J. Chem. Phys. 1991, 95, 5853–5860. [Google Scholar] [CrossRef] [Green Version]
- Tomasi, J.; Persico, M. Molecular Interactions in Solution: An Overview of Methods Based on Continuous Distributions of the Solvent. Chem. Rev. 1994, 94, 2027–2094. [Google Scholar] [CrossRef]
- Simkin, Y.; Sheikhet, I. Quantum Chemical and Statistical Theory of Solutions: A Computational Approach; Ellis Horwood: London, UK, 1995. [Google Scholar]
- Cossi, M.; Barone, V.; Cammi, R.; Tomasi, J. Ab initio study of solvated molecules: A new implementation of the polarizable continuum model. Chem. Phys. Chem. 1996, 225, 327–335. [Google Scholar] [CrossRef]
- Cances, E. A new integral equation formalism for the polarizable continuum model: Theoretical background and applications to isotropic and anisotropic dielectrics. J. Chem. Phys. 1997, 107, 3032–3041. [Google Scholar] [CrossRef]
- Barone, V.; Cossi, M.; Tomasi, J. Geometry optimization of molecular structures in solution by the polarizable continuum model. J. Comput. Chem. 1998, 19, 404–417. [Google Scholar] [CrossRef]
- Reed, A.E.; Weinstock, R.B.; Weinhold, F. Natural population analysis. J. Chem. Phys. 1985, 83, 735–746. [Google Scholar] [CrossRef]
- Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
- Domingo, L.R.; Chamorro, E.; Pérez, P. Understanding the Reactivity of Captodative Ethylenes in Polar Cycloaddition Reactions. A Theoretical Study. J. Org. Chem. 2008, 73, 4615–4624. [Google Scholar] [CrossRef] [PubMed]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, 1133–1138. [Google Scholar] [CrossRef] [Green Version]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Fox, D.J.; et al. (Eds.) Gaussian 16; Revision, A.03; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Noury, S.; Krokidis, X.; Fuster, F.; Silvi, B. Computational tools for the electron localization function topological analysis. Comput. Chem. 1999, 23, 597–604. [Google Scholar] [CrossRef]
- Dennington, R.; Keith, T.A.; Millam, J.M. (Eds.) Gauss View, Version 6; Semichem Inc.: Shawnee Mission, KS, USA, 2016. [Google Scholar]



| Method | Base | Temp. [°C] | Time [h] | Molar Ratio Hydroxamoyl Chlorides/Nitroalkene | Yield [%] | |
|---|---|---|---|---|---|---|
| Isoxazoline | Furoxan | |||||
| 1 | K2CO3 | 25 (r.t.) | 24 | 1:1.25 | 40.0 | 1.0 |
| 66 (reflux) | 6 | 1:1.25 | 40.0 | 8.1 | ||
| 2 | TEA | 25 (r.t.) | 24 | 1:1.25 | 44.4 | 0.9 |
| 66 (reflux) | 6 | 1:1.25 | 43.5 | 5.0 | ||
| 1 | K2CO3 | 25 (r.t.) | 24 | 1:2 | 9.8 | 0.8 |
| 66 (reflux) | 6 | 1:2 | 25.6 | 7.5 | ||
| 2 | TEA | 25 (r.t.) | 24 | 1:2 | 20.8 | 0.7 |
| 66 (reflux) | 6 | 1:2 | 47.6 | 10.6 | ||
| Compound | μ | η | ω | N |
|---|---|---|---|---|
| 1b | −3.42 | 4.91 | 1.19 | 3.24 |
| 1a | −3.69 | 4.97 | 1.37 | 2.95 |
| 1c | −3.85 | 5.02 | 1.47 | 2.76 |
| 1d | −4.12 | 4.96 | 1.71 | 2.52 |
| 1e | −5.04 | 4.03 | 3.15 | 2.07 |
| 2 | −5.84 | 5.22 | 3.27 | 0.67 |
| 3 | 4 | |
|---|---|---|
| Cl (d) | 91.4 | 8.6 |
| MeO (b) | 98.0 | 2.0 |
| NO2 (e) | 88.7 | 11.3 |
| F (c) | 97.1 | 2.9 |
| Me (a) | 98.1 | 1.9 |
| TS-o-b | S1-b | S2-b | S3-b | S4-b | 3b | |
|---|---|---|---|---|---|---|
| d(O1-C4) | 2.051 | 1.865 | 1.856 | 1.760 | 1.751 | 1.428 |
| d(C3-C5) | 2.253 | 1.999 | 1.988 | 1.862 | 1.850 | 1.512 |
| V(O1,N2) | 1.40 | 1.31 | 1.30 | 1.23 | 1.23 | 1.07 |
| V(N2) | 2.09 | 2.44 | 2.46 | 2.58 | 2.60 | 2.80 |
| V(N2,C3) | 2.17 | 1.81 | 1.80 | 1.75 | 1.74 | 1.67 |
| V′(N2,C3) | 2.12 | 1.90 | 1.89 | 1.81 | 1.81 | 1.60 |
| V(C4,C5) | 3.45 | 2.47 | 2.45 | 2.29 | 2.27 | 2.03 |
| V(O1) | 2.83 | 2.73 | 2.72 | 2.65 | 2.62 | 2.47 |
| V′(O1) | 2.82 | 2.89 | 2.89 | 2.59 | 2.56 | 2.42 |
| V′′(O1) | 0.51 | |||||
| V(C4) | 0.26 | 0.27 | 0.18 | |||
| V(C3) | 0.51 | |||||
| V(C5) | 0.79 | |||||
| V(C3,C5) | 1.32 | 1.56 | 1.57 | 2.01 | ||
| V(O1,C4) | 0.79 | 1.33 |
| TS-o-e | S1-e | S2-e | S3-e | S4-e | 3e | |
|---|---|---|---|---|---|---|
| d(O1-C4) | 2.105 | 1.932 | 1.924 | 1.770 | 1.761 | 1.429 |
| d(C3-C4) | 2.217 | 1.972 | 1.960 | 1.771 | 1.761 | 1.509 |
| V(O1,N2) | 1.44 | 1.34 | 1.33 | 1.23 | 1.23 | 1.08 |
| V(N2) | 2.01 | 2.39 | 2.41 | 2.61 | 2.62 | 2.79 |
| V(N2,C3) | 2.25 | 1.83 | 1.83 | 1.74 | 1.73 | 1.67 |
| V′(N2,C3) | 2.15 | 1.91 | 1.90 | 1.78 | 1.78 | 1.61 |
| V(C4,C5) | 3.43 | 2.49 | 2.47 | 2.23 | 2.21 | 2.04 |
| V(O1) | 2.82 | 2.74 | 2.73 | 2.64 | 2.62 | 2.47 |
| V′(O1) | 2.79 | 2.84 | 2.85 | 2.57 | 2.54 | 2.40 |
| V′′(O1) | 0.53 | |||||
| V(C4) | 0.23 | 0.24 | 0.20 | |||
| V(C3) | 0.56 | |||||
| V(C5) | 0.75 | |||||
| V(C3,C5) | 1.33 | 1.67 | 1.68 | 2.02 | ||
| V(O1,C4) | 0.81 | 1.34 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zawadzińska, K.; Ríos-Gutiérrez, M.; Kula, K.; Woliński, P.; Mirosław, B.; Krawczyk, T.; Jasiński, R. The Participation of 3,3,3-Trichloro-1-nitroprop-1-ene in the [3 + 2] Cycloaddition Reaction with Selected Nitrile N-Oxides in the Light of the Experimental and MEDT Quantum Chemical Study. Molecules 2021, 26, 6774. https://doi.org/10.3390/molecules26226774
Zawadzińska K, Ríos-Gutiérrez M, Kula K, Woliński P, Mirosław B, Krawczyk T, Jasiński R. The Participation of 3,3,3-Trichloro-1-nitroprop-1-ene in the [3 + 2] Cycloaddition Reaction with Selected Nitrile N-Oxides in the Light of the Experimental and MEDT Quantum Chemical Study. Molecules. 2021; 26(22):6774. https://doi.org/10.3390/molecules26226774
Chicago/Turabian StyleZawadzińska, Karolina, Mar Ríos-Gutiérrez, Karolina Kula, Przemysław Woliński, Barbara Mirosław, Tomasz Krawczyk, and Radomir Jasiński. 2021. "The Participation of 3,3,3-Trichloro-1-nitroprop-1-ene in the [3 + 2] Cycloaddition Reaction with Selected Nitrile N-Oxides in the Light of the Experimental and MEDT Quantum Chemical Study" Molecules 26, no. 22: 6774. https://doi.org/10.3390/molecules26226774
APA StyleZawadzińska, K., Ríos-Gutiérrez, M., Kula, K., Woliński, P., Mirosław, B., Krawczyk, T., & Jasiński, R. (2021). The Participation of 3,3,3-Trichloro-1-nitroprop-1-ene in the [3 + 2] Cycloaddition Reaction with Selected Nitrile N-Oxides in the Light of the Experimental and MEDT Quantum Chemical Study. Molecules, 26(22), 6774. https://doi.org/10.3390/molecules26226774










