Ferroelectric Particles in Nematic Liquid Crystals with Soft Anchoring
Abstract
:1. Introduction
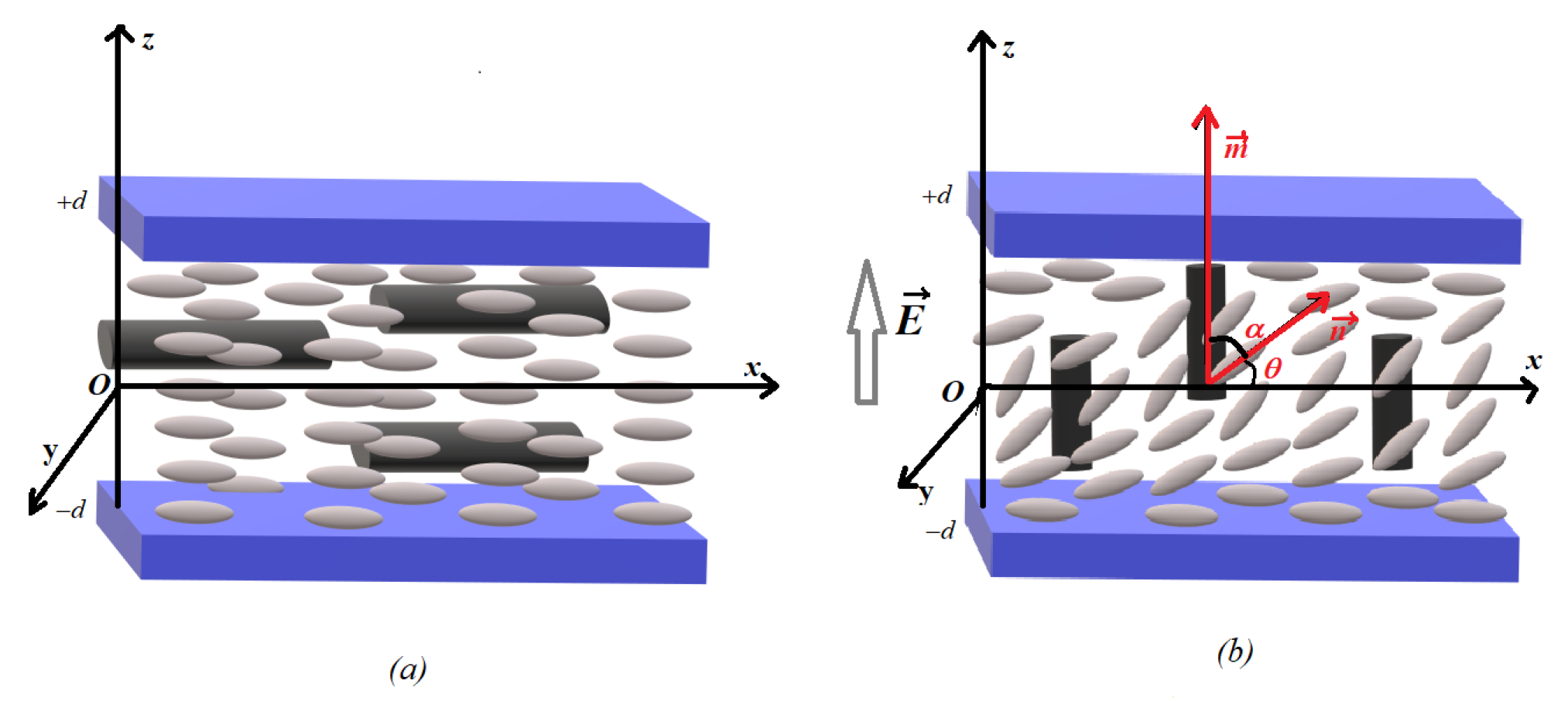
2. Theory and Calculations
2.1. Theory and Calculations
2.2. Freedericksz Transition Threshold
2.3. Saturation Field
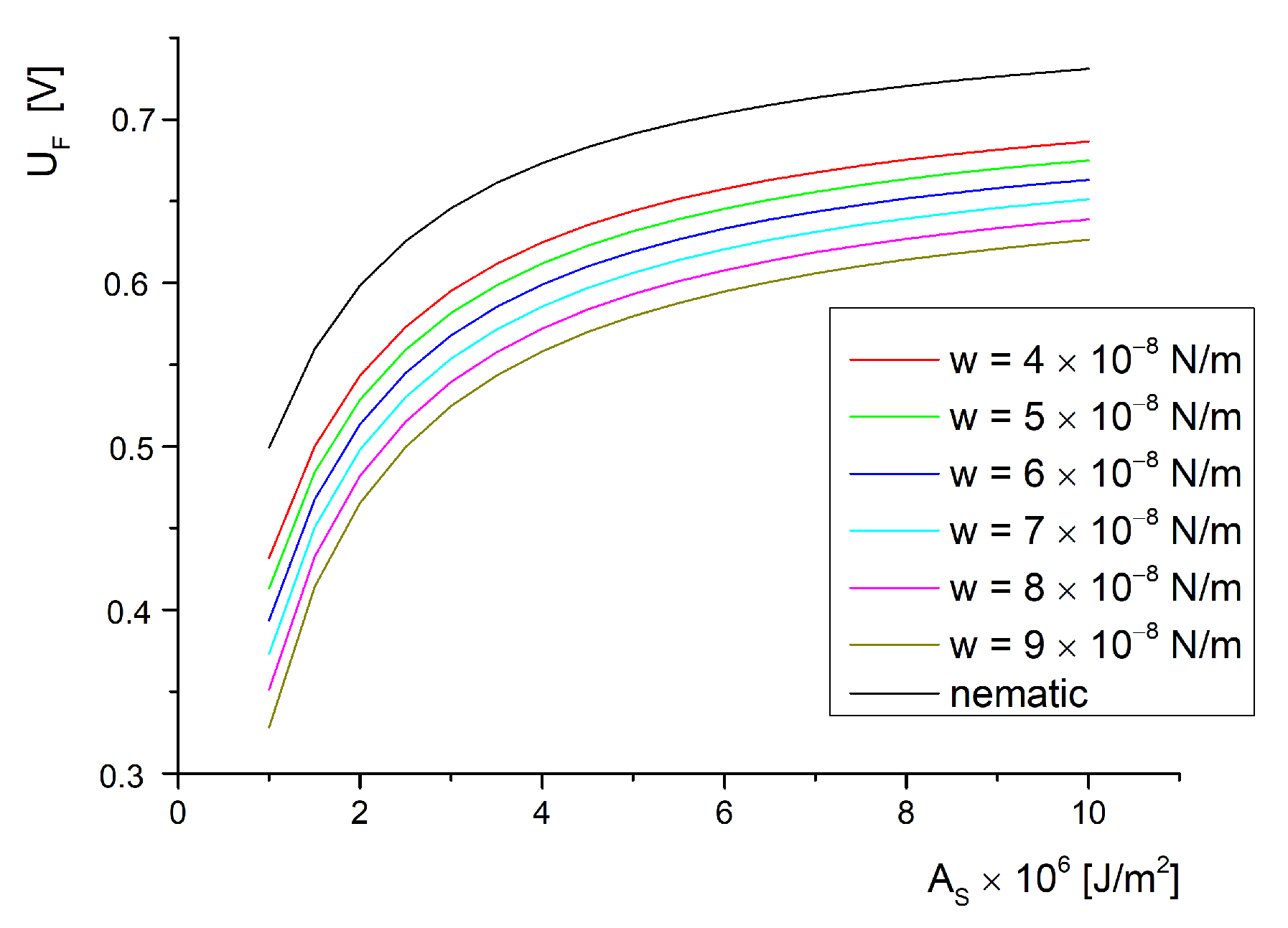
3. Results and Discussions
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Guo, Q.; Srivastava, A.K.; Chigrinov, V.G.; Kwok, H.S. Polymer and azo-dye composite:a photo-alignment layer for liquid crystals. Liq. Cryst. 2014, 41, 1465–1472. [Google Scholar] [CrossRef]
- Motoc, C.; Iacobescu, G. Magnetic field effects on the optical properties of an azo-dye doped liquid crystal. J. Magn. Magn. Mater. 2006, 306, 103–107. [Google Scholar] [CrossRef]
- Singh, S. Impact of Dispersion of Nanoscale Particles on the Properties of Nematic Liquid Crystals. Crystals 2019, 9, 475. [Google Scholar] [CrossRef] [Green Version]
- Petrescu, E.; Cirtoaje, C.; Danila, O. Dynamic behaviour of nematic liquid crystal mixtures with quantum dots in electric fields. Beilstein J. Nanotechnol. 2018, 9, 399–406. [Google Scholar] [CrossRef] [Green Version]
- Pandey, F.P.; Rastogi, A.; Singh, S. Optical properties and zeta potential of carbon quantum dots (CQDs) dispersed nematic liquid crystal 4′-heptyl-4-biphenylcarbonitrile (7CB). Opt. Mater. 2020, 105, 109849. [Google Scholar] [CrossRef]
- Barar, A.; Manaila-Maximean, D.; Vladescu, M.; Schiopu, P. Simulation of charge carrier transport mechanisms for quantum dot-sensitized solar cell structures. Univ. Politeh. Buchar. Ser. A 2019, 81, 265–270. [Google Scholar]
- Zakhlevnykh, A.N.; Petrov, D.A. Orientational bistability in ferronematic liquid crystals with negative diamagnetic anisotropy. J. Magn. Magn. Mater. 2015, 393, 517–525. [Google Scholar] [CrossRef]
- Petrescu, E.; Bena, R.; Cristina, C. Polarisation gratings using ferronematics-an elastic continuum theory. J. Magn. Magn. Mater. 2013, 336, 44–48. [Google Scholar] [CrossRef]
- Jepu, I.; Porosnicu, C.; Lungu, C.P.; Mustata, I.; Luculescu, C.; Kuncser, V.; Iacobescu, G.; Marin, A.; Ciupina, V. Combinatorial Fe–Co thin film magnetic structures obtained by thermionic vacuum arc method. Surf. Coat. Technol. 2014, 240, 344–352. [Google Scholar] [CrossRef] [Green Version]
- Maximean, D.M. New grafted ferrite particles/liquid crystal composite under magnetic field. J. Magn. Magn. Mater. 2018, 452, 343–348. [Google Scholar] [CrossRef]
- Petrov, D.A.; Skokov, P.K.; Zakhlevnykh, A.N. Magnetic field induced orientational transitions in liquid crystals doped with carbon nanotubes. Beilstein J. Nanotechnol. 2017, 8, 2807–2817. [Google Scholar] [CrossRef] [Green Version]
- Staic, M.D.; Petrescu-Nita, A. Symmetry group of two special types of carbon nanotori. Acta Cryst. 2013, A69, 435–439. [Google Scholar] [CrossRef]
- Lisetski, L.; Fedoryako, A.P.; Samoilov, A.N.; Minenko, S.S.; Soskin, M.S.; Lebovka, N.I. Optical transmission of nematic liquid crystal 5CB doped by single-walled and multi-walled carbon nanotubes. Eur. Phys. 2014, 37. [Google Scholar] [CrossRef] [PubMed]
- Il’in, V.A.; Mordvinov, A.N.; Petrov, D.A. Electroconvection of a poorly conducting fluid under unipolar charge injection in a steady electric field. J. Exp. Theor. Phys. 2015, 120, 161–168. [Google Scholar] [CrossRef]
- Reshetnyak, Y.Y.; Shelestiuk, S.A.; Sluckin, T.J. Fredericksz Transition Threshold in Nematic Liquid Crystals Filled with Ferroelectric Nano-Particles. Mol. Cryst. Liq. Cryst. 2006, 454. [Google Scholar] [CrossRef]
- Reshetnyak, Y.Y.; Shelestiuk, S.A.; Sluckin, T.J. Frederiks transition in ferroelectric liquid-crystal nanosuspensions. Phys. Rev. E 2011, 83, 041705. [Google Scholar] [CrossRef] [Green Version]
- Cirtoaje, C.; Petrescu, E.; Stoian, V. Electrical Freedericksz transitions in nematic liquid crystals containing ferroelectric nanoparticles. Phys. E 2015, 67, 23–27. [Google Scholar] [CrossRef]
- Paul, S.N.; Dhar, R.; Verma, R.; Sharma, S.; Dabrowski, R. Molecular Crystals and Liquid Crystals Change in Dielectric and Electro-Optical Properties of a Nematic Material (6CHBT) Due to the Dispersion of BaTiO 3 Nanoparticles. Mol. Cryst. Liq. Cryst. 2011, 545. [Google Scholar] [CrossRef]
- Scolari, L.; Gauza, S.; Xianyu, H.; Zhai, L.; Eskildsen, L.; Alkeskjold, T.T.; Wu, S.T.; Bjarklev, A. Frequency tunability of solid-core photonic crystal fibers filled with nanoparticle-doped liquid crystals. Opt. Express 2009, 17, 3754–3764. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Garbovskiy, Y.; Glushchenko, A. Ferroelectric Nanoparticles in Liquid Crystals: Recent Progress and Current Challenges. Nanomaterials 2017, 7, 361. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Blach, J.F.; Saitzek, S.; Legrand, C.; Dupont, L.; Henninot, J.F.; Warenghem, M. BaTiO3 ferroelectric nanoparticles dispersed in 5CB nematic liquid crystal: Synthesis and electro-optical characterization. J. Appl. Phys. 2010, 107, 074102. [Google Scholar] [CrossRef]
- Klein, S.; Richardson, R.M.; Greasty, R.J.; Jenkins, R.; Stone, J.; Thomas, M.R.; Sarua, A. The influence of suspended nanoparticles on the Frederiks threshold of the nematic host. Philos. Trans. R. Soc. A 2013, 371, 20120253. [Google Scholar] [CrossRef] [PubMed]
- Mishra, M.; Dabrowski, R.S.; Dhar, R. Thermodinamical, optical and electro-optical studies of a room temperature liquid crystal 4-pentyl-4′-cyanobiphenyl dispersed with barium titanate nanoparticles. J. Mol. Liq. 2016, 213, 247–254. [Google Scholar] [CrossRef]
- Ibragimov, T.D.; Imamaliyev, A.R.; Bayramov, G.M. Electro-optic properties of the BaTiO3-Liquid crystal 5CB colloid. Optik 2016, 127, 2278–2281. [Google Scholar] [CrossRef]
- Burylov, S.V.; Zakhlevnykh, A.N. Orientational energy of anisometric particles in liquid-crystalline suspensions. Phys. Rev. E 2013, 88, 012511. [Google Scholar] [CrossRef]
- Knyazeva, L.I.; Makarov, D.V. Effects of High Order Surface Anchoring Anisotropy in Ferronematic Liquid Crystals. Liq. Cryst. Their Appl. 2018, 18, 78–87. [Google Scholar] [CrossRef] [Green Version]
- Rapini, A.; Papoular, M. Distorsion D’Une Lamelle NéMatique Sous Champ MagnéTique Conditions D’Ancrage Aux Parois. J. Physique Colloq. 1969, 30, C4-54–C4-56. [Google Scholar] [CrossRef]
- Guochen, Y.; Jianru, S.; Ying, L. Surface anchoring energy and the first order Freedericksz transition of a NLC cell. Liq. Cryst. 2000, 27, 875–882. [Google Scholar] [CrossRef]
- Petrescu, E.; Teodorescu, S.; Iuciuc, E.; Alexandru, V. Temperature dependence of Freedericksz transition in nematic liquid crystals with quantum dots. Univ. Politeh. Buchar. Sci. Bull. Ser. A 2018, 80, 281–288. [Google Scholar]
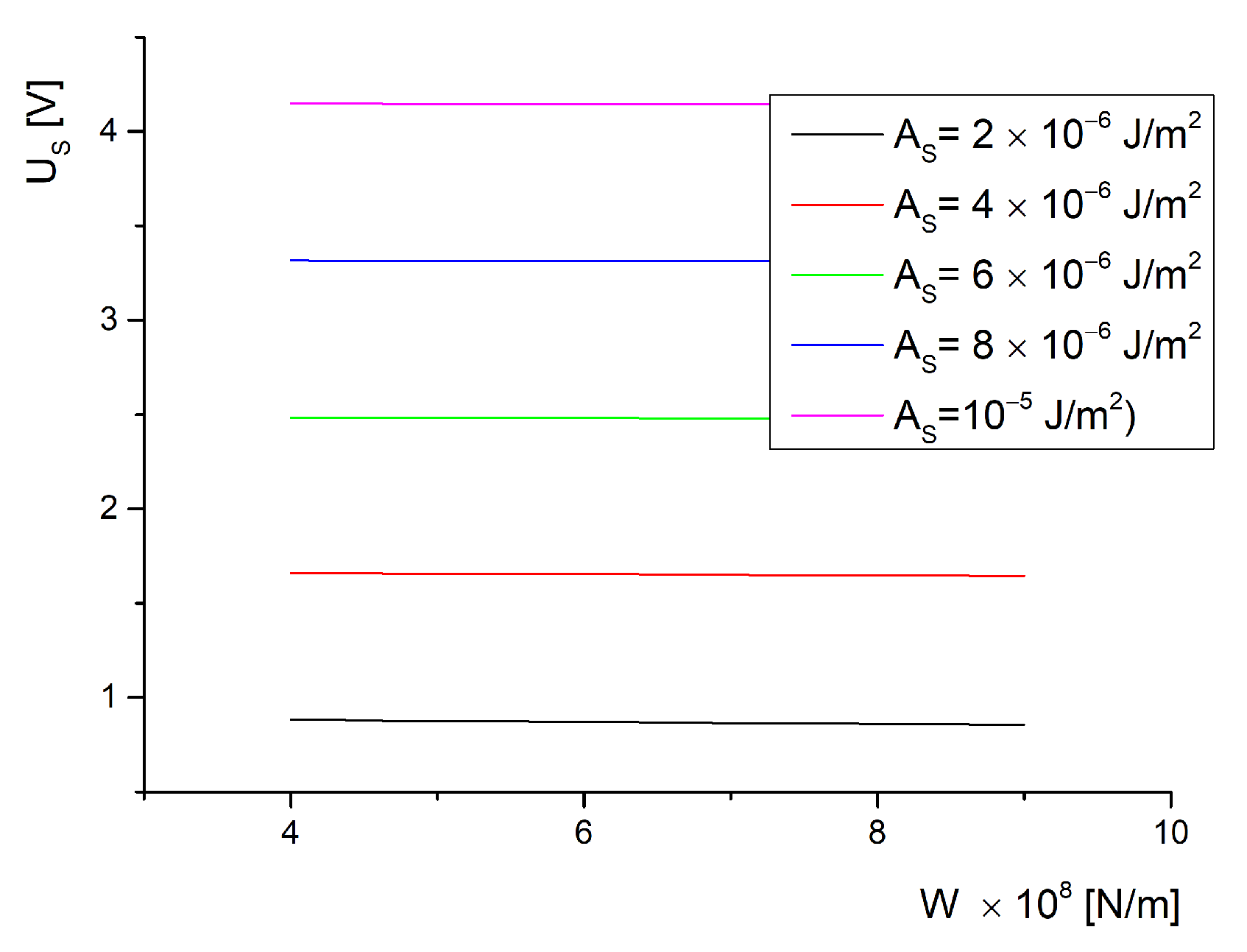


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cirtoaje, C. Ferroelectric Particles in Nematic Liquid Crystals with Soft Anchoring. Molecules 2021, 26, 1166. https://doi.org/10.3390/molecules26041166
Cirtoaje C. Ferroelectric Particles in Nematic Liquid Crystals with Soft Anchoring. Molecules. 2021; 26(4):1166. https://doi.org/10.3390/molecules26041166
Chicago/Turabian StyleCirtoaje, Cristina. 2021. "Ferroelectric Particles in Nematic Liquid Crystals with Soft Anchoring" Molecules 26, no. 4: 1166. https://doi.org/10.3390/molecules26041166
APA StyleCirtoaje, C. (2021). Ferroelectric Particles in Nematic Liquid Crystals with Soft Anchoring. Molecules, 26(4), 1166. https://doi.org/10.3390/molecules26041166






