Quasi-Classical Trajectory Study of the CN + NH3 Reaction Based on a Global Potential Energy Surface
Abstract
:1. Introduction
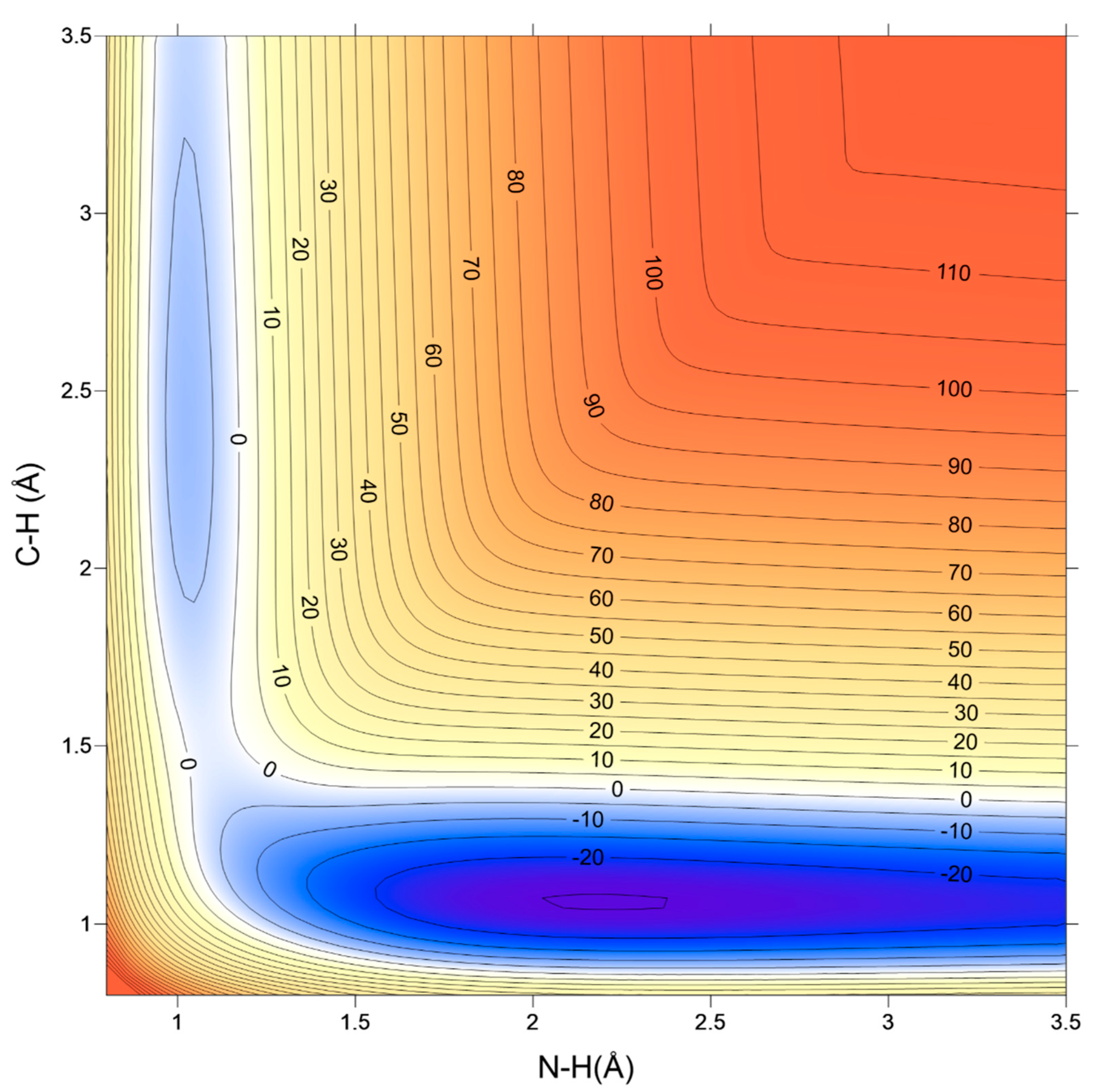
2. Global Potential Energy Surface
3. Kinetics and Dynamic Tools
4. Results and Discussion
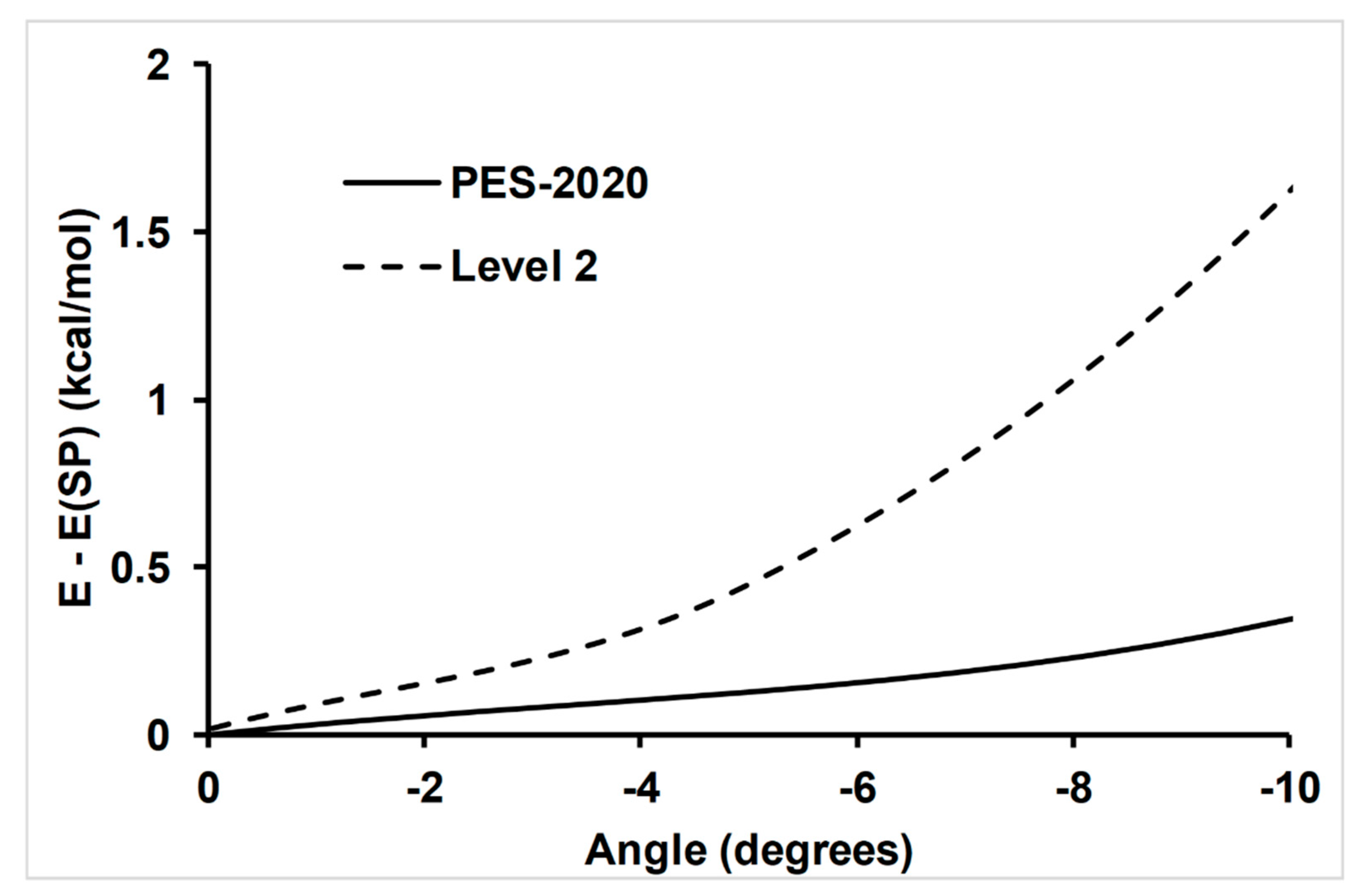
4.1. Accuracy of the Fitting Process; Self-Consistency Test
4.2. Kinetics Results
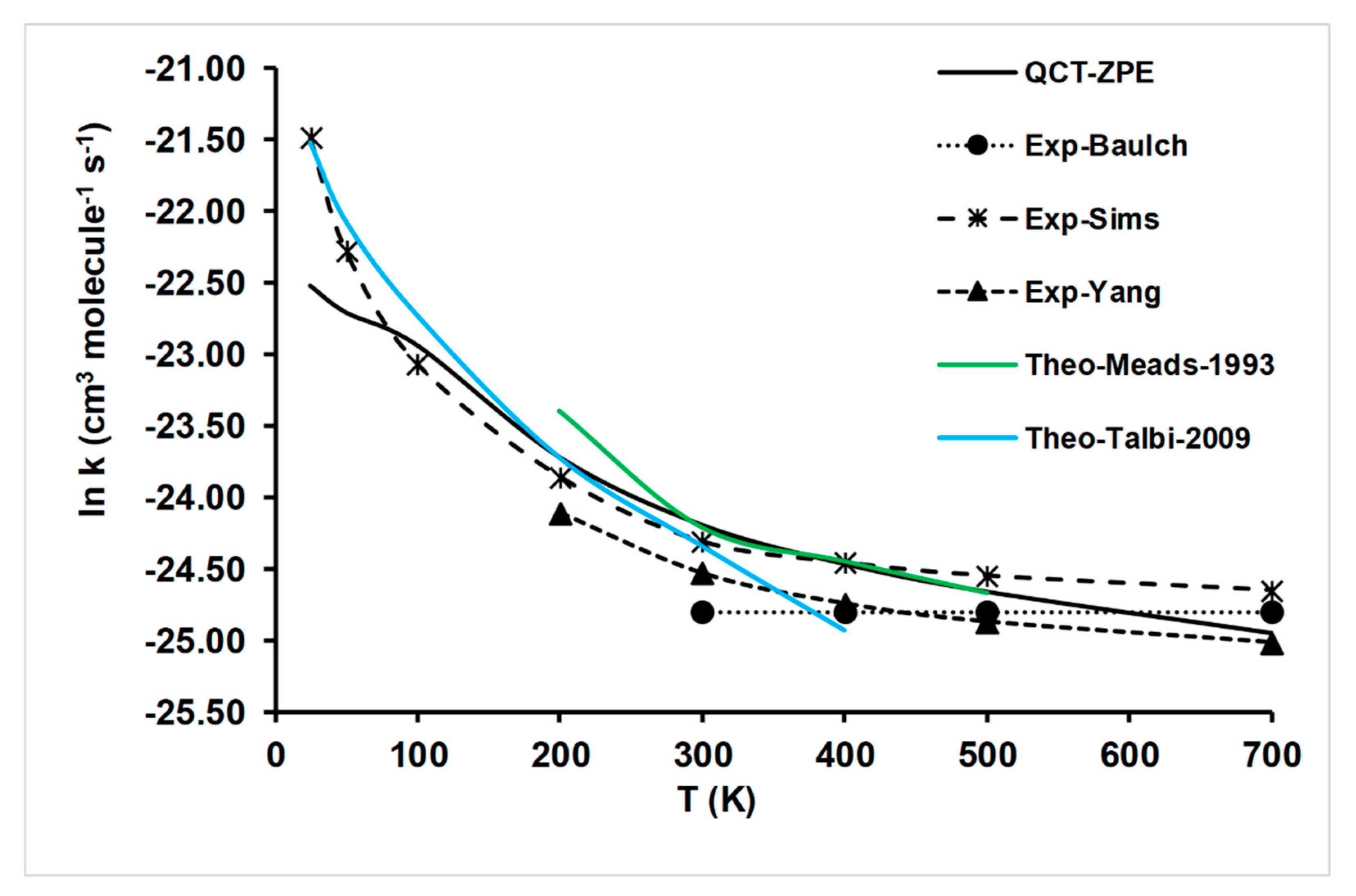
4.2.1. Rate Constant Calculations
4.2.2. Kinetics Isotope Effects (KIEs)
4.3. Dynamics Results
4.3.1. Effect of the CN (v = 1) Vibrational Excitation on Reactivity
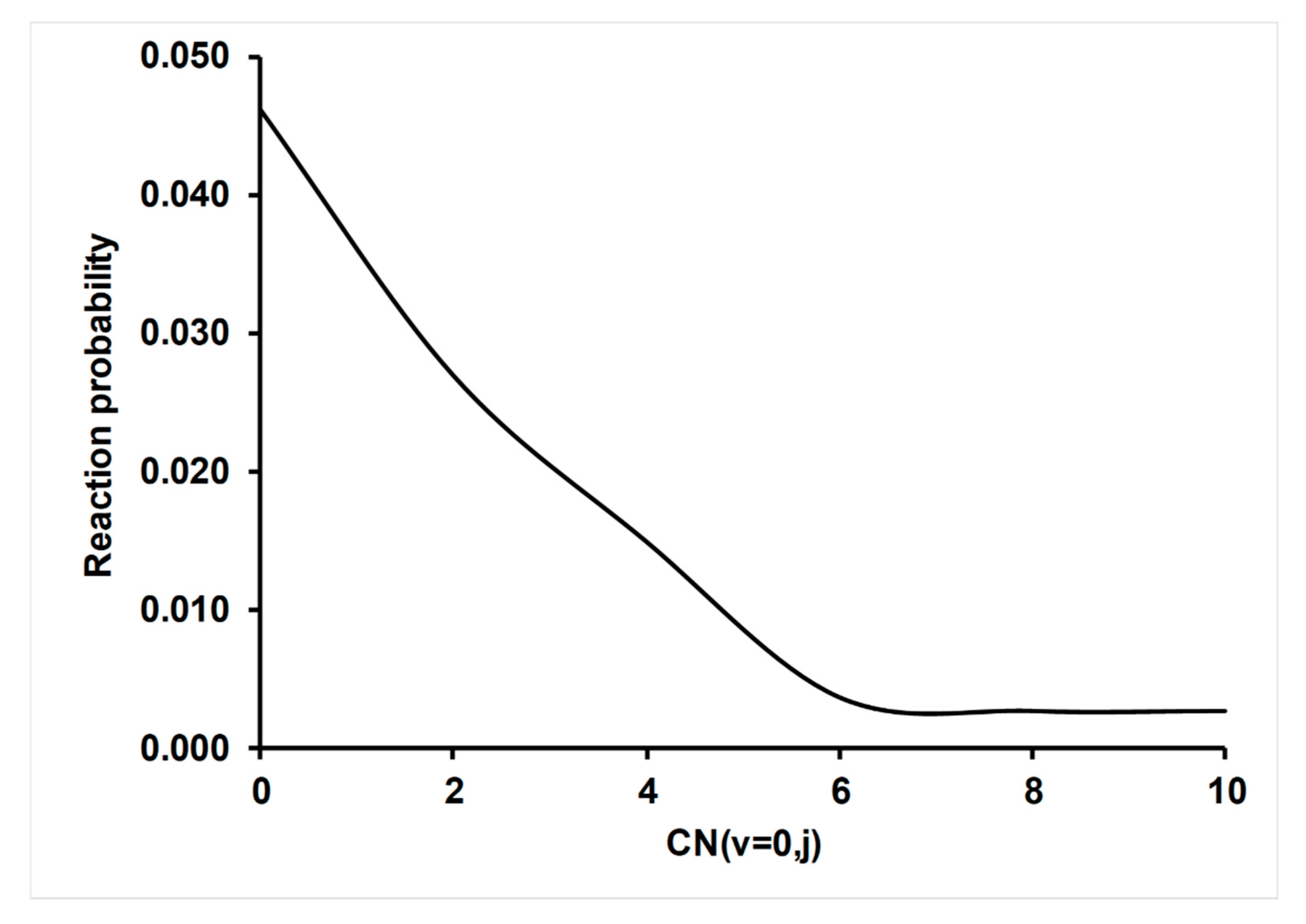
4.3.2. Effect of CN (v,j) Rotational Excitation on Reactivity
4.3.3. Product Angular Distribution
5. Conclusions
- In general, PES-2020 simulates the properties (geometry, vibrational frequency and energy) of reactants, products and saddle points reasonably, showing an exothermicity of ∆Hr(298K) = −20.05 kcal mol−1, reproducing the theoretical and experimental evidence, and a “submerged” barrier of −1.45 kcal mol−1, simulating the ab initio information used as input. However, due to the complicated topology of the title reaction, with deep wells in the entrance and exit channels, the description of the intermediate complexes is poorer. The stability, ∆H(0K), of the reactant complex is therefore underestimated by 1–2 kcal mol−1, while the stability of the product complex is overestimated by 3–4 kcal mol−1. Nevertheless, as in the case of the ab initio values used as a reference, PES-2020 also presents deep wells, and in the light of the results obtained, we believe that these differences are not determinant. Thus, PES-2020 represents a first approximation to the problem of the consequence of a compromise between time, efficacy and accuracy. Obviously, future theoretical studies will almost certainly improve the fitting, but we do not think that they will substantially modify the main conclusions obtained in the present work.
- Based on PES-2020, a kinetics study was performed using QCT calculations. With respect to previous theoretical results, the rate constants obtained in the present work noticeably improve the agreement with the experimental evidence in the wide temperature range of 25–700 K. In addition, the experimental KIEs are reproduced for the first time. These comparisons represent a stringent test, and the good agreement with experiments lends confidence to the quality of PES-2020.
- A dynamics study based on QCT/PES-2020 was also performed, for which experimental information for comparison was scarce. Firstly, vibrational excitation by one quantum of the CN (v = 1) reactant increased reactivity slightly with respect to the vibrational ground-state, by factors between 21 and 5% in the temperature range of 300–700 K, thus reproducing qualitatively the only experimental study. This behavior was explained by the coupling of this vibrational mode with the reaction coordinate. Secondly, CN(j) rotational excitation decreased reactivity. Finally, product angular distribution presented a forward–backward behavior, which is characteristic of reactions with deep wells in the entrance and exit channels. This tendency is additional proof of the existence of a complex mechanism for the title reaction. These last two effects, rotational excitation and angular distribution, can be explained by a disorientation effect in the entrance channel and so losing the appropriate orientation for effective collisions. These two theoretical predictions await experimental confirmation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Yang, D.L.; Lin, M.C. The Reactions of the CN Radical with Molecules Relevant to Combustion and Atmospheric Chemistry. In The Chemical Dynamics and Kinetics of Small Radicals; Liu, K., Wagner, A., Eds.; World Scientific Publishing: Singapore, 1995; Part. 1, Chapter 5; pp. 164–213. [Google Scholar]
- Standard Reference Database 17, Version 7.0 (web version), Release 1.6.8. Data version 2015.09; NIST Chemical Kinetics Database web page: Gaithersburg, MD, USA.
- Stoecklin, T.; Clary, D.C. Fast Reactions between a Linear Molecule and a Polar Symmetric Top. J. Mol. Struct. (Theochem) 1995, 341, 53–61. [Google Scholar] [CrossRef]
- Faure, A.; Rist, C.; Valiron, P. Ab initio Determination of the CN–NH3 Capture Potential Energy Surface. Chem. Phys. 1999, 241, 29–42. [Google Scholar] [CrossRef]
- Faure, A.; Rist, C.; Valiron, P. Temperature Dependence for the CN+NH3 Reaction under Interstellar Conditions: Beyond Capture Theories? Astron. Astrophys. 1999, 348, 972–977. [Google Scholar]
- Meads, R.F.; Maclagan, R.G.A.R.; Phillips, L.F. Kinetics, Energetics, and Dynamics of the Reactions of CN with NH3 and ND3. J. Phys. Chem. 1993, 97, 3257–3265. [Google Scholar] [CrossRef]
- Talbi, D.; Smith, I.W.M. A Theoretical Analysis of the Reaction between CN Radicals and NH3. Phys. Chem. Chem. Phys. 2009, 11, 8477–8483. [Google Scholar] [CrossRef] [PubMed]
- Boden, J.C.; Thrush, B.A. Kinetics of Reactions Involving CN Emission. IV. Study of the Reactions of CN by Electronic Absorption Spectroscopy. Proc. R. Soc. Lond. A 1968, 305, 107. [Google Scholar]
- Baulch, D.L.; Duxbury, J.; Grant, S.J.; Montague, D.C. Evaluated kinetic Data for High Temperature Reactions. Volume 4. Homogeneous Gas Phase Reactions of Halogen- and Cyanide-Containing Species. J. Phys. Chem. Ref. Data 1981, 10. [Google Scholar]
- Sims, I.R.; Smith, I.W.M. Pulsed Laser Photolysis-Laser-induced Fluorescence Measurements on the Kinetics of CN(v= 0) and CN(v = 1) with O2, NH3, and NO between 294 and 761 K. J. Chem. Soc. Faraday Trans. 2 1988, 84, 527–539. [Google Scholar] [CrossRef]
- Sims, I.R.; Queffelec, J.L.; Defrance, A.; Rebrion-Rowe, C.; Travers, D.; Bocherel, P.; Rowe, B.R.; Smith, I.W.M. Ultra-low Temperature Kinetics of Neutral-Neutral Reactions: The Technique, and Results for the Reactions CN + O2, down to 13 K and CN + NH3 down to 25 K. J. Chem. Phys. 1994, 100, 4229. [Google Scholar] [CrossRef]
- Clary, D.C. Fast Chemical Reactions: Theory Challenges Experiment. Annu. Rev. Phys. Chem. 1990, 41, 61. [Google Scholar] [CrossRef]
- Troe, J. Recent Advances in Statistical Adiabatic Channel Calculations of State-Specific Dissociation Dynamics. Adv. Chem. Phys. 1997, 101, 819–851. [Google Scholar]
- Stoecklin, T.; Dateo, C.E.; Clary, D.C. Rate Constant Calculations on Fast Diatom–Diatom Reactions. J. Chem. Soc. Faraday Trans. 1991, 87, 1667. [Google Scholar] [CrossRef]
- Greenwald, E.E.; North, S.W.; Georgievskii, Y.; Klippenstein, S.J. A Two Transition State Model for Radical−Molecule Reactions: A Case Study of the Addition of OH to C2H4. J. Phys. Chem. A 2005, 109, 6031–6044. [Google Scholar] [CrossRef]
- Georgievskii, Y.; Klippenstein, S.J. Long-range Transition State Theory. J. Chem. Phys. 2005, 122, 194103. [Google Scholar] [CrossRef]
- Georgievskii, Y.; Klippenstein, S.J. Strange Kinetics of the C2H6 + CN Reaction Explained. J. Phys. Chem. A 2007, 111, 3802–3811. [Google Scholar] [CrossRef] [PubMed]
- Sabbah, H.; Biennier, L.; Sims, I.R.; Georgievskii, Y.; Klippenstein, S.J.; Smith, I.W.M. Understanding Reactivity at Very Low Temperatures: The Reactions of Oxygen Atoms with Alkenes. Science 2007, 317, 102–105. [Google Scholar] [CrossRef] [Green Version]
- Burkholder, J.B.; Abbatt, J.P.D.; Huie, R.E.; Kurylo, M.J.; Wilmouth, D.M.; Sander, S.P.; Barker, J.R.; Kolb, C.E.; Orkin, V.L.; Wine, P.H. Chemical Kinetics and Photochemical Data for Use in Atmospheric Studies; Evaluation Number 19; JPL Publication: Pasadena, CA, USA, 2015. [Google Scholar]
- Ruscic, B.; Pinzon, R.E.; von Laszewski, G.; Kodeboyina, D.; Burcat, A.; Leahy, D.; Montoy., D.; Wagner, A.F. Active Thermochemical Tables. J. Phys. Conf. Ser. 2005, 16, 078. [Google Scholar] [CrossRef]
- Neese, F. The ORCA Program System. Wiley Interdiscip. Rev.-Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision A0.3; Gaussian Inc.: Wallinford, CT, USA.
- Espinosa-Garcia, J.; Corchado, J.C. Analytical Surface for the Reaction with No Saddle-Point NH3 + F → NH2 + FH. Application of Variational Transition State Theory. J. Phys. Chem. A 1997, 101, 7336–7344. [Google Scholar] [CrossRef]
- Corchado, J.C.; Espinosa-Garcia, J. Analytical Potential Energy Surface for the NH3+H → NH2+H2 Reaction: Application of Variational Transition-state Theory and Analysis of the Equilibrium Constants and Kinetic Isotope Effects using Curvilinear and Rectilinear Coordinates. J. Chem. Phys. 1997, 106, 4013–4021. [Google Scholar] [CrossRef]
- Espinosa Garcia, J. Capability of LEP-type Surfaces to Describe Non-Collinear Reactions. 2. Polyatomic Systems. J. Phys. Chem. A 2001, 105, 8748–8755. [Google Scholar] [CrossRef]
- Monge-Palacios, M.; Rangel, C.; Espinosa-Garcia, J. Ab initio based Potential Energy Surface and Kinetics Study of the OH + NH3 Hydrogen Abstraction Reaction. J. Chem. Phys. 2013, 138, 084305. [Google Scholar] [CrossRef] [PubMed]
- Monge-Palacios, M.; Rangel, C.; Corchado, J.C.; Espinosa-Garcia, J. Analytical Potential Energy Surface for the Reaction with Intermediate Complexes NH3 + Cl → NH2 + HCl: Application to the Kinetics Study. Int. J. Quantum Chem. 2012, 112, 1887–1903. [Google Scholar] [CrossRef]
- Corchado, J.C.; Bravo, J.L.; Espinosa-Garcia, J. The Hydrogen Abstraction Reaction H+CH4. I. New Analytical Potential Energy Surface based on Fitting to Ab initio Calculations. J. Chem. Phys. 2009, 130, 184314. [Google Scholar] [CrossRef] [PubMed]
- Duchovic, R.J.; Volobuev, Y.L.; Lynch, G.C.; Jasper, A.W.; Truhlar, D.G.; Allison, T.C.; Wagner, A.F.; Garrett, B.C.; Espinosa-Garcia, J.; Corchado, J.C. POTLIB 2020. Available online: http://comp.chem.umn.edu/potlib (accessed on 12 February 2021).
- Hu, X.; Hase, W.L.; Pirraglia, T. Vectorization of the General Monte Carlo Classical Trajectory Program VENUS. J. Comput. Chem. 1991, 12, 1014–1024. [Google Scholar] [CrossRef]
- Hase, W.L.; Duchovic, R.J.; Hu, X.; Komornicki, A.; Lim, K.F.; Lu, D.-H.; Peslherbe, G.H.; Swamy, K.N.; Linde, S.R.V.; Varandas, A.J.C.; et al. A general chemical dynamics computer program. Quantum Chem. Program. Exch. Bull. 1996, 16, 671. [Google Scholar]
- Truhlar, D.G.; Muckerman, J.T. Atom-Molecule Collision Theory: A Guide for the Experimentalist; Bernstein, R.B., Ed.; Plenum Press: New York, NY, USA, 1979; pp. 505–566. [Google Scholar]
- Peslherbe, G.H.; Wang, H.; Hase, W.L. Monte Carlo Methods in Chemical Physics; Prigogine, I., Rice, S.A., Eds.; Advances in Chemical Physics; Wiley: Hoboken, NJ, USA, 2007; pp. 171–201. [Google Scholar]
- Nyman, G.; Davisson, J. A Low-energy Quasiclassical Trajectory Study of O(3P)+OH(2Π)→O2(3Σ−g)+H(2S). II. Rate Constants and Recrossing, Zero-point Energy Effects. J. Chem. Phys. 1990, 92, 2415–2422. [Google Scholar] [CrossRef]
- Varandas, A.J.C.; Marques, J.M.C. A Detailed State-to-State Low-energy Dynamics Study of the Reaction O(3P)+OH(2Π)→O2(X~ 3Σg−)+H(2S) using a Quasiclassical Trajectory–Internal-Energy Quantum-Mechanical-Threshold Method. J. Chem. Phys. 1992, 97, 4050–4065. [Google Scholar] [CrossRef]
- Varandas, A.J.C. Excitation Function for H+O2 Reaction: A Study of Zero-Point Energy Effects and Rotational Distributions in Trajectory Calculations. J. Chem. Phys. 1993, 99, 1076–1085. [Google Scholar] [CrossRef]
- Nyman, G. Dynamical and Statistical Behaviour of O(3P) + OH(2Π) → H(2S) + O2(3∑−g). Chem. Phys. 1993, 173, 159–166. [Google Scholar] [CrossRef]
- Varandas, A.J.C. A Novel Non-active Model to Account for the Leak of Zero-point Energy in Trajectory Calculations. Application to H + O2 Reaction Near Threshold. Chem. Phys. Lett. 1994, 225, 18–27. [Google Scholar] [CrossRef]
- Kudla, K.; Schatz, G.C. A Quasiclassical Trajectory Study of Mode Specific Reaction Dynamics in the Cl + HOD and H + HOD Reactions. Chem. Phys. 1993, 175, 71–82. [Google Scholar] [CrossRef]
- Bethardy, G.A.; Wagner, A.F.; Schatz, G.C.; ter Horst, M.A. A Quasiclassical Trajectory Study of Product State Distributions from the CN+H2→HCN+H Reaction. J. Chem. Phys. 1997, 106, 6001–6015. [Google Scholar] [CrossRef]
- Corchado, J.C.; Espinosa-Garcia, J.; Yang, M. Kinetics and Dynamics of the NH3 + H→NH2 + H2 Reaction using Transition State Methods, Quasi-classical Trajectories, and Quantum-Mechanical Scattering. J. Chem. Phys. 2011, 135, 014303. [Google Scholar] [CrossRef]
- Monge-Palacios, M.; Espinosa-Garcia, J. Reaction-Path Dynamics Calculations of the Cl + NH3 Hydrogen Abstraction Reaction: The Role of the Intermediate Complexes. J. Phys. Chem. A 2010, 114, 4418–4426. [Google Scholar] [CrossRef]
- Lee, T.J.; Taylor, P.R. A diagnostic for determining the quality of single-reference electron correlation methods. Int. J. Quantum Chem. Quantum Chem. Symp. 1989, 23, 199–207. [Google Scholar] [CrossRef] [Green Version]
- Lique, F.; Jorfi, M.; Honvoult, P.; Halvick, P.; Lin, S.Y.; Guo, H.; Xie, D.Q.; Dagdigian, P.J.; Klos, J.; Alexander, M.H. O + OH →O2 + H: A Key Reaction for Interstellar Chemistry. New Theoretical Results and Comparison with Experiment. J. Chem. Phys. 2009, 131, 221104. [Google Scholar] [CrossRef] [Green Version]
- Texeidor, M.M.; Varandas, A.J.C. Quantum Dynamics Study on the CHIPR Potential Energy Surface for the Hydroperoxyl Radical: The Reactions O + OH →O2 + H. J. Chem. Phys. 2015, 142, 014309. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Xie, D.; Zhang, D.H.; Lin, S.Y.; Guo, H. A New Ab initio Potential-Energy Surface of HO2(X2A″) and Quantum Studies of HO2 Vibrational Spectrum and Rate Constants for the H+O2↔O+OH Reactions. J. Chem. Phys. 2005, 122, 244305. [Google Scholar] [CrossRef]
- Xu, C.; Xie, D.; Honvault, P.; Lin, S.Y.; Guo, H. Rate Constant for OH(2Π)+O(3P)→H(2S)+O2(3Σg−) Reaction on an Improved Ab initio Potential Energy Surface and Implications for the Interstellar Oxygen Problem. J. Chem. Phys. 2007, 127, 024304. [Google Scholar] [CrossRef] [PubMed]
- Miller, W.H.; Handy, N.C.; Adams, J.E. Reaction Path Hamiltonian for Polyatomic Molecules. J. Chem. Phys. 1980, 72, 99–112. [Google Scholar] [CrossRef] [Green Version]
- Jiang, B.; Guo, H. Relative Efficacy of Vibrational vs. Translational Excitation in Promoting Atom−Diatom Reactivity: Rigorous Examination of Polanyi’s rules and Proposition of Sudden Vector Projection (SVP) Model. J. Chem. Phys. 2013, 138, 234104. [Google Scholar] [CrossRef]
- Li, J.; Guo, H. Mode Specificity and Product Energy Disposal in Unimolecular Reactions: Insights from the Sudden Vector Projection Model. J. Phys. Chem. A 2014, 118, 2419–2425. [Google Scholar] [CrossRef]
- Jiang, B.; Guo, H. Mode Specificity, Bond Selectivity, and Product Energy Disposal in X + CH4/CHD3 (X = H, F, O(3P), Cl, and OH) Hydrogen Abstraction Reactions: Perspective from Sudden Vector Projection Model. J. Chin. Chem. Soc. 2014, 61, 847–859. [Google Scholar] [CrossRef]
- Polanyi, J.C. Concepts in Reaction Dynamics. Acc. Chem. Res. 1972, 5, 161–168. [Google Scholar] [CrossRef]
- Nobusada, K.; Moribayashi, K.; Nakamura, H. Quantum Dynamics of O(3P)+HCl→OH+Cl Effects of Reagent Rotational Excitation. J. Chem. Soc. Faraday Trans. 1997, 93, 721–726. [Google Scholar] [CrossRef]
- Schatz, G.C. A Quasiclassical Trajectory Study of Reagent Vibrational Excitation Effects in the OH+H2→H2O+H Reaction. J. Chem. Phys. 1981, 74, 1133–1139. [Google Scholar] [CrossRef]
- Zhang, D.H.; Lee, S.-Y. Effects of Reagent Rotation on the Dynamics of the Reaction: A Full Dimension Quantum Study. J. Chem. Phys. 1998, 109, 2708–2716. [Google Scholar] [CrossRef]
- Zhang, D.H.; Lee., S.-Y. Effects of Reagent Rotation and the Accuracy of the Centrifugal Sudden Approximation in the H2 + CN Reaction. J. Chem. Phys. 2000, 112, 203–211. [Google Scholar] [CrossRef]
- Smith, G.P.; Zare, R.N. Angular Distribution of Product Internal States using Laser Fluorescence Detection: The Ba + KCl Reaction. J. Chem. Phys. 1976, 64, 2632–2640. [Google Scholar] [CrossRef] [Green Version]
- Truhlar, D.G.; Blais, N.C. Legendre Moment Method for Calculation Differential Cross Sections from Classical Trajectories with Monte Carlo Initial Conditions. J. Chem. Phys. 1977, 67, 1532–1539. [Google Scholar] [CrossRef]
- Monge-Palacios, M.; Yang, M.; Espinosa-Garcia, J. QCT and QM Calculations of the Cl(2P) + NH3 Reaction: Influence of the Reactant Well on the Dynamics. Phys. Chem. Chem. Phys. 2012, 14, 4824–4834. [Google Scholar] [CrossRef] [PubMed]
- Monge-Palacios, M.; Corchado, J.C.; Espinosa-Garcia, J. Dynamics Study of the OH + NH3 Hydrogen Abstraction Reaction using QCT Calculations based on an Analytical Potential Energy Surface. J. Chem. Phys. 2013, 138, 214306. [Google Scholar] [CrossRef] [PubMed]


| Property | CN | NH3 | HCN | NH2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PES | Level 1 | Level 2 | PES | Level 1 | Level 2 | PES | Level 1 | Level 2 | PES | Level 1 | Level 2 | |
| Geometry | ||||||||||||
| C–N | 1.172 | 1.175 | 1.180 | 1.172 | 1.157 | 1.165 | ||||||
| H-C | 1.059 | 1.069 | 1.071 | |||||||||
| <HCN | 180.00 | 180.00 | 180.00 | |||||||||
| N–H | 1.014 | 1.014 | 1.017 | 1.028 | 1.026 | 1.031 | ||||||
| <HNH | 109.00 | 106.37 | 106.81 | 103.40 | 102.84 | 102.30 | ||||||
| Frequency | ||||||||||||
| 2114 | 2103 | 2096 | 3684 | 3603 | 3621 | 3364 | 3434 | 3447 | 3553 | 3463 | 3458 | |
| 3684 | 3603 | 3621 | 2014 | 2118 | 2098 | 3252 | 3369 | 3363 | ||||
| 3312 | 3474 | 3486 | 756 | 715 | 713 | 1489 | 1547 | 1515 | ||||
| 1676 | 1676 | 1662 | 756 | 715 | 713 | |||||||
| 1676 | 1676 | 1662 | ||||||||||
| 1076 | 1085 | 1096 | ||||||||||
| Energy | ||||||||||||
| ZPE | 3.02 | 3.01 | 3.00 | 21.60 | 21.61 | 21.65 | 9.85 | 9.98 | 9.96 | 11.86 | 11.98 | 11.58 |
| ∆ER | −17.51 | −17.35 | −18.41 | |||||||||
| ∆HR (0 K) | −20.42 | −19.89 | −21.18 | |||||||||
| ∆HR (298 K) | −20.05 | −20.01 | −21.0.6 | |||||||||
| Property | SP | RC2 | PC | ||||||
|---|---|---|---|---|---|---|---|---|---|
| PES | Level 1 | Level 2 | PES | Level 1 | Level 2 | PES | Level 1 | Level 2 | |
| Geometry | |||||||||
| N–H | 1.031 | 1.020 | 1.022 | 1.018 | 1.012 | 1.012 | 1.032 | 1.025 | 1.029 |
| N–H’ | 1.088 | 1.119 | 1.099 | 1.018 | 1.012 | 1.012 | 2.195 | 2.165 | 2.193 |
| C–H’ | 1.512 | 1.485 | 1.539 | 1.062 | 1.078 | 1.080 | |||
| C–N | 3.197 | 2.000 | 2.060 | ||||||
| C–N(CN) | 1.173 | 1.168 | 1.173 | 1.172 | 1.183 | 1.181 | 1.172 | 1.158 | 1.165 |
| <NH’C | 177.13 | 137.93 | 135.30 | 180.00 | 180.00 | 180.00 | |||
| Frequency | |||||||||
| 3260 | 3551 | 3579 | 3604 | 3665 | 3652 | 3461 | 3485 | 3483 | |
| 3247 | 3450 | 3474 | 3604 | 3655 | 3648 | 3341 | 3391 | 3387 | |
| 2166 | 2184 | 2259 | 3239 | 3481 | 3486 | 3186 | 3297 | 3326 | |
| 1836 | 1922 | 2155 | 2115 | 2386 | 2107 | 2015 | 2108 | 2091 | |
| 1465 | 1594 | 1606 | 1659 | 1636 | 1621 | 1444 | 1551 | 1540 | |
| 1274 | 1461 | 1496 | 1659 | 1617 | 1617 | 769 | 858 | 889 | |
| 895 | 858 | 868 | 1071 | 902 | 996 | 769 | 831 | 875 | |
| 538 | 551 | 535 | 118 | 792 | 513 | 124 | 299 | 320 | |
| 516 | 387 | 360 | 118 | 603 | 455 | 87 | 226 | 250 | |
| 246 | 172 | 121 | 7118 | 456 | 360 | 84 | 149 | 148 | |
| 246 | 138 | 120 | 72 | 318 | 112 | 63 | 116 | 122 | |
| 810 i | 878 i | 697 i | 72 | 243 | 91 | 58 | 87 | 107 | |
| Energy | |||||||||
| ZPE | 20.99 | 23.30 | 23.70 | 24.95 | 27.75 | 26.55 | 22.02 | 23.44 | 23.65 |
| ∆E | −1.45 | −1.62 | −1.10 | −8.12 | −12.03 | −11.16 | −25.70 | −23.00 | −24.57 |
| ∆H (0 K) | −3.63 | −2.94 | −2.05 | −7.80 | −8.90 | −9.27 | −28.29 | −24.17 | −25.57 |
| T(K) | QCT | Exp-1988 a | Exp-1994 b | Exp-1995 c |
|---|---|---|---|---|
| 25 | 1.65 × 10−10 | 4.7 × 10−10 | ||
| 50 | 1.37 × 10−10 | 2.1 × 10−10 | ||
| 100 | 1.09 × 10−10 | 9.6 × 10−11 | ||
| 200 | 5.00 × 10−11 | 4.4 × 10−11 | 3.40 × 10−11 | |
| 300 | 3.12 × 10−11 | 2.77 × 10−11 | 2.23 × 10−11 | |
| 400 | 2.38 × 10−11 | 2.39 × 10−11 | 1.80 × 10−11 | |
| 500 | 1.96 × 10−11 | 2.17 × 10−11 | 1.59 × 10−11 | |
| 700 | 1.47 × 10−11 | 1.97 × 10−11 | 1.37 × 10−11 |
| T(K) | QCT | Exp.a | Exp.b |
|---|---|---|---|
| 200 | 1.99 | 1.72 | |
| 300 | 2.02 | 1.89 | 2.01 |
| 500 | 2.10 | 2.04 | |
| 700 | 2.18 | 2.11 |
| T(K) | QCT | Exp. a |
|---|---|---|
| 300 | 1.21 | 1.55 |
| 500 | 1.16 | 1.40 |
| 700 | 1.05 | 1.31 |
| Species | Mode | Frequency a | Bi,F(s) b | SVP |
|---|---|---|---|---|
| CN | Stretching | 2114 | 0.66 | 0.085 |
| NH3 | Stretching | 3684(d) | 0.11 | 0.244 |
| Stretching | 3313 | 1.74 | 0.230 | |
| Deformation | 1676(d) | 2.05 | 0.260 | |
| Deformation | 1076 | 1.31 | 0.347 | |
| CN···NH3 | Translation | - | 0.795 | |
| Rotation | - | 0.118 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Espinosa-Garcia, J.; Rangel, C.; Garcia-Chamorro, M.; Corchado, J.C. Quasi-Classical Trajectory Study of the CN + NH3 Reaction Based on a Global Potential Energy Surface. Molecules 2021, 26, 994. https://doi.org/10.3390/molecules26040994
Espinosa-Garcia J, Rangel C, Garcia-Chamorro M, Corchado JC. Quasi-Classical Trajectory Study of the CN + NH3 Reaction Based on a Global Potential Energy Surface. Molecules. 2021; 26(4):994. https://doi.org/10.3390/molecules26040994
Chicago/Turabian StyleEspinosa-Garcia, Joaquin, Cipriano Rangel, Moises Garcia-Chamorro, and Jose C. Corchado. 2021. "Quasi-Classical Trajectory Study of the CN + NH3 Reaction Based on a Global Potential Energy Surface" Molecules 26, no. 4: 994. https://doi.org/10.3390/molecules26040994
APA StyleEspinosa-Garcia, J., Rangel, C., Garcia-Chamorro, M., & Corchado, J. C. (2021). Quasi-Classical Trajectory Study of the CN + NH3 Reaction Based on a Global Potential Energy Surface. Molecules, 26(4), 994. https://doi.org/10.3390/molecules26040994








