Next Article in Journal
Counteracting the Ramifications of UVB Irradiation and Photoaging with Swietenia macrophylla King Seed
Next Article in Special Issue
Design, Characterization and Applications of Functional Nanomaterials
Previous Article in Journal
Effect of Korean Red Ginseng and Rg3 on Asian Sand Dust-Induced MUC5AC, MUC5B, and MUC8 Expression in Bronchial Epithelial Cells
Previous Article in Special Issue
Probing Molybdenum Active Sites during In Situ Photoreduction of the Mo6+/SiO2 Catalyst
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Molecules
Volume 26
Issue 7
10.3390/molecules26071988
molecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

The Early Steps of Molecule-to-Material Conversion in Chemical Vapor Deposition (CVD): A Case Study

by
Davide Barreca
1,
Ettore Fois
2,
Alberto Gasparotto
3,
Chiara Maccato
3,
Mario Oriani
2 and
Gloria Tabacchi
2,*
1
CNR-ICMATE and INSTM, Department of Chemical Sciences, Padova University, 35131 Padova, Italy
2
Department of Science and High Technology, Insubria University and INSTM, 22100 Como, Italy
3
Department of Chemical Sciences, Padova University and INSTM, 35131 Padova, Italy
*
Author to whom correspondence should be addressed.
Molecules 2021, 26(7), 1988; https://doi.org/10.3390/molecules26071988
Submission received: 26 February 2021 / Revised: 27 March 2021 / Accepted: 29 March 2021 / Published: 1 April 2021
(This article belongs to the Special Issue Design, Characterization and Applications of Functional Nanomaterials)
Browse Figures
Versions Notes

Abstract

:
Transition metal complexes with β-diketonate and diamine ligands are valuable precursors for chemical vapor deposition (CVD) of metal oxide nanomaterials, but the metal-ligand bond dissociation mechanism on the growth surface is not yet clarified in detail. We address this question by density functional theory (DFT) and ab initio molecular dynamics (AIMD) in combination with the Blue Moon (BM) statistical sampling approach. AIMD simulations of the Zn β-diketonate-diamine complex Zn(hfa)2TMEDA (hfa = 1,1,1,5,5,5-hexafluoro-2,4-pentanedionate; TMEDA = N,N,N′,N′-tetramethylethylenediamine), an amenable precursor for the CVD of ZnO nanosystems, show that rolling diffusion of this precursor at 500 K on a hydroxylated silica slab leads to an octahedral-to-square pyramidal rearrangement of its molecular geometry. The free energy profile of the octahedral-to-square pyramidal conversion indicates that the process barrier (5.8 kcal/mol) is of the order of magnitude of the thermal energy at the operating temperature. The formation of hydrogen bonds with surface hydroxyl groups plays a key role in aiding the dissociation of a Zn-O bond. In the square-pyramidal complex, the Zn center has a free coordination position, which might promote the interaction with incoming reagents on the deposition surface. These results provide a valuable atomistic insight on the molecule-to-material conversion process which, in perspective, might help to tailor by design the first nucleation stages of the target ZnO-based nanostructures.

Graphical Abstract

1. Introduction

The control and modulation of nanometer-level structures are of paramount importance in the fabrication of functional materials for advanced applications, encompassing gas sensing, energy, environmental sciences, and biomedical areas [1]. The consequent extensive research efforts have recently triggered the introduction of nanoarchitectonics, a novel paradigm of materials science and technology on the nanoscale [2] involving the combination of nanotechnologies with other specific disciplines to produce systems with emerging functionalities [3]. In this regard, tailoring of structure, composition, and morphology offers unique opportunities for the applications of metal oxide nanomaterials, which are an endless source of functionalities thanks to the multitude of valence states/structures and the widely diversified chemical reactivity that they exhibit [4,5,6,7,8]. The rational design of such systems is directly dependent on the availability of versatile preparation routes enabling their growth onto suitable substrates allowing, in turn, their direct integration into functional devices [9]. In the current tide of nanomaterial preparation routes, chemical vapor deposition (CVD)-related technologies hold a significant promise thanks to their inherent flexibility, adaptability to large-scale processing, and possibility to yield a broad range of material features by a proper choice of the operational conditions. CVD processes are based on the nucleation and growth of the target materials on solid surfaces starting from suitable molecular precursors in the vapor phase, whose features significantly influence the subsequent molecule-to-material conversion [10,11,12,13,14]. Important research progresses in this area are directly dependent on the attainment of additional insights into the involved reactive processes at the molecular scale, that can be successfully achieved by the combination of advanced experimental techniques and computational modeling [11,15,16,17,18].
Over the last decade, we have focused our attention on the extensive investigation of CVD precursors based on first-row transition metal oxides of general formula ML2TMEDA, where L is a fluorine-containing β-diketonate moiety (such as 1,1,1,5,5,5-hexafluoro-2,4-pentanedionate, hfa) and TMEDA is N,N,N′,N′-tetramethylethylenediamine. The joint use of both ligands yields the full saturation of metal coordination sphere, ultimately resulting in improved stability, volatility, and mass-transport behavior for CVD applications [19,20,21]. In particular, we have evidenced, in the case of the Cu(hfa)2TMEDA compound, a “rock-and-roll over a hot floor” motion consisting in a fast diffusion involving a vibrational excitation of metal-ligand bonds, paving the way to the subsequent precursor decomposition to copper oxide (CuxO, with x = 1, 2) nanomaterials [22]. Such investigations have been partly extended to the homologous Zn(hfa)2TMEDA [23] and Fe(hfa)2TMEDA [24] complexes, and the outcomes have revealed different high temperature behaviors for the three systems, which might be responsible for diverse decomposition pathways on the growth surface. In spite of these efforts, an open and hot challenge remains a thorough atomistic comprehension of the metal-ligand bond dissociation, related to the first stages of the molecule-to-material conversion in CVD processes. The understanding of this issue is indeed a crucial step towards the ultimate prediction of material properties, which would indeed disclose general concepts to boost the development of novel functional nanosystems.
On the basis of these results, the present research work aims at providing a step forward in the investigation of these issues by combined calculations involving the density functional theory (DFT) coupled with ab initio molecular dynamics (AIMD) [25]. It is worth noticing that, despite the growing interest in understanding via quantum chemical approaches the microscopic details of molecule-to-material conversion in CVD or ALD processes [26,27,28,29,30,31,32,33], most literature data refer to geometry optimization or transition state calculations performed at 0 K. Whereas these studies contribute to shedding light on the binding of the metal center with substrate atoms, the formation of metal-surface linkages for the target CVD precursors, where the metal center is completely surrounded by ligands, requires the dissociation of at least one metal-ligand bond, and remains a key issue to be further investigated.
The use of computational methodologies capable of taking into account thermal motion would be crucial to identifying possible molecular rearrangement events which, in turn, could promote the metal-ligand bond dissociation in the above molecular systems. Indeed, the rolling diffusion of Cu(hfa)2TMEDA [22] and Zn(hfa)2TMEDA [23] complexes, accompanied by large temperature-induced molecular distortions, suggests that thermal activation processes on the heated substrate surface might be responsible for both metal-ligand bond dissociation and metal center binding to surface atoms. Unfortunately, the mechanisms of these events are not only unknown, but also difficult to be foreseen on the basis of the sole precursors structure. Additionally, the thermal behavior of the precursor on the heated substrate may depend on the nature of the metal center. As an example, AIMD simulation on Fe(hfa)2TMEDA at 750 K revealed that the thermally-promoted rolling motion was sufficient to detach TMEDA from Fe(II) as a neutral ligand, leading to two separately physisorbed Fe(hfa)2 and TMEDA moieties [24]. On the other hand, the thermal behavior of the homologous Zn complex on the growth surface evidenced a preferential dissociation of one Zn-O bond [23], suggesting that a change of Zn coordination number from six to five could be the initial reaction step. Nonetheless, the simulation of reactive process such as bond dissociation events at finite temperature conditions generally requires statistical sampling techniques, such as the Blue Moon ensemble [34] approach, which have been successfully applied to the gas-phase fragmentation of Cu(hfa)2TMEDA [35]. In this perspective, herein we used a combined Blue Moon-AIMD approach to capture at the molecular level the mechanism of the metal-ligand bond breakage in the target molecular systems. This strategy enables to gather insight on the first stages of the precursor fragmentation on the growth surface and, most importantly, to evaluate the process energy barrier.
As a case study, we focus herein our attention on Zn(hfa)2TMEDA as a molecular precursor to Zn(II) oxide nanomaterials, in view of the paramount importance of ZnO for a huge variety of technological end-uses encompassing piezoelectric nanogenerators, sensors, lasers and optoelectronic devices, photocatalysts, solar cells, and supercapacitors [36,37,38,39,40,41].

2. Methods

Zn(hfa)2TMEDA was synthesized following a previously reported procedure [42]. The compound UV-Vis absorption spectrum was recorded on a Cary 5E (Agilent, Santa Clara, CA, USA) dual-beam spectrophotometer, using a 1.25 × 10−5 M ethanolic solution and quartz cuvettes with an optical path length of 1 cm.
The behavior of the Zn(hfa)2TMEDA complex on the growth surface was modeled in the framework of DFT. The PBE functional [43] with dispersion corrections [44] was employed along with plane wave (PW) basis sets and a PW cut-off of 25 and 200 Ry for wavefunction coefficients and electronic density, respectively. All simulations were performed with periodic boundary conditions.
The experimental conditions required for the deposition of transition metal oxides from Zn(hfa)2TMEDA precursors, i.e., oxidizing atmosphere (O2 + H2O), support heated in the 523–773 K interval [4], imply the formation of hydroxyl groups on the support, hence an outermost hydroxylated SiO2 layer. Accordingly, we employed a hydroxylated SiO2 slab model as in previous work on this precursor family [22,23,24]. The slab was characterized by 1 nm thickness, 1.7 × 1.7 nm2 surface area, and chemical composition Si36O72·8H2O. The simulation periodic box was 1.7 × 1.7 × 2.6 nm3. The 2.6 nm height, which included circa 1 nm vacuum, allowed for good decoupling of periodic images along the z directions. The slab contained 2.75 surface hydroxyls per nm2, in line with data on hydroxylated silica surfaces [45,46].
All the simulated [Zn(hfa)2TMEDA + surface] models contained a total of 185 atoms (132 atoms for the slab + 53 atoms for the complex). The guess geometry of the systems for simulation runs were built by placing the precursor complex in different and randomly selected positions and orientations in the proximity of the slab. From such geometries, structural optimizations were carried out, and the resulting sets of nuclei positions were used to start AIMD simulations [25,47] using the CPMD program (Version 4.1, ©2019–2021 IBM Corp. & MPI für Festkörperforschung Stuttgart, Zürich (CH) & Stuttgart (D)) [47]. To treat the electron-cores interaction, a norm-conserving pseudopotential [48,49,50] was employed for Si, along with ultrasoft pseudopotentials of the Vanderbilt type [51] for all other atoms. All pseudopotentials are available in the CPMD library. A spin multiplicity of 1 was adopted, consistently with the singlet spin state of the isolated Zn complex [23]. This calculation scheme for the electronic structure yielded a good representation of the behavior of molecules adsorbed on oxide surfaces as well as organic-inorganic materials both at 0 K (optimized geometry) and at finite temperature conditions (molecular dynamics simulations) [22,52]. For the AIMD, a 0.121 fs time step was selected, along with a 500 au fictitious mass for the wavefunction coefficients. After equilibration, the trajectory was followed for 20 ps in the NVT canonical ensemble, with 500 K target temperature and Nose–Hoover chain thermostats [53,54].
The free energy curve for the conversion from hexa- to penta-coordinated Zn in the Zn(hfa)2TMEDA complex was computed via a statistical sampling approach known as Blue Moon (BM) ensemble [34], in conjunction with AIMD. As reaction coordinate (or constraint), we selected the distance between the Zn atom and one of the diketonate oxygen atoms (namely, O2′, see Figure 1), r = r(Zn-O2′). This reaction coordinate was sampled by carrying out, along an interval of 2.72 Å, 18 BM-AIMD simulations. Each simulation was performed by fixing the constraint at the selected value and prolonged until the convergence of the constraint force. The entire set of BM simulations lasted ≈ 130 ps elapsed time. All the constrained simulations were performed by selecting 500 K as the target temperature and by employing Nose–Hoover chain thermostats [53,54].
At the end of the BM-AIMD simulations, selected configurations were extracted from the trajectories corresponding to the initial value of the reaction coordinate (“reactant”: octahedral hexa-coordinated complex) and to the final value of the reaction coordinate (“product”: penta-coordinated complex), as well as from the activated complex region. After simulated annealing, these configurations were subjected to geometry optimization, leading to the 0 K structures of the octahedral complex (Oct@SiO2), the pyramidal complex (Pyr@SiO2), and the transition state (TS@SiO2).
The binding energy (BE) of the Oct and Pyr forms of Zn(hfa)2TMEDA on the hydroxylated SiO2 surface was calculated using the abovementioned optimized geometries computed for the Zn(hfa)2TMEDA/slab system. BEs were computed using the formula:
−BE = E(complex + slab) − E(isolated complex) − E(slab)
where E(complex + slab) is the total energy of Zn(hfa)2TMEDA adsorbed on the hydroxylated SiO2 surface, and E(complex) and E(slab) are, respectively, the total energies of a single isolated Zn(hfa)2TMEDA molecule and of the bare hydroxylated silica slab model, whose geometries have been optimized using the same computational setup and the same periodic simulation box adopted for the (complex + slab) system. With this definition, binding energies are positive.
All the structural optimizations presented in this work were performed by employing a quasi-Newton algorithm [55]. The convergence criterion was set to a maximum of 1 × 10−4 atomic units (au) for the maximum value of the gradient per ionic degree of freedom, as done in previous work on these complexes [23]. All the PW calculations were performed with the CPMD code [47].
Hybrid DFT calculations on the Oct and Pyr forms of the isolated Zn(hfa)2TMEDA complex in the gas phase were performed using the M06 functional [56], the ECP10-MDF pseudopotential [57] with the correlation-consistent aug-cc-pVDZ-PP basis set for Zn [58], and full double-ζ basis sets augmented with diffuse and polarization functions (D95+(d,p)) [59] for the atoms of the TMEDA and hfa ligands. Basis sets not available in the Gaussian 09 were taken from the basissetexchange.org library [60].
Electronic excitation spectra on the PBE-D2 optimized geometries of the Oct and Pyr forms of the isolated Zn(hfa)2TMEDA were computed in implicit solvent ethanol [61] using time-dependent DFT (TD-DFT) with the CAM-B3LYP functional [62] and the standard 6-311++g(2d,p) basis set (available in the Gaussian 09 library [63]), by considering the first 20 lower energy excitations. To obtain the simulated spectra, the obtained TD-DFT values were broadened using a 2-nm width Gaussian function.
All the Gaussian calculations were performed with spin multiplicity = 1 (singlet) using the Gaussian 09 code (Revision B.01, Gaussian, Inc., Wallingford, CT, USA, 2010) [63]. Visualization of molecular structures and supporting movie (Movie S1, Supporting Information) were created with the VMD code (version 1.9.3, TCB Group, University of Illinois, Urbana-Champaign, IL, USA) [64].

3. Results

3.1. The Square-Pyramidal Zn(hfa)2TMEDA Complex

The exploratory AIMD simulation at 500 K shows that the Zn(hfa)2TMEDA complex, initially adsorbed with an octahedral geometry, underwent diffusion on the heated substrate via a rolling motion triggered by thermal energy exchange with the substrate, in line with previous AIMD simulations in the 363–750 K temperature range [23]. During this rolling diffusion motion, sketched in Movie S1, the Zn-O and Zn-N bonds showed large oscillations and, in some cases, metal-ligand bonds were transiently broken, thus determining a ligand rearrangement around the metal center (see Movie S1, Supporting Information).
This behavior can be quantitatively described by the time evolution of the metal-ligand distances along the trajectory (Figure 1) and the corresponding statistical values (Table 1). At about 7 ps, one of the Zn-O distances (Zn-O2′ from now on) drastically increased up to a maximum value of 5.21 Å, remaining above 3.5 Å for the rest of the simulation, whereas the other metal-ligand distances kept oscillating around typical Zn-O and Zn-N coordination distances, with lower amplitude (see Figure 1 and Table 1). The significant lengthening of the Zn-O2′ distance during the simulation was also evidenced by the high value of the average Zn-O2′ distance (3.62 Å) and standard deviation (0.91 Å), which is an estimate of the thermal fluctuation of the Zn-O2′ distance and was much larger compared to the other Zn-ligand bonds (Table 1). These results indicate that thermal motion on the silica surface had induced a change in zinc coordination number from six to five. Indeed, the Zn-O bond dissociation was followed by a partial detachment of one hfa ligand, leading to the formation of a Zn(hfa)2TMEDA characterized by a penta-coordinated Zn center and a square-pyramidal geometry (See Movie S1, Supporting Information).
These data suggest that the square-pyramidal arrangement of the Zn(hfa)2TMEDA compound, although never observed at room temperature, might be formed at elevated temperature on a hydroxylated surface.
To investigate whether the pyramidal geometry of the Zn complex could be stable even in the gas phase at 0 K (in the absence of a surface), we optimized the geometry of an isolated Zn(hfa)2TMEDA molecule by using as a guess the final configuration of the 500 K trajectory. The calculation resulted in a stable square-pyramidal geometry, depicted in Figure 2b, in which the pyramid base was characterized by a N’NO1′O1 dihedral angle of 8.3°. Compared with the standard octahedral geometry of this compound, characterized by a C2 symmetry (Figure 2a), the pyramidal structure was 10.02 kcal/mol higher in energy. This result can be easily understood by taking into account that in the pyramidal complex, Zn formed only five bonds with the ligands, i.e., its coordination environment was not fully saturated. Indeed, the minimum energy structure of isolated Zn(hfa)2TMEDA, shown in Figure 2a, exhibited six Zn-ligands coordination bonds, and had the C2 symmetry documented in previous investigations on β-diketonate-diamine compounds [23,42,65].
On the other hand, the Pyr form was characterized by the detachment of one of the β-diketonate oxygens, O2′, which was separated by about 4.3 Å from the metal center (see Table 2). The other oxygen atom of the same diketonate ligand, O2, is bound more strongly to Zn, as indicated by the pronounced shortening of the Zn-O2 bond distance (see Table 2). In addition, even the bond distances of Zn with the two oxygens (O1 and O1′) of the second hfa moiety, and with the N atoms of TMEDA, became shorter than in the octahedral structure. These findings suggested a strengthening of metal-ligand interactions as an effect of the loss of the Zn-O2′ bond in the Pyr complex. Another interesting consequence of the Zn-O2′ bond dissociation was the loss of conjugation of the hfa moiety. The O2′-C2′ distance elongation was accompanied by the shortening of the O2-C2 bond: as a result, the C2*-C2′ and C2*-C2 bonds became no longer equivalent. Such an effect was indeed significant, especially in comparison with the other hfa ligand, which had very close C-O and C-C bond lenghts.
The DFT results with plane waves (PBE-D2/PW) on the two forms of the complexes agreed quite satisfactorily with calculations at higher level of theory performed with the hybrid DFT functional M06 and D95+(d,p) Gaussian basis sets (M06/D95+(d,p)). In particular, the metal-ligand bond distances of the Oct complex calculated with PBE-D2/PW were slightly higher (on average, by about 1.4%) than the corresponding M06/D95+(d,p) values (Table 2). The same effect was observed even for the Pyr structure: specifically, the PBE-D2/PW metal-ligand bond distances were overestimated by 1.4% with respect to the M06/D95+(d,p) ones. Importantly, the distances of the detached oxygen atom O2′ from Zn obtained with the two methodologies differed by only 0.7%, and also the N’NO1′O1 dihedral angles defining the square-pyramidal geometry were very close (8.3° vs. 9.0° for PBE-D2/PW and M06/D95+(d,p), respectively). Finally, even the diketonate C-C and C-O bond distances, as well as the Zn-centered bond angles computed with the hybrid functional, were fairly well reproduced by the PBE-D2/PW approach for both the Oct and Pyr forms of the complex (see Table 2).
The energy difference between the Pyr and Oct form at the M06/D95+(d,p) level (ΔE = 13.06 kcal/mol) indicated that, in line with the PBE-D2/PW results, the octahedral complex was appreciably more stable than the pyramidal form. Overall, these results could be taken as a validation of our modeling strategy for the finite temperature reactivity of Zn(hfa)2TMEDA on the CVD growth surface. As a matter of fact, due to the high computational overhead of statistical sampling approaches on oxide material surfaces [11,52,66,67,68], the simulation of the Zn-ligand bond dissociation process is currently viable at reasonable time scales only through (dispersion-corrected) generalized gradient approximation DFT approaches such as the PBE-D2/PW one.
Before investigating the octahedral-to-pyramidal conversion of Zn(hfa)2TMEDA on a hydroxylated silica slab by BM-AIMD simulations, we checked if the structural differences between Oct and Pyr may have consequences also on the electronic structure of the corresponding complexes. To this aim, we computed electronic excitation spectra and compared them with the experimental UV-Vis spectrum of Zn(hfa)2TMEDA (octahedral) in ethanol solution (Figure 3). Although the TD-DFT-predicted position of the absorption maximum was shifted towards lower wavelengths, the peak intensity was close to the experimental spectrum, which presented a net UV absorption centered at 303 nm. Overall, the agreement of the Oct simulated spectrum with the experimental one may be considered satisfactory, taking into account that it was obtained from a single configuration—the 0 K minimum energy structure of the complex. Moreover, Figure 3 shows that the two forms (Oct and Pyr) had very close absorption maxima and might not have been experimentally distinguishable. On this basis, we concluded that possible Oct → Pyr isomerization events should not have had appreciable effects on the electronic excitation properties of the Zn(hfa)2TMEDA precursor.
Regarding the nature of the electronic transitions, the Oct absorption maximum was mainly due to the HOMO → LUMO+1 and HOMO−1 → LUMO excitations. The four Oct molecular orbitals (MOs) involved in the excitations are shown in Figure 4a. These MOs are spread on both hfa moieties. Whereas HOMO and HOMO−1 had a dominant π-character, LUMO and LUMO+1 were essentially π*. Hence, in the octahedral complex, the occurring transition was ligand-ligand π-π*.
Even in the pyramidal complex, the electronic absorption maximum was mainly ligand-ligand π-π*. However, the relevant Pyr MOs were preferentially localized on a single hfa ligand (Figure 4b). The main transition component was the HOMO → LUMO+1 excitation, involving the π and π* states of the partially detached hfa. The other component was the HOMO−2 → LUMO excitation: the HOMO−2 also contained σ and n-contributions from the oxygen lone pairs, whereas the LUMO was composed by the π*-states of the doubly coordinated hfa. The reason for which the dominant Pyr-Zn(hfa)2TMEDA excitation was essentially localized on a single hfa moiety (the mono-coordinated one) with negligible participation of the other hfa ligand could be the symmetry loss upon passing from the Oct (C2) to the Pyr (C1) geometry.

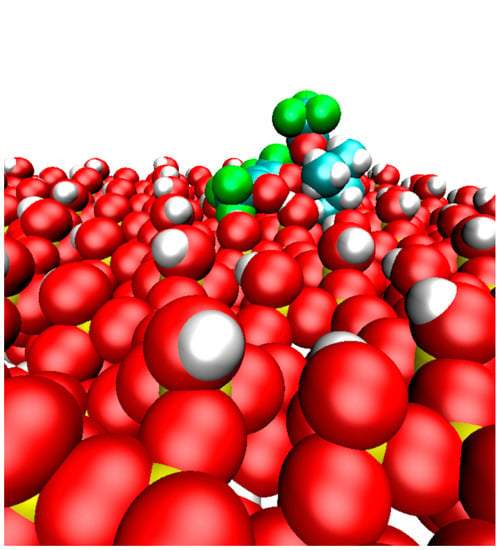
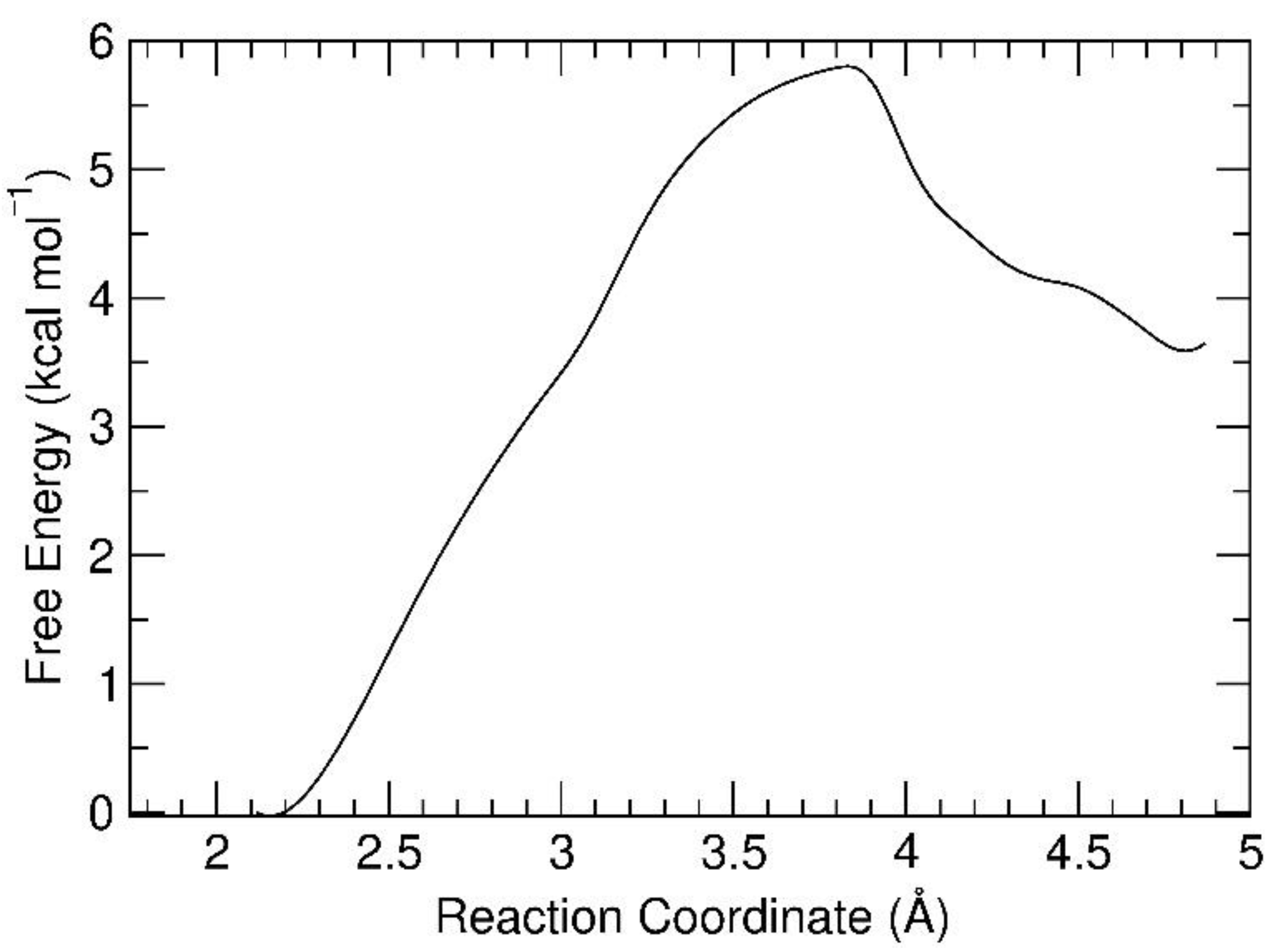
3.2. Free Energy Profile for the Octahedral-to-Pyramidal Conversion on the Hydroxylated Silica Surface

Having verified the stability of the square-pyramidal Zn(hfa)2TMEDA complex both in the gas phase at 0 K and in contact with the silica slab at 500 K, we tackled, using BM-AIMD, the question of how this geometry could be obtained from the octahedral structure under conditions close to the experimental ones. Hence, we positioned the Oct optimized complex on the silica surface and, after equilibration at 500 K, we started the BM sampling from octahedral Zn(hfa)2TMEDA stably physisorbed on the slab. As a reaction coordinate, we chose the Zn-O2′ bond length, which was progressively elongated from 2.146 Å (a distance typical of the octahedral complex) to 4.869 Å (pyramidal complex) by performing 18 BM-AIMD simulations, each characterized by a fixed Zn-O2′ distance (see Methods section). The resulting free energy profile (Figure 5) indicated that the octahedral to pyramidal conversion of the precursor complex was clearly endoergonic, as the free energy difference ΔG of the final product (Pyr@SiO2) with respect to the initial state (Oct@SiO2) was +3.6 kcal/mol (Table 3). This result might have been expected, since the pyramidal structure was energetically unfavored also in the gas phase. We note, however, that this free energy difference at 500 K was considerably lower than the energy difference between the two forms in the gas phase (10.02 kcal/mol), indicating that thermal activation played a key role in the overall process.
The estimated barrier for the octahedral-to-pyramidal rearrangement amounted to 5.8 kcal/mol, which was comparable to the thermal energy available in the environment (kT at 500 K ≈ 1 kcal/mol). Hence, although the pyramidal geometry was unfavored in the isolated complex at 0 K, this unusual structure became easily accessible if the precursor was in contact with a heated substrate due to the low activation barrier. Interestingly, the BM-AIMD simulations confirmed that the formation of a hydrogen bond between O2′ and a surface hydroxyl proton accompanied the generation of the activated complex, contributing thus to the achievement of a low barrier for this process.
The activated complex was formed at a Zn-O2′ value of ≈ 3.7 Å, i.e., it was closer to the product side than to the reactant side. Accordingly, the geometry of the complex during the corresponding BM-AIMD trajectory was quite reminiscent of the pyramidal Zn(hfa)2TMEDA structure.
The energy difference ΔE between (Pyr@SiO2) and (Oct@SiO2) and the energy barrier calculated at 0 K are also reported in Table 3. The ΔE value between pyramidal and octahedral geometry (2.23 kcal/mol) was substantially lower than the value for the isolated complexes (10.03 kcal/mol) and confirmed the essential contribution of surface hydroxyls in stabilizing the pyramidal structure via hydrogen bonding. The barrier was found to be 2 kcal/mol higher at 0 K than at 500 K, highlighting thus the vital role of thermal effects in promoting the conversion process.
Table 4 reports relevant geometrical parameters of the 0 K transition state (TS@SiO2), along with those for the optimized structures of (Oct@SiO2) and (Pyr@SiO2), while graphical representations of these structures can be found in Figure 6. First of all, we noticed the formation of a strong hydrogen bond (1.885 Å) between the O2′ oxygen atom (involved in the reaction coordinate) and a surface hydroxyl proton H*. In spite of this interaction, the geometry of physisorbed octahedral Zn(hfa)2TMEDA did not show substantial distortions with respect to the isolated Oct complex (Figure 6a). On the other hand, the geometry of the transition state was trigonal bipyramidal, as the Zn-O2′ bond was practically broken (Zn-O2′ distance being 3.818 Å) and the metal center was 5-coordinated. The N’NO1′O1 dihedral angle in the transition state was ≈ 55°, indicating that the conversion to the square-pyramidal complex was already at an advanced stage, although not fully completed (Figure 6b). Importantly, the H*-O2′ hydrogen bond distance shortened to 1.630 Å, indicating a further strengthening of this interaction, which played a crucial role in stabilizing the transition state. Furthermore, the final state was characterized by the accomplishment of the Zn(hfa)2TMEDA square-planar structure (Figure 6c). The N’NO1′O1 dihedral angle was 23°, indicating that the precursor interaction with the surface led to a pyramidal geometry slightly distorted with respect to the isolated Pyr complex. In addition, in the Pyr@SiO2 structure, the distances of both O2′ and O2 atoms from the metal center were higher than in the isolated precursor (see Table 4). These differences could be attributed to the presence of a very strong hydrogen bond, characterized by a distance (1.586 Å) close to those typical of proton-sharing moieties on oxide surfaces [17,66,69,70,71,72]. Moreover, the complex pyramidal geometry also favored the formation of a hydrogen bond between a surface -OH proton and an F atom of the hfa ligand (F-H distance = 2.002 Å). These interactions counterbalanced the partial detachment of the hfa ligand, thus providing an effective stabilization to the pyramidal complex.
A more detailed insight into the mechanism of the octahedral-to-pyramidal isomerization process was provided by the analysis of structural changes that the complex underwent as a function of the reaction coordinate (i.e., the Zn-O2′ distance). Figure 7 shows relevant snapshots taken from the BM-AIMD simulations for increasing values of the Zn-O2′ distance. During the first part of the reaction profile (Figure 7a,b), the complex maintained approximately an octahedral geometry, in spite of the significant Zn-O2′ bond weakening. Notably, in this part of the reaction, no stable hydrogen bond was formed between O2′ and surface hydroxyl proton H*, as evidenced in Figure 8. Indeed, the conversion of the precursor to the pyramidal form started to occur only upon formation of the O2′-H* hydrogen bond, corresponding to a Zn-O2′ value of 3.6 Å (Figure 8). Figure 7c shows the trigonal bipyramidal structure of the activated complex, which was stabilized by the O2′-H* hydrogen bond.
As shown in Figure 8, for larger values of the reaction coordinate, the O2′-H* hydrogen bond was always maintained, although with large thermal oscillations. In spite of the high simulation temperature, the average hydrogen bond distances were rather short, indicating a strong hydrogen bond interaction. The latter resulted in a considerable stabilization of the penta-coordinated form of the complex, which could thus evolve to its final square-pyramidal geometry (Figure 7d,e). Hence, the present analysis disclosed the atomistic structural changes of the Zn precursor along the reaction path which showcase the key role of hydrogen bonding with surface hydroxyl groups in the precursor isomerization process.

4. Discussion

As a matter of fact, the binding energy of the square-pyramidal Zn(hfa)2TMEDA with the surface was 7.81 kcal/mol greater than that obtained for the octahedral Zn(hfa)2TMEDA complex (Table 3). Hence, the lower energy of (Oct@SiO2) with respect to (Pyr@SiO2) could essentially be ascribed to the fact that the octahedral geometry of Zn(hfa)2TMEDA was intrinsically energetically favored with respect to the pyramidal structure, since it was characterized by a fully saturated coordination environment, which also implies greater dispersion effects.
The reason why dispersion effects favor the octahedral form of Zn(hfa)2TMEDA may be visually appreciated by comparing Figure 6a (Oct@SiO2) and Figure 6c (Pyr@SiO2). Indeed, the more compact structure of the Oct complex maximized intramolecular dispersion interactions. In a different way, the structure of the pyramidal complex was more prone to undergo hydrogen bonding interactions with the surface atoms. In addition, the pyramidal form exposed a free coordination position of the metal center, which could more efficiently interact with an incoming reagent (e.g., O2) on the growth surface. Following this suggestion, an interesting future development of this work might be the study of the interaction of O2 with the Zn center in the physisorbed pyramidal complex (Pyr@SiO2) and the subsequent oxidation reaction, which would, however, require the use of more computationally expensive spin-polarized calculations.
An unexpected result emerging from this study is the great relevance of the dispersion interactions in the complex-surface binding energy. Indeed, the binding energy of octahedral Zn(hfa)2TMEDA computed with the dispersion-corrected PBE-D2 functional (28.6 kcal/mol, Table 3) was significantly higher than the one computed by the PBE functional without dispersion interactions (5.6 kcal/mol, [23]). Actually, previous studies on metal organic precursors on silica slabs have also evidenced an important role of dispersion interactions on the physisorption process [31].
In a more general scenario, the present quantitative results on the energy barrier for the metal-ligand bond dissociation step underline that at temperatures close to the conditions adopted in CVD processes, the thermal energy (kT) is comparable with the bond stretching energies (at T = 500 K, kT ≈ 1 kcal/mol), and it can be of the same order of magnitude of the activation barrier, as found for Zn(hfa)2TMEDA. Consequently, thermal effects may significantly influence the precursor chemical behavior in the first key stages of vapor deposition processes and affect the whole decomposition mechanism.
In this context, further insight could be gained by comparing the thermal behavior of the Zn complex with that predicted by our previous AIMD studies on the Fe [24] and Cu [22] homologues. In all these cases, a high-temperature-induced rolling diffusion of the metal precursor took place on the substrate surface, accompanied by large-amplitude oscillations of metal-ligand bond distances. In the case of Fe(hfa)2TMEDA, the oscillations of Fe-N bonds were larger with respect to Fe-O ones: In particular, one of the Fe-N distances averaged to 4.52 ± 0.73 Å over the trajectory, indicating that the rolling motion caused a partial TMEDA detachment already in the early simulation stages. This behavior finally led to a TMEDA ligand loss of the iron complex (as reported in Ref. [24]) with formation of the tetra-coordinated Fe(hfa)2 moiety.
On the other hand, in the case of the Zn complex, the oscillations of Zn-O bonds were larger than those of Zn-N distances, as evidenced in Figure 1, Table 1, and in [23]. Additionally, here we have shown that the Zn complex could isomerize to a penta-coordinated pyramidal structure stabilized by hydrogen-bonding with a surface hydroxyl group, and that the process barrier was of the same order of magnitude of the thermal energy available in the system at the deposition conditions (500–750 K). Finally, even the diffusional rolling motion of the Cu(hfa)2TMEDA precursors on a hydroxylated silica surface led preferentially to larger-amplitude Cu-O oscillations [22], suggesting that Cu-O bond dissociation might be favored over the Cu-N one. On this basis, it would be reasonable to expect that a similar octahedral-to-pyramidal conversion could take place even for Cu(hfa)2TMEDA.
Finally, an interesting question is whether the thermal behavior and bond dissociation mechanism deduced for Zn(hfa)2TMEDA on hydroxylated silica might be extended to other kinds of substrates—for example, electrically conductive tin dioxide and other transparent oxidic supports used for ZnO deposition. Whereas the metal oxide nature may undoubtedly influence the activation barrier, it is worthwhile highlighting that the presence of surface hydroxyl groups is rather ubiquitous on many oxide-based materials (see, e.g., [73,74,75]). Hence, it can be argued that the hydrogen bond-assisted formation of the square-pyramidal complex reported in our work might be quite general and not limited to hydroxylated silica.

5. Conclusions

This study has elucidated the metal-ligand bond dissociation process of a β-diketonate-diamine Zn precursor for the CVD of zinc oxide nanomaterials. An octahedral-to-pyramidal isomerization of the Zn(hfa)2TMEDA complex involving a Zn-O bond dissociation can be triggered by the rolling diffusion of this molecule on a heated hydroxylated silica surface, which causes the partial detachment of an hfa ligand. The free energy barrier calculated for the octahedral-to-pyramidal conversion is of the same order of magnitude of thermal energy at 500 K. Stabilization of the activated complex, which exhibits a trigonal-bipyramidal geometry, is provided by strong hydrogen bonding interactions between the uncoordinated hfa oxygen and a surface hydroxyl group. This finding clearly highlights that under CVD conditions, activation mechanisms very different from those typical of (room temperature) chemistry may be viable, thus yielding species obtainable only under high-temperature conditions. Comparison of the thermal behavior of Zn(hfa)2TMEDA with previously studied homologues suggests that even the copper homologue may exhibit a similar isomerization to a pyramidal form in contact with hydroxylated oxide surfaces. Interesting future perspectives for the development of the present research activities might concern the investigation of the fate of this family of precursors on other kinds of substrates or in the presence of oxygen.
Overall, this work highlights the role of rolling molecular diffusion in surface processes typical of vapor deposition fabrication routes of oxide nanomaterials. The octahedral-to-pyramidal conversion unraveled here may be crucial for the subsequent reactive event, since it may enable the metal center to come into direct contact with other reagents on the substrate surface.

Supplementary Materials

The following are available online. Movie S1: movie from the AIMD PBE-D2/PW trajectory evidencing the rolling diffusion of Zn(hfa)2TMEDA.

Author Contributions

Conceptualization, G.T., E.F. and D.B.; writing—original draft preparation, A.G. and C.M.; investigation, G.T. and E.F.; data curation, G.T.; formal analysis, E.F., G.T. and M.O.; validation, M.O.; project administration, D.B., E.F., G.T.; visualization, E.F. and M.O.; funding acquisition, D.B., E.F., A.G. and C.M.; writing—reviewing and editing, all authors. All authors have read and agreed to the published version of the manuscript.

Funding

We gratefully acknowledge University of Insubria FAR2020, Padova University (DOR 2018–2020, P-DiSC#04BIRD2020-UNIPD EUREKA) and the INSTM Consortium (INSTM21PDBARMAC–ATENA; NSTM21PDGASPAROTTO–NANOMAT) for financial support.

Data Availability Statement

Data is contained within the article or supplementary material.

Conflicts of Interest

The authors declare no conflict of interests. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

Sample Availability

Samples of the compounds M(hfa)2TMEDA (M = Fe, Cu, Zn) are available from the authors.

References

  1. Ariga, K.; Ji, Q.; Nakanishi, W.; Hill, J.P.; Aono, M. Nanoarchitectonics: A new materials horizon for nanotechnology. Mater. Horiz. 2015, 2, 406–413. [Google Scholar] [CrossRef]
  2. Ariga, K.; Li, J. Nanoarchitectonics for advanced materials: Strategy beyond nanotechnology. Adv. Mater. 2016, 28, 987–988. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  3. Komiyama, M.; Mori, T.; Ariga, K. Molecular imprinting: Materials nanoarchitectonics with molecular information. Bull. Chem. Soc. Jpn. 2018, 91, 1075–1111. [Google Scholar] [CrossRef]
  4. Bekermann, D.; Barreca, D.; Gasparotto, A.; Maccato, C. Multi-component oxide nanosystems by Chemical Vapor Deposition and related routes: Challenges and perspectives. CrystEngComm 2012, 14, 6347–6358. [Google Scholar] [CrossRef]
  5. Mohd Abdah, M.A.A.; Azman, N.H.N.; Kulandaivalu, S.; Sulaiman, Y. Review of the use of transition-metal-oxide and conducting polymer-based fibres for high-performance supercapacitors. Mater. Des. 2020, 186, 108199. [Google Scholar] [CrossRef]
  6. Maduraiveeran, G.; Sasidharan, M.; Jin, W. Earth-abundant transition metal and metal oxide nanomaterials: Synthesis and electrochemical applications. Prog. Mater. Sci. 2019, 106, 100574. [Google Scholar] [CrossRef]
  7. Zappa, D.; Galstyan, V.; Kaur, N.; Munasinghe Arachchige, H.M.M.; Sisman, O.; Comini, E. “Metal oxide -based heterostructures for gas sensors”—A review. Anal. Chim. Acta 2018, 1039, 1–23. [Google Scholar] [CrossRef] [PubMed]
  8. Peng, Y.K.; Tsang, S.C.E. Facet-dependent photocatalysis of nanosize semiconductive metal oxides and progress of their characterization. Nano Today 2018, 18, 15–34. [Google Scholar] [CrossRef]
  9. Gasparotto, A.; Barreca, D.; Bekermann, D.; Devi, A.; Fischer, R.A.; Maccato, C.; Tondello, E. Plasma processing of nanomaterials: Emerging technologies for sensing and energy applications. J. Nanosci. Nanotechnol. 2011, 11, 8206–8213. [Google Scholar] [CrossRef]
  10. McElwee-White, L. Design of precursors for the CVD of inorganic thin films. Dalton Trans. 2006, 5327–5333. [Google Scholar] [CrossRef]
  11. Tabacchi, G.; Fois, E.; Barreca, D.; Gasparotto, A. Opening the Pandora’s jar of molecule-to-material conversion in chemical vapor deposition: Insights from theory. Int. J. Quantum Chem. 2014, 114, 1–7. [Google Scholar] [CrossRef] [Green Version]
  12. Devi, A. “Old chemistries” for new applications: Perspectives for development of precursors for MOCVD and ALD applications. Coord. Chem. Rev. 2013, 257, 3332–3384. [Google Scholar] [CrossRef]
  13. Mishra, S.; Daniele, S. Metal-organic derivatives with fluorinated ligands as precursors for inorganic nanomaterials. Chem. Rev. 2015, 115, 8379–8448. [Google Scholar] [CrossRef] [PubMed]
  14. Mishra, S.; Daniele, S. Molecular Engineering of Metal Alkoxides for Solution Phase Synthesis of High-Tech Metal Oxide Nanomaterials. Chem. A Eur. J. 2020, 26, 9292–9303. [Google Scholar] [CrossRef]
  15. Ferreira Da Silva, F.; Thorman, R.M.; Bjornsson, R.; Lu, H.; Mcelwee-White, L.; Ingólfsson, O. Dissociation of the FEBID precursor: Cis-Pt(CO)2Cl2 driven by low-energy electrons. Phys. Chem. Chem. Phys. 2020, 22, 6100–6108. [Google Scholar] [CrossRef]
  16. Cipriani, M.; Thorman, R.M.; Brewer, C.R.; McElwee-White, L.; Ingólfsson, O. Dissociative ionization of the potential focused electron beam induced deposition precursor π-allyl ruthenium(II) tricarbonyl bromide, a combined theoretical and experimental study. Eur. Phys. J. D 2019, 73, 1–7. [Google Scholar] [CrossRef]
  17. Bigiani, L.; Andreu, T.; Maccato, C.; Fois, E.; Gasparotto, A.; Sada, C.; Tabacchi, G.; Krishnan, D.; Verbeeck, J.; Morante, J.R.; et al. Engineering Au/MnO2 hierarchical nanoarchitectures for ethanol electrochemical valorization. J. Mater. Chem. A 2020, 8, 16902. [Google Scholar] [CrossRef]
  18. Bigiani, L.; Zappa, D.; Barreca, D.; Gasparotto, A.; Sada, C.; Tabacchi, G.; Fois, E.; Comini, E.; Maccato, C. Sensing nitrogen mustard gas simulant at the ppb scale via selective dual-site activation at Au/Mn3O4 interfaces. ACS Appl. Mater. Interfaces 2019, 11, 23692–23700. [Google Scholar] [CrossRef]
  19. Barreca, D.; Carraro, G.; Devi, A.; Fois, E.; Gasparotto, A.; Seraglia, R.; Maccato, C.; Sada, C.; Tabacchi, G.; Tondello, E.; et al. β-Fe2O3 nanomaterials from an iron(ii) diketonate-diamine complex: A study from molecular precursor to growth process. Dalt. Trans. 2012, 41, 149–155. [Google Scholar] [CrossRef]
  20. Barreca, D.; Carraro, G.; Gasparotto, A.; Maccato, C.; Seraglia, R.; Tabacchi, G. An iron(II) diamine diketonate molecular complex: Synthesis, characterization and application in the CVD of Fe2O3 thin films. Inorg. Chim. Acta 2012, 380, 161–166. [Google Scholar] [CrossRef]
  21. Bandoli, G.; Barreca, D.; Gasparotto, A.; Seraglia, R.; Tondello, E.; Devi, A.; Fischer, R.A.; Winter, M.; Fois, E.; Tabacchi, G. An integrated experimental and theoretical investigation on Cu (hfa)2‧TMEDA: Structure, bonding and reactivity. Phys. Chem. Chem. Phys. 2009, 11, 5998–6007. [Google Scholar] [CrossRef]
  22. Fois, E.; Tabacchi, G.; Barreca, D.; Gasparotto, A.; Tondello, E. “Hot” surface activation of molecular complexes: Insight from modeling studies. Angew. Chem. Int. Ed. 2010, 49, 1944–1948. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  23. Tabacchi, G.; Fois, E.; Barreca, D.; Gasparotto, A. CVD precursors for transition metal oxide nanostructures: Molecular properties, surface behavior and temperature effects. Phys. Status Solidi A 2014, 211, 251–259. [Google Scholar] [CrossRef]
  24. Tabacchi, G.; Fois, E.; Barreca, D.; Carraro, G.; Gasparotto, A.; Maccato, C. Modeling the first activation stages of the Fe(hfa)2‧TMEDA CVD precursor on a heated growth surface. In Advanced Processing and Manufacturing Technologies for Nanostructured and Multifunctional Materials II; Ceramic Engineering and Science, Proceedings; Ohji, T., Singh, M., Halbig, M., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2016; pp. 83–90. ISBN 9781119211662. [Google Scholar]
  25. Car, R.; Parrinello, M. Unified approach for molecular dynamics and density-functional theory. Phys. Rev. Lett. 1985, 55, 2471–2474. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  26. Fang, G.; Xu, L.; Cao, Y.; Li, A. Theoretical design and computational screening of precursors for atomic layer deposition. Coord. Chem. Rev. 2016, 322, 94–103. [Google Scholar] [CrossRef]
  27. Pedersen, H.; Elliott, S.D. Studying chemical vapor deposition processes with theoretical chemistry. Theor. Chem. Acc. 2014, 133, 1–10. [Google Scholar] [CrossRef] [Green Version]
  28. Takeuchi, N.; Ventura-Macias, E.; Guerrero-Sánchez, J.; Zaera, F. Density functional theory study of the adsorption and dissociation of copper(I) acetamidinates on Ni(110): The effect of the substrate. J. Phys. Chem. C 2020, 124, 15366–15376. [Google Scholar] [CrossRef]
  29. Sukkaew, P.; Danielsson, Ö.; Kordina, O.; Janzén, E.; Ojamäe, L. Ab initio study of growth mechanism of 4H-SiC: Adsorption and Surface Reaction of C2H2, C2H4, CH4, and CH3. J. Phys. Chem. C 2017, 121, 1249–1256. [Google Scholar] [CrossRef] [Green Version]
  30. Avila, J.R.; Peters, A.W.; Li, Z.; Ortuño, M.A.; Martinson, A.B.F.; Cramer, C.J.; Hupp, J.T.; Farha, O.K. Atomic layer deposition of Cu(I) oxide films using Cu(II) bis(dimethylamino-2-propoxide) and water. Dalton Trans. 2017, 46, 5790–5795. [Google Scholar] [CrossRef]
  31. Shen, J.; Muthukumar, K.; Jeschke, H.O.; Valentí, R. Physisorption of an organometallic platinum complex on silica: An ab initio study. New J. Phys. 2012, 14, 073040. [Google Scholar] [CrossRef]
  32. Krasnov, P.O.; Mikhaleva, N.S.; Kuzubov, A.A.; Nikolaeva, N.S.; Zharkova, G.I.; Sheludyakova, L.A.; Morozova, N.B.; Basova, T.V. Prediction of the relative probability and the kinetic parameters of bonds breakage in the molecules of palladium MOCVD precursors. J. Mol. Struct. 2017, 1139, 269–274. [Google Scholar] [CrossRef]
  33. Lang, H.; Adner, D.; Georgi, C. Advances in deposition of transition metal oxides from metal enolates. In PATAI’S Chemistry of Functional Groups; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2016; pp. 1–38. [Google Scholar]
  34. Carter, E.A.; Ciccotti, G.; Hynes, J.T.; Kapral, R. Constrained reaction coordinate dynamics for the simulation of rare events. Chem. Phys. Lett. 1989, 156, 472–477. [Google Scholar] [CrossRef]
  35. Barreca, D.; Fois, E.; Gasparotto, A.; Seraglia, R.; Tondello, E.; Tabacchi, G. How does CuII convert into CuI? An unexpected ring-mediated single-electron reduction. Chem. A Eur. J. 2011, 17, 10864–10870. [Google Scholar] [CrossRef] [PubMed]
  36. Theerthagiri, J.; Salla, S.; Senthil, R.A.; Nithyadharseni, P.; Madankumar, A.; Arunachalam, P.; Maiyalagan, T.; Kim, H.S. A review on ZnO nanostructured materials: Energy, environmental and biological applications. Nanotechnology 2019, 30, 392001. [Google Scholar] [CrossRef]
  37. Le, A.T.; Ahmadipour, M.; Pung, S.Y. A review on ZnO-based piezoelectric nanogenerators: Synthesis, characterization techniques, performance enhancement and applications. J. Alloys Compd. 2020, 844, 156172. [Google Scholar] [CrossRef]
  38. Constantinoiu, I.; Viespe, C. ZnO metal oxide semiconductor in surface acoustic wave sensors: A Review. Sensors 2020, 20, 5118. [Google Scholar] [CrossRef]
  39. Özgür, Ü.; Alivov, Y.I.; Liu, C.; Teke, A.; Reshchikov, M.A.; Doǧan, S.; Avrutin, V.; Cho, S.J.; Morko, H. A comprehensive review of ZnO materials and devices. J. Appl. Phys. 2005, 98, 1–103. [Google Scholar] [CrossRef] [Green Version]
  40. Wang, J.; Chen, R.; Xiang, L.; Komarneni, S. Synthesis, properties and applications of ZnO nanomaterials with oxygen vacancies: A review. Ceram. Int. 2018, 44, 7357–7377. [Google Scholar] [CrossRef]
  41. Kołodziejczak-Radzimska, A.; Jesionowski, T. Zinc Oxide—from synthesis to application: A review. Materials 2014, 7, 2833–2881. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  42. Ni, J.; Yan, H.; Wang, A.; Yang, Y.; Stern, C.L.; Metz, A.W.; Jin, S.; Wang, L.; Marks, T.J.; Ireland, J.R.; et al. MOCVD-derived highly transparent, conductive zinc- and tin-doped indium oxide thin films: Precursor synthesis, metastable phase film growth and characterization, and application as anodes in polymer light-emitting diodes. J. Am. Chem. Soc. 2005, 127, 5613–5624. [Google Scholar] [CrossRef] [PubMed]
  43. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  44. Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
  45. Tabacchi, G.; Gianotti, E.; Fois, E.; Martra, G.; Marchese, L.; Coluccia, S.; Gamba, A. Understanding the vibrational and electronic features of Ti(IV) sites in mesoporous silicas by integrated ab initio and spectroscopic investigations. J. Phys. Chem. C 2007, 111, 4946–4955. [Google Scholar] [CrossRef]
  46. Fois, E.; Gamba, A.; Tabacchi, G.; Coluccia, S.; Martra, G. Ab initio study of defect sites at the inner surfaces of mesoporous silicas. J. Phys. Chem. B 2003, 107, 10767–10772. [Google Scholar] [CrossRef]
  47. IBM Corp. MPI für Festkörperforschung Stuttgart 1997–2001 CPMD: Car Parrinello Molecular Dynamics 2019, Version 4.1; IBM Corp: Zürich, Switzerland, 2019. [Google Scholar]
  48. Tabacchi, G. Supramolecular organization in confined nanospaces. ChemPhysChem 2018, 19, 1249–1297. [Google Scholar] [CrossRef]
  49. Kleinman, L.; Bylander, D.M. Efficacious form for model pseudopotentials. Phys. Rev. Lett. 1982, 48, 1425–1428. [Google Scholar] [CrossRef]
  50. Troullier, N.; Martins, J.L. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B 1991, 43, 1993–2006. [Google Scholar] [CrossRef]
  51. Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 1990, 41, 7892–7895. [Google Scholar] [CrossRef]
  52. Martínez-Suarez, L.; Siemer, N.; Frenzel, J.; Marx, D. Reaction Network of Methanol Synthesis over Cu/ZnO Nanocatalysts. ACS Catal. 2015, 5, 4201–4218. [Google Scholar] [CrossRef]
  53. Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef] [Green Version]
  54. Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  55. Gatta, G.D.; Lotti, P.; Tabacchi, G. The effect of pressure on open-framework silicates: Elastic behaviour and crystal–fluid interaction. Phys. Chem. Miner. 2018, 45, 115–138. [Google Scholar] [CrossRef]
  56. Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef] [Green Version]
  57. Figgen, D.; Rauhut, G.; Dolg, M.; Stoll, H. Energy-consistent pseudopotentials for group 11 and 12 atoms: Adjustment to multi-configuration Dirac-Hartree-Fock data. Chem. Phys. 2005, 311, 227–244. [Google Scholar] [CrossRef]
  58. Peterson, K.A.; Puzzarini, C. Systematically convergent basis sets for transition metals. II. Pseudopotential-based correlation consistent basis sets for the group 11 (Cu, Ag, Au) and 12 (Zn, Cd, Hg) elements. Theor. Chem. Acc. 2005, 114, 283–296. [Google Scholar] [CrossRef]
  59. Dunning, T.H.; Hay, P.J. Gaussian Basis Sets for Molecular Calculations. In Methods of Electronic Structure Theory; Springer: New York, NY, USA, 1977; pp. 1–27. [Google Scholar]
  60. Pritchard, B.P.; Altarawy, D.; Didier, B.; Gibson, T.D.; Windus, T.L. New Basis Set Exchange: An Open, Up-to-Date Resource for the Molecular Sciences Community. J. Chem. Inf. Model. 2019, 59, 4814–4820. [Google Scholar] [CrossRef]
  61. Tomasi, J.; Mennucci, B.; Cammi, R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105, 2999–3094. [Google Scholar] [CrossRef]
  62. Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef] [Green Version]
  63. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision B.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
  64. Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
  65. Halz, J.H.; Heiser, C.; Wagner, C.; Merzweiler, K. Syntheses and crystal structures of three [ M(acac)2(TMEDA)] complexes (M = Mn, Fe and Zn). Acta Crystallogr. Sect. E Crystallogr. Commun. 2020, 76, 66–71. [Google Scholar] [CrossRef]
  66. Tabacchi, G.; Fabbiani, M.; Mino, L.; Martra, G.; Fois, E. The case of formic acid on anatase TiO2 (101): Where is the acid proton? Angew. Chem. Int. Ed. 2019, 58, 12431–12434. [Google Scholar] [CrossRef] [PubMed]
  67. Fois, E.; Gamba, A.; Medici, C.; Tabacchi, G.; Quartieri, S.; Mazzucato, E.; Arletti, R.; Vezzalini, G.; Dmitriev, V. High pressure deformation mechanism of Li-ABW: Synchrotron XRPD study and ab initio molecular dynamics simulations. Microporous Mesoporous Mater. 2008, 115, 267–280. [Google Scholar] [CrossRef]
  68. Frank, I. A single-molecule reaction cascade: First-principles molecular dynamics simulation. Int. J. Quantum Chem. 2017, 117, e25395. [Google Scholar] [CrossRef]
  69. Fois, E.; Gamba, A.; Tabacchi, G. Structure and dynamics of a Brønsted acid site in a zeolite: An ab initio study of hydrogen sodalite. J. Phys. Chem. B 1998, 102, 3974–3979. [Google Scholar] [CrossRef]
  70. Litman, Y.; Donadio, D.; Ceriotti, M.; Rossi, M. Decisive role of nuclear quantum effects on surface mediated water dissociation at finite temperature. J. Chem. Phys. 2018, 148, 102320. [Google Scholar] [CrossRef] [Green Version]
  71. Arletti, R.; Fois, E.; Gigli, L.; Vezzalini, G.; Quartieri, S.; Tabacchi, G. Irreversible conversion of a water–ethanol solution into an organized two-dimensional network of alternating supramolecular units in a hydrophobic zeolite under pressure. Angew. Chem. Int. Ed. 2017, 56, 2105–2109. [Google Scholar] [CrossRef]
  72. Konuk, M.; Sellschopp, K.; Vonbun-Feldbauer, G.B.; Meißner, R.H. Modeling charge redistribution at magnetite interfaces in empirical force fields. J. Phys. Chem. C 2021. [Google Scholar] [CrossRef]
  73. Harju, M.; Mäntylä, T.; Vähä-Heikkilä, K.; Lehto, V.P. Water adsorption on plasma sprayed transition metal oxides. Appl. Surf. Sci. 2005, 249, 115–126. [Google Scholar] [CrossRef]
  74. Boehm, H.P.; Knoezinger, H. Nature and estimation of functional groups on solid surfaces. In Catalysis—Science and Technology; Anderson, J.R., Boudart, M., Eds.; Springer: Berlin/Heidelberg, Germany, 1983; Volume 4, pp. 39–209. [Google Scholar] [CrossRef]
  75. Védrine, J.C. Recent developments and prospectives of acid-base and redox catalytic processes by metal oxides. Appl. Catal. A Gen. 2019, 575, 170–179. [Google Scholar] [CrossRef]
Molecules 26 01988 g001 550
Figure 1. Variation of four Zn-O distances (red solid lines) and two Zn-N distances (black solid line) along the exploratory ab initio molecular dynamics (AIMD) simulation of the octahedral Zn(hfa)2TMEDA molecular complex on the hydroxylated silica surface.
Figure 1. Variation of four Zn-O distances (red solid lines) and two Zn-N distances (black solid line) along the exploratory ab initio molecular dynamics (AIMD) simulation of the octahedral Zn(hfa)2TMEDA molecular complex on the hydroxylated silica surface.
Molecules 26 01988 g001
Molecules 26 01988 g002 550
Figure 2. Optimized geometries of the (a) octahedral and (b) pyramidal forms of the complex Zn(hfa)2TMEDA (computed at the M06/D95+(d,p) level of theory). (a) Octahedral complex (Oct), which is the minimum energy structure, evidencing the pseudo-octahedral Zn coordination environment. (b) Pyramidal complex (Pyr), highlighting the breakage of the bond between the β-diketonate oxygen O2′ and the Zn center. Pyr is higher in energy than Oct by 13.06 kcal/mol at the M06/D95+(d,p) level, and by 10.02 kcal/mol at the PBE-D2/PW level. C1* and C2* indicate the central C atoms of the hfa ligands. Color codes: Zn, grey; F, green; O, red; N, blue; C, cyan; H, white.
Figure 2. Optimized geometries of the (a) octahedral and (b) pyramidal forms of the complex Zn(hfa)2TMEDA (computed at the M06/D95+(d,p) level of theory). (a) Octahedral complex (Oct), which is the minimum energy structure, evidencing the pseudo-octahedral Zn coordination environment. (b) Pyramidal complex (Pyr), highlighting the breakage of the bond between the β-diketonate oxygen O2′ and the Zn center. Pyr is higher in energy than Oct by 13.06 kcal/mol at the M06/D95+(d,p) level, and by 10.02 kcal/mol at the PBE-D2/PW level. C1* and C2* indicate the central C atoms of the hfa ligands. Color codes: Zn, grey; F, green; O, red; N, blue; C, cyan; H, white.
Molecules 26 01988 g002
Molecules 26 01988 g003 550
Figure 3. Simulated electronic spectra of the octahedral and pyramidal forms of Zn(hfa)2TMEDA along with the experimental spectrum obtained at room temperature in 1.25 × 10−5 M ethanol solution.
Figure 3. Simulated electronic spectra of the octahedral and pyramidal forms of Zn(hfa)2TMEDA along with the experimental spectrum obtained at room temperature in 1.25 × 10−5 M ethanol solution.
Molecules 26 01988 g003
Molecules 26 01988 g004 550
Figure 4. (a) Molecular orbitals (MOs) involved in the π–π* ligand-to-ligand electronic transitions for Zn(hfa)2TMEDA-Oct in ethanol. The main components of the transition were at λ = 273 nm (oscillator strength = 0.376) (HOMO → LUMO+1 and HOMO−1 → LUMO excitations) and λ = 281 nm (oscillator strength = 0.109) (HOMO → LUMO and HOMO−1 → LUMO+1 excitations). (b) MOs involved in the π–π* ligand-to-ligand electronic transitions for Zn(hfa)2TMEDA-Pyr in ethanol. Main components at λ = 269 nm (oscillator strength = 0.383) (HOMO→ LUMO+1 excitation) and λ = 276 nm (oscillator strength = 0.252) (HOMO−2 → LUMO excitation). Blue and yellow colors mark positive and negative phases of the MOs, respectively.
Figure 4. (a) Molecular orbitals (MOs) involved in the π–π* ligand-to-ligand electronic transitions for Zn(hfa)2TMEDA-Oct in ethanol. The main components of the transition were at λ = 273 nm (oscillator strength = 0.376) (HOMO → LUMO+1 and HOMO−1 → LUMO excitations) and λ = 281 nm (oscillator strength = 0.109) (HOMO → LUMO and HOMO−1 → LUMO+1 excitations). (b) MOs involved in the π–π* ligand-to-ligand electronic transitions for Zn(hfa)2TMEDA-Pyr in ethanol. Main components at λ = 269 nm (oscillator strength = 0.383) (HOMO→ LUMO+1 excitation) and λ = 276 nm (oscillator strength = 0.252) (HOMO−2 → LUMO excitation). Blue and yellow colors mark positive and negative phases of the MOs, respectively.
Molecules 26 01988 g004
Molecules 26 01988 g005 550
Figure 5. Free energy profile of the octahedral-to-pyramidal conversion of Zn(hfa)2TMEDA on the hydroxylated SiO2 surface. The reaction coordinate is the Zn-O2′ distance.
Figure 5. Free energy profile of the octahedral-to-pyramidal conversion of Zn(hfa)2TMEDA on the hydroxylated SiO2 surface. The reaction coordinate is the Zn-O2′ distance.
Molecules 26 01988 g005
Molecules 26 01988 g006 550
Figure 6. Optimized geometries of the (a) octahedral Zn(hfa)2TMEDA complex (initial state), (b) transition state, and (c) pyramidal Zn(hfa)2TMEDA (final state) on the hydroxylated silica slab (PBE-D2/PW level of theory). The insets on the right side of the (a–c) panels highlight the coordination environment of Zn and the O2′-H* hydrogen bond. Color codes: Zn, gray; F, green; O, red; N, blue; C, cyan; H, white; Si: yellow. Labels as in Figure 1 and Table 1 and Table 3. The hydrogen bond of the detached hfa oxygen O2′ with the surface proton H* is indicated as a dotted line.
Figure 6. Optimized geometries of the (a) octahedral Zn(hfa)2TMEDA complex (initial state), (b) transition state, and (c) pyramidal Zn(hfa)2TMEDA (final state) on the hydroxylated silica slab (PBE-D2/PW level of theory). The insets on the right side of the (a–c) panels highlight the coordination environment of Zn and the O2′-H* hydrogen bond. Color codes: Zn, gray; F, green; O, red; N, blue; C, cyan; H, white; Si: yellow. Labels as in Figure 1 and Table 1 and Table 3. The hydrogen bond of the detached hfa oxygen O2′ with the surface proton H* is indicated as a dotted line.
Molecules 26 01988 g006
Molecules 26 01988 g007 550
Figure 7. Five snapshots taken from the Blue Moon AIMD (BM-AIMD) simulations corresponding to the following values of the Zn-O2′ distance (reaction coordinate): (a) Zn-O2′ = 2.12 Å, Oct- Zn(hfa)2TMEDA; (b) Zn-O2′ = 3.18 Å, Oct- Zn(hfa)2TMEDA; (c) Zn-O2′ = 3.81 Å, trigonal- bipyramidal Zn(hfa)2TMEDA (transition state); (d) Zn-O2′ = 4.23 Å, Pyr-Zn(hfa)2TMEDA; (e) Zn-O2′ = 4.87 Å, Pyr- Zn(hfa)2TMEDA. Color codes: Zn, gray; F, green; O, red; N, blue; C, cyan; H, white; Si: yellow. The hydrogen bond of the detached hfa oxygen O2′ with the surface hydroxyl proton H* is indicated as a dotted line.
Figure 7. Five snapshots taken from the Blue Moon AIMD (BM-AIMD) simulations corresponding to the following values of the Zn-O2′ distance (reaction coordinate): (a) Zn-O2′ = 2.12 Å, Oct- Zn(hfa)2TMEDA; (b) Zn-O2′ = 3.18 Å, Oct- Zn(hfa)2TMEDA; (c) Zn-O2′ = 3.81 Å, trigonal- bipyramidal Zn(hfa)2TMEDA (transition state); (d) Zn-O2′ = 4.23 Å, Pyr-Zn(hfa)2TMEDA; (e) Zn-O2′ = 4.87 Å, Pyr- Zn(hfa)2TMEDA. Color codes: Zn, gray; F, green; O, red; N, blue; C, cyan; H, white; Si: yellow. The hydrogen bond of the detached hfa oxygen O2′ with the surface hydroxyl proton H* is indicated as a dotted line.
Molecules 26 01988 g007
Molecules 26 01988 g008 550
Figure 8. Variation of the average distance between the surface hydroxyl proton H* and the hfa oxygen O2′ as a function of the Zn-O2′ distance (reaction coordinate). Vertical bars represent the standard deviations, which are an estimate of the amplitude of the thermal oscillations of the O2′-H* distance. The black dots correspond to the BM-sampled values of the Zn-O2′ distance.
Figure 8. Variation of the average distance between the surface hydroxyl proton H* and the hfa oxygen O2′ as a function of the Zn-O2′ distance (reaction coordinate). Vertical bars represent the standard deviations, which are an estimate of the amplitude of the thermal oscillations of the O2′-H* distance. The black dots correspond to the BM-sampled values of the Zn-O2′ distance.
Molecules 26 01988 g008
Table
Table 1. Average metal-ligand bond distances <r>, standard deviation σ, minimum rmin and maximum rmax distance values sampled from the AIMD simulation of Zn(hfa)2TMEDA on the hydroxylated SiO2 surface at the PBE-D2/PW level. All distances are in Å. For atom labeling, see Figure 2.
Table 1. Average metal-ligand bond distances <r>, standard deviation σ, minimum rmin and maximum rmax distance values sampled from the AIMD simulation of Zn(hfa)2TMEDA on the hydroxylated SiO2 surface at the PBE-D2/PW level. All distances are in Å. For atom labeling, see Figure 2.
Distance<r>σrminrmax
Zn-O12.230.251.823.24
Zn-O1′2.040.121.752.43
Zn-O22.150.211.822.89
Zn-O2′3.620.911.865.21
Zn-N2.260.181.852.93
Zn-N′2.330.191.942.89
Table
Table 2. Geometrical parameters calculated in the gas phase at 0 K for octahedral (Oct) and pyramidal (Pyr) forms of Zn(hfa)2TMEDA at PBE-D2/PW and M06/D95+(d,p) levels (labels in Figure 2). Distances in Å, angles in degrees (°).
Table 2. Geometrical parameters calculated in the gas phase at 0 K for octahedral (Oct) and pyramidal (Pyr) forms of Zn(hfa)2TMEDA at PBE-D2/PW and M06/D95+(d,p) levels (labels in Figure 2). Distances in Å, angles in degrees (°).
ParameterOct- PBE-D2/PWPyr- PBE-D2/PWOct- M06/D95+(d,p)Pyr- M06/D95+(d,p)
Zn-O12.1152.0572.0742.031
Zn-O1′2.1162.0642.0972.039
Zn-O22.1151.9642.0741.942
Zn-O2′2.1164.3342.0974.302
Zn-N2.1962.1882.1622.152
Zn-N’2.1962.1672.1622.123
O2′-C2′1.2691.2411.2511.225
O2-C21.2701.2821.2541.267
O1′-C1′1.2691.2711.2511.254
O1- C11.2701.2731.2541.256
C2*-C2′1.4081.4371.4041.437
C2*-C21.4051.3871.4001.378
C1*-C1′1.4081.4051.4041.399
C1*-C11.4051.4041.4001.400
O2-Zn-O188.0111.987.3111.8
O2-Zn-O1′86.7108.186.6107.0
O2-Zn-N93.899.394.299.8
O2-Zn-N’91.691.592.092.2
Table
Table 3. Free energy differences ΔG and energy differences ΔE for the transition state and Pyr with respect to Oct. Binding energies BE (kcal/mol) of the octahedral (Oct) and pyramidal (Pyr) structures of the Zn complex adsorbed on the SiO2 silica slab. Binding energy difference Δ(BE) relative to Oct.
Table 3. Free energy differences ΔG and energy differences ΔE for the transition state and Pyr with respect to Oct. Binding energies BE (kcal/mol) of the octahedral (Oct) and pyramidal (Pyr) structures of the Zn complex adsorbed on the SiO2 silica slab. Binding energy difference Δ(BE) relative to Oct.
(kcal/mol)Oct@SiO2TS@SiO2Pyr@SiO2
ΔG0+5.80+3.57
ΔE0+7.80+2.23
BE28.27-36.07
Δ(BE)0-7.81
Table
Table 4. Geometrical parameters of the octahedral (Oct), pyramidal (Pyr), and transition state (TS) structures of the Zn complex adsorbed on the hydroxylated SiO2 surface at the PBE-D2/PW level. Isolated complex data at the same theory level are reported to facilitate comparison. Distances in Å.
Table 4. Geometrical parameters of the octahedral (Oct), pyramidal (Pyr), and transition state (TS) structures of the Zn complex adsorbed on the hydroxylated SiO2 surface at the PBE-D2/PW level. Isolated complex data at the same theory level are reported to facilitate comparison. Distances in Å.
DistanceOct@SiO2TS@SiO2Pyr@SiO2Isolated-OctIsolated-Pyr
Zn-O12.0872.0902.0442.1152.057
Zn-O1′2.1392.0182.0912.1162.064
Zn-O22.1152.0422.0502.1151.964
Zn-O2′2.2633.8184.8732.1164.334
Zn-N2.1772.1412.1602.1962.188
Zn-N’2.1492.1452.1472.1962.167
O2′-H*1.8851.6301.586--
O2′-C2′1.2791.2481.2511.2691.241
O2-C21.2641.2651.2771.2701.282
O1′-C1′1.2671.2771.2691.2691.271
O1- C11.2711.2691.2721.2701.273
H* indicates the surface hydroxyl proton involved in the O2′-H* hydrogen bond.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Barreca, D.; Fois, E.; Gasparotto, A.; Maccato, C.; Oriani, M.; Tabacchi, G. The Early Steps of Molecule-to-Material Conversion in Chemical Vapor Deposition (CVD): A Case Study. Molecules 2021, 26, 1988. https://doi.org/10.3390/molecules26071988

AMA Style

Barreca D, Fois E, Gasparotto A, Maccato C, Oriani M, Tabacchi G. The Early Steps of Molecule-to-Material Conversion in Chemical Vapor Deposition (CVD): A Case Study. Molecules. 2021; 26(7):1988. https://doi.org/10.3390/molecules26071988

Chicago/Turabian Style

Barreca, Davide, Ettore Fois, Alberto Gasparotto, Chiara Maccato, Mario Oriani, and Gloria Tabacchi. 2021. "The Early Steps of Molecule-to-Material Conversion in Chemical Vapor Deposition (CVD): A Case Study" Molecules 26, no. 7: 1988. https://doi.org/10.3390/molecules26071988

Article Metrics

Back to TopTop