Monte Carlo Simulation and Experimental Studies of CO2, CH4 and Their Mixture Capture in Porous Carbons
Abstract
1. Introduction
2. Methodology
2.1. Fluid-Fluid Potential Models
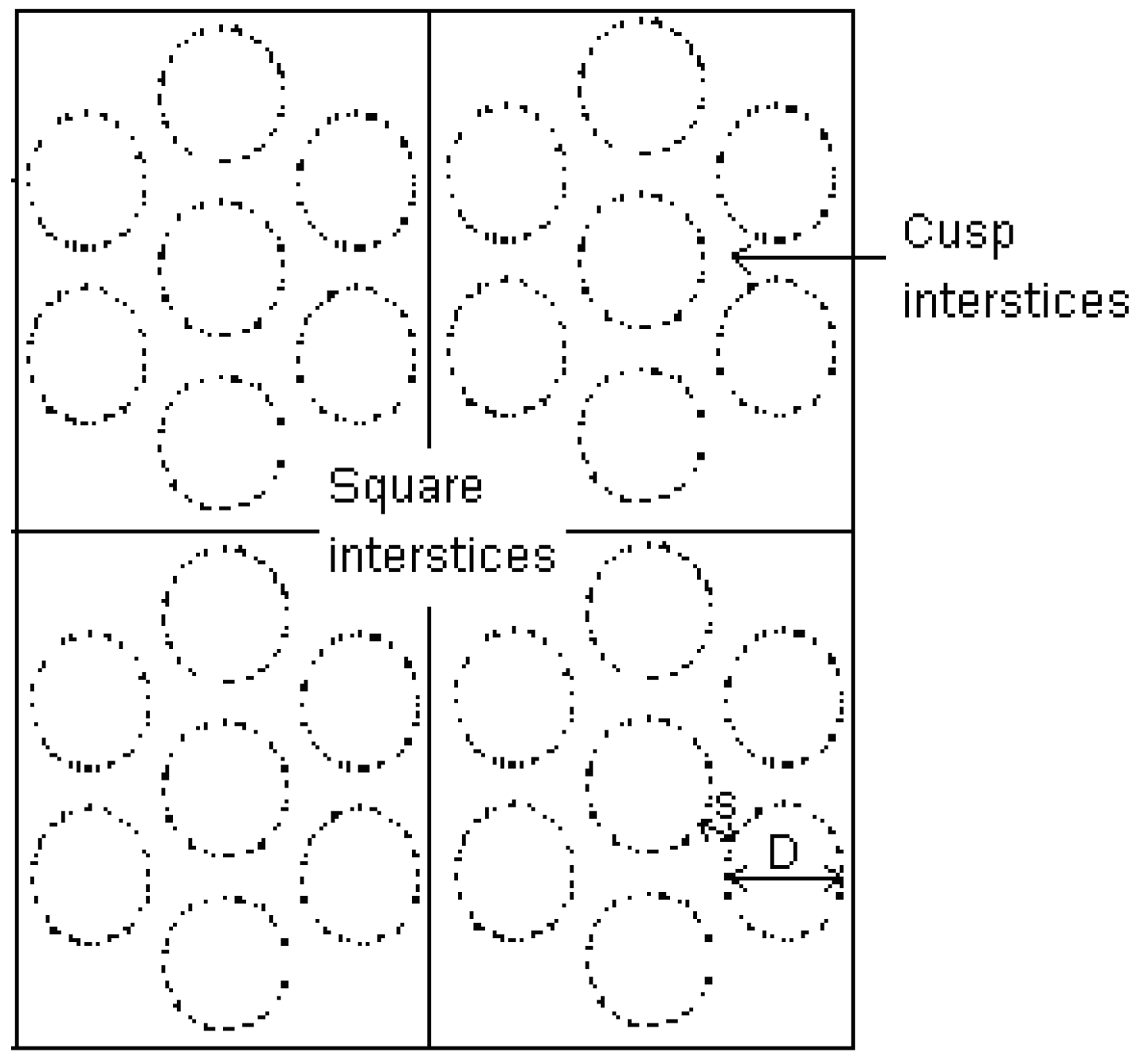
2.2. Solid Models
2.3. Monte Carlo Simulation
2.4. Experiments
3. Results and Discussions
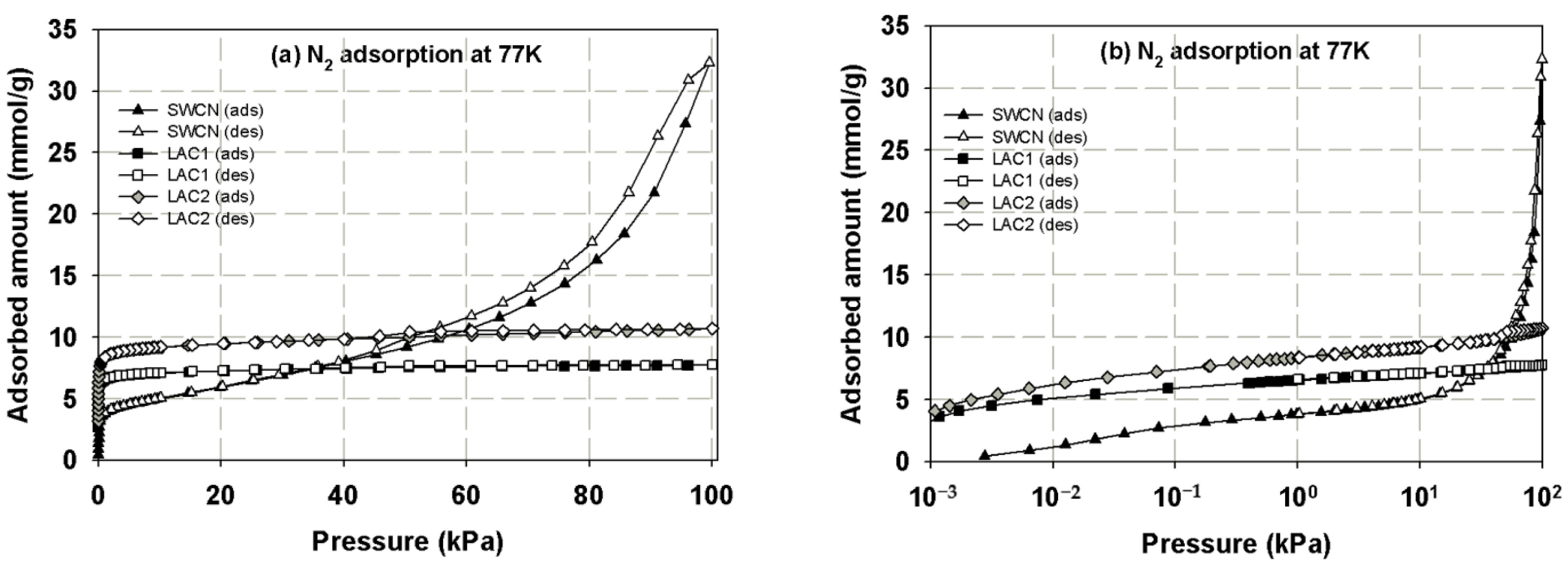
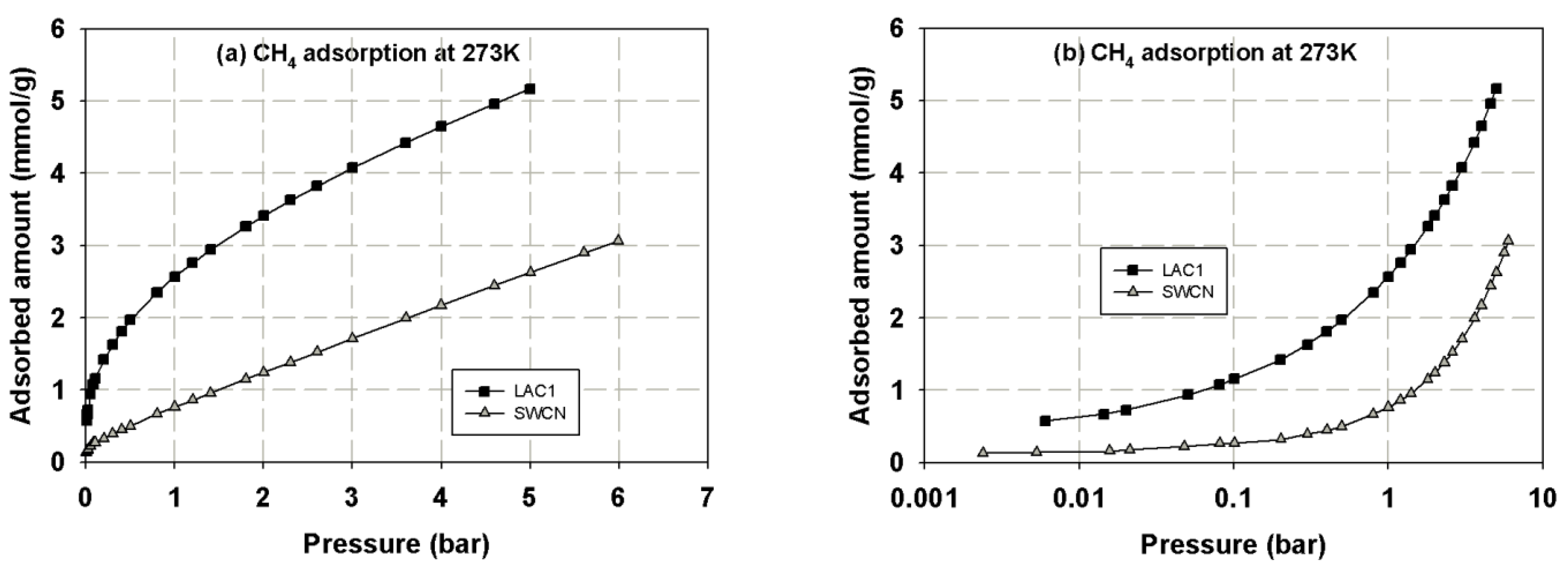
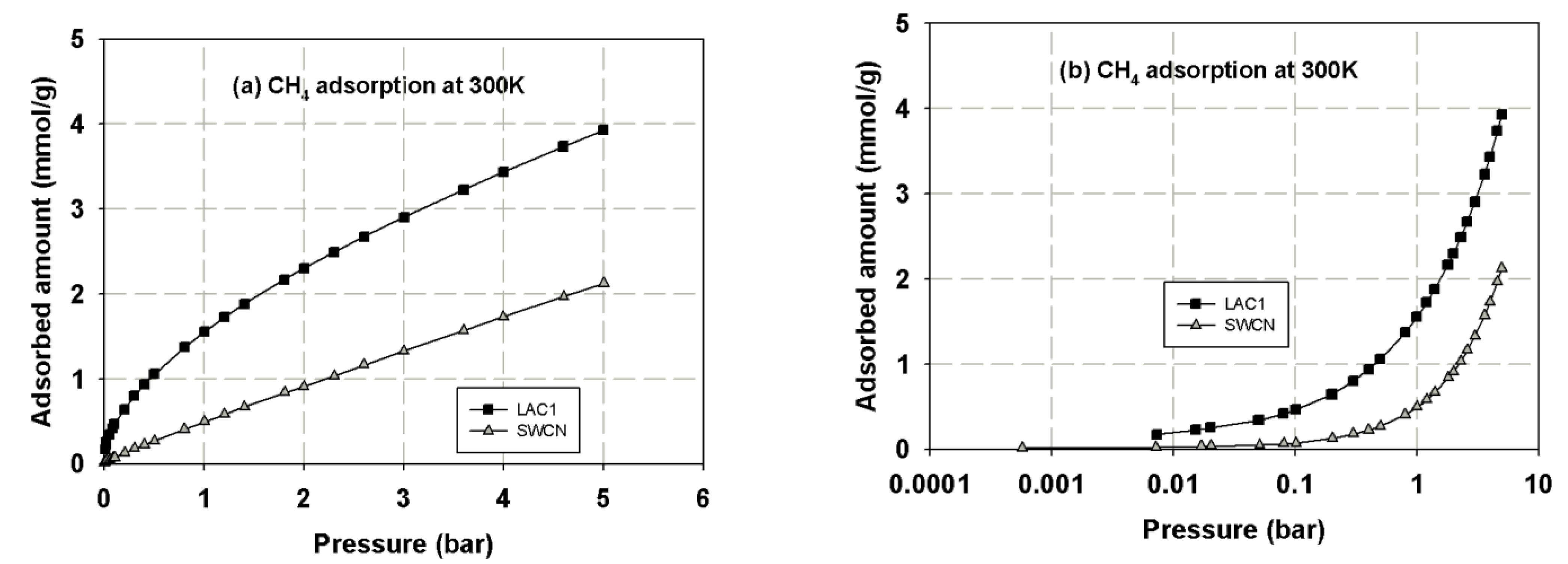
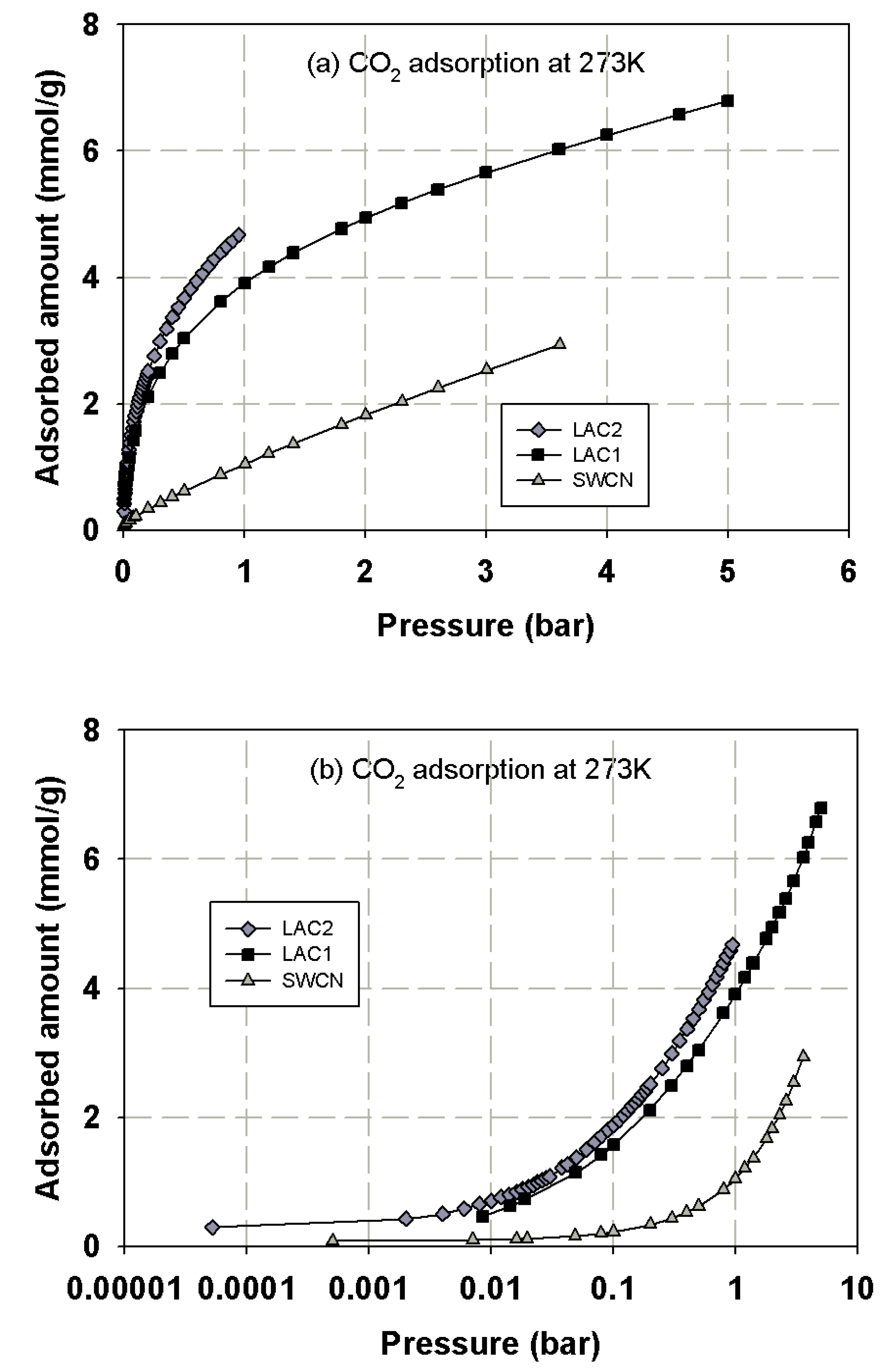
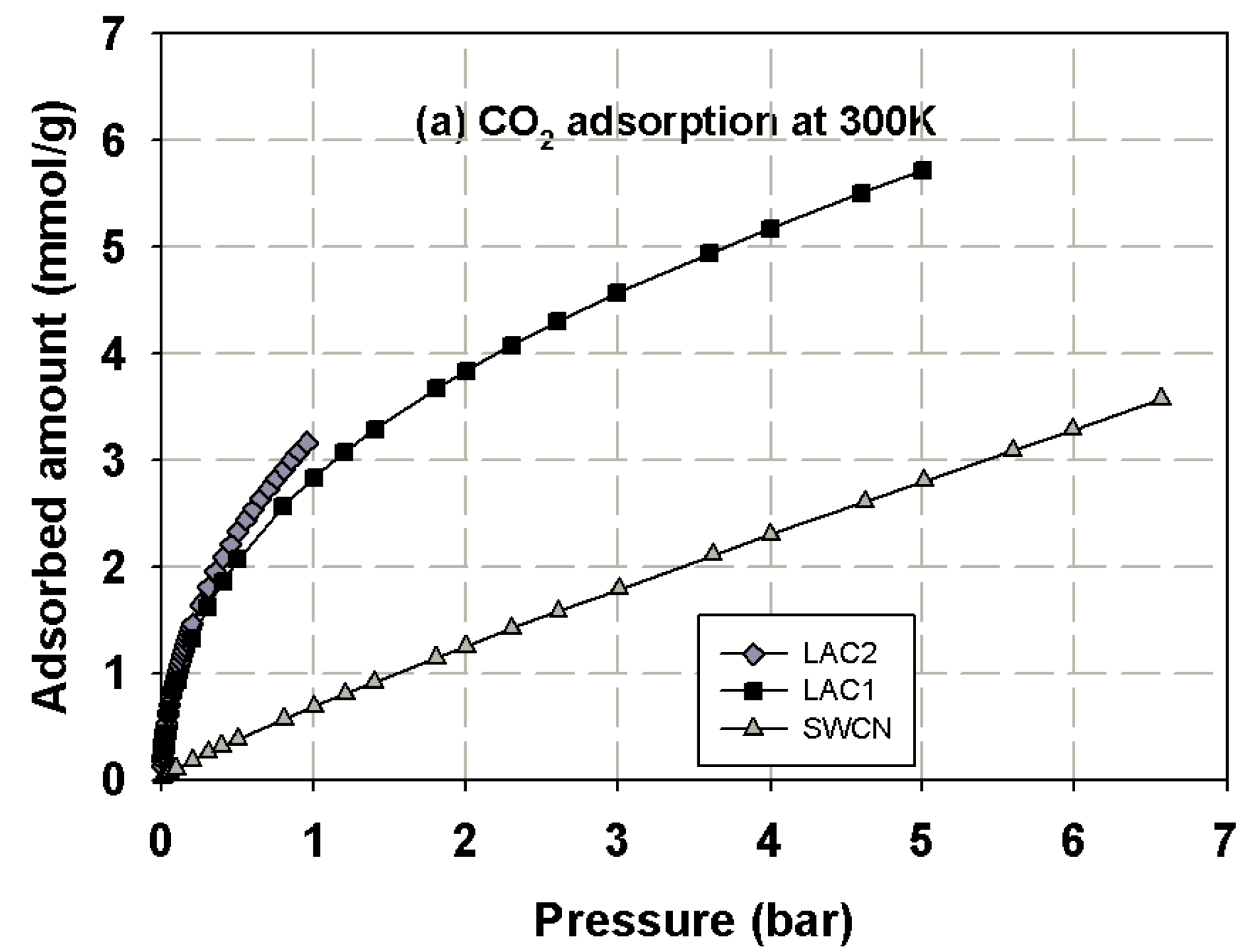
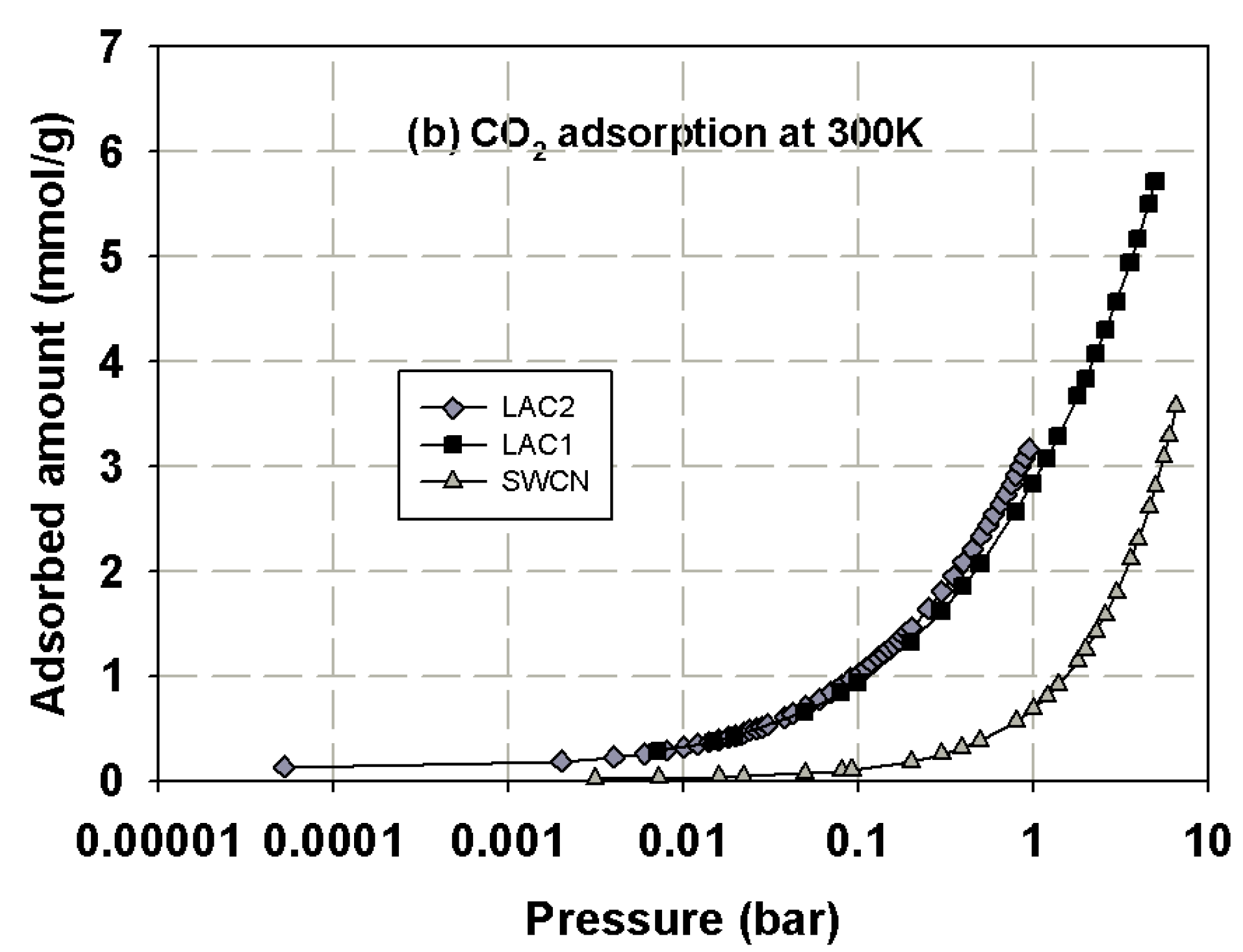
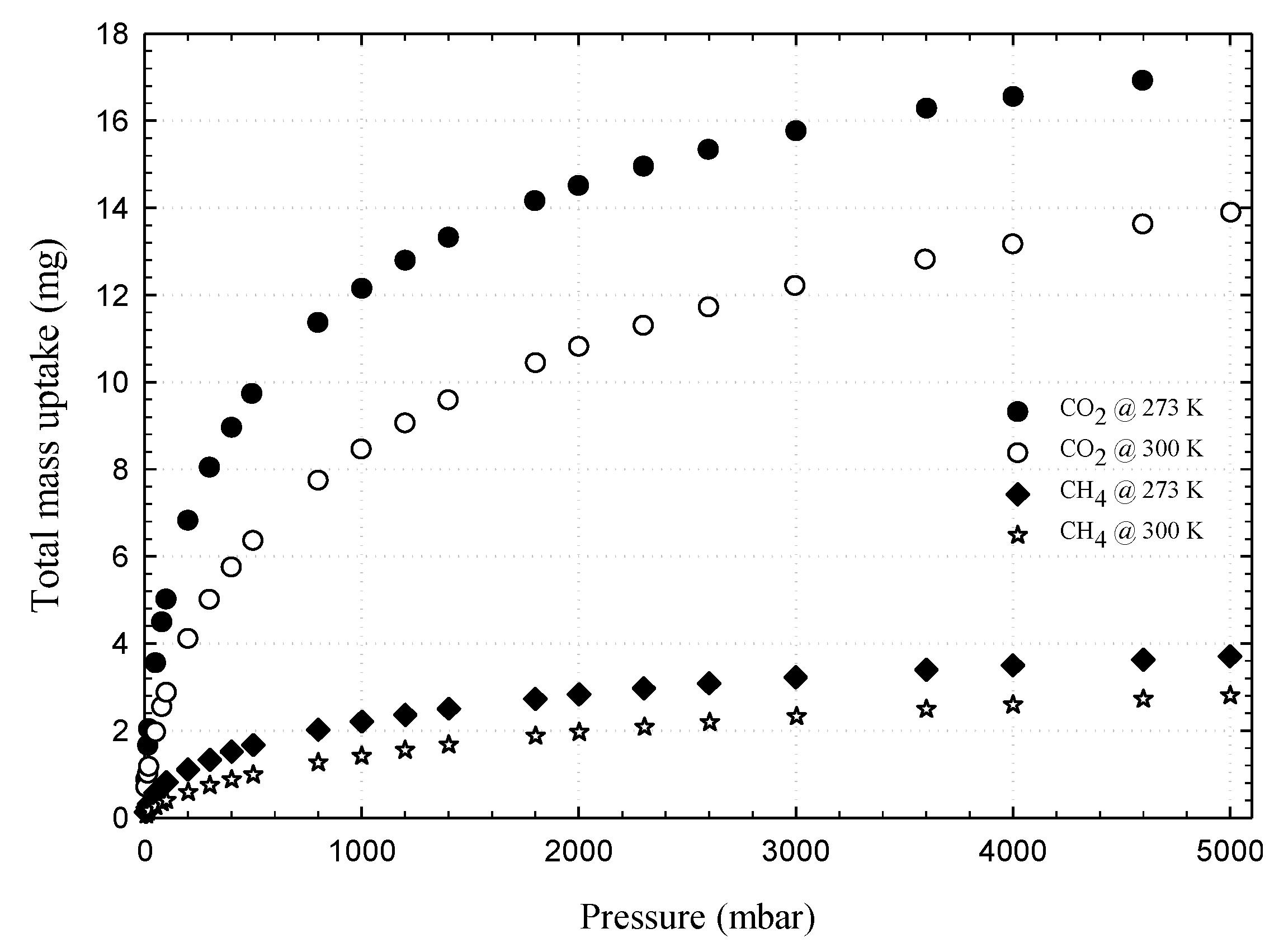
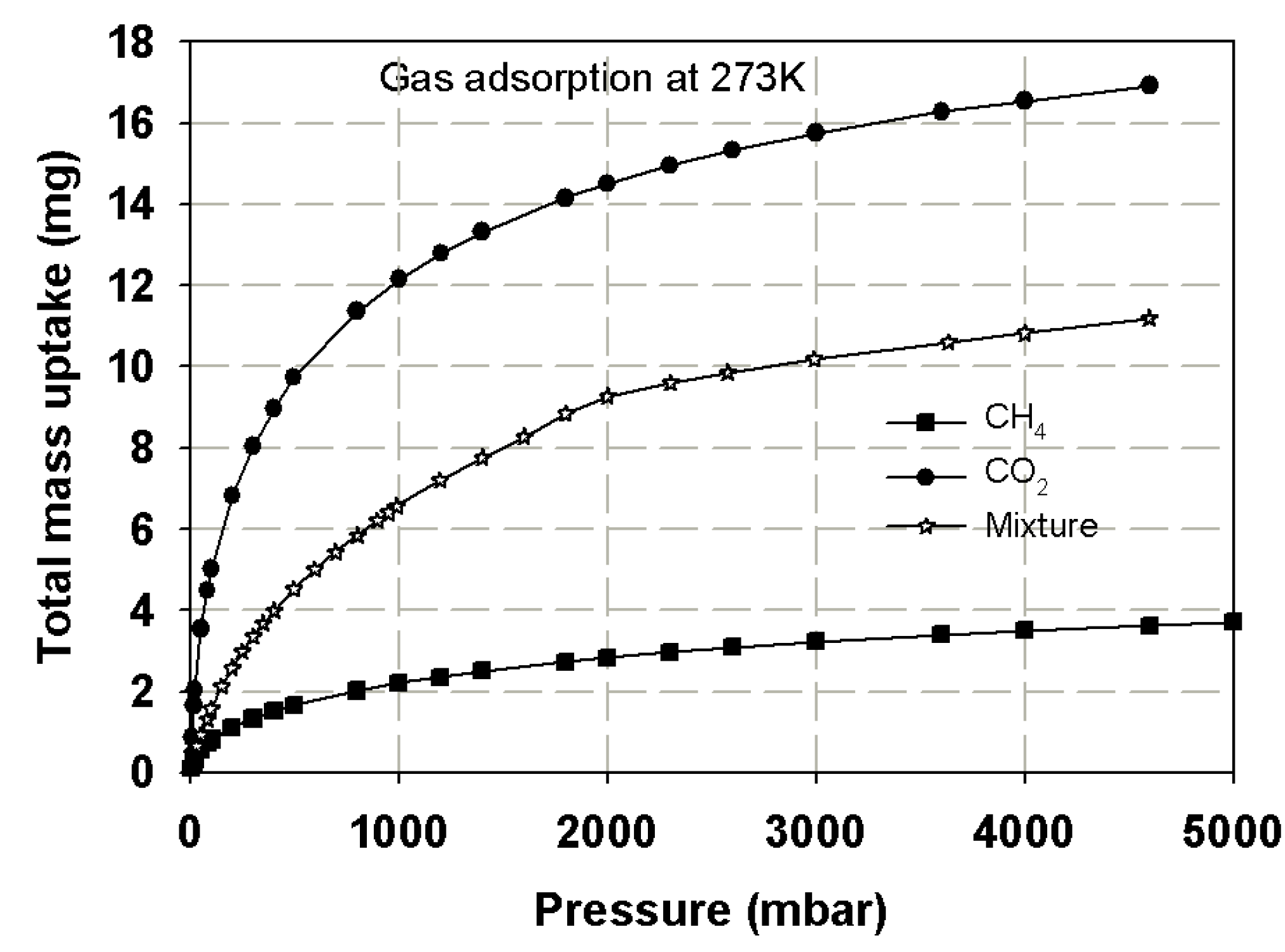
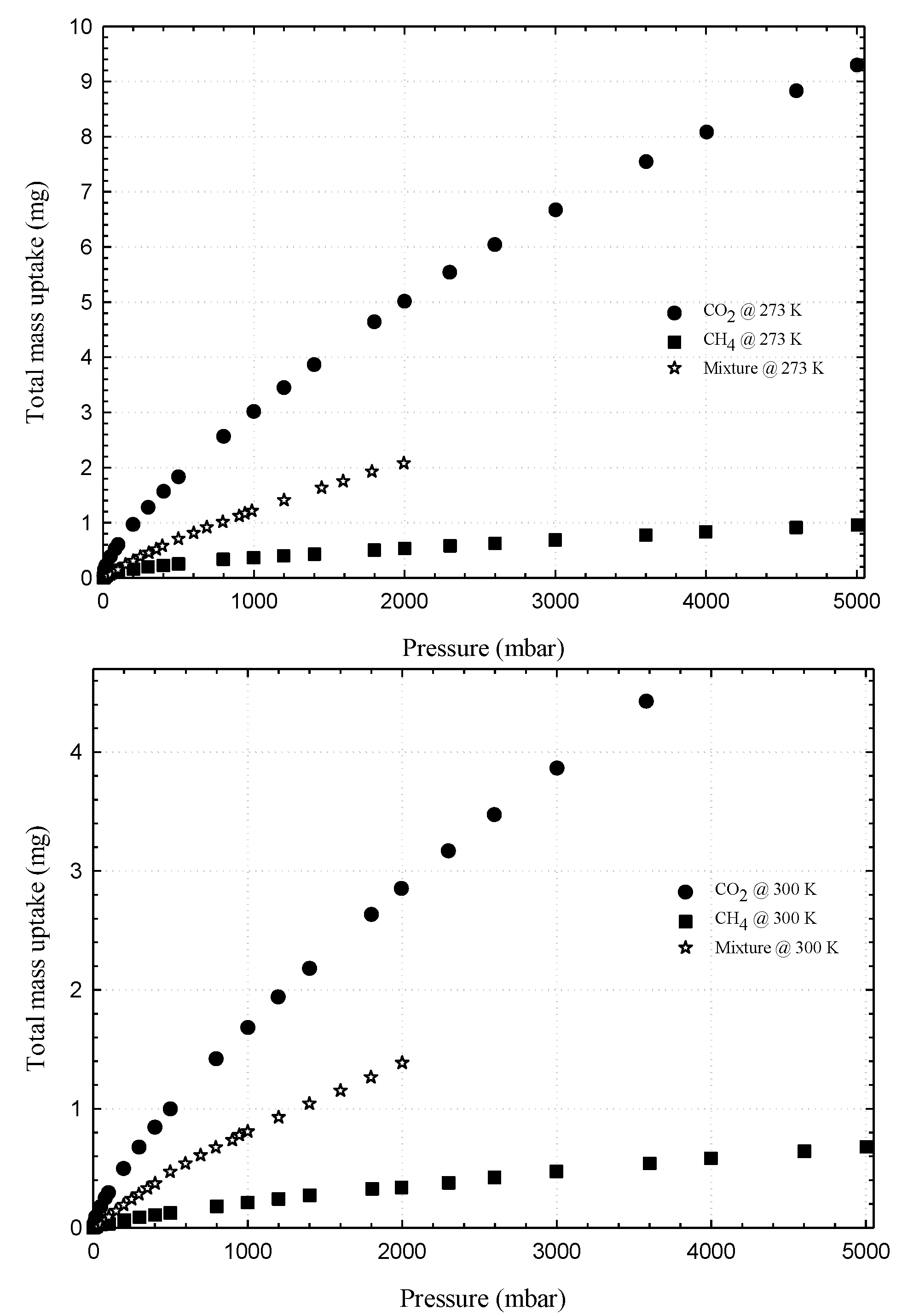
3.1. Experimental Isotherms
3.2. Simulation Isotherm for Gas Adsorption in Finite-Length Slit Pore
3.3. Simulation Isotherm for Gas Adsorption in Finite Length Tube Bundle Model
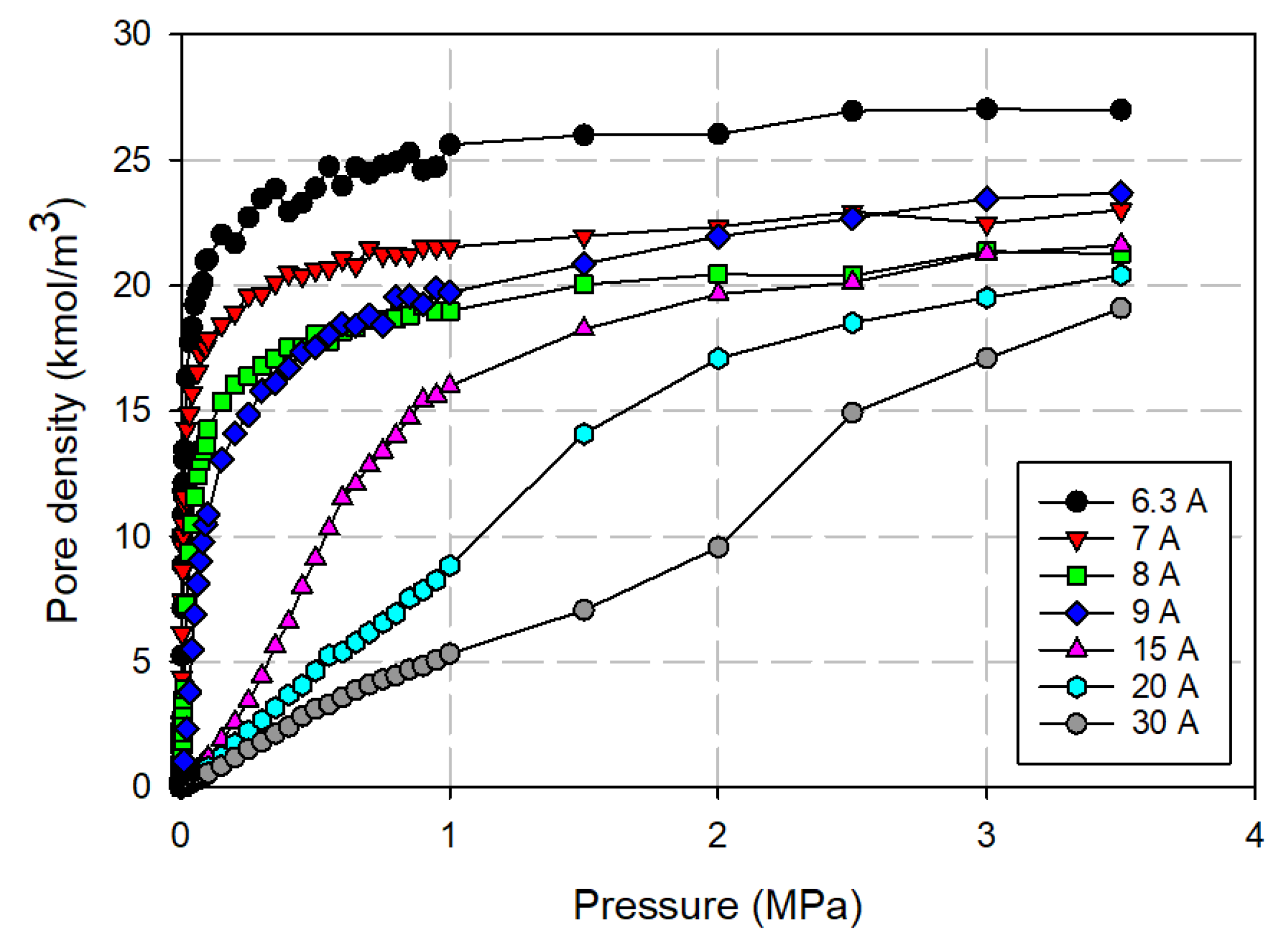
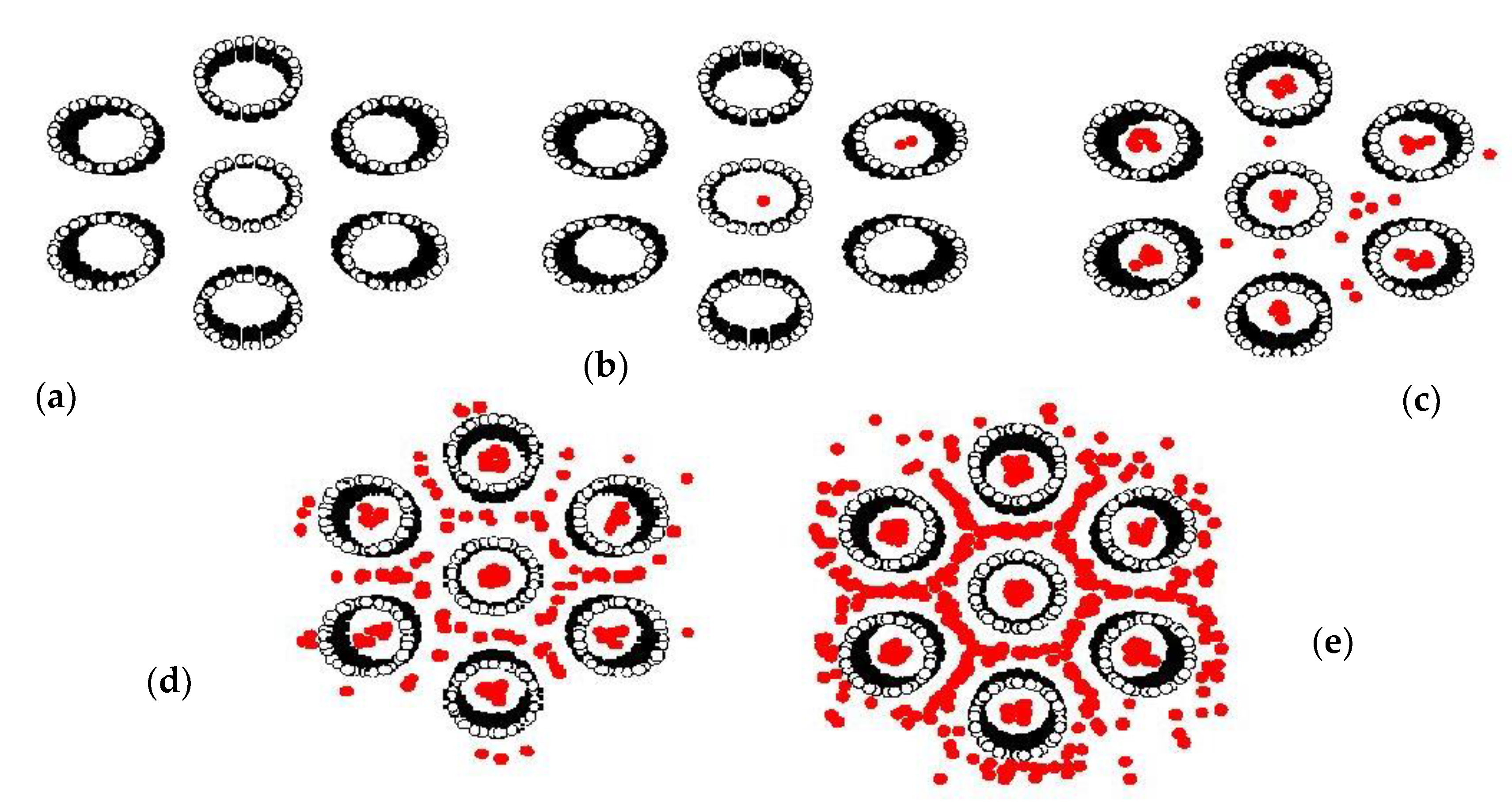
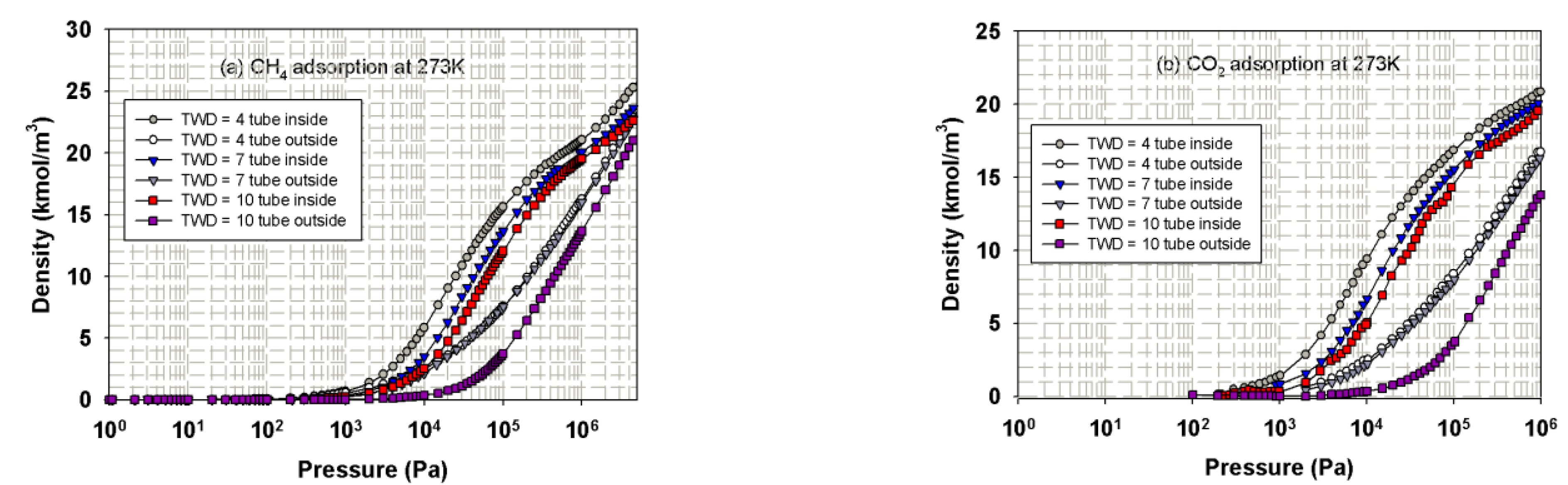
3.3.1. Effects of Tube Diameter on Adsorption Isotherm
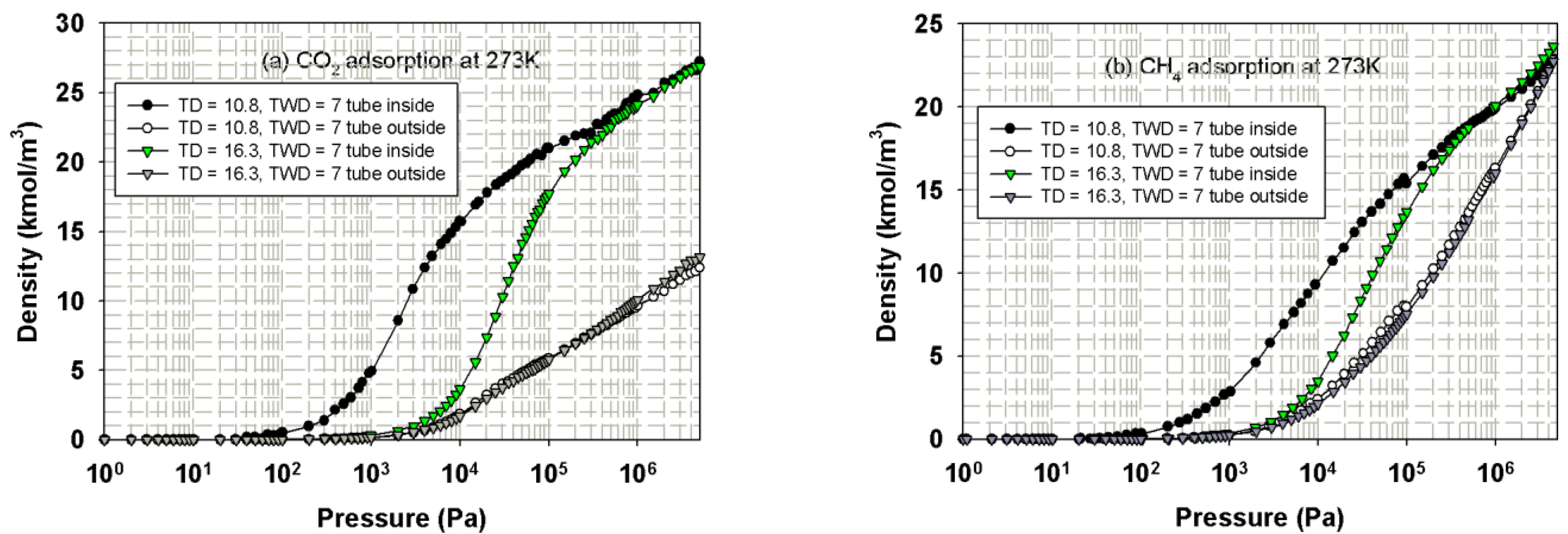
3.3.2. Effects of Tube Wall Distance
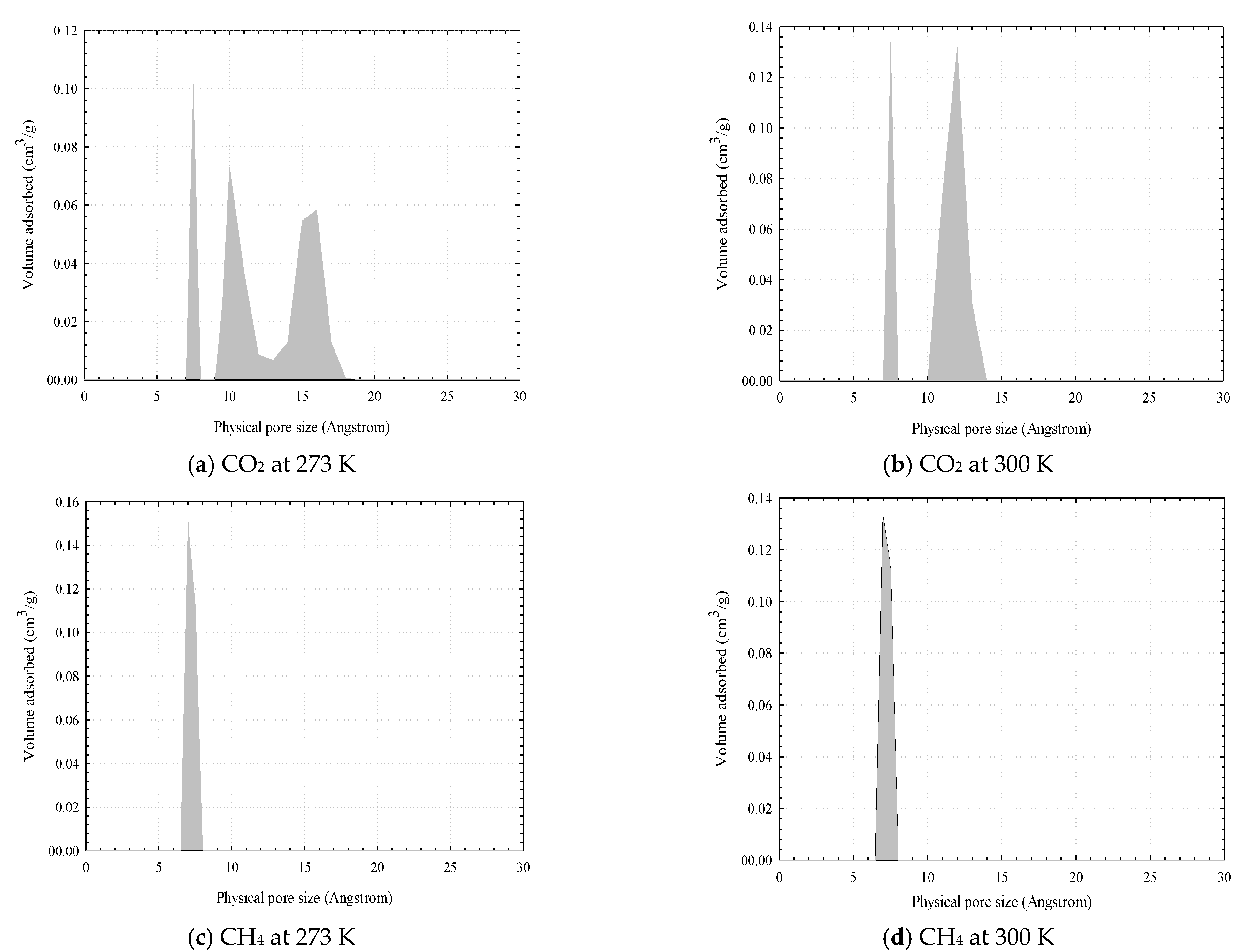
3.4. Pore Size Distribution (PSD) Determination
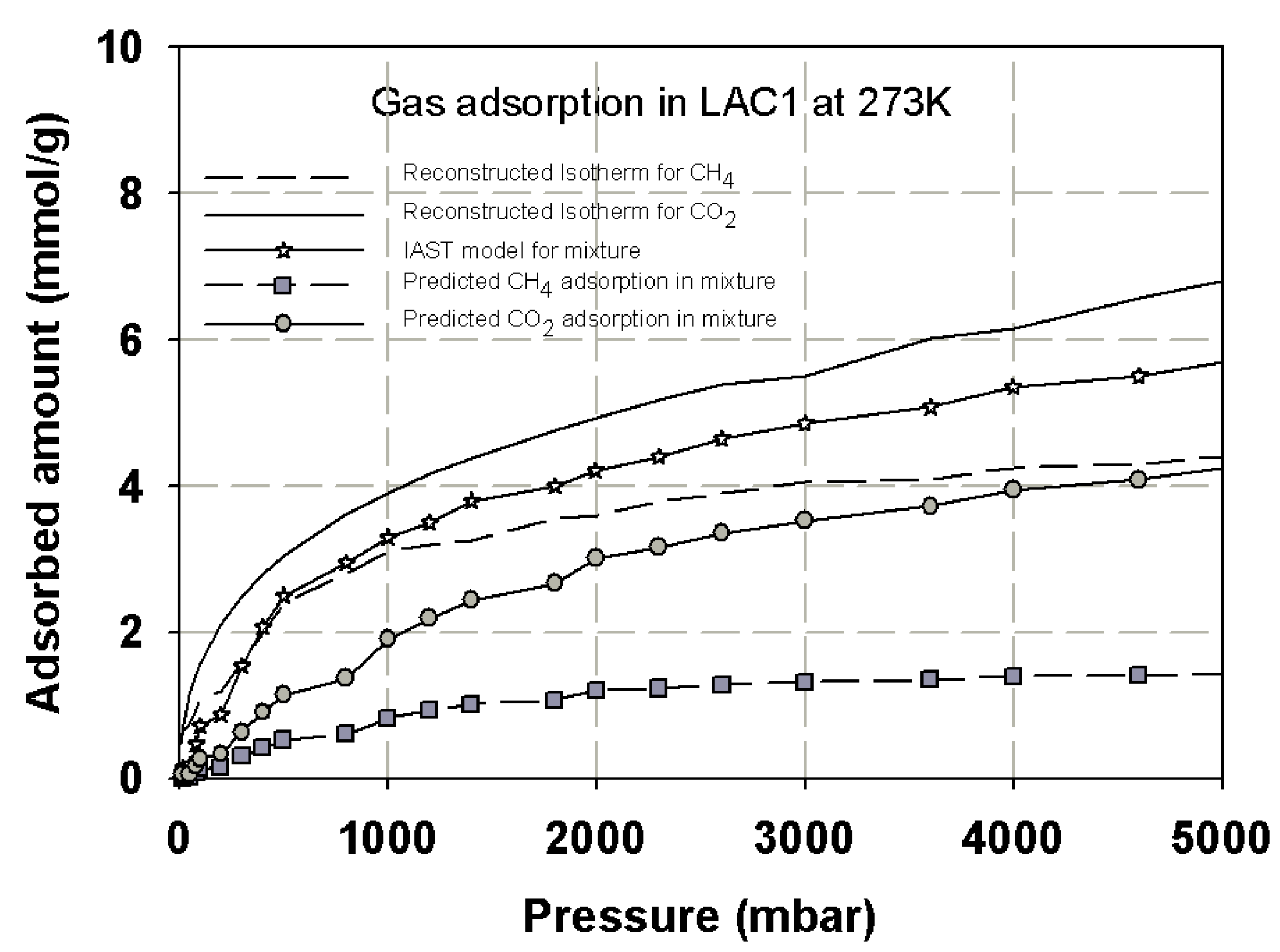
3.5. Prediction Adsorption Isotherm of CO2/CH4 Mixture
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Ravikovitch, P.I.; Vishnyakov, A.; Russo, R.; Neimark, A.V. Unified Approach to Pore Size Characterization of Microporous Carbonaceous Materials from N2, Ar, and CO2 Adsorption Isotherms. Langmuir 2000, 16, 2311–2320. [Google Scholar] [CrossRef]
- Yang, R.T. Adsorbents Fundamentals and Applications; John Wiley & Sons, Inc. Publication: Hoboken, NJ, USA, 2003. [Google Scholar]
- Park, J.; Attia, N.F.; Jung, M.; Lee, M.E.; Lee, K.; Chung, J.; Oh, H. Sustainable nanoporous carbon for CO2, CH4, N2, H2 adsorption and CO2/CH4 and CO2/N2 separation. Energy 2018, 158, 9–16. [Google Scholar] [CrossRef]
- Fan, W.; Chakraborty, A.; Kayal, S. Adsorption cooling cycles: Insights into carbon dioxide adsorption on activated carbons. Energy 2016, 102, 491–501. [Google Scholar] [CrossRef]
- Hug, S.; Stegbauer, L.; Oh, H.; Hirscher, M.; Lotsch, B.V. Nitrogen-Rich Covalent Triazine Frameworks as High-Performance Platforms for Selective Carbon Capture and Storage. Chem. Mater. 2015, 27, 8001–8010. [Google Scholar] [CrossRef]
- Feng, L.; Shen, Y.; Wu, T.; Liu, B.; Zhang, D.; Tang, Z. Adsorption equilibrium isotherms and thermodynamic analysis of CH4, CO2, CO, N2 and H2 on NaY Zeolite. Adsorpt 2020, 26, 1101–1111. [Google Scholar] [CrossRef]
- Heuchel, M.; Davies, G.M.; Buss, E.; Seaton, N.A. Adsorption of Carbon Dioxide and Methane and Their Mixtures on an Activated Carbon: Simulation and Experiment. Langmuir 1999, 15, 8695–8705. [Google Scholar] [CrossRef]
- Álvarez-Gutiérrez, N.; Gil, M.; Rubiera, F.; Pevida, C. Adsorption performance indicators for the CO2/CH4 separation: Application to biomass-based activated carbons. Fuel Process. Technol. 2016, 142, 361–369. [Google Scholar] [CrossRef]
- Esteves, I.A.; Lopes, M.S.; Nunes, P.M.; Mota, J.P. Adsorption of natural gas and biogas components on activated carbon. Sep. Purif. Technol. 2008, 62, 281–296. [Google Scholar] [CrossRef]
- Kayal, S.; Sun, B.; Chakraborty, A. A Study of metal-organic framwork MIL-101(Cr) for natural gas (methane) storage and compare with other MOFs (metal-organic-framworks). Energy 2015, 91, 772–781. [Google Scholar] [CrossRef]
- Kaźmierczak, J.; Nowicki, P.; Pietrzak, R. Sorption properties of activated carbons obtained from corn cops by chemical and physical activation. Adsorption 2013, 19, 273–281. [Google Scholar] [CrossRef]
- Junpirom, S.; Do, D.; Tangsathitkulchai, C.; Tangsathitkulchai, M. A carbon activation model with application to longan seed char gasification. Carbon 2005, 43, 1936–1943. [Google Scholar] [CrossRef]
- Mintmire, J.W.; Dunlap, B.I.; White, C.T. Are fullerene tubules metallic? Phys. Rev. Lett. 1992, 68, 631–634. [Google Scholar] [CrossRef]
- Hamada, N.; Sawada, S.-I.; Oshiyama, A. New one-dimensional conductors: Graphitic microtubules. Phys. Rev. Lett. 1992, 68, 1579–1581. [Google Scholar] [CrossRef]
- Lozano-Castelló, D.; Alcañiz-Monge, J.; de la Casa-Lillo, M.; Cazorla-Amorós, D.; Linares-Solano, A. Advances in the study of methane storage in porous carbonaceous materials. Fuel 2002, 81, 1777–1803. [Google Scholar] [CrossRef]
- Molashahi, M.; Hashemipour, H. Experimental study and artificial neural network simulation of methane adsorption on activated carbon. Korean J. Chem. Eng. 2012, 29, 601–605. [Google Scholar] [CrossRef]
- Parkyns, N.D.; Quinn, D.F. Porosity in Carbons; Patrick, J.W., Ed.; Edward Arnold: London, UK, 1995; pp. 293–325. [Google Scholar]
- Nguyen, C.; Do, D.D. A New Method for the Characterization of Porous Materials. Langmuir 1999, 15, 3608–3615. [Google Scholar] [CrossRef]
- Gauden, P.A.; Terzyk, A.P.; Rychlicki, G.; Kowalczyk, P.; Cwiertnia, M.S.; Garbacz, J.K. Estimating the pore size distribution of activated carbons from adsorption data of different adsorbates by various methods. J. Colloid Interface Sci. 2004, 273, 39–63. [Google Scholar] [CrossRef] [PubMed]
- Mazzoldi, A.; Hill, T.; Colls, J.J. CFD and Gaussian atmospheric dispersion models: A comparison for leak from carbon dioxide transportation and storage facilities. Atmos. Environ. 2008, 42, 8046–8054. [Google Scholar] [CrossRef]
- Maddox, M.; Ulberg, D.; Gubbins, K. Molecular simulation of simple fluids and water in porous carbons. Fluid Phase Equilibria 1995, 104, 145–158. [Google Scholar] [CrossRef]
- Alexiadis, A.; Kassinos, S. Molecular Simulation of Water in Carbon Nanotubes. Chem. Rev. 2008, 108, 5014–5034. [Google Scholar] [CrossRef] [PubMed]
- Franklin, R.E. Crystallite growth in graphitizing and non-graphitizing carbons. Proc. Roy. Soc. 1951, 209, 196–218. [Google Scholar]
- Do, D.D. Adsorption Analysis: Equilibria and Kinetics; Imperial College Press: London, UK, 1998. [Google Scholar]
- Yin, Y.F.; Mays, T.; McEnaney, B. Adsorption of Nitrogen in Carbon Nanotube Arrays. Langmuir 1999, 15, 8714–8718. [Google Scholar] [CrossRef]
- Agnihotri, S.; Mota, J.P.B.; Rostam-Abadi, M.; Rood, M.J. Theoretical and Experimental Investigation of Morphology and Temperature Effects on Adsorption of Organic Vapors in Single-Walled Carbon Nanotubes. J. Phys. Chem. B 2006, 110, 7640–7647. [Google Scholar] [CrossRef] [PubMed]
- Wongkoblap, A.; Junpirom, S.; Do, D.D. Adsorption of Lennard-Jones Fluids in Carbon Slit Pores of a Finite Length. A Computer Simulation Study. Adsorpt. Sci. Technol. 2005, 23, 1–18. [Google Scholar] [CrossRef]
- Wongkoblap, A.; Do, D.; Wang, K. Adsorption of polar and non-polar fluids in carbon nanotube bundles: Computer simulation and experimental studies. J. Colloid Interface Sci. 2009, 331, 65–76. [Google Scholar] [CrossRef]
- Harris, J.G.; Yung, K.H. Carbon Dioxide’s Liquid-Vapor Coexistence Curve and Critical Properties as Predicted by a Simple Molecular Model. J. Phys. Chem. 1995, 99, 12021–12024. [Google Scholar] [CrossRef]
- Murthy, C.S.; O’Shea, S.F.; McDonald, I.R. Electrostatic interactions in molecular crystals: Lattice dynamics of solid nitrogen and carbon dioxide. Mol. Phys. 1983, 50, 531–541. [Google Scholar] [CrossRef]
- Vernov, A.; Steele, W. Simulation studies of bilayers of N2 adsorbed on graphite at 25 and 35 K. Surf. Sci. 1986, 171, 83–102. [Google Scholar] [CrossRef]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation, 2nd ed.; Academic Press: New York, NY, USA, 2002. [Google Scholar]
- Allen, M.P.; Tildesley, D. Computer Simulation of Liquid; Oxford University Press: Oxford, UK, 1987. [Google Scholar]
- Johnson, J.K.; Zollweg, J.A.; Gubbins, K.E. The Lennard-Jones equation of state revisited. Mol. Phys. 1993, 78, 591–618. [Google Scholar] [CrossRef]
- Vishnyakov, A.; Ravikovitch, P.I.; Neimark, A.V. Molecular Level Models for CO2 Sorption in Nanopores. Langmuir 1999, 15, 8736–8742. [Google Scholar] [CrossRef]
- Yang, R.T. Gas Separation by Adsorption Processes; Imperial College Press, Butterworths: Boston, MA, USA, 1997. [Google Scholar]
- Huang, L.; Zhang, L.; Shao, Q.; Lu, L.; Lü, X.; Jiang, S.; Shen, W. Simulations of Binary Mixture Adsorption of Carbon Dioxide and Methane in Carbon Nanotubes: Temperature, Pressure, and Pore Size Effects. J. Phys. Chem. C 2007, 111, 11912–11920. [Google Scholar] [CrossRef]
- Tangsathitkulchai, C. Adsorption Processes; Suranaree University of Technology Press: Nakhon Ratchasima, Thailand, 2011. [Google Scholar]
- Kirk, R.E.; Othmer, D.F. Encyclopedia of Chemical Technology; Wiley & Sons, Inc. Publication: Chichester, UK; New York, NY, USA, 2004; pp. 493–527. [Google Scholar]
- Choi, B.-U.; Choi, D.-K.; Lee, Y.-W.; Lee, B.-K.; Kim, S.-H. Adsorption Equilibria of Methane, Ethane, Ethylene, Nitrogen, and Hydrogen onto Activated Carbon. J. Chem. Eng. Data 2003, 48, 603–607. [Google Scholar] [CrossRef]
- Lithoxoos, G.P.; Labropoulos, A.; Peristeras, L.D.; Kanellopoulos, N.; Samios, J.; Economou, I.G. Adsorption of N2, CH4, CO and CO2 gases in single walled carbon nanotubes: A combined experimental and Monte Carlo molecular simulation study. J. Supercrit. Fluids 2010, 55, 510–523. [Google Scholar] [CrossRef]
- Buss, E. Gravimetric measurement of binary gas adsorption equilibria of methane-carbon dioxide mixtures on activated carbon. Gas Sep. Purif. 1995, 9, 189–197. [Google Scholar] [CrossRef]
- Van Der Vaart, R.; Husiskes, C.; Bosch, H.; Reith, T. Single and Mixed Gas Adsorption Equilibria of Carbon Dioxide/Methane on Activated Carbon. Adsorption 2000, 6, 311–323. [Google Scholar] [CrossRef]
- Dreisbach, F.; Staudt, R.; Keller, J.U. High Pressure Adsorption Data of Methane, Nitrogen, Carbon Dioxide and their Binary and Ternary Mixtures on Activated Carbon. Adsorption 1999, 5, 215–227. [Google Scholar] [CrossRef]
- Goetz, V.; Pupier, O.; Guillot, A. Guillot, Carbon dioxide-methane mixture adsorption on activated carbon. Adsorption 2006, 12, 55–63. [Google Scholar] [CrossRef]
- Wongkoblap, A.; Intomya, W.; Somrup, W.; Charoensuk, S.; Junpirom, S.; Tangsathitkulchai, C. Pore Size Distribution of Carbon with Different Probe Molecules. Eng. J. 2010, 14, 45–56. [Google Scholar] [CrossRef][Green Version]
- Bottani, E.; Bakaev, V. The Grand Canonical Ensemble Monte Carlo Simulation of Nitrogen on Graphite. Langmuir 1994, 10, 1550. [Google Scholar] [CrossRef]
- Samios, S.; Stubos, A.K.; Kanellopoulos, N.K.; Cracknell, R.F.; Papadopoulos, G.K.; Nicholson, D. Determination of micropore size distribution from Grand Canonical Monte Carlo simulations and experimental CO2 isotherm data. Langmuir 1997, 13, 2795–2802. [Google Scholar] [CrossRef]
- Cazorla-Amorós, D.; Alcañiz-Monge, J.; De La Casa-Lillo, M.A.; Linares-Solano, A. CO2 As an Adsorptive To Characterize Carbon Molecular Sieves and Activated Carbons. Langmuir 1998, 14, 4589–4596. [Google Scholar] [CrossRef]
- Kurniawan, Y.; Bhatia, S.K.; Rudolph, V. Monte Carlo simulation of binary mixture adsorption of methane and carbon dioxide in carbon slit pore. Ann. Univ. Mariae Curie-Sklodowska Sect. AA Chem. 2005, 60, 79–92. [Google Scholar]





| Fluid | |||
|---|---|---|---|
| CH4 | 3.730 | 148.0 | - |
| N2 (2 LJ sites) | 3.320 | 36.4 | 1.1 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| σc-c | 2.757 Å | εc-c/k | 28.129 K |
| σo-o | 3.033 Å | εo-o/k | 80.507 K |
| qc | 0.6512e | qo | −0.3256e |
| λc-o | 1.149 Å |
| Sample | BET Surface Area (m2/g) | Micropore Volume (cm3/g) | Meso- and Macropores Volume (cm3/g) | Total Pore Volume (cm3/g) |
|---|---|---|---|---|
| SWCN | 853 | 0.18 | 1.11 | 1.29 |
| LAC1 | 538 | 0.20 | 0.07 | 0.27 |
| LAC2 | 705 | 0.26 | 0.11 | 0.37 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kohmuean, P.; Inthomya, W.; Wongkoblap, A.; Tangsathitkulchai, C. Monte Carlo Simulation and Experimental Studies of CO2, CH4 and Their Mixture Capture in Porous Carbons. Molecules 2021, 26, 2413. https://doi.org/10.3390/molecules26092413
Kohmuean P, Inthomya W, Wongkoblap A, Tangsathitkulchai C. Monte Carlo Simulation and Experimental Studies of CO2, CH4 and Their Mixture Capture in Porous Carbons. Molecules. 2021; 26(9):2413. https://doi.org/10.3390/molecules26092413
Chicago/Turabian StyleKohmuean, Pakamas, Worapoj Inthomya, Atichat Wongkoblap, and Chaiyot Tangsathitkulchai. 2021. "Monte Carlo Simulation and Experimental Studies of CO2, CH4 and Their Mixture Capture in Porous Carbons" Molecules 26, no. 9: 2413. https://doi.org/10.3390/molecules26092413
APA StyleKohmuean, P., Inthomya, W., Wongkoblap, A., & Tangsathitkulchai, C. (2021). Monte Carlo Simulation and Experimental Studies of CO2, CH4 and Their Mixture Capture in Porous Carbons. Molecules, 26(9), 2413. https://doi.org/10.3390/molecules26092413






