Group Contribution Estimation of Ionic Liquid Melting Points: Critical Evaluation and Refinement of Existing Models

Abstract

While several group contribution method (GCM) models have been developed in recent years for the prediction of ionic liquid (IL) properties, some challenges exist in their effective application. Firstly, the models have been developed and tested based on different datasets; therefore, direct comparison based on reported statistical measures is not reliable. Secondly, many of the existing models are limited in the range of ILs for which they can be used due to the lack of functional group parameters. In this paper, we examine two of the most diverse GCMs for the estimation of IL melting point; a key property in the selection and design of ILs for materials and energy applications. A comprehensive database consisting of over 1300 data points for 933 unique ILs, has been compiled and used to critically evaluate the two GCMs. One of the GCMs has been refined by introducing new functional groups and reparametrized to give improved performance for melting point estimation over a wider range of ILs. This work will aid in the targeted design of ILs for materials and energy applications.

1. Introduction

Over the past two decades, interest in ionic liquids (ILs) has grown significantly, both in terms of academic research and industrial applications. ILs are loosely defined as salts that exist as liquids below 100 °C [1]. Their relatively low melting points result from their chemical structure; they are made of bulky, asymmetric organic cations in combination with organic or inorganic anions that do not easily form a tightly packed lattice structure [2]. ILs also exhibit several unique and interesting properties. They exhibit negligible volatility, high thermal and chemical stability, and high solubility towards a wide range of solutes. Due to the wide range of possible ILs, each with different chemical and physical properties, they are often described as “designer” liquids [3]. These characteristics make them potential candidates for various applications such as separation processes [4], heat transfer fluids [5], thermal energy storage [6], batteries [7], fuel cells [8], and tribology, both as lubricants [9] and lubricant additives [10], and even space technology [11]. Improvements in IL synthesis technology in recent years has also facilitated their large-scale production [12]. Today, there are multiple manufacturers with the ability to mass produce ILs [12,13].

Melting point is one of the fundamental defining characteristics of ILs and also a key physical property in selecting and designing ILs for materials and energy applications. For example, the use of ILs as solvents or heat transfer fluids in industrial processes requires ILs that remain in the liquid phase over the full range of process conditions involved. Melting point defines the lower limit of the liquidus range of ILs, with the upper limit usually defined by the decomposition temperature. In addition, the application of ILs as phase change materials for thermal energy storage necessitates the selection of an IL with a specific melting point suited to the temperature at which thermal energy absorption or release is required [14].

One of the most important characteristics of ILs is their “designer” nature. IL properties can be tuned by varying the cation-anion combination, changing the hydrocarbon chain length on the cation, or by adding various functional groups. It has been estimated that there are in the order of 10⁶ possible ILs, yet only a few thousand have actually been synthesized and characterized. [15,16]. This vast number of possible ILs means that it should be possible, in theory, to design ILs with optimized properties for any selected application. In practice, however, this does not happen, due to the obvious cost and time constraints. To resolve this issue and allow ILs to truly become designer liquids, predictive models are an essential component in the screening of the almost limitless array of possible ILs.

Models for estimating physical properties can be categorized as either theoretical, semi-empirical or empirical [17]. Theoretical methods, such as molecular modeling, are derived from first principles and are usually extremely computationally intensive. They are most useful for developing a fundamental understanding of physical property behavior on a molecular level, but are usually impractical for large scale computational screening of molecules. On the other end of the scale, empirical methods are fast and easy to apply, and are useful for interpolation when sufficient data already exists. However, they are significantly limited in their predictive capabilities. The semi-empirical method is the most useful approach when predictive modelling and efficient screening of large numbers of molecules is required. These models use previously regressed parameters in combination with an equation that models the relationships between the structure of the molecule and its physical properties.

There are primarily two semi-empirical approaches available for predicting IL properties: group contribution methods (GCMs) and quantitative structure property relationship (QSPR) models. QSPR models use the physical, chemical, or physicochemical properties as descriptors, upon which the predictive mathematical model is built [18]. QSPR models mainly rely on quantum calculations to attain the values of the various descriptors used for predicting the IL properties [19]. On the other hand, GCMs mainly use the frequency of occurrence of functional groups within the chemical structure for calculating properties [17]. The fundamental assumption in GCMs is that the physical property of the whole molecule can be represented by the additive contribution of its functional groups. The key advantage of this approach is that all the information needed to use the model is available in the chemical structure. There is no need to make any experimental measurements or perform quantum calculations before applying the GCM for property estimation. For many engineering applications, such as process simulation or computer-aided molecular design, GCMs are preferable to QSPR models, as they are less computationally intensive and are more flexible in their application. In the past decade, GCMs have been developed to estimate IL thermodynamic and physical properties such as melting point [19,20,21], density [22,23,24,25,26,27], viscosity [28,29,30,31], heat capacity [32,33,34,35,36], and thermal conductivity [37,38,39]. However, most of these GCMs were developed several years ago and are based on different and limited datasets. As a result, it is meaningless to compare their reported statistical measures, such as coefficient of determination (R²) or average absolute relative deviation (AARD), since these are not calculated against the same test sets. Furthermore, since the models were developed at a time when significantly fewer ILs had been characterized experimentally, the group contribution parameters available in such models are insufficient for property prediction of many new types to ILs. This presents a major problem in selecting an appropriate GCM for future use. In recent years, a wealth of experimental data has been published; therefore, it is necessary to revisit, reevaluate, improve, and extend such models.

GCMs have been used for property prediction extensively since the 1980s. One of the earliest models was developed by Joback and Reid [40], which estimated a wide variety of thermophysical properties of pure molecular compounds and greatly expanded on the work done by Lydersen [41]. Group contribution models are based on the fundamental assumption that the property of a compound depends upon the type and quantity of functional groups that the compound is composed of. Each functional group makes a certain contribution towards the overall physical property of the compound. In the simple GCMs, these contributions are assumed to be additive; the frequencies of occurrence of each functional group are multiplied by their contribution parameters and added together to obtain the property for the whole compound [40]. More advanced GCMs involve more complex procedures for obtaining the overall property from the individual functional group parameters; for example, they may have parameters to represent the interaction between functional groups, thereby accounting for the dependence of the physical property on such interactions. The main advantages of the GCM approach are its ease of application, breadth of applicability, low computational cost, and its reliance only on structural information without the need for more complex parameters. This is in contrast to the QSPR approach, for example, which often relies upon descriptors derived from quantum calculations or other experimentally measured physical properties. It is also comparatively easy to understand the physical meaning of the parameters in GCMs, as well as extend the applicability of these models by estimating the values for new groups that might not have been incorporated into the initial model. Finally, group contribution models have the benefit of being extendable to work for multiple properties while using the same structural building blocks. Depending on the property being modeled, the fundamental equation for the group contribution models may remain the same, while the group contribution parameters will be regressed according to the new property. Alternatively, the same building blocks can be used, but with new parameters and a new equation more suited to the new property. This greatly reduces the setup time for modeling various properties and provides a consistent platform to build on. Furthermore, often several GCMs are needed to work together for molecular design, since several physical properties are important in the design of molecules for specific applications. Having several GCMs that use the same structural building blocks facilitates their incorporation into an integrated design framework.

Many researchers have developed models for the estimation of IL melting points.

Table 1. Summary of existing models for IL melting point estimation.

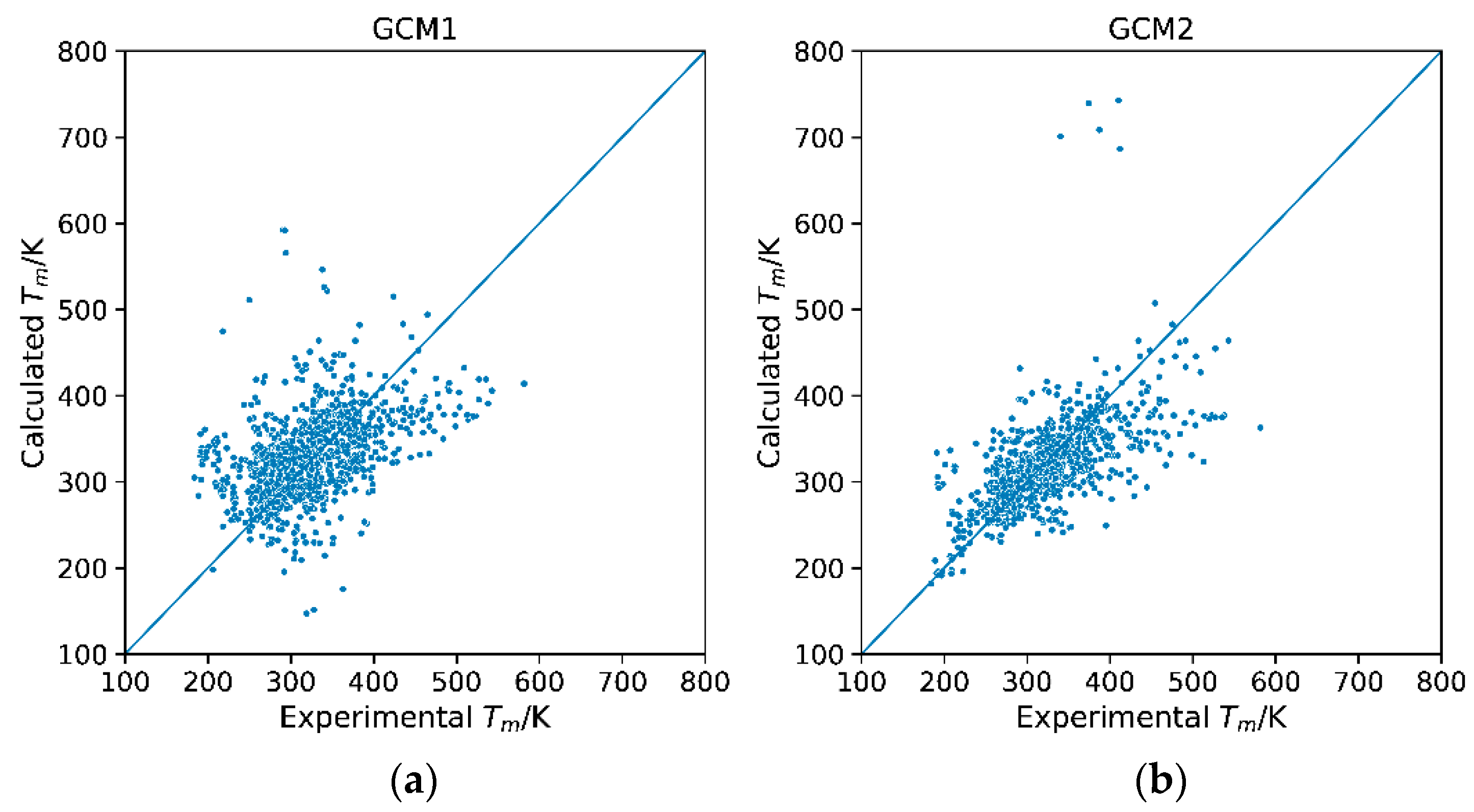
Work	Type of Model	Applicability	Number of ILs Used	R2	AARD
Huo et. al. [42]	GCM	Imidazolium/Benzimidazolium	190	0.8984	5.86%
Aguirre et. al. [43]	GCM	Diverse	136		7.8%
Chen et. al. [44]	GCM	Diverse	111		4.7%
Katritzky et. al. [45]	QSPR	Imidazolium/Benzimidazolium bromides	149	0.7442/0.7517/0.6899
Katritzky et. al. [19]	QSPR	Pyridinium bromides	126	0.788/0.713
Trohalaki and Pachter [46]	QSPR	Triazolium bromides, Triazolium nitrates	26	0.8730/0.8390
Farahani et. al. [47]	QSPR	Diverse	805	0.721	7.3%
Bini et. al. [48]	RNN	Pyridinium bromides	126	0.872
Carrera and Aires-de-Sousa [49]	QSPR	Pyridinium bromides	126	0.933
Zhang et. al. [50]	QSPR	Imidazolium tetrafluoroborates, Imidazolium hexafluorophos-phates	41	0.776/0.842
Eike et. al. [51]	QSPR	Ammonium Bromides	75	0.790/0.775
Varnek et. al. [52]	QSPR	Diverse Bromides	717	0.61
López-Martin et. al. [53]	QSPR	Imidazolium	62	0.8690
Yan et. al. [54]	QSPR	Imidazolium bromides, Imidazolium chlorides	50	0.8900
Lazzús [20]	GCM	Diverse	400	0.8841	7.07%
Gharagheizi et. al. [21]	GCM	Diverse	799	0.811	5.82%

provides a summary of the models reported in literature. It was observed that they generally fall under the categories of QSPR or GCM, with a recurrent neural network (RNN) also included. However, many of the models are limited to specific families of ILs, such as imidazolium halides, for example. Such models have a low range of applicability and are of very limited use in computer-aided molecular design (CAMD) of ILs for different applications. In all cases, the number of compounds used in the test set and training set is lower than the currently available data for IL melting points, often by a significant margin. Therefore, significant scope exists to build upon this previous work by compiling an updated database of IL melting point data, and using it to test, update, and extend the models.

Typically, two statistical measures are used in testing the accuracy of such models: coefficient of determination (R²) and average absolute relative deviation (AARD). As seen in Table 1, some authors reported R², others reported AARD, and a few reported both. Therefore, it is difficult to decide which model is performing the best, since these different statistical measures have been used. This is further compounded by the fact that different test sets, with different numbers of unique ILs, have been used in calculating the statistical measures. A fair comparison can only be made when using the same test set of data, which should be as comprehensive as possible.

It should also be mentioned that there are several difficulties in determining the melting points of ILs which, thereby, can impact the accuracy of data-driven predictive models. Valderrama and Campusano [55] summarized some of the key issues in two major areas: glass formation and multiple transitions. While cooling, there is the possibility of incorrect measurement due to the IL going through glass transition, where the kinetics are much slower. The difficulties in performing these experiments and estimating the melting point has somewhat reduced with the advent of more advanced Differential Scanning Calorimetry (DSC) machines. Conventional DSC machines suffered from various issues like insensitive sensors, requirement of external heat, inability to achieve constant cooling rates, and controlling drift in the temperature curves [56]. Most modern DSCs have rectified these errors, by introducing more thermocouples and heating elements, as well as measuring for any variations across the chamber, and accompany these with more optimized software and control mechanisms [57]. However, there are still aspects of the experimental process that can lead to errors, such as contamination of samples, humidity, formation of various liquid and plastic phases, pressure variations, thermal stability issues, and calibration and user errors [58]. There is also a lack of a universal testing protocol for such measurements, from material handling to temperature ranges and rates of change during the heating and cooling process, which can cause issues. Yamamoto [59] outlined these issues, and demonstrated the challenges in building a reliable predictive model as a result of the variance in the limited amount of experimental data available. Such issues lead to a certain amount of “noise” in the data. As long as the errors are randomly distributed about the mean, then this is not a major issue when applying regression-based models. Since GCMs are developed via parameter regression, the best fit parameters will be obtained by minimizing an objective function, such as the sum of the squares of residuals, for example. Random errors on the positive and negative side will effectively balance each other during regression to reach the best fit values of the parameters. However, the statistical measures used to test the models will also include the experimental error resulting from test set of data, and the measured performance of the model in terms of R² or AARD cannot, therefore, be better than that level of experimental error present within the test set.

As more melting point data has been gathered on a variety of ILs containing different cation and anion groups, it has become possible to develop more extensive models. The last two models in Table 1 are the most generic GCMs available today for IL melting point prediction and, thus, are the most useful for IL design for materials and energy applications. Therefore, we have selected these two GCMs for further detailed analysis in this work. Herein, the model by Lazzús [20] is referred to as GCM1 and the model by Gharagheizi et al. [21] is referred to as GCM2.

2. Results and Discussion

2.1. Database Development and Refinement

The new IL melting point database (see “Methodology” section) was used to evaluate the performance of the two selected group contribution models, GCM1 and GCM2. The preliminary database (DB-P) of raw data was initially compiled from a range of literature sources and the ILThermo website, without any data cleaning. However, it was noticed there were some issues that needed to be resolved before the database could be used for testing the selected GCMs. There was some duplication of datapoints that would cause undue weight to go towards those literature sources. Therefore, the database was carefully checked, and any duplicates were eliminated. The resulting refined database (DB-R) contained around 1500 datapoints.

Ideally, it would be possible to test both models against DB-R. However, due to limitations in each model resulting from the lack of certain required group contribution parameters, this was not possible. For example, the imidazolium functional group included in GCM1 was only designed to use substitutions on its 1st, 2nd, or 3rd positions. As such, it was not possible to represent the structures of ILs containing substitutions in other positions, such as 1,2,4-trialkylimdazolium ILs. In other cases, it was not possible to build the IL due to the lack of certain functional groups in each model. For example, metallic salts and ILs with unusual ring structures, such as benzotriazolium, could not be modeled in GCM1. Similarly, ILs containing the azido group were not represented by the functional groups in GCM1. The next necessary step, therefore, was to further reduce the database to include only those ILs for which each GCM could estimate the melting point. This resulted in a new, smaller database, DB-1, which was used for the analysis and comparison. It contains only GCM1- and GCM2-compatible data, consisting of 1305 datapoints, with 933 unique ILs made from 484 unique cations and 94 unique anions.

2.2. Model Evaluation and Comparison

Comparison of the two models begins with a qualitative analysis of the similarities and differences between their respective approaches. For GCM1, the cation is assumed to consist of a core group, such as imidazolium, pyridinium, or phosphonium, for example. Each cation core group has a number of available locations for attaching other functional groups. Imidazolium, for example, has three available locations: the two nitrogen atoms, and the carbon atom between the nitrogen. Smaller subgroups, such as -CH₂- or -CH₃, can be added to construct the alkyl chains typically present in IL cations. The model also allows for the addition of other functional groups, such as -OH. The anion is constructed from smaller subgroups, such as -SO₂ and CF₃, for example. Deconstructing the IL into its functional groups for the purpose of applying the GCM1 model is relatively straightforward. The functional groups used within the model are representative of the typical structures seen in commonly used ILs and, therefore, the application of the model is intuitive. In contrast, GCM2 is significantly more complicated to implement. The first issue is the larger number of functional groups that are used in GCM2; there are 67 functional groups in GCM1 compared with 80 groups in GCM2. Furthermore, the rules involved in deconstructing the IL into its functional groups using GCM2 are highly complex. It takes a much longer time to map each IL using GCM2 and there is a much greater chance of making an error due to several overlapping functional groups. Therefore, great care must be taken when implementing GCM2.

After the development of the most extensive database possible for testing both models, DB-1, the next step was to use GCM1 and GCM2 to estimate the melting points for every IL in the database. This involved breaking down and mapping out the IL structure in terms of its functional groups for each GCM, as illustrated in the “Methodology” section. Subsequently, the mapping for each IL was imported into the Python DataFrame and then each model was implemented to estimate the melting points for every ionic liquid in DB-1. The calculated melting points were then compared with the experimentally measured melting points. The parity plots of calculated versus experimental melting points for each model are shown in Figure 1. Ideally, the data points should follow the diagonal line, indicating that the calculated and experimental values are the same. However, we observe in both cases, the data is spread significantly. GCM2 performs overall somewhat better than GCM1, with its data points more tightly packed around the 45° line. However, for GCM2, there is a cluster of points which lies very far from the y = x line. These outliers will be discussed in more detail later. The average absolute relative deviation (AARD) was also calculated as a statistical measure of the performance of each model. For GCM1, the AARD was 13.98% while for GCM2, the AARD was 9.66%. This lower AARD indicates that GCM2 performs better than GCM1 overall; however, both models performed significantly worse when tested against the new database compared with their AARD values reported in literature using their original smaller and less diverse test datasets (Table 1).

There are several possible reasons why GCM2 performs better than GCM1. Firstly, the model was created based on a much larger training set of IL data; GCM1 had a training set of 200 IL datapoints, whereas GCM2 used a broader training set of around 400. Therefore, we would expect the parameters of GCM2 to be more robust and perform better when tested against the larger database. Secondly, the smaller functional groups used in GCM2 appear in a much broader range of ILs and, therefore, each functional group gets trained by a much wider range of ILs than those used in GCM1. This helps to improve the robustness of the model for application towards a wider range of ILs. Thirdly, the functional group definition for GCM2 was based on statistical significance, whereas, in GCM1, the functional groups were selected intuitively based on the typical structures observed in ILs. The use of statistical approach to guide functional group selection could be a significant factor in the overall better performance of GCM2.

To further analyze the performance of each model, the percentage AARD values for each cation type and anion type were determined, as illustrated in Figure 2. The general trend was that GCM2 exhibited a lower AARD than GCM1, except for piperidinium among the cations, and N(CN)₂ among the anions. This may be due to the fact that there are relatively few data points for ILs containing these types of cations and anions. Also, in the case of N(CN₂), the high error can be attributed to the existence of CN groups in both N(CN)₂ and B(CN)₄ anions. The contribution from CN towards T_m within B(CN)₄ was much larger than that in N(CN)₂. This may be due to symmetrical tetrahedral structure of B(CN)₄, which tends to cause an increased melting point. By contrast, N(CN)₂ is linear in orientation, which results in lower melting point. However, when the models were parametrized, CN was given equal weighting in both ions. This may have introduced a larger error in the regressed parameters of GCM2. The biggest differences between the performance of GCM1 and GCM2 occurred for the “other” category among the cations, which incorporates all those ILs containing cations that are not among the most frequently occurring cation types. Among the anions types, BF₄ exhibits the biggest difference. GCM1 is significantly worse for ILs containing BF₄ and PF₆, two of the most common anions found in ILs. This may be explained by the large difference between the number of BF₄ and PF₆ data points used to train each model. For GCM2, 70 data points for PF₆-based ILs and 56 data points for BF₄-based ILs were used in the training set. By comparison, only around 12 data points for PF₆-based ILs and 18 data points for BF₄-based ILs were included in the original training set of GCM1. Consequently, we would expect the relevant parameters for GCM2 to be much more accurate than those in GCM1.

The residual plot is an important tool for the interpretation of the errors present in predictive models. The most desirable models are those where the residuals are small and evenly distributed above and below the x-axis. The presence of any other trend in the residual plot could be indicative of systematic error in the model. Figure 3 shows the residual plots of error versus melting point for GCM1 and GCM2. In both cases, the data is relatively evenly distributed on the positive and negative sides of the residual plot. However, it is apparent that there was a slight trend in the data for both models, where the residuals were slightly more on the negative side, i.e., slightly more points below the x-axis, at low MW (<250 g∙mol⁻¹), and more on the positive side at medium MW (250 to 400 g∙mol⁻¹), then they become more negative again at high MW (>400 g∙mol⁻¹). This indicates that, to some extent, both models inaccurately represented the relationship between IL melting point and MW.

By examining the residual plots for different subcategories of IL melting point data, we can gain a better understanding on whether the model is performing adequately in each case. Figure 4 shows the individual residual plots for different cation types. For most cation types, we observed that the performance of both GCMs depends somewhat on the molecular weight of the IL. In many cases, at low MW, the error was negative, indicating that the model was underestimating T_m. In the mid-range MW, there tended to be more overestimation of T_m, and then for higher MW ILs, again there was more underestimation of T_m. This can be explained by the fact that both GCMs are additive in nature. That is, each functional group makes a fixed contribution towards the melting point. For example, in GCM1 the -CH₂- functional group had a contribution of 4.26 K, whereas, for GCM2, the -CH₂- contribution was 1.62 K. Since these contribution parameters are positive, each model assumes that every additional -CH₂- group added to the cation alkyl chain raises the melting point by that value. However, it has been well reported [60] that the melting points of ILs tend to decrease with increasing alkyl chain length until a minimum is reached at around 6 to 8 carbons, following which the melting point increases with increasing alkyl chain length. With increasing chain length, melting points decrease initially due to the increasing entropy. However, for larger chains, the Van der Waal’s interactions play a more dominant role, thus resulting in an increase in the melting point. These effects are further exacerbated with the energy differences due to changing bond and dihedral angles while undergoing phase change, creating a greater energy requirement and increasing the melting point [60]. Therefore, the additive nature of these GCMs is preventing each model from accurately representing the observed complex relationship between alkyl chain length and melting point. This explains why, at low MW, when the alkyl chains tend to be shorter, we observe that both GCMs tend to underestimate T_m. The additive nature of the GCM predicts that the melting point will be lowest for ILs with very short alkyl chains when, in fact, it tends to relatively high compared with those having medium alkyl chain length.

Among the various cation types, the largest spread is observed in imidazolium and ammonium. This is indicative of the very large number of data points available for these types of cations with a variety of counter anions.

Figure 5 shows the individual residual plots for different anion types. Again, we observe the trend that both models tend to underestimate T_m for low MW ILs, then overestimate for medium MW ILs, and again, underestimate for high MW ILs. Although NTf2 is the most frequent anion in the database, the greatest spread is observed in BF₄ and PF₆ for GCM1, whereas for GCM2, Cl based ILs have the largest spread. The reasons for this are discussed later.

Overall, GCM2 has been shown to outperform GCM1 based on the statistical measure, AARD. However, accuracy is only one of the desirable characteristics of a GCM. It is also important that the model should be easy to implement for the estimation of the physical property; furthermore, the model should be easy to implement within process simulation software and computer aided molecular design frameworks. This is where GCM2 has significant disadvantage compared with GCM1. As mentioned previously, it is difficult and time consuming to map out the structures of ILs for implementation of GCM2. Furthermore, due to the complexity of the functional group rules, it would be extremely difficult to combine this approach with structural constraints in a CAMD framework to allow the design of structurally feasible ILs. Another issue with GCM2 is the fact that, if a group or substructure is not present in the mapping table, its contribution is assumed to be zero. For example, the hexafluorotantalum and hexafluoroantimonate anion groups have the same contribution, as the model does not have either the tantalum or antimony groups. Although ammonium-based groups can be mapped out easily as a result of the availability of the N⁺ group, there is no such availability of a P⁺ group for phosphonium-based anions. This will inevitably lead to extrapolation of GCM2 beyond its reasonable range of applicable ILs and give the user a false sense of security. To further add to the problems of the mapping process, it is very difficult to generate the structural map from a holistic perspective taking into account the mapped data already available for other ILs. In conclusion, although GCM2 is more accurate, it comes at a cost to its utility as a quick and simple estimation tool, which is one of the main purposes of a GCM.

2.3. Refinement and Reparametrization of GCM1

While GCM1 has several advantages, including ease of use and applicability towards simulation software and CAMD frameworks, it displays significantly lower accuracy than GCM2. As discussed previously, this may be mainly attributed to the very small training set that was used to regress its group contribution parameters. Therefore, given that a much larger database has been compiled in this work, it was decided to further refine and reparametrize GCM1 to establish whether it can achieve an AARD comparable to that of GCM2. Firstly, some new functional groups were created to solve the problems identified in the model. New anion groups for BF₄, PF₆, B(CN)₄, oleate, and phosphate were created, since these were identified as structures for which original GCM1 was not giving adequate results. In addition, a new cation group (>P = O) was created to differentiate this functionality from the existing phosphonium group. After remapping the relevant ILs in the database according to these new functional groups, the model was fully reparametrized using Keras library in Python. The database was split into two separate parts: 50% of the data was used as the training set, the other 50% was used as the test set. The parameters were regressed by minimizing the objective function, MAE, via stochastic gradient descent (SGD). The new optimized parameter values for the cation functional groups and anion functional groups are shown in

Table 2. New and reparametrized cation functional group parameters for GCM1-R.

Group, i		ΔTm,i/K
T0		210.97
Imidazolium		6.00
Pyridinium		59.09
Pyrrolidinium		50.66
Pyrrolidinonium		0.07
Piperidinium		48.26
Morpholinium		39.74
Ammonium		−4.38
Sulfonium		5.00
Phosphonium		−10.01
Triazolium		31.15
Pyrazolium		0.11
Thiazolium		−0.19
-H		24.52
-CH3		30.98
-CH2-		−0.22
-CH<		−8.28
-OH		44.86
-O-		−18.99
>C<		12.71
-COO		9.88
-CN		40.01
-NH2		35.07
-F		22.38
-Br		22.24
-Cl		0.11
-SO2-		5.95
-Benzyl		52.26
-Vinyl		0.86
-CF2-		10.05
-CF3		30.22
-SF5		−5.79
>P = O		−36.95

and

Table 3. New and reparametrized anion functional group parameters for GCM1-R.

Group, i	ΔTm,i/K
-CH3	1.55
-CH2-	−2.71
>CH-	1.06
>C<	−0.77
>CO	−7.63
-COO-	−20.94
-HCOO	−24.97
-OH	−0.72
-O- [-O]	2.67
-CN	−16.50
-N- [>N-]	−3.87
-NO3	9.21
-S-	0.42
-SO2-	−4.82
-CF3	−10.06
-CF2-	4.27
-F	−4.74
-Cl	26.16
-Br	50.64
-P	4.77
-B	−11.05
-I	31.77
-Al	−5.92
-As	6.27
-Nb	−2.74
-Ta	0.25
-Sb	12.00
-Sn	0.23
-W	−0.28
-CB11H11- (carborane)	18.88
-CB11H12 (carborane)	18.19
-CB11H6 (carborane)	−16.68
CH- (ring)	0.18
=C< (ring)	17.02
>CO (ring)	3.72
-O- (ring)	3.34
PF6	28.32
BF4	1.18
B(CN)4	−8.80
Oleate	−12.14
Phosphate	18.23

, respectively. The reoptimized model, herein referred to as GCM1-R, demonstrated an AARD of 9.75% when tested against the test set, and 9.67% against the whole database, bringing it in close agreement with the AARD for GCM2.

The parity plot for the reparametrized model, GCM1-R, is compared with the parity plot for GCM1 in Figure 6. The significant improvement in the model performance can be observed, with the data points for GCM1-R more tightly packed around the y = x line. It is also notable that there was a significant reduction in the number of major outliers. One of these relates to the icosahedral anion, which had six bromide groups attached. Due to the large change in the weight of the -Br parameter after reparametrization, and the heavy influence of the -Br parameter in this IL, we observed a significant increase in the predicted melting point. This drastic change in the weighing of the bromide group in the overall model had the consequence of affecting the predicted melting point of the “hexabromide 1-carbon icosahedral” ionic liquid. The lack of data for multiple bromine-containing anions resulted in this datapoint having an error of around 200 K between the observed and predicted melting points of the sole datapoint. These groups were also extremely large and require multiples of various subgroups, mainly optimized for single occurrences in the overall IL. As a result, the overall error was compounded.

The performance of GCM1-R for estimating the melting points of different types of cations and anions is shown in Figure 7. In comparison with GCM1, we see improvements for most types of cations and anions. Compared with GCM2, the performance was similar for many types of cations and anions; however, GCM2 was still performing better for ILs containing the “other” category of cations, and ILs containing sulfate-based anions. This can be attributed to the method used to model such groups. GCM2 was built using groups of statistical significance relative to its database, which accounted for most trends and behaviors expected from the various cation and anion groups. The error, therefore, resulted from the uncertainty present in the less statistically or homologically significant groups. Since GCM1-R is derived from the original GCM1, it still suffers from some of its disadvantages. In the case of the “other” groups, the model uses more generalized subgroups that can be applicable to more datapoints, thereby trying to reduce overall error at the expense of accuracy in prediction. This also applies to the sulfate ions, which have functional groups in common with the sulfonyl-imide anions (NTf₂, BETI, OTf), which have been studied more intensively, and consequently have more datapoints in the overall dataset. This results in the SO₂ group being more optimized towards these groups, resulting in a higher error for the sulfates.

Figure 8 shows the residual plots of error versus MW for GCM1 and GCM1-R. Again, the improved performance of GCM1-R over GCM1 can be clearly seen. However, the same trend is still apparent; for ILs with low MW, the model underestimates T_m, for ILs with medium MW, the model overestimates T_m, and for high MW ILs, the model underestimates T_m. As explained previously, this is a problem that is inherent in additive GCM approach and cannot be overcome by new group definition or reparametrization. However, overall, it has been demonstrated that GCM1-R gives equivalent performance to GCM2 in terms of AARD, while having significant advantages in terms of ease of use, and applicability to simulation software and computer-aided molecular design frameworks.

3. Methodology

As a basis for testing and extending the selected GCM models, an Excel database of IL melting point data was compiled (see Supplementary Materials) from a variety of literature sources, including the NIST ILThermo database [61], a physicochemical properties reference book for ILs [62], and individual journal papers [14,45,51,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195,196,197,198,199,200,201,202,203,204,205,206,207,208,209,210,211,212,213,214,215,216,217,218,219,220,221,222,223,224,225,226,227,228,229,230,231,232,233,234,235,236,237,238,239,240,241,242,243,244,245,246,247,248,249,250,251,252,253,254,255,256,257,258,259,260,261,262,263,264,265,266,267,268,269,270,271,272,273,274,275,276,277,278,279,280,281,282,283,284,285,286,287,288,289,290,291,292,293,294,295,296,297,298,299,300,301,302,303,304,305,306,307,308,309,310,311,312,313,314,315,316,317,318,319,320,321,322,323,324,325,326,327,328,329,330,331,332,333,334,335,336,337,338,339,340,341,342,343,344,345,346,347,348,349,350,351,352,353,354,355,356,357,358,359,360,361]. This initial database contained 2061 data points from over 300 literature sources. Preliminary data cleansing was performed to remove duplicated data points and convert all IL synonyms to a single common name. For example, the anion ‘bis((trifluoromethyl)sulfonyl)imide’ was present in the database in 7 different ways, using a combination of different brackets and naming methods.

Following the initial data cleansing in Excel, the database was imported into Python as a DataFrame using the Pandas package [362]. The resulting DataFrame was then used as the basis for data segmentation and analysis. The seaborn [363] and matplotlib [364] packages in Python were used for generation of the various data visualizations.

In a separate Excel file, the various cations and anions were deconstructed and described in terms of the functional building blocks used for each model. This GCM mapping was subsequently imported into Python and merged with the existing DataFrame containing the experimental data points. GCM1 and GCM2 were implemented within Python to determine the corresponding calculated melting point for each experimental data point in the database.

Each of these models is linear and uses the same fundamental equation for estimating the melting point of the IL:

$$T_m=T_0+\mathsf{\Sigma }{n}_i\Delta T_{m,i}$$

(1)

where n_i represents the frequency of occurrence of functional group, i, ΔT_mi represents the contribution parameter of group, i, and T₀ is a global fitted parameter. For the GCM1, T₀ is 288.7 K, while for GCM2, T₀ is 264.29 K. An illustration of the procedure involved in applying each model for the estimation of one IL, 1-butyl-3-methylimidazolium bis((trifluoromethyl)sulfonyl)imide, is given in

Table 4. Estimation of the melting point of ILs using GCM1 and GCM2 with 1-butyl-3-methylimidazolium bis((trifluoromethyl)sulfonyl)imide as an illustration of the general procedure.

GCM1
Type	Group, i	ni	∆Tm,i/K	ni∆Tm,i/K
Cation	Imidazolium	1	22.837	22.837
	CH3	2	−4.384	−8.768
	CH2	3	−3.759	−11.277
	H	1	−20.98	−20.98
Anion	–N– [>N–]	1	−113.15	−113.15
	SO2	2	114.17	228.34
	CF3	2	−51.844	−103.688
T0				288.7
Tm/K = T0 + ∑ ni∆Tm,i				282.014
GCM2
Type	Group, i	ni	∆Tm,i/K	ni∆Tm,i/K
Cation	N+	1	7.8678	7.8678
	CH2R2	2	1.6214	3.2428
	CH3X	1	12.4075	12.4075
	CH2RX	1	6.5888	6.5888
	R-CH-X	1	−45.1417	−45.1417
	R-CH..X	1	18.6936	18.6936
	Ha attached to C° (sp3) no X attached to next C	5	−1.3355	−6.6775
Anion	Sulfones (SO2)	2	−35.6122	−71.2244
	Total number of Ns, Os, and Fs in the molecule, excluding N with a formal positive charge, higher oxidation states, and pyrrolyl form of N	11	8.2032	90.2352
	CX4	2	−30.3021	−60.6042
	Fa attached to C2 (sp2)-C4 (sp2)/ C1 (sp)/C4 (sp3)/X	6	0.7619	4.5714
	R-SO2-R	2	22.9432	45.8864
T0				264.29
Tm/K = T0 + ∑ ni∆Tm,i				270.136

. The chemical structure of this IL is shown in Figure 9. The cation and anion functional groups needed to construct this IL via GCM1 and GCM2, along with the frequency of occurrence and the associated contribution parameters, are shown in the table. For each group, the frequencies of occurrence are multiplied by the contribution parameters and the products are added along with the global parameter to obtain the estimate of the melting point. Further details on the functional group building blocks and their rules of application for GCM1 and GCM2 can be found in Lazzús [20] and Gharagheizi et al. [21], respectively.

For reparametrization of existing parameters and regression of new group parameters, the Keras package [365] was used in Python. The database was split into a training set and test set, each containing 50% of the available data. A single dense layer was created in Keras using the model parameters as the input and the mean absolute error (MAE) was used as the loss function. Optimization was performed using stochastic gradient descent (SGD).

Absolute average relative deviation (AARD) was used as the statistical measure of the performance of the models and was calculated according to the following equation:

$$\mathrm{ARD}(\%)=\frac{1}{\mathrm{n}}{\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{n}}\left|\frac{T_{m,calc}-T_{m,exp}}{T_{m,exp}}\right|\times 100\%$$

(2)

4. Conclusions

Over the past few decades, the GCM approach has been used extensively in process simulation and CAMD software, due to its reasonable accuracy, relative ease of use, wide range of applicability, and ease of integration into CAMD frameworks. In this paper, two of the most comprehensive GCMs for the estimation of IL melting points were critically examined. An up-to-date, comprehensive database of IL melting point data was compiled. The IL structures were mapped according to the functional group building blocks used for each GCM. The two GCMs were implemented against the full database, and the performance of each model was assessed based on its AARD for various categories of ILs. Both models were found to yield higher AARDs than those reported in the original papers. This is due to the much larger and more comprehensive test set used in this study. Both GCMs were also found to exhibit a certain amount of systematic error when examining the relationship between error and IL MW. This was attributed to the additive approach used in each model, that is unable to accurately represent the more complex relationship between the size of an IL and its melting point. It was found that GCM2 performed significantly better than GCM1 based on the statistical measure, AARD. However, due to the complexity of the functional groups used in GCM2, there is a high likelihood of user error, and it does not lend itself towards facile integration with structural constraints into a computational framework for IL design. On the other hand, GCM1 has straightforward functional building blocks that are simple and intuitive to use for IL melting point estimation. The fact that GCM1 was trained against a much smaller dataset than GCM2 was identified as a major reason for its significantly higher AARD. Furthermore, some problems with the functional group definitions, leading to increased error, were identified. To address these issues, several new functional groups were defined, and the whole model was reparametrized against a much larger training set than that used in the original model. The refined and reparametrized model, GCM1-R, was found to perform significantly better than the original GCM1, yielding a similar AARD to that obtained with GCM2. In combination with its ease of use and breadth of applicability, it is anticipated that this refined GCM will aid in the design of ILs for materials and energy applications, by reducing the need for extensive synthesis and experimental characterization of new ILs.