Zhang–Zhang Polynomials of Multiple Zigzag Chains Revisited: A Connection with the John–Sachs Theorem
Abstract
:1. Introduction
2. Preliminaries
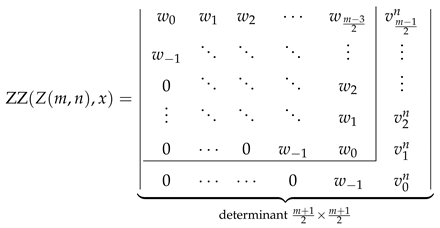
- The determinant of the John–Sachs matrix is equal to the number of Kekulé structures as stipulated by Equation (8). Similarly, we request that the determinant of the generalized John–Sachs matrix is equal to the ZZ polynomial of
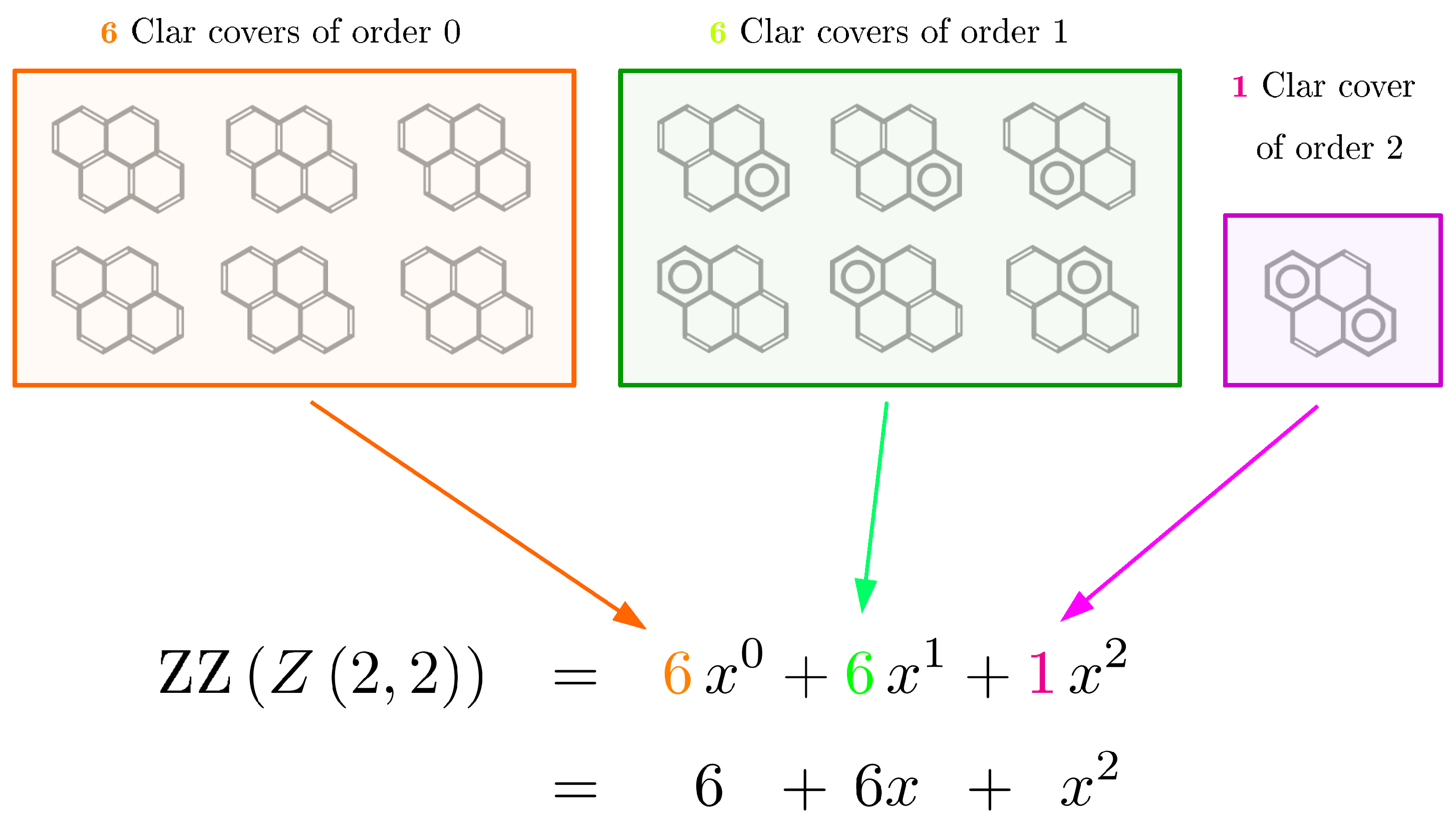
- As the Kekulé structures of are simply the Clar covers of of order 0, the number of Kekulé structures can be obtained from the ZZ polynomial of by evaluating it at ,which effectively corresponds to removing from the set of Clar covers those which contain at least one component . It is then only natural to request that in the same limiting process the John–Sachs path matrix is obtained from the generalized John–Sachs path matrix upon the evaluation at
3. Discovery of the Determinantal Formulas
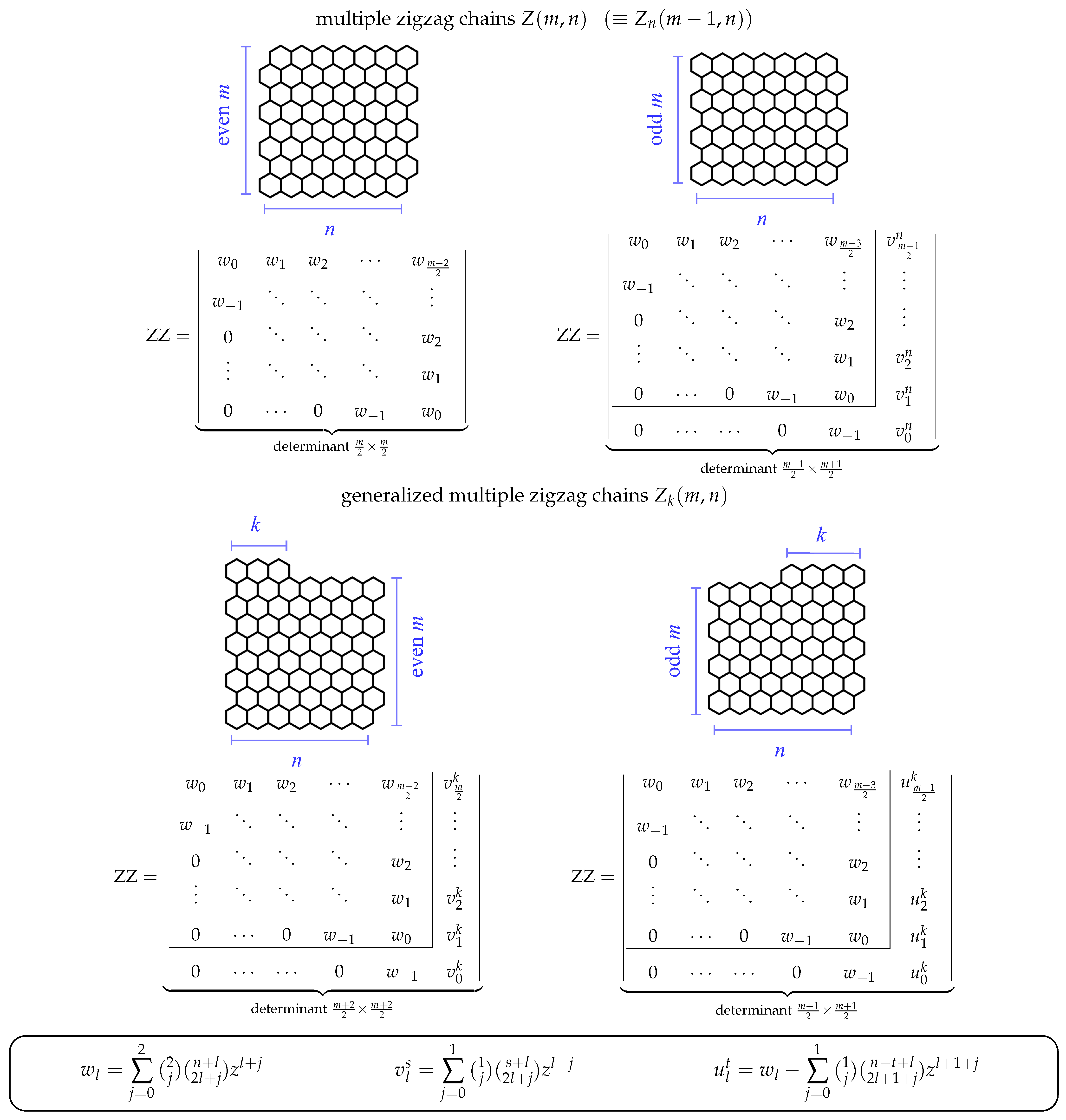
- The matrices are Toeplitz matrices with diagonals: 1 subdiagonal , 1 diagonal , and n consecutive superdiagonals .
- The value on the subdiagonal, , does not depend on n.
- The value of the diagonal element is equal to , given explicitly byThis value is consistent with the natural extension of the John–Sachs matrix diagonal elements, i.e., with replacing by .
- The value on the l-th superdiagonal is a product of a multiplicative factor , a numerical factor , and a polynomial of degree 2, 1, or 0.
- The polynomials always start from 1 and contain coefficients, which factorize into small primes. This suggests that they are hypergeometric polynomials, i.e., hypergeometric functions with at least one of the upper indices being a negative integer. As the formula for the diagonal elements in Equation (12) contains a hypergeometric function , it is natural to seek also in this form. The lower parameter is suggested by the denominator in the linear term of the polynomials , and it is equal to 3 for , 5 for , 7 for , etc. Therefore, in a general case, we can expect for a value of . Another observation is that the coefficient in the linear term of the polynomial, equal to , is always positive, which, taking into account that at least one of the upper indices should be negative, shows that actually both and are negative. One of these numbers, say , is immediately recognizable as , because of the constant degree of the polynomials for . The other index, , is a function , which for should be 0 (because of the degree 0 of the polynomial for ) and for should be 1 (because of the degree 0 of the polynomial for ). All these facts suggest that . A straightforward verification with Maple [78] shows that indeed the hypergeometric function reproduces all the reported polynomials in the matrix elements given above. Note that this polynomial reproduces somewhat fortuitously also the diagonal entry .
- The last remaining task is the identification of the two-dimensional sequence of numbers , which numerical values for small n and l are given by the following triangle:This task can be readily performed by typing, for example, the last rows of this triangle in the The On-Line Encyclopedia of Integer Sequences [79], which recognizes it as the sequence A085478 generated by
4. Formal Proof of Determinantal Formulas for and
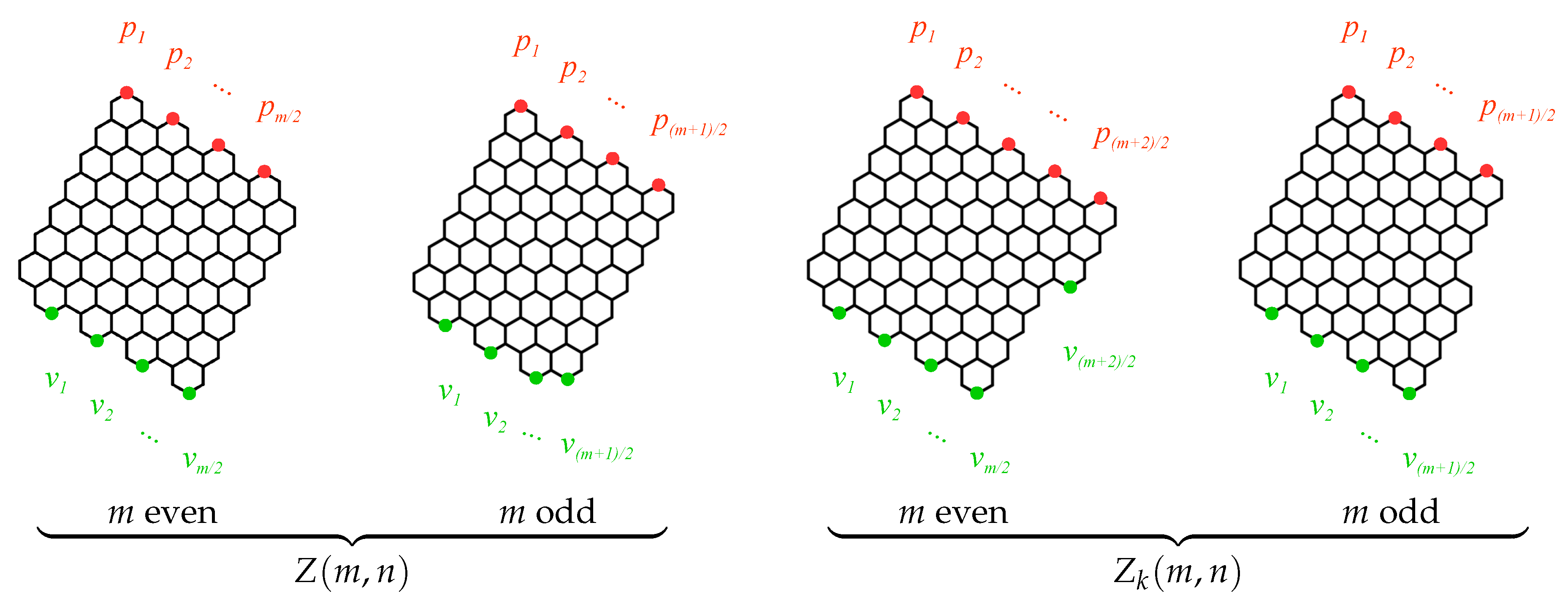
4.1. with Even m
4.2. with Odd m
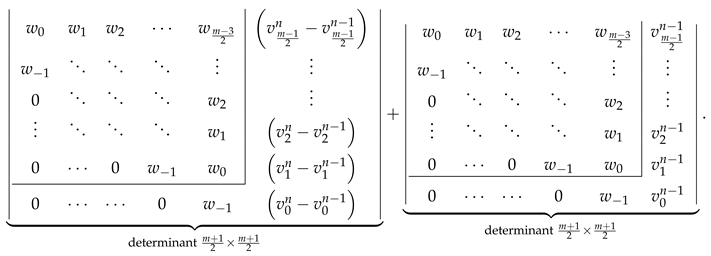
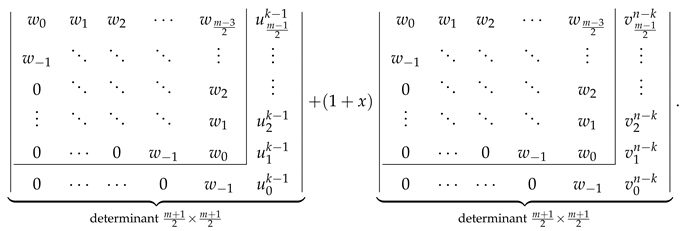
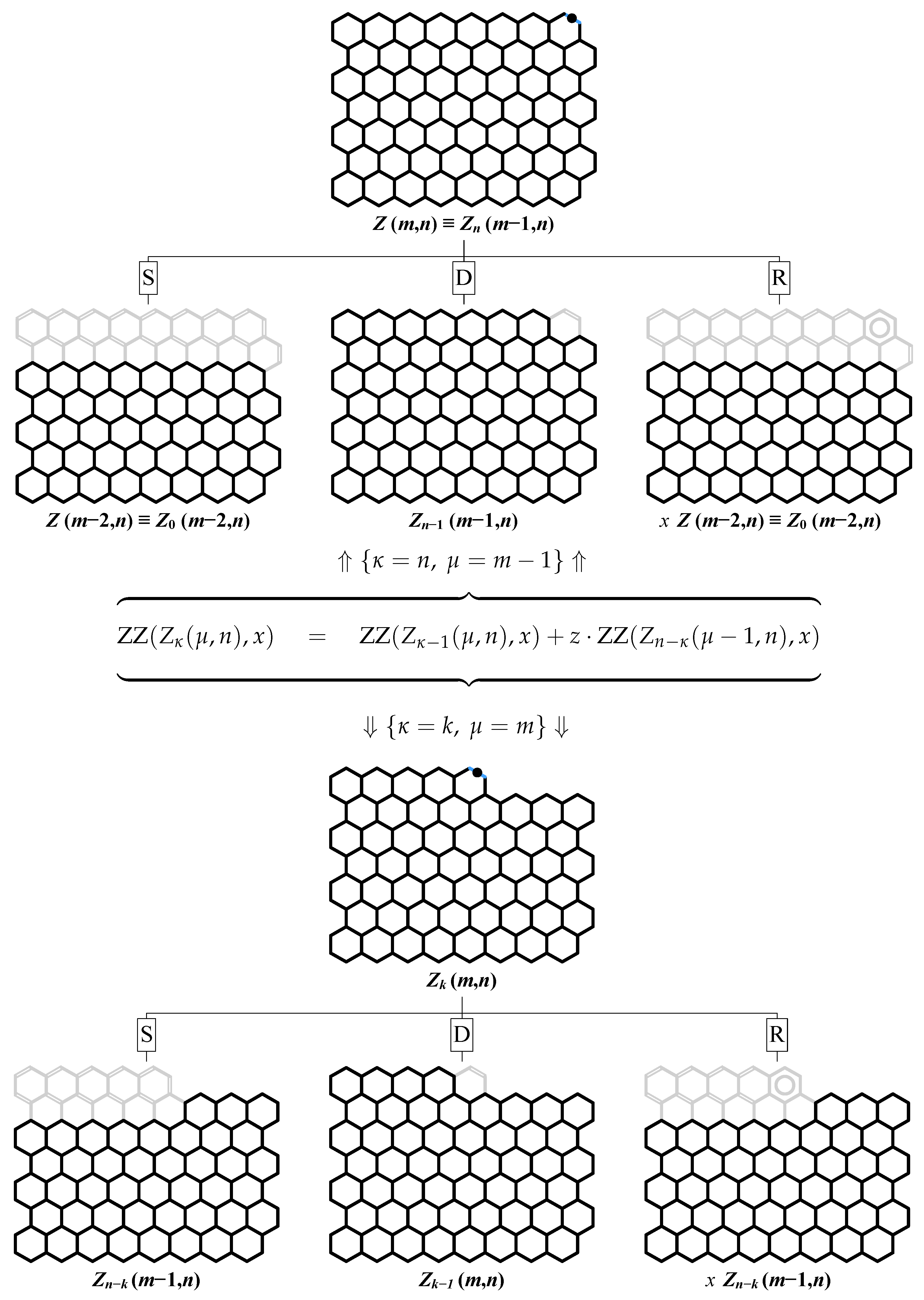
- Decompose the determinant into a sum of two determinants differing only by the last column [80]
- Rewrite the first determinant in Equation (40) by subtracting its last column from its last-but-one column obtaining
- Using these relations simplifies the determinant in Equation (41) to the following form:
4.3. with Even m
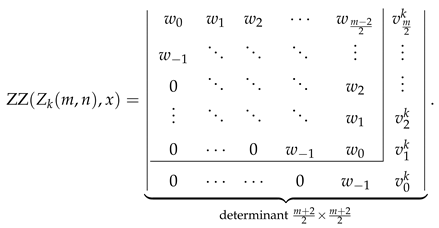
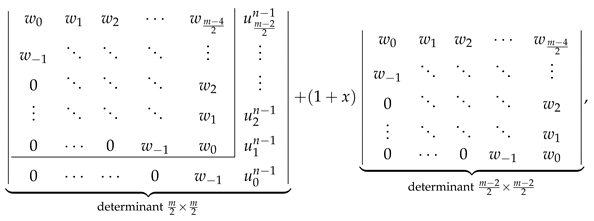
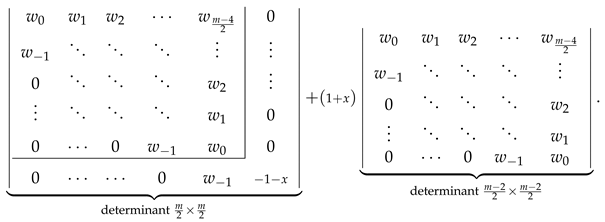
- We rewrite the last column of the determinant in Equation (44) as , with and .
- We decompose the determinant in Equation (44) as a sum of two determinants, the first one having in the last column and the second one having in the last column.
- We identify the second determinant with the help of Figure 2 as .
- In the first determinant, we subtract the last column from the last-but-one column obtaining
- Laplace expansion of the determinant in Equation (46) with respect to the last row givesallowing to identify this expression as .
4.4. with Odd m
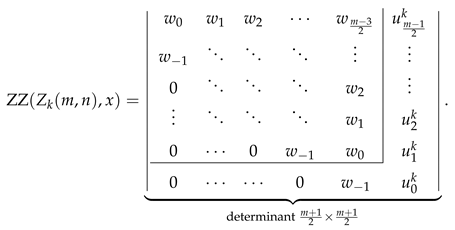
5. Chemical Applications
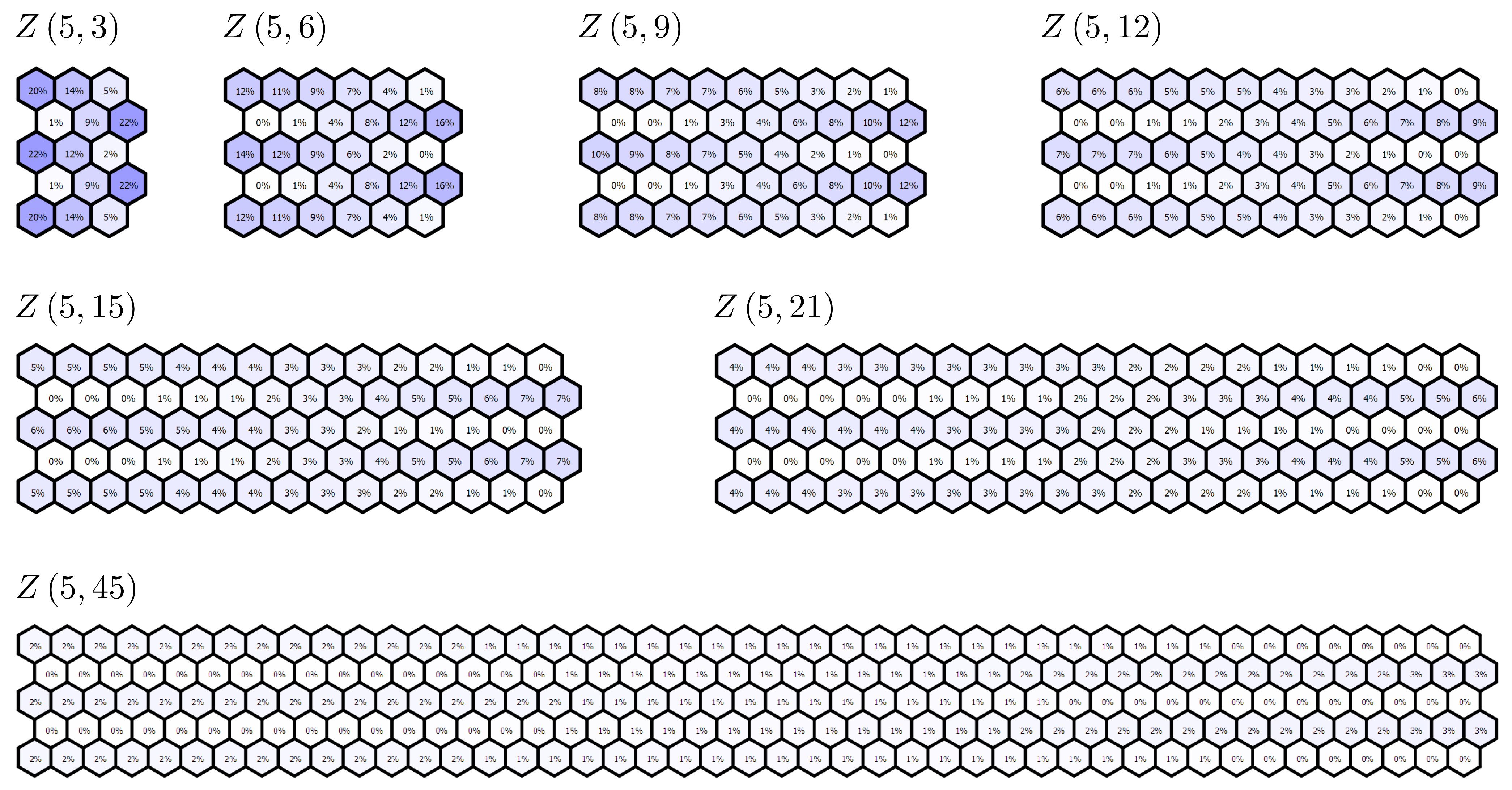
5.1. Local ZZ Aromaticity Indicators for Multiple Zigzag Chains
5.2. Spin Densities in Biradical Multiple Zigzag Chains
6. Conclusions

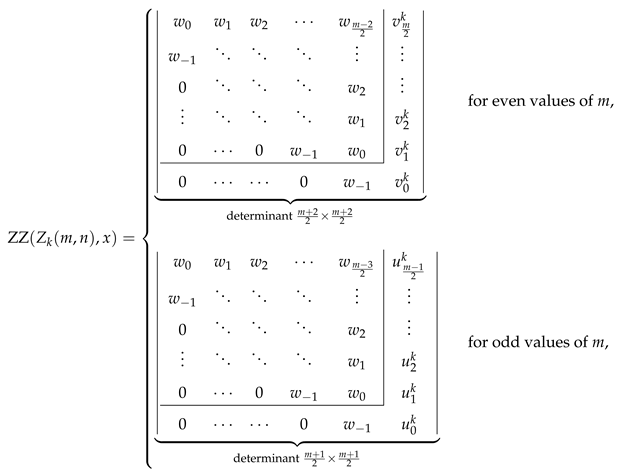
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Gutman, I. Clar formulas and Kekulé structures. MATCH Commun. Math. Comput. Chem. 1985, 17, 75–90. [Google Scholar]
- Cyvin, S.J.; Gutman, I. Kekulé Structures in Benzenoid Hydrocarbons; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Gutman, I.; Cyvin, S.J. Introduction to the Theory of Benzenoid Hydrocarbons; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Gutman, I.; Furtula, B.; Balaban, A.T. Algorithm for simultaneous calculation of Kekulé and Clar structure counts, and Clar number of benzenoid molecules. Polycycl. Aromat. Compd. 2006, 26, 17–35. [Google Scholar] [CrossRef]
- Zhang, F.J.; Guo, X.F.; Zhang, H.P. Advances of Clar’s aromatic sextet theory and Randić’s conjugated circuit model. Open Org. Chem. J. 2011, 5, 87–111. [Google Scholar] [CrossRef] [Green Version]
- Kekulé, A. Untersuchungen über aromatische Verbindungen Ueber die Constitution der aromatischen Verbindungen. I. Ueber die Constitution der aromatischen Verbindungen. Justus Liebigs Ann. Chem. 1866, 137, 129–196. [Google Scholar] [CrossRef] [Green Version]
- Clar, E. The Aromatic Sextet; Wiley: London, UK, 1972. [Google Scholar]
- Žigert Pleteršek, P. Equivalence of the generalized Zhang–Zhang polynomial and the generalized cube polynomial. MATCH Commun. Math. Comput. Chem. 2018, 80, 215–226. [Google Scholar]
- Zhang, H.P. The Clar covering polynomial of S,T–isomers. MATCH Commun. Math. Comput. Chem. 1993, 29, 189–197. [Google Scholar]
- Zhang, H.P. The Clar formulas of regular t–tier strip benzenoid systems. Syst. Sci. Math. Sci. 1995, 8, 327–337. [Google Scholar]
- Zhang, H.P.; Zhang, F.J. The Clar covering polynomial of hexagonal systems I. Discret. Appl. Math. 1996, 69, 147–167. [Google Scholar] [CrossRef]
- Zhang, F.J.; Zhang, H.P.; Liu, Y.T. The Clar covering polynomial of hexagonal systems II. Chin. J. Chem. 1996, 14, 321–325. [Google Scholar] [CrossRef]
- Zhang, H.P. The Clar covering polynomial of hexagonal systems with an application to chromatic polynomials. Discret. Math. 1997, 172, 163–173. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.P.; Zhang, F.J. The Clar covering polynomial of hexagonal systems III. Discret. Math. 2000, 212, 261–269. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.P.; Ji, N.D.; Yao, H.Y. Transfer–matrix calculation of the Clar covering polynomial of hexagonal systems. MATCH Commun. Math. Comput. Chem. 2010, 63, 379–392. [Google Scholar]
- Gutman, I.; Borovićanin, B. Zhang–Zhang polynomial of multiple linear hexagonal chains. Z. Naturforsch. A 2006, 61, 73–77. [Google Scholar] [CrossRef] [Green Version]
- Gojak, S.; Gutman, I.; Radenković, S.; Vodopivec, A. Relating resonance energy with the Zhang–Zhang polynomial. J. Serb. Chem. Soc. 2007, 72, 665–671. [Google Scholar] [CrossRef]
- Guo, Q.Z.; Deng, H.Y.; Chen, D.D. Zhang–Zhang polynomials of cyclo–polyphenacenes. J. Math. Chem. 2009, 46, 347–362. [Google Scholar] [CrossRef]
- Chen, D.D.; Deng, H.Y.; Guo, Q.Z. Zhang–Zhang polynomials of a class of pericondensed benzenoid graphs. MATCH Commun. Math. Comput. Chem. 2010, 63, 401–410. [Google Scholar]
- Chou, C.P.; Witek, H.A. An algorithm and FORTRAN program for automatic computation of the Zhang–Zhang polynomial of benzenoids. MATCH Commun. Math. Comput. Chem. 2012, 68, 3–30. [Google Scholar]
- Xu, L.Q.; Zhang, F.J. On the quasi–ordering of catacondensed hexagonal systems with respective to their Clar covering polynomials. Z. Naturforsch. A 2012, 67, 550–558. [Google Scholar] [CrossRef]
- Chou, C.P.; Witek, H.A. Comment on “Zhang–Zhang polynomials of cyclo-polyphenacenes” by Q. Guo, H. Deng, and D. Chen. J. Math. Chem. 2012, 50, 1031–1033. [Google Scholar] [CrossRef]
- Chou, C.P.; Li, Y.T.; Witek, H.A. Zhang–Zhang polynomials of various classes of benzenoid systems. MATCH Commun. Math. Comput. Chem. 2012, 68, 31–64. [Google Scholar]
- Chou, C.P.; Witek, H.A. Closed–form formulas for the Zhang–Zhang polynomials of benzenoid structures: Chevrons and generalized chevrons. MATCH Commun. Math. Comput. Chem. 2014, 72, 105–124. [Google Scholar]
- Chou, C.P.; Witek, H.A. Determination of Zhang–Zhang polynomials for various classes of benzenoid systems: Non–heuristic approach. MATCH Commun. Math. Comput. Chem. 2014, 72, 75–104. [Google Scholar]
- Chou, C.P.; Witek, H.A. ZZDecomposer: A graphical toolkit for analyzing the Zhang–Zhang polynomials of benzenoid structures. MATCH Commun. Math. Comput. Chem. 2014, 71, 741–764. [Google Scholar]
- Witek, H.A.; Moś, G.; Chou, C.P. Zhang–Zhang polynomials of regular 3– and 4–tier benzenoid strips. MATCH Commun. Math. Comput. Chem. 2015, 73, 427–442. [Google Scholar]
- Berlič, M.; Tratnik, N.; Žigert Pleteršek, P. Equivalence of Zhang–Zhang polynomial and cube polynomial for spherical benzenoid systems. MATCH Commun. Math. Comput. Chem. 2015, 73, 443–456. [Google Scholar]
- Chou, C.P.; Witek, H.A. Two examples for the application of the ZZDecomposer: Zigzag–edge coronoids and fenestrenes. MATCH Commun. Math. Comput. Chem. 2015, 73, 421–426. [Google Scholar]
- Chou, C.P.; Kang, J.S.; Witek, H.A. Closed–form formulas for the Zhang–Zhang polynomials of benzenoid structures: Prolate rectangles and their generalizations. Discret. Appl. Math. 2016, 198, 101–108. [Google Scholar] [CrossRef]
- Langner, J.; Witek, H.A. Connectivity graphs for single zigzag chains and their application for computing ZZ polynomials. Croat. Chem. Acta 2017, 90, 391–400. [Google Scholar] [CrossRef]
- Witek, H.A.; Langner, J.; Moś, G.; Chou, C.P. Zhang–Zhang polynomials of regular 5–tier benzenoid strips. MATCH Commun. Math. Comput. Chem. 2017, 78, 487–504. [Google Scholar]
- Langner, J.; Witek, H.A.; Moś, G. Zhang–Zhang polynomials of multiple zigzag chains. MATCH Commun. Math. Comput. Chem. 2018, 80, 245–265. [Google Scholar]
- Langner, J.; Witek, H.A. Equivalence between Clar covering polynomials of single zigzag chains and tiling polynomials of 2 × n rectangles. Discret. Appl. Math. 2018, 243, 297–303. [Google Scholar] [CrossRef]
- He, B.H.; Chou, C.P.; Langner, J.; Witek, H.A. Zhang-Zhang polynomials of ribbons. Symmetry 2020, 12, 2060. [Google Scholar] [CrossRef]
- Witek, H.A.; Kang, J.S. ZZ polynomials for isomers of (5, 6)-fullerenes Cn with n = 20–50. Symmetry 2020, 12, 1483. [Google Scholar] [CrossRef]
- Witek, H.A.; Langner, J.; Podeszwa, R. Closed-form Formulas for Zhang-Zhang Polynomials of Hexagonal Graphene Flakes O(k,m, n) with k,m = 1–7 and Arbitrary n. MATCH Commun. Math. Comput. Chem. 2021, 86, 165–194. [Google Scholar]
- Langner, J.; Witek, H.A. ZZ Polynomials of Regular m-tier Benzenoid Strips as Extended Strict Order Polynomials of Associated Posets Part 1. Proof of Equivalence. MATCH Commun. Math. Comput. Chem. 2021, submitted. [Google Scholar]
- Langner, J.; Witek, H.A. ZZ Polynomials of Regular m-tier Benzenoid Strips as Extended Strict Order Polynomials of Associated Posets Part 2. Guide to practical computations. MATCH Commun. Math. Comput. Chem. 2021, submitted. [Google Scholar]
- Langner, J.; Witek, H.A. ZZ Polynomials of Regular m-tier Benzenoid Strips as Extended Strict Order Polynomials of Associated Posets Part 3. Compilation of results for m = 1–6. MATCH Commun. Math. Comput. Chem. 2021. submitted. [Google Scholar]
- He, B.H.; Langner, J.; Witek, H.A. Hexagonal flakes as fused parallelograms: A determinantal formula for Zhang-Zhang polynomials of the O(2,m, n) benzenoids. J. Chin. Chem. Soc. 2021. [Google Scholar] [CrossRef]
- Aihara, J.; Makino, M. Constrained Clar formulas of coronoid hydrocarbons. J. Phys. Chem. A 2014, 118, 1258–1266. [Google Scholar] [CrossRef]
- Bašić, N.; Estélyi, I.; Škrekovski, R.; Tratnik, N. On the Clar number of benzenoid graphs. MATCH Commun. Math. Comput. Chem. 2018, 80, 173–188. [Google Scholar]
- Chan, D.W.H.; Xu, S.J.; Nong, G. A linear–time algorithm for computing the complete forcing number and the Clar number of catacondensed hexagonal systems. MATCH Commun. Math. Comput. Chem. 2015, 74, 201–216. [Google Scholar]
- Cruz, R.; Gutman, I.; Rada, J. Convex hexagonal systems and their topological indices. MATCH Commun. Math. Comput. Chem. 2012, 68, 97–108. [Google Scholar]
- Klavžar, S.; Žigert, P.; Gutman, I. Clar number of catacondensed benzenoid hydrocarbons. J. Mol. Struct. Theochem 2002, 586, 235–240. [Google Scholar] [CrossRef]
- Salem, K.; Klavžar, S.; Vesel, A.; Žigert, P. The Clar formulas of a benzenoid system and the resonance graph. Discrete Appl. Math. 2009, 157, 2565–2569. [Google Scholar] [CrossRef] [Green Version]
- Tratnik, N.; Žigert Pleteršek, P. Resonance graphs of fullerenes. ARS Math. Contemp. 2016, 11, 425–435. [Google Scholar] [CrossRef] [Green Version]
- Vesel, A. Fast computation of Clar formula for benzenoid graphs without nice coronenes. MATCH Commun. Math. Comput. Chem. 2014, 71, 717–740. [Google Scholar]
- Ahmadi, M.B.; Farhadi, E.; Khorasani, V.A. On computing the Clar number of a fullerene using optimization techniques. MATCH Commun. Math. Comput. Chem. 2016, 75, 695–701. [Google Scholar]
- Abeledo, H.; Atkinson, G.W. Unimodularity of the Clar number problem. Linear Algebra Appl. 2007, 420, 441–448. [Google Scholar] [CrossRef] [Green Version]
- Ashrafi, A.R.; Amini, K. Relations between Clar structures, Clar covers and sextet-rotations of dendrimer nanostars. Optoelectron. Adv. Mater. 2009, 3, 1076–1079. [Google Scholar]
- Ashrafi, A.R.; Amini, K. Clar structures, Clar covers and Kekulé index of dendrimer nanostars. Optoelectron. Adv. Mater. 2010, 4, 877–880. [Google Scholar]
- Balaban, A.T. Using Clar sextets for two- and three-dimensional aromatic systems. Phys. Chem. Chem. Phys. 2011, 13, 20649–20658. [Google Scholar] [CrossRef]
- Bérczi-Kovács, E.R.; Bernáth, A. The complexity of the Clar number problem and an exact algorithm. J. Math. Chem. 2018, 56, 597–605. [Google Scholar] [CrossRef]
- Carr, J.A.; Wang, X.F.; Ye, D. Packing resonant hexagons in fullerenes. Discret. Optim. 2014, 13, 49–54. [Google Scholar] [CrossRef]
- Chapman, J.; Foos, J.; Hartung, E.J.; Nelson, A.; Williams, A. Pairwise disagreements of Kekulé, Clar, and Fries numbers for benzenoids: A mathematical and computational investigation. MATCH Commun. Math. Comput. Chem. 2018, 80, 186–206. [Google Scholar]
- Hartung, E.J. Clar chains and a counterexample. J. Math. Chem. 2014, 52, 990–1006. [Google Scholar] [CrossRef]
- Salem, K.; Gutman, I. Clar number of hexagonal chains. Chem. Phys. Lett. 2004, 394, 283–286. [Google Scholar] [CrossRef]
- Zhou, S.; Zhang, H.P.; Gutman, I. Relations between Clar structures, Clar covers, and the sextet-rotation tree of a hexagonal system. Discret. Appl. Math. 2008, 156, 1809–1821. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.Q.; Zhang, H.P. Clar sets and maximum forcing numbers of hexagonal systems. MATCH Commun. Math. Comput. Chem. 2015, 74, 161–174. [Google Scholar]
- Cyvin, S.J.; Cyvin, B.N.; Brunvoll, J.; Gutman, I. Enumeration of Kekulé structures for multiple zigzag chains and related benzenoid hydrocarbons. Z. Naturforsch 1987, 42, 722–730. [Google Scholar] [CrossRef] [Green Version]
- He, B.H.; Langner, J.; Podeszwa, R.; Witek, H.A. Can the John-Sachs theorem be extended to Clar covers? MATCH Commun. Math. Comput. Chem. 2021, 86, 141–163. [Google Scholar]
- Son, Y.W.; Cohen, M.L.; Louie, S.G. Half-metallic graphene nanoribbons. Nature 2006, 444, 347–349. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Son, Y.W.; Cohen, M.L.; Louie, S.G. Energy Gaps in Graphene Nanoribbons. Phys. Rev. Lett. 2006, 97, 216803. [Google Scholar] [CrossRef] [Green Version]
- Trauzettel, B.; Bulaev, D.; Loss, D.; Burkard, G. Spin qubits in graphene quantum dots. Nat. Phys. 2007, 3, 192–196. [Google Scholar] [CrossRef] [Green Version]
- Yazyev, O.V.; Katsnelson, M.I. Magnetic Correlations at Graphene Edges: Basis for Novel Spintronics Devices. Phys. Rev. Lett. 2008, 100, 047209. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Soriano, D.; Muñoz-Rojas, F.; Fernández-Rossier, J.; Palacios, J.J. Hydrogenated graphene nanoribbons for spintronics. Phys. Rev. B 2010, 81, 165409. [Google Scholar] [CrossRef] [Green Version]
- Langner, J.; Witek, H.A. Algorithm for generating generalized resonance structures of single zigzag chains based on interface theory. J. Math. Chem. 2018, 56, 1393–1406. [Google Scholar] [CrossRef]
- Langner, J.; Witek, H.A. Interface theory of benzenoids. MATCH Commun. Math. Comput. Chem. 2020, 84, 143–176. [Google Scholar]
- Langner, J.; Witek, H.A. Interface theory of benzenoids: Basic applications. MATCH Commun. Math. Comput. Chem. 2020, 84, 177–215. [Google Scholar]
- Langner, J.; Witek, H.A. Extended strict order polynomial of a poset and fixed elements of linear extensions. Australas. J. Comb. 2021. under review. [Google Scholar]
- Page, A.J.; Chou, C.P.; Pham, B.Q.; Witek, H.A.; Irle, S.; Morokuma, K. Quantum chemical investigation of epoxide and ether groups in graphene oxide and their vibrational spectra. Phys. Chem. Chem. Phys. 2013, 15, 3725–3735. [Google Scholar] [CrossRef]
- Witek, H.A.; Langner, J. Clar covers of overlapping benzenoids: Case of two identically-oriented parallelograms. Symmetry 2020, 12, 1599. [Google Scholar] [CrossRef]
- Gutman, I.; Cyvin, S.J. A new method for the enumeration of Kekulé structures. Chem. Phys. Lett. 1987, 136, 137–140. [Google Scholar] [CrossRef]
- John, P.; Sachs, H. Calculating the numbers of perfect matchings and of spanning trees, Pauling’s orders, the characteristic polynomial, and the eigenvectors of a benzenoid system. Top. Curr. Chem. 1990, 153, 145–179. [Google Scholar]
- He, W.; He, W. P-V matrix and enumeration of Kekulé structures. Theor. Chim. Acta 1989, 75, 389–400. [Google Scholar]
- Maple 16. Maplesoft, a Division of Waterloo Maple Inc.; Maple Is a Trademark of Waterloo Maple Inc.: Waterloo, ON, Canada, 2012.
- The On-Line Encyclopedia of Integer Sequences. Available online: http://oeis.org/A085478 (accessed on 21 January 2021).
- Hogben, L. (Ed.) Handbook of Linear Algebra; Fact 10 in Section 4.1; Chapman & Hall: Boca Raton, FL, USA, 2007. [Google Scholar]
- Schleyer, P.; Maerker, C.; Dransfeld, A.; Jiao, H.; van Eikema Hommes, N.J.R. Nucleus-Independent Chemical Shifts: A Simple and Efficient Aromaticity Probe. J. Am. Chem. Soc. 1996, 118, 6317–6318. [Google Scholar] [CrossRef]
- Kruszewski, J.; Krygowski, T.M. Definition of aromaticity basing on the harmonic oscillator model. Tetrahedron Lett. 1972, 13, 3839–3842. [Google Scholar] [CrossRef]
- Krygowski, T.M. Crystallographic studies of inter- and intramolecular interactions reflected in aromatic character of π-electron systems. J. Chem. Inf. Comput. Sci. 1993, 33, 70–78. [Google Scholar] [CrossRef]
- Bird, C.W. A new aromaticity index and its application to five-membered ring heterocycles. Tetrahedron 1985, 41, 1409–1414. [Google Scholar] [CrossRef]
- Poater, J.; Fradera, X.; Duran, M.; Solá, M. The Delocalization Index as an Electronic Aromaticity Criterion: Application to a Series of Planar Polycyclic Aromatic Hydrocarbons. Chem. Eur. J. 2003, 9, 400–406. [Google Scholar] [CrossRef] [PubMed]
- Giambiagi, M.; de Giambiagi, M.; Mundim, K. Definition of a multicenter bond index. Struct. Chem. 1990, 1, 423–427. [Google Scholar] [CrossRef]
- Sablon, N.; Proft, F.D.; Solá, M.; Geerlings, P. The linear response kernel of conceptual DFT as a measure of aromaticity. Phys. Chem. Chem. Phys. 2012, 14, 3960–3967. [Google Scholar] [CrossRef]
- Fias, S.; Geerlings, P.; Ayers, P.; De Proft, F. σ, π aromaticity and anti-aromaticity as retrieved by the linear response kernel. Phys. Chem. Chem. Phys. 2013, 15, 2882–2889. [Google Scholar] [CrossRef] [PubMed]
- Sablon, N.; Proft, F.D.; Geerlings, P. The linear response kernel of conceptual DFT as a measure of electron delocalization. Chem. Phys. Lett. 2010, 498, 192–197. [Google Scholar] [CrossRef]
- Sablon, N.; Proft, F.D.; Geerlings, P. The linear response kernel: Inductive and resonance effects quantified. J. Phys. Chem. Lett. 2010, 1, 1228–1234. [Google Scholar] [CrossRef]
- Matito, E.; Duran, M.; Solá, M. The aromatic fluctuation index (FLU): A new aromaticity index based on electron delocalization. J. Chem. Phys. 2004, 122, 014109. [Google Scholar] [CrossRef] [Green Version]
- Chen, H. Development of a New Method Based on Clar Covers for Predicting Spin Populations and Aromaticities in Polycyclic Aromatic Hydrocarbons. Master’s Thesis, National Chiao Tung University, Hsinchu, Taiwan, 2019. [Google Scholar]
- Nakada, K.; Fujita, M.; Dresselhaus, G.; Dresselhaus, M.S. Edge state in graphene ribbons: Nanometer size effect and edge shape dependence. Phys. Rev. B 1996, 54, 17954. [Google Scholar] [CrossRef] [Green Version]
- Fujita, M.; Wakabayashi, K.; Nakada, K.; Kusakabe, K. Peculiar localized state at zigzag graphite edge. J. Phys. Soc. Jpn. 1996, 65, 1920–1923. [Google Scholar] [CrossRef] [Green Version]
- Pisani, L.; Chan, J.A.; Montanari, B.; Harrison, N.M. Electronic structure and magnetic properties of graphitic ribbons. Phys. Rev. B 2007, 75, 064418. [Google Scholar] [CrossRef]
- Feldner, H.; Meng, Z.Y.; Lang, T.C.; Assaad, F.F.; Wessel, S.; Honecker, A. Dynamical Signatures of Edge-State Magnetism of Graphene Nanoribbons. Phys. Rev. Lett. 2011, 106, 226401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Z.; Jin, S.; Liu, F. Spatially separated spin carriers in spin-semiconducting graphene nanoribbons. Phys. Rev. Lett. 2013, 111, 096803. [Google Scholar] [CrossRef] [Green Version]
- Culchac, F.J.; Latgé, A.; Costa, A.T. Spin waves in graphene nanoribbon devices. Phys. Rev. B 2012, 86, 115407. [Google Scholar] [CrossRef]
- Luo, M. Topological edge states of a graphene zigzag nanoribbon with spontaneous edge magnetism. Phys. Rev. B 2020, 102, 075421. [Google Scholar] [CrossRef]
- Sachs, H. Perfect matchings in hexagonal systems. Combinatorica 1984, 4, 89–99. [Google Scholar] [CrossRef]
- John, P.; Sachs, H. Calculating the number of perfect matching and Pauling’s bond orders in hexagonal systems whose inner dual is a tree. In Proceedings of the International Conference on Graph Theory, Los Angeles, CA, USA, 6–7 November 1985; pp. 80–91. [Google Scholar]
- John, P.; Rempel, J. Counting perfect matchings in hexagonal systems. In Proceedings of the International Conference on Graph Theory, Eyba, Germany, 1–5 October 1984; pp. 72–84. [Google Scholar]
- John, P.; Sachs, H. Wegesysteme und Linearfaktoren in hexagonalen und quadratischen Systemen. In Graphen in Forschung und Unterricht; Wagner, F.K., Bodendiek, R., Schumacher, H., Walther, G., Eds.; Verlag Barbara Franzbecker: Bad Salzdetfurth, Germany, 1985. [Google Scholar]
- John, P.E.; Sachs, H.; Zernitz, H. Counting perfect matchings in polyominoes with an application to the dimer problem. Appl. Math. 1987, 19, 465–477. [Google Scholar] [CrossRef]
- He, W.; He, W. Peak-Valley Path Method on Benzenoid and Coronoid System. Top. Curr. Chem. 1990, 153, 195–209. [Google Scholar]
- John, P.E.; Sachs, H.; Zheng, M. Kekulé patterns and Clar patterns in bipartite plane graphs. J. Chem. Inf. Comput. Sci. 1995, 35, 1019–1021. [Google Scholar] [CrossRef]
- He, B.H.; Witek, H.A. Clar theory for hexagonal benzenoids with corner defects. MATCH Commun. Math. Comput. Chem. 2020, 86, 121–140. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Witek, H.A. Zhang–Zhang Polynomials of Multiple Zigzag Chains Revisited: A Connection with the John–Sachs Theorem. Molecules 2021, 26, 2524. https://doi.org/10.3390/molecules26092524
Witek HA. Zhang–Zhang Polynomials of Multiple Zigzag Chains Revisited: A Connection with the John–Sachs Theorem. Molecules. 2021; 26(9):2524. https://doi.org/10.3390/molecules26092524
Chicago/Turabian StyleWitek, Henryk A. 2021. "Zhang–Zhang Polynomials of Multiple Zigzag Chains Revisited: A Connection with the John–Sachs Theorem" Molecules 26, no. 9: 2524. https://doi.org/10.3390/molecules26092524