Development of GBRT Model as a Novel and Robust Mathematical Model to Predict and Optimize the Solubility of Decitabine as an Anti-Cancer Drug
Abstract
1. Introduction
- Random Forest (Bagging of Regression Trees);
- Extra Trees (Bagging of Regression Trees);
- Gradient Boosting (Boosting of Regression Trees).
2. Dataset
3. Methodology
3.1. Random Forest Regression (RFR)
3.2. Extra Tree Regression (ETR)
3.3. Gradient Boosting Regression Trees (GBRT)
| Algorithm 1 |
| Initialize 1. Compute the negative gradient 2. Create a model 3. Select a gradient descent step size as 4. Modify the estimation of F(x) Output: the aggregated regression function |
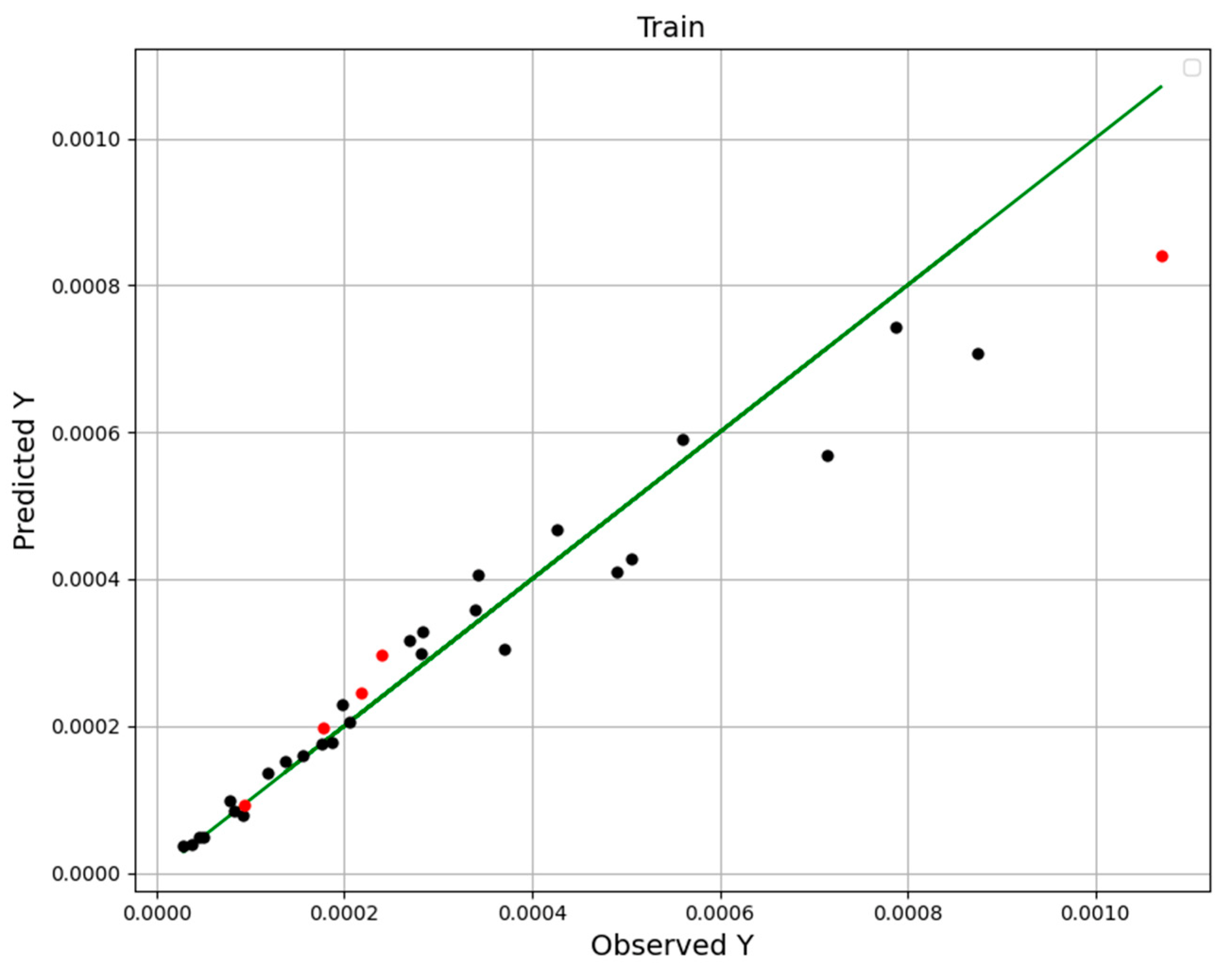
4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, Q.; Gilbert, J.A.; Zhu, H.; Huang, S.-M.; Kunkoski, E.; Das, P.; Bergman, K.; Buschmann, M.; ElZarrad, M.K. Emerging clinical pharmacology topics in drug development and precision medicine. In Atkinson’s Principles of Clinical Pharmacology; Elsevier: Amsterdam, The Netherlands, 2022; pp. 691–708. [Google Scholar]
- Docherty, J.R.; Alsufyani, H.A. Pharmacology of drugs used as stimulants. J. Clin. Pharmacol. 2021, 61, S53–S69. [Google Scholar] [CrossRef] [PubMed]
- Gore, S.D.; Jones, C.; Kirkpatrick, P. Decitabine. Nat. Rev. Drug Discov. 2006, 5, 891–893. [Google Scholar] [CrossRef] [PubMed]
- Jabbour, E.; Issa, J.P.; Garcia-Manero, G.; Kantarjian, H. Evolution of decitabine development: Accomplishments, ongoing investigations, and future strategies. Cancer Interdiscip. Int. J. Am. Cancer Soc. 2008, 112, 2341–2351. [Google Scholar] [CrossRef]
- Saba, H.I. Decitabine in the treatment of myelodysplastic syndromes. Ther. Clin. Risk Manag. 2007, 3, 807. [Google Scholar] [PubMed]
- Xiao, J.; Liu, P.; Wang, Y.; Zhu, Y.; Zeng, Q.; Hu, X.; Ren, Z.; Wang, Y. A Novel Cognition of Decitabine: Insights into Immunomodulation and Antiviral Effects. Molecules 2022, 27, 1973. [Google Scholar] [CrossRef]
- Senapati, J.; Shoukier, M.; Garcia-Manero, G.; Wang, X.; Patel, K.; Kadia, T.; Ravandi, F.; Pemmaraju, N.; Ohanian, M.; Daver, N. Activity of decitabine as maintenance therapy in core binding factor acute myeloid leukemia. Am. J. Hematol. 2022, 97, 574–582. [Google Scholar] [CrossRef]
- Issa, J.-P. Decitabine. Curr. Opin. Oncol. 2003, 15, 446–451. [Google Scholar] [CrossRef]
- Bhusnure, O.; Gholve, S.; Giram, P.; Borsure, V.; Jadhav, P.; Satpute, V.; Sangshetti, J. Importance of supercritical fluid extraction techniques in pharmaceutical industry: A Review. Indo Am. J. Pharm. Res. 2015, 5, 3785–3801. [Google Scholar]
- Khaw, K.-Y.; Parat, M.-O.; Shaw, P.N.; Falconer, J.R. Solvent supercritical fluid technologies to extract bioactive compounds from natural sources: A review. Molecules 2017, 22, 1186. [Google Scholar] [CrossRef]
- Tran, P.; Park, J.-S. Application of supercritical fluid technology for solid dispersion to enhance solubility and bioavailability of poorly water-soluble drugs. Int. J. Pharm. 2021, 610, 121247. [Google Scholar] [CrossRef]
- Zhuang, W.; Hachem, K.; Bokov, D.; Javed Ansari, M.; Taghvaie Nakhjiri, A. Ionic liquids in pharmaceutical industry: A systematic review on applications and future perspectives. J. Mol. Liq. 2022, 349, 118145. [Google Scholar] [CrossRef]
- Zhang, Q.-W.; Lin, L.-G.; Ye, W.-C. Techniques for extraction and isolation of natural products: A comprehensive review. Chin. Med. 2018, 13, 20. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Juarez, J.M.; Li, X. Data Mining for Biomedicine and Healthcare; Hindawi: London, UK, 2017. [Google Scholar]
- Zhang, Y.; Zhang, G.; Shang, Q. Computer-aided clinical trial recruitment based on domain-specific language translation: A case study of retinopathy of prematurity. J. Healthc. Eng. 2017, 2017, 7862672. [Google Scholar] [CrossRef] [PubMed]
- Seddon, G.; Lounnas, V.; McGuire, R.; van den Bergh, T.; Bywater, R.P.; Oliveira, L.; Vriend, G. Drug design for ever, from hype to hope. J. Comput.-Aided Mol. Des. 2012, 26, 137–150. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Mak, K.-K.; Pichika, M.R. Artificial intelligence in drug development: Present status and future prospects. Drug Discov. Today 2019, 24, 773–780. [Google Scholar] [CrossRef]
- Dietterich, T.G. Ensemble methods in machine learning. In Proceedings of the International Workshop on Multiple Classifier Systems, Cagliari, Italy, 21–23 June 2000. [Google Scholar]
- Izenman, A.J. Modern Multivariate Statistical Techniques—Regression, Classification, and Manifold Learning; Springer: New York, NY, USA, 2008; Volume 10. [Google Scholar]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. Experiments with a new boosting algorithm. In Proceedings of the 13th International Conference on Machine Learning (ICML’96), Bari, Italy, 3–6 July 1996; pp. 148–156. [Google Scholar]
- Kocev, D.; Ceci, M. Ensembles of extremely randomized trees for multi-target regression. In Proceedings of the International Conference on Discovery Science, Banff, AB, Canada, 4–6 October 2015. [Google Scholar]
- Wehenkel, L.; Ernst, D.; Geurts, P. Ensembles of extremely randomized trees and some generic applications. In Proceedings of the Workshop “Robust Methods for Power System State Estimation and Load Forecasting”; Paris, France, 29-–30 May 2006.
- Pishnamazi, M.; Zabihi, S.; Jamshidian, S.; Borousan, F.; Hezave, A.Z.; Marjani, A.; Shirazian, S. Experimental and thermodynamic modeling decitabine anti cancer drug solubility in supercritical carbon dioxide. Sci. Rep. 2021, 11, 1075. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Ghimire, B.; Rogan, J.; Chica-Olmo, M.; Rigol-Sanchez, J.P. An assessment of the effectiveness of a random forest classifier for land-cover classification. ISPRS J. Photogramm. Remote Sens. 2012, 67, 93–104. [Google Scholar] [CrossRef]
- Nguyen Duc, M.; Ho Sy, A.; Nguyen Ngoc, T.; Hoang Thi, T.L. An Artificial Intelligence Approach Based on Multi-layer Perceptron Neural Network and Random Forest for Predicting Maximum Dry Density and Optimum Moisture Content of Soil Material in Quang Ninh Province, Vietnam. In CIGOS 2021, Emerging Technologies and Applications for Green Infrastructure, Proceedings of the 6th International Conference on Geotechnics, Civil Engineering and Structures, Ha Long, Vietnam, 28–29 October 2021; Springer: Berlin/Heidelberg, Germany, 2022; pp. 1745–1754. [Google Scholar]
- Li, Y.; Zou, C.; Berecibar, M.; Nanini-Maury, E.; Chan, J.C.-W.; Van den Bossche, P.; Van Mierlo, J.; Omar, N. Random forest regression for online capacity estimation of lithium-ion batteries. Appl. Energy 2018, 232, 197–210. [Google Scholar] [CrossRef]
- Peters, J.; De Baets, B.; Verhoest, N.E.; Samson, R.; Degroeve, S.; De Becker, P.; Huybrechts, W. Random forests as a tool for ecohydrological distribution modelling. Ecol. Model. 2007, 207, 304–318. [Google Scholar] [CrossRef]
- Verikas, A.; Gelzinis, A.; Bacauskiene, M. Mining data with random forests: A survey and results of new tests. Pattern Recognit. 2011, 44, 330–349. [Google Scholar] [CrossRef]
- Gislason, P.O.; Benediktsson, J.A.; Sveinsson, J.R. Random forests for land cover classification. Pattern Recognit. Lett. 2006, 27, 294–300. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Ahmad, M.W.; Mourshed, M.; Rezgui, Y. Tree-based ensemble methods for predicting PV power generation and their comparison with support vector regression. Energy 2018, 164, 465–474. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Mason, L.; Baxter, J.; Bartlett, P.; Frean, M. Boosting algorithms as gradient descent. In Advances in Neural Information Processing Systems 12; MIT Press: Cambridge, MA, USA, 1999; Volume 12. [Google Scholar]
- Truong, V.-H.; Vu, Q.-V.; Thai, H.-T.; Ha, M.-H. A robust method for safety evaluation of steel trusses using Gradient Tree Boosting algorithm. Adv. Eng. Softw. 2020, 147, 102825. [Google Scholar] [CrossRef]
- Xu, Q.; Xiong, Y.; Dai, H.; Kumari, K.M.; Xu, Q.; Ou, H.-Y.; Wei, D.-Q. PDC-SGB: Prediction of effective drug combinations using a stochastic gradient boosting algorithm. J. Theor. Biol. 2017, 417, 1–7. [Google Scholar] [CrossRef]
- Willmott, C.J. Some comments on the evaluation of model performance. Bull. Am. Meteorol. Soc. 1982, 63, 1309–1313. [Google Scholar] [CrossRef]
- Gouda, S.G.; Hussein, Z.; Luo, S.; Yuan, Q. Model selection for accurate daily global solar radiation prediction in China. J. Clean. Prod. 2019, 221, 132–144. [Google Scholar] [CrossRef]
- Kim, S.; Kim, H. A new metric of absolute percentage error for intermittent demand forecasts. Int. J. Forecast. 2016, 32, 669–679. [Google Scholar] [CrossRef]
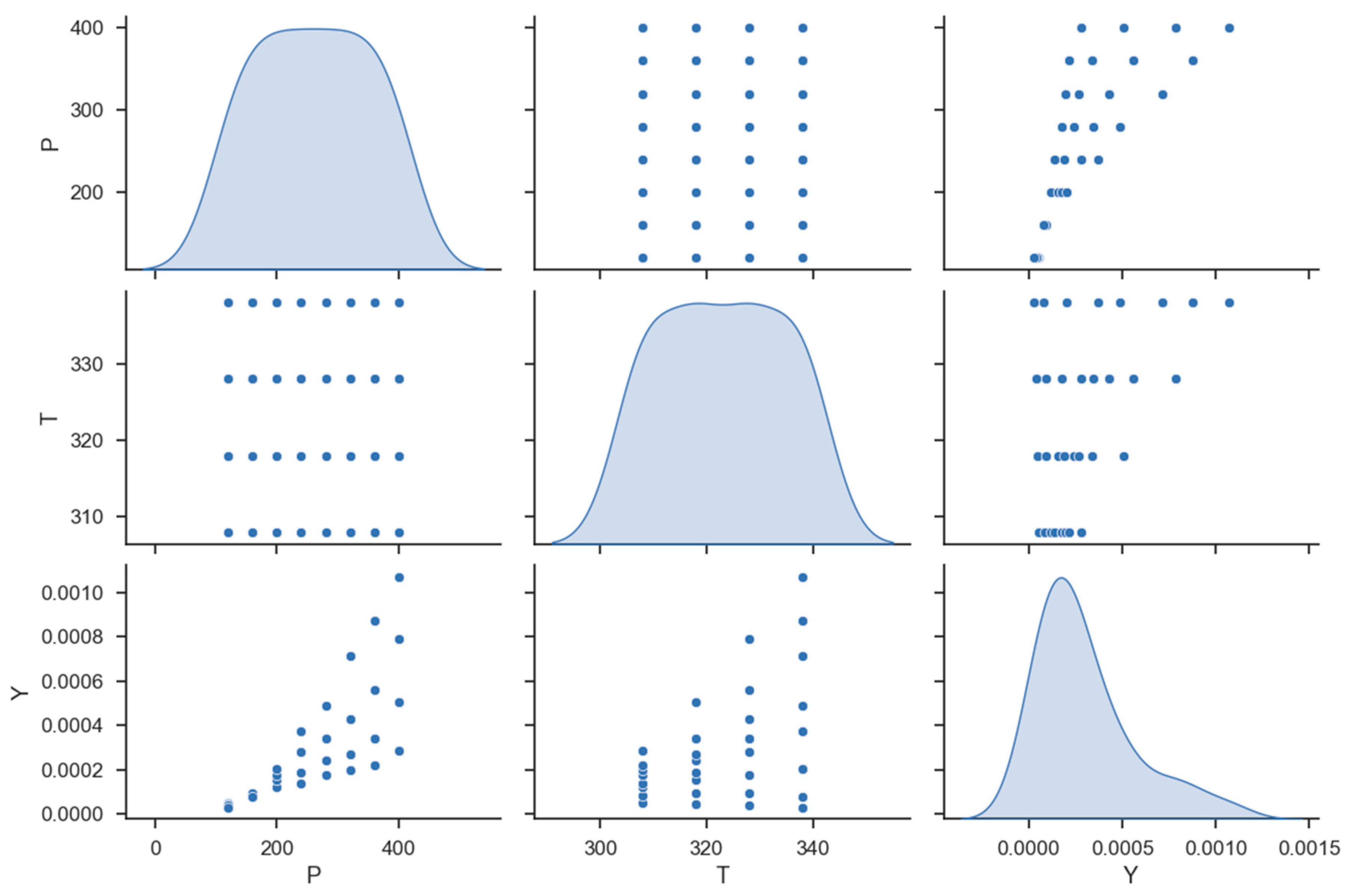



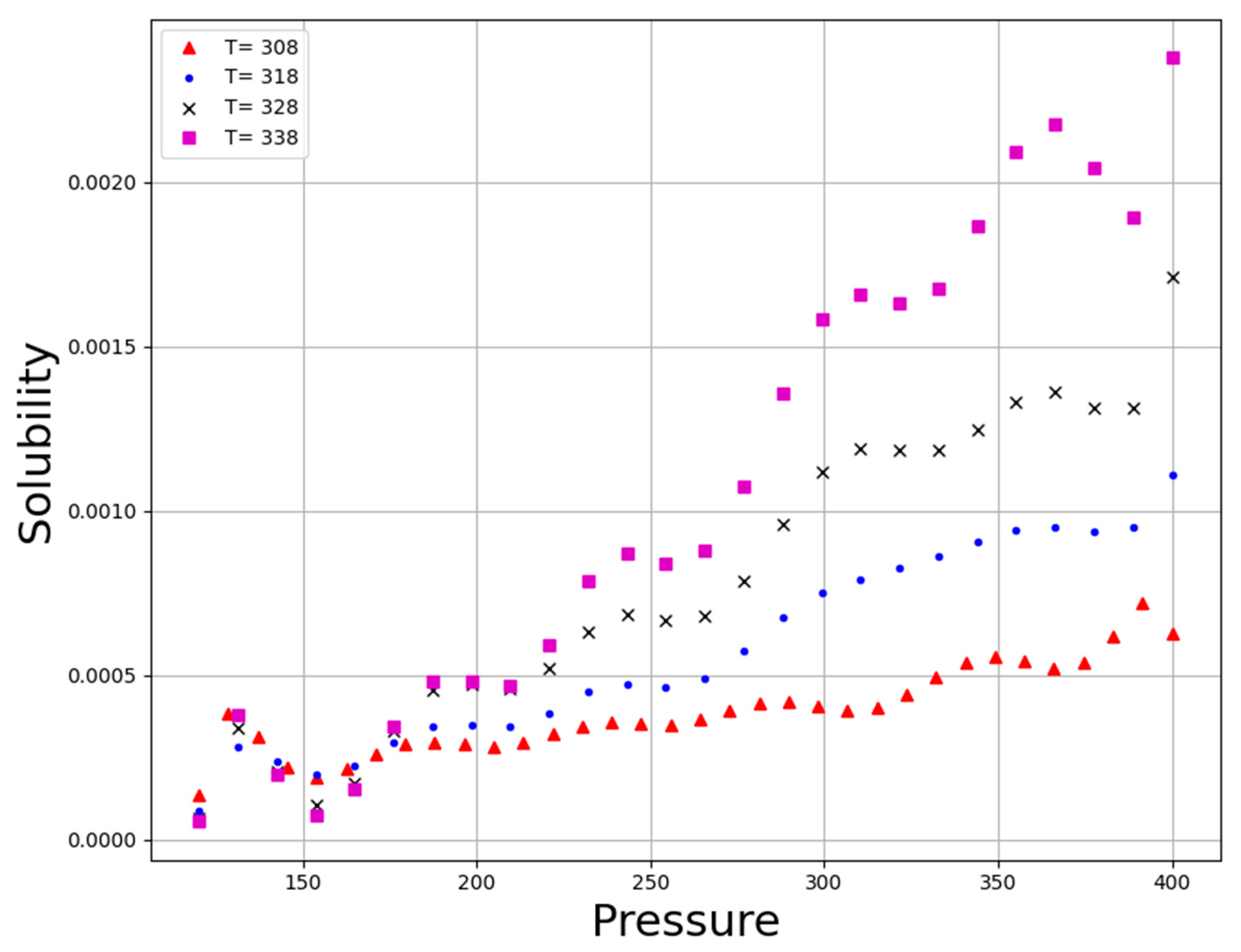
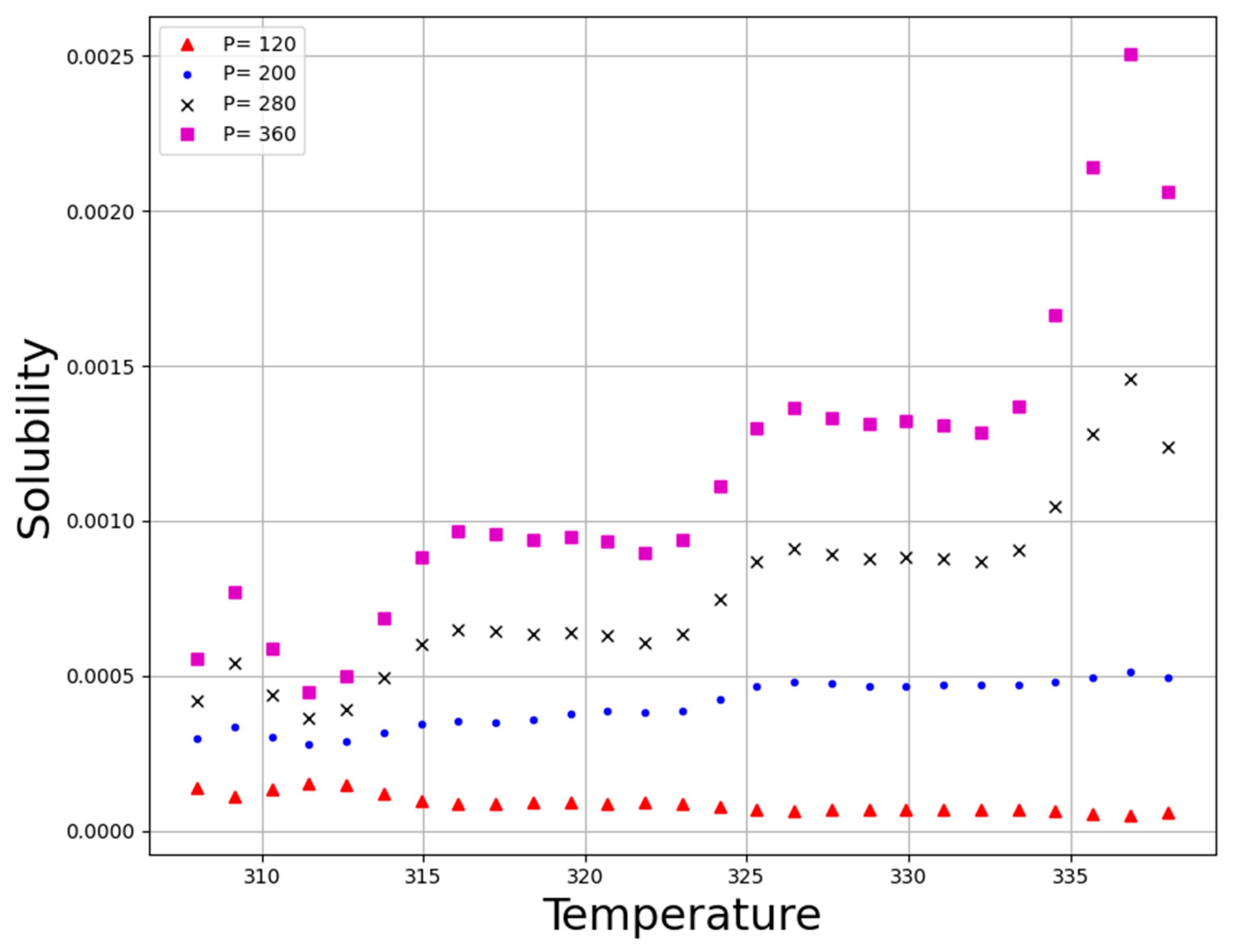
| No | X1 = P (Bar) | X2 = T (K) | Y = Solubility (Mole Fraction) |
|---|---|---|---|
| 1 | 120 | 308 | 5.04 × 10−5 |
| 2 | 120 | 318 | 4.51 × 10−5 |
| 3 | 120 | 328 | 3.69 × 10−5 |
| 4 | 120 | 338 | 2.84 × 10−5 |
| 5 | 160 | 308 | 8.23 × 10−5 |
| 6 | 160 | 318 | 9.37 × 10−5 |
| 7 | 160 | 328 | 9.11 × 10−5 |
| 8 | 160 | 338 | 7.79 × 10−5 |
| 9 | 200 | 308 | 1.18 × 10−4 |
| 10 | 200 | 318 | 1.55 × 10−4 |
| 11 | 200 | 328 | 1.77 × 10−4 |
| 12 | 200 | 338 | 2.05 × 10−4 |
| 13 | 240 | 308 | 1.37 × 10−4 |
| 14 | 240 | 318 | 1.87 × 10−4 |
| 15 | 240 | 328 | 2.82 × 10−4 |
| 16 | 240 | 338 | 3.71 × 10−4 |
| 17 | 280 | 308 | 1.76 × 10−4 |
| 18 | 280 | 318 | 2.40 × 10−4 |
| 19 | 280 | 328 | 3.42 × 10−4 |
| 20 | 280 | 338 | 4.90 × 10−4 |
| 21 | 320 | 308 | 1.97 × 10−4 |
| 22 | 320 | 318 | 2.69 × 10−4 |
| 23 | 320 | 328 | 4.27 × 10−4 |
| 24 | 320 | 338 | 7.15 × 10−4 |
| 25 | 360 | 308 | 2.18 × 10−4 |
| 26 | 360 | 318 | 3.40 × 10−4 |
| 27 | 360 | 328 | 5.60 × 10−4 |
| 28 | 360 | 338 | 8.74 × 10−4 |
| 29 | 400 | 308 | 2.83 × 10−4 |
| 30 | 400 | 318 | 5.06 × 10−4 |
| 31 | 400 | 328 | 7.88 × 10−4 |
| 32 | 400 | 338 | 1.07 × 10−3 |
| Models | R2 Score | MAPE |
|---|---|---|
| RFR | 0.925 | 1.423 × 10−1 |
| ETR | 0.999 | 7.573 × 10−2 |
| GBRT | 0.999 | 7.119 × 10−2 |
| P (Bar) | T (K) | Y |
|---|---|---|
| 380.88 | 333.01 | 0.001073 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdelbasset, W.K.; Elsayed, S.H.; Alshehri, S.; Huwaimel, B.; Alobaida, A.; Alsubaiyel, A.M.; Alqahtani, A.A.; El Hamd, M.A.; Venkatesan, K.; AboRas, K.M.; et al. Development of GBRT Model as a Novel and Robust Mathematical Model to Predict and Optimize the Solubility of Decitabine as an Anti-Cancer Drug. Molecules 2022, 27, 5676. https://doi.org/10.3390/molecules27175676
Abdelbasset WK, Elsayed SH, Alshehri S, Huwaimel B, Alobaida A, Alsubaiyel AM, Alqahtani AA, El Hamd MA, Venkatesan K, AboRas KM, et al. Development of GBRT Model as a Novel and Robust Mathematical Model to Predict and Optimize the Solubility of Decitabine as an Anti-Cancer Drug. Molecules. 2022; 27(17):5676. https://doi.org/10.3390/molecules27175676
Chicago/Turabian StyleAbdelbasset, Walid Kamal, Shereen H. Elsayed, Sameer Alshehri, Bader Huwaimel, Ahmed Alobaida, Amal M. Alsubaiyel, Abdulsalam A. Alqahtani, Mohamed A. El Hamd, Kumar Venkatesan, Kareem M. AboRas, and et al. 2022. "Development of GBRT Model as a Novel and Robust Mathematical Model to Predict and Optimize the Solubility of Decitabine as an Anti-Cancer Drug" Molecules 27, no. 17: 5676. https://doi.org/10.3390/molecules27175676
APA StyleAbdelbasset, W. K., Elsayed, S. H., Alshehri, S., Huwaimel, B., Alobaida, A., Alsubaiyel, A. M., Alqahtani, A. A., El Hamd, M. A., Venkatesan, K., AboRas, K. M., & Abourehab, M. A. S. (2022). Development of GBRT Model as a Novel and Robust Mathematical Model to Predict and Optimize the Solubility of Decitabine as an Anti-Cancer Drug. Molecules, 27(17), 5676. https://doi.org/10.3390/molecules27175676








