Understanding the Liquid States of Cyclic Hydrocarbons Containing N, O, and S Atoms via the 3D-RISM-KH Molecular Solvation Theory
Abstract
:1. Introduction
2. Results
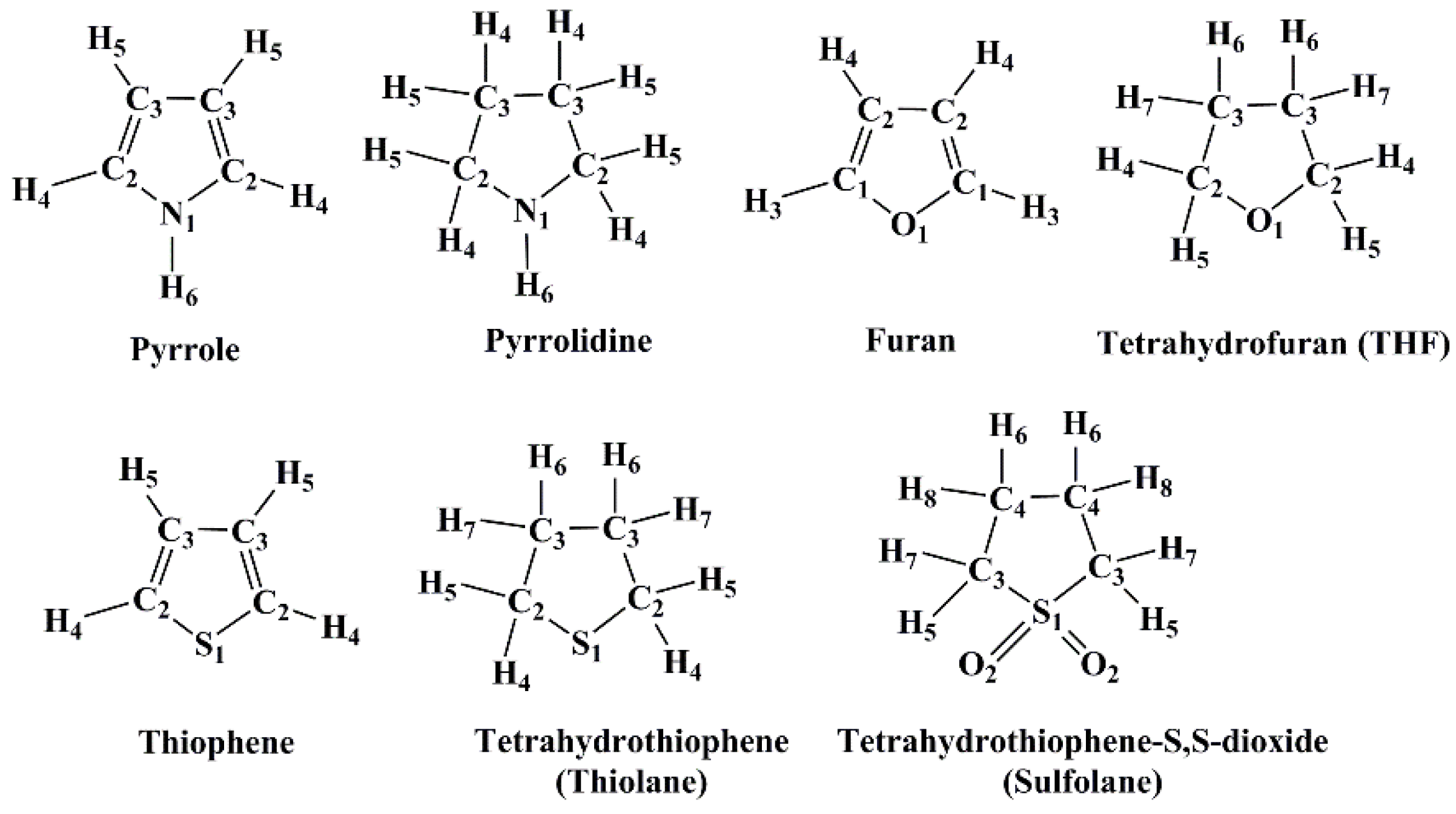
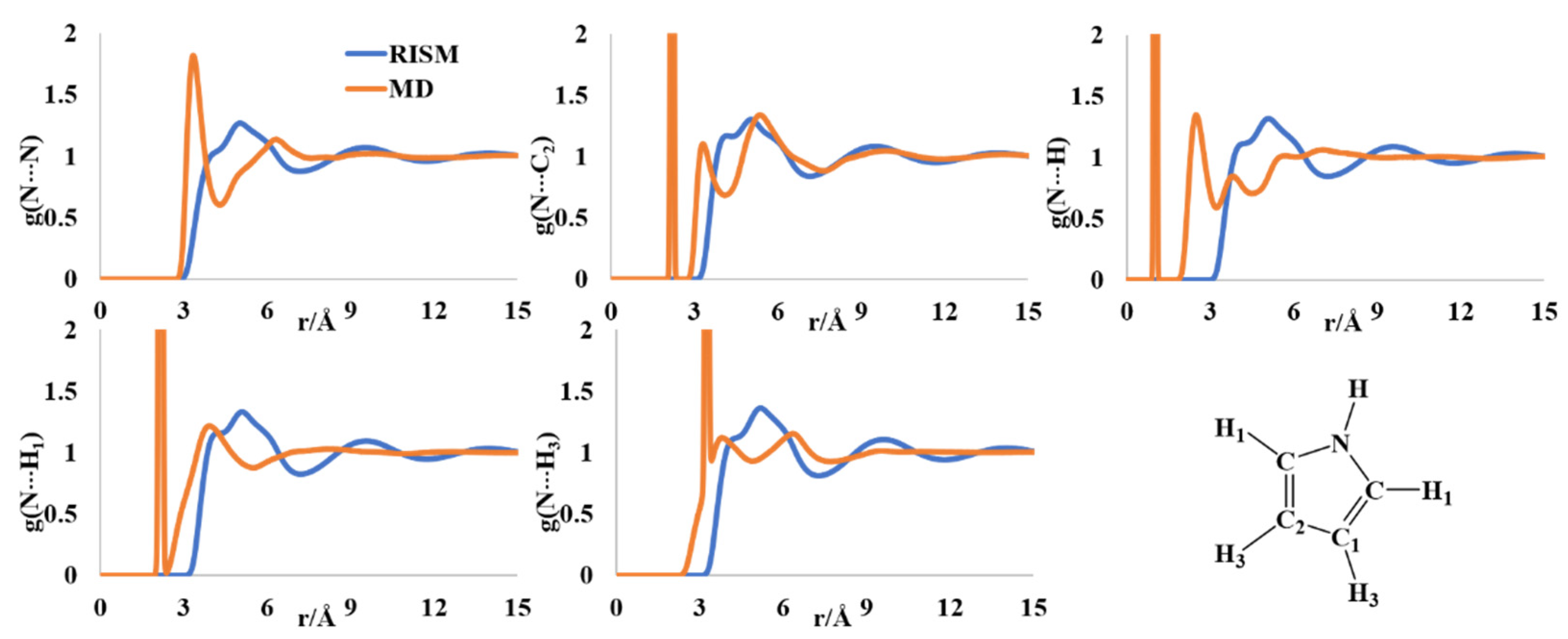
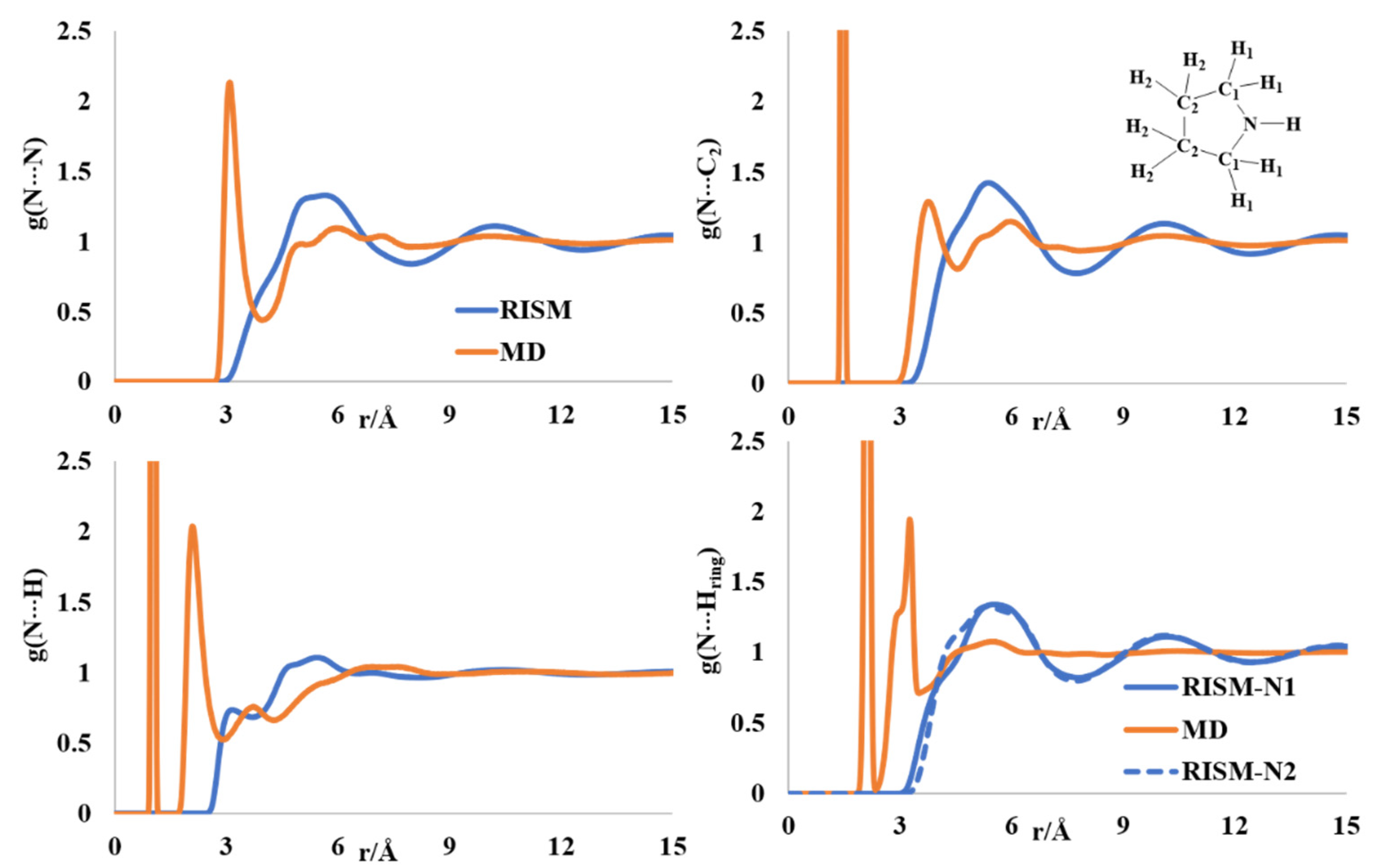
2.1. Liquid Structure of Pyrrole
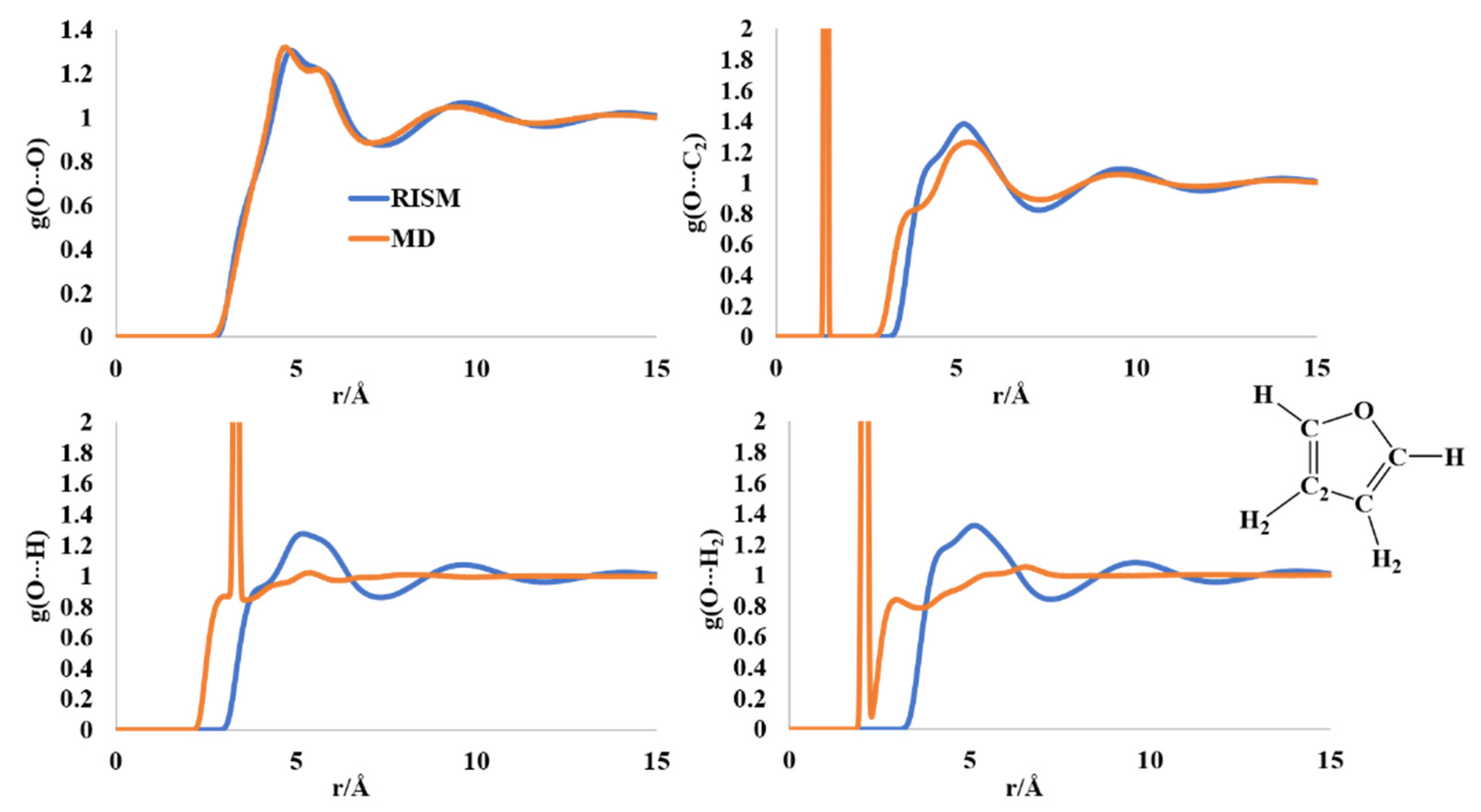
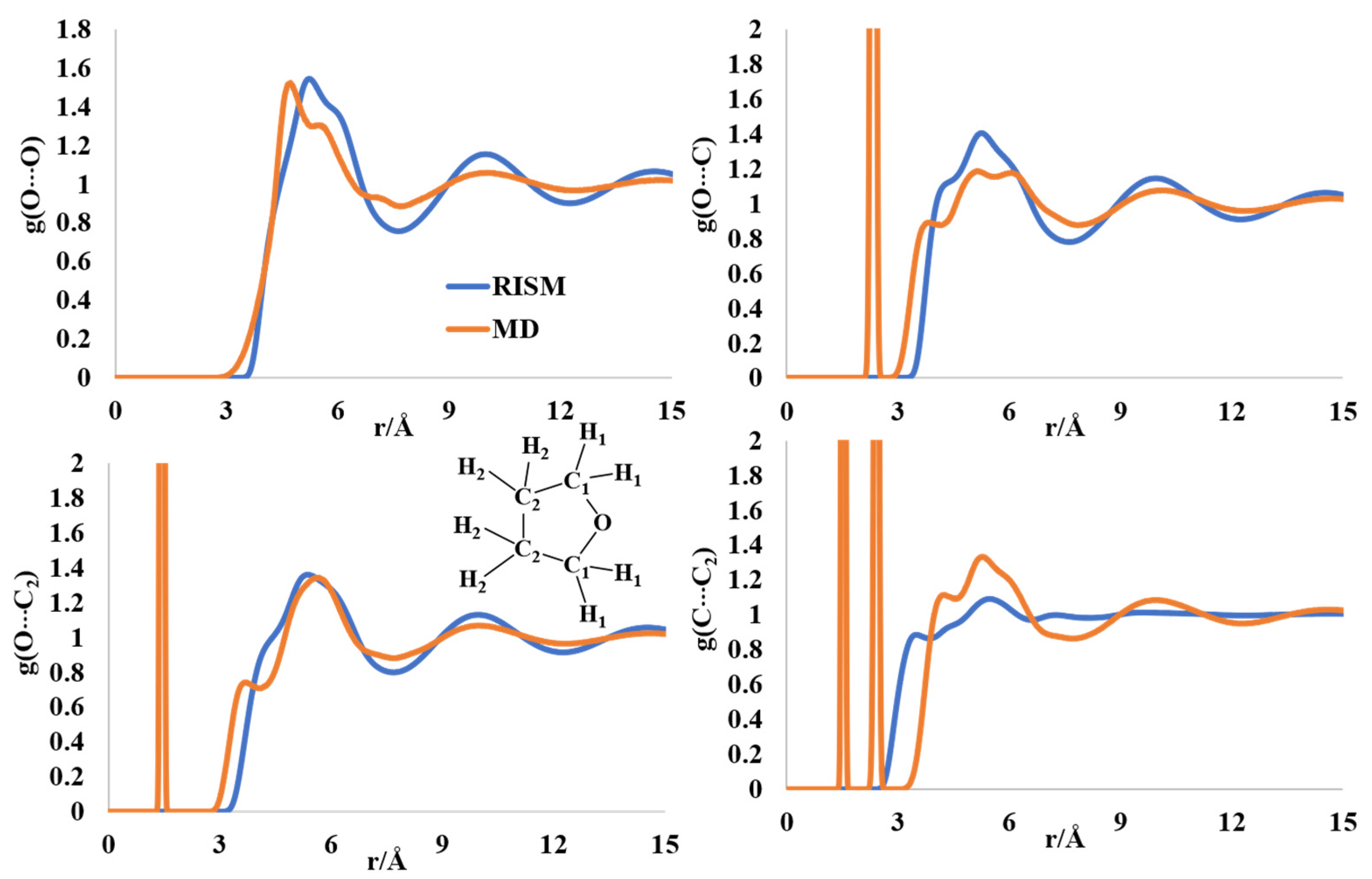
2.2. Liquid Structure of Furan
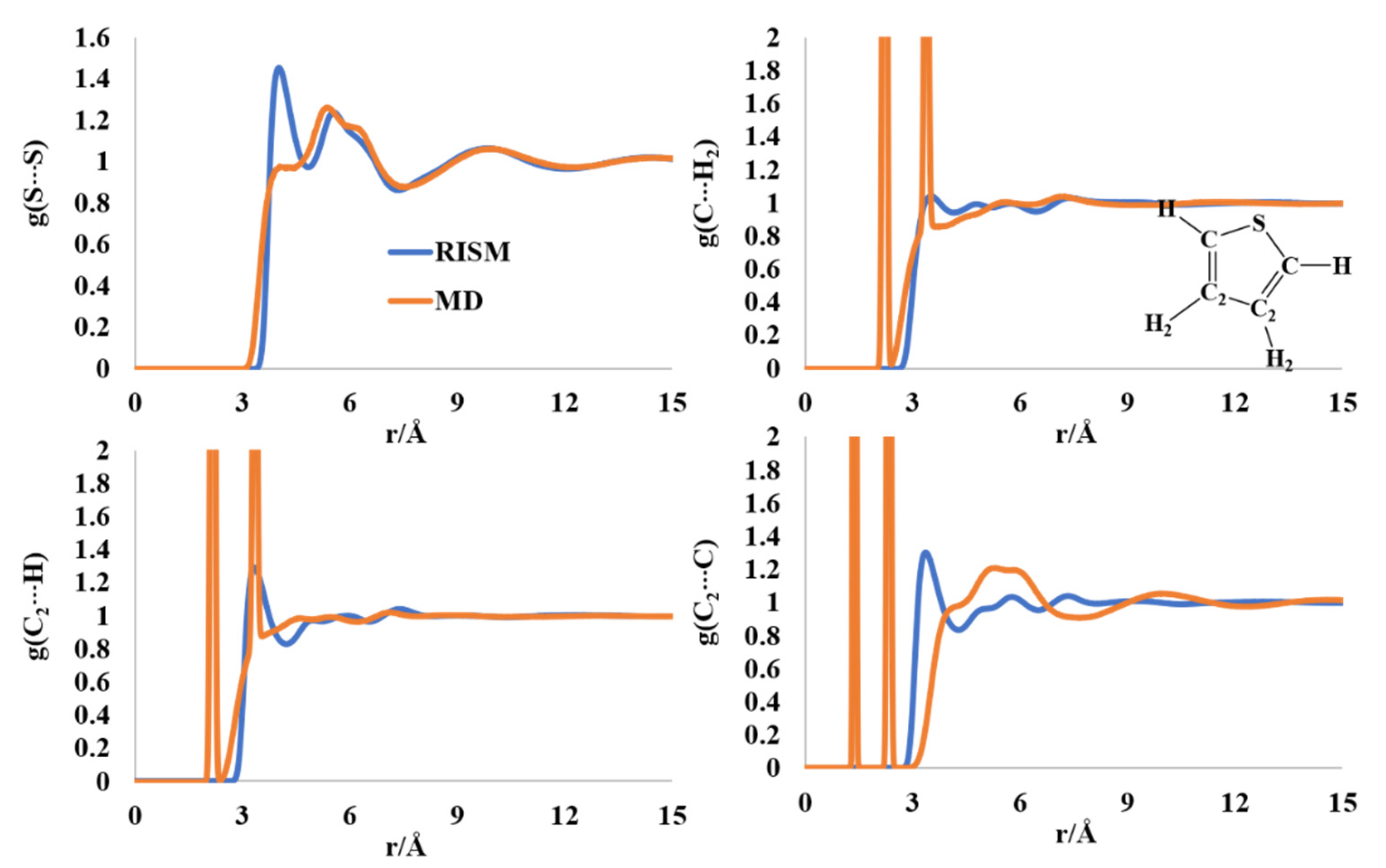
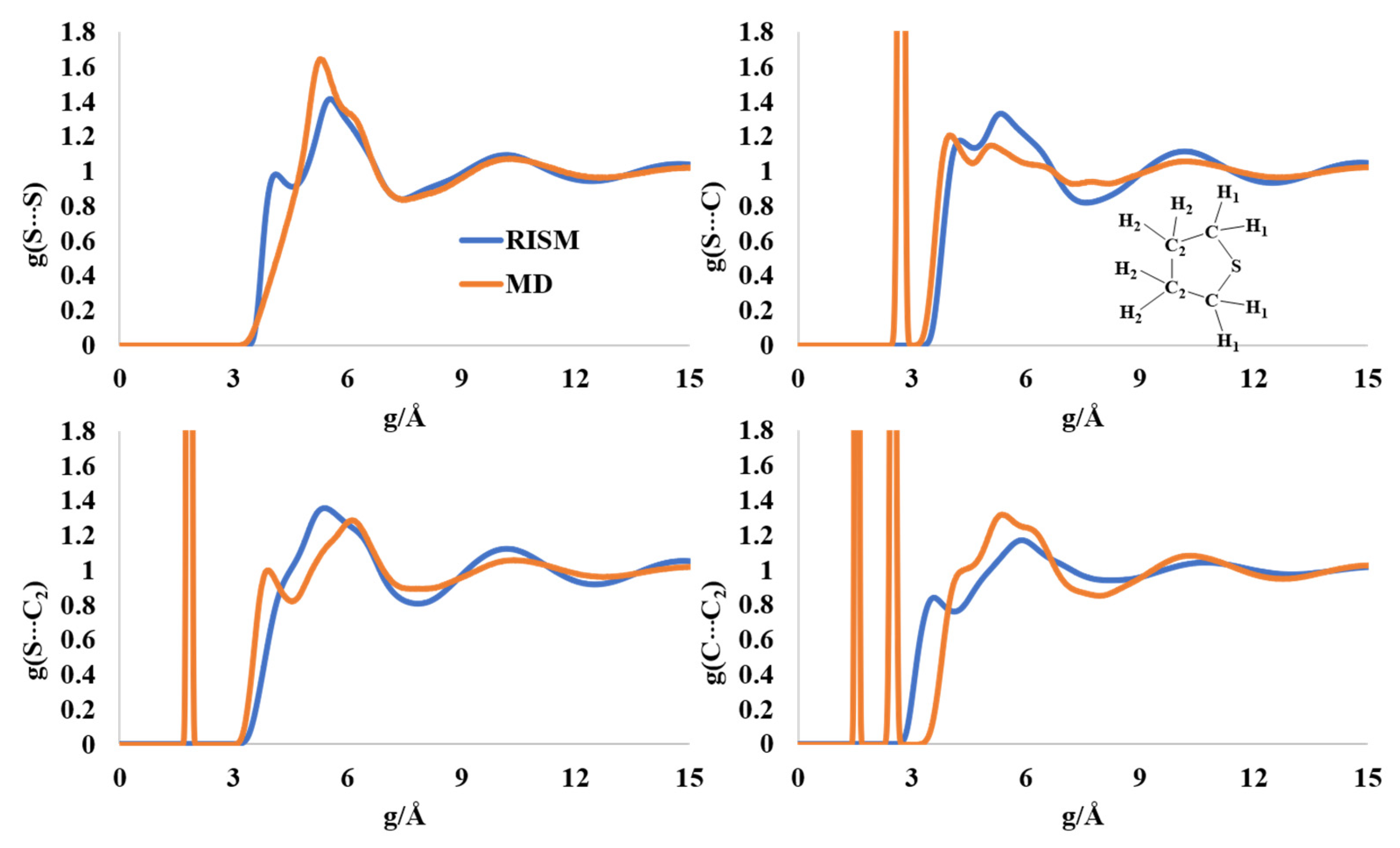
2.3. Liquid Structure of Thiophene
2.4. Liquid Structure of Pyrrolidine
2.5. Liquid Structure of Tetrahydrofuran (THF)
2.6. Liquid Structure of Tetrhydrothiophene (Thiolane)
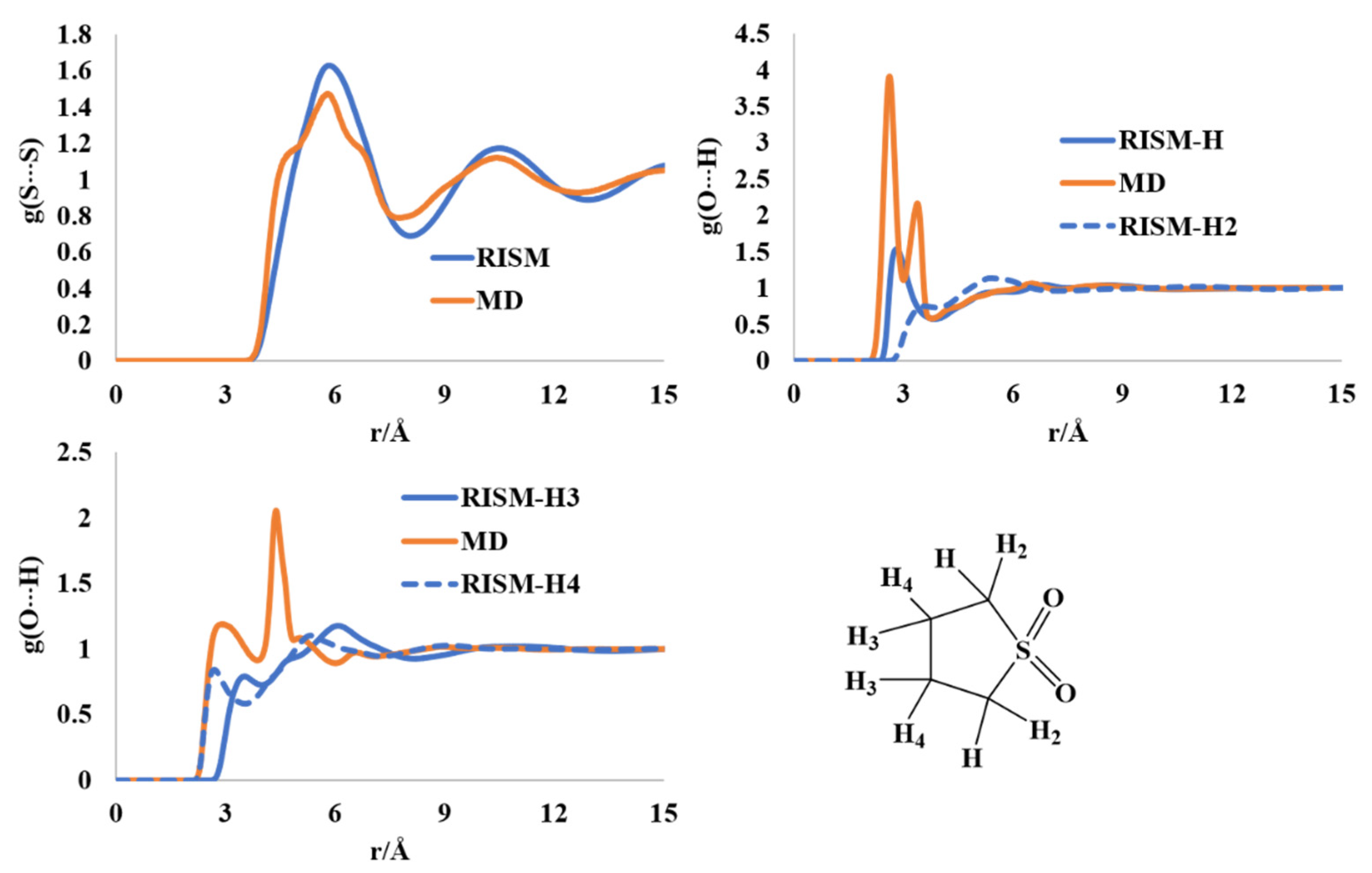
2.7. Liquid Structure of Tetrahydrothiophene-S,S-dioxide
2.8. SFEs in Tetrahydrofuran (THF) and Tetrahydrothiophene-S,S-dioxide (Thiolane) Solvents
3. Discussion
4. Materials and Methods
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Floris, F.; Tomasi, J. Evaluation of the dispersion contribution to the solvation energy. A simple computational model in the continuum approximation. J. Comput. Chem. 1989, 10, 616–627. [Google Scholar] [CrossRef]
- Roux, B.; Simonson, T. Implicit solvent models. Biophys. Chem. 1999, 78, 1–20. [Google Scholar] [CrossRef]
- Warshel, A.; Sharma, P.K.; Kato, M.; Parsonb, W.W. Modeling electrostatic effects in proteins. Biochim. Biophys. Acta Prot. Proteom. 2006, 1764, 1647–1676. [Google Scholar] [CrossRef] [PubMed]
- Wagoner, J.A.; Baker, N.A. Assessing implicit models for nonpolar mean solvation forces: The importance of dispersion and volume terms. Proc. Nat. Acad. Sci. USA 2006, 103, 8331–8336. [Google Scholar] [CrossRef] [Green Version]
- Schaefer, M.; Karplus, M. A Comprehensive Analytical Treatment of Continuum Electrostatics. J. Phys. Chem. 1996, 100, 1578–1599. [Google Scholar] [CrossRef]
- Lamm, G. The Poisson-Boltzmann Equation. In Reviews in Computational Chemistry; Lipkowitz, K.B., Larter, R., Cundari, T.R., Boyd, D.B., Eds.; Willey: Hoboken, NJ, USA, 2003; Volume 19, pp. 147–366. [Google Scholar]
- Tomasi, J. Selected features of the polarizable continuum model for the representation of solvation. WIREs Comp. Mol. Sci. 2011, 1, 855–867. [Google Scholar] [CrossRef]
- Herbert, J.M. Dielectric continuum methods for quantum chemistry. WIREs Comp. Mol. Sci. 2021, 11, e1519. [Google Scholar] [CrossRef]
- Klamt, A.; Schüürmann, G. COSMO: A new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient. J. Chem. Soc. Perkin Trans. 1993, 2, 799–805. [Google Scholar] [CrossRef]
- Klamt, A.; Moya, C.; Palomar, J. A Comprehensive Comparison of the IEFPCM and SS(V)PE Continuum Solvation Methods with the COSMO Approach. J. Chem. Theory Comput. 2015, 11, 4220–4225. [Google Scholar] [CrossRef] [Green Version]
- Mennucci, B. Polarizable continuum model. WIREs Comp. Mol. Sci. 2012, 2, 386–404. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
- Pliego, J.R., Jr.; Riveros, J.M. Hybrid discrete-continuum solvation methods. WIREs Comp. Mol. Sci. 2020, 10, e1440. [Google Scholar] [CrossRef]
- Pliego, J.R.; Riveros, J.M. The Cluster−Continuum Model for the Calculation of the Solvation Free Energy of Ionic Species. J. Phys. Chem. A 2001, 105, 7241–7247. [Google Scholar] [CrossRef]
- Ho, J.; Coote, M.L. A universal approach for continuum solvent pKa calculations: Are we there yet? Theor. Chem. Acc. 2009, 125, 3–21. [Google Scholar] [CrossRef]
- Pliego, J.R., Jr.; Riveros, J.M. Theoretical Calculation of pKa Using the Cluster-Continuum Model. J. Phys. Chem. A 2002, 106, 7434–7439. [Google Scholar] [CrossRef]
- Chandler, D.; Andersen, H.C. Optimized cluster expansions for classical fluids. II. Theory of molecular liquids. J. Chem. Phys. 1972, 57, 1930. [Google Scholar] [CrossRef]
- Chandler, D. Derivation of an integral equation for pair correlation functions in molecular fluids. J. Chem. Phys. 1973, 59, 2742. [Google Scholar] [CrossRef]
- Chandler, D.; McCoy, J.D.; Singer, S.J. Singer, Density functional theory of nonuniform polyatomic systems. I. General formulation. J. Chem. Phys. 1985, 85, 5971. [Google Scholar] [CrossRef]
- Chandler, D.; McCoy, J.D.; Singer, S.J. Density functional theory of nonuniform polyatomic systems. II. Rational closures for integral equations. J. Chem. Phys. 1986, 85, 5977. [Google Scholar] [CrossRef]
- Chandler, D. Equilibrium structure and molecular motion in liquids. Acc. Chem. Res. 1974, 7, 246–251. [Google Scholar] [CrossRef]
- Chandler, D.; Weeks, J.D.; Anderson, H.C. Van der Waals Picture of Liquids, Solids, and Phase Transformations. Science 1983, 220, 787–794. [Google Scholar] [CrossRef]
- Perkyns, J.S.; Pettitt, B.M. A site-site theory for finite concentration saline solutions. J. Chem. Phys. 1992, 97, 7656–7666. [Google Scholar] [CrossRef]
- Kovalenko, A.; Hirata, F. A molecular theory of liquid interfaces. Phys. Chem. Chem. Phys. 2005, 7, 1785–1793. [Google Scholar] [CrossRef]
- Palmer, D.S.; Frolov, A.; Ratkova, E.; Fedorov, M.V. Towards a universal method for calculating hydration free energies: A 3D reference interaction site model with partial molar volume correction. J. Phys. Condens. Matt. 2010, 22, 492101. [Google Scholar] [CrossRef]
- Kovalenko, A. Multiscale Modeling of Solvation. In Springer Handbook of Electro-Chemical Energy; Breitkopf, C., Swider-Lyons, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Roy, D.; Kovalenko, A. 3D-RISM-KH Molecular Solvation Theory. In Multiscale Dynamics Simulations: Nano and Nano-Bio Systems in Complex Environments; Salahub, D.R., Wei, D., Eds.; RSC Publishing: London, UK, 2021; pp. 254–286. [Google Scholar]
- Roy, D.; Kovalenko, A. Extension of the approximate 3D-RISM-KH molecular solvation theory to liquid aniline and pyridines. Res. Chem. 2022, 4, 100365. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.; Kollman, P.A.; Case, D.A. Automatic atom type and bond type perception in molecular mechanical calculations. J. Mol. Graph. Model. 2006, 25, 247260. [Google Scholar] [CrossRef]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general AMBER force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef] [PubMed]
- Rappe, A.K.; Casewit, C.J.; Colwell, K.S.; Goddard, W.A.; Skiff, W.M. UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations. J. Am. Chem. Soc. 1992, 114, 10024–10035. [Google Scholar] [CrossRef]
- Marenich, A.V.; Kelly, C.P.; Thompson, J.D.; Hawkins, G.D.; Chambers, C.C.; Giesen, D.J.; Winget, P.; Cramer, C.J.; Truhlar, D.G. Minnesota Solvation Database (MNSOL) Version 2012; University of Minnesota: Minneapolis, MN, USA, 2020. [Google Scholar] [CrossRef]
- Lide, D.R. (Ed.) CRC Handbook of Chemistry and Physics, 76th ed.; CRC Press Inc.: Boca Raton, FL, USA, 1995; pp. 3–474. [Google Scholar]
- O’Neil, M.J. (Ed.) The Merck Index—An Encyclopedia of Chemicals, Drugs, and Biologicals, 13th ed.; Merck and Co., Inc.: Whitehouse Station, NJ, USA, 2006; pp. 738–1597. [Google Scholar]
- Weast, R.C. (Ed.) Handbook of Chemistry and Physics, 60th ed.; CRC Press Inc.: Boca Raton, FL, USA, 1979; p. C-516. [Google Scholar]
- Gomez-Zavaglia, A.; Fausto, R. Self-Aggregation in Pyrrole: Matrix Isolation, Solid State Infrared Spectroscopy, and DFT Study. J. Phys. Chem. A 2004, 108, 6953–6967. [Google Scholar] [CrossRef]
- Goddard, R.; Heinemann, O.; Kruger, C. Pyrrole and a Co-crystal of 1H- and 2H-1,2,3-Triazole. Acta Crystallogr. 1997, 53, 1846–1850. [Google Scholar] [CrossRef]
- Wilcox, W.S.; Goldstein, J.H. Evidence for a Completely Planar Structure of Pyrrole from Its Microwave Spectrum. J. Chem. Phys. 1952, 20, 1656. [Google Scholar] [CrossRef]
- Gontrani, L.; Ramondo, F.; Caminiti, R. Energy dispersive X-ray diffraction and molecular dynamics meet: The structure of liquid pyrrole. Chem. Phys. Lett. 2006, 417, 200–205. [Google Scholar] [CrossRef]
- Schomaker, V.; Pauling, L. The Electron Diffraction Investigation of the Structure of Benzene, Pyridine, Pyrazine, Butadiene-1,3, Cyclopentadiene, Fur an, Pyrrole, and Thiophene. J. Am. Chem. Soc. 1939, 61, 1769–1780. [Google Scholar] [CrossRef]
- Gamba, Z.; Klein, M.L. Short-range structure of liquid pyrrole. J. Chem. Phys. 1990, 92, 697–698. [Google Scholar] [CrossRef]
- Lautie, A.; Novak, A. Effect of Hydrogen Bonding on the NH Stretching Raman Band of Pyrrole. J. Chem. Phys. 1972, 56, 2479. [Google Scholar] [CrossRef]
- McDonald, N.A.; Jorgensen, W.L. Development of an All-Atom Force Field for Heterocycles. Properties of Liquid Pyrrole, Furan, Diazoles, and Oxazoles. J. Phys. Chem. B 1998, 102, 8049–8059. [Google Scholar] [CrossRef]
- Macchiagodena, M.; Mancini, G.; Pagliai, M.; Cardini, G.; Barone, V. New atomistic model of pyrrole with improved liquid state properties and structure. Int. J. Quantum Chem. 2018, 118, e25554. [Google Scholar] [CrossRef] [Green Version]
- Gontrani, L.; Ramondo, F.; Caminiti, R. Furan and thiophene in liquid phase: An X-ray and molecular dynamics study. Chem. Phys. Lett. 2006, 422, 256–261. [Google Scholar] [CrossRef]
- Pfafferott, G.; Oberhammer, H.; Boggs, J.E.; Caminati, W. Geometric Structure and Pseudorational Potential of Pyrrolidine. An ab Initio and Electron Diffraction Study. J. Am. Chem. Soc. 1985, 107, 2305–2309. [Google Scholar] [CrossRef]
- Han, S.J.; Kang, Y.K. Pseudorotation in heterocyclic five-membered rings: Tetrahydrofuran and pyrrolidine. J. Mol. Struct. THEOCHEM 1996, 369, 157–165. [Google Scholar] [CrossRef]
- Stortz, C.A.; Sarotti, A.M. Exhaustive exploration of the conformational landscape of mono- and disubstituted five-membered rings by DFT and MP2 calculations. RSC Adv. 2019, 9, 24134–24145. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Denis, P.A. Coupled cluster investigation of the axial and equatorial isomers of pyrrolidine. Mol. Phys. 2012, 111, 9–17. [Google Scholar] [CrossRef]
- Hesse, S.; Wassermann, T.N.; Suhm, M.A. Brightening and Locking a Weak and Floppy N−H Chromophore: The Case of Pyrrolidine. J. Phys. Chem. A 2010, 114, 10492–10499. [Google Scholar] [CrossRef] [PubMed]
- Chandrasekhar, J.; Jorgensen, W.L. Monte Carlo simulations of liquid tetrahydrofuran including pseudorotation. J. Chem. Phys. 1982, 77, 5073. [Google Scholar] [CrossRef]
- Girard, S.; Müller-Plathe, F. Molecular dynamics simulation of liquid tetrahydrofuran: On the uniqueness of force fields. Mol. Phys. 2003, 106, 779–787. [Google Scholar] [CrossRef]
- Bowron, D.T.; Finney, J.L.; Soper, A.K. The Structure of Liquid Tetrahydrofuran. J. Am. Chem. Soc. 2006, 128, 5119–5126. [Google Scholar] [CrossRef]
- Houteghem, M.V.; Ghysels, A.; Verstraelen, T.; Poelmans, W.; Waroquier, M.; Speybroeck, V.V. Critical Analysis of the Accuracy of Models Predicting or Extracting Liquid Structure Information. J. Phys. Chem. B 2014, 118, 2451–2470. [Google Scholar] [CrossRef]
- Bedard-Hearn, M.J.; Larsen, R.E.; Schwartz, B.J. Understanding Nonequilibrium Solute and Solvent Motions through Molecular Projections: Computer Simulations of Solvation Dynamics in Liquid Tetrahydrofuran (THF). J. Phys. Chem. B 2003, 107, 14464–14475. [Google Scholar] [CrossRef]
- Johnsson, M.; Persson, I. The structure of silver(I) iodide and bromide, and the silver(I) solvate in tetrahydrothiophene solution: An X-ray scattering and raman spectroscopic study. Inorg. Chim. Acta 1987, 130, 215–220. [Google Scholar] [CrossRef]
- Naumov, V.A.; Semashko, V.N.; Shaidulin, S.A. Electron-diffraction investigation of the structure of the tetramethylene sulfone molecule. J. Struct. Chem. 1974, 14, 555–559. [Google Scholar] [CrossRef]
- Combet, J.; Bee, M.; Djurado, D.; D’Assenza, G.; Commandeur, G. Structural and dynamical aspects of solid sulpholan in the temperature range 160–300 K I.—X-ray powder diffraction study. Phys. B Condens. Matt. 1997, 233, 95–101. [Google Scholar] [CrossRef]
- Alonso, J.L. Microwave spectrum of sulfolane. J. Mol. Struct. 1981, 73, 71–78. [Google Scholar] [CrossRef]
- Hargittai, I. On the ring planarity of sulpholane. J. Mol. Struct. 1981, 77, 313–314. [Google Scholar] [CrossRef]
- Peemoeller, H.; Sharp, A.R.; Watton, A.; Kydon, D.W. Nuclear magnetic relaxation study of fully deuterated sulfolan. J. Chem. Phys. 1983, 78, 4337. [Google Scholar] [CrossRef]
- Mukherji, S.; Avula, N.V.S.; Balasubramanian, S. Refined Force Field for Liquid Sulfolane with Particular Emphasis to Its Transport Characteristics. ACS Omega 2020, 5, 28285–28295. [Google Scholar] [CrossRef] [PubMed]
- Hlushak, S.; Kovalenko, A. Effective Interactions and Adsorption of Heterocyclic Aromatic Hydrocarbons in Kaolinite Organic Solutions Studied by 3D-RISM-KH Molecular Theory of Solvation. J. Phys. Chem. C 2017, 121, 22092–22104. [Google Scholar] [CrossRef] [Green Version]
- Luchko, T.; Blinov, N.; Limon, G.C.; Joyce, K.P.; Kovalenko, A. SAMPL5: 3D-RISM partition coefficient calculations with partial molar volume corrections and solute conformational sampling. J. Comput. Aided Mol. Des. 2016, 30, 1115–1127. [Google Scholar] [CrossRef]
- Boyd, N.J.; Wilson, M.R. Optimization of the GAFF force field to describe liquid crystal molecules: The path to a dramatic improvement in transition temperature predictions. Phys. Chem. Chem. Phys. 2015, 17, 24851–24865. [Google Scholar] [CrossRef] [Green Version]
- Case, D.A.; Aktulga, H.M.; Belfon, K.; Ben-Shalom, I.Y.; Berryman, J.T.; Brozell, S.R.; Cerutti, D.S.; Cheatham, T.E., III; Cisneros, G.A.; Cruzeiro, V.W.D.; et al. Amber 2022; University of California, San Francisco: San Francisco, CA, USA, 2022. [Google Scholar]
- Frisch, M.J.; Head-Gordon, M.; Pople, J.A. Direct MP2 gradient method. Chem. Phys. Lett. 1990, 166, 275–280. [Google Scholar] [CrossRef]
- Head-Gordon, M.; Head-Gordon, T. Analytic MP2 Frequencies Without Fifth Order Storage: Theory and Application to Bifurcated Hydrogen Bonds in the Water Hexamer. Chem. Phys. Lett. 1994, 220, 122–128. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [Green Version]
- Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision B.01, Gaussian, Inc.: Wallingford, CT, USA, 2016.
- Dewar, M.J.S.; Zoebisch, E.G.; Healy, E.F. AM1: A New General Purpose Quantum Mechanical Molecular Model. J. Am. Chem. Soc. 1985, 107, 3902–3909. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1, 19–25. [Google Scholar] [CrossRef]
| Molecule | Dielectric Constant | Density (Experimental, g·cm−3) | Density (MD, g·cm−3) 1 |
|---|---|---|---|
| Pyrrole | 8.00 | 0.968 [33] | 1.009 |
| Furan | 2.94 | 0.973 [34] | 0.964 |
| Thiophene | 2.73 | 1.065 [33] | 1.033 |
| Pyrrolidine | 8.30 | 0.852 [34] | 0.892 |
| Tetrahydrofuran (THF) | 7.42 | 0.883 [33] | 0.899 |
| Tetrahydrothiophene | 8.61 | 0.998 [35] | 0.977 |
| Sulfolane | 43.96 | 1.2606 [34] | 1.298 |
| Solvent | a (kcal/mol/Å3) | b (kcal/mol) |
|---|---|---|
| THF | −0.1139 | −10.5505 |
| Sulfolane | −0.1715 | −7.1919 |
| Solute | Solvent | ΔGexpt (kcal/mol) | μGF (kcal/mol) | PMV (Å3) | ΔGcor (kcal/mol) |
|---|---|---|---|---|---|
| n-octane | THF | −5.39 | 44.13 | 352.55 | −6.57 |
| toluene | THF | −5.5 | 28.46 | 235.24 | −8.88 |
| ethanol | THF | −4.56 | 21.21 | 154.02 | −6.88 |
| tetrahydrofuran | THF | −4.25 | 24.21 | 192.77 | −8.29 |
| 1,4-dioxane | THF | −5.17 | 44.06 | 207.79 | 9.84 |
| 2-butanone | THF | −4.54 | 27.72 | 212.46 | −7.03 |
| nitromethane | THF | −5.09 | 21.21 | 152.51 | −6.71 |
| n-octane | sulfolane | −2.44 | 53.41 | 281.17 | −2.02 |
| toluene | sulfolane | −4.23 | 33.32 | 188.49 | −6.21 |
| ethanol | sulfolane | −4.3 | 22.90 | 114.90 | −4.00 |
| 1,4-dioxane | sulfolane | −4.9 | 30.16 | 163.54 | −5.09 |
| 2-butanone | sulfolane | −4.09 | 31.08 | 163.25 | −4.12 |
| butylamine | sulfolane | −4.25 | 35.56 | 182.73 | −2.98 |
| nitromethane | sulfolane | −5.28 | 20.98 | 110.01 | −5.09 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roy, D.; Kovalenko, A. Understanding the Liquid States of Cyclic Hydrocarbons Containing N, O, and S Atoms via the 3D-RISM-KH Molecular Solvation Theory. Molecules 2022, 27, 6563. https://doi.org/10.3390/molecules27196563
Roy D, Kovalenko A. Understanding the Liquid States of Cyclic Hydrocarbons Containing N, O, and S Atoms via the 3D-RISM-KH Molecular Solvation Theory. Molecules. 2022; 27(19):6563. https://doi.org/10.3390/molecules27196563
Chicago/Turabian StyleRoy, Dipankar, and Andriy Kovalenko. 2022. "Understanding the Liquid States of Cyclic Hydrocarbons Containing N, O, and S Atoms via the 3D-RISM-KH Molecular Solvation Theory" Molecules 27, no. 19: 6563. https://doi.org/10.3390/molecules27196563
APA StyleRoy, D., & Kovalenko, A. (2022). Understanding the Liquid States of Cyclic Hydrocarbons Containing N, O, and S Atoms via the 3D-RISM-KH Molecular Solvation Theory. Molecules, 27(19), 6563. https://doi.org/10.3390/molecules27196563






