Dephasing Processes in the Molecular Dye Lumogen-F Orange Characterized by Two-Dimensional Electronic Spectroscopy
Abstract
:1. Introduction
2. Results and Discussion
2.1. Sample Characterization
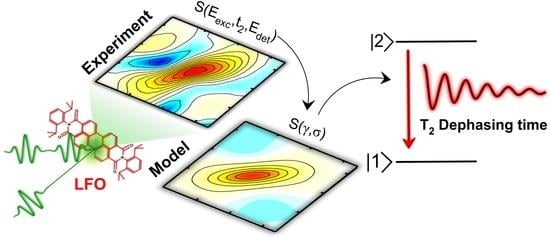
2.2. Two-Dimensional Electronic Spectroscopy of LFO
2.3. Temperature Dependent Dephasing Rate
2.4. Spectral Diffusion
3. Materials and Methods
3.1. Sample Preparation
3.2. Two-Dimensional Electronic Spectroscopy
3.3. Line Shape Data Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Schäfer, F.P. Dye Lasers; Springer: Berlin/Heidelberg, Germany, 1990; pp. 1–200. [Google Scholar]
- Dsouza, R.N.; Pischel, U.; Nau, W.M. Fluorescent Dyes and Their Supramolecular Host/Guest Complexes with Macrocycles in Aqueous Solution. Chem. Rev. 2011, 111, 7941–7980. [Google Scholar] [CrossRef] [PubMed]
- Zou, S.-J.; Shen, Y.; Xie, F.-M.; Chen, J.-D.; Li, Y.-Q.; Tang, J.X. Recent advances in organic light-emitting diodes: Toward smart lighting and displays. Mater. Chem. Front. 2020, 4, 788–820. [Google Scholar] [CrossRef]
- Toninelli, C.; Gerhardt, I.; Clark, A.S.; Reserbat-Plantey, A.; Götzinger, S.; Ristanović, Z.; Colautti, M.; Lombardi, P.; Major, K.D.; Deperasińska, I.; et al. Single organic molecules for photonic quantum technologies. Nat. Mater. 2021, 20, 1615–1628. [Google Scholar] [CrossRef] [PubMed]
- Skolnick, M.S.; Astratov, V.N.; Whittaker, D.M.; Armitage, A.; Emam-Ismael, M.; Stevenson, R.M.; Baumberg, J.J.; Roberts, J.S.; Lidzey, D.G.; Virgili, T.; et al. Exciton polaritons in single and coupled microcavities. J. Lumin. 2000, 87, 25–29. [Google Scholar] [CrossRef] [Green Version]
- Lidzey, D.G.; Bradley, D.D.C.; Skolnick, M.S.; Virgili, T.; Walker, S.; Whittaker, D.M. Strong exciton–photon coupling in an organic semiconductor microcavity. Nature 1998, 395, 53–55. [Google Scholar] [CrossRef]
- Byrnes, T.; Kim, N.Y.; Yamamoto, Y. Exciton–polariton condensates. Nat. Phys. 2014, 10, 803–813. [Google Scholar] [CrossRef] [Green Version]
- Quach, J.Q.; McGhee, K.E.; Ganzer, L.; Rouse, D.M.; Lovett, B.W.; Gauger, E.M.; Cerullo, G.; Lidzey, D.G.; Virgili, T. Superabsorption in an organic microcavity: Toward a quantum battery. Sci. Adv. 2022, 8, eabk3160. [Google Scholar] [CrossRef] [PubMed]
- Zondervan, R.; Kulzer, F.; Orlinskii, S.B.; Orrit, M. Photoblinking of Rhodamine 6G in Poly(vinyl alcohol): Radical Dark State Formed through the Triplet. J. Phys. Chem. A 2003, 107, 6770–6776. [Google Scholar] [CrossRef]
- Xu, Q.-H.; Scholes, G.D.; Yang, M.; Fleming, G.R. Probing Solvation and Reaction Coordinates of Ultrafast Photoinduced Electron-Transfer Reactions Using Nonlinear Spectroscopies: Rhodamine 6G in Electron-Donating Solvents. J. Phys. Chem. A 1999, 103, 10348–10358. [Google Scholar] [CrossRef]
- Mukamel, S. Principles of Nonlinear Optical Spectroscopy; Oxford University Press: Rochester, NY, USA, 1995; pp. 111–261. [Google Scholar]
- Volker, S. Hole-Burning Spectroscopy. Annu. Rev. Phys. Chem. 1989, 40, 499–530. [Google Scholar] [CrossRef]
- Weiner, A.M.; De Silvestri, S.; Ippen, E.P. Three-pulse scattering for femtosecond dephasing studies: Theory and experiment. J. Opt. Soc. Am. B 1985, 2, 654–662. [Google Scholar] [CrossRef]
- Scholes, G.D.; Larsen, D.S.; Fleming, G.R.; Rumbles, G.; Burn, P.L. Origin of line broadening in the electronic absorption spectra of conjugated polymers: Three-pulse-echo studies of MEH-PPV in toluene. Phys. Rev. B 2000, 61, 13670–13678. [Google Scholar] [CrossRef] [Green Version]
- Mukamel, S. Multidimensional femtosecond correlation spectroscopies of electronic and vibrational excitations. Annu. Rev. Phys. Chem. 2000, 51, 691–729. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jonas, D.M. Two-dimensional femtosecond spectroscopy. Annu. Rev. Phys. Chem. 2003, 54, 425–463. [Google Scholar] [CrossRef]
- Do, T.N.; Khyasudeen, M.F.; Nowakowski, P.J.; Zhang, Z.; Tan, H.-S. Measuring Ultrafast Spectral Diffusion and Correlation Dynamics by Two-Dimensional Electronic Spectroscopy. Chem. Asian J. 2019, 14, 3992–4000. [Google Scholar] [CrossRef] [PubMed]
- Cho, M.; Brixner, T.; Stiopkin, I.; Vaswanib, H.; Fleming, G.R. Two Dimensional Electronic Spectroscopy of Molecular Complexes. J. Chin. Chem. Soc. 2006, 53, 15–24. [Google Scholar] [CrossRef]
- Bardeen, C.J.; Cerullo, G.; Shank, C.V. Temperature-dependent electronic dephasing of molecules in polymers in the range 30 to 300 K. Chem. Phys. Lett. 1997, 280, 127–133. [Google Scholar] [CrossRef]
- Artur, C.; Le Ru, E.C.; Etchegoin, P.G. Temperature Dependence of the Homogeneous Broadening of Resonant Raman Peaks Measured by Single-Molecule Surface-Enhanced Raman Spectroscopy. J. Phys. Chem. Lett. 2011, 2, 3002–3005. [Google Scholar] [CrossRef]
- Hamm, P.; Zanni, M. Concepts and Methods of 2D Infrared Spectroscopy; Cambridge University Press: New York, NY, USA, 2011. [Google Scholar]
- Siemens, M.E.; Moody, G.; Li, H.; Bristow, A.D.; Cundiff, S.T. Resonance lineshapes in two-dimensional Fourier transform spectroscopy. Opt. Express. 2010, 18, 17699–17708. [Google Scholar] [CrossRef]
- Guo, L.; Chen, C.; Zhang, Z.; Monahan, D.M.; Lee, Y.; Fleming, G.R. Lineshape characterization of excitons in monolayer WS2 by two-dimensional electronic spectroscopy. Nanoscale Adv. 2020, 2, 2333–2338. [Google Scholar] [CrossRef]
- Khalil, M.; Demirdöven, N.; Tokmakoff, A. Obtaining Absorptive Line Shapes in Two-Dimensional Infrared Vibrational Correlation Spectra. Phys. Rev. Lett. 2003, 90, 047401. [Google Scholar] [CrossRef] [PubMed]
- Tokmakoff, A. Two-Dimensional Line Shapes Derived from Coherent Third-Order Nonlinear Spectroscopy. J. Phys. Chem. A 2000, 104, 4247–4255. [Google Scholar] [CrossRef]
- Katsuki, H.; Momose, T. Observation of Rovibrational Dephasing of Molecules in Parahydrogen Crystals by Frequency Domain Spectroscopy. Phys. Rev. Lett. 2000, 84, 15, 3286–3289. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Panitchayangkoon, G.; Hayes, D.; Fransted, K.A.; Caram, J.R.; Harel, E.; Wen, J.; Blankenship, R.E.; Engel, G.S. Long-lived quantum coherence in photosynthetic complexes at physiological temperature. PNAS 2010, 107, 12766–12770. [Google Scholar] [CrossRef] [Green Version]
- Roberts, S.T.; Loparo, J.J.; Tokmakoff, A. Characterization of spectral diffusion from two-dimensional line shapes. J. Chem. Phys. 2006, 125, 084502. [Google Scholar] [CrossRef]
- Moca, R.; Meech, S.R.; Heisler, I.A. Two-Dimensional Electronic Spectroscopy of Chlorophyll a: Solvent Dependent Spectral Evolution. J. Phys. Chem. B. 2015, 119, 8623–8630. [Google Scholar] [CrossRef] [Green Version]
- Šanda, F.; Perlík, V.; Lincoln, C.N.; Hauer, J. Center Line Slope Analysis in Two-Dimensional Electronic Spectroscopy. J. Phys. Chem. A. 2015, 119, 10893–10909. [Google Scholar] [CrossRef] [Green Version]
- Hamm, P.; Lim, M.; Hochstrasser, R.M. Non-Markovian Dynamics of the Vibrations of Ions in Water from Femtosecond Infrared Three-Pulse Photon Echoes. Phys. Rev. Lett. 1998, 24, 5326–5329. [Google Scholar] [CrossRef]
- Asbury, J.B.; Steinel, T.; Stromberg, C.; Corcelli, S.A.; Lawrence, C.P.; Skinner, J.L.; Fayer, M.D. Water Dynamics: Vibrational Echo Correlation Spectroscopy and Comparison to Molecular Dynamics Simulations. J. Phys. Chem. A 2004, 108, 1107–1119. [Google Scholar] [CrossRef]
- Fecko, C.J.; Loparo, J.J.; Roberts, S.T.; Tokmakoff, A. Local hydrogen bonding dynamics and collective reorganization in water: Ultrafast infrared spectroscopy of HOD/D2O. J. Chem. Phys. 2005, 122, 054506. [Google Scholar] [CrossRef]
- Zanni, M.T.; Asplund, M.C.; Hochstrasser, R.M. Two-dimensional heterodyned and stimulated infrared photon echoes of Nmethylacetamide-D. J. Chem. Phys. 2001, 114, 4579. [Google Scholar] [CrossRef]
- De Flores, L.P.; Nicodemus, R.A.; Tokmakoff, A. Two-dimensional Fourier transform spectroscopy in the pump–probe geometry. Opt. Lett. 2007, 32, 2966–2968. [Google Scholar] [CrossRef] [PubMed]
- Shim, S.-H.; Strasfeld, D.B.; Ling, Y.L.; Zanni, M.T. Automated 2D IR spectroscopy using a mid-IR pulse shaper and application of this technology to the human islet amyloid polypeptide. Proc. Natl. Acad. Sci. USA 2007, 104, 14197–14202. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shim, S.-H.; Zanni, M.T. How to turn your pump–probe instrument into a multidimensional spectrometer: 2D IR and Vis spectroscopies via pulse shaping. Phys. Chem. Chem. Phys. 2009, 11, 748–761. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Réhault, J.; Maiuri, M.; Oriana, A.; Cerullo, G. Two-dimensional electronic spectroscopy with birefringent wedges. Rev. Sci. Instrum. 2014, 85, 123107. [Google Scholar] [CrossRef] [PubMed]
- Zavelani, M.; Cerullo, G.; De Silvestri, S.; Gallmann, L.; Matuschek, N.; Steinmeyer, G.; Keller, U.; Angelow, G.; Scheuer, V.; Tschudi, T. Pulse compression over a 170-thz bandwidth in the visible by use of only chirped mirrors. Opt. Lett. 2001, 26, 1155–1157. [Google Scholar] [CrossRef]
- Brida, D.; Manzoni, C.; Cerullo, G. Phase-locked pulses for two-dimensional spectroscopy by a birefringent delay line. Optics Lett. 2012, 37, 3027–3029. [Google Scholar] [CrossRef]
- Wustholz, K.L.; Bott, E.D.; Kahr, B.; Reid, P.J. Memory and Spectral Diffusion in Single-Molecule Emission. J. Phys. Chem. C 2008, 112, 7877–7885. [Google Scholar] [CrossRef]
- Osad’ko, I.S.; Yershova, L.B. Exponential and logarithmic spectral diffusion in single molecule fluorescence. J. Chem. Phys. 2000, 112, 9645–9654. [Google Scholar] [CrossRef]






| Temperature (K) | γ (meV) | σ (meV) | S0R (10−5) | S0NR (10−5) |
|---|---|---|---|---|
| 86 | 7 | 18.7 | 1.8 | 1.4 |
| 140 | 8.8 | 24 | 2.46 | 1.53 |
| 180 | 9.6 | 19.2 | 1.87 | 1.14 |
| 240 | 10.8 | 20.2 | 2.39 | 0.7 |
| 295 | 12.4 | 21.8 | 2.92 | 1.43 |
| Temperature (K) | a (10−3) | τp (fs) | b (10−3) | τ (fs) | ωc (cm−1) | c (10−3) |
|---|---|---|---|---|---|---|
| 86 | 6 ± 2 | 35 ± 5 | 1.1 ± 0.3 | 260 ± 35 | 540 | 3 ± 1 |
| 295 | 5 ± 2 | 35 ± 5 | 1.1 ± 0.4 | 53 ± 4 | 540 | 1.1 ± 0.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Russo, M.; McGhee, K.E.; Virgili, T.; Lidzey, D.G.; Cerullo, G.; Maiuri, M. Dephasing Processes in the Molecular Dye Lumogen-F Orange Characterized by Two-Dimensional Electronic Spectroscopy. Molecules 2022, 27, 7095. https://doi.org/10.3390/molecules27207095
Russo M, McGhee KE, Virgili T, Lidzey DG, Cerullo G, Maiuri M. Dephasing Processes in the Molecular Dye Lumogen-F Orange Characterized by Two-Dimensional Electronic Spectroscopy. Molecules. 2022; 27(20):7095. https://doi.org/10.3390/molecules27207095
Chicago/Turabian StyleRusso, Mattia, Kirsty E. McGhee, Tersilla Virgili, David G. Lidzey, Giulio Cerullo, and Margherita Maiuri. 2022. "Dephasing Processes in the Molecular Dye Lumogen-F Orange Characterized by Two-Dimensional Electronic Spectroscopy" Molecules 27, no. 20: 7095. https://doi.org/10.3390/molecules27207095
APA StyleRusso, M., McGhee, K. E., Virgili, T., Lidzey, D. G., Cerullo, G., & Maiuri, M. (2022). Dephasing Processes in the Molecular Dye Lumogen-F Orange Characterized by Two-Dimensional Electronic Spectroscopy. Molecules, 27(20), 7095. https://doi.org/10.3390/molecules27207095