Preclinical MRI Using Hyperpolarized 129Xe
Abstract
1. Introduction
2. Gas Dynamics during the Breathing Cycle
3. Diffusive Dynamics in the Lung Parenchyma
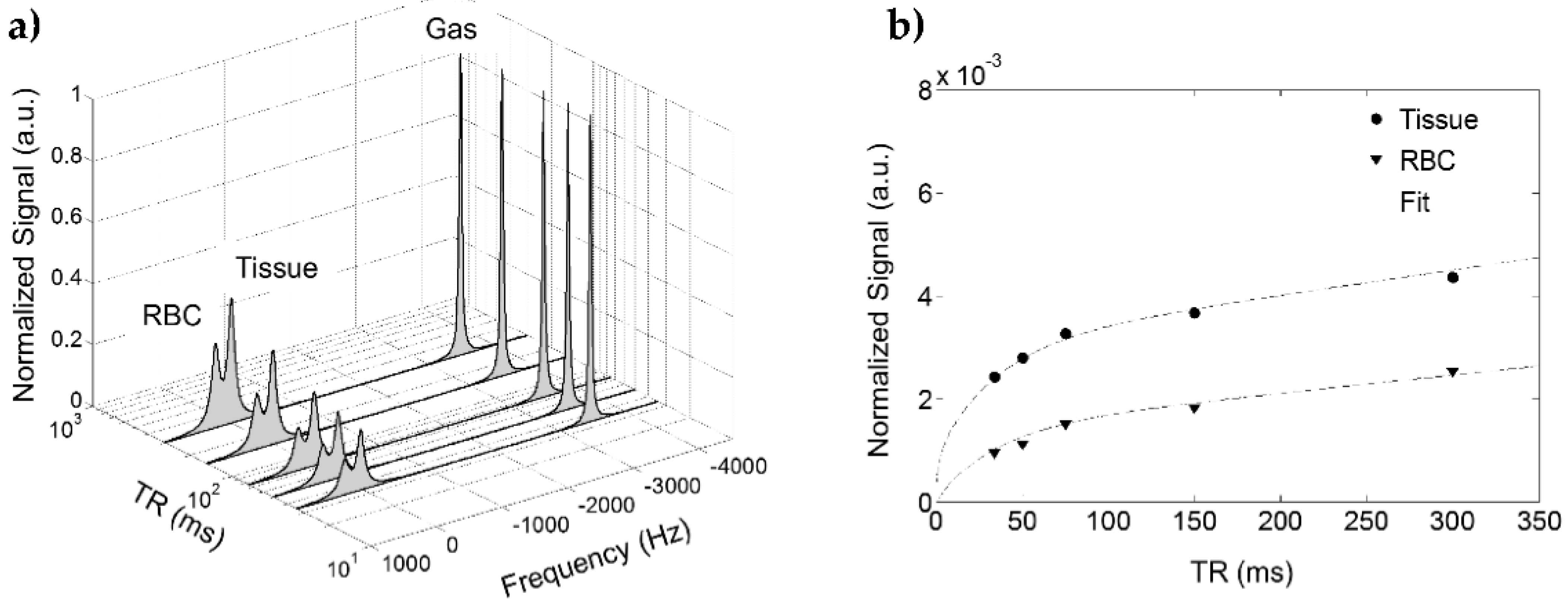
4. Spectra and Compartments
5. Quantification of Gas Dissolution and Uptake
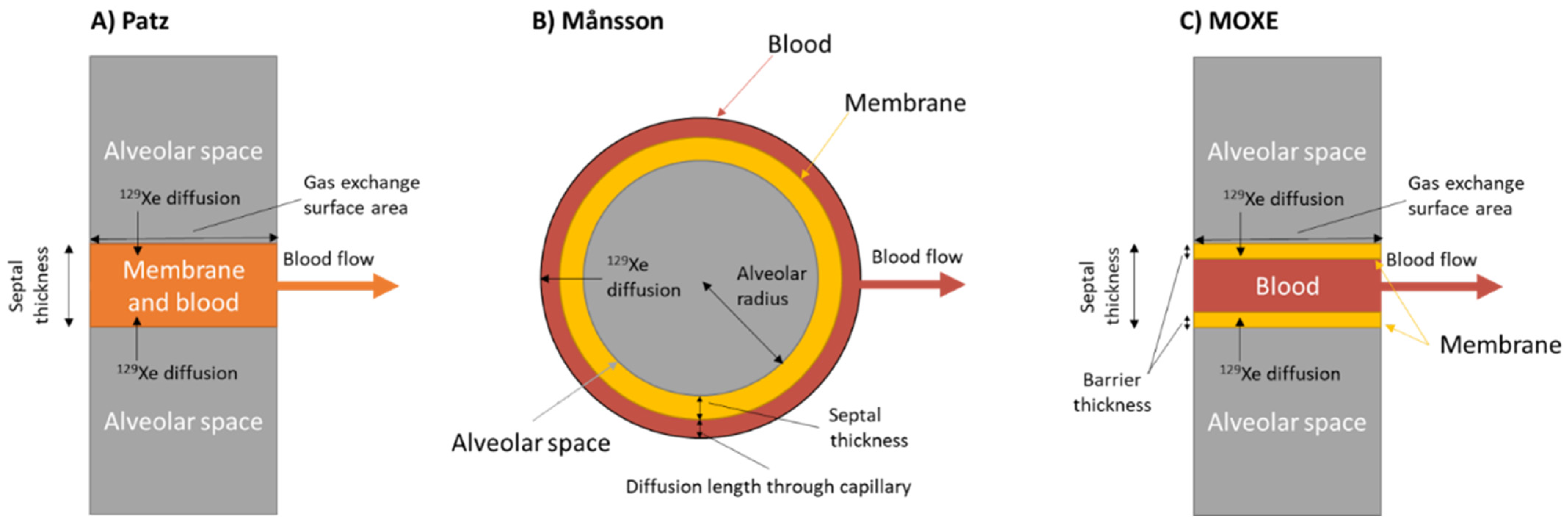
5.1. Models of Gas Exchange
5.2. Design Considerations
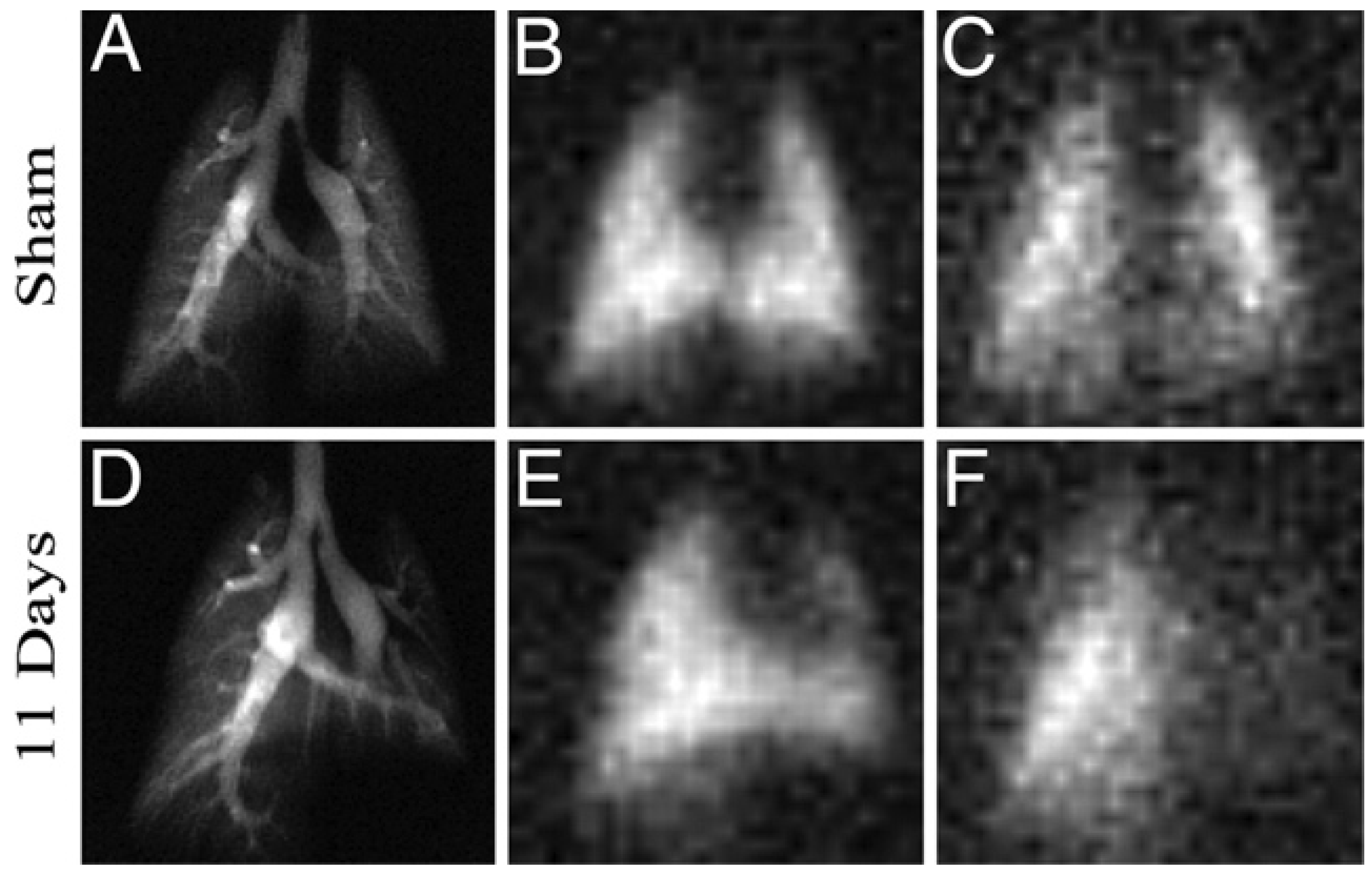
5.3. Applications of Gas Exchange MR in Animals
6. “Xenon Polarization Transfer Contrast” (XTC)-Based Techniques
6.1. Introduction
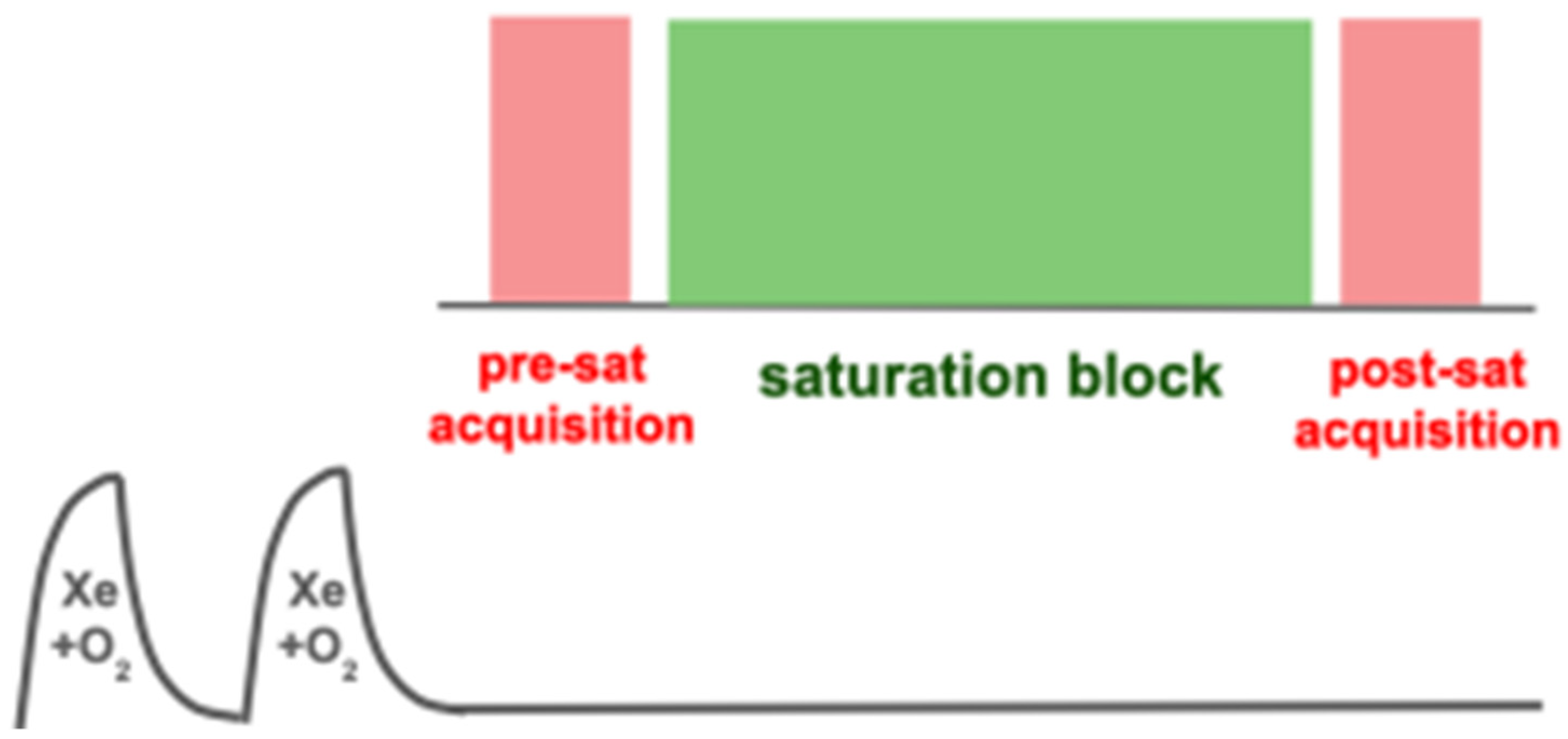
6.2. Saturation Schemes
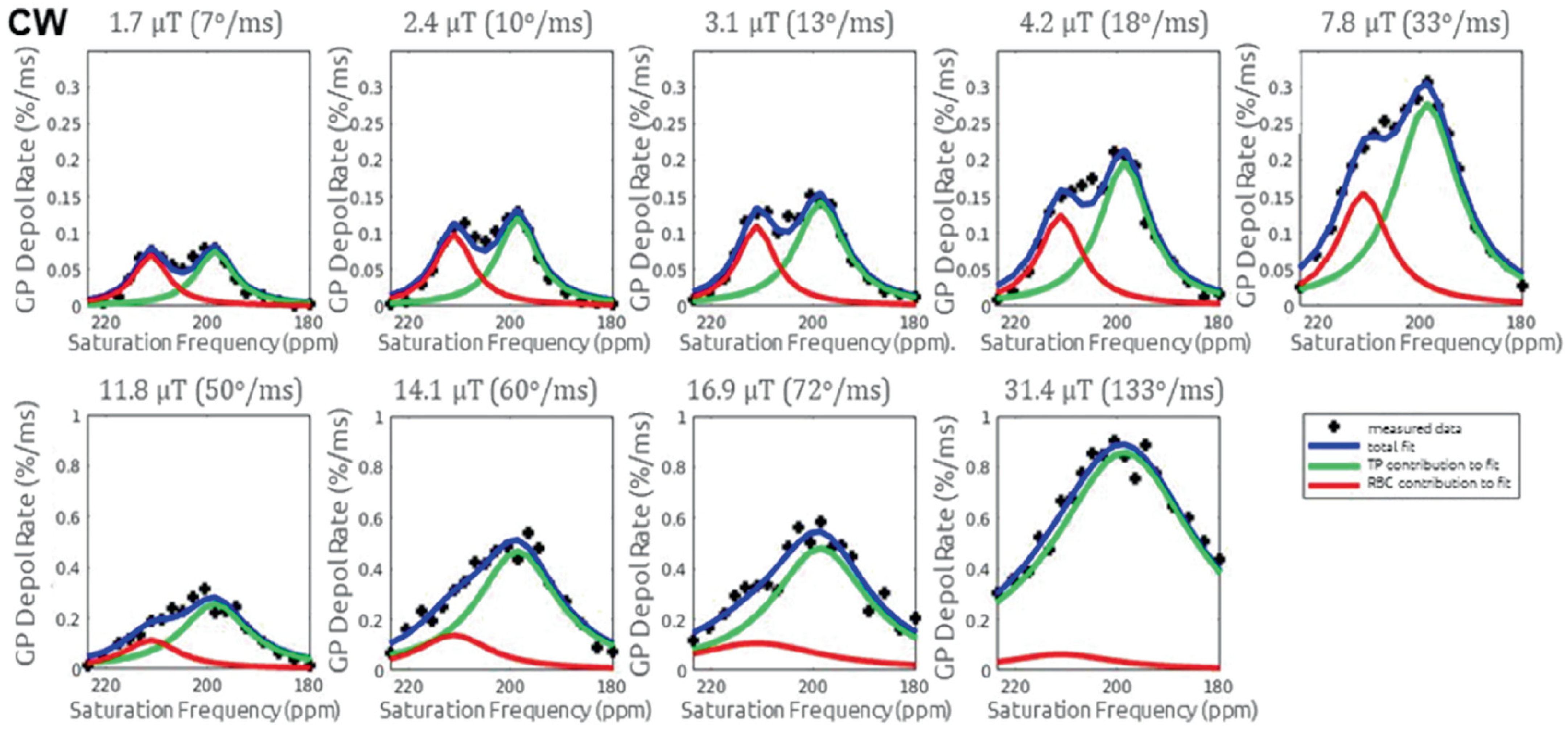
6.3. Interpretation of the XTC Effect
7. Whole Body and Brain Imaging
7.1. Whole-Body Gas Uptake and Distribution
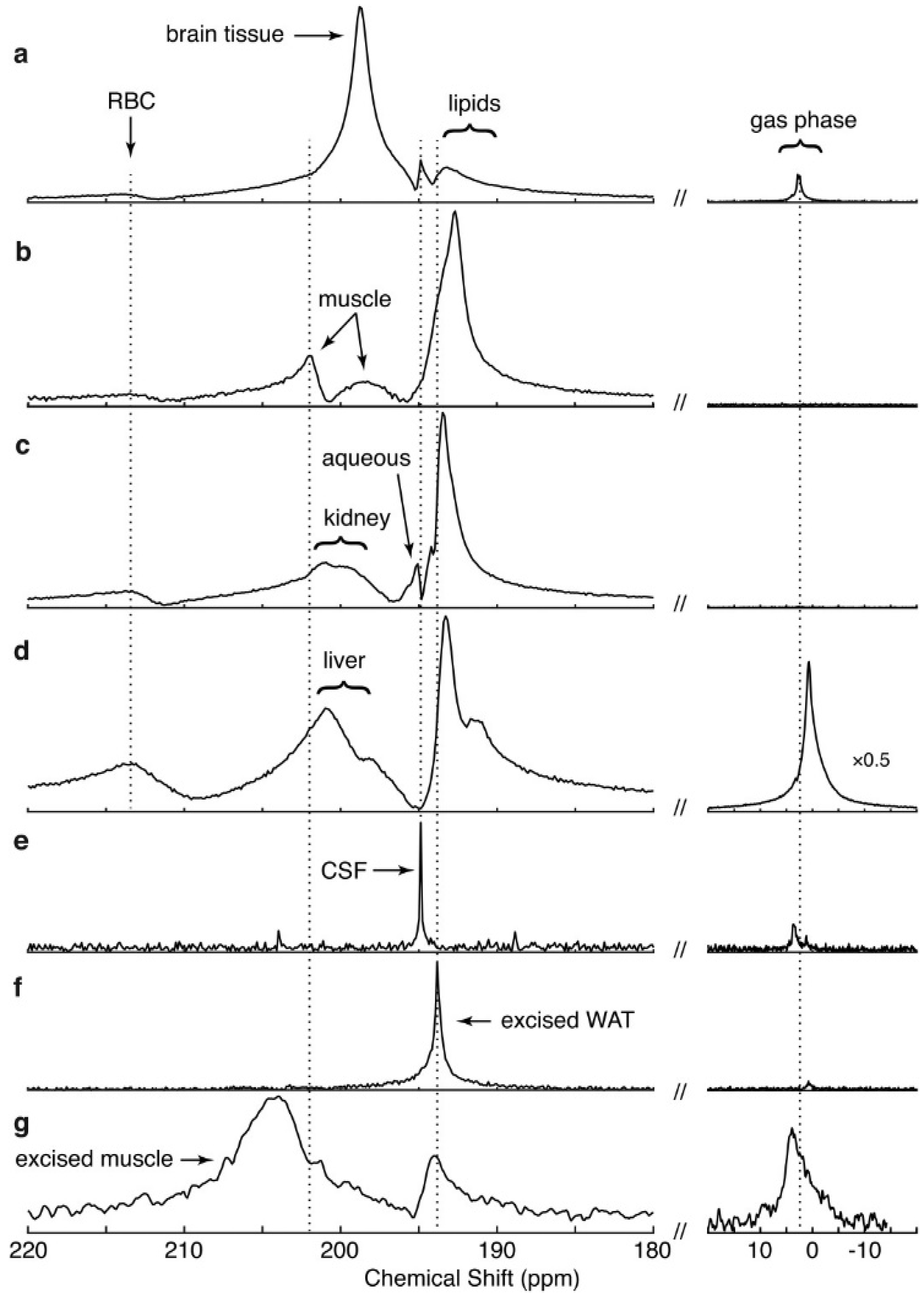
7.2. Imaging of HXe in the Rat Brain
7.3. HXe Signal Uptake in the Brain
7.4. Functional HXe Brain MRI
7.5. Hyperpolarized Chemical Exchange Saturation Transfer (HyperCEST) Imaging
8. Practical Imaging Considerations
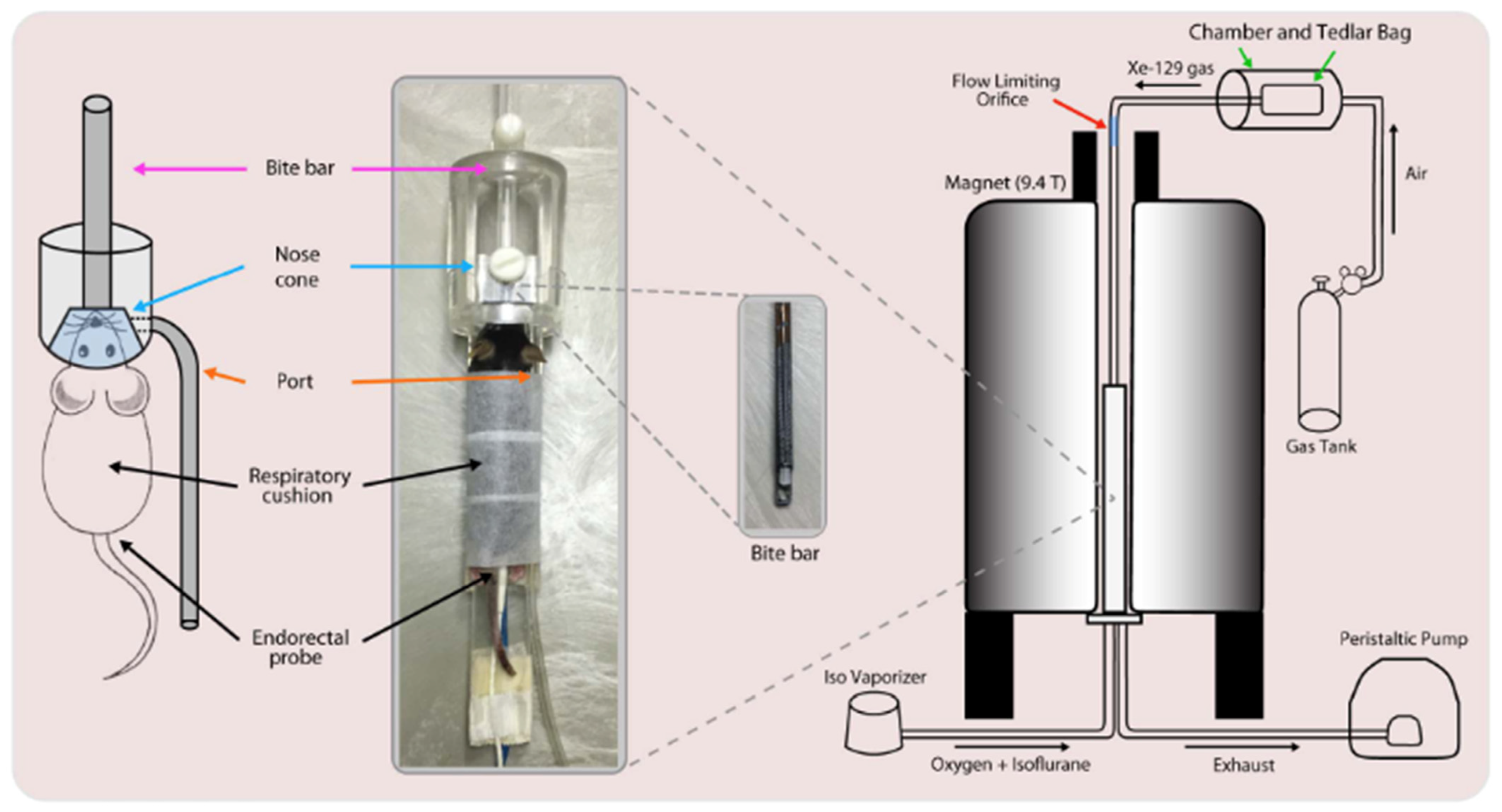
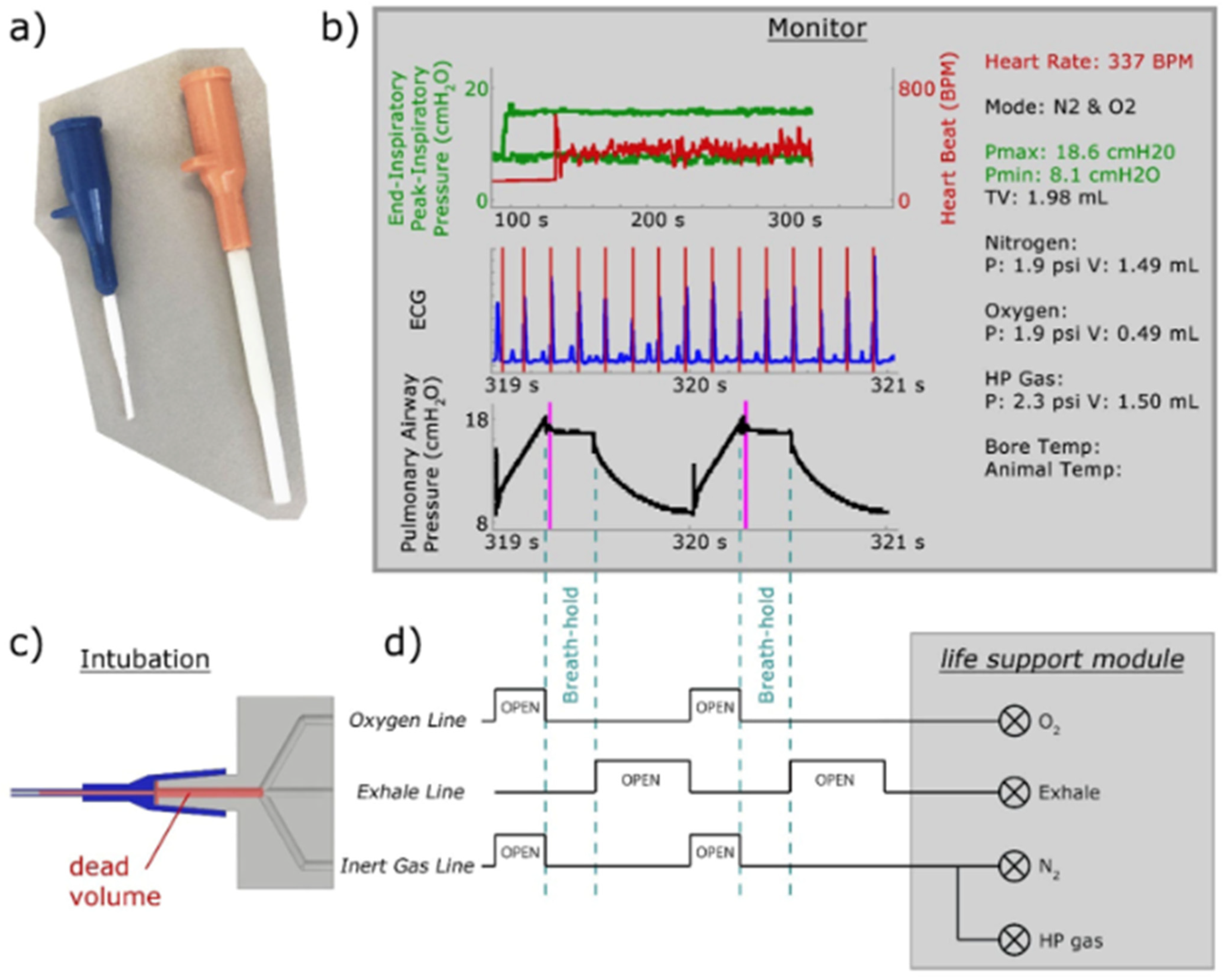
8.1. Gas Delivery and Animal Handling
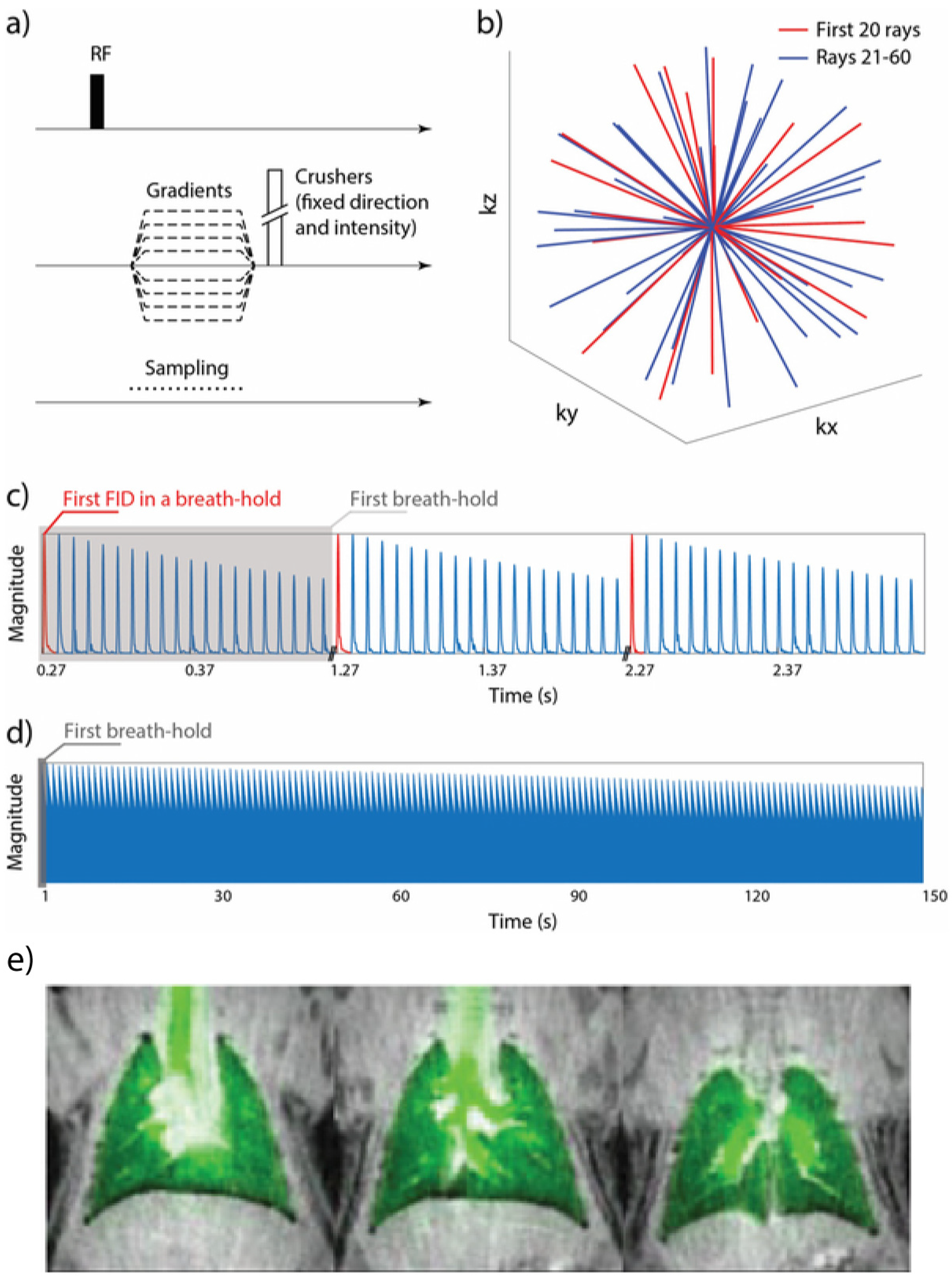
8.2. Imaging Considerations
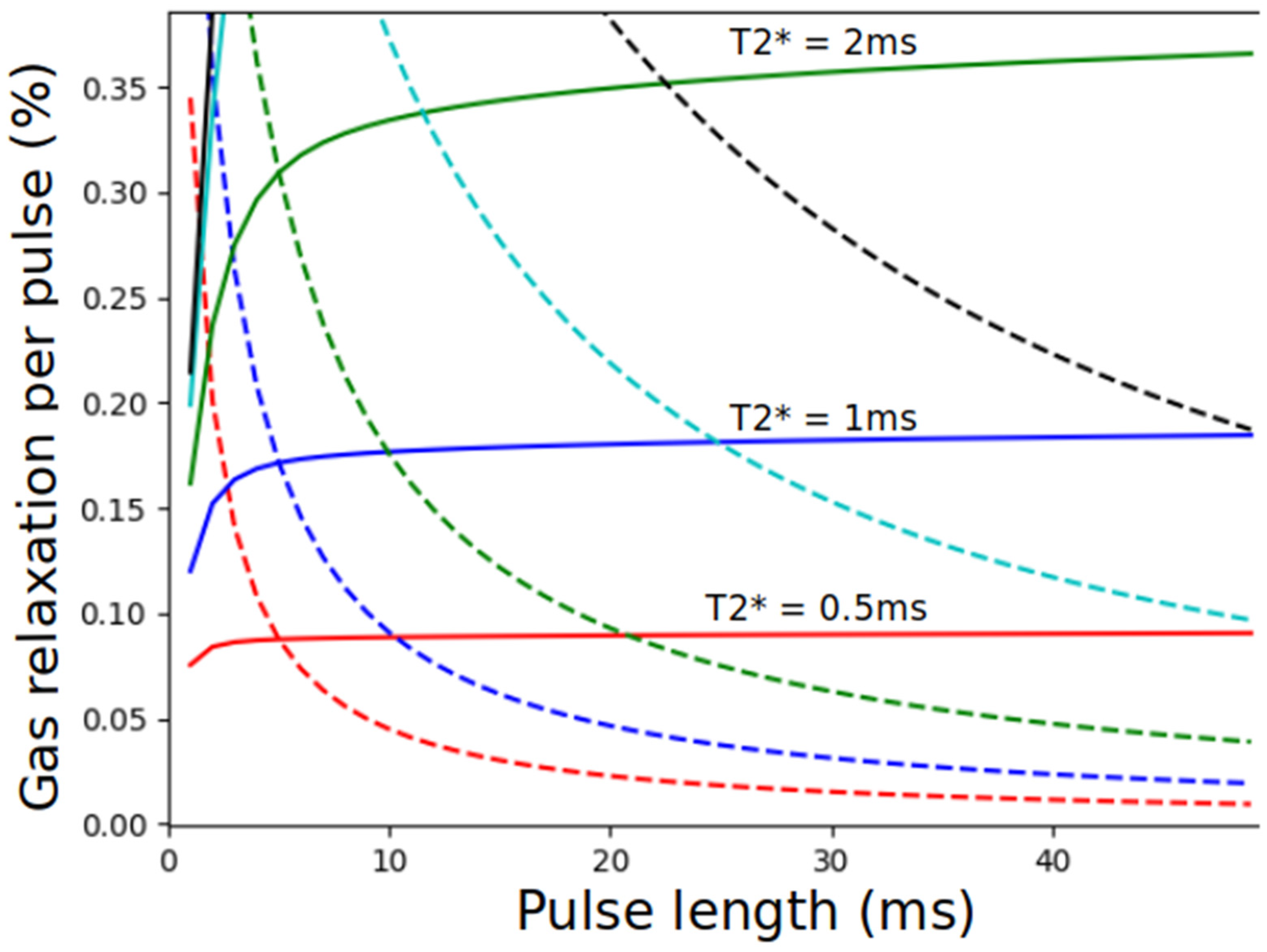
8.2.1. Magnetization Density
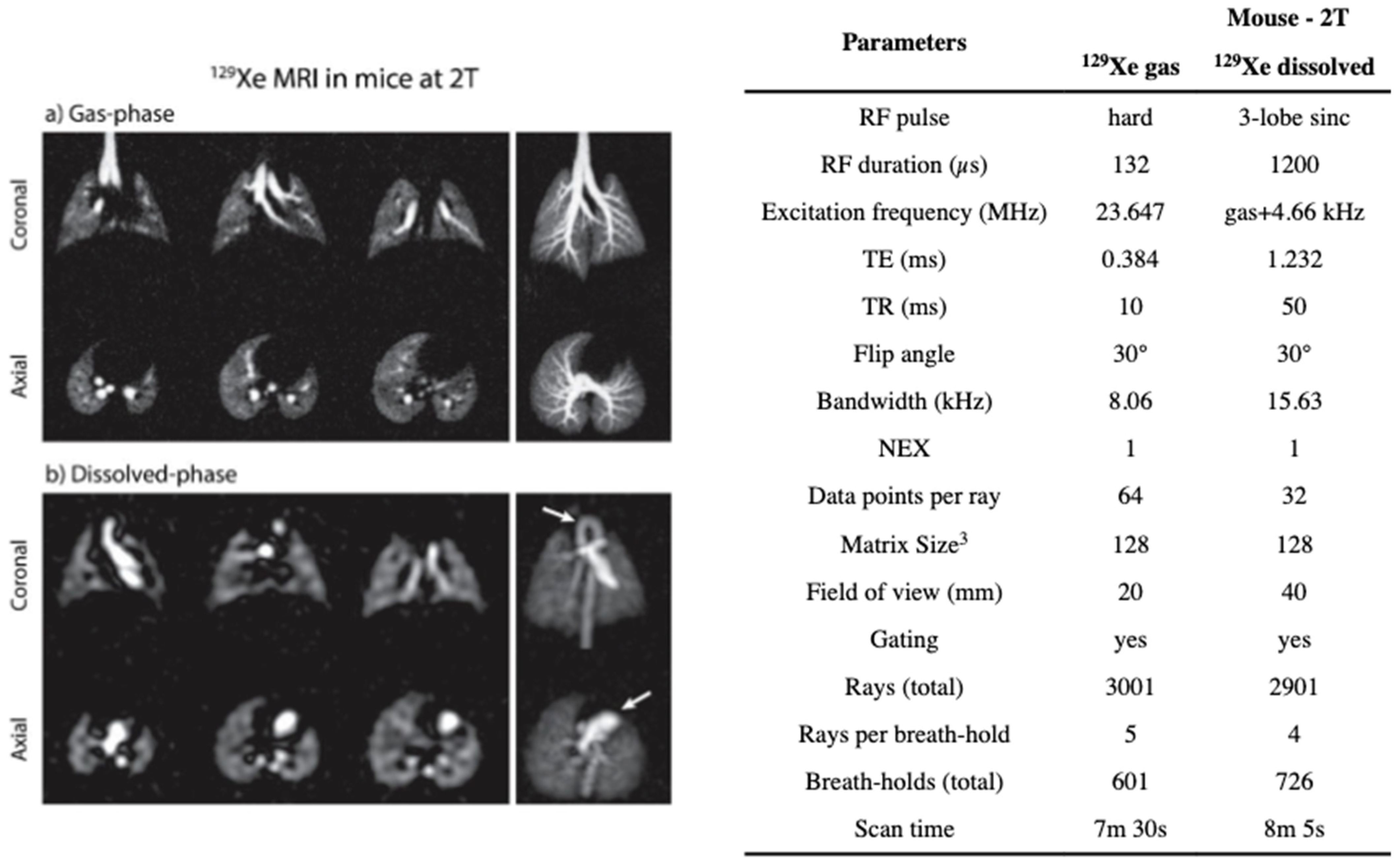
8.2.2. Imaging the Gas-Phase
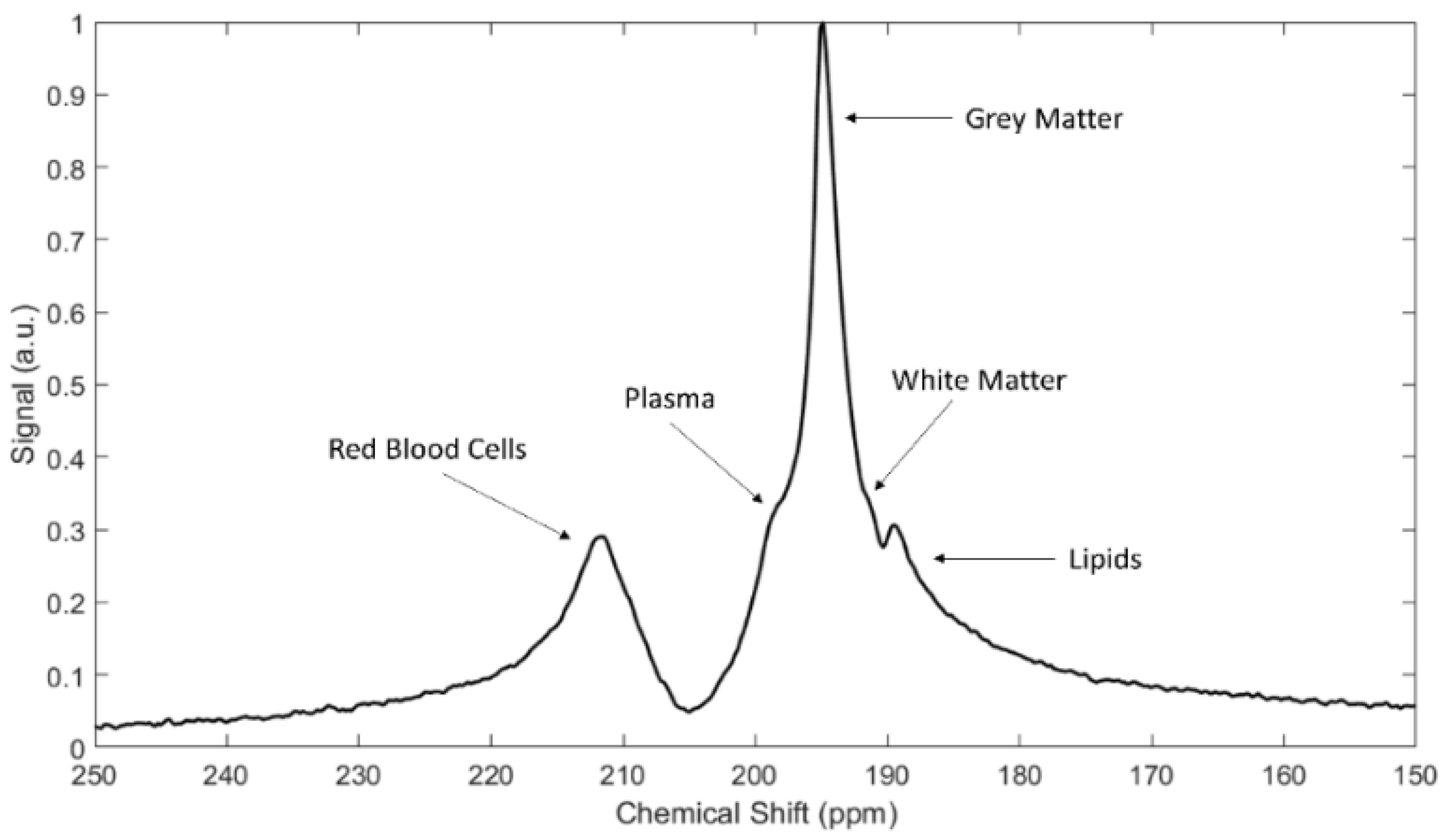
8.2.3. Imaging the Dissolved-Phase
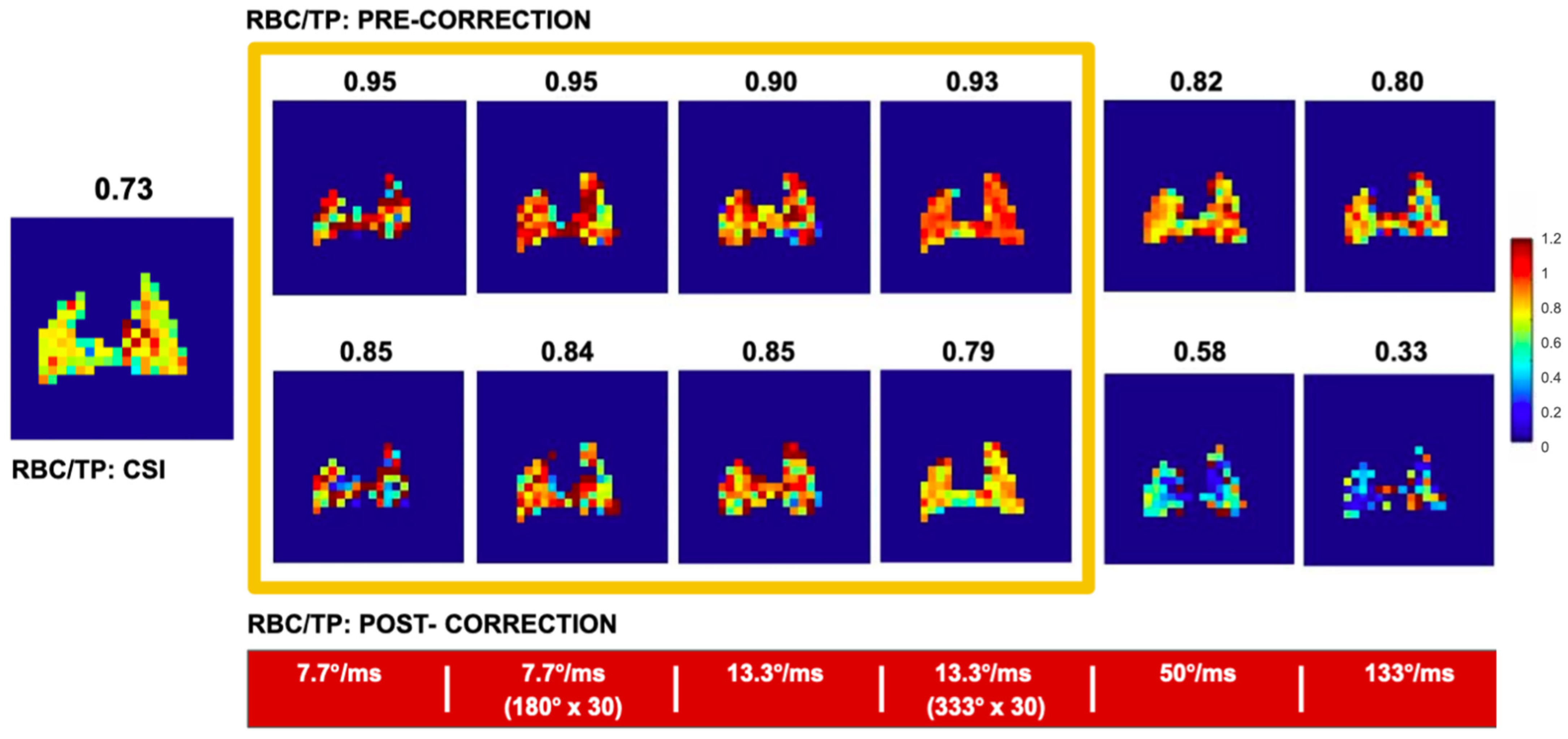
8.2.4. Separating the Dissolved Phase Image into Membrane and RBC Compartments
9. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Carvalho, A.R.; Zin, W.A. Respiratory System Dynamical Mechanical Properties: Modeling in Time and Frequency Domain. Biophys. Rev. 2011, 3, 71. [Google Scholar] [CrossRef] [PubMed]
- Bates, J.H.T.; Maksym, G.N.; Navajas, D.; Suki, B. Lung Tissue Rheology and 1/f Noise. Ann. Biomed. Eng. 1994, 22, 674–681. [Google Scholar] [CrossRef] [PubMed]
- Alvarado, A.; Arce, I. Metabolic Functions of the Lung, Disorders and Associated Pathologies. J. Clin. Med. Res. 2016, 8, 689–700. [Google Scholar] [CrossRef] [PubMed]
- de Wet, C.; Moss, J. METABOLIC FUNCTIONS OF THE LUNG. Anesthesiol. Clin. N. Am. 1998, 16, 181–199. [Google Scholar] [CrossRef]
- Labaki, W.W.; Martinez, C.H.; Martinez, F.J.; Galbán, C.J.; Ross, B.D.; Washko, G.R.; Barr, R.G.; Regan, E.A.; Coxson, H.O.; Hoffman, E.A.; et al. The Role of Chest Computed Tomography in the Evaluation and Management of the Patient with Chronic Obstructive Pulmonary Disease. Am. J. Respir. Crit. Care Med. 2017, 196, 1372–1379. [Google Scholar] [CrossRef]
- Ostridge, K.; Wilkinson, T.M.A. Present and Future Utility of Computed Tomography Scanning in the Assessment and Management of COPD. Eur. Respir. J. 2016, 48, 216–228. [Google Scholar] [CrossRef]
- Kakavas, S.; Kotsiou, O.S.; Perlikos, F.; Mermiri, M.; Mavrovounis, G.; Gourgoulianis, K.; Pantazopoulos, I. Pulmonary Function Testing in COPD: Looking beyond the Curtain of FEV1. npj Prim. Care Respir. Med. 2021, 31, 1–11. [Google Scholar] [CrossRef]
- Taylor-Robinson, D.; Whitehead, M.; Diderichsen, F.; Olesen, H.V.; Pressler, T.; Smyth, R.L.; Diggle, P. Understanding the Natural Progression in %FEV1 Decline in Patients with Cystic Fibrosis: A Longitudinal Study. Thorax 2012, 67, 860–866. [Google Scholar] [CrossRef]
- Siafakas, N.; Bizymi, N.; Mathioudakis, A.; Corlateanu, A. EARLY versus MILD Chronic Obstructive Pulmonary Disease (COPD). Respir. Med. 2018, 140, 127–131. [Google Scholar] [CrossRef]
- Ruparel, M.; Quaife, S.L.; Dickson, J.L.; Horst, C.; Tisi, S.; Hall, H.; Taylor, M.N.; Ahmed, A.; Shaw, P.J.; Burke, S.; et al. Prevalence, Symptom Burden, and Underdiagnosis of Chronic Obstructive Pulmonary Disease in a Lung Cancer Screening Cohort. Ann. ATS 2020, 17, 869–878. [Google Scholar] [CrossRef]
- Boventi, M.; Mauri, M.; Simonutti, R. 129Xe: A Wide-Ranging NMR Probe for Multiscale Structures. Appl. Sci. 2022, 12, 3152. [Google Scholar] [CrossRef]
- Hansen, A.L.; Lundström, P.; Velyvis, A.; Kay, L.E. Quantifying Millisecond Exchange Dynamics in Proteins by CPMG Relaxation Dispersion NMR Using Side-Chain 1H Probes. J. Am. Chem. Soc. 2012, 134, 3178–3189. [Google Scholar] [CrossRef]
- Ramey, K.C.; Louick, D.J.; Whitehurst, P.W.; Wise, W.B.; Mukherjee, R.; Moriarty, R.M. A Line Width Method for Determining Chemical Exchange Rates from NMR Spectra. Org. Magn. Reson. 1971, 3, 201–216. [Google Scholar] [CrossRef]
- Kleckner, I.R.; Foster, M.P. An Introduction to NMR-Based Approaches for Measuring Protein Dynamics. Biochim. Biophys. Acta 2011, 1814, 942–968. [Google Scholar] [CrossRef] [PubMed]
- Petersson, J.; Glenny, R.W. Gas Exchange and Ventilation–Perfusion Relationships in the Lung. Eur. Respir. J. 2014, 44, 1023–1041. [Google Scholar] [CrossRef]
- van Zijl, P.C.M.; Yadav, N.N. Chemical Exchange Saturation Transfer (CEST): What Is in a Name and What Isn’t? Magn Reson Med. 2011, 65, 927–948. [Google Scholar] [CrossRef] [PubMed]
- Sherry, A.D.; Woods, M. Chemical Exchange Saturation Transfer Contrast Agents for Magnetic Resonance Imaging. Annu. Rev. Biomed. Eng. 2008, 10, 391–411. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; van Zijl, P.C.M. Chemical Exchange Saturation Transfer Imaging and Spectroscopy. Prog. Nucl. Magn. Reson. Spectrosc. 2006, 48, 109–136. [Google Scholar] [CrossRef]
- Virgincar, R.S. Preclinical Hyperpolarized 129Xe MRI: Development, Applications and Dissemination. Ph.D. Thesis, Duke University, Durham, NC, USA, 2018. [Google Scholar]
- Virgincar, R.S.; Nouls, J.C.; Wang, Z.; Degan, S.; Qi, Y.; Xiong, X.; Rajagopal, S.; Driehuys, B. Quantitative 129Xe MRI Detects Early Impairment of Gas-Exchange in a Rat Model of Pulmonary Hypertension. Sci Rep. 2020, 10, 7385. [Google Scholar] [CrossRef]
- Rayment, J.H.; Couch, M.J.; McDonald, N.; Kanhere, N.; Manson, D.; Santyr, G.; Ratjen, F. Hyperpolarised 129Xe Magnetic Resonance Imaging to Monitor Treatment Response in Children with Cystic Fibrosis. Eur. Respir. J. 2019, 53, 1802188. [Google Scholar] [CrossRef] [PubMed]
- Svenningsen, S.; Kirby, M.; Starr, D.; Leary, D.; Wheatley, A.; Maksym, G.N.; McCormack, D.G.; Parraga, G. Hyperpolarized 3He and 129Xe MRI: Differences in Asthma before Bronchodilation. J. Magn. Reson. Imaging 2013, 38, 1521–1530. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; He, M.; Bier, E.; Rankine, L.; Schrank, G.; Rajagopal, S.; Huang, Y.-C.; Kelsey, C.; Womack, S.; Mammarappallil, J.; et al. Hyperpolarized 129Xe Gas Transfer MRI: The Transition from 1.5T to 3T. Magn. Reson. Med. 2018, 80, 2374–2383. [Google Scholar] [CrossRef] [PubMed]
- Thomen, R.P.; Walkup, L.L.; Roach, D.J.; Cleveland, Z.I.; Clancy, J.P.; Woods, J.C. Hyperpolarized 129Xe for Investigation of Mild Cystic Fibrosis Lung Disease in Pediatric Patients. J. Cyst. Fibros. 2017, 16, 275–282. [Google Scholar] [CrossRef] [PubMed]
- Jameson, C.J.; Jameson, A.K.; Hwang, J.K. Nuclear Spin Relaxation by Intermolecular Magnetic Dipole Coupling in the Gas Phase. 129Xe in Oxygen. J. Chem. Phys. 1988, 89, 4074–4081. [Google Scholar] [CrossRef]
- Deninger, A.J.; Månsson, S.; Petersson, J.S.; Pettersson, G.; Magnusson, P.; Svensson, J.; Fridlund, B.; Hansson, G.; Erjefeldt, I.; Wollmer, P.; et al. Quantitative Measurement of Regional Lung Ventilation Using 3He MRI. Magn. Reson. Med. 2002, 48, 223–232. [Google Scholar] [CrossRef]
- Hodono, S.; Shimokawa, A.; Stewart, N.J.; Yamauchi, Y.; Nishimori, R.; Yamane, M.; Imai, H.; Fujiwara, H.; Kimura, A. Ethyl Pyruvate Improves Pulmonary Function in Mice with Bleomycin-Induced Lung Injury as Monitored with Hyperpolarized 129Xe MR Imaging. Magn. Reson. Med. Sci. 2018, 17, 331. [Google Scholar] [CrossRef]
- Horn, F.C.; Deppe, M.H.; Marshall, H.; Parra-Robles, J.; Wild, J.M. Quantification of Regional Fractional Ventilation in Human Subjects by Measurement of Hyperpolarized 3He Washout with 2D and 3D MRI. J. Appl. Physiol. 2014, 116, 129–139. [Google Scholar] [CrossRef]
- Santyr, G.; Kanhere, N.; Morgado, F.; Rayment, J.H.; Ratjen, F.; Couch, M.J. Hyperpolarized Gas Magnetic Resonance Imaging of Pediatric Cystic Fibrosis Lung Disease. Acad. Radiol. 2019, 26, 344–354. [Google Scholar] [CrossRef]
- Hyperpolarized and Inert Gas MRI: From Technology to Application in Research and Medicine, 1st ed.; Albert, M.S., Hane, F., Eds.; Academic Press: London, UK; San Diego, CA, USA, 2016; ISBN 978-0-12-803675-4. [Google Scholar]
- Couch, M.J.; Ouriadov, A.; Santyr, G.E. Regional Ventilation Mapping of the Rat Lung Using Hyperpolarized 129Xe Magnetic Resonance Imaging. Magn. Reson. Med. 2012, 68, 1623–1631. [Google Scholar] [CrossRef]
- West, J.B.; Dollery, C.T. Distribution of Blood Flow and Ventilation-Perfusion Ratio in the Lung, Measured with Radioactive Carbon Dioxide. J. Appl. Physiol. 1960, 15, 405–410. [Google Scholar] [CrossRef]
- West, J.B.; Dollery, C.T.; Naimark, A. Distribution of Blood Flow in Isolated Lung; Relation to Vascular and Alveolar Pressures. J. Appl. Physiol. 1964, 19, 713–724. [Google Scholar] [CrossRef] [PubMed]
- Engel, L.A. Gas Mixing within the Acinus of the Lung. J. Appl. Physiol. 1983, 54, 609–618. [Google Scholar] [CrossRef] [PubMed]
- Parameswaran, H.; Bartolák-Suki, E.; Hamakawa, H.; Majumdar, A.; Allen, P.G.; Suki, B. Three-Dimensional Measurement of Alveolar Airspace Volumes in Normal and Emphysematous Lungs Using Micro-CT. J. Appl. Physiol. (Bethesda, Md.: 1985) 2009, 107, 583–592. [Google Scholar] [CrossRef] [PubMed]
- Ochs, M.; Nyengaard, J.R.; Jung, A.; Knudsen, L.; Voigt, M.; Wahlers, T.; Richter, J.; Gundersen, H.J.G. The Number of Alveoli in the Human Lung. Am. J. Respir. Crit. Care Med. 2012, 169, 120–124. [Google Scholar] [CrossRef]
- Watts, H. Diffusion in Multicomponent Gaseous Mixtures. Can J. Chem. 1964, 43, 431–435. [Google Scholar] [CrossRef]
- Yablonskiy, D.A.; Sukstanskii, A.I.; Leawoods, J.L.; Gierada, D.S.; Bretthorst, G.T.; Lefrak, S.S.; Cooper, J.; Conaradi, M.S. Quantitative in Vivo Assessment of Lung Microstructure at the Alveolar Level with Hyperpolarized 3He Diffusion MRI. Proc. Natl. Acad. Sci. USA 2002, 99, 3111–3116. [Google Scholar] [CrossRef]
- Mayer, O.; Campbell, R.; Cahill, P.; Redding, G. Thoracic Insufficiency Syndrome. Curr. Probl. Pediatr. Adolesc. Health Care 2016, 46, 72–97. [Google Scholar] [CrossRef]
- Halaweish, A.F.; Hoffman, E.A.; Thedens, D.R.; Fuld, M.K.; Sieren, J.P.; van Beek, E.J.R. Effect of Lung Inflation Level on Hyperpolarized 3He Apparent Diffusion Coefficient Measurements in Never-Smokers. Radiology 2013, 268, 572–580. [Google Scholar] [CrossRef][Green Version]
- Mata, J.; Altes, T.; Cai, J.; Ruppert, K.; Mitzner, W.; Hagspiel, K.D.; Patel, B.; Salerno, M.; Brookeman, J.; de Lange, E.E.; et al. Evaluation of Emphysema Severity and Progression in a Rabbit Model: Comparison of Hyperpolarized 3He and 129Xe Diffusion MRI with Lung Morphometry. J. Appl. Physiol. (Bethesda, Md.: 1985) 2007, 102, 1273–1280. [Google Scholar] [CrossRef]
- Wang, K.; Pan, T.; Yang, H.; Ruan, W.; Zhong, J.; Wu, G.; Zhou, X. Assessment of Pulmonary Microstructural Changes by Hyperpolarized 129Xe Diffusion-Weighted Imaging in an Elastase-Instilled Rat Model of Emphysema. J. Thorac. Dis. 2017, 9, 2572–2578. [Google Scholar] [CrossRef]
- Cereda, M.; Emami, K.; Kadlecek, S.; Xin, Y.; Mongkolwisetwara, P.; Profka, H.; Barulic, A.; Pickup, S.; Månsson, S.; Wollmer, P.; et al. Quantitative Imaging of Alveolar Recruitment with Hyperpolarized Gas MRI during Mechanical Ventilation. J. Appl. Physiol. 2011, 110, 499–511. [Google Scholar] [CrossRef] [PubMed]
- Sahetya, S.K.; Goligher, E.C.; Brower, R.G. Fifty Years of Research in ARDS. Setting Positive End-Expiratory Pressure in Acute Respiratory Distress Syndrome. Am. J. Respir. Crit. Care Med. 2017, 195, 1429–1438. [Google Scholar] [CrossRef] [PubMed]
- Komlosi, P.; Altes, T.A.; Qing, K.; Mooney, K.E.; Miller, G.W.; Mata, J.F.; de Lange, E.E.; Tobias, W.A.; Gordon, D.; Cates, J.; et al. Regional Anisotropy of Airspace Orientation in the Lung as Assessed with Hyperpolarized Helium-3 Diffusion MRI. J. Magn. Reson. Imaging: JMRI 2015, 42, 1777. [Google Scholar] [CrossRef] [PubMed]
- Boudreau, M.; Xu, X.; Santyr, G.E. Measurement of 129Xe Gas Apparent Diffusion Coefficient Anisotropy in an Elastase-Instilled Rat Model of Emphysema. Magn. Reson. Med. 2013, 69, 211–220. [Google Scholar] [CrossRef] [PubMed]
- Sukstanskii, A.L.; Yablonskiy, D.A. In Vivo Lung Morphometry with Hyperpolarized 3He Diffusion MRI. Theoretical Background. J. Magn. Reson. 2008, 190, 200–210. [Google Scholar] [CrossRef]
- Osmanagic, E.; Sukstanskii, A.L.; Quirk, J.D.; Woods, J.C.; Pierce, R.A.; Conradi, M.S.; Weibel, E.R.; Yablonskiy, D.A. Quantitative Assessment of Lung Microstructure in Healthy Mice Using an MR-Based 3He Lung Morphometry Technique. J. Appl. Physiol. 2010, 109, 1592. [Google Scholar] [CrossRef][Green Version]
- Ouriadov, A.; Farag, A.; Kirby, M.; McCormack, D.; Parraga, G.; Santyr, G. Lung Morphometry Using Hyperpolarized Xe-129 Apparent Diffusion Coefficient Anisotropy in Chronic Obstructive Pulmonary Disease. Magn. Reson. Med.: Off. J. Soc. Magn. Reson. Med./Soc. Magn. Reson. Med. 2013, 70, 1699–1706. [Google Scholar] [CrossRef]
- Lindenmaier, A.A. Hyperpolarized 129Xe Difussion Weighted MRI for Lung Morphometry of Bronchopulmonary Dysplasia. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 2022. [Google Scholar]
- Kallet, R.H.; Matthay, M.A. Hyperoxic Acute Lung Injury. Respir Care 2013, 58, 123–141. [Google Scholar] [CrossRef]
- Miller, K.W.; Reo, N.V.; Schoot Uiterkamp, A.J.; Stengle, D.P.; Stengle, T.R.; Williamson, K.L. Xenon NMR: Chemical Shifts of a General Anesthetic in Common Solvents, Proteins, and Membranes. Proc. Natl. Acad. Sci. USA 1981, 78, 4946–4949. [Google Scholar] [CrossRef]
- Antonacci, M.A.; Zhang, L.; Degan, S.; Erdmann, D.; Branca, R.T. Calibration of Methylene-Referenced Lipid-Dissolved Xenon Frequency for Absolute MR Temperature Measurements. Magn. Reson. Med. 2019, 81, 765–772. [Google Scholar] [CrossRef]
- Miller, J.B.; Walton, J.H.; Roland, C.M. NMR Chemical Shift of Xenon-129 Dissolved in Polymers. Macromolecules 1993, 26, 5602–5610. [Google Scholar] [CrossRef][Green Version]
- Roose, B.W.; Zemerov, S.D.; Dmochowski, I.J. Xenon-Protein Interactions: Characterization by X-Ray Crystallography and Hyper-CEST NMR. Methods Enzym. 2018, 602, 249–272. [Google Scholar] [CrossRef]
- Lepeshkevich, S.; Gilevich, S.; Parkhats, M.; Dzhagarov, B. Molecular Oxygen Migration through the Xenon Docking Sites of Human Hemoglobin in the R-State. Biochim. Et Biophys. Acta (BBA)—Proteins Proteom. 2016, 1864, 1110–1121. [Google Scholar] [CrossRef] [PubMed]
- Norquay, G.; Leung, G.; Stewart, N.J.; Wolber, J.; Wild, J.M. 129Xe Chemical Shift in Human Blood and Pulmonary Blood Oxygenation Measurement in Humans Using Hyperpolarized 129Xe NMR. Magn. Reson. Med. 2017, 77, 1399–1408. [Google Scholar] [CrossRef]
- Friedlander, Y.; Zanette, B.; Lindenmaier, A.A.; Fliss, J.; Li, D.; Emami, K.; Jankov, R.P.; Kassner, A.; Santyr, G. Effect of Inhaled Oxygen Concentration on 129Xe Chemical Shift of Red Blood Cells in Rat Lungs. Magn. Reson. Med. 2021, 86, 1187–1193. [Google Scholar] [CrossRef]
- Loza, L.A.; Kadlecek, S.J.; Pourfathi, M.; Hamedani, H.; Duncan, I.F.; Ruppert, K.; Rizi, R.R. Quantification of Ventilation and Gas Uptake in Free-Breathing Mice with Hyperpolarized 129Xe MRI. IEEE Trans Med. Imaging 2019, 38, 2081–2091. [Google Scholar] [CrossRef]
- Mugler, J.P.; Altes, T.A. Hyperpolarized 129Xe MRI of the Human Lung. J. Magn. Reson. Imaging 2013, 37, 313–331. [Google Scholar] [CrossRef]
- Qing, K.; Ruppert, K.; Jiang, Y.; Mata, J.F.; Miller, G.W.; Shim, Y.M.; Wang, C.; Ruset, I.C.; Hersman, F.W.; Altes, T.A.; et al. Regional Mapping of Gas Uptake by Blood and Tissue in the Human Lung Using Hyperpolarized Xenon-129 MRI. J. Magn. Reson. Imaging 2014, 39, 346–359. [Google Scholar] [CrossRef]
- Mammarappallil, J.G.; Rankine, L.; Chan, H.-F.; Weatherley, N.; Wild, J.; Driehuys, B. New Developments in Imaging Idiopathic Pulmonary Fibrosis with Hyperpolarized Xenon MRI. J. Thorac. Imaging 2019, 34, 136–150. [Google Scholar] [CrossRef]
- Niedbalski, P.J.; Cochran, A.S.; Akinyi, T.G.; Thomen, R.P.; Fugate, E.M.; Lindquist, D.M.; Pratt, R.G.; Cleveland, Z.I. Preclinical Hyperpolarized 129Xe MRI: Ventilation and T2* Mapping in Mouse Lungs at 7 T Using Multi-Echo Flyback UTE. NMR Biomed. 2020, 33, e4302. [Google Scholar] [CrossRef]
- Cleveland, Z.I.; Virgincar, R.S.; Qi, Y.; Robertson, S.H.; Degan, S.; Driehuys, B. 3D MR Imaging of Impaired Hyperpolarized 129Xe Uptake in a Rat Model of Pulmonary Fibrosis. NMR Biomed. 2014, 27, 1502–1514. [Google Scholar] [CrossRef] [PubMed]
- Zanette, B.; Stirrat, E.; Jelveh, S.; Hope, A.; Santyr, G. Detection of Regional Radiation-Induced Lung Injury Using Hyperpolarized 129Xe Chemical Shift Imaging in a Rat Model Involving Partial Lung Irradiation: Proof-of-Concept Demonstration. Adv Radiat. Oncol. 2017, 2, 475–484. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Driehuys, B.; Cofer, G.P.; Pollaro, J.; Mackel, J.B.; Hedlund, L.W.; Johnson, G.A. Imaging Alveolar–Capillary Gas Transfer Using Hyperpolarized 129Xe MRI. Proc. Natl. Acad. Sci. USA 2006, 103, 18278–18283. [Google Scholar] [CrossRef] [PubMed]
- Kershaw, J.; Nakamura, K.; Kondoh, Y.; Wakai, A.; Suzuki, N.; Kanno, I. Confirming the Existence of Five Peaks in 129Xe Rat Head Spectra. Magn. Reson. Med. 2007, 57, 791–797. [Google Scholar] [CrossRef] [PubMed]
- Albert, M.S.; Schepkin, V.D.; Budinger, T.F. Measurement of 129Xe T1 in Blood to Explore the Feasibility of Hyperpolarized 129Xe MRI. J. Comput. Assist. Tomogr. 1995, 19, 975–978. [Google Scholar] [CrossRef]
- Latour, L.L.; Svoboda, K.; Mitra, P.P.; Sotak, C.H. Time-Dependent Diffusion of Water in a Biological Model System. Proc. Natl. Acad. Sci. USA 1994, 91, 1229. [Google Scholar] [CrossRef]
- Mair, R.W.; Cory, D.G.; Peled, S.; Tseng, C.-H.; Patz, S.; Walsworth, R.L. Pulsed-Field-Gradient Measurements of Time-Dependent Gas Diffusion. J. Magn. Reson. 1998, 135, 478–486. [Google Scholar] [CrossRef]
- Mair, R.W.; Wong, G.P.; Hoffmann, D.; Hürlimann, M.D.; Patz, S.; Schwartz, L.M.; Walsworth, R.L. Probing Porous Media with Gas Diffusion NMR. Phys. Rev. Lett 1999, 83, 3324–3327. [Google Scholar] [CrossRef]
- Butler, J.P.; Mair, R.W.; Hoffmann, D.; Hrovat, M.I.; Rogers, R.A.; Topulos, G.P.; Walsworth, R.L.; Patz, S. Measuring Surface-Area-to-Volume Ratios in Soft Porous Materials Using Laser-Polarized Xenon Interphase Exchange Nuclear Magnetic Resonance. J. Phys. Condens. Matter: Inst. Phys. J. 2002, 14, L297–L304. [Google Scholar] [CrossRef]
- Ruppert, K.; Brookeman, J.R.; Hagspiel, K.D.; Driehuys, B.; Mugler III, J.P. NMR of Hyperpolarized 129Xe in the Canine Chest: Spectral Dynamics during a Breath-Hold. NMR Biomed. 2000, 13, 220–228. [Google Scholar] [CrossRef]
- Zhong, J.; Zhang, H.; Ruan, W.; Xie, J.; Li, H.; Deng, H.; Han, Y.; Sun, X.; Ye, C.; Zhou, X. Simultaneous Assessment of Both Lung Morphometry and Gas Exchange Function within a Single Breath-Hold by Hyperpolarized 129Xe MRI. NMR Biomed. 2017, 30, e3730. [Google Scholar] [CrossRef] [PubMed]
- Zanette, B.; Stirrat, E.; Jelveh, S.; Hope, A.; Santyr, G. Physiological Gas Exchange Mapping of Hyperpolarized 129Xe Using Spiral-IDEAL and MOXE in a Model of Regional Radiation-Induced Lung Injury. Med. Phys. 2018, 45, 803–816. [Google Scholar] [CrossRef] [PubMed]
- Patz, S.; Muradyan, I.; Hrovat, M.I.; Dabaghyan, M.; Washko, G.R.; Hatabu, H.; Butler, J.P. Diffusion of Hyperpolarized 129Xe in the Lung: A Simplified Model of 129Xe Septal Uptake and Experimental Results. New J. Phys. 2011, 13, 15009. [Google Scholar] [CrossRef]
- Patz, S.; Muradian, I.; Hrovat, M.I.; Ruset, I.C.; Topulos, G.; Covrig, S.D.; Frederick, E.; Hatabu, H.; Hersman, F.W.; Butler, J.P. Human Pulmonary Imaging and Spectroscopy with Hyperpolarized 129Xe at 0.2T. Acad. Radiol. 2008, 15, 713–727. [Google Scholar] [CrossRef]
- Månsson, S.; Wolber, J.; Driehuys, B.; Wollmer, P.; Golman, K. Characterization of Diffusing Capacity and Perfusion of the Rat Lung in a Lipopolysaccaride Disease Model Using Hyperpolarized 129Xe. Magn. Reson. Med. 2003, 50, 1170–1179. [Google Scholar] [CrossRef] [PubMed]
- Chang, Y.V. MOXE: A Model of Gas Exchange for Hyperpolarized 129Xe Magnetic Resonance of the Lung. Magn. Reson. Med. 2013, 69, 884–890. [Google Scholar] [CrossRef]
- Imai, H.; Kimura, A.; Iguchi, S.; Hori, Y.; Masuda, S.; Fujiwara, H. Noninvasive Detection of Pulmonary Tissue Destruction in a Mouse Model of Emphysema Using Hyperpolarized 129Xe MRS under Spontaneous Respiration. Magn. Reson. Med. 2010, 64, 929–938. [Google Scholar] [CrossRef] [PubMed]
- Freeman, M.S.; Cleveland, Z.I.; Qi, Y.; Driehuys, B. Enabling Hyperpolarized 129Xe MR Spectroscopy and Imaging of Pulmonary Gas Transfer to the Red Blood Cells in Transgenic Mice Expressing Human Hemoglobin. Magn. Reson. Med. 2013, 70, 1192–1199. [Google Scholar] [CrossRef]
- Fox, M.S.; Ouriadov, A.; Thind, K.; Hegarty, E.; Wong, E.; Hope, A.; Santyr, G.E. Detection of Radiation Induced Lung Injury in Rats Using Dynamic Hyperpolarized 129Xe Magnetic Resonance Spectroscopy. Med. Phys. 2014, 41, 072302. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Zhang, Z.; Zhao, X.; Sun, X.; Ye, C.; Zhou, X. Quantitative Evaluation of Radiation-Induced Lung Injury with Hyperpolarized Xenon Magnetic Resonance. Magn. Reson. Med. 2016, 76, 408–416. [Google Scholar] [CrossRef]
- Doganay, O.; Stirrat, E.; McKenzie, C.; Schulte, R.F.; Santyr, G.E. Quantification of Regional Early Stage Gas Exchange Changes Using Hyperpolarized 129Xe MRI in a Rat Model of Radiation-Induced Lung Injury. Med. Phys. 2016, 43, 2410–2420. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Li, H.; Li, H.; Zhao, X.; Zhou, Q.; Rao, Q.; Han, Y.; Lan, Y.; Deng, H.; Sun, X.; et al. Quantitative Evaluation of Lung Injury Caused by PM2.5 Using Hyperpolarized Gas Magnetic Resonance. Magn. Reson. Med. 2020, 84, 569–578. [Google Scholar] [CrossRef] [PubMed]
- Ruppert, K.; Amzajerdian, F.; Xin, Y.; Hamedani, H.; Loza, L.; Achekzai, T.; Duncan, I.F.; Profka, H.; Qian, Y.; Pourfathi, M.; et al. Investigating Biases in the Measurement of Apparent Alveolar Septal Wall Thickness with Hyperpolarized 129Xe MRI. Magn. Reson. Med. 2020, 84, 3027–3039. [Google Scholar] [CrossRef] [PubMed]
- Fliss, J.D.; Zanette, B.; Friedlander, Y.; Sadanand, S.; Lindenmaier, A.A.; Stirrat, E.; Li, D.; Post, M.; Jankov, R.P.; Santyr, G. Hyperpolarized 129Xe Magnetic Resonance Spectroscopy in a Rat Model of Bronchopulmonary Dysplasia. Am. J. Physiol.-Lung Cell. Mol. Physiol. 2021, 321, L507–L517. [Google Scholar] [CrossRef] [PubMed]
- Stewart, N.; Leung, G.; Norquay, G.; Marshall, H.; Parra-Robles, J.; Murphy, P.; Schulte, R.; Elliot, C.; Condliffe, R.; Griffiths, P.; et al. Experimental Validation of the Hyperpolarized 129Xe Chemical Shift Saturation Recovery Technique in Healthy Volunteers and Subjects with Interstitial Lung Disease. Magn. Reson. Med. 2014, 23, 44908. [Google Scholar] [CrossRef]
- Abdeen, N.; Cross, A.; Cron, G.; White, S.; Rand, T.; Miller, D.; Santyr, G. Measurement of Xenon Diffusing Capacity in the Rat Lung by Hyperpolarized 129Xe MRI and Dynamic Spectroscopy in a Single Breath-Hold. Magn. Reson. Med. 2006, 56, 255–264. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Rankine, L.; Bier, E.A.; Mummy, D.; Lu, J.; Church, A.; Tighe, R.M.; Swaminathan, A.; Huang, Y.-C.T.; Que, L.G.; et al. Using Hyperpolarized 129Xe Gas-Exchange MRI to Model the Regional Airspace, Membrane, and Capillary Contributions to Diffusing Capacity. J. Appl. Physiol. 2021, 130, 1398–1409. [Google Scholar] [CrossRef] [PubMed]
- Leung, G.; Norquay, G.; Schulte, R.F.; Wild, J.M. Radiofrequency Pulse Design for the Selective Excitation of Dissolved 129Xe. Magn. Reson. Med. 2015, 73, 21–30. [Google Scholar] [CrossRef]
- Hajari, A.J.; Yablonskiy, D.A.; Sukstanskii, A.L.; Quirk, J.D.; Conradi, M.S.; Woods, J.C. Morphometric Changes in the Human Pulmonary Acinus during Inflation. J. Appl. Physiol. 2011, 112, 937–943. [Google Scholar] [CrossRef]
- Stewart, N.J.; Parra-Robles, J.; Wild, J.M. Finite Element Modeling of 129Xe Diffusive Gas Exchange NMR in the Human Alveoli. J. Magn. Reson. 2016, 271, 21–33. [Google Scholar] [CrossRef]
- Stewart, N.J.; Horn, F.C.; Norquay, G.; Collier, G.J.; Yates, D.P.; Lawson, R.; Marshall, H.; Wild, J.M. Reproducibility of Quantitative Indices of Lung Function and Microstructure from 129Xe Chemical Shift Saturation Recovery (CSSR) MR Spectroscopy. Magn. Reson. Med. 2017, 77, 2107–2113. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Guan, Y.; Li, H.; Zhao, X.; Han, Y.; Xia, Y.; Sun, X.; Liu, S.; Ye, C.; Zhou, X. Quantitative Comparison of Lung Physiological Parameters in Single and Multiple Breathhold with Hyperpolarized Xenon Magnetic Resonance. Biomed. Phys. Eng. Express 2016, 2, 055013. [Google Scholar] [CrossRef]
- Ruppert, K.; Brookeman, J.R.; Hagspiel, K.D.; Mugler III, J.P. Probing Lung Physiology with Xenon Polarization Transfer Contrast (XTC). Magn. Reson. Med. 2000, 44, 349–357. [Google Scholar] [CrossRef]
- Ruppert, K.; Mata, J.F.; Brookeman, J.R.; Hagspiel, K.D.; Mugler III, J.P. Exploring Lung Function with Hyperpolarized 129Xe Nuclear Magnetic Resonance. Magn. Reson. Med. 2004, 51, 676–687. [Google Scholar] [CrossRef] [PubMed]
- Dregely, I.; Ruset, I.C.; Mata, J.F.; Ketel, J.; Ketel, S.; Distelbrink, J.; Altes, T.A.; Mugler, J.P.; Miller, G.W.; Hersman, F.W.; et al. Multiple-Exchange-Time Xenon Polarization Transfer Contrast (MXTC) MRI: Initial Results in Animals and Healthy Volunteers. Magn. Reson. Med. 2012, 67, 943–953. [Google Scholar] [CrossRef]
- Ruppert, K.; Mata, J.F.; Wang, H.-T.J.; Tobias, W.A.; Cates, G.D.; Brookeman, J.R.; Hagspiel, K.D.; Mugler, J.P., III. XTC MRI: Sensitivity Improvement through Parameter Optimization. Magn. Reson. Med. 2007, 57, 1099–1109. [Google Scholar] [CrossRef]
- Imai, H.; Kimura, A.; Hori, Y.; Iguchi, S.; Kitao, T.; Okubo, E.; Ito, T.; Matsuzaki, T.; Fujiwara, H. Hyperpolarized 129Xe Lung MRI in Spontaneously Breathing Mice with Respiratory Gated Fast Imaging and Its Application to Pulmonary Functional Imaging. NMR Biomed. 2011, 24, 1343–1352. [Google Scholar] [CrossRef]
- Dregely, I.; Mugler, J.P.; Ruset, I.C.; Altes, T.A.; Mata, J.F.; Miller, G.W.; Ketel, J.; Ketel, S.; Distelbrink, J.; Hersman, F.W.; et al. Hyperpolarized Xenon-129 Gas-Exchange Imaging of Lung Microstructure: First Case Studies in Subjects with Obstructive Lung Disease. J. Magn. Reson. Imaging 2011, 33, 1052–1062. [Google Scholar] [CrossRef]
- Marshall, H.; Stewart, N.J.; Chan, H.-F.; Rao, M.; Norquay, G.; Wild, J.M. In Vivo Methods and Applications of Xenon-129 Magnetic Resonance. Prog. Nucl. Magn. Reson. Spectrosc. 2021, 122, 42–62. [Google Scholar] [CrossRef]
- Achekzai, T.; Ruppert, K.; Loza, L.; Amzajerdian, F.; Profka, H.; Duncan, I.F.; Kadlecek, S.J.; Rizi, R.R. Investigating the Impact of RF Saturation-Pulse Parameters on Compartment-Selective Gas-Phase Depolarization with Xenon Polarization Transfer Contrast MRI. Magn. Reson. Med. 2022, 88, 2447–2460. [Google Scholar] [CrossRef]
- Muradyan, I.; Butler, J.P.; Dabaghyan, M.; Hrovat, M.; Dregely, I.; Ruset, I.; Topulos, G.P.; Frederick, E.; Hatabu, H.; Hersman, W.F.; et al. Single Breath Xenon Polarization Transfer Contrast (SB-XTC): Implementation and Initial Results in Healthy Humans. J. Magn. Reson. Imaging 2013, 37, 457–470. [Google Scholar] [CrossRef]
- Antonacci, M.A.; Zhang, L.; Burant, A.; McCallister, D.; Branca, R.T. Simple and Robust Referencing System Enables Identification of Dissolved-Phase Xenon Spectral Frequencies. Magn. Reson. Med. 2018, 80, 431–441. [Google Scholar] [CrossRef] [PubMed]
- Friedlander, Y.; Zanette, B.; Lindenmaier, A.; Li, D.; Kadlecek, S.; Santyr, G.; Kassner, A. Hyperpolarized 129Xe MRI of the Rat Brain with Chemical Shift Saturation Recovery and Spiral-IDEAL Readout. Magn. Reson. Med. 2021, 87, 1971–1979. [Google Scholar] [CrossRef] [PubMed]
- Ruppert, K.; Amzajerdian, F.; Hamedani, H.; Xin, Y.; Loza, L.; Achekzai, T.; Duncan, I.F.; Profka, H.; Siddiqui, S.; Pourfathi, M.; et al. Assessment of Flip Angle-TR Equivalence for Standardized Dissolved-Phase Imaging of the Lung with Hyperpolarized 129Xe MRI. Magn. Reson. Med. 2019, 81, 1784–1794. [Google Scholar] [CrossRef] [PubMed]
- Peled, S.; Jolesz, F.A.; Tseng, C.-H.; Nascimben, L.; Albert, M.S.; Walsworth, R.L. Determinants of Tissue Delivery for 129Xe Magnetic Resonance in Humans. Magn. Reson. Med. 1996, 36, 340–344. [Google Scholar] [CrossRef]
- Zhou, X.; Sun, Y.; Mazzanti, M.; Henninger, N.; Mansour, J.; Fisher, M.; Albert, M. MRI of Stroke Using Hyperpolarized 129Xe. NMR Biomed. 2011, 24, 170–175. [Google Scholar] [CrossRef] [PubMed]
- Kimura, A.; Imai, H.; Wakayama, T.; Fujiwara, H. A Simple Method for Quantitative Measurement and Analysis of Hyperpolarized 129Xe Uptake Dynamics in Mouse Brain under Controlled Flow. Magn. Reson. Med. Sci. 2008, 7, 179–185. [Google Scholar] [CrossRef] [PubMed]
- Imai, H.; Kimura, A.; Akiyama, K.; Ota, C.; Okimoto, K.; Fujiwara, H. Development of a Fast Method for Quantitative Measurement of Hyperpolarized 129Xe Dynamics in Mouse Brain. NMR Biomed. 2012, 25, 210–217. [Google Scholar] [CrossRef]
- Patz, S.; Hersman, F.W.; Muradian, I.; Hrovat, M.I.; Ruset, I.C.; Ketel, S.; Jacobson, F.; Topulos, G.P.; Hatabu, H.; Butler, J.P. Hyperpolarized 129Xe MRI: A Viable Functional Lung Imaging Modality? Eur. J. Radiol. 2007, 64, 335–344. [Google Scholar] [CrossRef]
- Wilson, G.J. NMR Relaxation Measurements of 129Xe in Tissue and Blood: Toward Imaging Laser-Polarized 129Xe in Tissue; University of Wisconsin: Madison, WI, USA, 1999. [Google Scholar]
- Norquay, G.; Leung, G.; Stewart, N.J.; Tozer, G.M.; Wolber, J.; Wild, J.M. Relaxation and Exchange Dynamics of Hyperpolarized 129Xe in Human Blood. Magn. Reson. Med. 2015, 74, 303–311. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Z.; Zhong, J.; Ruan, W.; Han, Y.; Sun, X.; Ye, C.; Zhou, X. Oxygen-Dependent Hyperpolarized 129Xe Brain MR. NMR Biomed. 2016, 29, 220–225. [Google Scholar] [CrossRef] [PubMed]
- Choquet, P.; Hyacinthe, J.-N.; Duhamel, G.; Grillon, E.; Leviel, J.-L.; Constantinesco, A.; Ziegler, A. Method to Determine in Vivo the Relaxation Time T1 of Hyperpolarized Xenon in Rat Brain. Magn. Reson. Med. 2003, 49, 1014–1018. [Google Scholar] [CrossRef] [PubMed]
- Wakai, A.; Nakamura, K.; Kershaw, J.; Kanno, I. In Vivo MR Spectroscopy of Hyperpolarized Xe-129 in Rat Brain. Int. Congr. Ser. 2004, 1265, 139–143. [Google Scholar] [CrossRef]
- Zhou, X. Hyperpolarized Xenon Brain MRI. In Advances in Brain Imaging; IntechOpen: London, UK, 2012; Volume 3. [Google Scholar] [CrossRef]
- Zhou, X.; Mazzanti, M.L.; Chen, J.J.; Tzeng, Y.-S.; Mansour, J.K.; Gereige, J.D.; Venkatesh, A.K.; Sun, Y.; Mulkern, R.V.; Albert, M.S. Reinvestigating Hyperpolarized 129Xe Longitudinal Relaxation Time in the Rat Brain with Noise Considerations. NMR Biomed. 2008, 21, 217–225. [Google Scholar] [CrossRef]
- Duhamel, G.; Choquet, P.; Grillon, E.; Leviel, J.L.; Décorps, M.; Ziegler, A.; Constantinesco, A. Global and Regional Cerebral Blood Flow Measurements Using NMR of Injected Hyperpolarized Xenon-129. Acad. Radiol. 2002, 9, S498–S500. [Google Scholar] [CrossRef]
- Mazzanti, M.L.; Walvick, R.P.; Zhou, X.; Sun, Y.; Shah, N.; Mansour, J.; Gereige, J.; Albert, M.S. Distribution of Hyperpolarized Xenon in the Brain Following Sensory Stimulation: Preliminary MRI Findings. PLoS ONE 2011, 6, e21607. [Google Scholar] [CrossRef]
- Martin, C.C.; Williams, R.F.; Gao, J.-H.; Nickerson, L.D.H.; Xiong, J.; Fox, P.T. The Pharmacokinetics of Hyperpolarized Xenon: Implications for Cerebral MRI. J. Magn. Reson. Imaging 1997, 7, 848–854. [Google Scholar] [CrossRef]
- McHugh, C.T.; Kelley, M.; Bryden, N.J.; Branca, R.T. In Vivo HyperCEST Imaging: Experimental Considerations for a Reliable Contrast. Magn. Reson. Med. 2022, 87, 1480–1489. [Google Scholar] [CrossRef]
- Hane, F.T.; Li, T.; Smylie, P.; Pellizzari, R.M.; Plata, J.A.; DeBoef, B.; Albert, M.S. In Vivo Detection of Cucurbit[6]Uril, a Hyperpolarized Xenon Contrast Agent for a Xenon Magnetic Resonance Imaging Biosensor. Sci. Rep. 2017, 7, 41027. [Google Scholar] [CrossRef]
- Lilburn, D.M.L.; Hughes-Riley, T.; Six, J.S.; Stupic, K.F.; Shaw, D.E.; Pavlovskaya, G.E.; Meersmann, T. Validating Excised Rodent Lungs for Functional Hyperpolarized Xenon-129 MRI. PLoS ONE 2013, 8, e73468. [Google Scholar] [CrossRef][Green Version]
- Imai, H.; Matsumoto, H.; Miyakoshi, E.; Okumura, S.; Fujiwara, H.; Kimura, A. Regional Fractional Ventilation Mapping in Spontaneously Breathing Mice Using Hyperpolarized 129Xe MRI. NMR Biomed. 2015, 28, 24–29. [Google Scholar] [CrossRef]
- Virgincar, R.S.; Dahlke, J.; Robertson, S.H.; Morand, N.; Qi, Y.; Degan, S.; Driehuys, B.; Nouls, J.C. A Portable Ventilator with Integrated Physiologic Monitoring for Hyperpolarized 129Xe MRI in Rodents. J. Magn. Reson. 2018, 295, 63–71. [Google Scholar] [CrossRef] [PubMed]
- Ouriadov, A.; Fox, M.; Hegarty, E.; Parraga, G.; Wong, E.; Santyr, G.E. Early Stage Radiation-Induced Lung Injury Detected Using Hyperpolarized 129Xe Morphometry: Proof-of-Concept Demonstration in a Rat Model. Magn. Reson. Med. 2016, 75, 2421–2431. [Google Scholar] [CrossRef] [PubMed]
- Ruppert, K.; Amzajerdian, F.; Hamedani, H.; Xin, Y.; Loza, L.; Achekzai, T.; Duncan, I.F.; Profka, H.; Siddiqui, S.; Pourfathi, M.; et al. Rapid Assessment of Pulmonary Gas Transport with Hyperpolarized 129Xe MRI Using a 3D Radial Double Golden-Means Acquisition with Variable Flip Angles. Magn. Reson. Med. 2018, 80, 2439–2448. [Google Scholar] [CrossRef] [PubMed]
- Doganay, O.; Wade, T.; Hegarty, E.; McKenzie, C.; Schulte, R.F.; Santyr, G.E. Hyperpolarized 129Xe Imaging of the Rat Lung Using Spiral IDEAL. Magn. Reson. Med. 2016, 76, 566–576. [Google Scholar] [CrossRef] [PubMed]
- Niedbalski, P.J.; Cleveland, Z.I. Improved Preclinical Hyperpolarized 129Xe Ventilation Imaging with Constant Flip Angle 3D Radial Golden Means Acquisition and Keyhole Reconstruction. NMR Biomed. 2021, 34, e4464. [Google Scholar] [CrossRef]
- Ouriadov, A.V.; Lam, W.W.; Santyr, G.E. Rapid 3-D Mapping of Hyperpolarized 3He Spin-Lattice Relaxation Times Using Variable Flip Angle Gradient Echo Imaging with Application to Alveolar Oxygen Partial Pressure Measurement in Rat Lungs. MAGMA 2009, 22, 309–318. [Google Scholar] [CrossRef]
- Zhong, J.; Ruan, W.; Han, Y.; Sun, X.; Ye, C.; Zhou, X. Fast Determination of Flip Angle and T1 in Hyperpolarized Gas MRI During a Single Breath-Hold. Sci. Rep. 2016, 6, 25854. [Google Scholar] [CrossRef] [PubMed]
- Dixon, W.T. Simple Proton Spectroscopic Imaging. Radiology 1984, 153, 189–194. [Google Scholar] [CrossRef]
- Costa, D.N.; Pedrosa, I.; McKenzie, C.; Reeder, S.B.; Rofsky, N.M. Body MRI Using IDEAL. AJR Am. J. Roentgenol. 2008, 190, 1076–1084. [Google Scholar] [CrossRef]
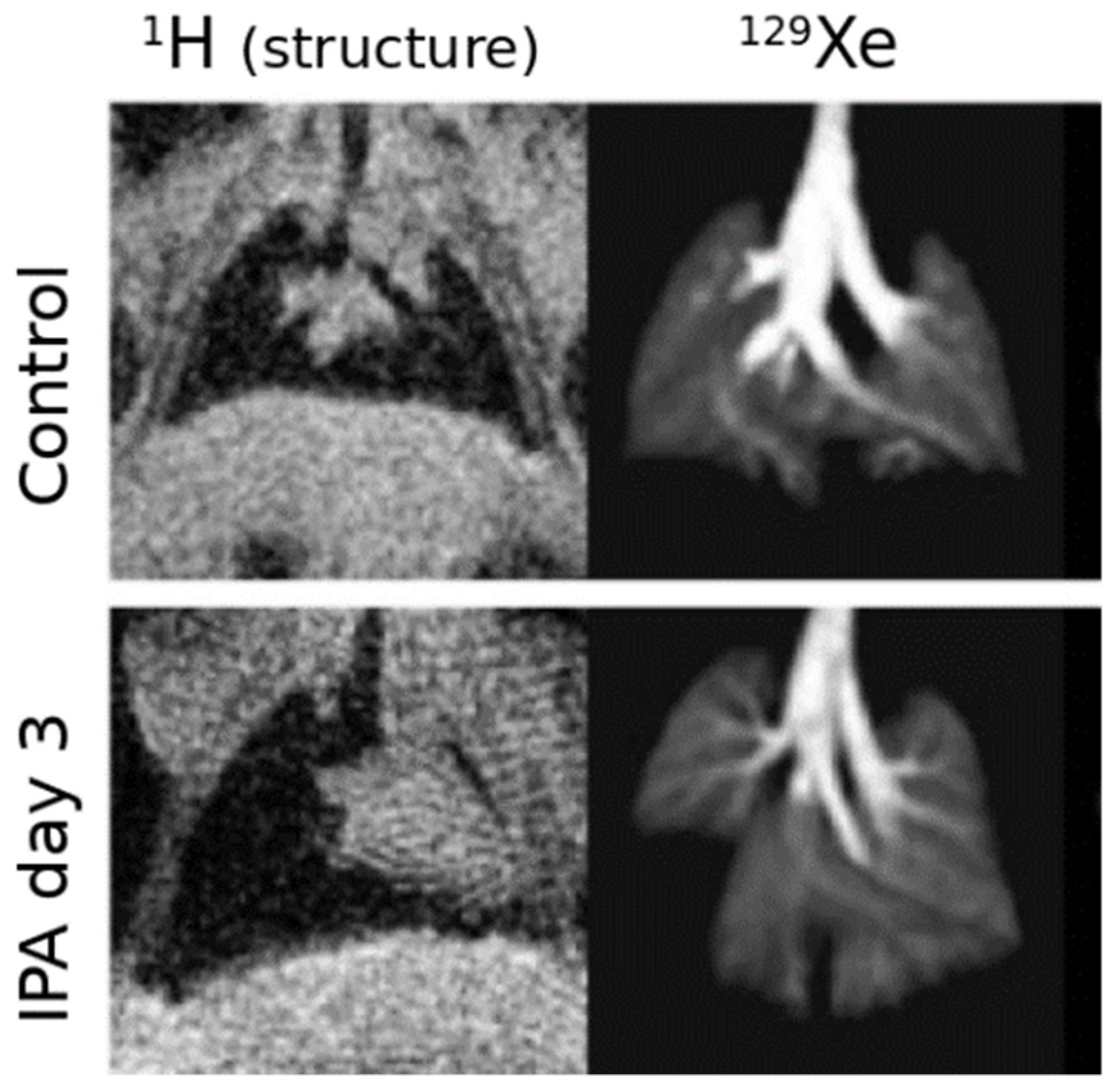
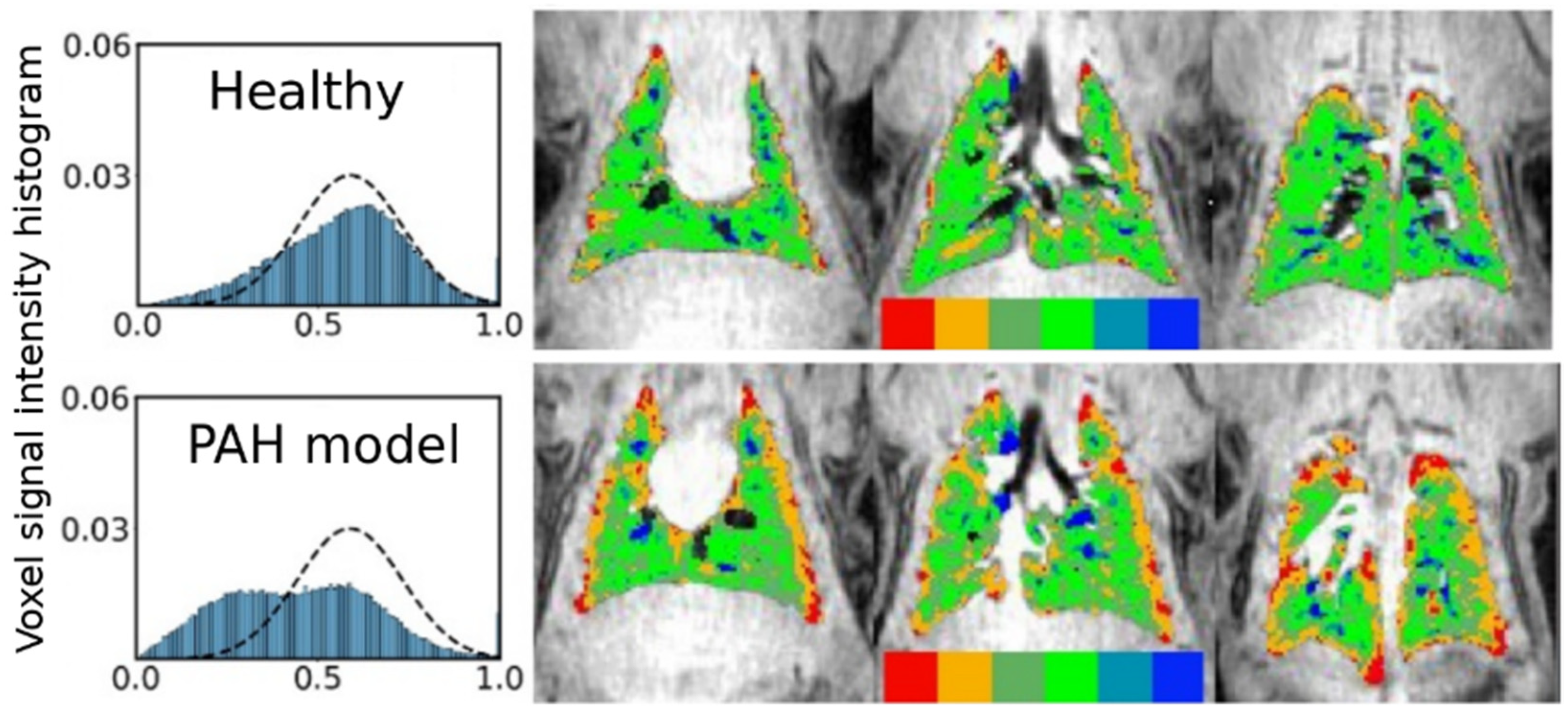
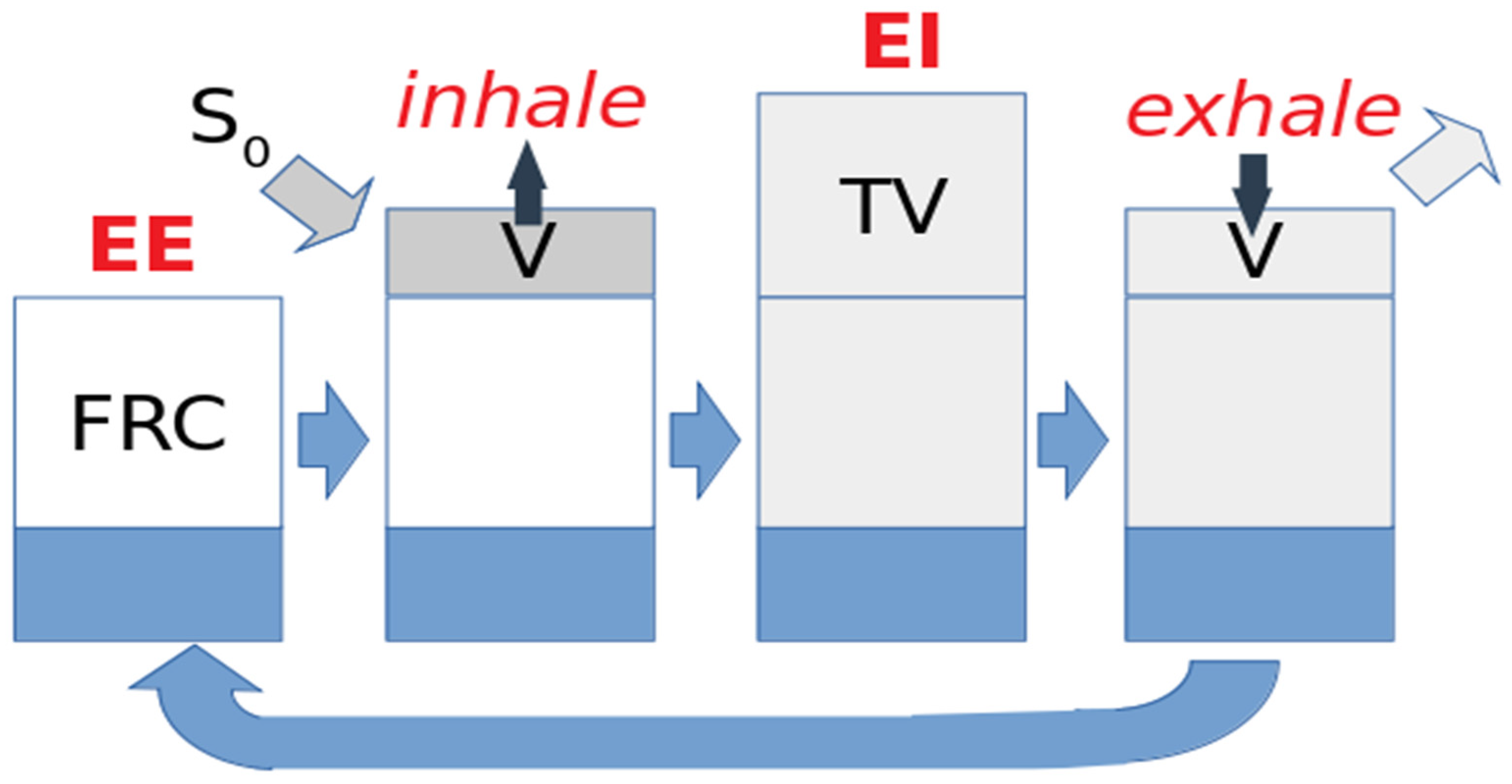


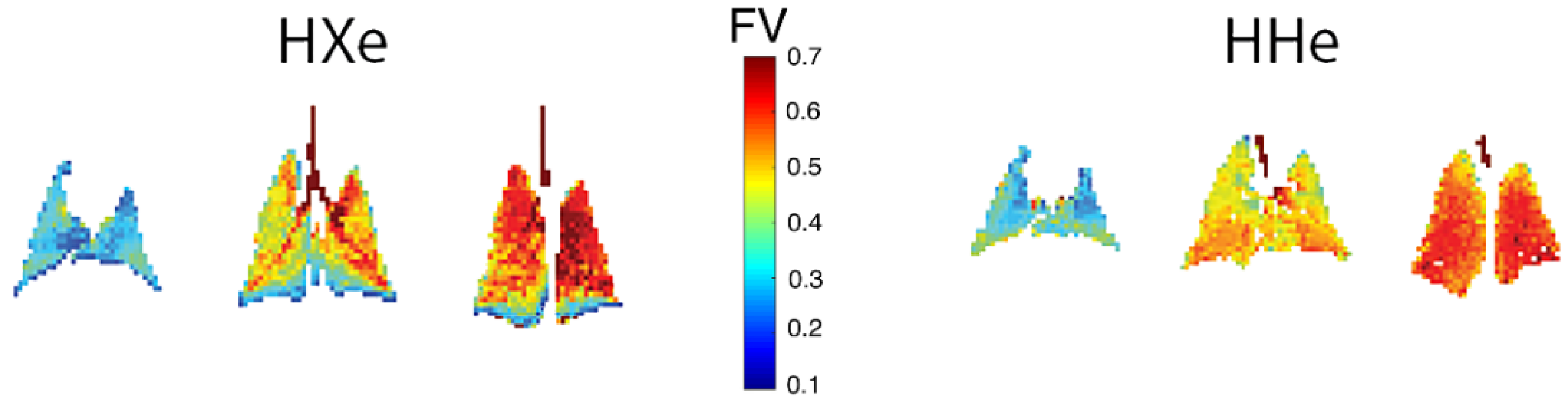
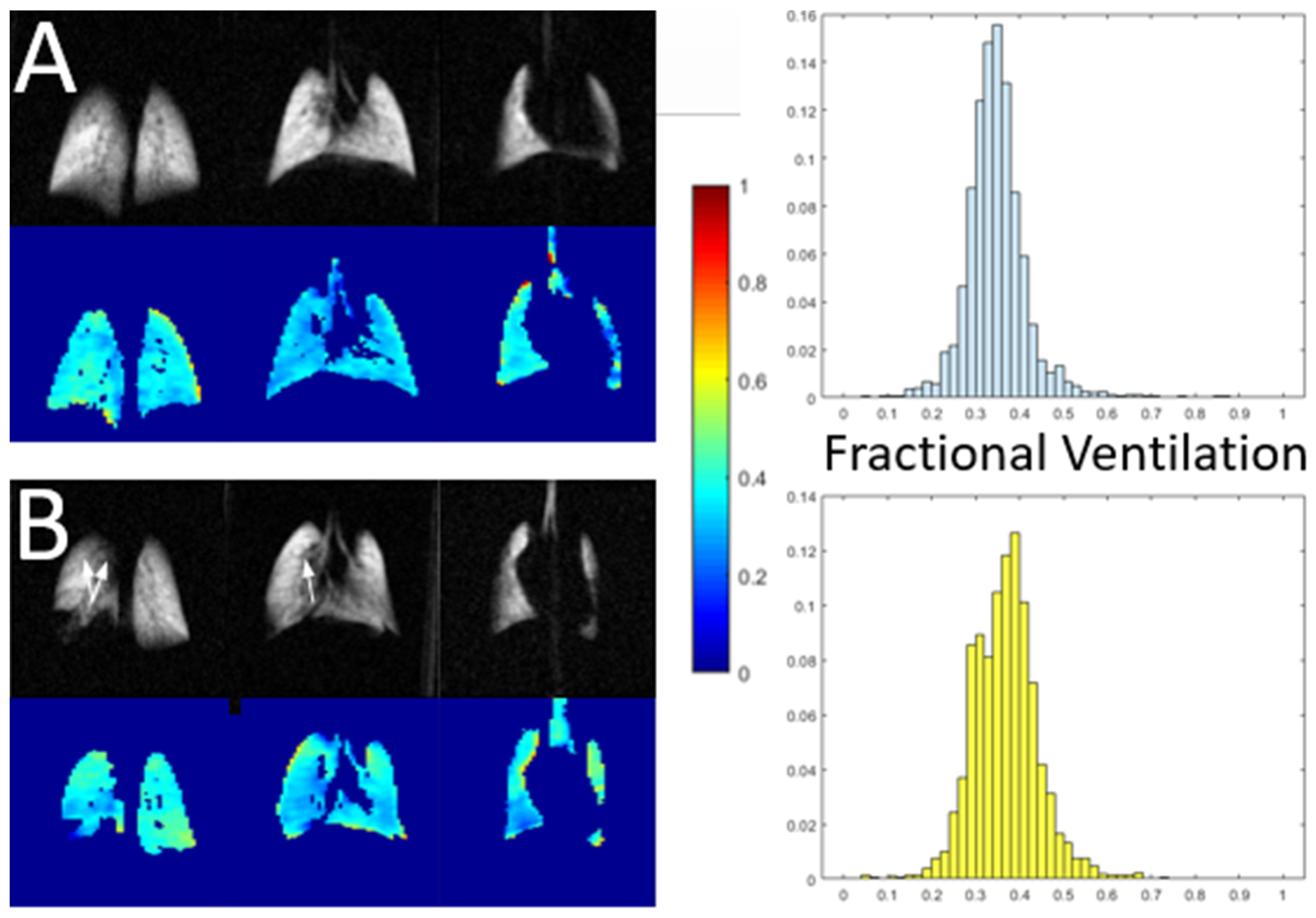

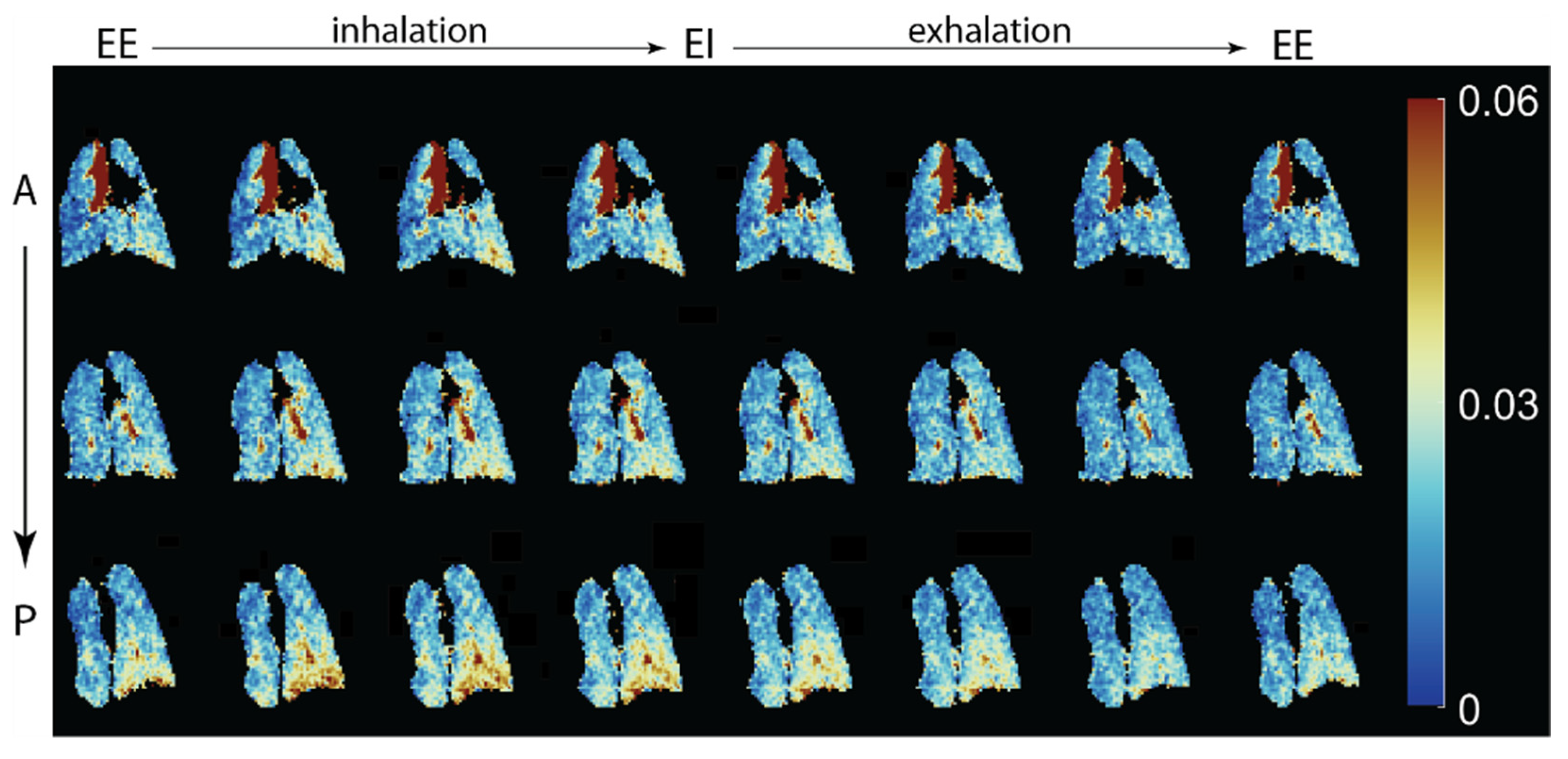
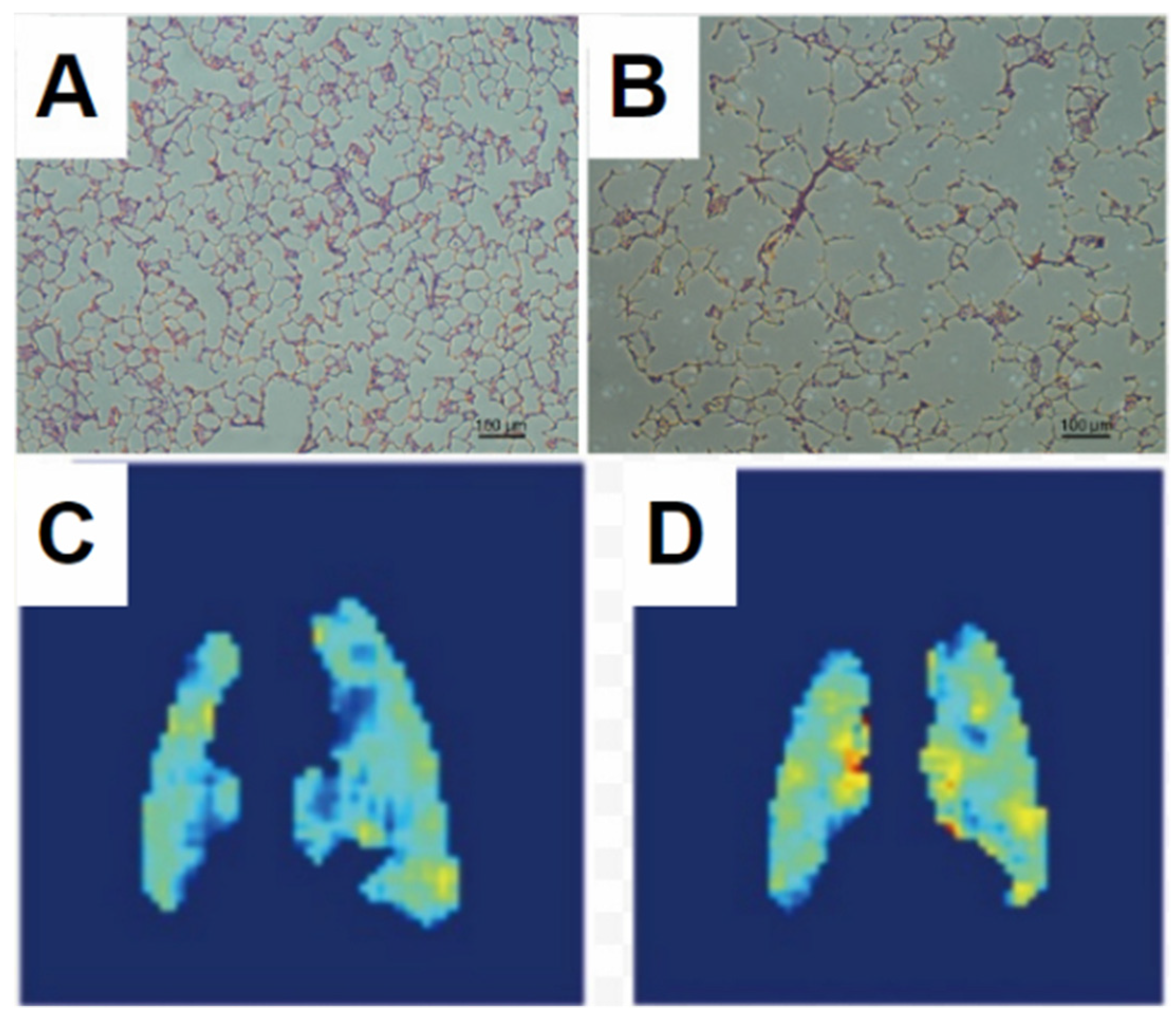
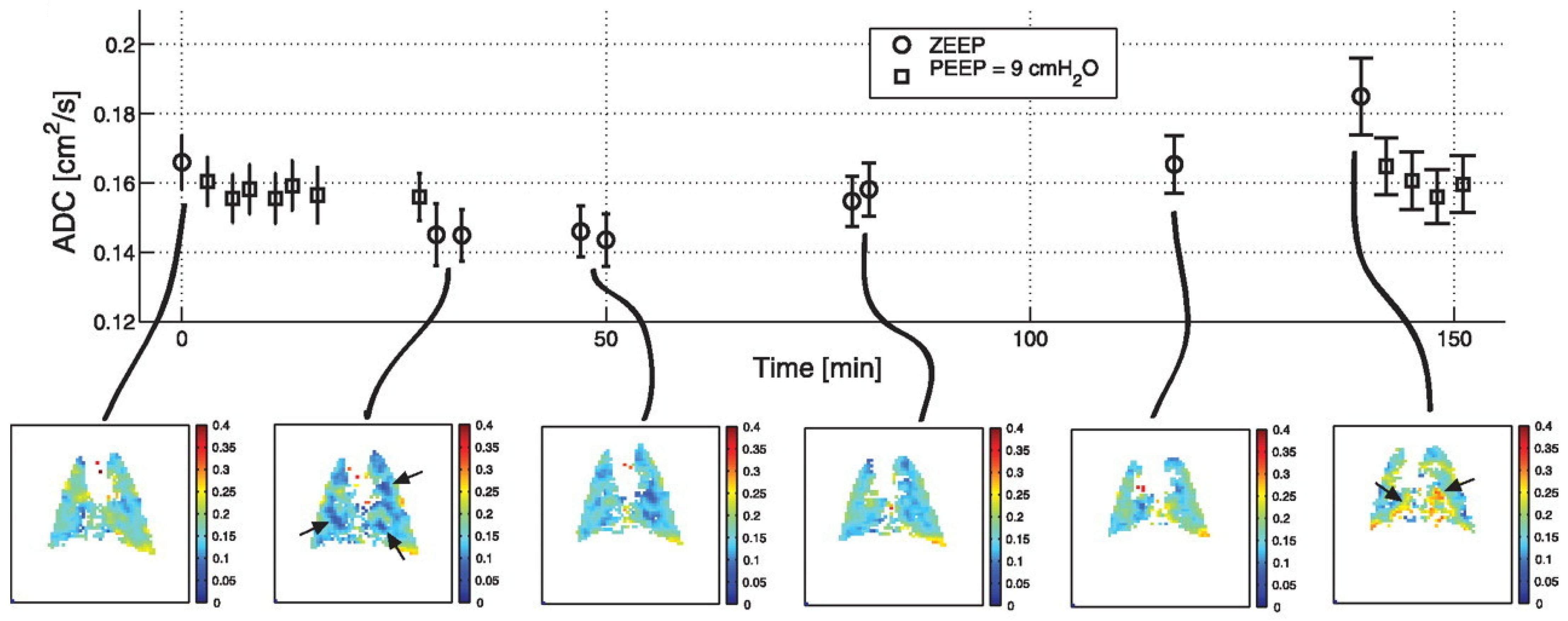
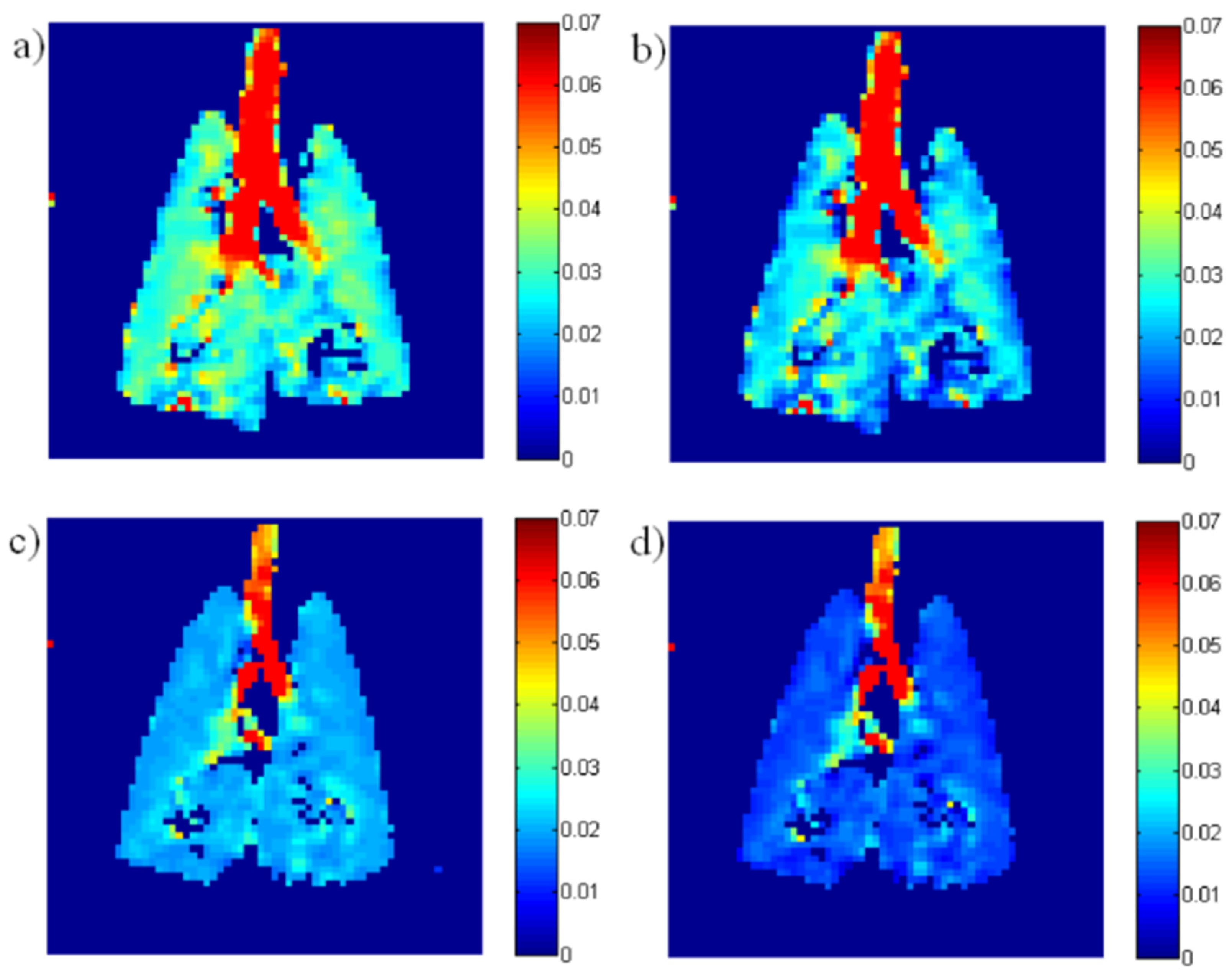
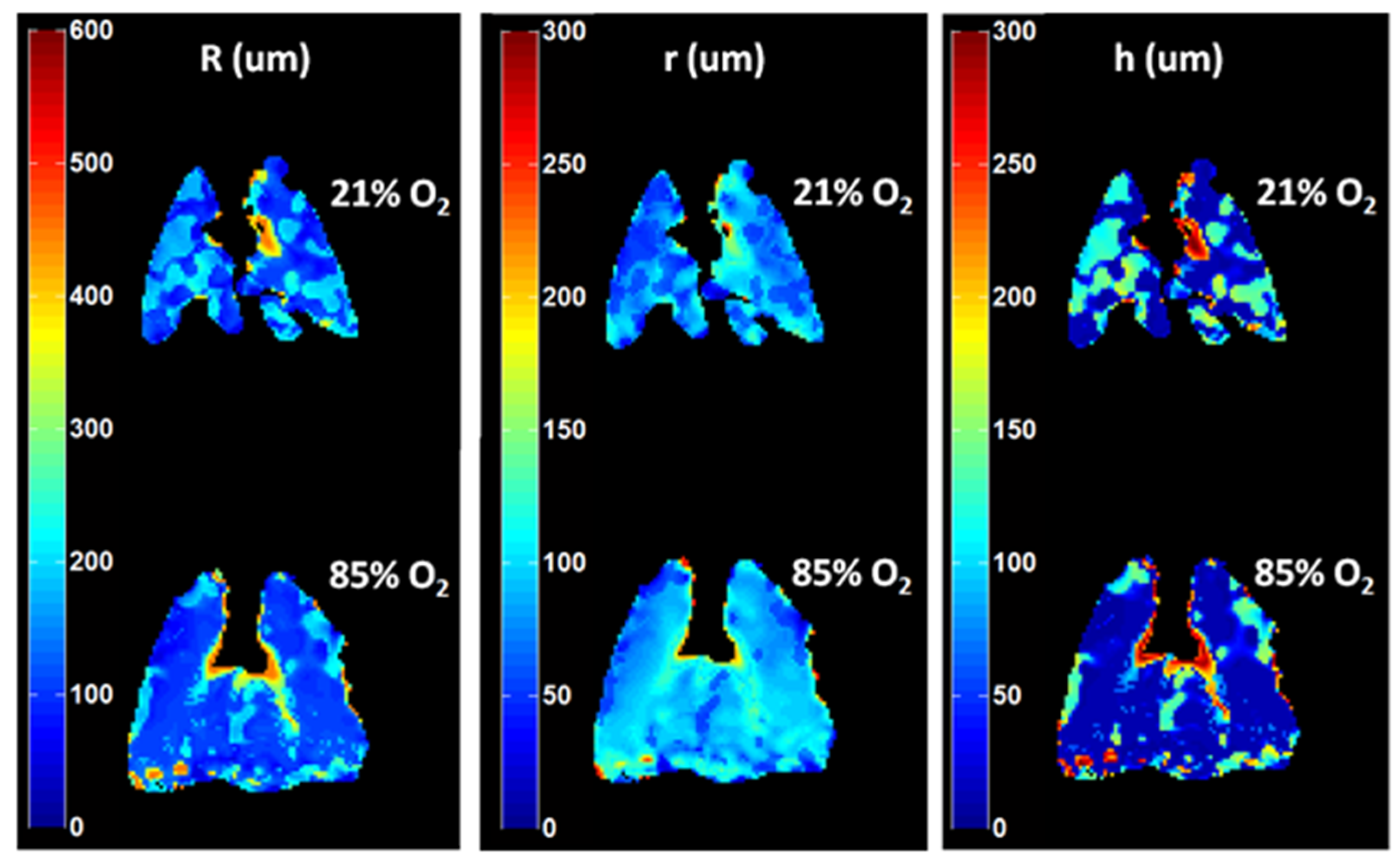
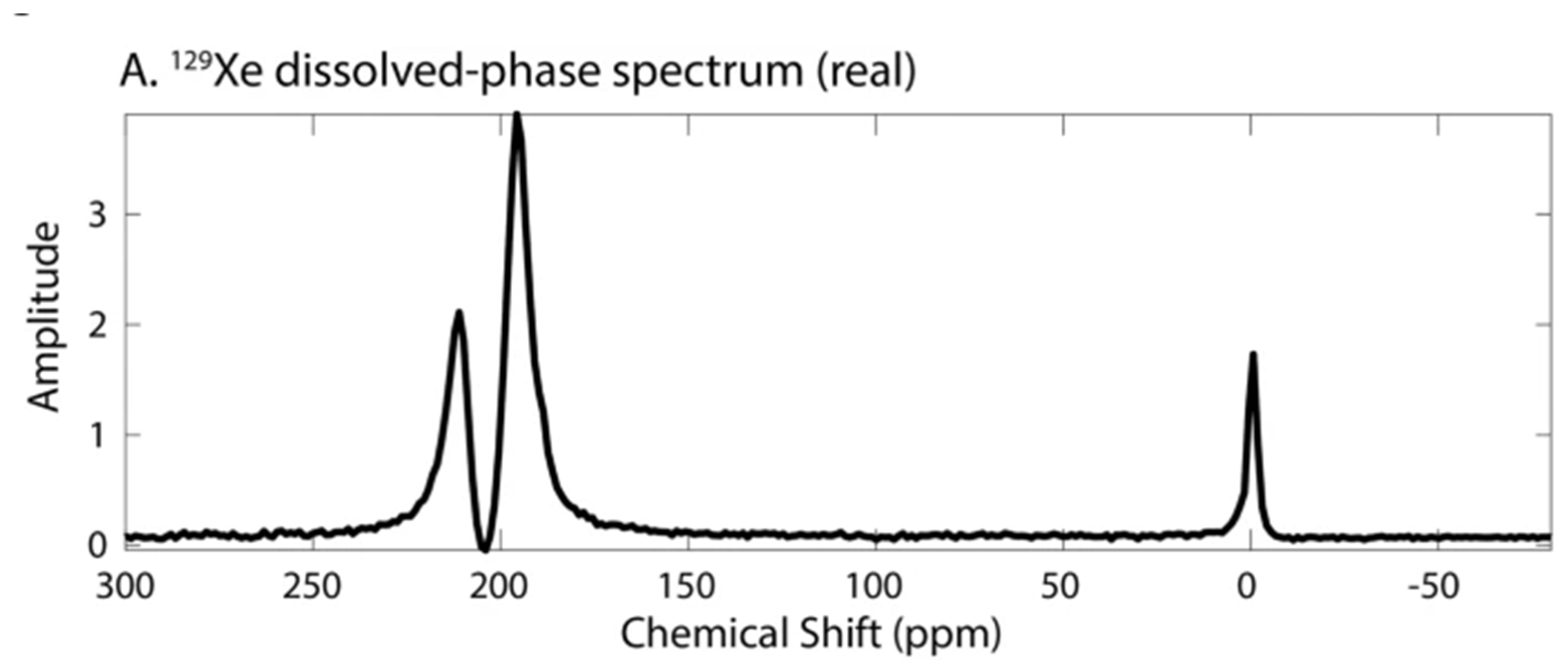
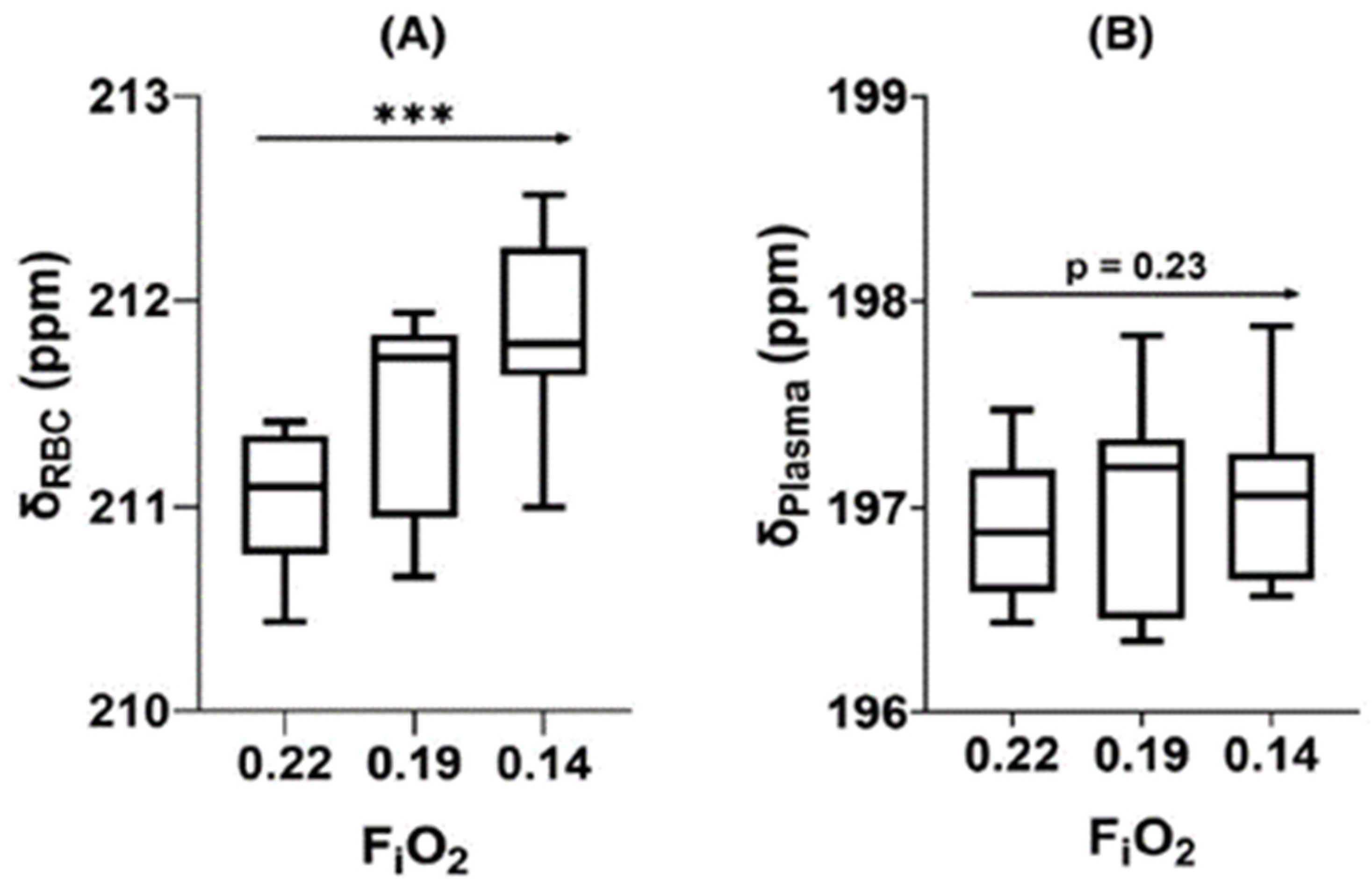
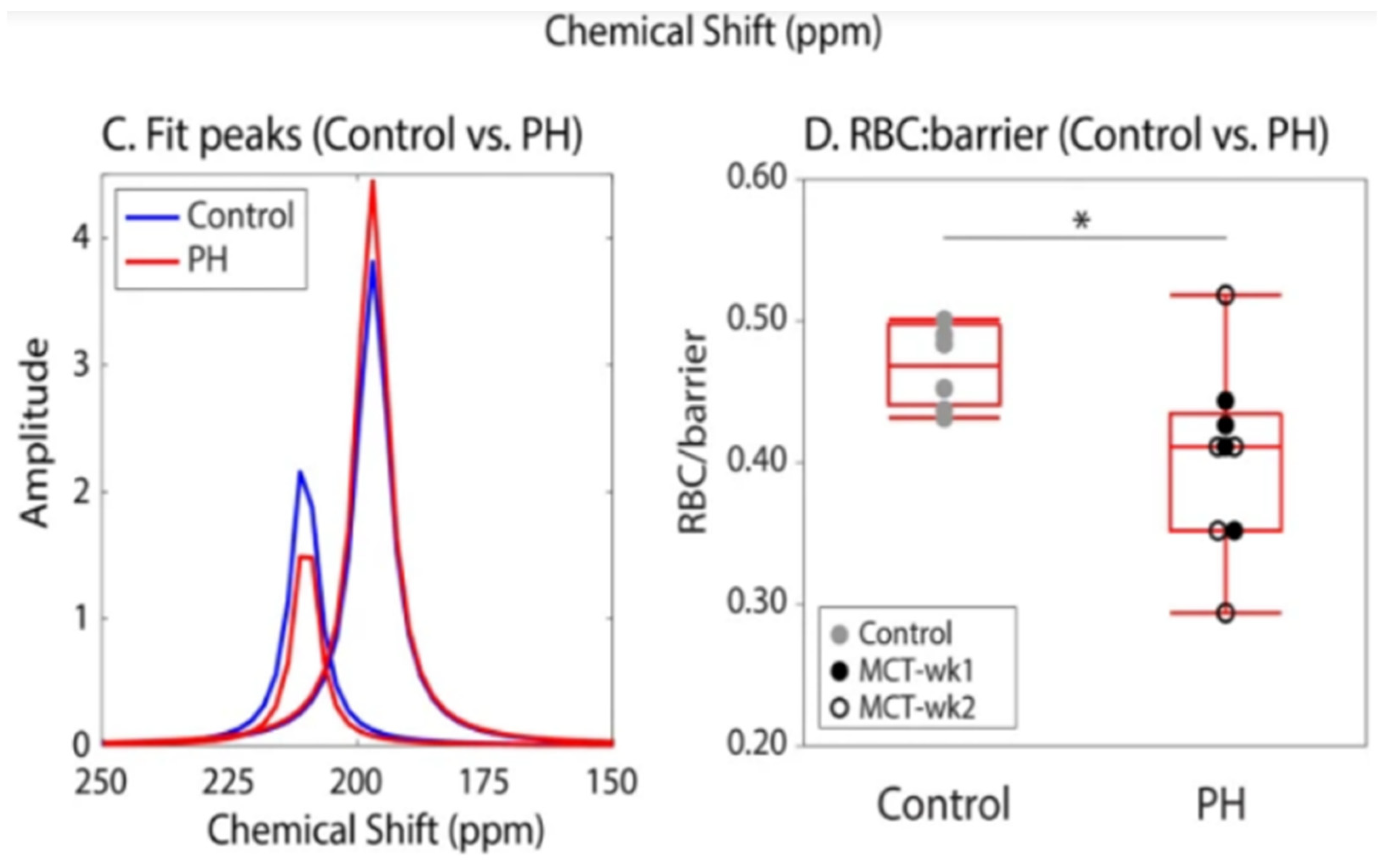
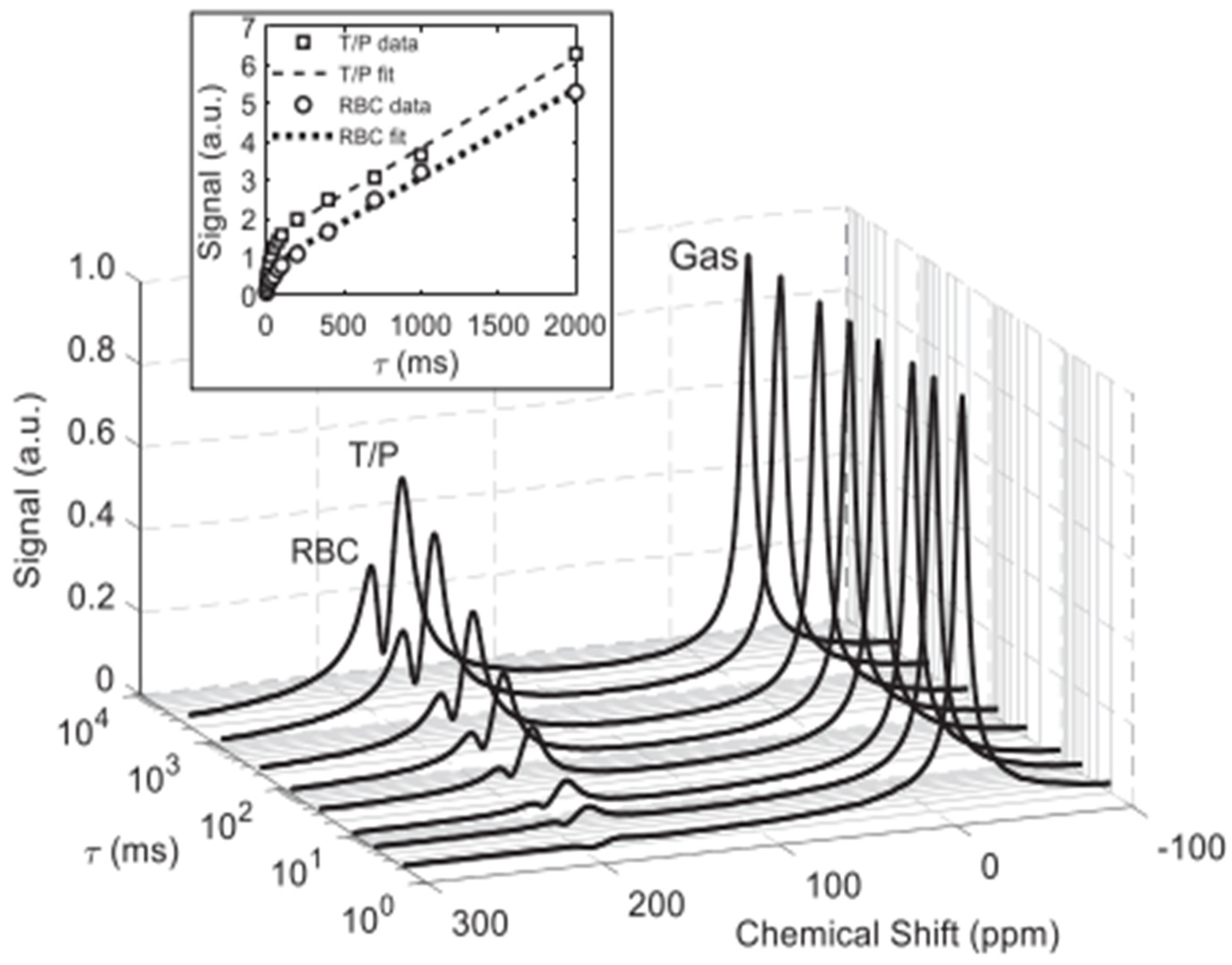
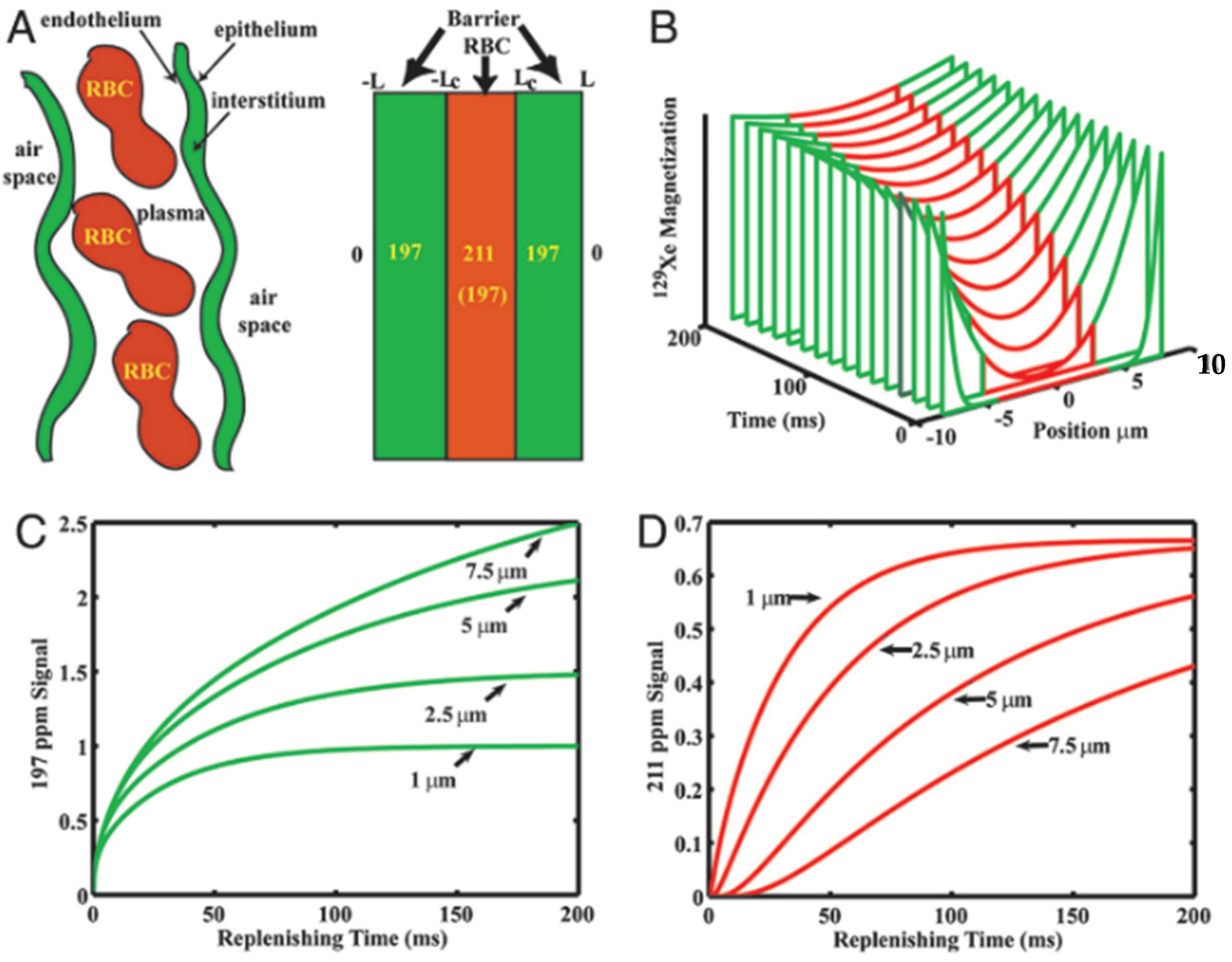
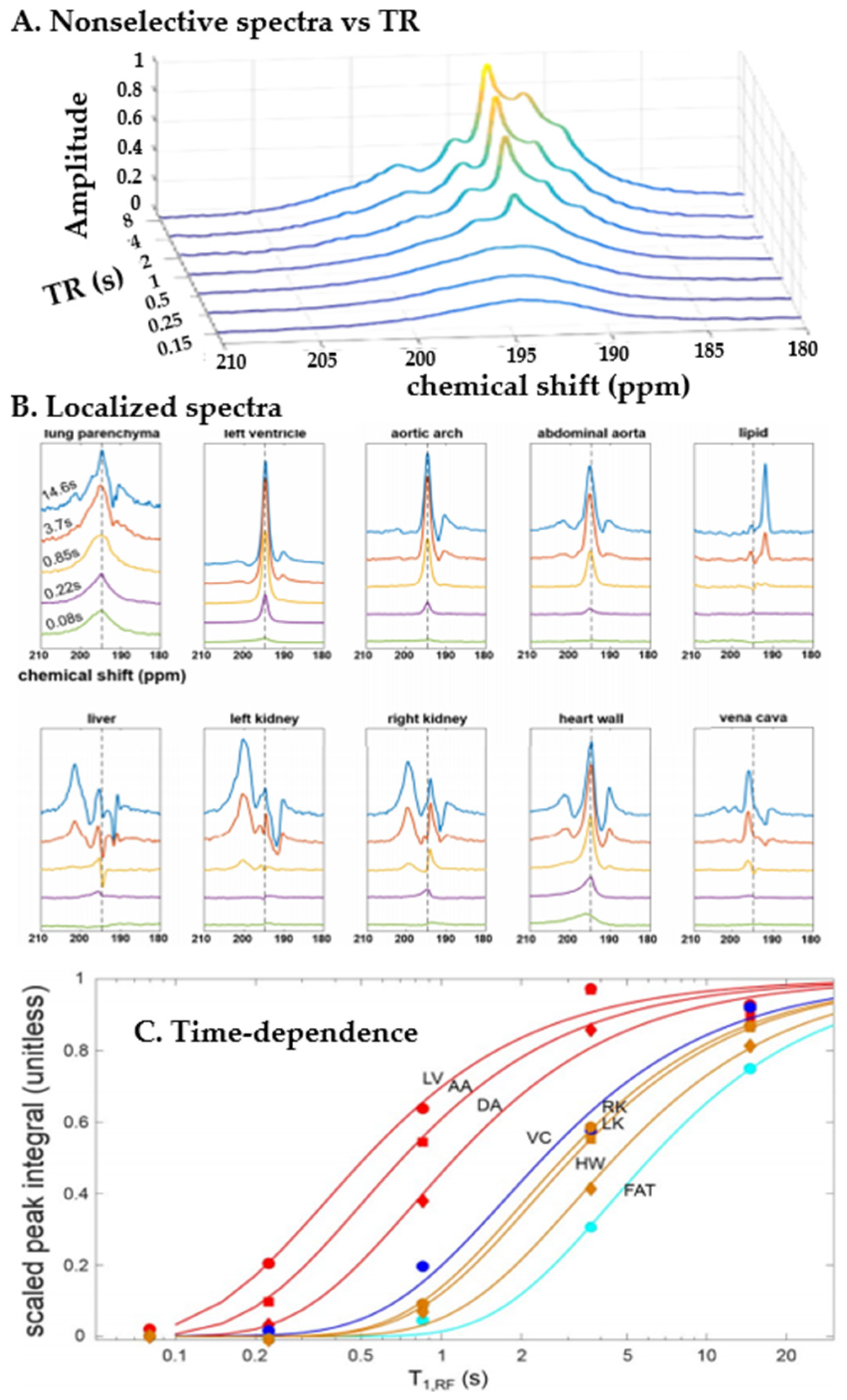
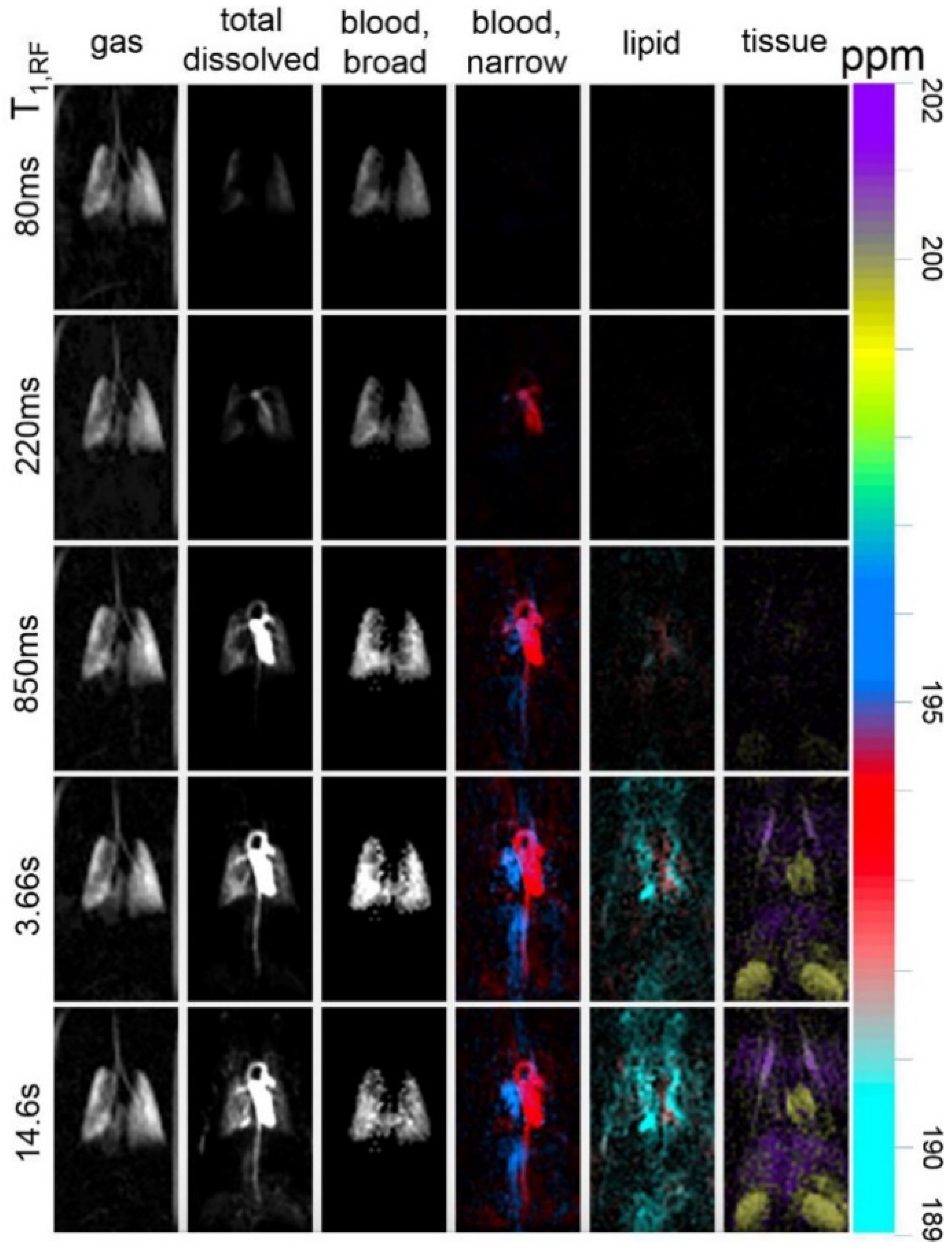
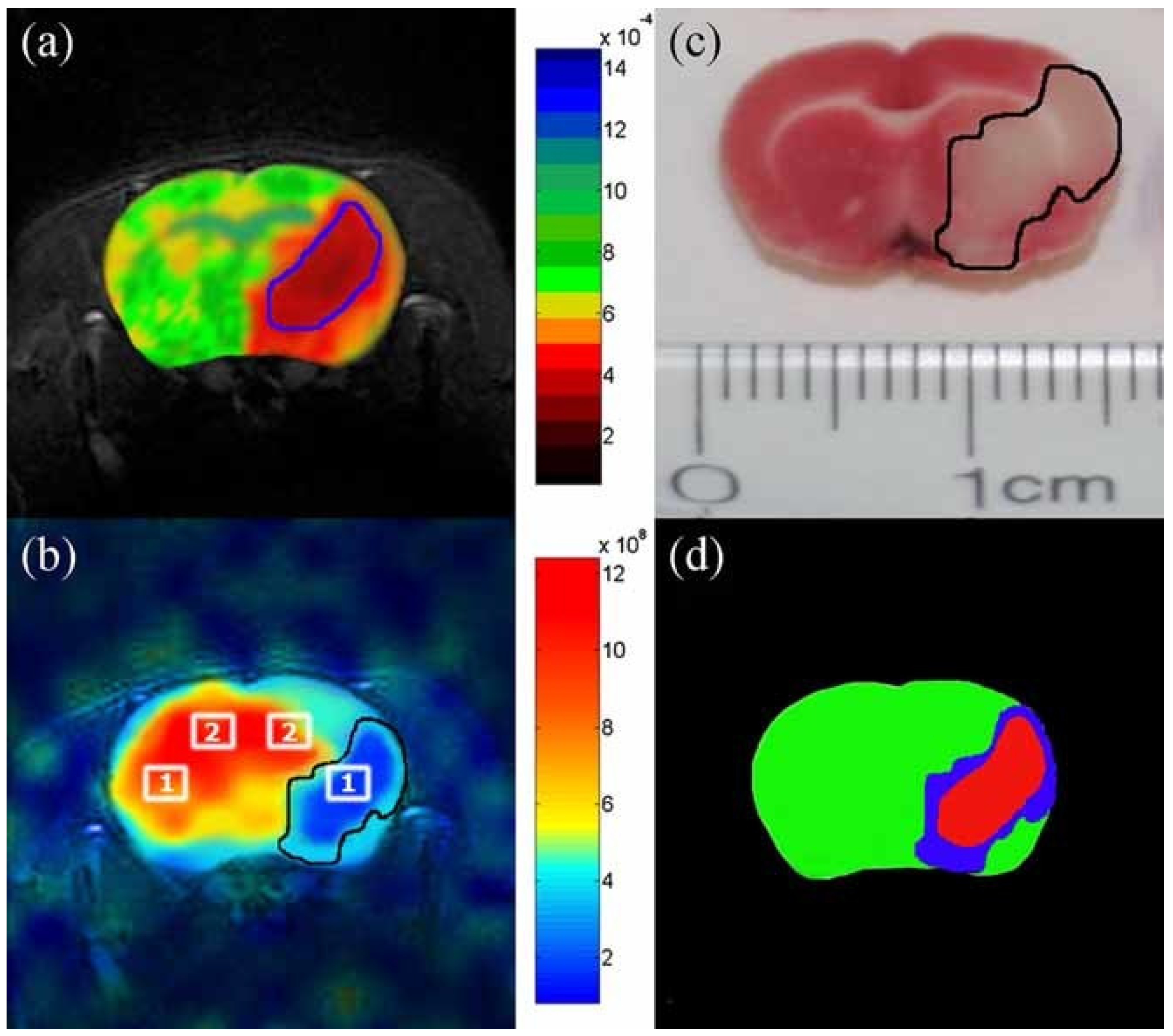
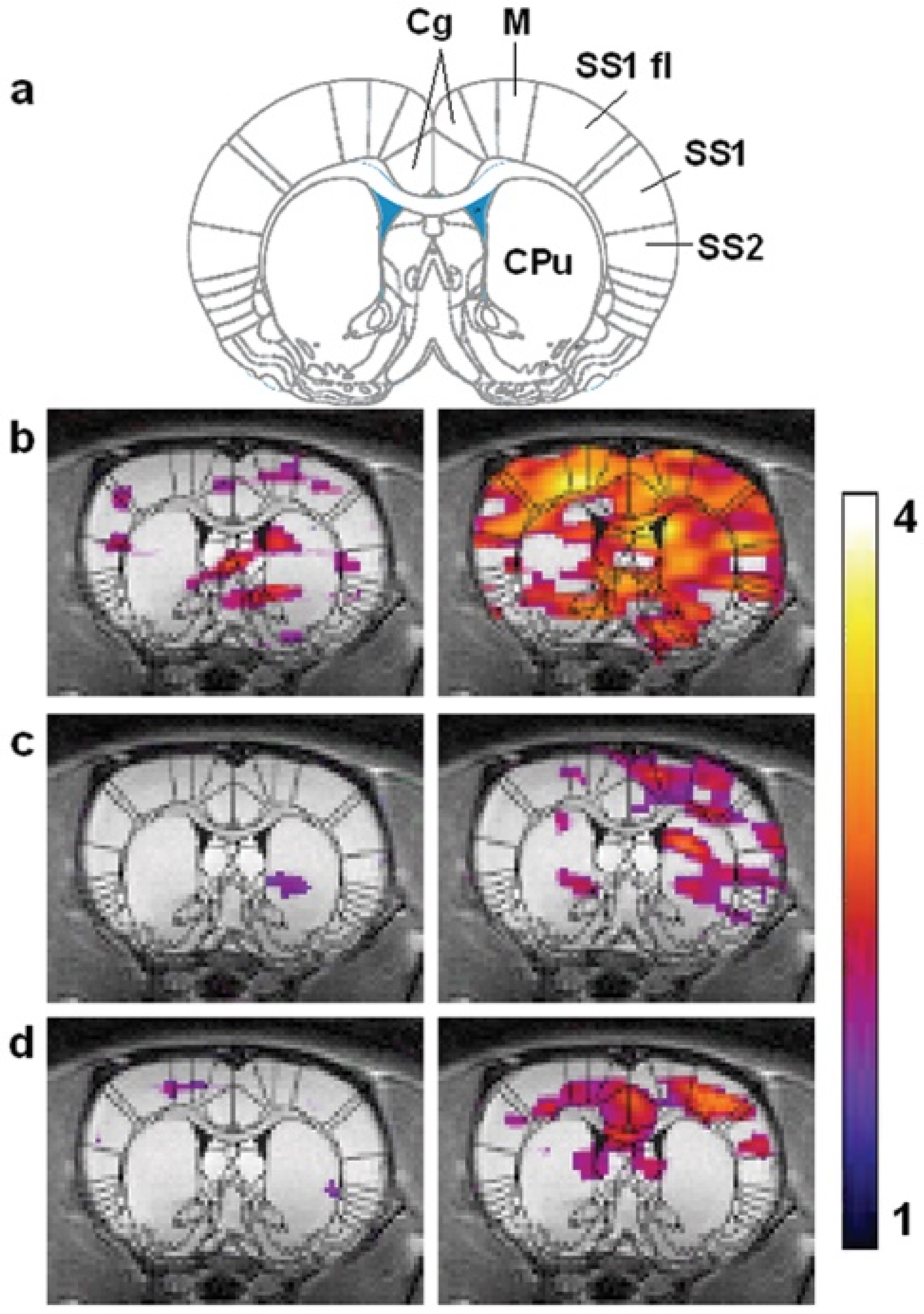
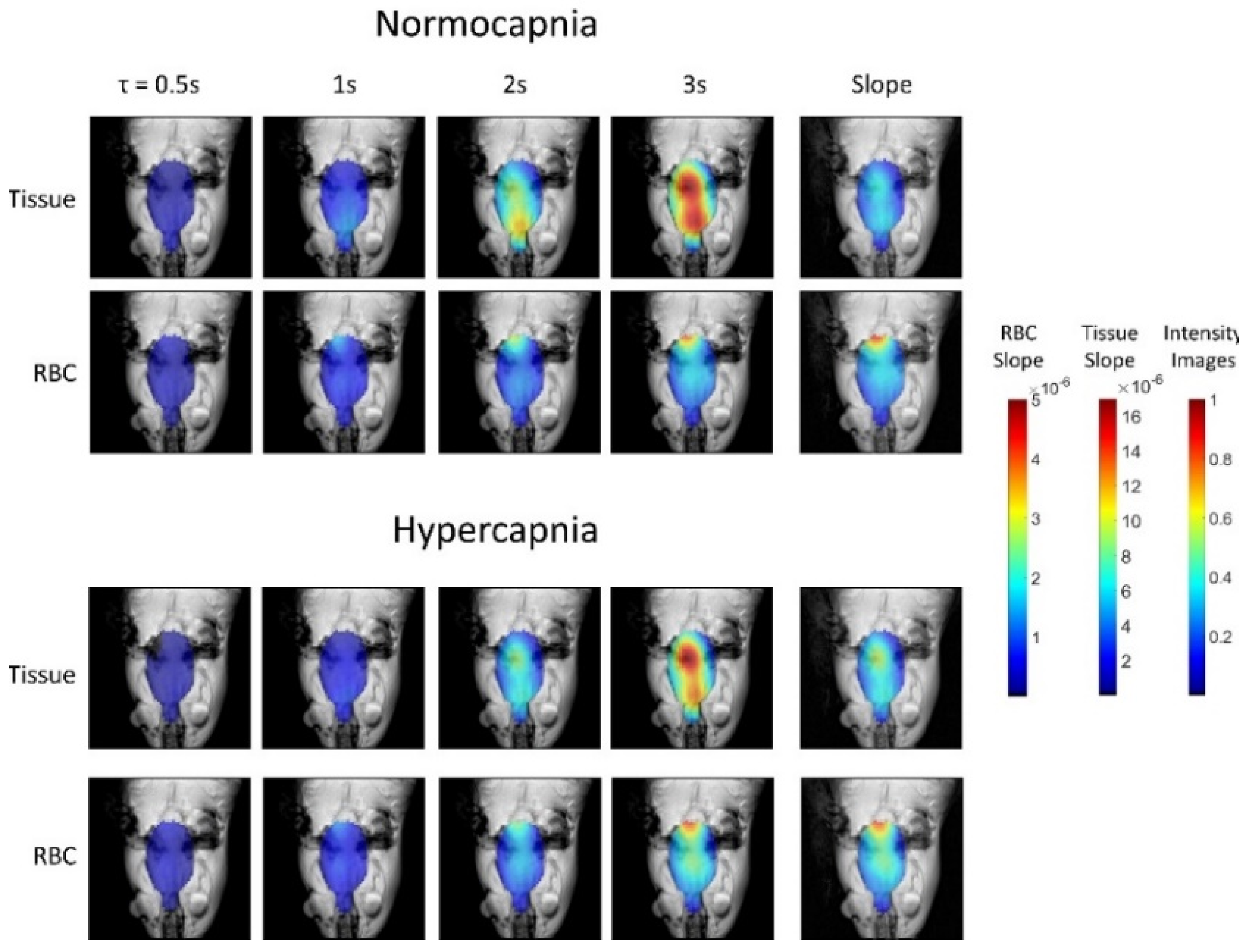



| Paper | Model | Species | Disease Model | Statistically Significant Outcome Measurements |
|---|---|---|---|---|
| Imai et al. (2010) [80] | Patz | Mice | Emphysema | SVR |
| Freeman et al. (2013) [81] | MOXE | Mice | -- | -- |
| Fox et al. (2014) [82] | Månsson | Rats | Radiation induced lung injury | TTR_Tissue † |
| Li et al. (2016) [83] | MOXE | Rats | Radiation induced lung injury | Capillary transit time, septal wall thickness, haematocrit |
| Zhang et al. (2016) [83] | MOXE | Rats | Cigarette smoke injury | Septal wall thickness, air-capillary barrier thickness |
| Doganay et al. (2016) [84] | Månsson | Rats | Radiation induced lung injury | Pulmonary tissue thickness, relative blood volume |
| Zhong et al. (2017) [74] | MOXE | Rats | -- | -- |
| Zanette et al. (2018) [75] | MOXE | Rats | Radiation induced lung injury | Air-capillary barrier thickness, haematocrit |
| Zhang et al. (2020) [85] | MOXE | Rats | Fine particulate matter pollution | Septal wall thickness |
| Ruppert et al. (2020) [86] | Patz | Rabbits | -- | -- |
| Fliss et al. (2021) [87] | MOXE | Rats | Bronchopulmonary dysplasia | Mean chord length, SVR, haematocrit |
| Nuclear Density | Polarization (%) | Gyromagnetic Ratio | Magnetization @ 3 T | |
|---|---|---|---|---|
| 1H (conventional MRI) | 30 M | 3.3 × 10−4 × (B/T) | γP | 1 |
| HXe Gas phase | 0.03 M | ~20 | 0.28 γP | 9 |
| HXe Dissolved phase | 0.0006 M | ~20 | 0.28 γP | 0.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kadlecek, S.; Friedlander, Y.; Virgincar, R.S. Preclinical MRI Using Hyperpolarized 129Xe. Molecules 2022, 27, 8338. https://doi.org/10.3390/molecules27238338
Kadlecek S, Friedlander Y, Virgincar RS. Preclinical MRI Using Hyperpolarized 129Xe. Molecules. 2022; 27(23):8338. https://doi.org/10.3390/molecules27238338
Chicago/Turabian StyleKadlecek, Stephen, Yonni Friedlander, and Rohan S. Virgincar. 2022. "Preclinical MRI Using Hyperpolarized 129Xe" Molecules 27, no. 23: 8338. https://doi.org/10.3390/molecules27238338
APA StyleKadlecek, S., Friedlander, Y., & Virgincar, R. S. (2022). Preclinical MRI Using Hyperpolarized 129Xe. Molecules, 27(23), 8338. https://doi.org/10.3390/molecules27238338




