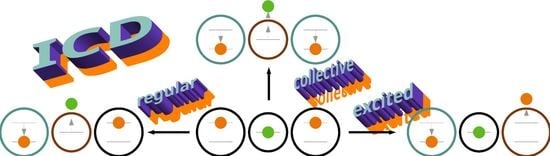
Three-Electron Dynamics of the Interparticle Coulombic Decay in Doubly Excited Clusters with One-Dimensional Continuum Confinement
Abstract
:1. Introduction
2. Theory
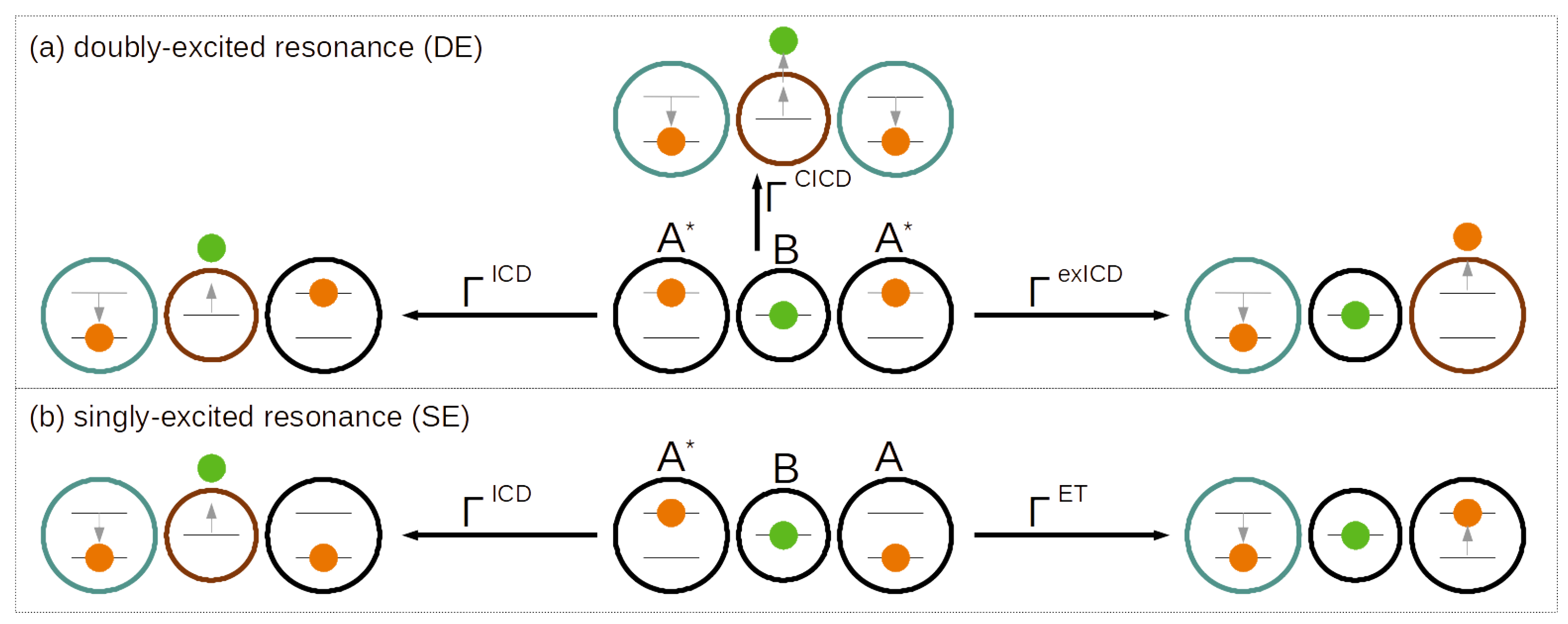
2.1. Pathways of the Inter-Coulombic Decay in a Linear Array
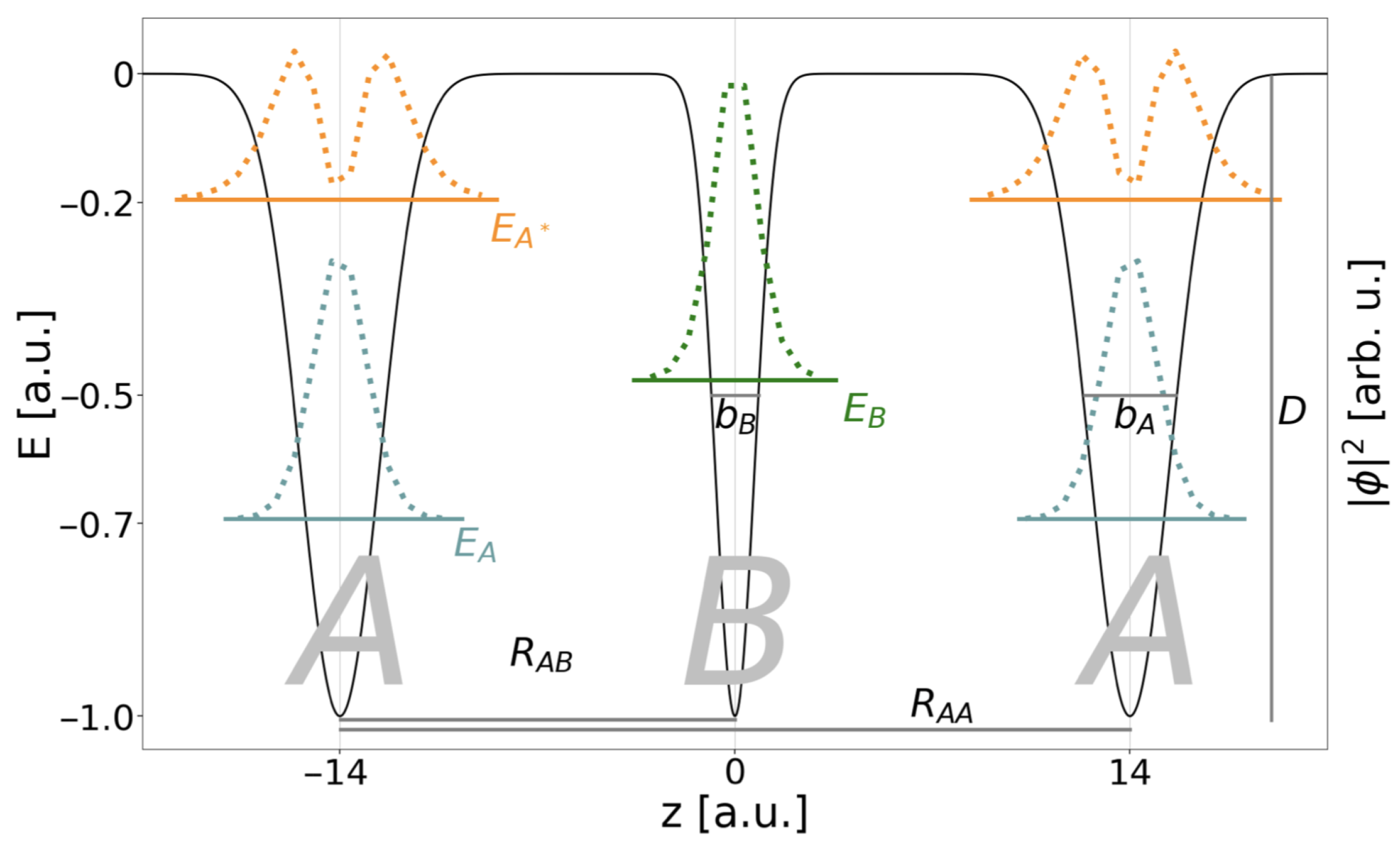
2.2. Electron Dynamics in Model Potentials
3. Computational Details
4. Results
4.1. Electronic Structure
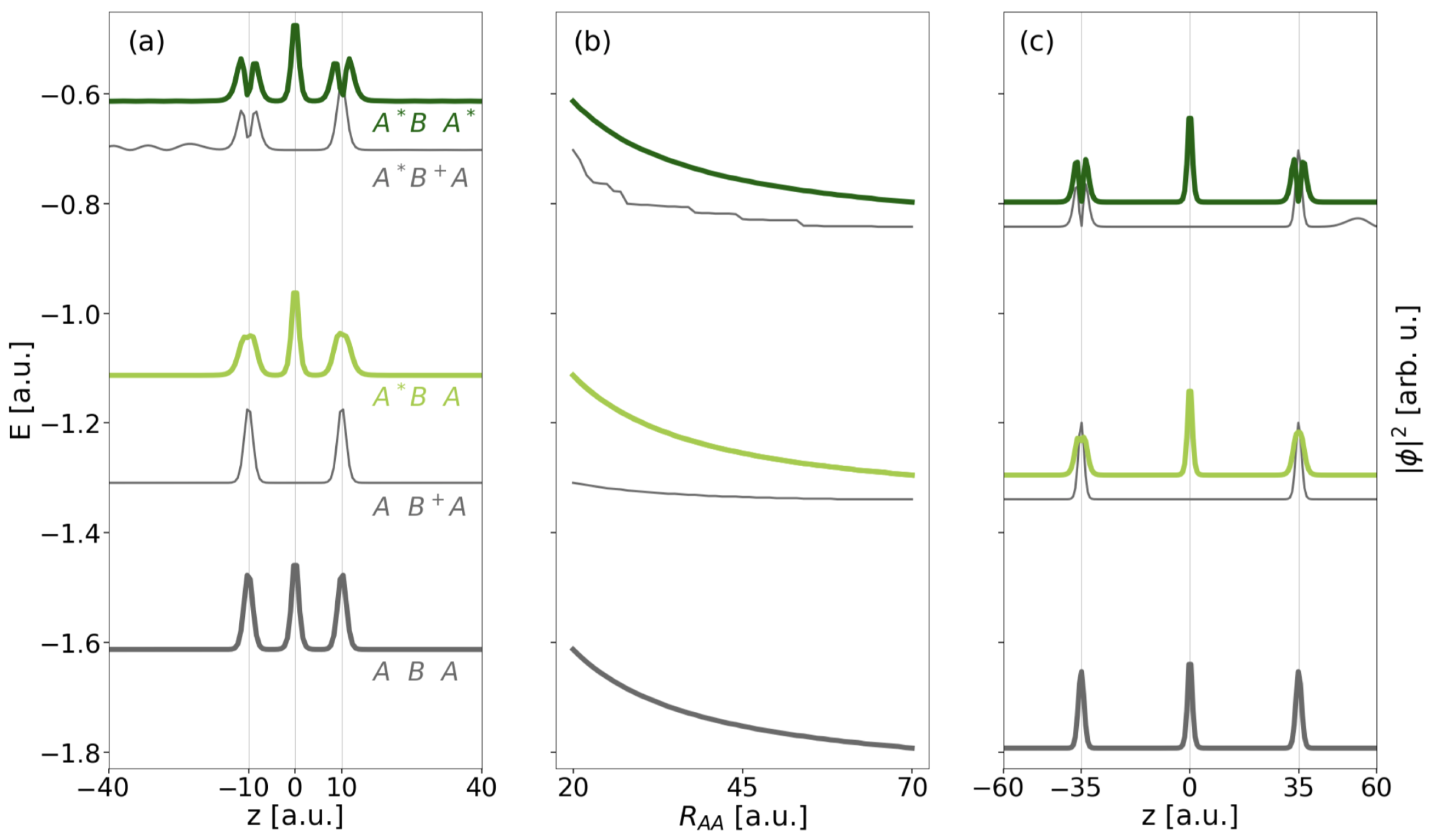
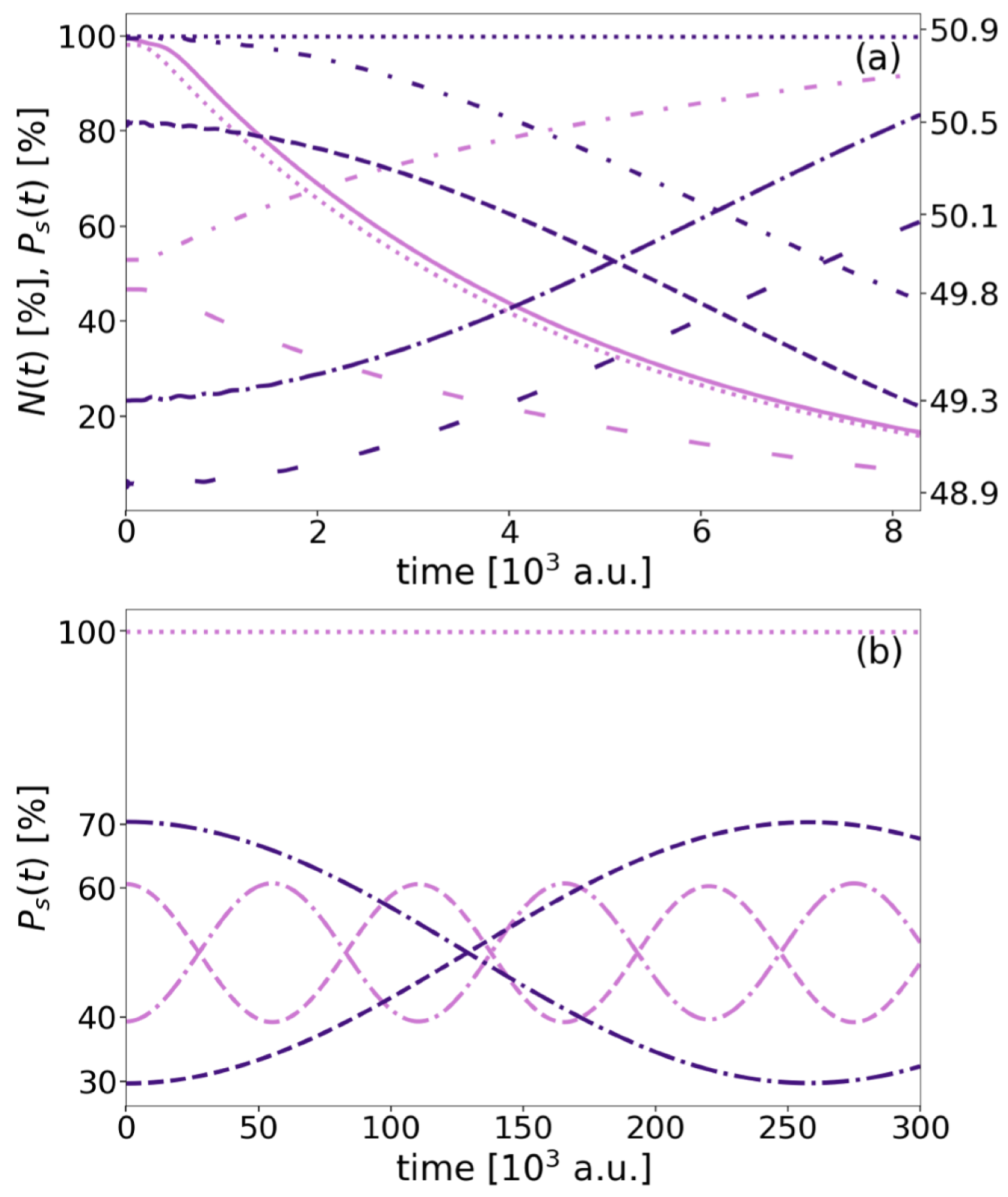
4.2. Electron Dynamics
4.2.1. Dynamics of the Doubly Excited Resonance
4.2.2. Dynamics of the Singly Excited Resonance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cederbaum, L.S.; Zobeley, J.; Tarantelli, F. Giant Intermolecular Decay and Fragmentation of Clusters. Phys. Rev. Lett. 1997, 79, 4778–4781. [Google Scholar] [CrossRef]
- Feshbach, H. Unified theory of nuclear reactions. Ann. Phys. 1958, 5, 357. [Google Scholar] [CrossRef]
- Morishita, Y.; Liu, X.J.; Saito, N.; Lischke, T.; Kato, M.; Prümper, G.; Oura, M.; Yamaoka, H.; Tamenori, Y.; Suzuki, I.H.; et al. Experimental Evidence of Interatomic Coulombic Decay from the Auger Final States in Argon Dimers. Phys. Rev. Lett. 2006, 96, 243402. [Google Scholar] [CrossRef] [PubMed]
- Sisourat, N.; Kryzhevoi, N.V.; Kolorenc, P.; Scheit, S.; Jahnke, T.; Cederbaum, L.S. Ultralong-range energy transfer by interatomic Coulombic decay in an extreme quantum system. Nature Phys. 2010, 6, 508–511. [Google Scholar] [CrossRef]
- Unger, I.; Hollas, D.; Seidel, R.; Thürmer, S.; Aziz, E.F.; Slavíček, P.; Winter, B. Control of X-ray Induced Electron and Nuclear Dynamics in Ammonia and Glycine Aqueous Solution via Hydrogen Bonding. J. Phys. Chem. B 2015, 119, 10750. [Google Scholar] [CrossRef] [PubMed]
- Averbukh, V.; Cederbaum, L.S. Interatomic Electronic Decay in Endohedral Fullerenes. Phys. Rev. Lett. 2006, 96, 053401. [Google Scholar] [CrossRef]
- De, R.; Magrakvelidze, M.; Madjet, M.E.; Manson, S.T.; Chakraborty, H.S. First prediction of inter-Coulombic decay of C60 inner vacancies through the continuum of confined atoms. J. Phys. B 2016, 49, 11LT01. [Google Scholar] [CrossRef] [Green Version]
- Bande, A.; Gokhberg, K.; Cederbaum, L.S. Dynamics of interatomic Coulombic decay in quantum dots. J. Chem. Phys. 2011, 135, 144112. [Google Scholar] [CrossRef]
- Cherkes, I.; Moiseyev, N. Electron relaxation in quantum dots by the interatomic Coulombic decay mechanism. Phys. Rev. B 2011, 83, 113303. [Google Scholar] [CrossRef]
- Förster, T. Energiewanderung und fluoreszenz. Naturwissenschaften. Naturwiss 1946, 33, 166. [Google Scholar] [CrossRef]
- Stryer, L.; Haugland, R.P. Energy transfer: A spectroscopic ruler. Proc. Natl. Acad. Sci. USA 1967, 58, 719–726. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Santra, R.; Cederbaum, L.S. Non-Hermitian electronic theory and applications to clusters. Phys. Rep. 2002, 368, 1. [Google Scholar] [CrossRef]
- Averbukh, V.; Müller, I.B.; Cederbaum, L.S. Mechanism of Interatomic Coulombic Decay in Clusters. Phys. Rev. Lett. 2004, 93, 263002. [Google Scholar] [CrossRef] [PubMed]
- Jones, G.A.; Bradshaw, D.S. Resonance Energy Transfer: From Fundamental Theory to Recent Applications. Front. Phys. 2019, 7, 100. [Google Scholar] [CrossRef] [Green Version]
- Weber, F.; Aziz, E.F.; Bande, A. Interdependence of ICD rates in paired quantum dots on geometry. J. Comput. Chem. 2017, 38, 2141. [Google Scholar] [CrossRef] [Green Version]
- Stumpf, V.; Brunken, C.; Gokhberg, K. Impact of metal ion’s charge on the interatomic Coulombic decay widths in microsolvated clusters. J. Chem. Phys. 2016, 145, 104306. [Google Scholar] [CrossRef]
- Haller, A.; Peláez, D.; Bande, A. Inter-Coulombic Decay in Laterally Arranged Quantum Dots Controlled by Polarized Lasers. J. Phys. Chem. C 2019, 123, 14754–14765. [Google Scholar] [CrossRef]
- Guskov, V.A.; Langkabel, F.; Berg, M.; Bande, A. An Impurity Effect for the Rates of the Interparticle Coulombic Decay. QUARKS Braz. Electron. J. Phys. Chem. Mat. Sci. 2020, 3, 31928. [Google Scholar] [CrossRef]
- Miteva, T.; Kazandjian, S.; Kolorenč, P.; Votavová, P.; Sisourat, N. Interatomic Coulombic Decay Mediated by Ultrafast Superexchange Energy Transfer. Phys. Rev. Lett. 2017, 119, 083403. [Google Scholar] [CrossRef] [Green Version]
- Votavová, P.; Miteva, T.; Engin, S.; Kazandjian, S.; Kolorenč, P.; Sisourat, N. Mechanism of superexchange interatomic Coulombic decay in rare-gas clusters. Phys. Rev. A 2019, 100, 022706. [Google Scholar] [CrossRef]
- Bennett, R.; Votavová, P.; Kolorenč, P.; Miteva, T.; Sisourat, N.; Buhmann, S.Y. Virtual Photon Approximation for Three-Body Interatomic Coulombic Decay. Phys. Rev. Lett. 2019, 122, 153401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Agueny, H.; Pesche, M.; Lutet-Toti, B.; Miteva, T.; Molle, A.; Caillat, J.; Sisourat, N. Interparticle coulombic decay in coupled quantum dots: Enhanced energy transfer via bridge assisted mechanisms. Phys. Rev. B 2020, 101, 195431. [Google Scholar] [CrossRef]
- Kuleff, A.I.; Gokhberg, K.; Kopelke, S.; Cederbaum, L.S. Ultrafast Interatomic Electronic Decay in Multiply Excited Clusters. Phys. Rev. Lett. 2010, 105, 043004. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Averbukh, V.; Kolorenč, P. Collective Interatomic Decay of Multiple Vacancies in Clusters. Phys. Rev. Lett. 2009, 103, 183001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Langkabel, F.; Lützner, M.; Bande, A. Interparticle Coulombic Decay Dynamics along Single- and Double-Ionization Pathways. J. Phys. Chem. C 2019, 123, 21757. [Google Scholar] [CrossRef]
- Langkabel, F.; Bande, A. Three-electron dynamics of the interparticle Coulombic decay with two-dimensional continuum confinement. J. Chem. Phys. 2021, 154, 054111. [Google Scholar] [CrossRef] [PubMed]
- Santra, R.; Zobeley, J.; Cederbaum, L.S. Electronic decay of valence holes in clusters and condensed matter. Phys. Rev. B 2001, 64, 245104. [Google Scholar] [CrossRef]
- Fasshauer, E.; Förstel, M.; Pallmann, S.; Pernpointner, M.; Hergenhahn, U. Using ICD for structural analysis of clusters: A case study on NeAr clusters. New J. Phys. 2014, 16, 103026. [Google Scholar] [CrossRef]
- Förstel, M.; Mucke, M.; Arion, T.; Lischke, T.; Pernpointner, M.; Hergenhahn, U.; Fasshauer, E. Long-Range Interatomic Coulombic Decay in ArXe Clusters: Experiment and Theory. J. Phys. Chem. C 2016, 120, 22957. [Google Scholar] [CrossRef]
- Demekhin, P.V.; Gokhberg, K.; Jabbari, G.; Kopelke, S.; Kuleff, A.I.; Cederbaum, L.S. Overcoming blockade in producing doubly excited dimers by a single intense pulse and their decay. J. Phys. B At. Mol. Opt. Phys. 2013, 46, 021001. [Google Scholar] [CrossRef]
- Takanashi, T.; Golubev, N.V.; Callegari, C.; Fukuzawa, H.; Motomura, K.; Iablonskyi, D.; Kumagai, Y.; Mondal, S.; Tachibana, T.; Nagaya, K.; et al. Time-Resolved Measurement of Interatomic Coulombic Decay Induced by Two-Photon Double Excitation of Ne2. Phys. Rev. Lett. 2017, 118, 033202. [Google Scholar] [CrossRef] [Green Version]
- Nagaya, K.; Iablonskyi, D.; Golubev, N.V.; Matsunami, K.; Fukuzawa, H.; Motomura, K.; Nishiyama, T.; Sakai, T.; Tachibana, T.; Mondal, S.; et al. Interatomic Coulombic decay cascades in multiply excited neon clusters. Nat. Commun. 2016, 7, 13477. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- LaForge, A.C.; Drabbels, M.; Brauer, N.B.; Coreno, M.; Devetta, M.; Di Fraia, M.; Finetti, P.; Grazioli, C.; Katzy, R.; Lyamayev, V.; et al. Collective Autoionization in Multiply-Excited Systems: A novel ionization process observed in Helium Nanodroplets. Sci. Rep. 2014, 4, 3621. [Google Scholar] [CrossRef] [Green Version]
- Ovcharenko, Y.; Lyamayev, V.; Katzy, R.; Devetta, M.; LaForge, A.; O’Keeffe, P.; Plekan, O.; Finetti, P.; Di Fraia, M.; Mudrich, M.; et al. Novel collective autoionization process observed in electron spectra of He clusters. Phys. Rev. Lett. 2014, 112, 073401. [Google Scholar] [CrossRef] [Green Version]
- Averbukh, V.; Cederbaum, L.S. Ab initio calculation of interatomic decay rates by a combination of the Fano ansatz, Green’s-function methods, and the Stieltjes imaging technique. J. Chem. Phys. 2005, 123, 204107. [Google Scholar] [CrossRef] [PubMed]
- Gokhberg, K.; Averbukh, V.; Cederbaum, L.S. Decay rates of inner-valence excitations in noble gas atoms. J. Chem. Phys. 2007, 126, 154107. [Google Scholar] [CrossRef]
- Kolorencč, P.; Averbukh, V.; Gokhberg, K.; Cederbaum, L.S. Ab initio calculation of interatomic decay rates of excited doubly ionized states in clusters. J. Chem. Phys. 2008, 129, 244102. [Google Scholar] [CrossRef] [Green Version]
- Averbukh, V.; Kolorencč, P.; Gokhberg, K.; Cederbaum, L.S. Quantum Chemical Approach to Interatomic Decay Rates in Clusters. In Advances in the Theory of Atomic and Molecular Systems; Springer: Dordreht, The Netherlands, 2009; Volume 20, p. 155. [Google Scholar]
- Kreidi, K.; Demekhin, P.V.; Jahnke, T.; Weber, T.; Havermeier, T.; Liu, X.; Morishita, Y.; Schössler, S.; Schmidt, L.; Schöffler, M.; et al. Photo- and Auger-Electron Recoil Induced Dynamics of Interatomic Coulombic Decay. Phys. Rev. Lett. 2009, 103, 033001. [Google Scholar] [CrossRef] [PubMed]
- Miteva, T.; Kazandjian, S.; Sisourat, N. On the computations of decay widths of Fano resonances. Chem. Phys. 2017, 482, 208. [Google Scholar] [CrossRef] [Green Version]
- Åberg, T.; Howat, G. Corpuscles and Radiation in Matter I. In Handbuch der Physick; Springer: Berlin/Heidelberg, Germany, 1982; Volume 31, p. 419. [Google Scholar]
- Matsakis, D.; Coster, A.; Laster, B.; Sime, R. A renaming proposal: “The Auger–Meitner effect”. Phys. Today 2019, 72, 10–11. [Google Scholar] [CrossRef]
- Santra, R.; Zobeley, J.; Cederbaum, L.S.; Moiseyev, N. Interatomic Coulombic Decay in van der Waals Clusters and Impact of Nuclear Motion. Phys. Rev. Lett. 2000, 85, 4490. [Google Scholar] [CrossRef] [PubMed]
- Moiseyev, N.; Santra, R.; Zobeley, J.; Cederbaum, L.S. Fingerprints of the nodal structure of autoionizing vibrational wave functions in clusters: Interatomic Coulombic decay in Ne dimer. J. Chem. Phys. 2001, 114, 7351. [Google Scholar] [CrossRef]
- Scheit, S.; Cederbaum, L.S.; Meyer, H.D. Time-dependent interplay between electron emission and fragmentation in the interatomic Coulombic decay. J. Chem. Phys. 2003, 118, 2092. [Google Scholar] [CrossRef]
- Sisourat, N.; Kryzhevoi, N.V.; Kolorencč, P.; Scheit, S.; Cederbaum, L.S. Impact of nuclear dynamics on interatomic Coulombic decay in a He dimer. Phys. Rev. A 2010, 82, 053401. [Google Scholar] [CrossRef]
- Chiang, Y.C.; Otto, F.; Meyer, H.D.; Cederbaum, L.S. Interrelation between the distributions of kinetic energy release and emitted electron energy following the decay of electronic states. Phys. Rev. Lett. 2011, 107, 173001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bande, A. Acoustic phonon impact on the inter-Coulombic decay process in charged quantum dot pairs. Mol. Phys. 2019, 117, 2014–2028. [Google Scholar] [CrossRef] [Green Version]
- Pont, F.M.; Bande, A.; Cederbaum, L.S. Controlled energy-selected electron capture and release in double quantum dots. Phys. Rev. B 2013, 88, 241304. [Google Scholar] [CrossRef] [Green Version]
- Bednarek, S.; Szafran, B.; Chwiej, T.; Adamowski, J. Effective interaction for charge carriers confined in quasi-one-dimensional nanostructures. Phys. Rev. B 2003, 68, 045328. [Google Scholar] [CrossRef] [Green Version]
- Meyer, H.D.; Manthe, U.; Cederbaum, L. The multi-configurational time-dependent Hartree approach. Chem. Phys. Lett. 1990, 165, 73–78. [Google Scholar] [CrossRef]
- Manthe, U.; Meyer, H.; Cederbaum, L.S. Wave-packet dynamics within the multiconfiguration Hartree framework: General aspects and application to NOCl. J. Chem. Phys. 1992, 97, 3199–3213. [Google Scholar] [CrossRef]
- Beck, M.; Jäckle, A.; Worth, G.; Meyer, H.D. The multiconfiguration time-dependent Hartree (MCTDH) method: A highly efficient algorithm for propagating wavepackets. Phys. Rep. 2000, 324, 1–105. [Google Scholar] [CrossRef]
- Light, J.C. Time-Dependent Quantum Molecular Dynamics; Plenum: New York, NY, USA, 1992; p. 185. [Google Scholar]
- Light, J.C.; Carrington Jr, T. Discrete-Variable Representations and their Utilization. Adv. Chem. Phys. 2000, 114, 263. [Google Scholar] [CrossRef]
- Bande, A. Electron dynamics of interatomic Coulombic decay in quantum dots induced by a laser field. J. Chem. Phys. 2013, 138, 214104. [Google Scholar] [CrossRef] [PubMed]
- Meyer, H.D.; Gatti, F.; Worth, G.A. (Eds.) Multidimensional Quantum Dynamics: MCTDH Theory and Applications; Wiley-VCH: Weinheim, Germany, 2009. [Google Scholar]
- Jäckle, A.; Meyer, H.D. Product representation of potential energy surfaces. J. Chem. Phys. 1996, 104, 7974. [Google Scholar] [CrossRef]
- Meyer, H.D.; Worth, G.A. Quantum molecular dynamics: Propagating wavepackets and density operators using the Multi-configuration time-dependent Hartree (MCTDH) method. Theor. Chem. Acc. 2003, 109, 251. [Google Scholar] [CrossRef]
- Meyer, H.D.; Le Quere, F.; Leonard, C.; Gatti, F. Calculation and selective population of the vibrational levels with the Multiconfiguration Time-Dependent Hartree (MCTDH) algorithm. Chem. Phys. 2006, 329, 179. [Google Scholar] [CrossRef]
- Bande, A.; Pont, F.M.; Dolbundalchok, P.; Gokhberg, K.; Cederbaum, L.S. Dynamics of Interatomic Coulombic Decay in Quantum Dots: Singlet Initial State. EPJ Web Conf. 2013, 41, 04031. [Google Scholar] [CrossRef] [Green Version]
- Berg, M.; Uranga-Piña, L.; Martínez-Mesa, A.; Bande, A. Wavepacket golden rule treatment of interparticle Coulombic decay in paired quantum dots. J. Chem. Phys. 2019, 151, 244111. [Google Scholar] [CrossRef]
- Juzeliūnas, G.; Andrews, D.L. Quantum electrodynamics of resonant energy transfer in condensed matter. Phys. Rev. B 1994, 49, 8751. [Google Scholar] [CrossRef]
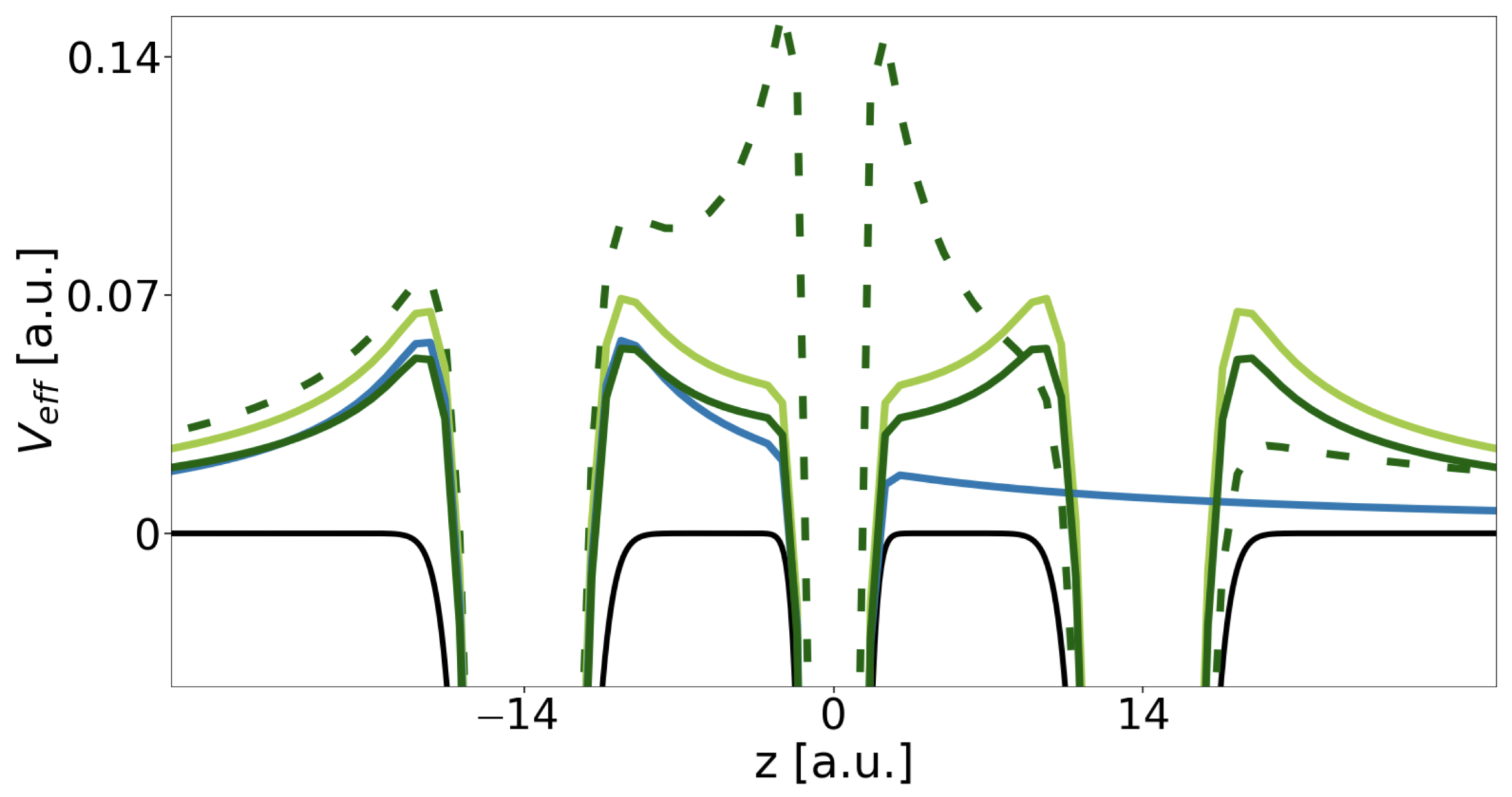
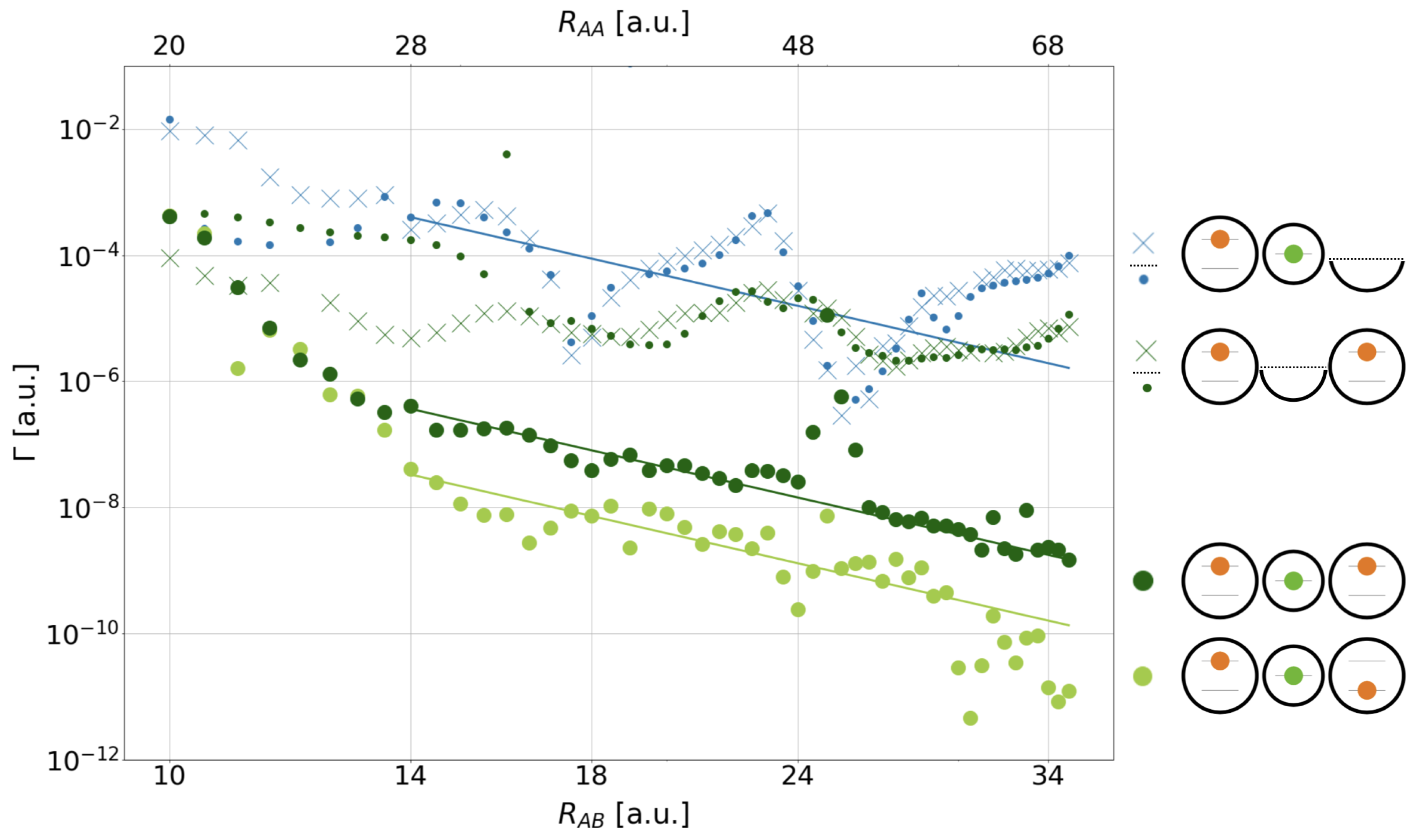
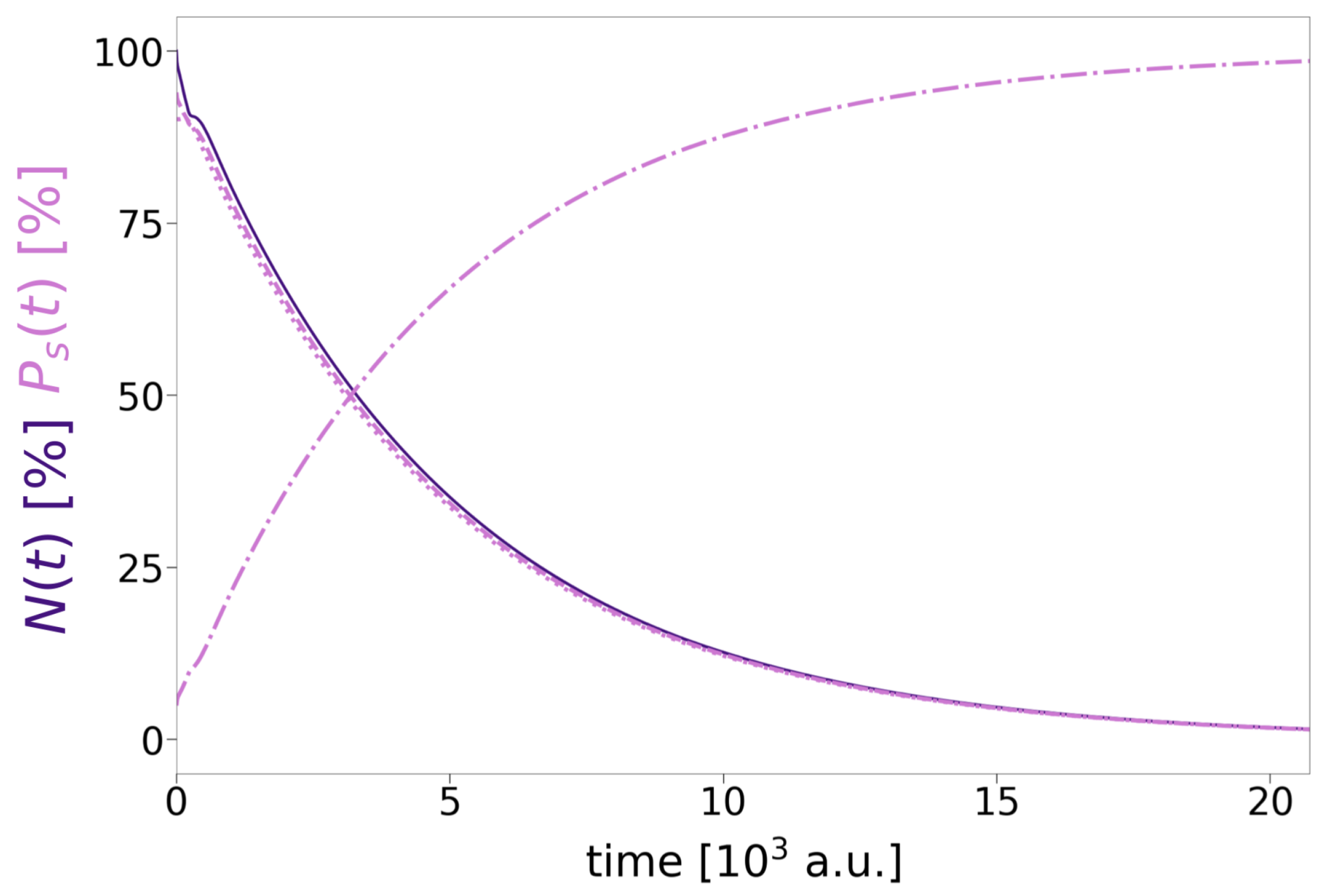


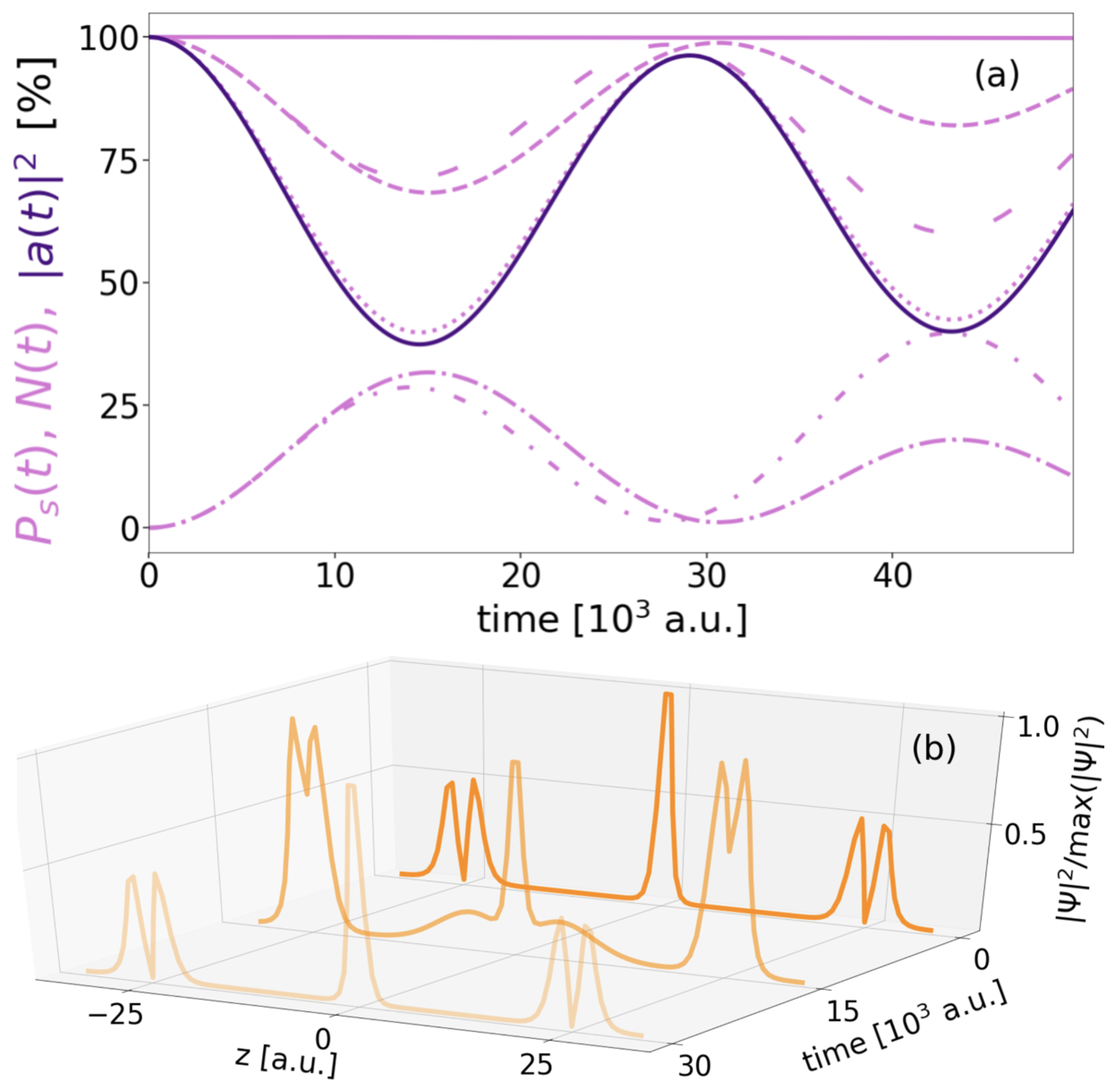


| DE | SE | ICD | exICD | |
|---|---|---|---|---|
| (a.u.) | ||||
| (a.u.) | > |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schäfer, J.-L.; Langkabel, F.; Bande, A. Three-Electron Dynamics of the Interparticle Coulombic Decay in Doubly Excited Clusters with One-Dimensional Continuum Confinement. Molecules 2022, 27, 8713. https://doi.org/10.3390/molecules27248713
Schäfer J-L, Langkabel F, Bande A. Three-Electron Dynamics of the Interparticle Coulombic Decay in Doubly Excited Clusters with One-Dimensional Continuum Confinement. Molecules. 2022; 27(24):8713. https://doi.org/10.3390/molecules27248713
Chicago/Turabian StyleSchäfer, Joana-Lysiane, Fabian Langkabel, and Annika Bande. 2022. "Three-Electron Dynamics of the Interparticle Coulombic Decay in Doubly Excited Clusters with One-Dimensional Continuum Confinement" Molecules 27, no. 24: 8713. https://doi.org/10.3390/molecules27248713