Theoretical, Equilibrium, Kinetics and Thermodynamic Investigations of Methylene Blue Adsorption onto Lignite Coal
Abstract
:1. Introduction
2. Results and Discussion
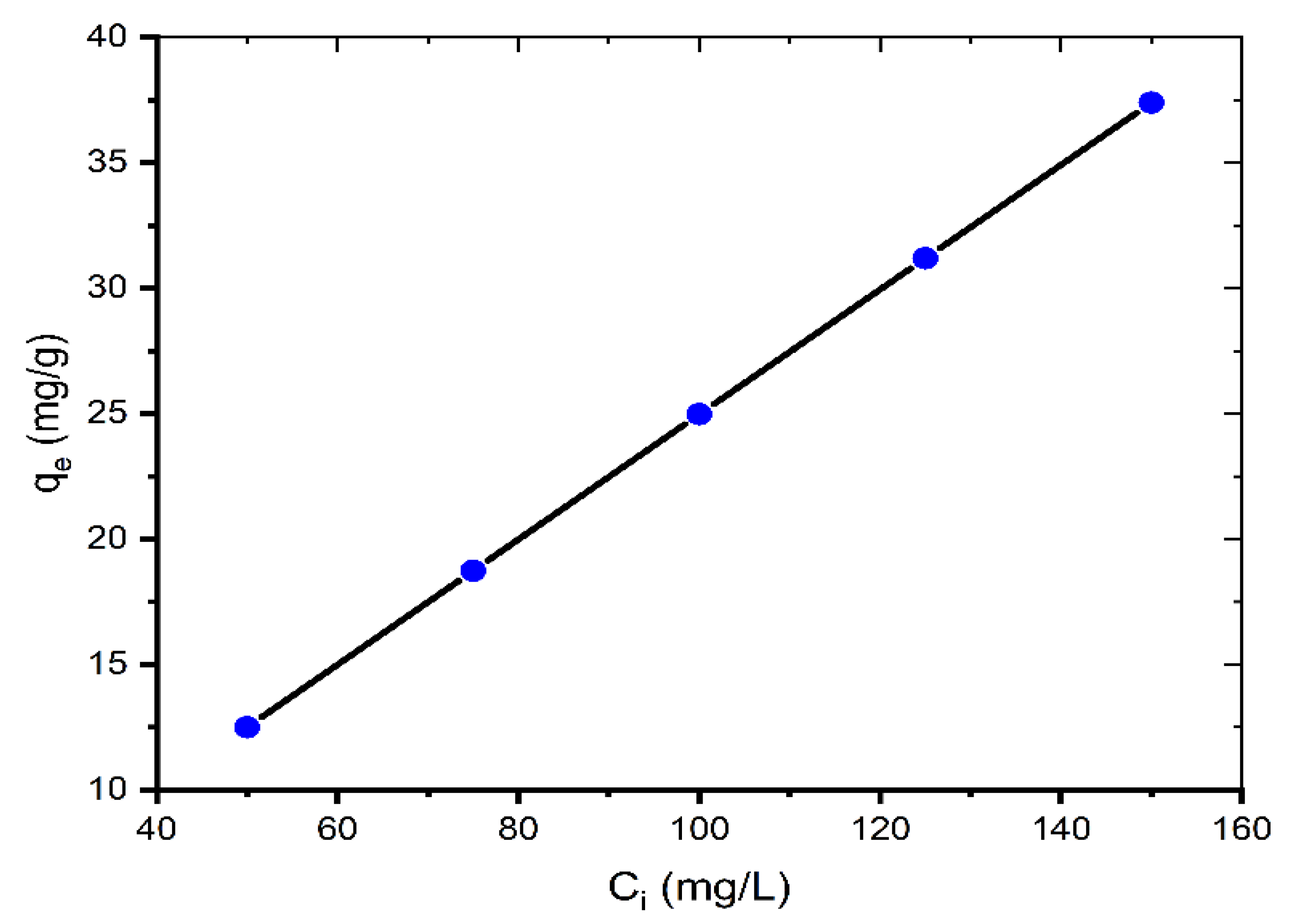
2.1. Effect of Contact Time and Initial MB Concentration
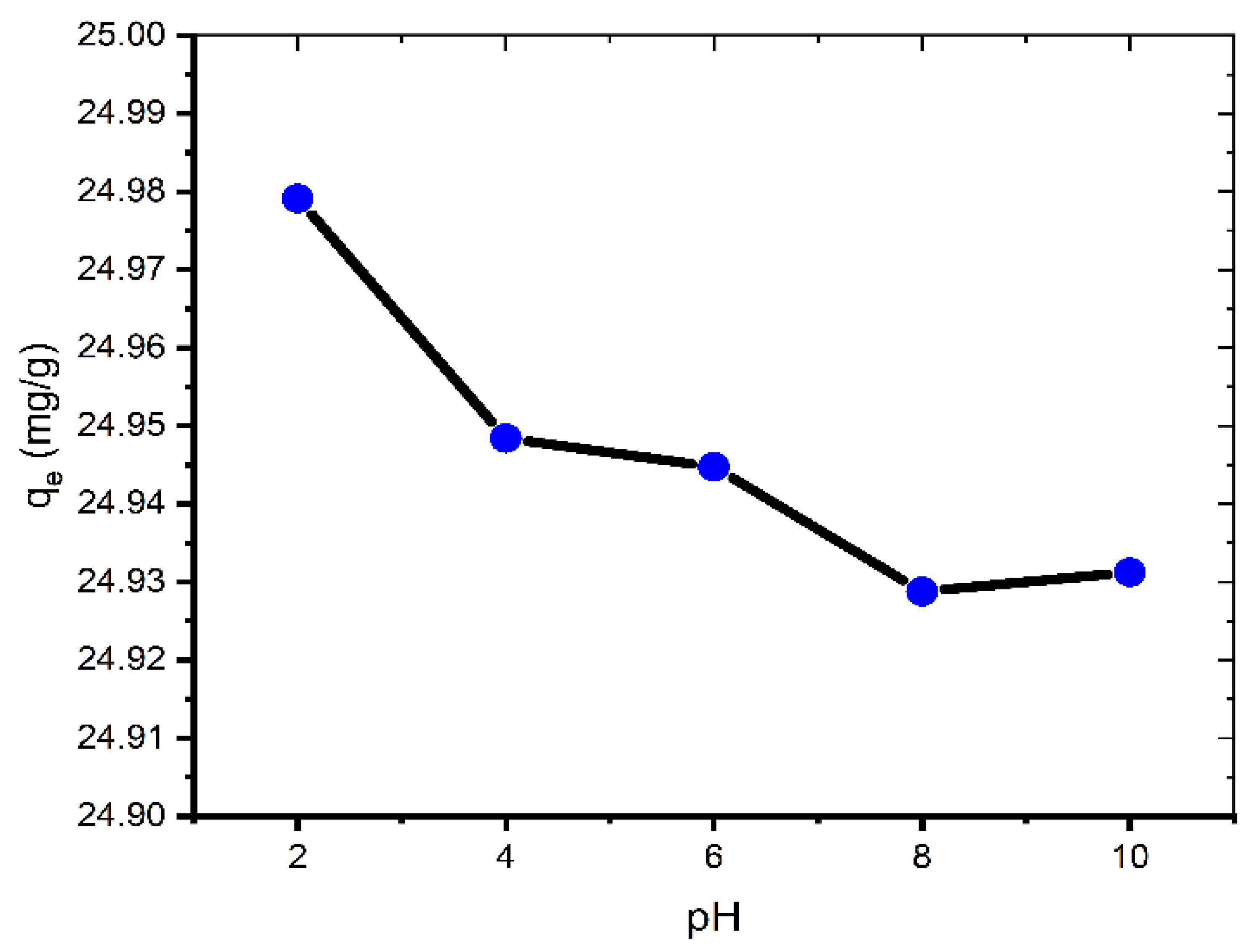
2.2. Effect of pH
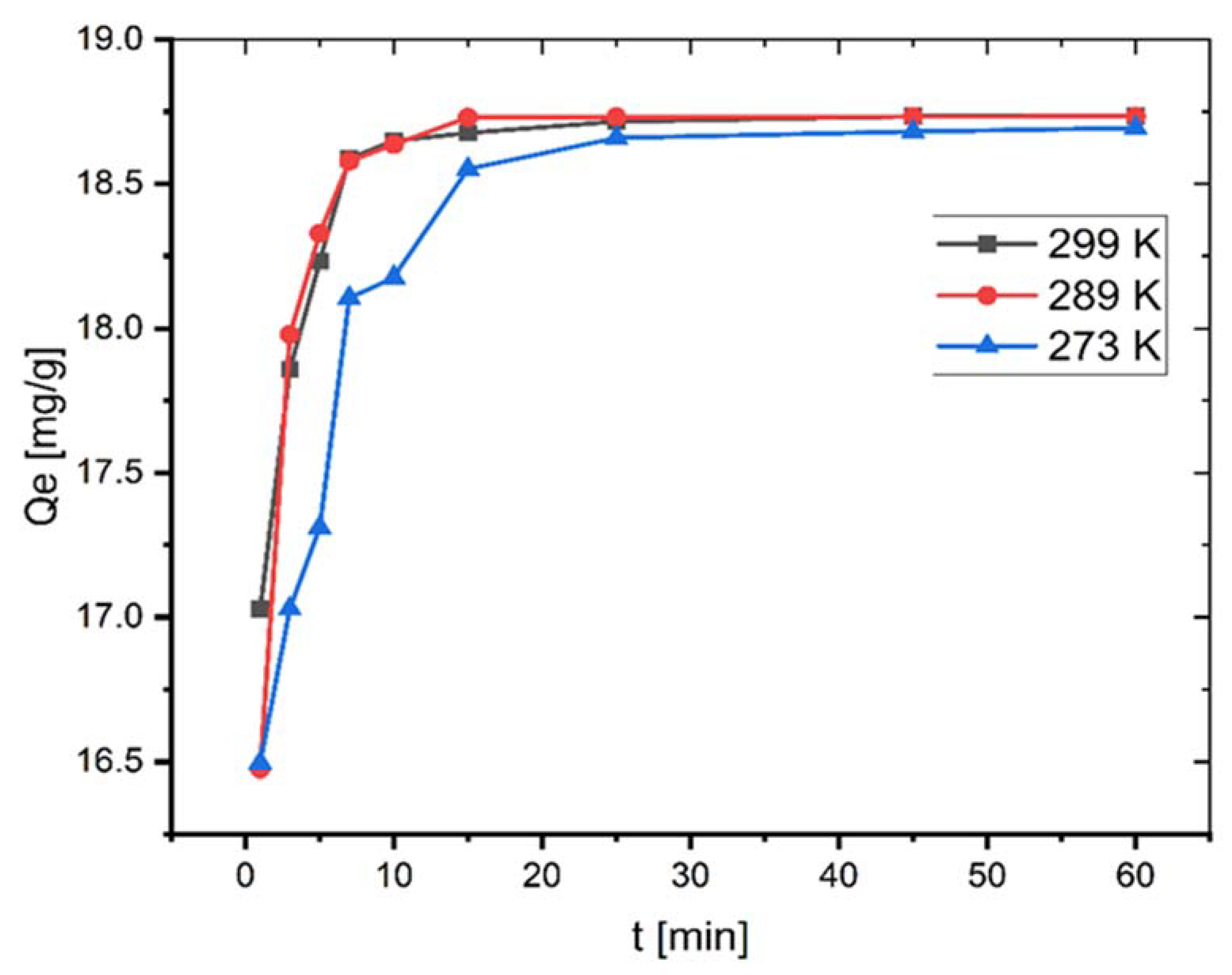
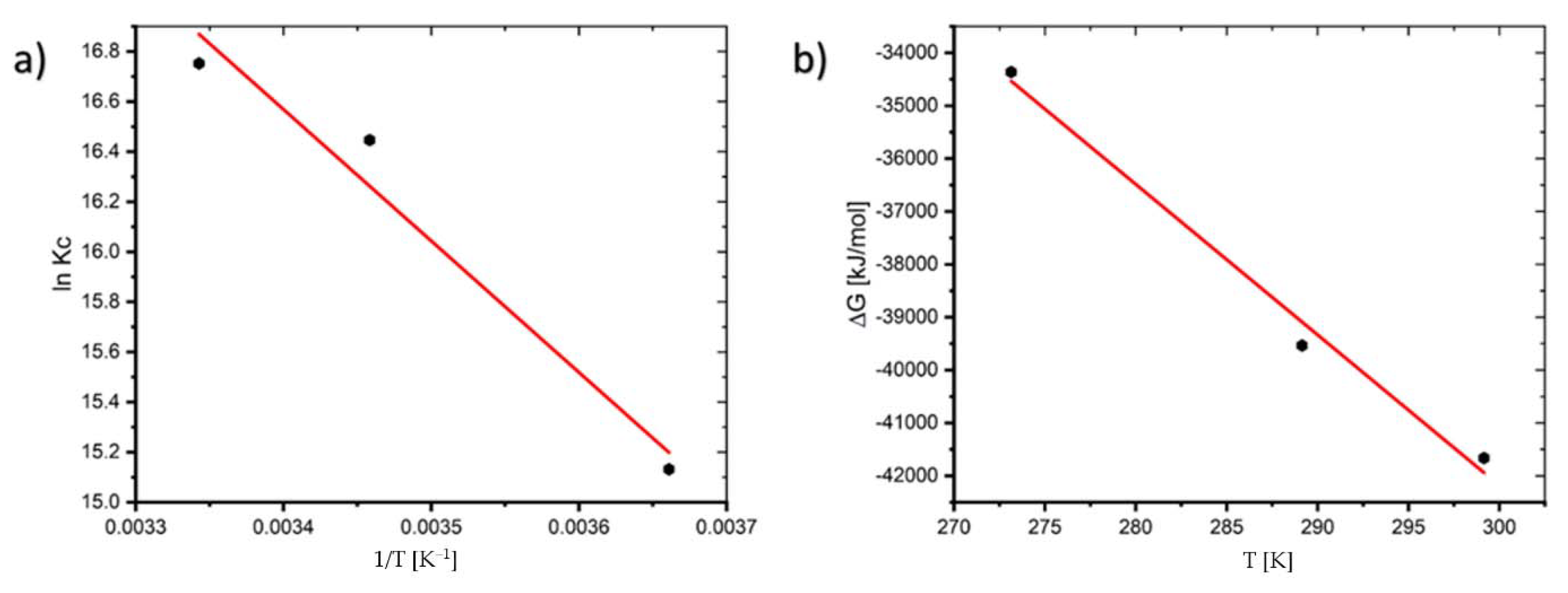
2.3. Effect of Temperature and Thermodynamic Parameters
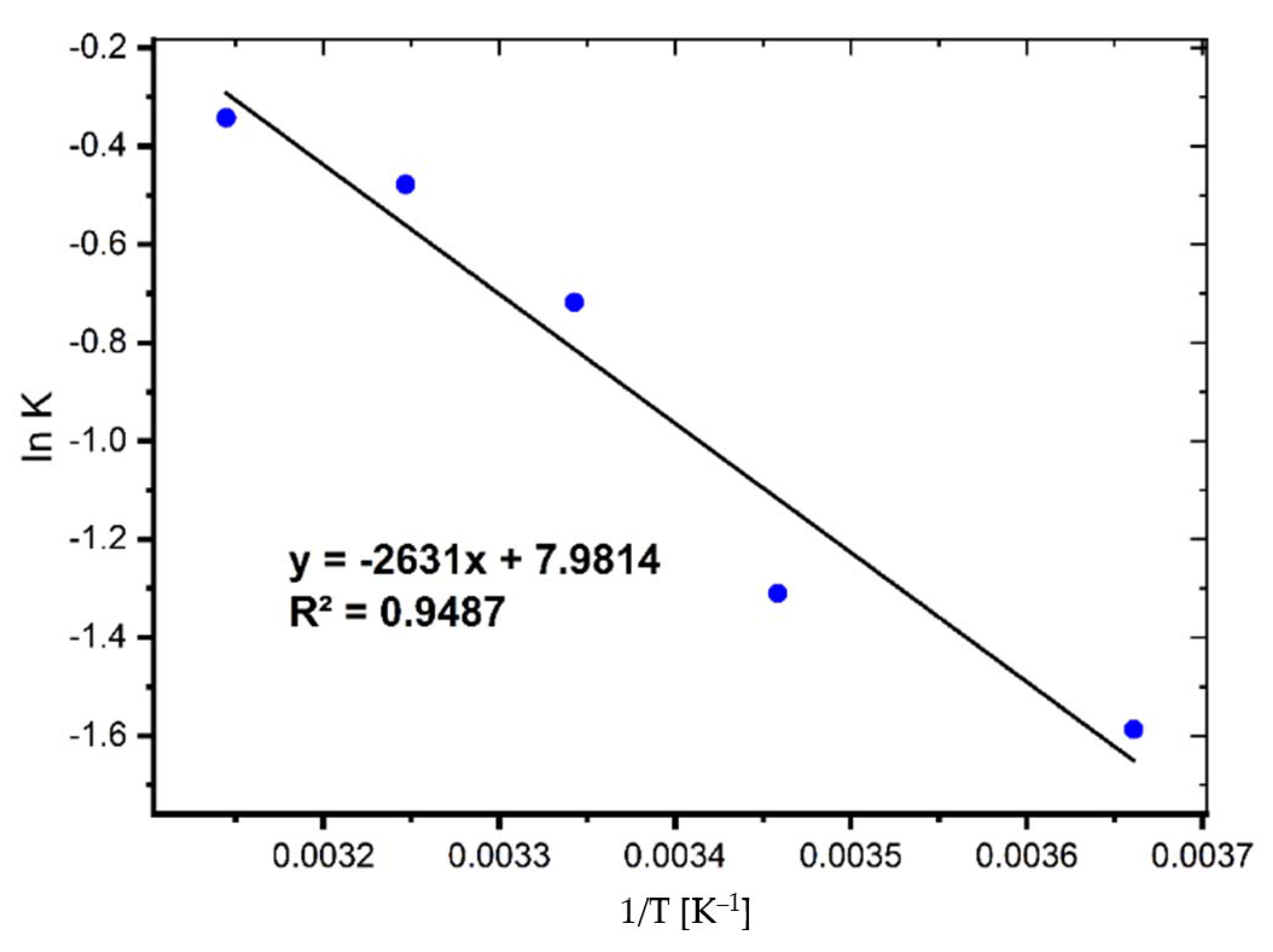
Activation Energy
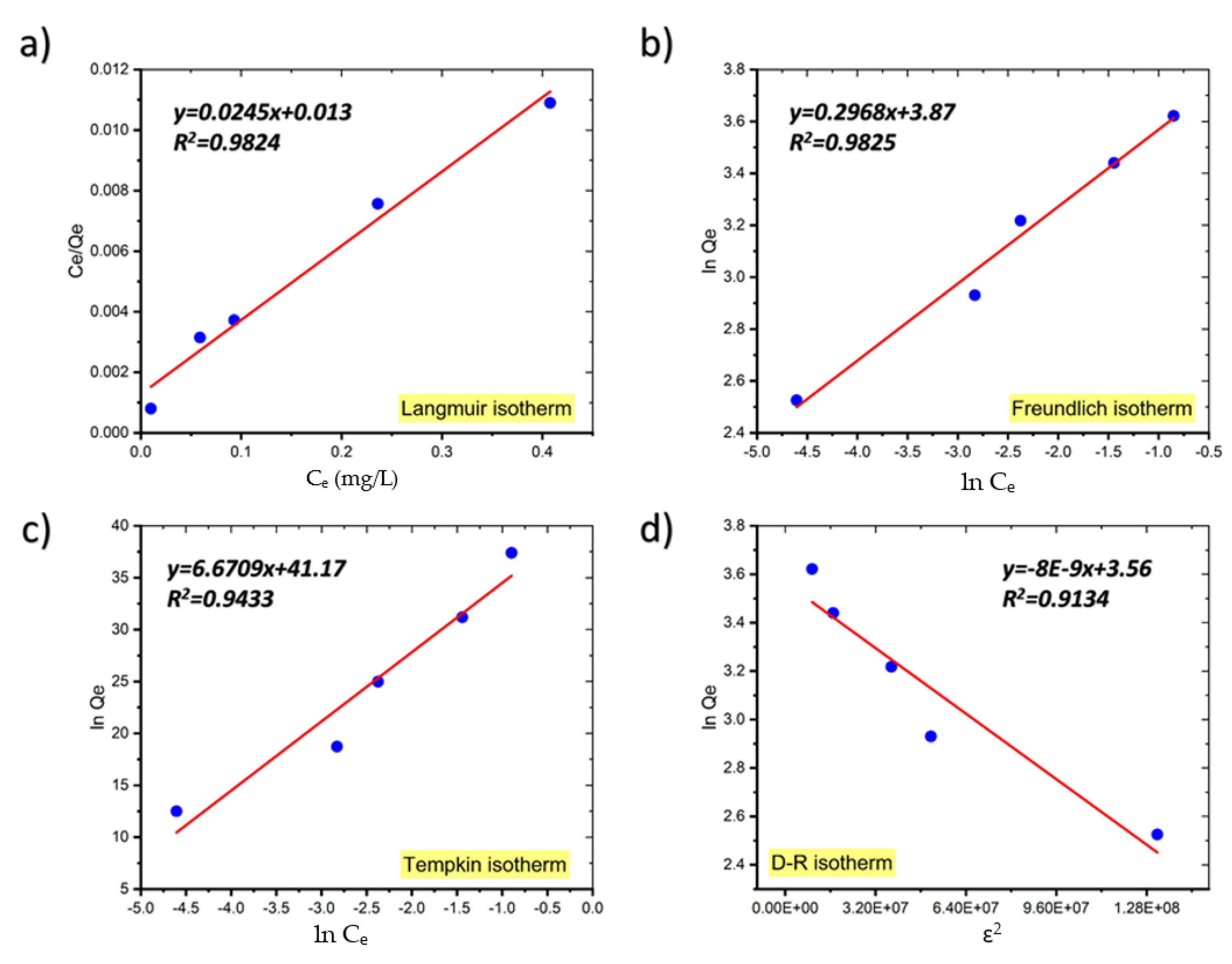
2.4. Adsorption Isotherms
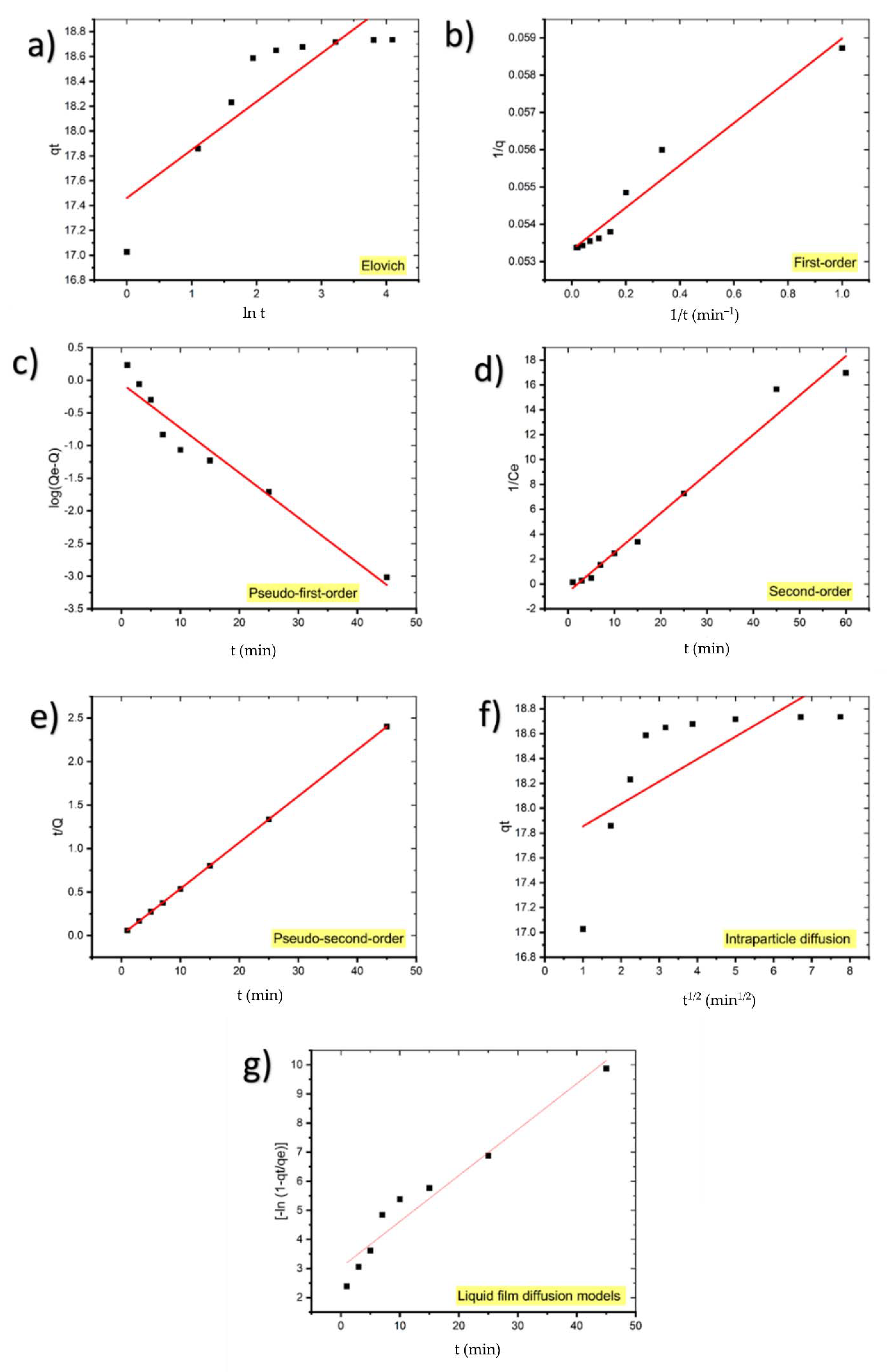
2.5. Kinetics
Diffusion Models
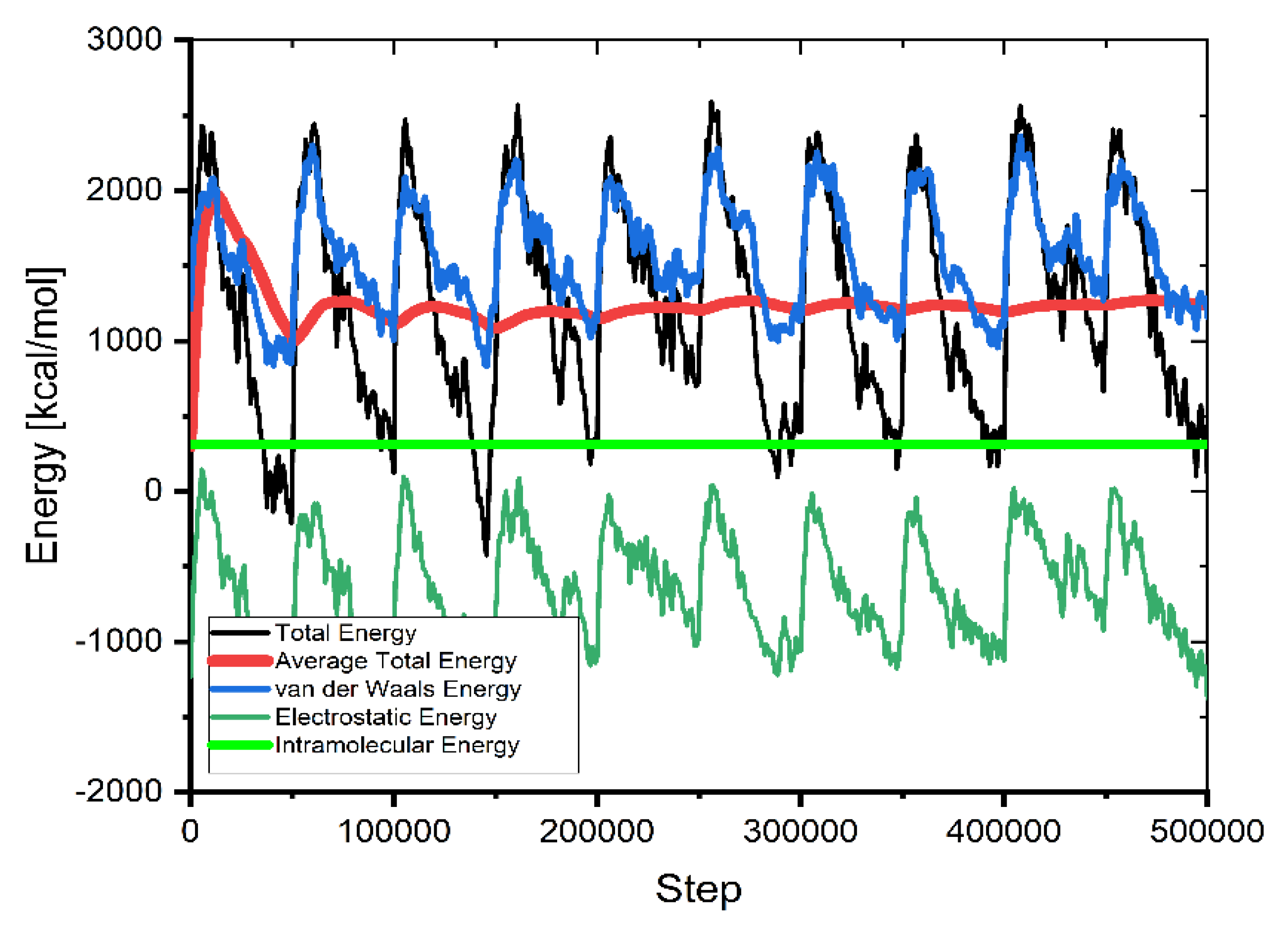
2.6. MC Calculations
2.7. FTIR Spectroscopy
3. Materials and Methods
3.1. Adsorbent and Adsorbate
3.2. Adsorption Experiments
3.3. Adsorption Isotherms
3.4. Adsorption Kinetics
Diffusion Models
3.5. Molecular Modelling and Monte Carlo (MC) Calculations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Renou, S.; Givaudan, J.G.; Poulain, S.; Dirassouyan, F.; Moulin, P. Landfill leachate treatment: Review and opportunity. J. Hazard. Mater. 2008, 150, 468–493. [Google Scholar] [CrossRef] [PubMed]
- Benitez, S.O.; Lozano, J.L.B. The municipal solid waste cycle in Mexico: Final disposal. Resour. Conserv. Recycl. 2003, 39, 239–250. [Google Scholar]
- Nagano, S.; Tamon, H.; Adzumi, T.; Nakagawa, K.; Suzuki, T. Activated carbon from municipal waste. Carbon 2000, 38, 915–920. [Google Scholar] [CrossRef]
- Montagnaro, F.; Santoro, L. Reuse of coal combustion ashes as dyes and heavy metal adsorbents: Effect of sieving and demineralization on waste properties and adsorption capacity. Chem. Eng. J. 2009, 150, 174–180. [Google Scholar] [CrossRef]
- Bello, O.S.; Adegoke, K.A.; Olaniyan, A.A.; Abdulazeez, H. Dye adsorption using biomass wastes and natural adsorbents: Overview and future prospects. Desalin. Water Treat. 2015, 53, 1292–1315. [Google Scholar] [CrossRef]
- Ali, S.Z.; Athar, M.; Farooq, U.; Salman, M. Insight into Equilibrium and Kinetics of the Binding of Cadmium Ions on Radiation-Modified Straw from Oryza sativa. J. Appl. Chem. 2013, 12. [Google Scholar] [CrossRef] [Green Version]
- Ravikumar, K.; Deebika, B.; Balu, K. Decolourization of aqueous dye solutions by a novel adsorbent: Application of statistical designs and surface plots for the optimization and regression analysis. J. Hazard. Mater. 2005, 122, 75–83. [Google Scholar] [CrossRef]
- Abidi, N.; Errais, E.; Duplay, J.; Berez, A.; Jrad, A.; Schäfer, G.; Ghazi, M.; Semhi, K.; Trabelsi-Ayadi, M. Treatment of dye containing effluent by natural clay. J. Clean. Prod. 2015, 86, 432–440. [Google Scholar] [CrossRef]
- Omer, S.O.; Hussein, M.A.; Hussein, B.H.M.; Mgaidi, A. Adsorption thermodynamics of cationic dyes (methylene blue and crystal violet) to a natural clay mineral from aqueous solution between 293.15 and 323.15 K. Arab. J. Chem. 2018, 11, 615–623. [Google Scholar] [CrossRef]
- Morais, L.C.; Freitas, O.M.; Gonçalves, E.P.; Vascancelos, L.T.; González Beça, C.G. Reactive dyes removal from wastewaters by adsorption on eucalyptus bark: Variables that define the process. Water Res. 1999, 33, 979–988. [Google Scholar] [CrossRef]
- Chiou, M.S.; Li, H.Y. Equilibrium and kinetic modeling of adsorption of reactive dye on cross-linked chitosan beads. J. Hazard. Mater. 2002, 93, 233–248. [Google Scholar] [CrossRef]
- Meshko, V.; Markovska, L.; Mincheva, M.; Rodrigues, A.E. Adsorption of basic dyes on granular activated carbon and natural zeolite. Water Res. 2001, 35, 3357–3366. [Google Scholar] [CrossRef]
- Sari, A.; Tuzen, M. Biosorption of cadmium(II) from aqueous solution by red algae (Ceramium virgatum): Equilibrium, kinetic and thermodynamic studies. J. Hazard. Mater. 2008, 157, 448–454. [Google Scholar] [CrossRef] [PubMed]
- Anayurt, R.A.; Sari, A.; Tuzen, M. Equilibrium, thermodynamic and kinetic studies on biosorption of Pb(II) and Cd(II) from aqueous solution by macrofungus (Lactarius scrobiculatus) biomass. Chem. Eng. J. 2009, 151, 255–261. [Google Scholar] [CrossRef]
- Sari, A.; Tuzen, M. Biosorption of Pb(II) and Cd(II) from aqueous solution using green alga (Ulva lactuca) biomass. J. Hazard. Mater. 2008, 152, 302–308. [Google Scholar] [CrossRef] [PubMed]
- Sari, A.; Tuzen, M.; Uluozlu, O.D.; Soylak, M. Biosorption of Pb(II) and Ni(II) from aqueous solution by lichen (Cladonia furcata) biomass. Biochem. Eng. J. 2007, 37, 151–158. [Google Scholar] [CrossRef]
- Crini, G.; Peindy, H.N.; Gimbert, F.; Robert, C. Removal of C.I. basic green 4 (malachite green) from aqueous solutions by adsorption using cyclodextrinbased adsorbent: Kinetic and equilibrium studies. Sep. Purif. Technol. 2007, 53, 97–110. [Google Scholar] [CrossRef]
- Altınıșik, A.; Gür, E.; Seki, Y. A natural sorbent, Luffa cylindrica for the removal of a model basic dye. J. Hazard. Mater. 2010, 179, 658–664. [Google Scholar] [CrossRef] [PubMed]
- Mane, V.S.; Mall, I.D.; Srivastava, V.C. Kinetic and equilibrium isotherm studies for the adsorptive removal brilliant green dye from aqueous solution by rice husk ash. J. Environ. Manag. 2007, 84, 390–400. [Google Scholar] [CrossRef]
- Dahri, M.K.; Kooh, M.R.R.; Lim, L.B.L. Removal of Methyl Violet 2B from Aqueous Solution Using Casuarina equisetifolia Needle. ISRN Environ. Chem. 2013, 2013, 619819. [Google Scholar] [CrossRef] [Green Version]
- Inyinbor, A.A.; Adekola, F.A.; Olatunji, G.A. Adsorption of Rhodamine B Dye from Aqueous Solution on Irvingia gabonensis Biomass: Kinetics and Thermodynamics Studies. S. Afr. J. Chem. 2015, 68, 115–125. [Google Scholar] [CrossRef] [Green Version]
- Aljeboreea, A.M.; Alkaima, A.F.; Al-Dujaili, A.H. Adsorption isotherm, kinetic modeling and thermodynamics of crystal violet dye on coconut huskbased activated carbon. Desalin. Water Treat. 2015, 53, 3656–3667. [Google Scholar] [CrossRef]
- Felista, M.M.; Wanyonyi, W.C.; Gilbert, O. Adsorption of anionic dye (Reactive Black 5) using macadamia seed husks: Kinetics and equilibrium studies. Sci. Afr. 2020, 7, 10. [Google Scholar] [CrossRef]
- da Fontoura, J.T.; Rolim, G.S.; Mella, B.; Farenzena, M.; Gutterres, M. Defatted microalgal biomass as biosorbent for the removal of Acid Blue 161 dye from tannery effluent. J. Environ. Chem. Eng. 2017, 5, 5076–5084. [Google Scholar] [CrossRef]
- Zamouche, M.; Hamdaoui, O. Sorption of Rhodamine B by cedar cone: Effect of pH and ionic strength. Energy Procedia 2012, 18, 1228–1239. [Google Scholar] [CrossRef] [Green Version]
- Chang, S.; Wang, K.; Li, H.; Wey, M.; Chou, J. Enhancement of Rhodamine B removal by low-cost fly ash sorption with Fenton pre-oxidation. J. Hazard. Mater. 2009, 172, 1131–1136. [Google Scholar] [CrossRef] [PubMed]
- Sureshkumar, M.V.; Namasivayam, C. Adsorption behavior of direct red 12B and Rhodamine B from water unto surfactant-modified coconut coir pith. Colloid Surf. A Physicochem. Chem. Eng. Asp. 2008, 317, 277–283. [Google Scholar] [CrossRef]
- Santhi, T.; Prasad, A.L.; Manonmani, S. A comparative studof microwave and chemically treated Acacia nilotica leaf as an eco friendly adsorbent for the removal of rhodamine B dye from aqueous solution. Arab. J. Chem. 2014, 7, 494–503. [Google Scholar] [CrossRef] [Green Version]
- Yu, J.; Li, B.; Sun, X.; Jun, Y.; Chi, R. Adsorption of methylene blue and rhodamine B on baker’s yeast and photocatalytic regeneration of the biosorbent. BioChem. Eng. J. 2009, 45, 145–151. [Google Scholar] [CrossRef]
- Khan, T.; Dahiya, A.S.; Ali, I. Use of kaolinite as adsorbent: Equilibrium, dynamics and thermodynamic studies on the adsorption of Rhodamine B from aqueous solution. Appl. Clay Sci. 2012, 69, 58–66. [Google Scholar]
- Zhang, Z.; O’Hara, I.M.; Kent, G.A.; Doherty, W.O.S. Comparative study on adsorption of two cationic dyes by milled sugarcane bagasse. Indust. Crops Prod. 2013, 42, 41–49. [Google Scholar] [CrossRef] [Green Version]
- Panda, G.C.; Das, S.K.; Guha, A.K. Jute stick powder as a potential biomass for the removal of congo red and rhodamine B from their aqueous solution. J. Hazard. Mater. 2009, 164, 374–379. [Google Scholar] [CrossRef] [PubMed]
- Tong, Z.; Zheng, P.; Bai, B.; Wang, H.; Suo, Y. Adsorption Performance of Methyl Violet via α-Fe2O3@Porous Hollow Carbonaceous Microspheres and Its Effective Regeneration through a Fenton-Like Reaction. Catalysts 2016, 6, 58. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, M.A.; Ahmad, N.; Bello, O.S. Adsorption kinetic studies for the removal of synthetic dye using durian seed activated carbon. J. Dispers. Sci. Technol. 2015, 36, 670–684. [Google Scholar] [CrossRef]
- Machrouhi, A.; Elhalil, A.; Farnane, M.; Mahjoubi, F.Z.; Tounsadi, H.; Sadiq, M.; Abdennouri, M.; Barka, N. Adsorption behavior of methylene blue onto powdered Ziziphus lotus fruit peels and Avocado kernels seeds. J. Appl. Surf. Interfaces 2017, 1, 49–56. [Google Scholar]
- El Farissi, H.; Lakhmiri, R.; Albourine, A.; Safi, M.; Cherkaoui, O. Removal of anionic dyes from aqueous solutions by cistus ladaniferus shells and their biochar: Isotherms, kinetic and thermodynamic studies. Int. J. Sci. Eng. Res. 2018, 9, 200–211. [Google Scholar] [CrossRef]
- Nourmoradi, H.; Moghadam, K.F.; Jafari, A.; Kamarehie, B. Removal of Acetaminophen and Ibuprofen from Aqueous Solutions by Activated Carbon Derived from Quercus Brantii (Oak) Acorn as a Low-cost Biosorbent. J. Environ. Chem. Eng. 2018, 6, 6807–6815. [Google Scholar] [CrossRef]
- Mansouri, F.E.; Farissi, H.E.; Zerrouk, M.H.; Cacciola, F.; Bakkali, C.; Brigui, J.; Lovillo, M.P.; Esteves da Silva, J.C.G. Dye Removal from Colored Textile Wastewater Using Seeds and Biochar of Barley (Hordeum vulgare L.). Appl. Sci. 2021, 11, 5125. [Google Scholar] [CrossRef]
- Chowdhury, S.; Mishra, R.; Saha, P.; Kushwaha, P. Adsorption thermodynamics, kinetics and isosteric heat of adsorption of malachite green onto chemically modified rice husk. Desalination 2011, 265, 159–168. [Google Scholar] [CrossRef]
- Núñez-gómez, D.; Rodrigues, C.; Rubens, F. Adsorption of heavy metals from coal acid mine drainage by shrimp shell waste: Isotherm and continuous-flow studies. J. Environ. Chem. Eng. 2019, 7, 102787. [Google Scholar] [CrossRef]
- Popa, N.; Visa, M. The synthesis, activation and characterization of charcoal powder for the removal of methylene blue and cadmium from wastewater. Adv. Powder Technol. 2017, 28, 1866–1876. [Google Scholar] [CrossRef]
- Dash, S.; Chaudhuri, H.; Gupta, R.; Nair, U.G. Adsorption Study of Modified Coal Fly Ash with Sulfonic Acid as a Potential Adsorbent for the Removal of Toxic Reactive Dyes from Aqueous Solution: Kinetics and Thermodynamics. J. Environ. Chem. Eng. 2018, 6, 5897–5905. [Google Scholar] [CrossRef]
- Murugesan, A.; Divakaran, M.; Raveendran, P.; Nitin Nikamanth, A.B.; Thelly, K.J. An Eco-friendly Porous Poly(imide-ether)s for the Efficient Removal of Methylene Blue: Adsorption Kinetics, Isotherm, Thermodynamics and Reuse Performances. J. Polym. Environ. 2019, 27, 1007–1024. [Google Scholar] [CrossRef]
- Ahmad, M.; Bachmann, R.T.; Khan, M.A.; Edyvean, R.G.J.; Farooq, U.; Athar, M.M. Dye removal using carbonized biomass, isotherm and kinetic studies. Desalin. Water Treat. 2015, 53, 2289–2298. [Google Scholar] [CrossRef]
- Jadhav, D.N.; Vanjara, A.K. A Study: Removal of Dyestuff Effluent Using Sawdust, Polymerized Sawdust and Sawdust Carbon-II. Indian J. Chem. Technol. 2004, 11, 42–50. [Google Scholar]
- ALzaydien, A.S. Adsorption of Methylene Blue from Aqueous Solution onto a Low-Cost Natural Jordanian Tripoli. Am. J. Appl. Sci. 2009, 5, 197–208. [Google Scholar] [CrossRef] [Green Version]
- Khalaf, B.; Hamed, O.; Jodeh, S.; Bol, R.; Hanbali, G.; Safi, Z.; Dagdag, O.; Berisha, A.; Samhan, S. Cellulose-Based Hectocycle Nanopolymers: Synthesis, Molecular Docking and Adsorption of Difenoconazole from Aqueous Medium. Int. J. Mol. Sci. 2021, 22, 6090. [Google Scholar] [CrossRef] [PubMed]
- Hamed, O.A.; Qaisi, M.; Abushqair, I.; Berisha, A.; Dagdag, O.; Janem, A.; Azzaoui, K.; Al-Kerm, R.; Al-Kerm, R.; Hammouti, B. Cellulose Powder Functionalized with Phenyl Biguanide: Synthesis, Cross-Linking, Metal Adsorption, and Molecular Docking. BioResources 2021, 16, 7263–7282. [Google Scholar] [CrossRef]
- Greathouse, J.A.; Geatches, D.; Pike, D.Q.; Greenwell, H.C.; Johnston, C.T.; Wilcox, J.; Cygan, R.T. Methylene Blue Adsorption on the Basal Surfaces of Kaolinite: Structure and Thermodynamics from Quantum and Classical Molecular Simulation. Clays Clay Miner. 2015, 63, 185–198. [Google Scholar] [CrossRef]
- Rauf, M.A.; Shehadeh, I.; Ahmed, A.; Al-Zamly, A. Removal of Methylene Blue from Aqueous Solution by Using Gypsum as a Low Cost Adsorbent. Int. J. Chem. Mol. Eng. 2009, 3, 367–374. [Google Scholar]
- Tran, H.N.; You, S.J.; Chao, H.P. Thermodynamic parameters of cadmium adsorption onto orange peel calculated from various methods: A comparison study. J. Environ. Chem. Eng. 2016, 4, 2671–2682. [Google Scholar] [CrossRef]
- Xie, S.; Zhang, C.; Zhou, X.; Yang, J.; Zhang, X.; Wang, J. Comments on “removal of uranium (VI) from aqueous solution by adsorption of hematite”. J. Environ. Radioact. 2009, 100, 921–922. [Google Scholar]
- Weber, T.W.; Chakkravorti, R.K. Pore and solid diffusion models for fixed-bed adsorbers. AlChE J. 1974, 20, 228–238. [Google Scholar] [CrossRef]
- Tan, I.A.W.; Ahmad, A.L.; Hameed, B.H. Adsorption isotherms, kinetics, thermodynamics and desorption studies of 2,4,6-trichlorophenol on oil palm empty fruit bunch-based activated carbon. J. Hazard. Mater. 2009, 164, 473–482. [Google Scholar] [CrossRef] [PubMed]
- Elmorsi, T.M. Equilibrium Isotherms and Kinetic Studies of Removal of Methylene Blue Dye by Adsorption onto Miswak Leaves as a Natural Adsorbent. J. Environ. Prot. 2011, 2, 817–827. [Google Scholar] [CrossRef] [Green Version]
- Vaghetti, J.C.P.; Lima, E.C.; Royer, B.; Cardoso, N.F.; Martins, B.; Calvete, T. Pecan nutshell as biosorbent to remove toxic metals from aqueous solution. Sep. Sci. Technol. 2009, 44, 615–644. [Google Scholar] [CrossRef]
- Lazaridis, N.K.; Asouhidou, D.D. Kinetics of sorptive removal of chromium (VI) from aqueous solutions by calcined Mg-Al-CO3 hydrotalcite. Water Res. 2003, 37, 2875–2882. [Google Scholar] [CrossRef]
- Alkan, M.; Demirbas, O.; Dogan, M. Adsorption kinetics and thermodynamics of an anionic dye onto sepiolite. Microporous Mesoporous Mater. 2007, 101, 388–396. [Google Scholar] [CrossRef]
- El Gaayda, J.; Ezzahra Titchou, F.; Oukhrib, R.; Karmal, I.; Abou Oualid, H.; Berisha, A.; Zazou, H.; Swanson, C.; Hamdani, M.; Ait Akbour, R. Removal of cationic dye from coloured water by adsorption onto hematite-humic acid composite: Experimental and theoretical studies. Sep. Purif. Technol. 2022, 288, 120607. [Google Scholar] [CrossRef]

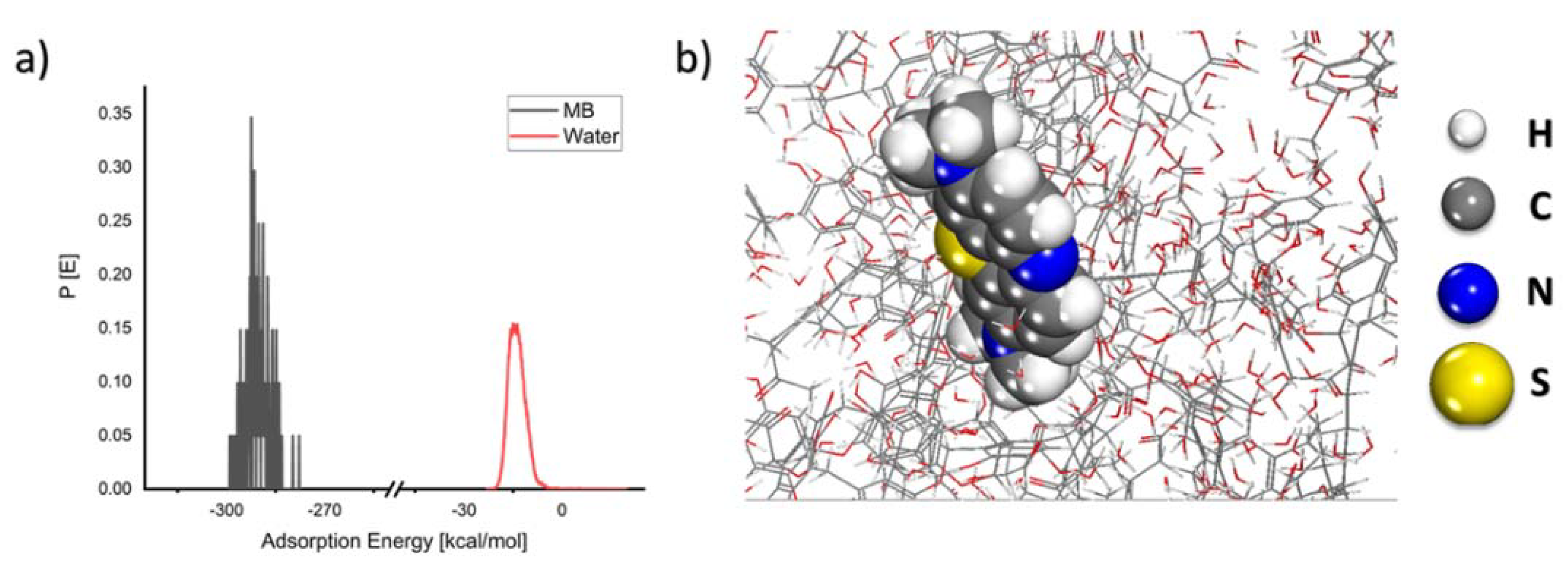
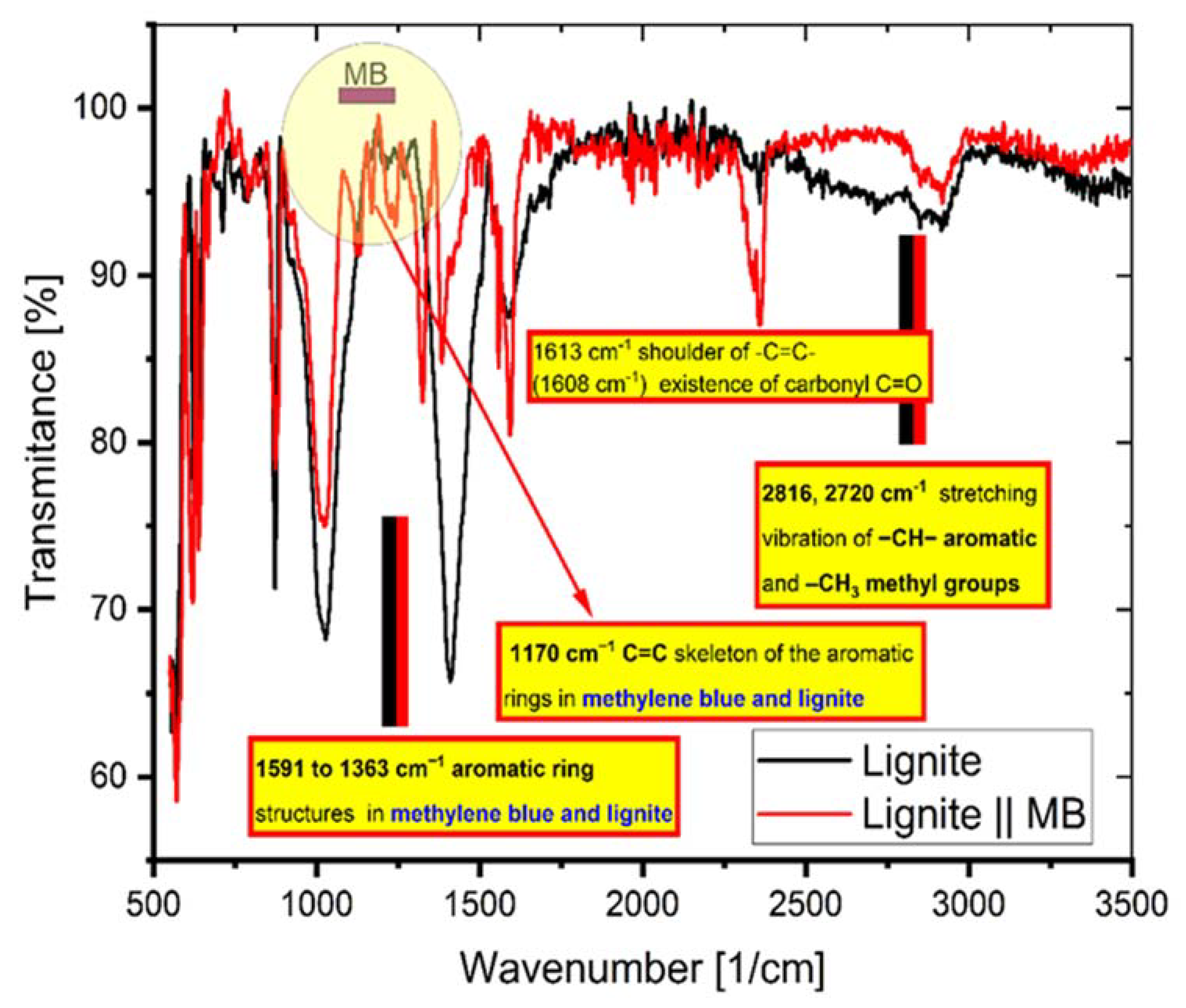
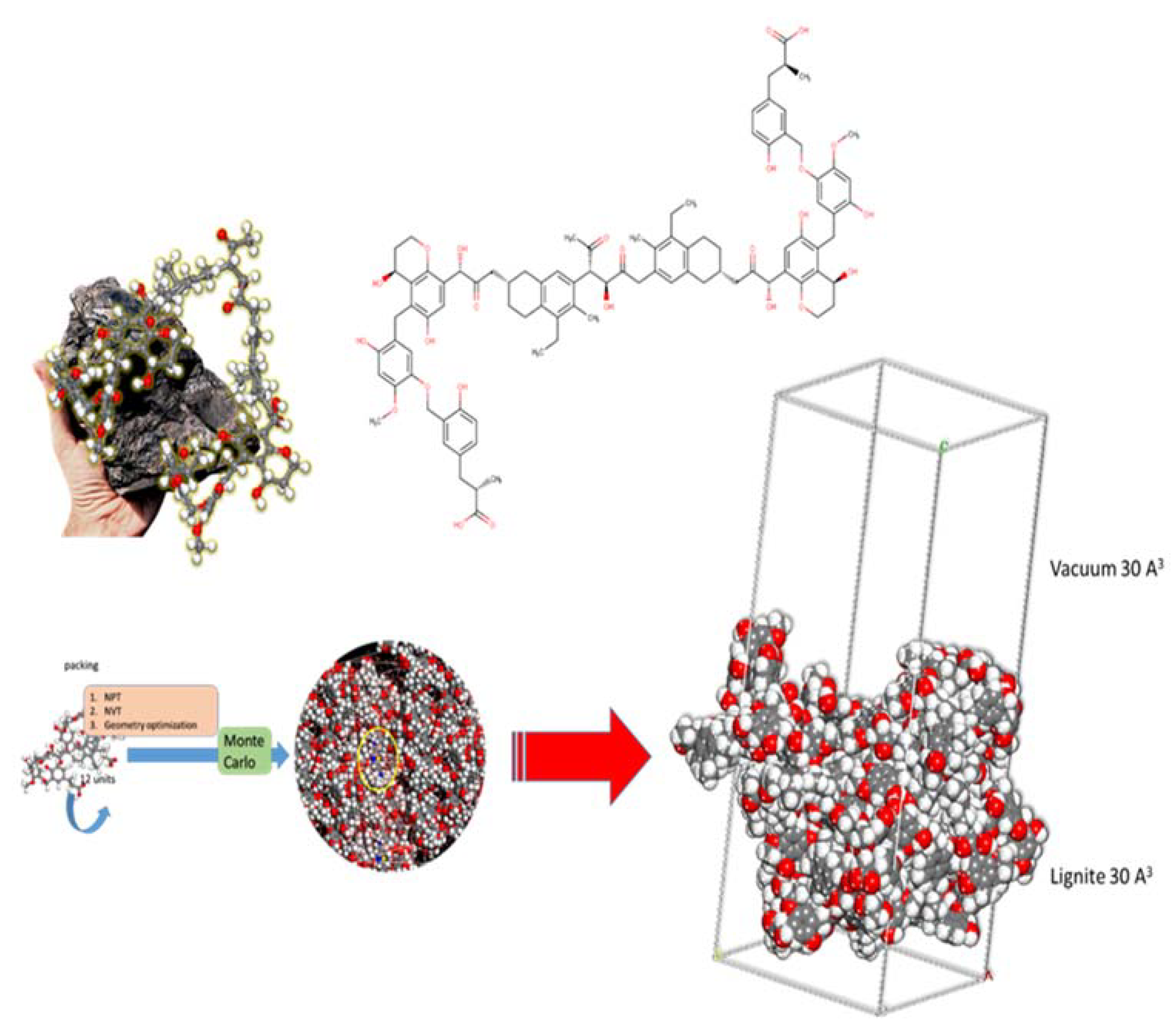
| Temperature (K) | ΔG0 (kJ/mol) | ΔH0 (kJ/mol) | ΔS0 (J/mol∙K) |
|---|---|---|---|
| 273.15 | −41.66 | 43.645 | 286.14 |
| 289.15 | −39.54 | ||
| 299.15 | −34.36 |
| Model | Equation | Parameters | |||
|---|---|---|---|---|---|
| 299.15 K | 289.15 K | 273.15 K | |||
| Langmuir | qm (mg g−1) | 40.82 | 42.37 | 48.78 | |
| KL (L mg−1) | 18.85 | 13.88 | 3.73 | ||
| RL | 0.0007 | 0.0005 | 0.0053 | ||
| R2 | 0.9824 | 0.9897 | 0.9584 | ||
| RMSE | 3.18 | 4.54 | 23.14 | ||
| Freundlich | KF (mg g−1) | 48.13 | 51.41 | 41.37 | |
| n | 3.34 | 2.77 | 2.17 | ||
| R2 | 0.9825 | 0.991 | 0.9620 | ||
| RMSE | 2.12 | 0.87 | 1.91 | ||
| Temkin | KT (L mg−1) | 476.32 | 196.29 | 40.50 | |
| RT/b (kJ/mol) | 6.67 | 8.17 | 10.28 | ||
| R2 | 0.9433 | 0.9814 | 0.9336 | ||
| RMSE | 2.09 | 1.20 | 2.26 | ||
| D–R | qm (mg g−1) | 35.35 | 38.48 | 36.23 | |
| β | 8 × 10–9 | 1 × 10−8 | 3 × 10−8 | ||
| E (kJ/mol) | 7.9 | 7.07 | 4.082 | ||
| R2 | 0.9134 | 0.9682 | 0.8935 | ||
| RMSE | 2.99 | 1.80 | 3.08 | ||
| Adsorbent | qmax/mg g–1 | Ref. |
|---|---|---|
| Cedar cone | 4.55 | [25] |
| Fly ash | 10 | [26] |
| Modified coir pit | 14.9 | [27] |
| Microwave-treated nilotica leaf | 24.39 | [28] |
| Baker’s yeast | 25 | [29] |
| Natural coal | 40.82 | This study |
| Kaolinite | 46.08 | [30] |
| Sugarcane baggas | 51.5 | [31] |
| Jute stick powder | 87.7 | [32] |
| Acid-treated dika nut | 232 | [33] |
| Model | Linear Equation | qeexp (mg/g) | Parameters | |
|---|---|---|---|---|
| Elovich | 18.7353 | a (mg g−1 min−1) | 1.34 × 1019 | |
| 𝑏 (gmg−1) | 2.58 | |||
| R2 | 0.7755 | |||
| First-order | k1 (min−1) | 0.1418 | ||
| qe,calc (mg g−1) | 18.8679 | |||
| R2 | 0.9592 | |||
| Pseudo-first-order | k1 (min−1) | 0.158 | ||
| qe,calc (mg g−1) | 0.8993 | |||
| R2 | 0.9454 | |||
| Second-order | k2 (gmg−1 min−1) | 0.3162 | ||
| R2 | 0.9796 | |||
| Pseudo-second-order | k2 (gmg−1 min−1) | 0.488 | ||
| qe,calc (mg g−1) | 18.797 | |||
| R2 | 1 | |||
| Intraparticle diffusion | ki (mg g−1 min−1/2) | 0.1805 | ||
| C | 17.673 | |||
| R2 | 0.5065 | |||
| Liquid film diffusion | Kfd | 0.158 | ||
| C | 3.037 | |||
| R2 | 0.9454 | |||
| Adsorbent | Adsorbate | Kinetic | Ref. |
|---|---|---|---|
| Chitosan composite MCs/MS | RB19 | Pseudo-second-order | [36] |
| Carbon of Quercus brantii (oak) | ACT | Pseudo-second-order | [37] |
| BS−HVL | MGC | Pseudo-second-order | [38] |
| α-Fe2O3@PHCMs | Methyl violet | Pseudo-second-order | [33] |
| Modified rice husk | Malachite green | Pseudo-second-order | [39] |
| Natural coal | MB | Pseudo-second-order | This study |
| Coal acid mine drainage | Fe | Pseudo-second-order | [40] |
| Charcoal (tree branches) | MB | Pseudo-second-order | [41] |
| Coal fly ash (CFA) | MG | Pseudo-second-order | [42] |
| Porous poly(imide-ether)s | MB | Pseudo-second-order | [43] |
| Dye Name | Methylene Blue |
|---|---|
| Suggested name | Methylene blue |
| Abbreviation | MB |
| C.I. name | Basic blue 9 |
| C.I. number | 52015 |
| Class | Thiazin |
| λmax | 668 nm |
| Color | Blue |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hasani, N.; Selimi, T.; Mele, A.; Thaçi, V.; Halili, J.; Berisha, A.; Sadiku, M. Theoretical, Equilibrium, Kinetics and Thermodynamic Investigations of Methylene Blue Adsorption onto Lignite Coal. Molecules 2022, 27, 1856. https://doi.org/10.3390/molecules27061856
Hasani N, Selimi T, Mele A, Thaçi V, Halili J, Berisha A, Sadiku M. Theoretical, Equilibrium, Kinetics and Thermodynamic Investigations of Methylene Blue Adsorption onto Lignite Coal. Molecules. 2022; 27(6):1856. https://doi.org/10.3390/molecules27061856
Chicago/Turabian StyleHasani, Naim, Teuta Selimi, Altin Mele, Veprim Thaçi, Jeton Halili, Avni Berisha, and Makfire Sadiku. 2022. "Theoretical, Equilibrium, Kinetics and Thermodynamic Investigations of Methylene Blue Adsorption onto Lignite Coal" Molecules 27, no. 6: 1856. https://doi.org/10.3390/molecules27061856
APA StyleHasani, N., Selimi, T., Mele, A., Thaçi, V., Halili, J., Berisha, A., & Sadiku, M. (2022). Theoretical, Equilibrium, Kinetics and Thermodynamic Investigations of Methylene Blue Adsorption onto Lignite Coal. Molecules, 27(6), 1856. https://doi.org/10.3390/molecules27061856







