In Silico Screening of Metal−Organic Frameworks and Zeolites for He/N2 Separation
Abstract
1. Introduction
2. Results and Discussion
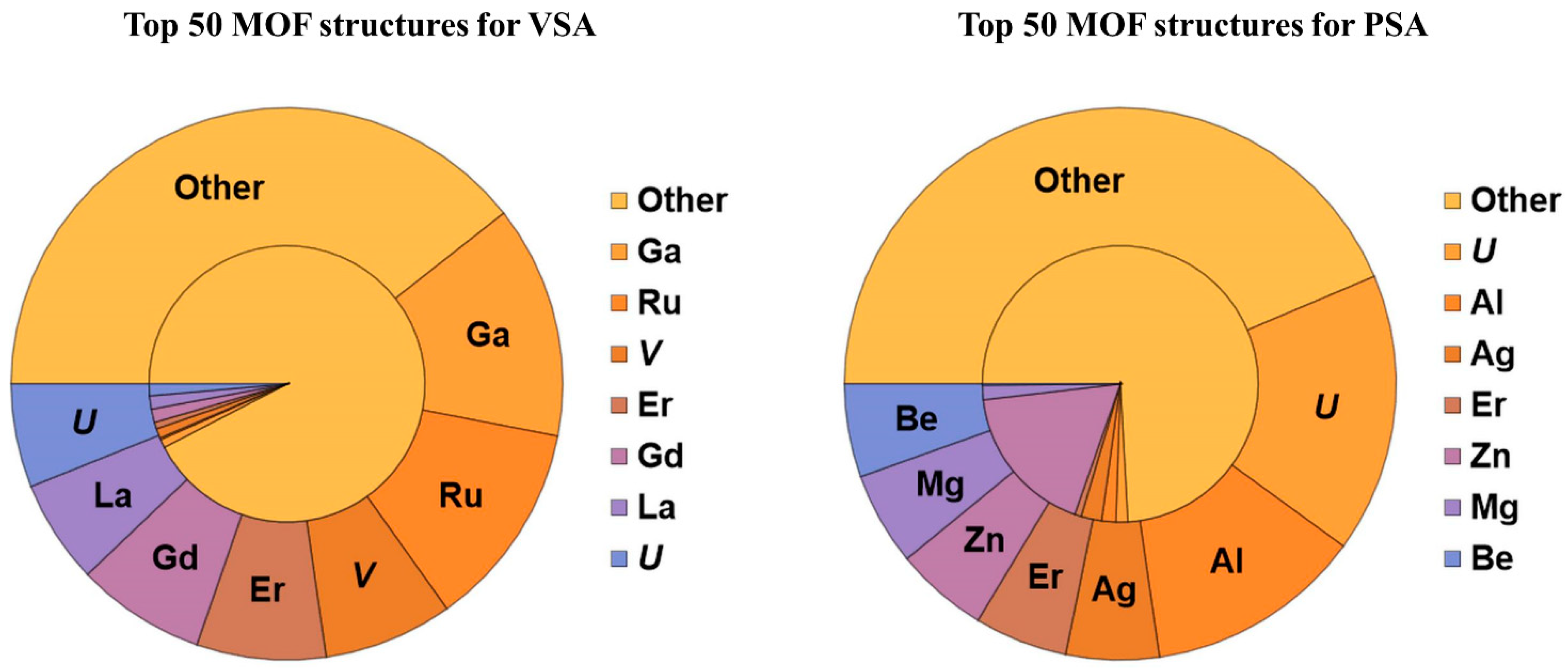
2.1. Adsorption-Based Gas Separation
2.2. Membrane-Based Gas Separation
3. Computational Methods
3.1. MOF and Zeolite Databases
3.2. Simulation Details
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Berganza, C.J.; Zhang, J.H. The Role of Helium Gas in Medicine. Med. Gas Res. 2013, 3, 18. [Google Scholar] [CrossRef] [PubMed]
- Mahesh, M.; Barker, P.B. The MRI Helium Crisis: Past and Future. J. Am. Coll. Radiol. 2016, 13, 1536–1537. [Google Scholar] [CrossRef] [PubMed]
- Rufford, T.E.; Chan, K.I.; Huang, S.H.; May, E.F. A Review of Conventional and Emerging Process Technologies for the Recovery of Helium from Natural Gas. Adsorpt. Sci. Technol. 2014, 32, 49–72. [Google Scholar] [CrossRef]
- Dai, Z.; Deng, J.; He, X.; Scholes, C.A.; Jiang, X.; Wang, B.; Guo, H.; Ma, Y.; Deng, L. Helium Separation Using Membrane Technology: Recent Advances and Perspectives. Sep. Purif. Technol. 2021, 274, 119044. [Google Scholar] [CrossRef]
- Sunarso, J.; Hashim, S.S.; Lin, Y.S.; Liu, S.M. Membranes for Helium Recovery: An Overview on the Context, Materials and Future Directions. Sep. Purif. Technol. 2017, 176, 335–383. [Google Scholar] [CrossRef]
- Scholes, C.A.; Ghosh, U. Helium Separation through Polymeric Membranes: Selectivity Targets. J. Membr. Sci. 2016, 520, 221–230. [Google Scholar] [CrossRef]
- Scholes, C.; Ghosh, U. Review of Membranes for Helium Separation and Purification. Membranes 2017, 7, 9. [Google Scholar] [CrossRef]
- Alders, M.; Winterhalder, D.; Wessling, M. Helium Recovery Using Membrane Processes. Sep. Purif. Technol. 2017, 189, 433–440. [Google Scholar] [CrossRef]
- Scholes, C.A. Helium Recovery through Inorganic Membranes Incorporated with a Nitrogen Rejection Unit. Ind. Eng. Chem. Res. 2018, 57, 3792–3799. [Google Scholar] [CrossRef]
- Daglar, H.; Keskin, S. Recent Advances, Opportunities, and Challenges in High-Throughput Computational Screening of MOFs for Gas Separations. Coord. Chem. Rev. 2020, 422, 213470. [Google Scholar] [CrossRef]
- Yang, S.; Yin, K.; Wu, J.; Wu, Z.; Chu, D.; He, J.; Duan, J.-A. Ultrafast Nano-Structuring of Superwetting Ti Foam with Robust Antifouling and Stability towards Efficient Oil-in-Water Emulsion Separation. Nanoscale 2019, 11, 17607–17614. [Google Scholar] [CrossRef] [PubMed]
- Robeson, L.M. The Upper Bound Revisited. J. Membr. Sci. 2008, 320, 390–400. [Google Scholar] [CrossRef]
- Yin, K.; Chu, D.; Dong, X.; Wang, C.; Duan, J.-A.; He, J. Femtosecond Laser Induced Robust Periodic Nanoripple Structured Mesh for Highly Efficient Oil–Water Separation. Nanoscale 2017, 9, 14229–14235. [Google Scholar] [CrossRef] [PubMed]
- Malbrunot, P.; Vidal, D.; Vermesse, J.; Chahine, R.; Bose, T.K. Adsorbent Helium Density Measurement and Its Effect on Adsorption Isotherms at High Pressure. Langmuir 1997, 13, 539–544. [Google Scholar] [CrossRef]
- Khoramzadeh, E.; Mofarahi, M.; Lee, C.-H. Equilibrium Adsorption Study of CO2 and N2 on Synthesized Zeolites 13X, 4A, 5A, and Beta. J. Chem. Eng. Data 2019, 64, 5648–5664. [Google Scholar] [CrossRef]
- Gong, C.; Peng, X.; Zhu, M.; Zhou, T.; You, L.; Ren, S.; Wang, X.; Gu, X. Synthesis and Performance of STT Zeolite Membranes for He/N2 and He/CH4 Separation. Sep. Purif. Technol. 2022, 301, 121927. [Google Scholar] [CrossRef]
- Xu, X.; Yang, W.; Liu, J.; Lin, L.; Stroh, N.; Brunner, H. Synthesis of NaA Zeolite Membrane on a Ceramic Hollow Fiber. J. Membr. Sci. 2004, 229, 81–85. [Google Scholar] [CrossRef]
- Aoki, K.; Kusakabe, K.; Morooka, S. Separation of Gases with an A-Type Zeolite Membrane. Ind. Eng. Chem. Res. 2000, 39, 2245–2251. [Google Scholar] [CrossRef]
- Aoki, K.; Kusakabe, K.; Morooka, S. Gas Permeation Properties of A-Type Zeolite Membrane Formed on Porous Substrate by Hydrothermal Synthesis. J. Membr. Sci. 1998, 141, 197–205. [Google Scholar] [CrossRef]
- Guan, G.; Kusakabe, K.; Morooka, S. Gas Permeation Properties of Ion-Exchanged LTA-Type Zeolite Membranes. Sep. Sci. Technol. 2001, 36, 2233–2245. [Google Scholar] [CrossRef]
- Himeno, S.; Tomita, T.; Suzuki, K.; Nakayama, K.; Yajima, K.; Yoshida, S. Synthesis and Permeation Properties of a DDR-Type Zeolite Membrane for Separation of CO2/CH4 Gaseous Mixtures. Ind. Eng. Chem. Res. 2007, 46, 6989–6997. [Google Scholar] [CrossRef]
- Tomita, T.; Nakayama, K.; Sakai, H. Gas Separation Characteristics of DDR Type Zeolite Membrane. Microporous Mesoporous Mater. 2004, 68, 71–75. [Google Scholar] [CrossRef]
- Yu, L.; Mayne, B.; Nobandegani, M.S.; Grekou, T.; Hedlund, J. Recovery of Helium from Natural Gas Using MFI Membranes. J. Membr. Sci. 2022, 644, 120113. [Google Scholar] [CrossRef]
- Drobek, M.; Bechelany, M.; Vallicari, C.; Abou Chaaya, A.; Charmette, C.; Salvador-Levehang, C.; Miele, P.; Julbe, A. An Innovative Approach for the Preparation of Confined ZIF-8 Membranes by Conversion of ZnO ALD Layers. J. Membr. Sci. 2015, 475, 39–46. [Google Scholar] [CrossRef]
- Hara, N.; Yoshimune, M.; Negishi, H.; Haraya, K.; Hara, S.; Yamaguchi, T. ZIF-8 Membranes Prepared at Miscible and Immiscible Liquid–Liquid Interfaces. Microporous Mesoporous Mater. 2015, 206, 75–80. [Google Scholar] [CrossRef]
- Hara, N.; Yoshimune, M.; Negishi, H.; Haraya, K.; Hara, S.; Yamaguchi, T. Diffusive Separation of Propylene/Propane with ZIF-8 Membranes. J. Membr. Sci. 2014, 450, 215–223. [Google Scholar] [CrossRef]
- Chen, C.; Ozcan, A.; Yazaydin, A.O.; Ladewig, B.P. Gas Permeation through Single-Crystal ZIF-8 Membranes. J. Membr. Sci. 2019, 575, 209–216. [Google Scholar] [CrossRef]
- Hara, N.; Yoshimune, M.; Negishi, H.; Haraya, K.; Hara, S.; Yamaguchi, T. Metal–Organic Framework Membranes with Layered Structure Prepared within the Porous Support. RSC Adv. 2013, 3, 14233. [Google Scholar] [CrossRef]
- Yoo, Y.; Varela-Guerrero, V.; Jeong, H.-K. Isoreticular Metal−Organic Frameworks and Their Membranes with Enhanced Crack Resistance and Moisture Stability by Surfactant-Assisted Drying. Langmuir 2011, 27, 2652–2657. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, Q.; Lin, Z.; Zhang, T.; Xu, J.; Tan, Y.; Tian, W.; Jiang, L. Constructing Free Standing Metal Organic Framework MIL-53 Membrane Based on Anodized Aluminum Oxide Precursor. Sci. Rep. 2015, 4, 4947. [Google Scholar] [CrossRef] [PubMed]
- Huang, A.; Chen, Y.; Liu, Q.; Wang, N.; Jiang, J.; Caro, J. Synthesis of Highly Hydrophobic and Permselective Metal–Organic Framework Zn(BDC)(TED)0.5 Membranes for H2/CO2 Separation. J. Membr. Sci. 2014, 454, 126–132. [Google Scholar] [CrossRef]
- Database of Zeolite Structures. Available online: http://www.iza-structure.org/databases/ (accessed on 3 November 2022).
- Moghadam, P.Z.; Li, A.; Wiggin, S.B.; Tao, A.; Maloney, A.G.P.; Wood, P.A.; Ward, S.C.; Fairen-Jimenez, D. Development of a Cambridge Structural Database Subset: A Collection of Metal–Organic Frameworks for Past, Present, and Future. Chem. Mater. 2017, 29, 2618–2625. [Google Scholar] [CrossRef]
- Chung, Y.G.; Haldoupis, E.; Bucior, B.J.; Haranczyk, M.; Lee, S.; Zhang, H.; Vogiatzis, K.D.; Milisavljevic, M.; Ling, S.; Camp, J.S.; et al. Advances, Updates, and Analytics for the Computation-Ready, Experimental Metal–Organic Framework Database: CoRE MOF 2019. J. Chem. Eng. Data 2019, 64, 5985–5998. [Google Scholar] [CrossRef]
- Altintas, C.; Avci, G.; Daglar, H.; Nemati Vesali Azar, A.; Erucar, I.; Velioglu, S.; Keskin, S. An Extensive Comparative Analysis of Two MOF Databases: High-Throughput Screening of Computation-Ready MOFs for CH4 and H2 Adsorption. J. Mater. Chem. A 2019, 7, 9593–9608. [Google Scholar] [CrossRef]
- Solanki, V.A.; Borah, B. High-Throughput Computational Screening of 12,351 Real Metal–Organic Framework Structures for Separation of Hexane Isomers: A Quest for a Yet Better Adsorbent. J. Phys. Chem. C 2020, 124, 4582–4594. [Google Scholar] [CrossRef]
- Basdogan, Y.; Sezginel, K.B.; Keskin, S. Identifying Highly Selective Metal Organic Frameworks for CH4/H2 Separations Using Computational Tools. Ind. Eng. Chem. Res. 2015, 54, 8479–8491. [Google Scholar] [CrossRef]
- Fischer, M. Computational Evaluation of Aluminophosphate Zeotypes for CO2/N2 Separation. Phys. Chem. Chem. Phys. 2017, 19, 22801–22812. [Google Scholar] [CrossRef]
- Erdős, M.; Geerdink, D.F.; Martin-Calvo, A.; Pidko, E.A.; van den Broeke, L.J.P.; Calero, S.; Vlugt, T.J.H.; Moultos, O.A. In Silico Screening of Zeolites for High-Pressure Hydrogen Drying. ACS Appl. Mater. Interfaces 2021, 13, 8383–8394. [Google Scholar] [CrossRef]
- Daglar, H.; Keskin, S. High-Throughput Screening of Metal Organic Frameworks as Fillers in Mixed Matrix Membranes for Flue Gas Separation. Adv. Theory Simul. 2019, 2, 1900109. [Google Scholar] [CrossRef]
- Budhathoki, S.; Ajayi, O.; Steckel, J.A.; Wilmer, C.E. High-Throughput Computational Prediction of the Cost of Carbon Capture Using Mixed Matrix Membranes. Energy Environ. Sci. 2019, 12, 1255–1264. [Google Scholar] [CrossRef]
- Krishna, R.; van Baten, J.M. In Silico Screening of Zeolite Membranes for CO2 Capture. J. Membr. Sci. 2010, 360, 323–333. [Google Scholar] [CrossRef]
- Nazarian, D.; Camp, J.S.; Chung, Y.G.; Snurr, R.Q.; Sholl, D.S. Large-Scale Refinement of Metal−Organic Framework Structures Using Density Functional Theory. Chem. Mater. 2017, 29, 2521–2528. [Google Scholar] [CrossRef]
- Zarabadi-Poor, P.; Marek, R. Metal–Organic Frameworks for Helium Recovery from Natural Gas via N2/He Separation: A Computational Screening. J. Phys. Chem. C 2019, 123, 3469–3475. [Google Scholar] [CrossRef]
- Wiersum, A.D.; Chang, J.-S.; Serre, C.; Llewellyn, P.L. An Adsorbent Performance Indicator as a First Step Evaluation of Novel Sorbents for Gas Separations: Application to Metal–Organic Frameworks. Langmuir 2013, 29, 3301–3309. [Google Scholar] [CrossRef]
- Daglar, H.; Erucar, I.; Keskin, S. Recent Advances in Simulating Gas Permeation through MOF Membranes. Mater. Adv. 2021, 2, 5300–5317. [Google Scholar] [CrossRef] [PubMed]
- Kadioglu, O.; Keskin, S. Efficient Separation of Helium from Methane Using MOF Membranes. Sep. Purif. Technol. 2018, 191, 192–199. [Google Scholar] [CrossRef]
- Yang, W.; Liang, H.; Peng, F.; Liu, Z.; Liu, J.; Qiao, Z. Computational Screening of Metal–Organic Framework Membranes for the Separation of 15 Gas Mixtures. Nanomaterials 2019, 9, 467. [Google Scholar] [CrossRef]
- Daglar, H.; Aydin, S.; Keskin, S. MOF-Based MMMs Breaking the Upper Bounds of Polymers for a Large Variety of Gas Separations. Sep. Purif. Technol. 2022, 281, 119811. [Google Scholar] [CrossRef]
- Ongari, D.; Yakutovich, A.V.; Talirz, L.; Smit, B. Building a Consistent and Reproducible Database for Adsorption Evaluation in Covalent–Organic Frameworks. ACS Cent. Sci. 2019, 5, 1663–1675. [Google Scholar] [CrossRef]
- Aydin, S.; Altintas, C.; Keskin, S. High-Throughput Screening of COF Membranes and COF/Polymer MMMs for Helium Separation and Hydrogen Purification. ACS Appl. Mater. Interfaces 2022, 14, 21738–21749. [Google Scholar] [CrossRef]
- Feng, M.; Cheng, M.; Deng, J.; Ji, X.; Zhou, L.; Dang, Y.; Bi, K.; Dai, Z.; Dai, Y. High-Throughput Computational Screening of Covalent−Organic Framework Membranes for Helium Purification. Results Eng. 2022, 15, 100538. [Google Scholar] [CrossRef]
- Sava Gallis, D.F.; Parkes, M.V.; Greathouse, J.A.; Zhang, X.; Nenoff, T.M. Enhanced O2 Selectivity versus N2 by Partial Metal Substitution in Cu-BTC. Chem. Mater. 2015, 27, 2018–2025. [Google Scholar] [CrossRef]
- Chowdhury, P.; Bikkina, C.; Meister, D.; Dreisbach, F.; Gumma, S. Comparison of Adsorption Isotherms on Cu-BTC Metal Organic Frameworks Synthesized from Different Routes. Microporous Mesoporous Mater. 2009, 117, 406–413. [Google Scholar] [CrossRef]
- Saha, D.; Bao, Z.; Jia, F.; Deng, S. Adsorption of CO2, CH4, N2O, and N2 on MOF-5, MOF-177, and Zeolite 5A. Environ. Sci. Technol. 2010, 44, 1820–1826. [Google Scholar] [CrossRef]
- Kloutse, F.A.; Hourri, A.; Natarajan, S.; Benard, P.; Chahine, R. Experimental Benchmark Data of CH4, CO2 and N2 Binary and Ternary Mixtures Adsorption on MOF-5. Sep. Purif. Technol. 2018, 197, 228–236. [Google Scholar] [CrossRef]
- Li, T.; Chen, D.-L.; Sullivan, J.E.; Kozlowski, M.T.; Johnson, J.K.; Rosi, N.L. Systematic Modulation and Enhancement of CO2:N2 Selectivity and Water Stability in an Isoreticular Series of Bio-MOF-11 Analogues. Chem. Sci. 2013, 4, 1746. [Google Scholar] [CrossRef]
- Cmarik, G.E.; Kim, M.; Cohen, S.M.; Walton, K.S. Tuning the Adsorption Properties of UiO-66 via Ligand Functionalization. Langmuir 2012, 28, 15606–15613. [Google Scholar] [CrossRef]
- Dubskikh, V.A.; Lysova, A.A.; Samsonenko, D.G.; Lavrov, A.N.; Kovalenko, K.A.; Dybtsev, D.N.; Fedin, V.P. 3D Metal–Organic Frameworks Based on Co(II) and Bithiophendicarboxylate: Synthesis, Crystal Structures, Gas Adsorption, and Magnetic Properties. Molecules 2021, 26, 1269. [Google Scholar] [CrossRef]
- Mayo, S.L.; Olafson, B.D.; Goddard, W.A. DREIDING: A Generic Force Field for Molecular Simulations. J. Phys. Chem. 1990, 94, 8897–8909. [Google Scholar] [CrossRef]
- Bai, P.; Tsapatsis, M.; Siepmann, J.I. TraPPE-Zeo: Transferable Potentials for Phase Equilibria Force Field for All-Silica Zeolites. J. Phys. Chem. C 2013, 117, 24375–24387. [Google Scholar] [CrossRef]
- Vujić, B.; Lyubartsev, A.P. Transferable Force-Field for Modelling of CO2, N2, O2 and Ar in All Silica and Na+ Exchanged Zeolites. Model. Simul. Mater. Sci. Eng. 2016, 24, 045002. [Google Scholar] [CrossRef]
- Pham, T.D.; Xiong, R.; Sandler, S.I.; Lobo, R.F. Experimental and Computational Studies on the Adsorption of CO2 and N2 on Pure Silica Zeolites. Microporous Mesoporous Mater. 2014, 185, 157–166. [Google Scholar] [CrossRef]
- Predescu, L.; Tezel, F.H.; Chopra, S. Adsorption of Nitrogen, Methane, Carbon Monoxide, and Their Binary Mixtures on Aluminophosphate Molecular Sieves. Adsorption 1997, 3, 7–25. [Google Scholar] [CrossRef]
- Li, S.; Chen, J.; Wang, Y.; Li, K.; Li, K.; Guo, W.; Zhang, X.; Liu, J.; Tang, X.; Yang, J.; et al. Adsorption and Separation of CH4/N2 by Electrically Neutral Skeleton AlPO Molecular Sieves. Sep. Purif. Technol. 2022, 286, 120497. [Google Scholar] [CrossRef]
- Zhao, Z.; Ma, X.; Li, Z.; Lin, Y.S. Synthesis, Characterization and Gas Transport Properties of MOF-5 Membranes. J. Membr. Sci. 2011, 382, 82–90. [Google Scholar] [CrossRef]
- Cao, F.; Zhang, C.; Xiao, Y.; Huang, H.; Zhang, W.; Liu, D.; Zhong, C.; Yang, Q.; Yang, Z.; Lu, X. Helium Recovery by a Cu-BTC Metal–Organic-Framework Membrane. Ind. Eng. Chem. Res. 2012, 51, 11274–11278. [Google Scholar] [CrossRef]
- Kasik, A.; Dong, X.; Lin, Y.S. Synthesis and Stability of Zeolitic Imidazolate Framework-68 Membranes. Microporous Mesoporous Mater. 2015, 204, 99–105. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, B.; Liu, D.; Sheng, P.; Lai, Z. Fabrication and Molecular Transport Studies of Highly C-Oriented AFI Membranes. J. Membr. Sci. 2017, 528, 46–54. [Google Scholar] [CrossRef]
- Nishiyama, N.; Ueyama, K.; Matsukata, M. Gas Permeation through Zeolite-Alumina Composite Membranes. AIChE J. 1997, 43, 2724–2730. [Google Scholar] [CrossRef]
- Zhang, P.; Gong, C.; Zhou, T.; Du, P.; Song, J.; Shi, M.; Wang, X.; Gu, X. Helium Extraction from Natural Gas Using DD3R Zeolite Membranes. Chin. J. Chem. Eng. 2021, 49, 122–129. [Google Scholar] [CrossRef]
- Robeson, L.M. Correlation of Separation Factor versus Permeability for Polymeric Membranes. J. Membr. Sci. 1991, 62, 165–185. [Google Scholar] [CrossRef]
- Wu, A.X.; Drayton, J.A.; Smith, Z.P. The Perfluoropolymer Upper Bound. AIChE J. 2019, 65, e16700. [Google Scholar] [CrossRef]
- Willems, T.F.; Rycroft, C.H.; Kazi, M.; Meza, J.C.; Haranczyk, M. Algorithms and Tools for High-Throughput Geometry-Based Analysis of Crystalline Porous Materials. Microporous Mesoporous Mater. 2012, 149, 134–141. [Google Scholar] [CrossRef]
- Dubbeldam, D.; Calero, S.; Ellis, D.E.; Snurr, R.Q. RASPA: Molecular Simulation Software for Adsorption and Diffusion in Flexible Nanoporous Materials. Mol. Simul. 2016, 42, 81–101. [Google Scholar] [CrossRef]
- Dubbeldam, D.; Calero, S.; Vlugt, T.J.H. IRASPA: GPU-Accelerated Visualization Software for Materials Scientists. Mol. Simul. 2018, 44, 653–676. [Google Scholar] [CrossRef]
- Potoff, J.J.; Siepmann, J.I. Vapor–Liquid Equilibria of Mixtures Containing Alkanes, Carbon Dioxide, and Nitrogen. AIChE J. 2001, 47, 1676–1682. [Google Scholar] [CrossRef]
- Jhirschfelder, J.O.; Curtiss, R.B. Bird Molecular Theory of Gases and Liquids; Wiley: New York, NY, USA, 1954. [Google Scholar]
- Rappe, A.K.; Casewit, C.J.; Colwell, K.S.; Goddard, W.A.; Skiff, W.M. UFF, a Full Periodic Table Force Field for Molecular Mechanics and Molecular Dynamics Simulations. J. Am. Chem. Soc. 1992, 114, 10024–10035. [Google Scholar] [CrossRef]
- Campañá, C.; Mussard, B.; Woo, T.K. Electrostatic Potential Derived Atomic Charges for Periodic Systems Using a Modified Error Functional. J. Chem. Theory Comput. 2009, 5, 2866–2878. [Google Scholar] [CrossRef]
- Manz, T.A.; Limas, N.G. Introducing DDEC6 Atomic Population Analysis: Part 1. Charge Partitioning Theory and Methodology. RSC Adv. 2016, 6, 47771–47801. [Google Scholar] [CrossRef]
- Sladekova, K.; Campbell, C.; Grant, C.; Fletcher, A.J.; Gomes, J.R.B.; Jorge, M. The Effect of Atomic Point Charges on Adsorption Isotherms of CO2 and Water in Metal Organic Frameworks. Adsorption 2019, 26, 663–685. [Google Scholar] [CrossRef]
- Grenev, I.V.; Klimkin, N.D.; Shamanaeva, I.A.; Shubin, A.A.; Chetyrin, I.A.; Gavrilov, V.Y. A Novel Adsorption-Based Method for Revealing the Si Distribution in SAPO Molecular Sieves: The Case of SAPO-11. Microporous Mesoporous Mater. 2021, 328, 111503. [Google Scholar] [CrossRef]
- Grenev, I.V.; Shubin, A.A.; Solovyeva, M.V.; Gordeeva, L.G. The Impact of Framework Flexibility and Defects on the Water Adsorption in CAU-10-H. Phys. Chem. Chem. Phys. 2021, 23, 21329–21337. [Google Scholar] [CrossRef] [PubMed]
- Nazarian, D.; Camp, J.S.; Sholl, D.S. A Comprehensive Set of High-Quality Point Charges for Simulations of Metal–Organic Frameworks. Chem. Mater. 2016, 28, 785–793. [Google Scholar] [CrossRef]
- Kancharlapalli, S.; Gopalan, A.; Haranczyk, M.; Snurr, R.Q. Fast and Accurate Machine Learning Strategy for Calculating Partial Atomic Charges in Metal–Organic Frameworks. J. Chem. Theory Comput. 2021, 17, 3052–3064. [Google Scholar] [CrossRef] [PubMed]
- Chung, Y.G.; Gómez-Gualdrón, D.A.; Li, P.; Leperi, K.T.; Deria, P.; Zhang, H.; Vermeulen, N.A.; Stoddart, J.F.; You, F.; Hupp, J.T.; et al. In Silico Discovery of Metal-Organic Frameworks for Precombustion CO2 Capture Using a Genetic Algorithm. Sci. Adv. 2016, 2, e1600909. [Google Scholar] [CrossRef] [PubMed]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation: From Algorithms to Applications; Academic Press: Bodmin, UK, 2001; ISBN 978-0-08-051998-2. [Google Scholar]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grenev, I.V.; Gavrilov, V.Y. In Silico Screening of Metal−Organic Frameworks and Zeolites for He/N2 Separation. Molecules 2023, 28, 20. https://doi.org/10.3390/molecules28010020
Grenev IV, Gavrilov VY. In Silico Screening of Metal−Organic Frameworks and Zeolites for He/N2 Separation. Molecules. 2023; 28(1):20. https://doi.org/10.3390/molecules28010020
Chicago/Turabian StyleGrenev, Ivan V., and Vladimir Yu. Gavrilov. 2023. "In Silico Screening of Metal−Organic Frameworks and Zeolites for He/N2 Separation" Molecules 28, no. 1: 20. https://doi.org/10.3390/molecules28010020
APA StyleGrenev, I. V., & Gavrilov, V. Y. (2023). In Silico Screening of Metal−Organic Frameworks and Zeolites for He/N2 Separation. Molecules, 28(1), 20. https://doi.org/10.3390/molecules28010020





