Prediction of Ethanol-Mediated Growth Morphology of Ammonium Dinitramide/Pyrazine-1,4-Dioxide Cocrystal at Different Temperatures
Abstract
1. Introduction
2. Results and Discussion
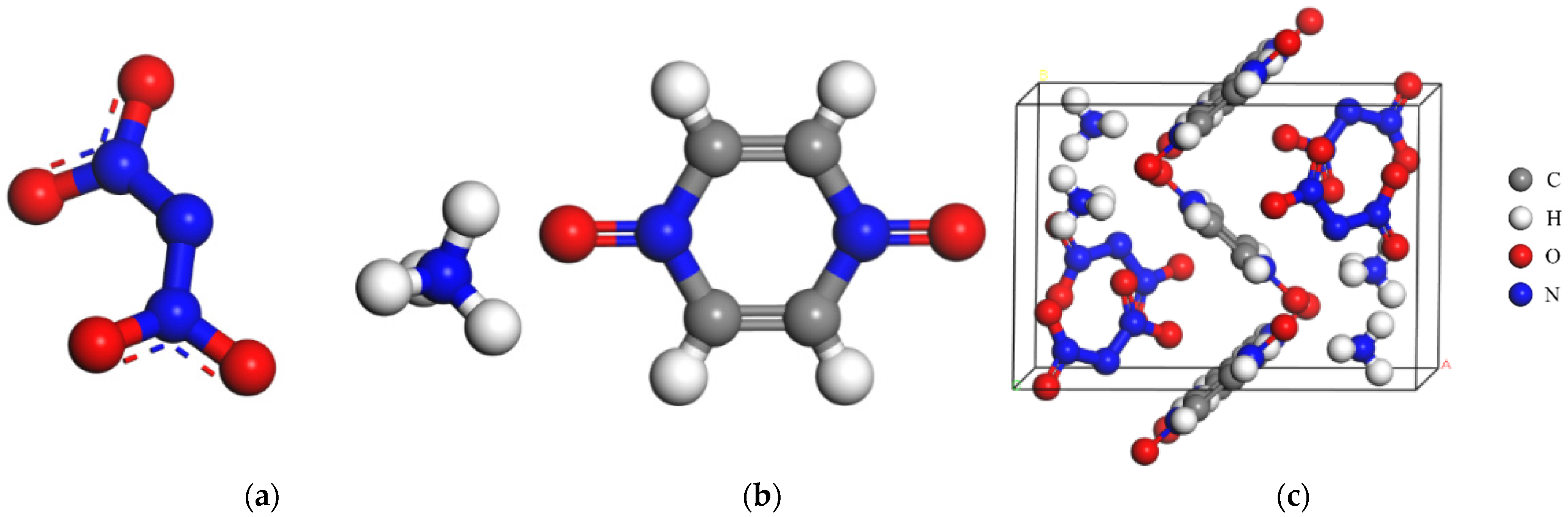
2.1. Force Field Verification
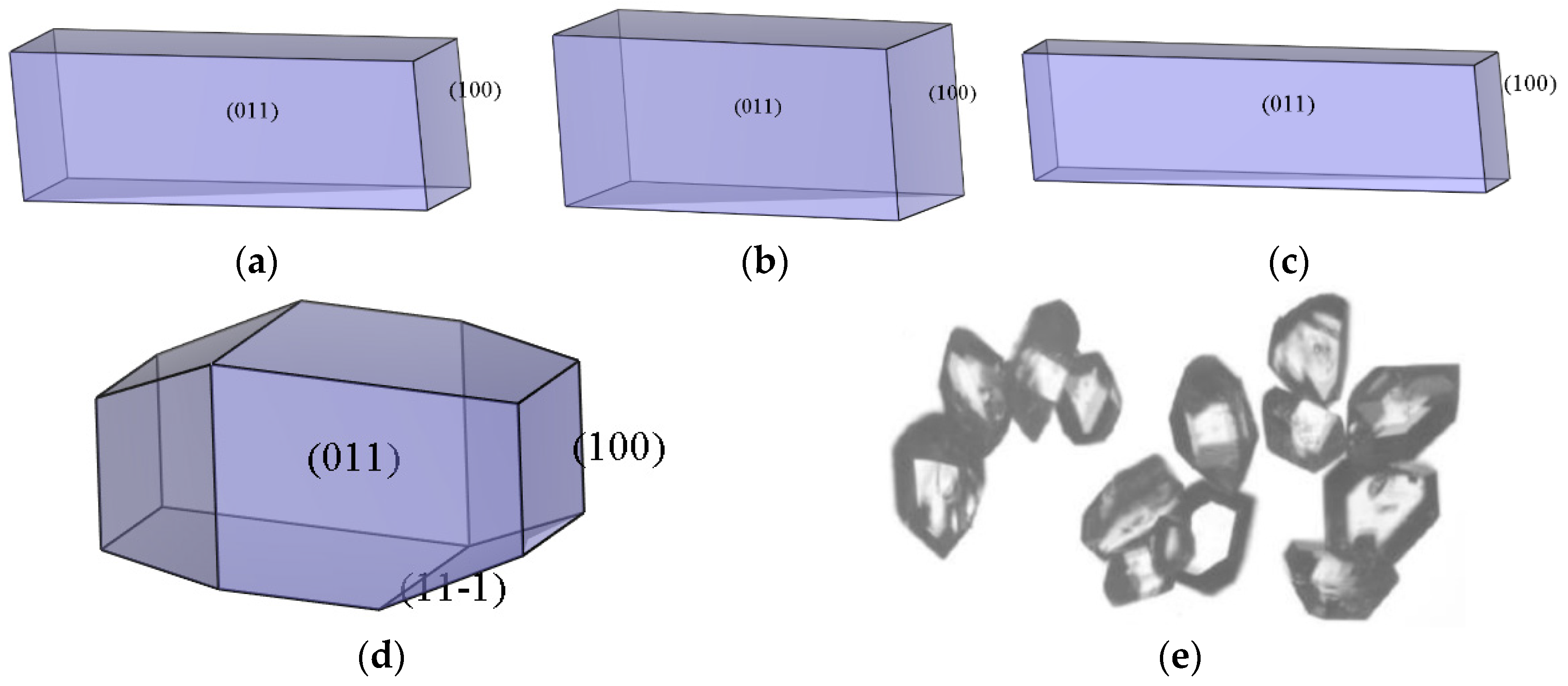
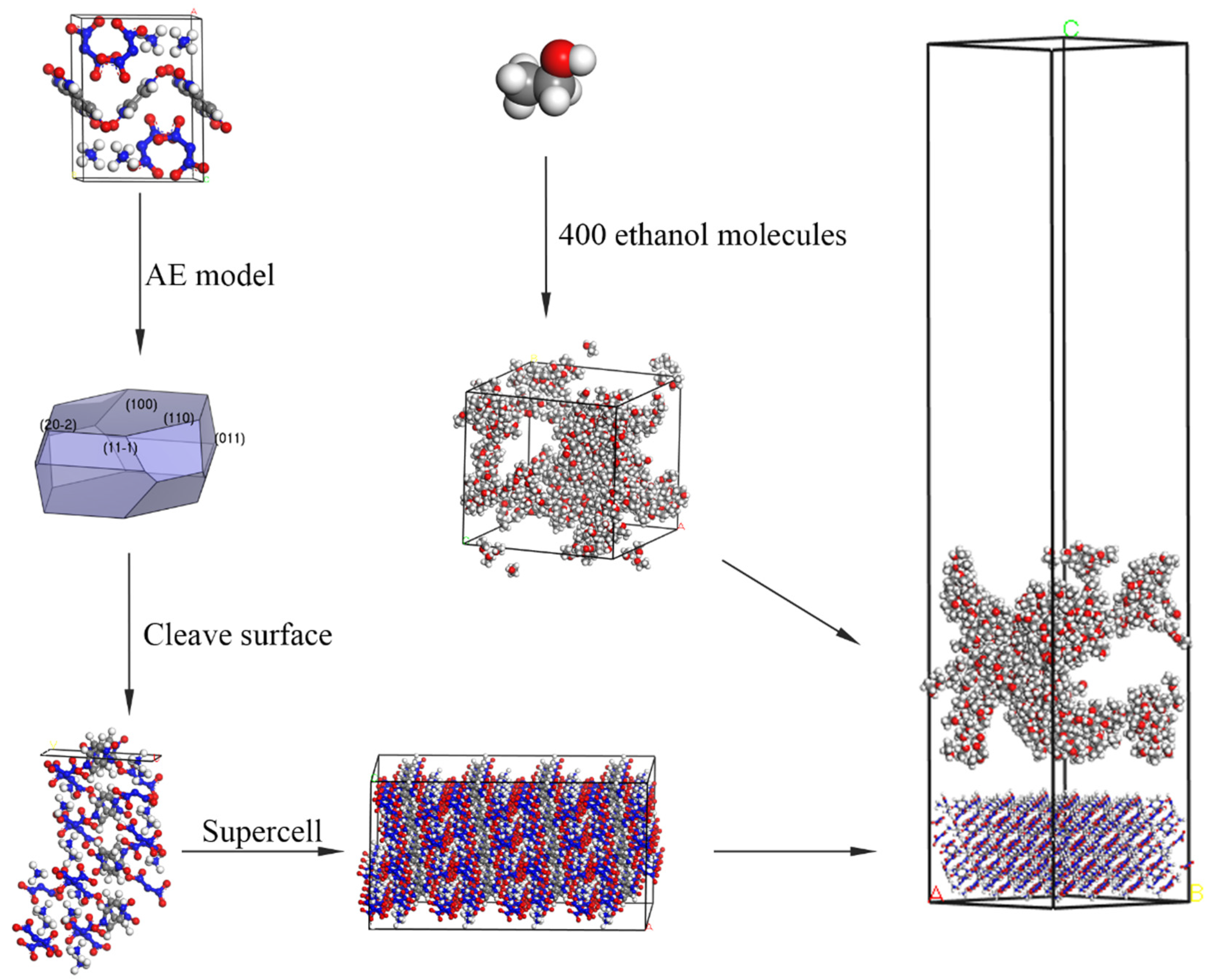
2.2. Morphology of the ADN/PDO in Vacuum
2.3. Morphology of the AND/PDO in Solvent
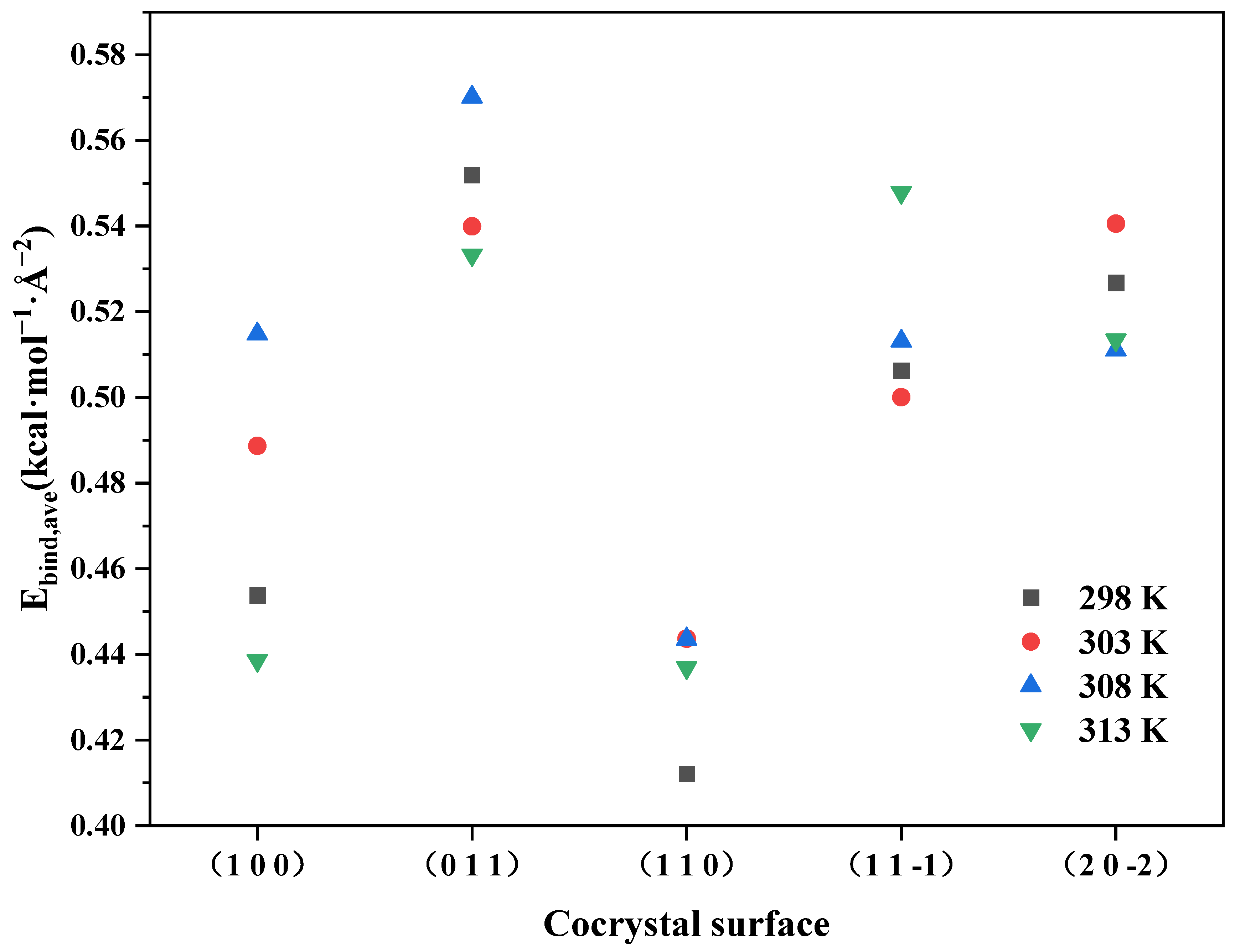
2.3.1. Binding Energy
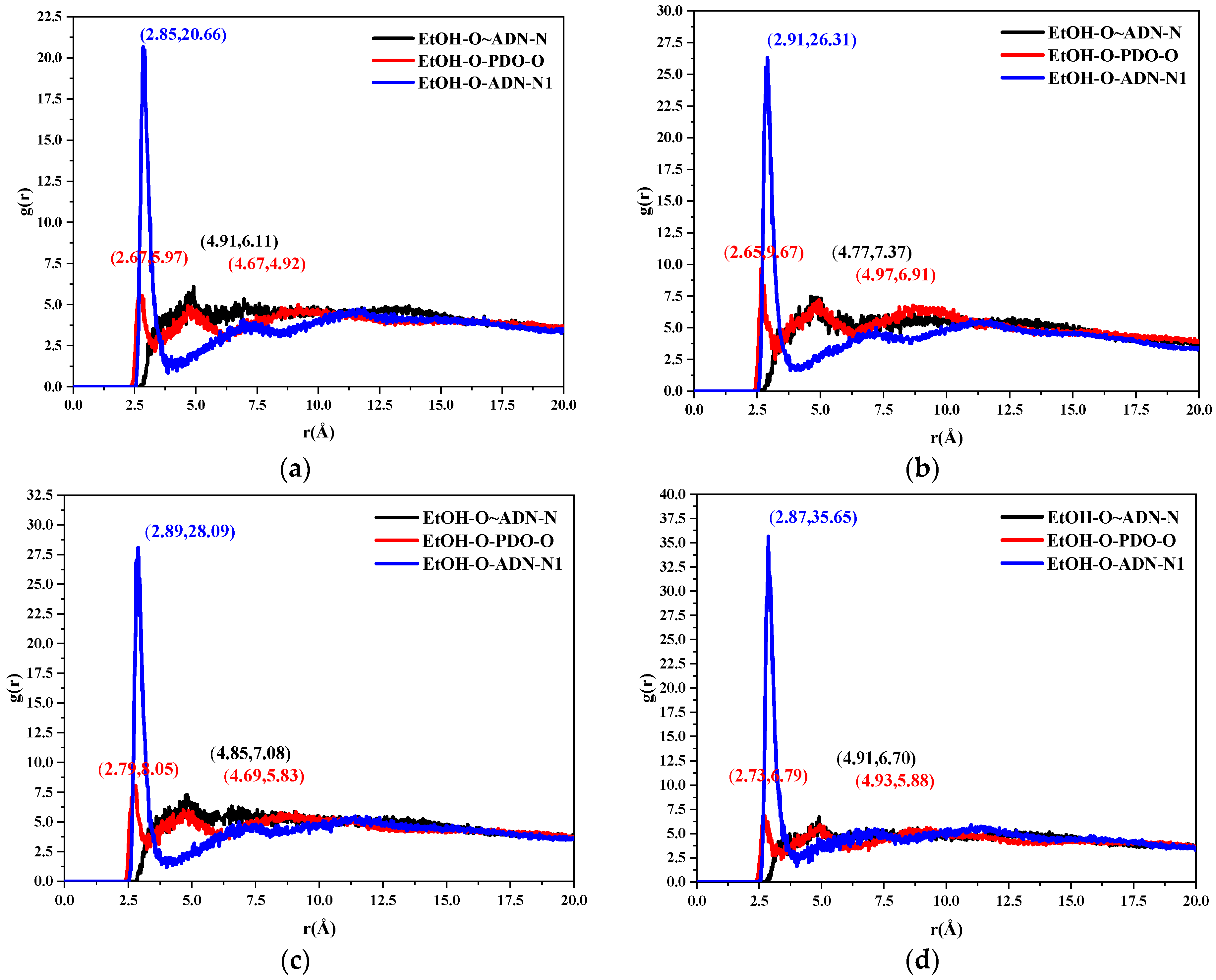
2.3.2. Radial Distribution Function
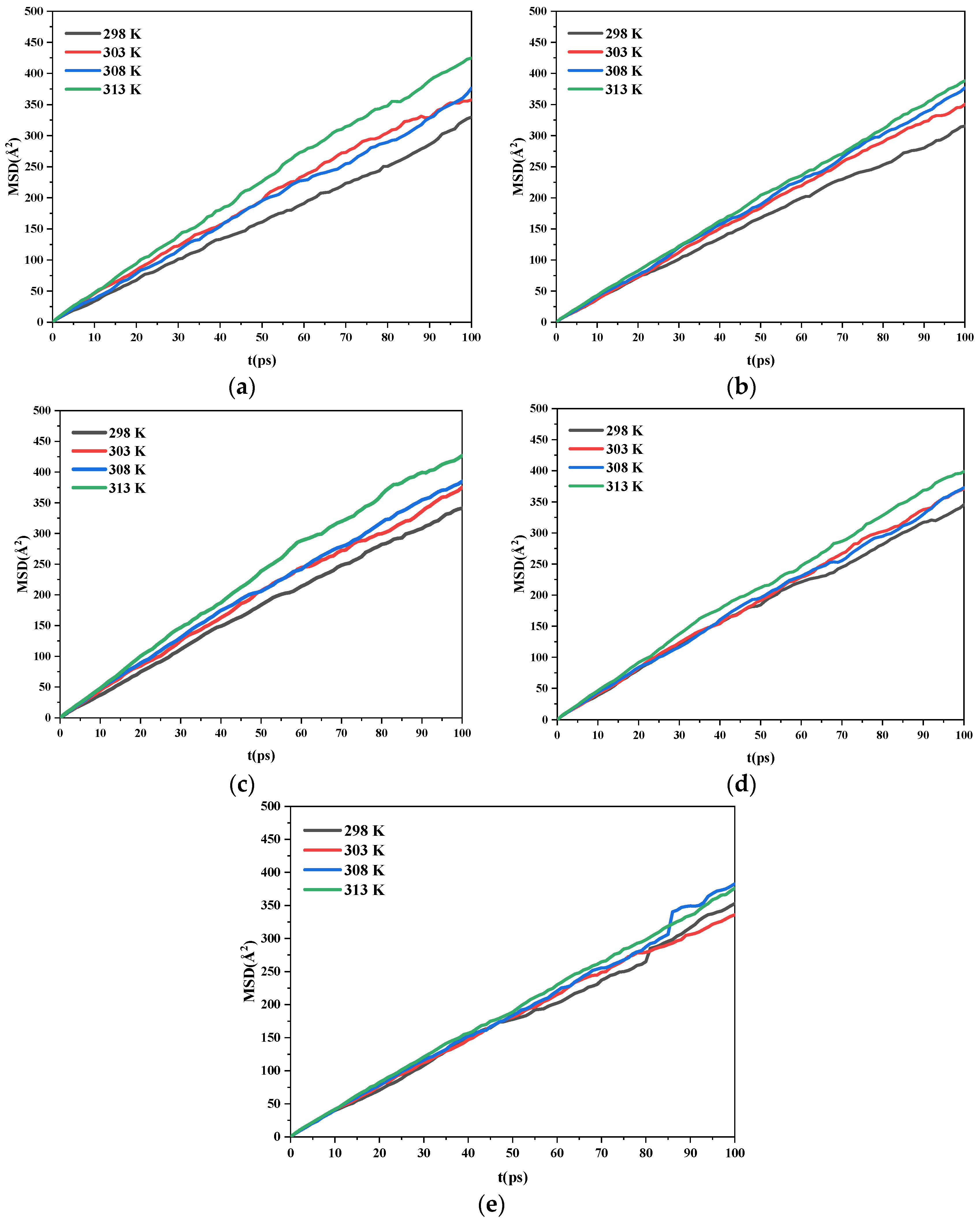
2.3.3. Diffusion Coefficients
2.3.4. Morphology Analysis
3. Modeling and Simulation
3.1. Modified Attachment Energy Model
3.2. Computational Methods
4. Conclusions
- (1)
- The growth morphology of the ADN/PDO is hexagonal prism in vacuum, and the five main crystal surfaces are (1 0 0), (0 1 1), (1 1 0), (1 1 −1), and (2 0 −2). Among them, the (1 0 0) surface has the largest exposed area, accounting for 40.744%.
- (2)
- The binding energy between the ADN/PDO cocrystal and ethanol solvent is positive on all important growth planes. The order of binding energy is (0 1 1) > (1 1 −1) > (2 0 −2) > (1 1 0) > (1 0 0). The binding effect between the ethanol and ADN/PDO is strongest on the (0 1 1) crystal plane.
- (3)
- The radial distribution function analysis of the (0 1 1) crystal plane showed that there are hydrogen bonds between the ethanol and ADN cations, van der Waals interactions with the ADN anions, and hydrogen bonds and van der Waals interactions with the PDO at the same time. In the (0 1 1) crystal plane, the value of S is 1.513, which indicates that this surface has a large roughness. This is more conducive to the adsorption of ethanol molecules.
- (4)
- As the temperature increases, the diffusion coefficient of the ethanol under the same crystal plane increases gradually. Meanwhile, the morphology analysis indicated that increasing the temperature is beneficial to reducing the aspect ratio of the crystal. This is conducive to the reduction of explosive sensitivity.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Östmark, H.; Bemm, U.; Langlet, A.; Sandén, R.; Wingborg, N. The Properties of Ammonium Dinitramide (ADN): Part 1, Basic Properties and Spectroscopic Data. J. Energ. Mater 2000, 18, 123–138. [Google Scholar] [CrossRef]
- Venkatachalam, S.; Santhosh, G.; Ninan Ninan, K. An Overview on the Synthetic Routes and Properties of Ammonium Dinitramide (ADN) and Other Dinitramide Salts. Propell. Explos. Pyrot. 2004, 29, 178–187. [Google Scholar] [CrossRef]
- Kon’kova, T.S.; Matyushin, Y.N.; Miroshnichenko, E.A.; Vorob’ev, A.B. Thermochemical properties of dinitramidic acid salts. Russ. Chem. Bulletin. 2009, 58, 2020–2027. [Google Scholar] [CrossRef]
- Chen, F.; Xuan, C.; Lu, Q.; Xiao, L.; Yang, J.; Hu, Y.; Zhang, G.-P.; Wang, Y.; Zhao, F.; Hao, G.; et al. A Review on the High Energy Oxidizer Ammonium Dinitramide: Its Synthesis, Thermal Decomposition, Hygroscopicity, and Application in Energetic Materials. Def. Technol. 2023, 19, 163–195. [Google Scholar] [CrossRef]
- Kumar, P. An Overview on Properties, Thermal Decomposition, and Combustion Behavior of ADN and ADN Based Solid Propellants. Def. Technol. 2018, 14, 661–673. [Google Scholar] [CrossRef]
- Cui, J.; Han, J.; Wang, J.; Huang, R. Study on the Crystal Structure and Hygroscopicity of Ammonium Dinitramide. J. Chem. Eng. Data 2010, 55, 3229–3234. [Google Scholar] [CrossRef]
- Chen, X.; He, L.; Li, X.; Zhou, Z.; Ren, Z. Molecular Simulation Studies on the Growth Process and Properties of Ammonium Dinitramide Crystal. J. Phys. Chem. C 2019, 123, 10940–10948. [Google Scholar] [CrossRef]
- Zhang, J.; Shreeve, J.M. Time for pairing: Cocrystals as advanced energetic materials. CrystEngComm 2016, 18, 6124–6133. [Google Scholar] [CrossRef]
- Muravyev, N.V.; Fershtat, L.L.; Dalinger, I.L.; Suponitsky, K.Y.; Ananyev, I.V.; Melnikov, I.N. Rational Screening of Cocrystals using Thermal Analysis: Benchmarking on Energetic Materials. Cryst. Growth Des. 2022, 22, 7349–7362. [Google Scholar] [CrossRef]
- Hu, D.; Wang, Y.; Xiao, C.; Hu, Y.; Zhou, Z.; Ren, Z. Studies on Ammonium Dinitramide and 3, 4-Diaminofurazan Cocrystal for Tuning the Hygroscopicity. Chinese J. Chem. Eng. 2023, in press. [Google Scholar] [CrossRef]
- Ren, Z.; Chen, X.; Yu, G.; Wang, Y.; Chen, B.; Zhou, Z. Molecular Simulation Studies on the Design of Energetic Ammonium Dinitramide Co-Crystals for Tuning Hygroscopicity. CrystEngComm 2020, 22, 5237–5244. [Google Scholar] [CrossRef]
- Qiao, S.; Li, H.; Yang, Z. Decreasing the Hygroscopicity of Ammonium Dinitramide (ADN) through Cocrystallization. Energetic Mater. Front. 2022, 3, 84–89. [Google Scholar] [CrossRef]
- Xie, H.; Gou, R.; Zhang, S. Theoretical Study on the Effect of Solvent Behavior on Ammonium Dinitramide (ADN)/1,4,7,10,13,16-Hexaoxacyclooctadecane (18-Crown-6) Cocrystal Growth Morphology at Different Temperatures. Cryst. Res. Technol. 2021, 56, 2000203. [Google Scholar] [CrossRef]
- Bellas, M.K.; Matzger, A.J. Achieving Balanced Energetics through Cocrystallization. Angew. Chem. Int. Ed. 2019, 58, 17185–17188. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Niu, S.; Lai, W.; Yu, T.; Ma, Y.; Gao, H.; Zhao, F.; Ge, Z. Crystal Morphology Prediction of Energetic Materials Grown from Solution: Insights into the Accurate Calculation of Attachment Energies. CrystEngComm 2019, 21, 4910–4917. [Google Scholar] [CrossRef]
- Esfahani, R.E.; Zahedi, P.; Zarghami, R. 5-Fluorouracil-Loaded Poly(Vinyl Alcohol)/Chitosan Blend Nanofibers: Morphology, Drug Release and Cell Culture Studies. Iran Polym. J. 2021, 30, 167–177. [Google Scholar] [CrossRef]
- Sun, L.; Wang, Y.; Yang, F.; Zhang, X.; Hu, W. Cocrystal Engineering: A Collaborative Strategy toward Functional Materials. Adv. Mater. 2019, 31, 1902328. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, T.; Lai, W.; Ma, Y.; Kang, Y.; Ge, Z. Adsorption Behavior of Acetone Solvent at the HMX Crystal Faces: A Molecular Dynamics Study. J. Mol. Graph. Model. 2017, 74, 38–43. [Google Scholar] [CrossRef]
- Lovette, M.A.; Browning, A.R.; Griffin, D.W.; Sizemore, J.P.; Snyder, R.C.; Doherty, M.F. Crystal Shape Engineering. Ind. Eng. Chem. Res. 2008, 47, 9812–9833. [Google Scholar] [CrossRef]
- Dandekar, P.; Kuvadia, Z.B.; Doherty, M.F. Engineering Crystal Morphology. Annu. Rev. Mater. Res. 2013, 43, 359–386. [Google Scholar] [CrossRef]
- Yusop, S.N.; Anuar, N.; Salwani, M.A.N.; Abu Bakar, N.H. Molecular Dynamic Investigation on the Dissolution Behaviour of Carbamazepine Form III in Ethanol Solution. Key Eng. Mater. 2019, 797, 149–157. [Google Scholar] [CrossRef]
- Liu, Y. Crystal Morphology Prediction Method of Energetic Materials: Attachment Energy Model and Its Development. Chin. J. Explos. Propellant 2021, 44, 578–588. [Google Scholar] [CrossRef]
- Liu, Y.; Lai, W.; Yu, T.; Ma, Y.; Kang, Y.; Ge, Z. Understanding the Growth Morphology of Explosive Crystals in Solution: Insights from Solvent Behavior at the Crystal Surface. RSC Adv. 2017, 7, 1305–1312. [Google Scholar] [CrossRef]
- Liu, Y.; Lai, W.; Ma, Y.; Yu, T.; Kang, Y.; Ge, Z. Face-Dependent Solvent Adsorption: A Comparative Study on the Interfaces of HMX Crystal with Three Solvents. J. Phys. Chem. B 2017, 121, 7140–7146. [Google Scholar] [CrossRef] [PubMed]
- Hartman, P. The Attachment Energy as a Habit Controlling Factor: III. Application to Corundum. J. Cryst. Growth. 1980, 49, 166–170. [Google Scholar] [CrossRef]
- Bonaccorso, A.; Gigliobianco, M.R.; Pellitteri, R.; Santonocito, D.; Carbone, C.; Di Martino, P.; Puglisi, G.; Musumeci, T. Optimization of curcumin nanocrystals as promising strategy for nose-to-brain delivery application. Pharmaceutics 2020, 12, 476. [Google Scholar] [CrossRef]
- Rakotoarisoa, M.; Angelov, B.; Espinoza, S.; Khakurel, K.; Bizien, T.; Drechsler, M.; Angelova, A. Composition-switchable liquid crystalline nanostructures as green formulations of curcumin and fish oil. ACS Sustain. Chem. Eng. 2021, 9, 14821–14835. [Google Scholar] [CrossRef]
- Rakotoarisoa, M.; Angelov, B.; Espinoza, S.; Khakurel, K.; Bizien, T.; Angelova, A. Cubic Liquid Crystalline Nanostructures Involving Catalase and Curcumin: BioSAXS Study and Catalase Peroxidatic Function after Cubosomal Nanoparticle Treatment of Differentiated SH-SY5Y Cells. Molecules 2019, 24, 3058. [Google Scholar] [CrossRef]
- Hartman, P.; Bennema, P. The Attachment Energy as a Habit Controlling Factor: I. Theoretical Considerations. J. Cryst. Growth. 1980, 49, 145–156. [Google Scholar] [CrossRef]
- Liu, Y.; Bi, F.; Lai, W.; Wei, T.; Ma, Y.; Ge, Z. Crystal Morphology Prediction od Dihydroxylammonium 5,5′-Bistetrazole-1,1′-diolate Under Different Growth Conditions. Chin. J. Energetic Mater. 2018, 26, 210–217. [Google Scholar] [CrossRef]
- Zhou, T.; Chen, F.; Li, J.; Cao, D.; Wang, J. Growth Morphology of TKX-50 in Formic Acid/Water Mixed Solvent by Molecular Dynamics Simulation. Chin. J. Energetic Mater. 2020, 28, 865–873. [Google Scholar] [CrossRef]
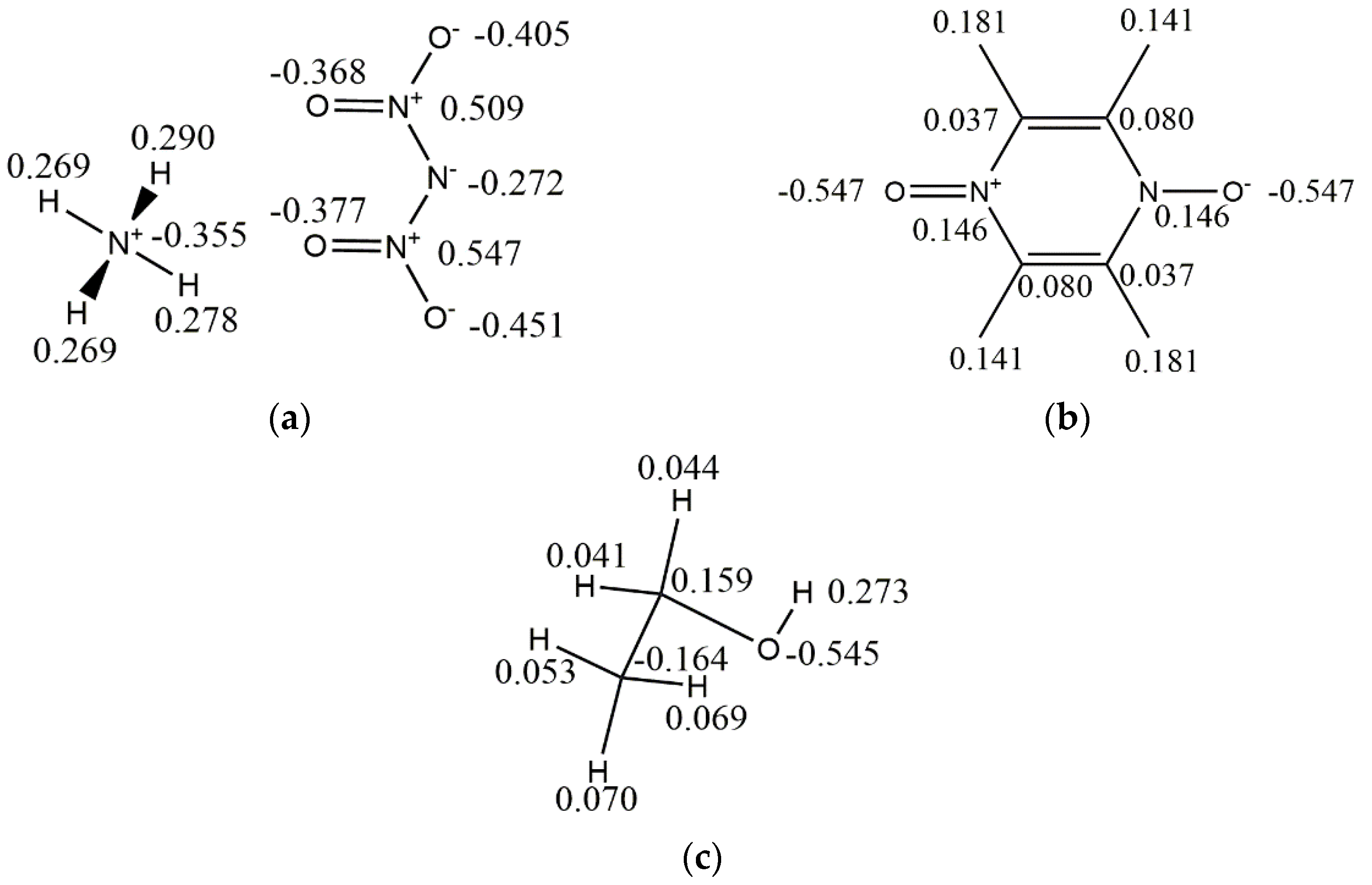
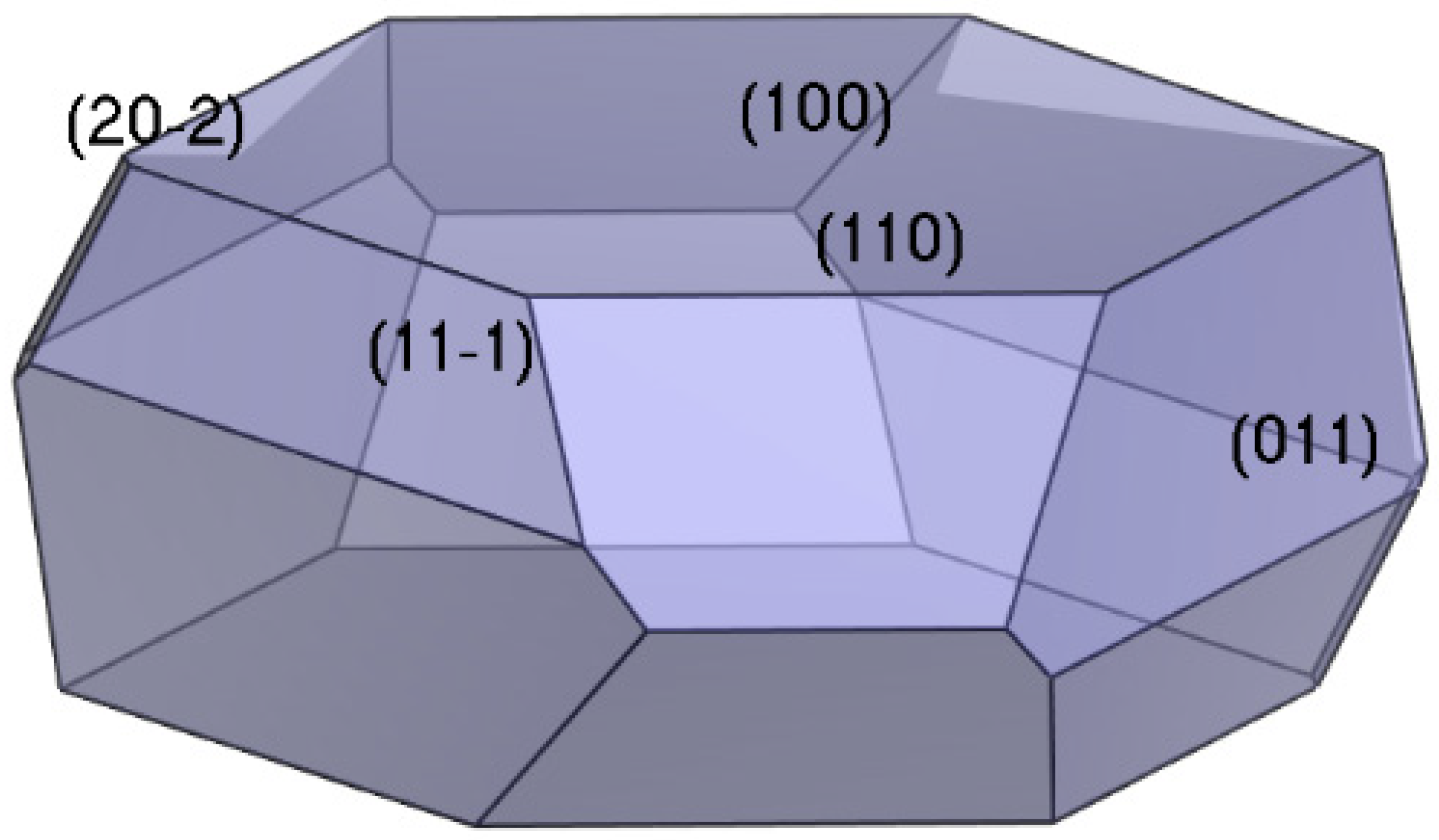

| Parameters | Exp | COMPASSIII | PCFF | CVFF | Universal | Dreiding |
|---|---|---|---|---|---|---|
| a/Å | 11.592 | 10.946 | 11.533 | 11.626 | 11.819 | 11.347 |
| b/Å | 8.188 | 8.143 | 9.167 | 8.504 | 8.472 | 7.960 |
| c/Å | 7.227 | 6.832 | 6.946 | 7.217 | 7.687 | 7.696 |
| α/° | 90.000 | 90.000 | 90.000 | 90.000 | 90.000 | 90.000 |
| β/° | 101.236 | 99.546 | 93.744 | 101.050 | 100.974 | 100.628 |
| γ/° | 90.000 | 90.000 | 90.000 | 90.000 | 90.000 | 90.000 |
| REa | 0.00% | −5.57% | −0.51% | 0.29% | 1.96% | −2.12% |
| REb | 0.00% | −0.54% | 11.96% | 3.86% | 3.47% | −2.78% |
| REc | 0.00% | −5.47% | −3.89% | −0.14% | 6.36% | 6.49% |
| REα | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% |
| REβ | 0.00% | −1.67% | −7.40% | −0.18% | −0.26% | −0.60% |
| REγ | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% |
| (h k l) | dhkl | Surface Area/Å2 | Eatt (total)/(kcal·mol−1) | Total Facet Area/% | Aspect Ratio |
|---|---|---|---|---|---|
| (1 0 0) | 11.411 | 61.370 | −61.570 | 40.744 | 2.569 |
| (0 1 1) | 5.442 | 128.669 | −117.417 | 26.208 | |
| (1 1 0) | 6.818 | 102.703 | −109.348 | 18.177 | |
| (1 1 −1) | 5.220 | 134.151 | −119.789 | 14.450 | |
| (2 0 −2) | 3.306 | 105.900 | −148.904 | 0.422 |
| T/K | (h k l) | Etot/ (kcal·mol−1) | Esol/ (kcal·mol−1) | Ecry/ (kcal·mol−1) | Ebind/ (kcal·mol−1) |
|---|---|---|---|---|---|
| 298 | (1 0 0) | −31,481.17 | −977.69 | −30,057.88 | 445.60 |
| (0 1 1) | −30,628.73 | −1821.46 | −27,671.08 | 1136.19 | |
| (1 1 0) | −34,837.67 | −1936.03 | −32,224.39 | 677.25 | |
| (1 1 −1) | −36,757.43 | −1570.34 | −34,100.57 | 1086.52 | |
| (2 0 −2) | −13,735.02 | −1740.63 | −11,101.82 | 892.57 | |
| 303 | (1 0 0) | −31,274.01 | −817.80 | −29,976.35 | 479.86 |
| (0 1 1) | −30,552.83 | −1790.10 | −27,651.20 | 1111.53 | |
| (1 1 0) | −34,632.60 | −1770.36 | −32,133.13 | 729.11 | |
| (1 1 −1) | −36,837.35 | −1703.37 | −34,060.68 | 1073.30 | |
| (2 0 −2) | −13,690.91 | −1658.16 | −11,116.84 | 915.91 | |
| 308 | (1 0 0) | −31,210.31 | −829.50 | −29,875.30 | 505.50 |
| (0 1 1) | −30,341.76 | −1626.49 | −27,541.56 | 1173.72 | |
| (1 1 0) | −34,523.77 | −1706.96 | −32,087.83 | 728.98 | |
| (1 1 −1) | −36,633.24 | −1583.95 | −33,947.88 | 1101.40 | |
| (2 0 −2) | −13,497.78 | −1561.47 | −11,070.35 | 865.96 | |
| 313 | (1 0 0) | −31,010.92 | −714.65 | −29,865.60 | 430.68 |
| (0 1 1) | −30,239.24 | −1560.73 | −27,580.70 | 1097.81 | |
| (1 1 0) | −34,250.38 | −1550.09 | −31,982.37 | 717.92 | |
| (1 1 −1) | −36,502.03 | −1486.06 | −33,840.10 | 1175.87 | |
| (2 0 −2) | −13,428.79 | −1492.03 | −11,066.84 | 869.92 |
| (h k l) | D/(×10−8 m2·s−1) | |||
|---|---|---|---|---|
| 298 K | 303 K | 308 K | 313 K | |
| (1 0 0) | 0.53 | 0.61 | 0.60 | 0.71 |
| (0 1 1) | 0.52 | 0.59 | 0.62 | 0.64 |
| (1 1 0) | 0.57 | 0.61 | 0.63 | 0.73 |
| (1 1 −1) | 0.56 | 0.61 | 0.60 | 0.66 |
| (2 0 −2) | 0.57 | 0.56 | 0.62 | 0.61 |
| T/K | (h k l) | Eint/ (kcal·mol−1) | Es/ (kcal·mol−1) | Eatt′/ (kcal·mol−1) | Total Facet Area/% | Aspect Ratio |
|---|---|---|---|---|---|---|
| 298 | (1 0 0) | −445.60 | −27.85 | −27.51 | 15.37 | 3.324 |
| (0 1 1) | −1136.19 | −71.01 | −10.00 | 84.63 | ||
| (1 1 0) | −677.25 | −42.33 | −51.81 | - | ||
| (1 1 −1) | −1086.52 | −67.91 | −25.46 | - | ||
| (2 0 −2) | −892.57 | −55.79 | −46.46 | - | ||
| 303 | (1 0 0) | −479.86 | −29.99 | −24.90 | 19.85 | 2.653 |
| (0 1 1) | −1111.54 | −69.47 | −12.33 | 80.15 | ||
| (1 1 0) | −729.11 | −45.57 | −47.40 | - | ||
| (1 1 −1) | −1073.30 | −67.08 | −26.61 | - | ||
| (2 0 −2) | −915.91 | −57.24 | −43.78 | - | ||
| 308 | (1 0 0) | −505.50 | −31.59 | −22.94 | 12.33 | 4.090 |
| (0 1 1) | −1173.72 | −73.36 | −6.45 | 87.67 | ||
| (1 1 0) | −728.98 | −45.56 | −47.41 | - | ||
| (1 1 −1) | −1101.40 | −68.84 | −24.17 | - | ||
| (2 0 −2) | −865.96 | −54.12 | −49.52 | - | ||
| 313 | (1 0 0) | −430.68 | −26.92 | −28.65 | 10.70 | 2.353 |
| (0 1 1) | −1097.81 | −68.61 | −13.63 | 61.50 | ||
| (1 1 0) | −717.92 | −44.87 | −48.35 | - | ||
| (1 1 −1) | −1175.87 | −73.49 | −17.71 | 27.80 | ||
| (2 0 −2) | −869.92 | −54.37 | −49.06 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Ma, B.; Jia, X.; Hou, C. Prediction of Ethanol-Mediated Growth Morphology of Ammonium Dinitramide/Pyrazine-1,4-Dioxide Cocrystal at Different Temperatures. Molecules 2023, 28, 4534. https://doi.org/10.3390/molecules28114534
Zhang Y, Ma B, Jia X, Hou C. Prediction of Ethanol-Mediated Growth Morphology of Ammonium Dinitramide/Pyrazine-1,4-Dioxide Cocrystal at Different Temperatures. Molecules. 2023; 28(11):4534. https://doi.org/10.3390/molecules28114534
Chicago/Turabian StyleZhang, Yuanping, Boyu Ma, Xinlei Jia, and Conghua Hou. 2023. "Prediction of Ethanol-Mediated Growth Morphology of Ammonium Dinitramide/Pyrazine-1,4-Dioxide Cocrystal at Different Temperatures" Molecules 28, no. 11: 4534. https://doi.org/10.3390/molecules28114534
APA StyleZhang, Y., Ma, B., Jia, X., & Hou, C. (2023). Prediction of Ethanol-Mediated Growth Morphology of Ammonium Dinitramide/Pyrazine-1,4-Dioxide Cocrystal at Different Temperatures. Molecules, 28(11), 4534. https://doi.org/10.3390/molecules28114534






