On Integral INICS Aromaticity of Pyridodiazepine Constitutional Isomers and Tautomers
Abstract
:1. Introduction
2. Results and Discussion
2.1. Energetics
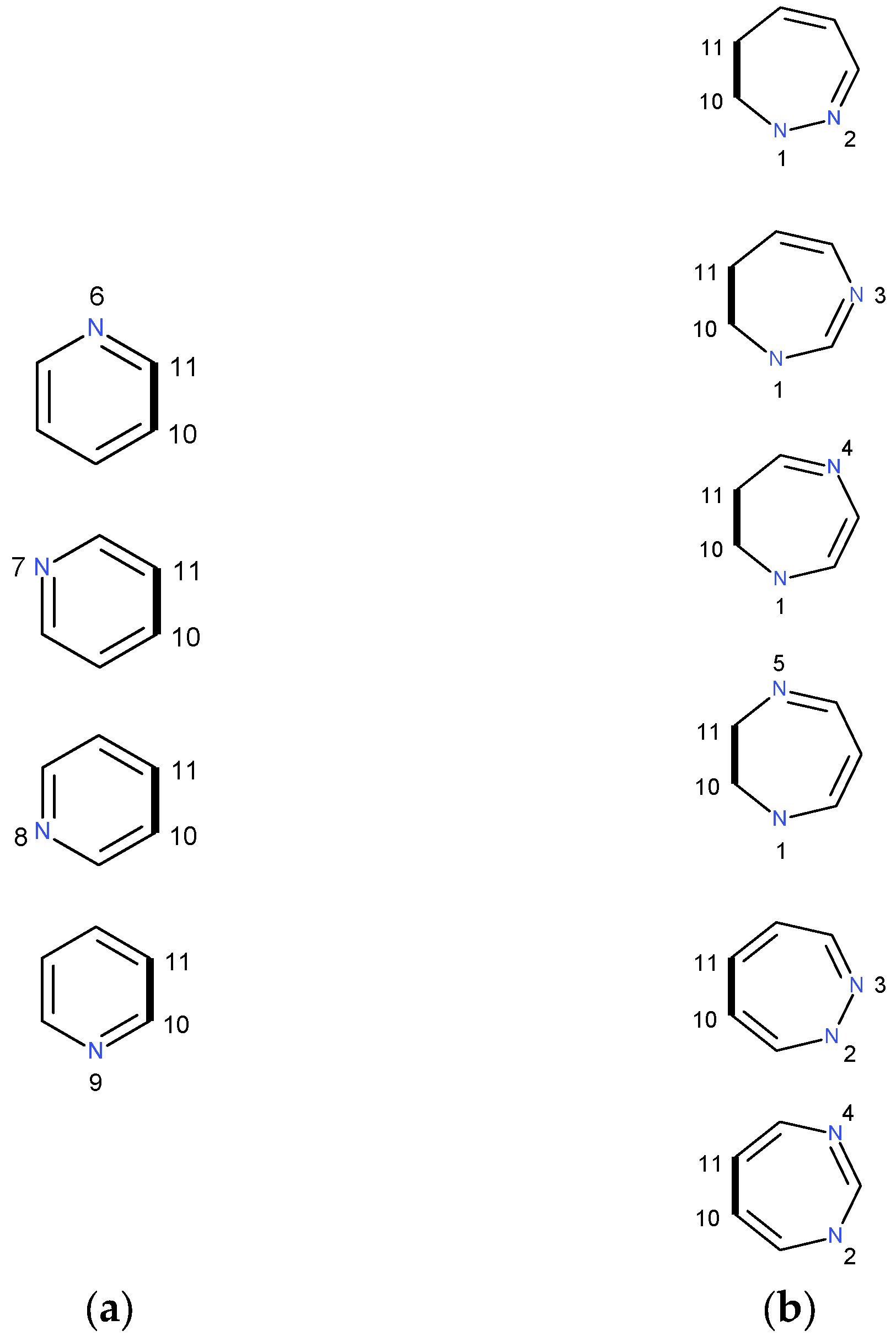
2.1.1. [m,n]diazepine Isomers
2.1.2. Pyridine–Diazepine Rings Condensation
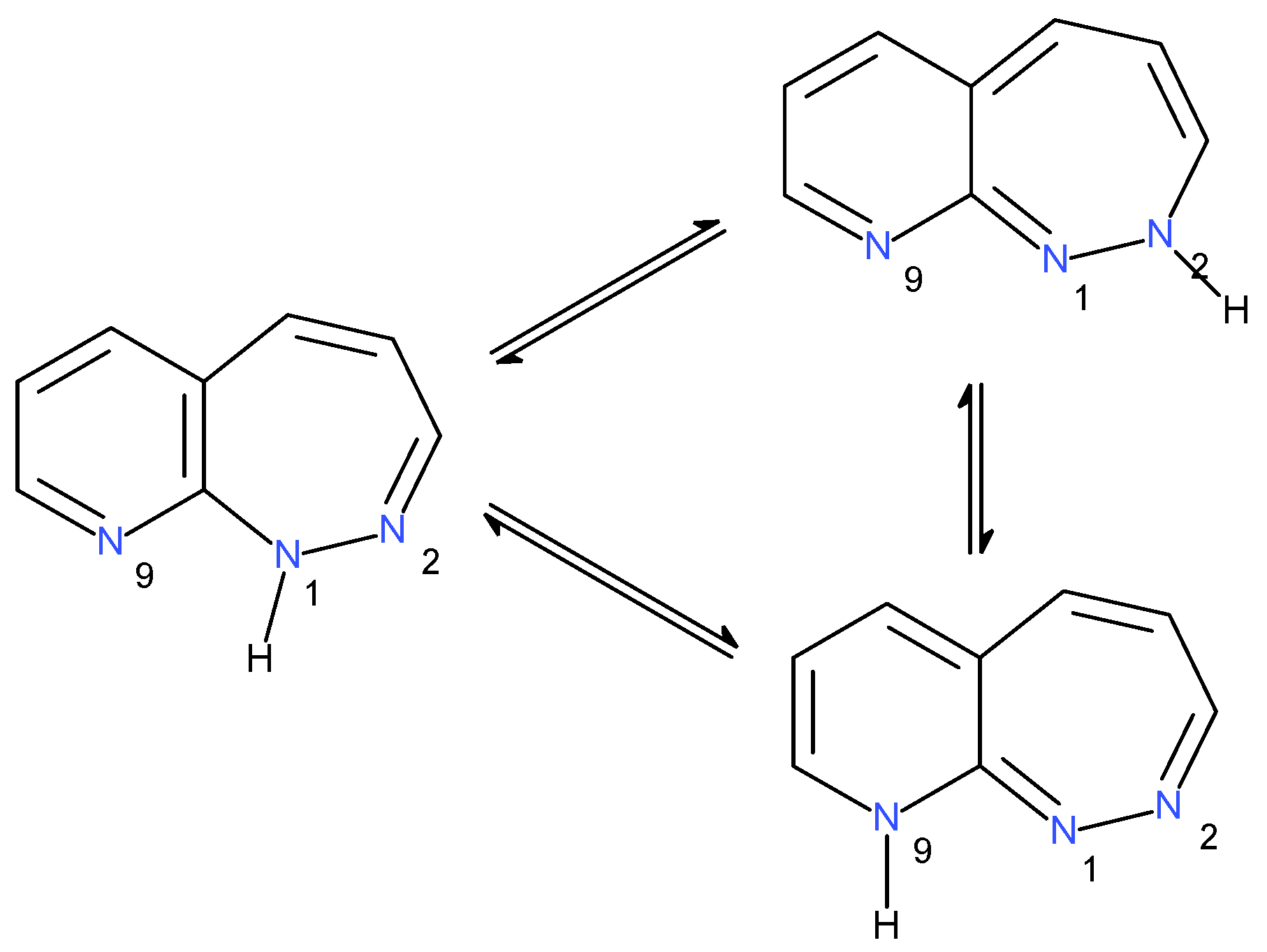
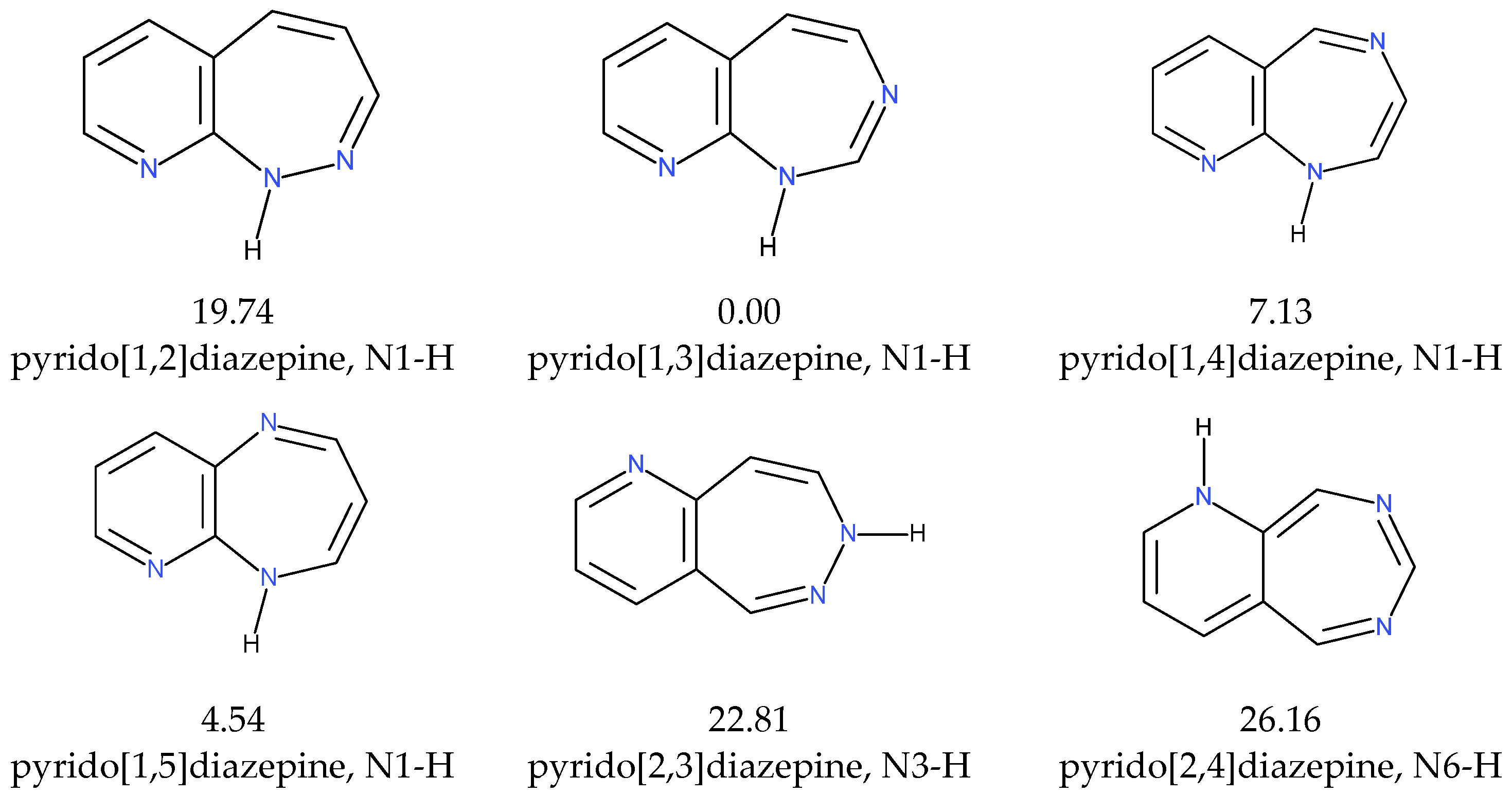
2.1.3. Tautomers
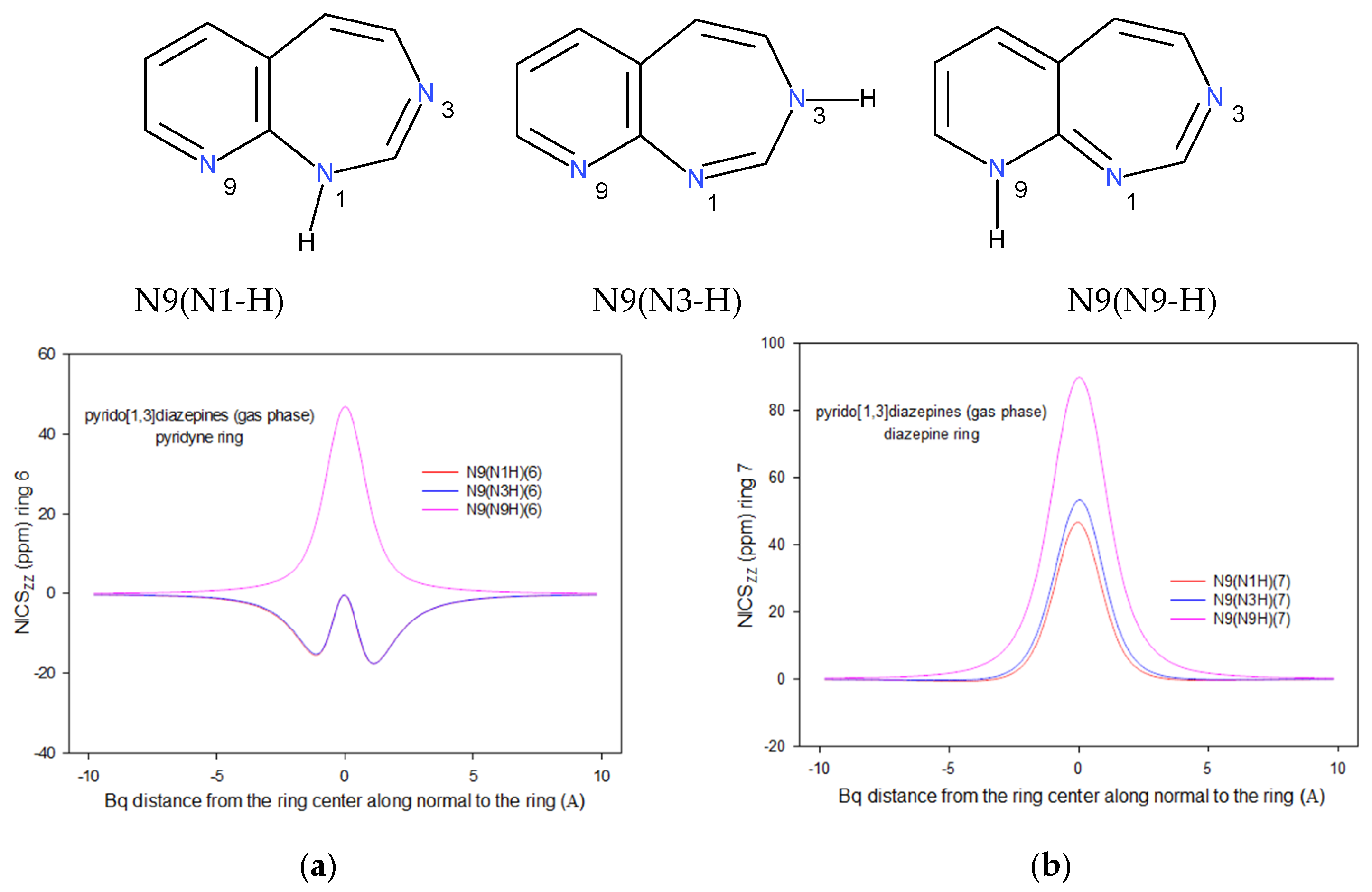
2.2. Integral INICS Aromaticity
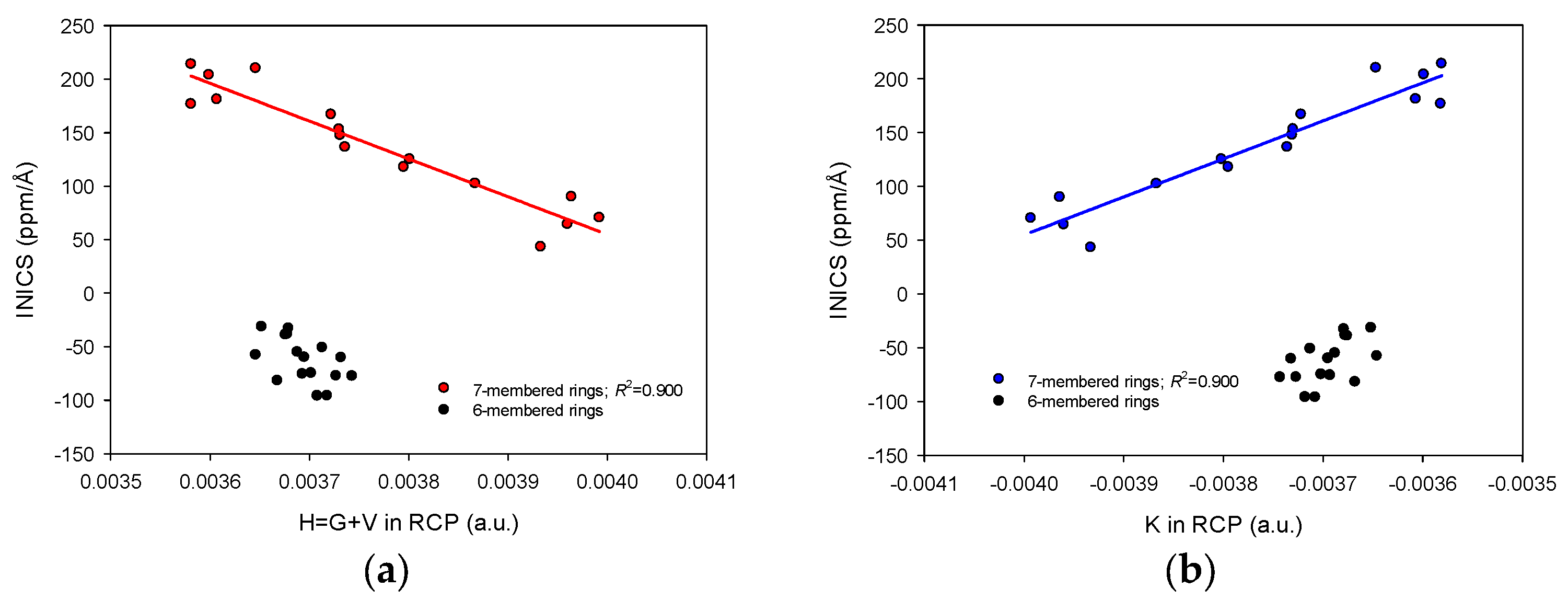
2.3. INICS vs. Electron Density Parameters at the Ring Critical Points
3. Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Laar, C. Ueber die Möglichkeit mehrerer Strukturformeln für dieselbe chemische Verbindung. Ber. Dtsch. Chem. Ges. 1885, 18, 648–657. [Google Scholar] [CrossRef] [Green Version]
- Raczyńska, E.D.; Kosińska, W.; Ośmiałowski, B.; Gawinecki, R. Tautomeric Equilibria in Relation to Pi-Electron Delocalization. Chem. Rev. 2005, 105, 3561–3612. [Google Scholar] [CrossRef] [PubMed]
- Raczyńska, E.D.; Kamińska, B. Structural and thermochemical consequences of prototropy and ionization for the biomolecule xanthine in vacuo. J. Chem. Thermodyn. 2022, 171, 106788. [Google Scholar] [CrossRef]
- Raczyńska, E.D.; Krygowski, T.M.; Zachara, J.E.; Ośmiałowski, B.; Gawinecki, R. Tautomeric equilibria, H-bonding and π-electron delocalization in o -nitrosophenol. A B3LYP/6-311 + G(2df,2p) study. J. Phys. Org. Chem. 2005, 18, 892–897. [Google Scholar] [CrossRef]
- Raczyńska, E.D.; Kamińska, B. Variations of the tautomeric preferences and π-electron delocalization for the neutral and redox forms of purine when proceeding from the gas phase (DFT) to water (PCM). J. Mol. Model. 2013, 19, 3947–3960. [Google Scholar] [CrossRef] [Green Version]
- Raczyńska, E.D.; Gal, J.-F.; Maria, P.-C.; Sajek, M. Proton transfer chemistry in the gas phase. Is a spontaneous “neutralization” reaction a myth or a reality? Croat. Chem. Acta 2009, 82, 87–103. [Google Scholar]
- Raczyńska, E.D.; Decouzon, M.; Gal, J.-F.; Maria, P.-C.; Taft, R.W.; Anvia, F. Gas-Phase Basicity of Polyfunctional Amidinazines: Experimental Evidence of Preferred Site(s) of Protonation. J. Org. Chem. 2000, 65, 4635–4640. [Google Scholar] [CrossRef]
- Taylor, P.J.; van der Zwan, G.; Antonov, L. Tautomerism: Introduction, History, and Recent Developments in Experimental and Theoretical Methods. In Tautomerism; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2013; pp. 1–24. [Google Scholar]
- Liu, Q.; Yang, D.; Zhuang, Y.; Croll, T.I.; Cai, X.; Dai, A.; He, X.; Duan, J.; Yin, W.; Ye, C.; et al. Ligand recognition and G-protein coupling selectivity of cholecystokinin A receptor. Nat. Chem. Biol. 2021, 17, 1238–1244. [Google Scholar] [CrossRef]
- Raczyńska, E.D. On Analogies in Proton-Transfers for Pyrimidine Bases in the Gas Phase (Apolar Environment)—Cytosine Versus Isocytosine. Symmetry 2023, 15, 342. [Google Scholar] [CrossRef]
- Barclay, T.; Ginic-Markovic, M.; Johnston, M.R.; Cooper, P.; Petrovsky, N. Observation of the keto tautomer of d-fructose in D2O using 1H NMR spectroscopy. Carbohydr. Res. 2012, 347, 136–141. [Google Scholar] [CrossRef] [Green Version]
- Raczyńska, E.D.; Gal, J.-F.; Maria, P.-C.; Fontaine-Vive, F. Biguanide Antidiabetic Drugs: Imeglimin Exhibits Higher Proton Basicity but Smaller Lithium-Cation Basicity than Metformin in Vacuo. ACS Omega 2018, 3, 17842–17852. [Google Scholar] [CrossRef]
- Raczyńska, E.D.; Gal, J.-F.; Maria, P.-C.; Michalec, P.; Zalewski, M. Exceptionally High Proton and Lithium Cation Gas-Phase Basicity of the Anti-Diabetic Drug Metformin. J. Phys. Chem. A 2017, 121, 8706–8718. [Google Scholar] [CrossRef]
- Katritzky, A.R.; Hall, C.D.; El-Gendy, B.E.-D.M.; Draghici, B. Tautomerism in drug discovery. J. Comput. Aided. Mol. Des. 2010, 24, 475–484. [Google Scholar] [CrossRef]
- Graff, M.; Dobrowolski, J.C. On tautomerism of diazinones. Comput. Theor. Chem. 2013, 1026, 55–64. [Google Scholar] [CrossRef]
- Karpińska, G.; Mazurek, A.P.; Dobrowolski, J.C. On substituent effect on the benzodiazepinone system. Comput. Theor. Chem. 2012, 993, 13–19. [Google Scholar] [CrossRef]
- Jarończyk, M.; Dobrowolski, J.C. The 1-deazapurine derivatives, tautomerism, substituent effect, and aromaticity: A computational study. Comput. Theor. Chem. 2011, 974, 9–15. [Google Scholar] [CrossRef]
- Jarończyk, M.; Dobrowolski, J.C. On isomers and tautomers of Nitro-1-deazapurine: A DFT study. J. Mol. Struct. THEOCHEM 2008, 858, 77–84. [Google Scholar] [CrossRef]
- Ozimiński, W.P.; Dobrowolski, J.C.; Mazurek, A.P. DFT studies on tautomerism of C5-substituted 1,2,4-triazoles. J. Mol. Struct. THEOCHEM 2004, 680, 107–115. [Google Scholar] [CrossRef]
- Jarończyk, M.; Dobrowolski, J.C.; Mazurek, A.P. Theoretical studies on tautomerism and IR spectra of pyrazole derivatives. J. Mol. Struct. THEOCHEM 2004, 673, 17–28. [Google Scholar] [CrossRef]
- Karpińska, G.; Dobrowolski, J.C.; Mazurek, A.P. Conformation and tautomerism of the cimetidine molecule: A theoretical study. J. Mol. Struct. 2003, 645, 37–43. [Google Scholar] [CrossRef]
- Ozimiński, W.P.; Dobrowolski, J.C.; Mazurek, A.P. DFT studies on tautomerism of C5-substituted 1,2,3-triazoles. J. Mol. Struct. 2003, 651–653, 697–704. [Google Scholar] [CrossRef]
- Kurzepa, M.; Dobrowolski, J.C.; Mazurek, A.P. Theoretical studies on tautomerism and IR spectra of C-5 substituted imidazoles. J. Mol. Struct. 2001, 565–566, 107–113. [Google Scholar] [CrossRef]
- Fernandez, I. (Ed.) Aromaticity. Modern Computational Methods and Applications; Elsevier: Amsterdam, The Netherlands, 2021; ISBN 9780128227237. [Google Scholar]
- Krygowski, T.M.; Szatylowicz, H. Aromaticity: What does it mean? ChemTexts 2015, 1, 12. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alonso, M.; Fernández, I. Quantifying aromaticity according to the energetic criterion. In Aromaticity; Elsevier: Amsterdam, The Netherlands, 2021; pp. 195–235. [Google Scholar]
- Szatylowicz, H.; Wieczorkiewicz, P.A.; Krygowski, T.M. Molecular geometry as a source of electronic structure of π-electron systems and their physicochemical properties. In Aromaticity; Elsevier: Amsterdam, The Netherlands, 2021; pp. 71–99. [Google Scholar]
- Gershoni-Poranne, R.; Stanger, A. NICS—Nucleus-independent Chemical Shift. In Aromaticity; Elsevier: Amsterdam, The Netherlands, 2021; pp. 99–154. [Google Scholar]
- Szczepanik, D.W.; Solà, M. The electron density of delocalized bonds (EDDBs) as a measure of local and global aromaticity. In Aromaticity; Elsevier: Amsterdam, The Netherlands, 2021; pp. 259–284. [Google Scholar]
- Aihara, J. Graph Theory of Aromatic Stabilization. Bull. Chem. Soc. Jpn. 2016, 89, 1425–1454. [Google Scholar] [CrossRef] [Green Version]
- Randić, M. Aromaticity of Polycyclic Conjugated Hydrocarbons. Chem. Rev. 2003, 103, 3449–3606. [Google Scholar] [CrossRef]
- Raczyńska, E. Application of the Extended HOMED (Harmonic Oscillator Model of Aromaticity) Index to Simple and Tautomeric Five-Membered Heteroaromatic Cycles with C, N, O, P, and S Atoms. Symmetry 2019, 11, 146. [Google Scholar] [CrossRef] [Green Version]
- Raczyńska, E.D.; Kurpiewski, J.; Igielska, M.; Kamińska, B. Quantitative description of bond lengths alternation for caffeine−effects of ionization, proton-transfer, and noncovalent interaction. Comput. Theor. Chem. 2020, 1180, 112811. [Google Scholar] [CrossRef]
- Raczyńska, E.D.; Hallman, M.; Kolczyńska, K.; Stępniewski, T.M. On the Harmonic Oscillator Model of Electron Delocalization (HOMED) Index and its Application to Heteroatomic π-Electron Systems. Symmetry 2010, 2, 1485–1509. [Google Scholar] [CrossRef] [Green Version]
- Von Schleyer, P.R.; Maerker, C.; Dransfeld, A.; Jiao, H.; van Eikema Hommes, N.J.R. Nucleus-Independent Chemical Shifts: A Simple and Efficient Aromaticity Probe. J. Am. Chem. Soc. 1996, 118, 6317–6318. [Google Scholar] [CrossRef]
- Von Schleyer, P.R.; Manoharan, M.; Wang, Z.-X.; Kiran, B.; Jiao, H.; Puchta, R.; van Eikema Hommes, N.J.R. Dissected Nucleus-Independent Chemical Shift Analysis of π-Aromaticity and Antiaromaticity. Org. Lett. 2001, 3, 2465–2468. [Google Scholar] [CrossRef]
- Schleyer, P.V.R.; Jiao, H.; Hommes, N.J.V.E.; Malkin, V.G.; Malkina, O.L. An Evaluation of the Aromaticity of Inorganic Rings: Refined Evidence from Magnetic Properties. J. Am. Chem. Soc. 1997, 119, 12669–12670. [Google Scholar] [CrossRef]
- Fowler, P.W.; Steiner, E.; Zanasi, R.; Cadioli, B. Electric and magnetic properties of hexaethynylbenzene. Mol. Phys. 1999, 96, 1099–1108. [Google Scholar] [CrossRef]
- Corminboeuf, C.; Heine, T.; Seifert, G.; von Schleyer, P.R.; Weber, J. Induced magnetic fields in aromatic [n]-annulenes—Interpretation of NICS tensor components. Phys. Chem. Chem. Phys. 2004, 6, 273–276. [Google Scholar] [CrossRef]
- Stanger, A. Nucleus-Independent Chemical Shifts (NICS): Distance Dependence and Revised Criteria for Aromaticity and Antiaromaticity. J. Org. Chem. 2006, 71, 883–893. [Google Scholar] [CrossRef]
- Stanger, A. Reexamination of NICS π,zz: Height Dependence, Off-Center Values, and Integration. J. Phys. Chem. A 2019, 123, 3922–3927. [Google Scholar] [CrossRef]
- Berger, R.J.F.; Dimitrova, M.; Nasibullin, R.T.; Valiev, R.R.; Sundholm, D. Integration of global ring currents using the Ampère–Maxwell law. Phys. Chem. Chem. Phys. 2022, 24, 624–628. [Google Scholar] [CrossRef]
- Berger, R.J.F.; Dimitrova, M. A natural scheme for the quantitative analysis of the magnetically induced molecular current density using an oriented flux-weighted stagnation graph. I. A minimal example for LiH. Phys. Chem. Chem. Phys. 2022, 24, 23089–23095. [Google Scholar] [CrossRef]
- Dudek, W.M.; Ostrowski, S.; Dobrowolski, J.C. On Aromaticity of the Aromatic α-Amino Acids and Tuning of the NICS Indices to Find the Aromaticity Order. J. Phys. Chem. A 2022, 126, 3433–3444. [Google Scholar] [CrossRef] [PubMed]
- Dudek, W.M. ARONICS; Institute of Chemistry and Nuclear Technology: Warsaw, Poland, 2022. [Google Scholar]
- Leimgruber, W.; Stefanović, V.; Schenker, F.; Karr, A.; Berger, J. Isolation and Characterization of Anthramycin, a New Antitumor Antibiotic. J. Am. Chem. Soc. 1965, 87, 5791–5793. [Google Scholar] [CrossRef]
- Leimgruber, W.; Batcho, A.D.; Czajkowski, R.C. Total synthesis of anthramycin. J. Am. Chem. Soc. 1968, 90, 5641–5643. [Google Scholar] [CrossRef]
- Leimgruber, W.; Batcho, A.D.; Schenker, F. The Structure of Anthramycin. J. Am. Chem. Soc. 1965, 87, 5793–5795. [Google Scholar] [CrossRef]
- Balon, R.; Starcevic, V. Role of Benzodiazepines in Anxiety Disorders. Adv. Exp. Med. Biol. 2020, 1191, 367–388. [Google Scholar] [PubMed]
- Peng, L.; Morford, K.L.; Levander, X.A. Benzodiazepines and Related Sedatives. Med. Clin. N. Am. 2022, 106, 113–129. [Google Scholar] [CrossRef] [PubMed]
- Fabian, A.; Röhmel, R.; Kubicki, S. Changes in the length of sleep cycles during administration of flurazepam and lopirazepam. EEG. EMG. Z. Elektroenzephalogr. Elektromyogr. Verwandte Geb. 1984, 15, 151–158. [Google Scholar] [PubMed]
- Saletu, M.; Saletu, B.; Grünberger, J.; Mader, R.; Karobath, M. Clinical Symptomatology and Computer Analyzed EEG before, during and after Anxiolytic Therapy of Alcohol Withdrawal Patients. Neuropsychobiology 1983, 9, 119–134. [Google Scholar] [CrossRef]
- Jacoviev, V.; Thiemer, K.; Engel, J. Zapizolam. Drugs Future 1982, 7, 831. [Google Scholar] [CrossRef]
- Liszkiewicz, H.; Kowalska, M.W.; Rutkowska, M.; Gliniak, H. Synthesis and anxiolytic activity of 1-phenyl-2-(4-aryl-1,3,4,5-tetrahydropyrido[2,3-b][1,4]diazepin-2-ylidene)-ethanone. Pharmazie 2006, 61, 517–521. [Google Scholar] [CrossRef]
- Liszkiewicz, H.; Kowalsk, M.W.; Glowiak, T.; Wietrzyk, J.; Opolski, A. Synthesis and antiproliferative activity in vitro of 1-phenyl-2-(4-aryl-1,3,4,5-tetrahydropyrido[2,3-b][1,4]diazepin-2-ylidene) ethanone. Part I. Pol. J. Chem. 2002, 76, 1607–1617. [Google Scholar] [CrossRef]
- Liszkiewicz, H.; Nawrocka, W.P.; Sztuba, B.; Wietrzyk, J.; Jaroszewicz, J.; Nasulewicz, A.; Pełczyńska, M. Synthesis and antiproliferative activity in vitro of new pyrido[1,4-b]diazepine derivatives and imidazo[4,5-b]pyridine. Acta Pol. Pharm. 2011, 68, 349–355. [Google Scholar]
- Liegeois, J.F.F.; Bruhwyler, J.; Damas, J.; Nguyen, T.P.; Chleide, E.M.G.; Mercier, M.G.A.; Rogister, F.A.; Delarge, J.E. New pyridobenzodiazepine derivatives as potential antipsychotics: Synthesis and neurochemical study. J. Med. Chem. 1993, 36, 2107–2114. [Google Scholar] [CrossRef]
- Sanabria, E.; Cuenca, R.E.; Esteso, M.Á.; Maldonado, M. Benzodiazepines: Their Use either as Essential Medicines or as Toxics Substances. Toxics 2021, 9, 25. [Google Scholar] [CrossRef]
- De Jonge, B.L.M.; Kutschke, A.; Newman, J.V.; Rooney, M.T.; Yang, W.; Cederberg, C. Pyridodiazepine Amines Are Selective Therapeutic Agents for Helicobacter pylori by Suppressing Growth through Inhibition of Glutamate Racemase but Are Predicted to Require Continuous Elevated Levels in Plasma to Achieve Clinical Efficacy. Antimicrob. Agents Chemother. 2015, 59, 2337–2342. [Google Scholar] [CrossRef] [Green Version]
- Lv, M.; Xu, H. Dipyridodiazepinone Analogs as Human Immunodeficiency Virus Type 1- Specific Non-Nucleoside Reverse Transcriptase Inhibitors: An Overview. Curr. Med. Chem. 2010, 17, 1874–1898. [Google Scholar] [CrossRef]
- Milinkovic, A.; Martínez, E. Nevirapine in the treatment of HIV. Expert Rev. Anti. Infect. Ther. 2004, 2, 367–373. [Google Scholar] [CrossRef]
- Novelli, F.; Sparatore, A.; Tasso, B.; Sparatore, F. Quinolizidinyl derivatives of 5,11-dihydro-6H-pyrido[2,3-b][1,4]benzodiazepin-6-one as ligands for muscarinic receptors. Bioorg. Med. Chem. Lett. 1999, 9, 3031–3034. [Google Scholar] [CrossRef]
- Carmine, A.A.; Brogden, R.N. Pirenzepine. A review of its pharmacodynamic and pharmacokinetic properties and therapeutic efficacy in peptic ulcer disease and other allied diseases. Drugs 1985, 30, 85–126. [Google Scholar] [CrossRef]
- Czepita, M.; Iomdina, E.N. The possibilities of pharmacological intervention in myopia. Ophthalmol. J. 2020, 5, 150–153. [Google Scholar] [CrossRef]
- Tamizharasan, N.; Gajendran, C.; Kristam, R.; Sulochana, S.P.; Sivanandhan, D.; Mullangi, R.; Mathivathanan, L.; Hallur, G.; Suresh, P. Discovery and optimization of novel phenyldiazepine and pyridodiazepine based Aurora kinase inhibitors. Bioorg. Chem. 2020, 99, 103800. [Google Scholar] [CrossRef]
- Antonow, D.; Thurston, D.E. Synthesis of DNA-Interactive Pyrrolo[2,1-c ][1,4]benzodiazepines (PBDs). Chem. Rev. 2011, 111, 2815–2864. [Google Scholar] [CrossRef]
- Verdecia Reyes, Y.; Rodríguez, E.O.; Reyes, A.R.; Figueredo, Y.N.; Domínguez, C.C.; Tacoronte Morales, J.E.; Alba Gutiérrez, L.L.; Pardo Andreu, G.L. Tricyclic and tetracyclic systems with activity on the central nervous and vascular systems. U.S. Patent 9315497B2, 19 April 2016. [Google Scholar]
- Fun, H.-K.; Yeap, C.S.; Hazra, A.; Jana, S.; Goswami, S. 2,4-Diphenyl-4,5-dihydro-3 H -pyrido[2,3- b ][1,4]diazepine. Acta Crystallogr. Sect. E Struct. Reports Online 2009, 65, o1139–o1140. [Google Scholar] [CrossRef]
- Ahmad, R.; Zia-ul-Haq, M.; Duddeck, H.; Stefaniak, L.; Sitkowski, J. Study of the conformational equilibria of some 2-(2’-hydroxyphenyl)-4-aryl-3H-1,5-benzodiazepines using 1H, 13C, and 15N NMR spectroscopy. Monatshefte Chemie Chem. Mon. Chemie Chem. Mon. 1997, 128, 633–640. [Google Scholar] [CrossRef]
- Claramunt, R.M.; Alkorta, I.; Elguero, J. A theoretical study of the conformation and dynamic properties of 1,5-benzodiazepines and their derivatives. Comput. Theor. Chem. 2013, 1019, 108–115. [Google Scholar] [CrossRef]
- Bojarska, J.; Maniukiewicz, W.; Sieroń, L. Three new olanzapine structures: The acetic acid monosolvate, and the propan-2-ol and propan-2-one hemisolvate monohydrates. Acta Crystallogr. Sect. C Cryst. Struct. Commun. 2013, 69, 781–786. [Google Scholar] [CrossRef] [PubMed]
- Meagher, T.P.; Murugan, R. 1,2-Diazepines. In Comprehensive Heterocyclic Chemistry III; Elsevier: Amsterdam, The Netherlands, 2008; pp. 143–160. [Google Scholar]
- De Borggraeve, W.M.; Van den Bogaert, A.M. 1,3-Diazepines. In Comprehensive Heterocyclic Chemistry III; Elsevier: Amsterdam, The Netherlands, 2008; pp. 161–182. [Google Scholar]
- Meanwell, N.A.; Walker, M.A. 1,4-Diazepines. In Comprehensive Heterocyclic Chemistry III; Elsevier: Amsterdam, The Netherlands, 2008; pp. 183–235. [Google Scholar]
- Pertejo, P.; García-Valverde, M.; Peña, P.; Cordero, N.A.; Torroba, T.; González-Ortega, A. Experimental and theoretical studies on the effect of the oxo group in 1,4-benzodiazepines. Org. Biomol. Chem. 2014, 12, 4905. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ramig, K. Stereodynamic properties of medium-ring benzo-fused nitrogenous heterocycles: Benzodiazepines, benzazepines, benzazocines, and benzazonines. Tetrahedron 2013, 69, 10783–10795. [Google Scholar] [CrossRef]
- Mayer, I. Analytical derivation of the Hückel “4n + 2 rule”. Theor. Chem. Acc. 2010, 125, 203–206. [Google Scholar] [CrossRef]
- Buck, H. Calculated geometries of dications of bis odd-membered pi-ring systems containing a NCN fragment and related pi-systems. An opposite out-of-plane rotation of the 4n pi-ring subsystems. Int. J. Quantum Chem. 2002, 87, 37–48. [Google Scholar] [CrossRef]
- Nagami, T.; Fujiyoshi, J.; Tonami, T.; Watanabe, K.; Yamane, M.; Okada, K.; Kishi, R.; Nakano, M.; Champagne, B.; Liégeois, V. Evaluation of Aromaticity for Open-Shell Singlet Dicyclopenta-Fused Acenes and Polyacenes Based on a Magnetically Induced Current. Chem.—A Eur. J. 2018, 24, 13457–13466. [Google Scholar] [CrossRef]
- Dobrowolski, J.C.; Lipiński, P.F.J. On splitting of the NICS(1) magnetic aromaticity index. RSC Adv. 2016, 6, 23900–23904. [Google Scholar] [CrossRef]
- Ferreira, J.M.; Anacleto, J. Ampère–Maxwell law for a conducting wire: A topological perspective. Eur. J. Phys. 2013, 34, 1403–1410. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Clarendon Press: Oxford, UK, 1990. [Google Scholar]
- Popelier, P.L.A. Atoms in Molecules. An Introduction; Pearson Education Ltd.: Harlow, UK, 2000. [Google Scholar]
- Palusiak, M.; Krygowski, T.M. Application of AIM Parameters at Ring Critical Points for Estimation of π-Electron Delocalization in Six-Membered Aromatic and Quasi-Aromatic Rings. Chem.—A Eur. J. 2007, 13, 7996–8006. [Google Scholar] [CrossRef]
- Todd, A.K. AIMAll, Version 16.01.09; TK Gristmill Software: Overland Park, KS, USA, 2016.
- Murray, J.S.; Politzer, P. The electrostatic potential: An overview. WIREs Comput. Mol. Sci. 2011, 1, 153–163. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.; Yang, W.; Parr, R. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B. Condens. Matter 1988, 37, 785–789. [Google Scholar] [CrossRef] [Green Version]
- Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef] [Green Version]
- Kendall, R.A.; Dunning, T.H.; Harrison, R.J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar] [CrossRef] [Green Version]
- Janoschek, R. Quantum chemical B3LYP/cc-pvqz computation of ground-state structures and properties of small molecules with atoms of Z ≤ 18 (hydrogen to argon)(IUPAC Technical Report). Pure Appl. Chem. 2001, 73, 1521–1553. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian, version 09; Gaussian Inc.: Wallingford, CT, USA, 2009.
- Pulay, P.; Hinton, J.F.; Wolinski, K. Efficient Implementation of the GIAO Method for Magnetic Properties: Theory and Application. In Nuclear Magnetic Shieldings and Molecular Structure; Springer: Dordrecht, The Netherlands, 1993; pp. 243–262. [Google Scholar]
- Geerlings, P.; De Proft, F.; Langenaeker, W. Conceptual Density Functional Theory. Chem. Rev. 2003, 103, 1793–1874. [Google Scholar] [CrossRef]
- Mardirossian, N.; Head-Gordon, M. Thirty years of density functional theory in computational chemistry: An overview and extensive assessment of 200 density functionals. Mol. Phys. 2017, 115, 2315–2372. [Google Scholar] [CrossRef] [Green Version]
- Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef] [Green Version]
- Peach, M.J.G.; Helgaker, T.; Sałek, P.; Keal, T.W.; Lutnæs, O.B.; Tozer, D.J.; Handy, N.C. Assessment of a Coulomb-attenuated exchange–correlation energy functional. Phys. Chem. Chem. Phys. 2006, 8, 558–562. [Google Scholar] [CrossRef] [PubMed]
- Yu, W.; Liang, L.; Lin, Z.; Ling, S.; Haranczyk, M.; Gutowski, M. Comparison of some representative density functional theory and wave function theory methods for the studies of amino acids. J. Comput. Chem. 2009, 30, 589–600. [Google Scholar] [CrossRef] [PubMed]
- Pyrka, M.; Maciejczyk, M. Theoretical investigations of tautomeric equilibrium of 9-methyl-8-aza-iso-Guanine and its electrostatic properties. Comput. Theor. Chem. 2016, 1091, 1–7. [Google Scholar] [CrossRef]
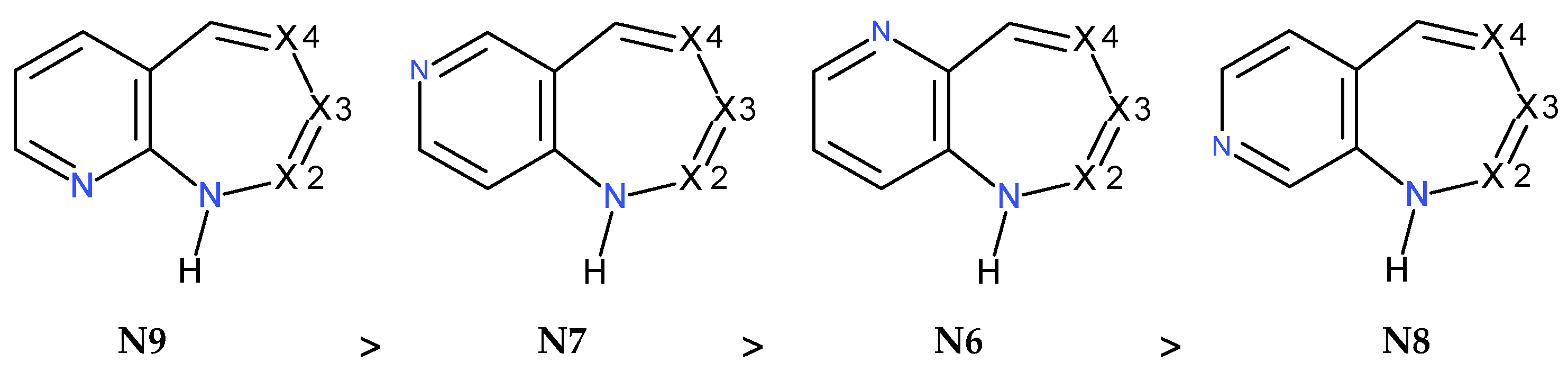



| PC | T | P | ΔGPDZ | ΔGPC | ΔET | ΔGT | PC | T | P | ΔGPDZ | ΔGPC | ΔET | ΔGT | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| pyrido[1,2]diazepines | N6 | N1-H | n | 4.89 | 0.00 | 0.00 | pirydo[1,4]diazepinese | N6 | N1-H | n | 6.63 | 0.00 | 0.00 | ||
| N2-H | n | 19.64 | 19.03 | N4-H | n | 19.98 | 19.40 | ||||||||
| N2-H | p | 22.09 | 21.38 | N6-H | n | 18.63 | 17.16 | ||||||||
| N6-H | n | 36.20 | 34.53 | N7 | N1-H | n | 5.00 | 0.00 | 0.00 | ||||||
| N7 | N1-H | n | 4.22 | 0.00 | 0.00 | N4-H | p | 20.39 | 19.51 | ||||||
| N2-H | n | 18.89 | 18.63 | N4-H | n | 20.20 | 19.51 | ||||||||
| N7-H | n | 22.44 | 21.33 | N7-H | n | 15.05 | 14.37 | ||||||||
| N8 | N1-H | n | 6.17 | 0.00 | 0.00 | N8 | N1-H | n | 7.45 | 0.00 | 0.00 | ||||
| N2-H | p | 19.69 | 19.15 | N4-H | n | 22.86 | 22.04 | ||||||||
| N2-H | n | 23.56 | 22.69 | N8-H | p | 19.06 | 17.37 | ||||||||
| N8-H | n | 27.69 | 26.39 | ||||||||||||
| N9 | N1-H | n | 19.74 | 0.00 | 0.00 | 0.00 | N9 | N1-H | n | 7.13 | 0.00 | 0.00 | 0.00 | ||
| N2-H | p | 25.61 | 24.75 | N4-H | n | 27.60 | 26.63 | ||||||||
| N2-H | n | 28.71 | 27.78 | N9-H | p | 13.03 | 12.02 | ||||||||
| N9-H | n | 21.08 | 19.34 | ||||||||||||
| pyrido [1,3]diazepines | N6 | N1-H | n | 2.06 | 2.37 | pirydo [1,5]diazepines | N6 | N1-H | n | 8.06 | 7.73 | ||||
| N3-H | n | 3.86 | 0.00 | 0.00 | N5-H | n | 4.54 | 0.00 | 0.00 | 0.00 | |||||
| N6-H | n | 16.70 | 16.16 | N6-H | p | 11.65 | 10.82 | ||||||||
| N7 | N1-H | n | 0.52 | 1.84 | N7 | N1-H | n | 5.92 | 0.00 | 0.00 | |||||
| N3-H | n | 3.62 | 0.00 | 0.00 | N5-H | n | 0.58 | 0.66 | |||||||
| N7-H | n | 16.49 | 16.90 | N7-H | p | 13.18 | 12.12 | ||||||||
| N8 | N1-H | n | 1.07 | 1.75 | N8 | N1-H | p | 0.58 | 0.66 | ||||||
| N3-H | n | 4.83 | 0.00 | 0.00 | N5-H | n | 5.92 | 0.00 | 0.00 | ||||||
| N8-H | n | 17.96 | 17.85 | N8-H | p | 13.18 | 12.12 | ||||||||
| N9 | N1-H | n | 0.00 | 0.00 | 0.00 | 0.00 | N9 | N1-H | n | 0.00 | 0.00 | 0.00 | |||
| N3-H | n | 6.10 | 5.63 | N5-H | n | 8.06 | 7.73 | ||||||||
| N9-H | n | 12.64 | 11.95 | N9-H | n | 11.65 | 10.82 |
| PC | T | P | ΔGPDZ | ΔGPC | ΔET | ΔGT | PC | T | P | ΔGPDZ | ΔGPC | ΔET | ΔGT | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| pyrido[2,3]diazepines | N6 | N2-H | p | 18.64 | 18.63 | pirydo[2,4]diazepinese | N6 | N2-H | p | 5.58 | 5.42 | ||||
| N3-H | n | 22.81 | 0.00 | 0.00 | 0.00 | N4-H | n | 3.97 | 4.24 | ||||||
| N6-H | n | 21.90 | 21.15 | N6-H | p | 26.16 | 0.00 | 0.00 | 0.00 | ||||||
| N7 | N2-H | p | 18.22 | 18.47 | N7 | N2-H | p | 4.77 | 4.75 | ||||||
| N3-H | n | 1.77 | 0.00 | 0.00 | N4-H | p | 6.26 | 6.32 | |||||||
| N7-H | n | 30.11 | 28.89 | N7-H | n | 0.05 | 0.00 | 0.00 | |||||||
| N8 | N2-H | n | 18.23 | 0.00 | 0.00 | N8 | N2-H | p | 6.26 | 6.32 | |||||
| N3-H | p | 1.93 | 2.01 | N4-H | p | 4.77 | 4.75 | ||||||||
| N8-H | n | 4.57 | 3.76 | N8-H | n | 0.05 | 0.00 | 0.00 | |||||||
| N9 | N2-H | n | 17.89 | 0.00 | 0.00 | N9 | N2-H | n | 3.97 | 4.24 | |||||
| N3-H | p | 0.83 | 0.74 | N4-H | p | 5.58 | 5.42 | ||||||||
| N9-H | p | 11.38 | 9.71 | N9-H | p | 26.16 | 0.00 | 0.00 | 0.00 |
| PC | T | I(R6) | I(R7) | ISUM | PC | T | I(R6) | I(R7) | ISUM | PC | T | I(R6) | I(R7) | ISUM | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| pyrido[1,2]diazepines | N6 | N1-H | −95.9 | 64.5 | −31.4 | pyrido[1,3]diazepines | N6 | N1-H | −85.0 | 94. 6 | 9.5 | pyrido[1,4]diazepines | N6 | N1-H | −77.5 | 118.0 | 40.4 |
| N2-H | 158.8 | 588.8 | 747.6 | N3-H | −50.9 | 176.8 | 125.9 | N4-H | 73.4 | 255.0 | 328.4 | ||||||
| N6-H | 171.5 | 329.4 | 501.0 | N6-H | 120.8 | 280.9 | 401.8 | N6-H | 243.2 | 431.0 | 674.2 | ||||||
| N7 | N1-H | −81.7 | 90.1 | 8.3 | N7 | N1-H | −78.4 | 107.6 | 29.1 | N7 | N1-H | −57.7 | 147.8 | 90.2 | |||
| N2-H | 168.6 | 569.4 | 738.0 | N3-H | −31.4 | 214.0 | 182.5 | N4-H | 128.8 | 371.9 | 500.8 | ||||||
| N7-H | 74.7 | 163.5 | 238.2 | N7-H | 106.0 | 265.1 | 371.1 | N7-H | 122.6 | 246.4 | 369.0 | ||||||
| N8 | N1-H | −96.0 | 70.5 | −25.5 | N8 | N1-H | −85.3 | 99.0 | 13.7 | N8 | N1-H | −77.3 | 125.3 | 48.0 | |||
| N2-H | 170.2 | 604.5 | 774.6 | N3-H | −38.3 | 204.0 | 165.7 | N4-H | 65.0 | 236.1 | 301.1 | ||||||
| N8-H | 75.7 | 128.2 | 203.8 | N8-H | 129.1 | 293.0 | 422.2 | N8-H | 278.3 | 514.2 | 792.5 | ||||||
| N9 | N1-H | −75.6 | 92.1 | 16.5 | N9 | N1-H | −74.8 | 102.5 | 27.7 | N9 | N1-H | −55.0 | 136.6 | 81.6 | |||
| N2-H | 173.3 | 580.5 | 753.8 | N3-H | −73.0 | 128.1 | 55.2 | N4-H | 71.4 | 221.7 | 293.1 | ||||||
| N9-H | 146.7 | 287.5 | 434.1 | N9-H | 278.3 | 114.4 | 392.7 | N9-H | 170.3 | 320.9 | 491.2 | ||||||
| pyrido[1,5]diazepines | N6 | N1-H | −84.5 | 114.1 | 29.7 | pyrido[2,3]diazepines | N6 | N2-H | 186.9 | 554.0 | 740.9 | pyrido[2,4]diazepines | N2-H | 808.0 | 325.1 | 1133.0 | |
| N5-H | −60.3 | 153.2 | 92.9 | N3-H | −38.9 | 181.2 | 142.3 | N6 | N4-H | 651.9 | 246.4 | 898.3 | |||||
| N6-H | 133.1 | 343.9 | 477.0 | N6-H | 91.0 | 127.9 | 218.9 | N6-H | 278.7 | 230.5 | 509.2 | ||||||
| N7 | N1-H | −60.0 | 167.0 | 107.0 | N7 | N2-H | 168.4 | 549.5 | 717.9 | N2-H | 820.6 | 331.3 | 1151.8 | ||||
| N5-H | −72.9 | 146.1 | 73.2 | N3-H | −32.8 | 210.2 | 177.4 | N7 | N4-H | 913.7 | 383.9 | 1297.6 | |||||
| N7-H | 144.4 | 373.5 | 518.0 | N7-H | 191.8 | 327.3 | 519.2 | N7-H | 252.1 | 187.4 | 439.4 | ||||||
| N8 | N1-H | −72.9 | 146.1 | 73.2 | N8 | N2-H | 198.2 | 582.1 | 780.3 | N2-H | 913.7 | 383.9 | 1297.6 | ||||
| N5-H | −60.0 | 167.0 | 107.0 | N3-H | 168.4 | 549.5 | 717.9 | N8 | N4-H | 820.6 | 331.3 | 1151.8 | |||||
| N8-H | 144.4 | 373.5 | 518.0 | N8-H | 77.0 | 118.8 | 195.8 | N8-H | 252.1 | 187.4 | 439.4 | ||||||
| N9 | N1-H | −60.3 | 153.2 | 92.9 | N9 | N2-H | 165.6 | 543.7 | 709.4 | N2-H | 651.9 | 246.4 | 898.3 | ||||
| N5-H | −84.5 | 114.1 | 29.7 | N3-H | 186.9 | 186.9 | 373.9 | N9 | N4-H | 807.9 | 325.2 | 1133.1 | |||||
| N9-H | 133.1 | 343.9 | 477.0 | N9-H | 240.5 | 392.9 | 633.4 | N9-H | 278.7 | 230.5 | 509.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jarończyk, M.; Ostrowski, S.; Dobrowolski, J.C. On Integral INICS Aromaticity of Pyridodiazepine Constitutional Isomers and Tautomers. Molecules 2023, 28, 5684. https://doi.org/10.3390/molecules28155684
Jarończyk M, Ostrowski S, Dobrowolski JC. On Integral INICS Aromaticity of Pyridodiazepine Constitutional Isomers and Tautomers. Molecules. 2023; 28(15):5684. https://doi.org/10.3390/molecules28155684
Chicago/Turabian StyleJarończyk, Małgorzata, Sławomir Ostrowski, and Jan Cz. Dobrowolski. 2023. "On Integral INICS Aromaticity of Pyridodiazepine Constitutional Isomers and Tautomers" Molecules 28, no. 15: 5684. https://doi.org/10.3390/molecules28155684








