Prediction of Xe/Kr Separation in Metal-Organic Frameworks by a Precursor-Based Neural Network Synergistic with a Polarizable Adsorbate Model
Abstract
:1. Introduction
2. Results and Discussion
2.1. Adsorption Isotherms of Xe and Kr
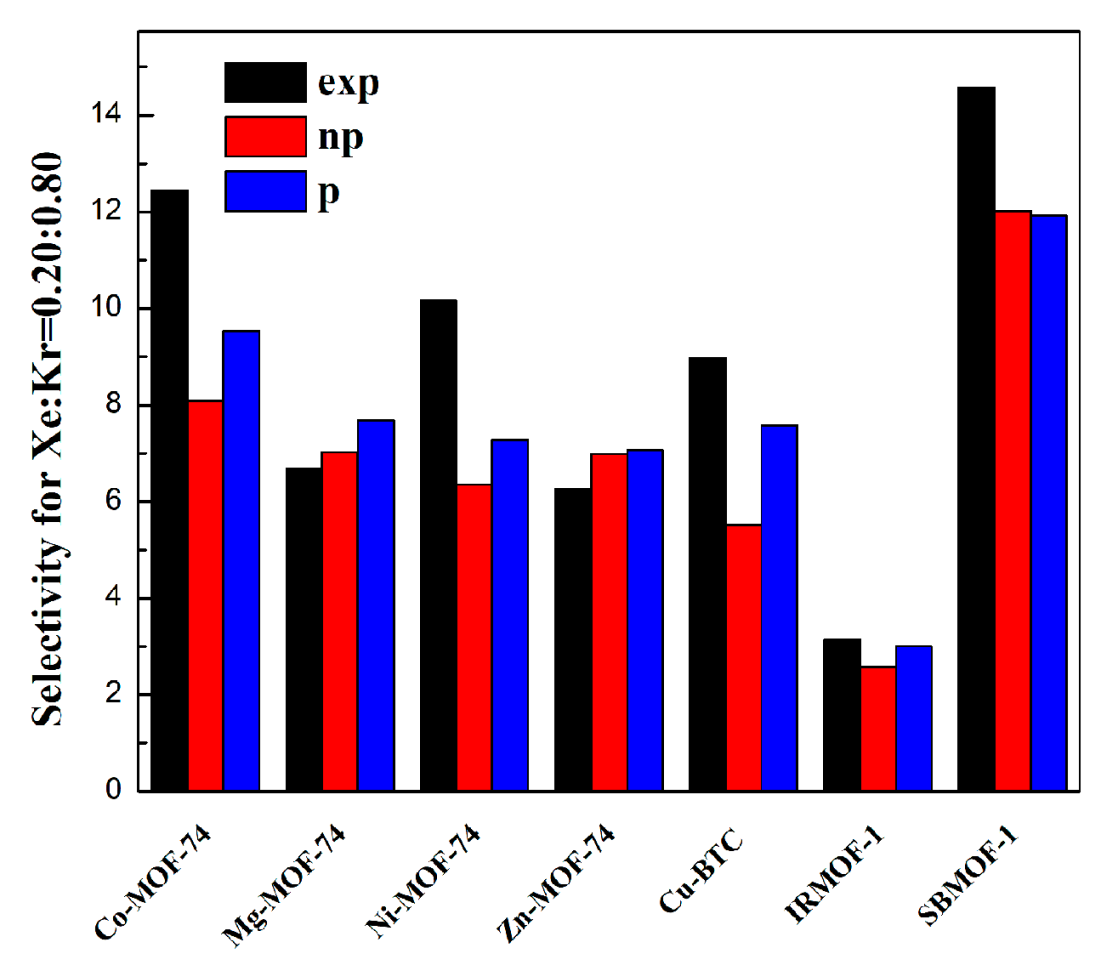
2.2. Selectivity of Xe/Kr Mixture
2.3. ANN Model
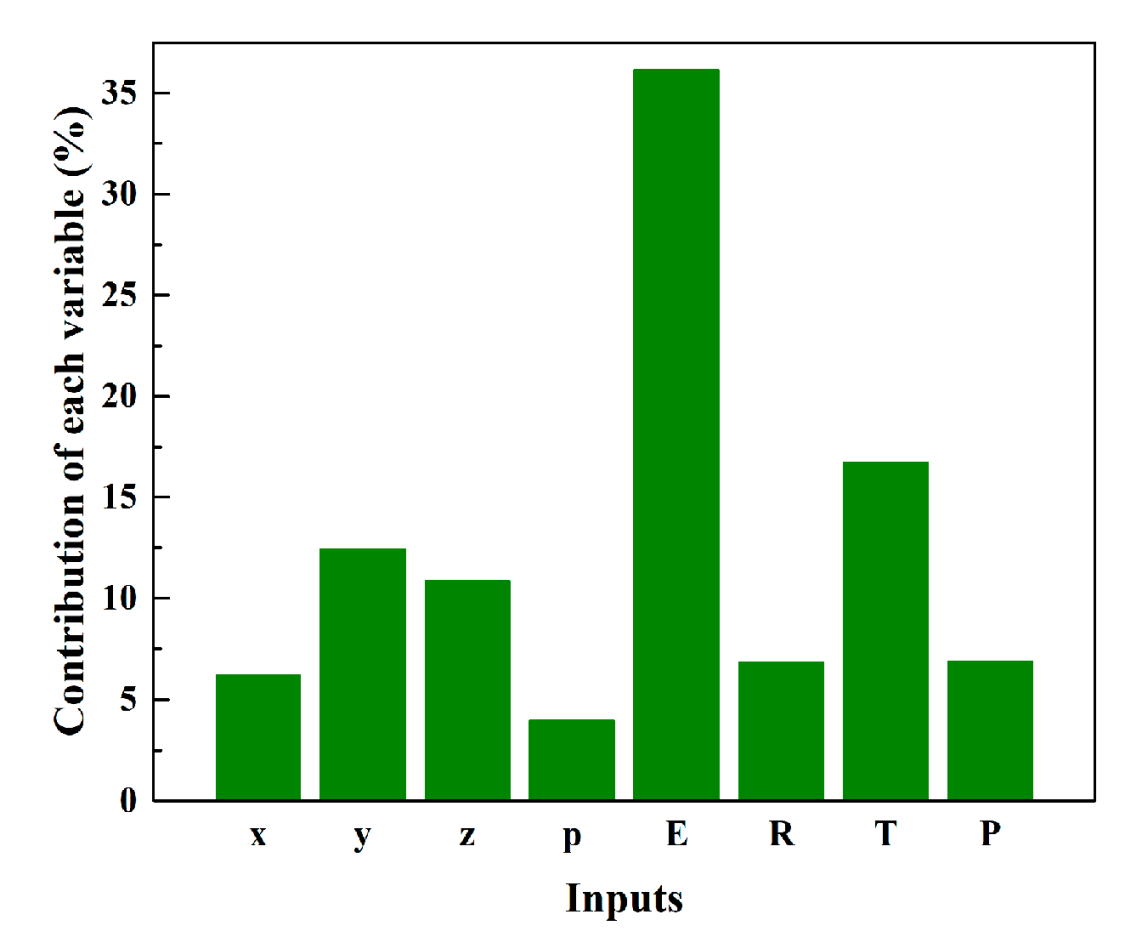
2.4. Sensitivity Analysis
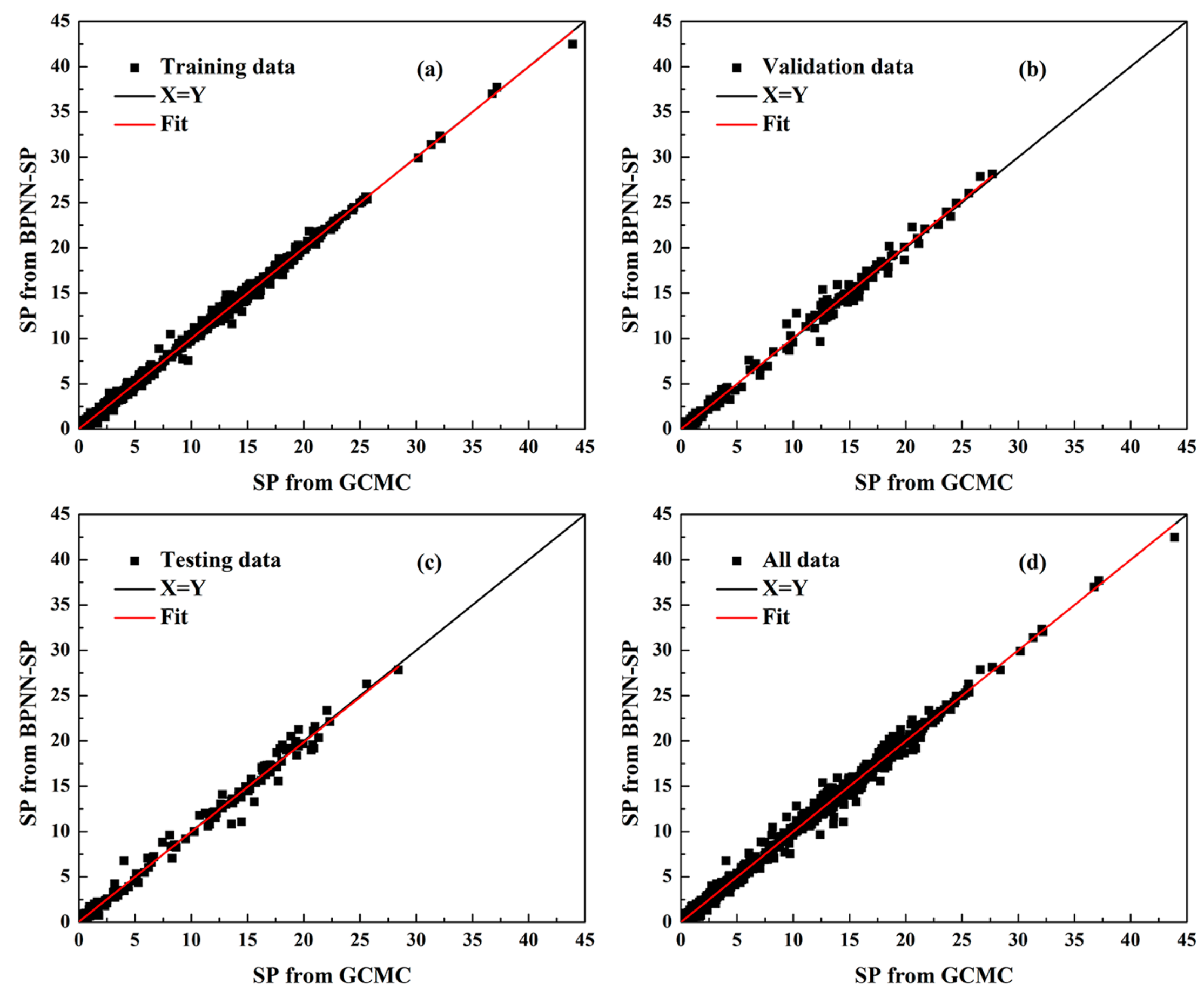
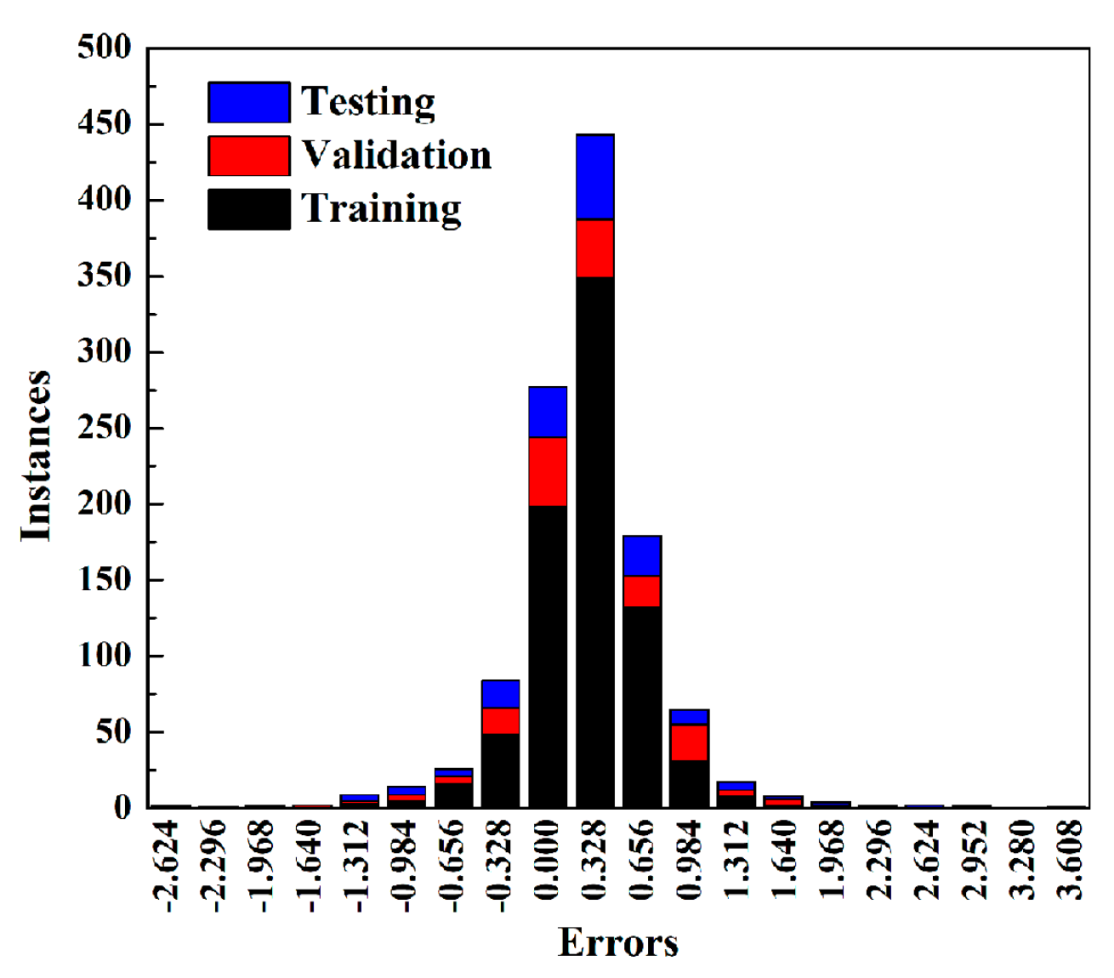
2.5. Validation of ANN Model
3. Methods
3.1. Model Construction and Structure Characterization
3.2. Simulation Details
3.3. ANN Model
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Holsträter, T.F.; Georgieff, M.; Föhr, K.J.; Klingler, W.; Uhl, M.E.; Walker, T.; Köster, S.; Grön, G.; Adolph, O. Intranasal application of xenon reduces opioid requirement and postoperative pain in patients undergoing major abdominal surgery: A randomized controlled trial. Anesthesiology 2011, 115, 398–407. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Reiss, P.S.; Chong, S.Y.; Holden, D.; Jelfs, K.E.; Hasell, T.; Little, M.A.; Kewley, A.; Briggs, M.E.; Stephenson, A.; et al. Separation of rare gases and chiral molecules by selective binding in porous organic cages. Nat. Mater. 2014, 13, 954–960. [Google Scholar] [CrossRef]
- Auer, M.; Kumberg, T.; Sartorius, H.; Wernsperger, B.; Schlosser, C. Ten years of development of equipment for measurement of atmospheric radioactive xenon for the verification of the CTBT. Pure Appl. Geophys. 2010, 167, 471–486. [Google Scholar] [CrossRef]
- Hoff, P.W.; Swingle, J.C.; Rhodes, C.K. Observations of stimulated emission from high-pressure krypton and argon/xenon mixtures. Appl. Phys. Lett. 1973, 23, 245–246. [Google Scholar] [CrossRef]
- Gong, W.; Xie, Y.; Pham, T.D.; Shetty, S.; Son, F.A.; Idrees, K.B.; Chen, Z.; Xie, H.; Snurr, R.Q.; Chen, B.L.; et al. Creating optimal pockets in a clathrochelate-based metal–organic framework for gas adsorption and separation: Experimental and computational studies. J. Am. Chem. Soc. 2022, 144, 3737–3745. [Google Scholar] [CrossRef] [PubMed]
- Sun, W.; Hu, J.; Duttwyler, S.; Wang, L.; Krishna, R.; Zhang, Y. Highly selective gas separation by two isostructural boron cluster pillared MOFs. Sep. Purif. Technol. 2022, 283, 120220. [Google Scholar] [CrossRef]
- Cai, Z.; Bien, C.E.; Liu, Q.; Wade, C.R. Insights into CO2 adsorption in M–OH functionalized MOFs. Chem. Mater. 2020, 32, 4257–4264. [Google Scholar] [CrossRef]
- He, X.; Chen, D.R.; Wang, W.N. Bimetallic metal-organic frameworks (MOFs) synthesized using the spray method for tunable CO2 adsorption. Chem. Eng. J. 2020, 382, 122825. [Google Scholar] [CrossRef]
- Wang, S.; Cheng, M.; Luo, L.; Ji, X.; Liu, C.; Bi, K.; Zhou, L. High-throughput screening of metal-organic frameworks for hydrogen purification. Chem. Eng. J. 2023, 451, 138436. [Google Scholar] [CrossRef]
- Duan, C.; Yu, Y.; Li, J.; Li, L.; Huang, B.; Chen, D.; Xi, H. Recent advances in the synthesis of monolithic metal-organic frameworks. Sci. China Mater. 2021, 64, 1305–1319. [Google Scholar] [CrossRef]
- Wang, T.; Peng, Y.L.; Lin, E.; Niu, Z.; Li, P.; Ma, S.; Zhao, P.; Chen, Y.; Cheng, P.; Zhang, Z. Robust bimetallic ultramicroporous metal-organic framework for separation and purification of noble gases. Inorg. Chem. 2020, 59, 4868–4873. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.J.; Yoon, T.U.; Kim, A.R.; Kim, S.Y.; Cho, K.H.; Hwang, Y.K.; Yeon, J.W.; Bae, Y.S. Adsorptive separation of xenon/krypton mixtures using a zirconium-based metal-organic framework with high hydrothermal and radioactive stabilities. J. Hazard. Mater. 2016, 320, 513–520. [Google Scholar] [CrossRef] [PubMed]
- Mohamed, M.H.; Elsaidi, S.K.; Pham, T.; Forrest, K.A.; Schaef, H.T.; Hogan, A.; Wojtas, L.; Xu, W.; Space, B.; Zaworotko, M.J.; et al. Hybrid Ultra-microporous materials for selective xenon adsorption and separation. Angew. Chem. Int. Ed. Engl. 2016, 55, 8425–8429. [Google Scholar] [CrossRef]
- Xiong, S.; Gong, Y.; Hu, S.; Wu, X.; Li, W.; He, Y.; Chen, B.; Wang, X. A microporous metal–organic framework with commensurate adsorption and highly selective separation of xenon. J. Mater. Chem. A 2018, 6, 4752–4758. [Google Scholar] [CrossRef]
- Gong, W.; Wang, X.; Kirlikovali, K.O.; Idrees, K.B.; Sha, F.; Xie, H.; Liu, Y.; Chen, B.; Cui, Y.; Farha, O.K. Programmed polarizability engineering in a cyclen-based cubic Zr(IV) metal–organic framework to boost Xe/Kr Separation. J. Am. Chem. Soc. 2023, 145, 2679–2689. [Google Scholar] [CrossRef]
- Banerjee, D.; Simon, C.M.; Plonka, A.M.; Motkuri, R.K.; Liu, J.; Chen, X.; Smit, B.; Parise, J.B.; Haranczyk, M.; Thallapally, P.K. Metal-organic framework with optimally selective xenon adsorption and separation. Nat. Commun. 2016, 7, ncomms11831. [Google Scholar] [CrossRef]
- Perry, J.J.; Teich, M.S.L.; Meek, S.T.; Greathouse, J.A.; Haranczyk, M.; Allendorf, M.D. Noble gas adsorption in metal–organic frameworks containing open metal sites. J. Phys. Chem. C 2014, 118, 11685–11698. [Google Scholar] [CrossRef]
- Li, L.Y.; Guo, L.; Zhang, Z.G.; Yang, Q.W.; Yang, Y.W.; Bao, Z.B.; Ren, Q.L.; Li, J. A robust squarate-based metal–organic framework demonstratesrecord-high affinity and selectivity for xenon over krypton. J. Am. Chem. Soc. 2019, 141, 9358–9364. [Google Scholar] [CrossRef]
- Altintas, C.; Avci, G.; Daglar, H.; Azar, A.N.V.; Velioglu, S.; Erucar, I.; Keskin, S. Database for CO2 separation performances of MOFs based on computational materials screening. ACS Appl. Mater. Interfaces 2018, 10, 17257–17268. [Google Scholar] [CrossRef]
- Krishna, R. Screening metal–organic frameworks for mixture separations in fixed-bed adsorbers using a combined selectivity/capacity metric. RSC Adv. 2017, 7, 35724–35737. [Google Scholar] [CrossRef]
- Fu, X.; Li, Z.; Liu, Q.; Guan, H.; Wang, Y. Microporous metal–organic framework with cage-within-cage structures for xenon/krypton separation. Ind. Eng. Chem. Res. 2022, 61, 7397–7402. [Google Scholar] [CrossRef]
- Magdysyuk, O.V.; Adams, F.; Liermann, H.P.; Spanopoulos, I.; Trikalitis, P.N.; Hirscher, M.; Morris, R.E.; Duncan, M.J.; McCormick, L.J.; Dinnebier, R.E. Understanding the adsorption mechanism of noble gases Kr and Xe in CPO-27-Ni, CPO-27-Mg, and ZIF-8. Phys. Chem. Chem. Phys. 2014, 16, 23908–23914. [Google Scholar] [CrossRef] [PubMed]
- Sumer, Z.; Keskin, S. Molecular simulations of MOF adsorbents and membranes for noble gas separations. Chem. Eng. Sci. 2017, 164, 108–121. [Google Scholar] [CrossRef]
- Tao, Y.; Fan, Y.; Xu, Z.; Feng, X.; Krishna, R.; Luo, F. Boosting selective adsorption of Xe over Kr by double-accessible open-metal site in metal-organic framework: Experimental and theoretical research. Inorg. Chem. 2010, 59, 11793–11800. [Google Scholar] [CrossRef] [PubMed]
- Xiong, X.L.; Chen, G.H.; Xiao, S.T.; Ouyang, Y.G.; Li, H.B.; Wang, Q. New discovery of metal–organic framework UTSA-280: Ultrahigh adsorption selectivity of krypton over xenon. J. Phys. Chem. C 2020, 124, 14603–14612. [Google Scholar] [CrossRef]
- Meek, S.T.; McGoldrick, S.L.T.; Perry, J.J.; Greathouse, J.A.; Allendorf, M.D. Effects of polarizability on the adsorption of noble gases at low pressures in monohalogenated isoreticular metal–organic frameworks. J. Phys. Chem. C 2012, 116, 19765–19772. [Google Scholar] [CrossRef]
- Demir, H.; Greathouse, J.A.; Staiger, C.L.; Perry, J.J.; Allendorf, M.D.; Sholl, D.S. DFT-based force field development for noble gas adsorption in metal organic frameworks. J. Mater. Chem. A 2015, 3, 23539–23548. [Google Scholar] [CrossRef]
- Vazhappilly, T.; Ghanty, T.K.; Jagatap, B.N. Computational modeling of adsorption of Xe and Kr in M-MOF-74 metal organic frame works with different metal atoms. J. Phys. Chem. C 2016, 120, 10968–10974. [Google Scholar] [CrossRef]
- Halder, P.; Singh, J.K. High-throughput screening of metal–organic frameworks for ethane–ethylene separation using the machine learning technique. Energy Fuels 2020, 34, 14591–14597. [Google Scholar] [CrossRef]
- Feng, M.; Cheng, M.; Ji, X.; Zhou, L.; Dang, Y.; Bi, K.; Dai, Z.; Dai, Y. Finding the optimal CO2 adsorption material: Prediction of multi-properties of metal-organic frameworks (MOFs) based on DeepFM. Sep. Purif. Technol. 2022, 302, 122111. [Google Scholar] [CrossRef]
- Liu, X.; Wang, R.; Wang, X.; Xu, D. High-throughput computational screening and machine learning model for accelerated metal-organic frameworks discovery in toluene vapor adsorption. J. Phys. Chem. C 2023, 127, 11268–11282. [Google Scholar] [CrossRef]
- Sikora, B.J.; Wilmer, C.E.; Greenfield, M.L.; Snurr, R.Q. Thermodynamic analysis of Xe/Kr selectivity in over 137 000 hypothetical metal–organic frameworks. Chem. Sci. 2012, 3, 2217–2223. [Google Scholar] [CrossRef]
- Simon, C.M.; Mercado, R.; Schnell, S.K.; Smit, B.; Haranczyk, M. What are the best materials to separate a xenon/krypton mixture? Chem. Mater. 2015, 27, 4459–4475. [Google Scholar] [CrossRef]
- Avci, G.; Velioglu, S.; Keskin, S. High-throughput screening of MOF adsorbents and membranes for H2 purification and CO2 capture. ACS Appl. Mater. Interfaces 2018, 10, 33693–33706. [Google Scholar] [CrossRef]
- Rogacka, J.; Seremak, A.; Luna, T.A.; Formalik, F.; Matito, M.I.; Firlej, L.; Calero, S.; Kuchta, B. High-throughput screening of metal-organic frameworks for CO2 and CH4 separation in the presence of water. Chem. Eng. J. 2021, 403, 126392. [Google Scholar] [CrossRef]
- Altintas, C.; Erucar, I.; Keskin, S. High-throughput computational screening of the metal organic framework database for CH4/H2 separations. ACS Appl. Mater. Interfaces 2018, 10, 3668–3679. [Google Scholar] [CrossRef]
- Ozonoh, M.; Oboirien, B.O.; Higginson, A.; Daramola, M.O. Performance evaluation of gasification system efficiency using artificial neural network. Renew. Energy 2020, 145, 2253–2270. [Google Scholar] [CrossRef]
- Zheng, Z.Y.; Guo, X.N.; Zhu, K.X.; Peng, W.; Zhou, H.M. Artificial neural network—Genetic algorithm to optimize wheat germ fermentation condition: Application to the production of two anti-tumor benzoquinones. Food. Chem. 2017, 227, 264–270. [Google Scholar] [CrossRef]
- Chenar, S.S.; Deng, Z. Development of artificial intelligence approach to forecasting oyster norovirus outbreaks along Gulf of Mexico coast. Environ. Int. 2018, 111, 212–223. [Google Scholar] [CrossRef]
- An, J.; He, G.; Qin, F.; Li, R.; Huang, Z. A new framework of global sensitivity analysis for the chemical kinetic model using PSO-BPNN. Comput. Chem. Eng. 2018, 112, 154–164. [Google Scholar] [CrossRef]
- Yan, Z.; Gong, Y.; Chen, B.; Wu, X.; Liu, Q.; Cui, L.; Xiong, S.; Peng, S. Methyl functionalized Zr-Fum MOF with enhanced xenon adsorption and separation. Sep. Purif. Technol. 2020, 239, 116514. [Google Scholar] [CrossRef]
- Borycz, J.; Tiana, D.; Haldoupis, E.; Sung, J.C.; Farha, O.K.; Siepmann, J.I.; Gagliardi, L. CO2 adsorption in M-IRMOF-10 (M = Mg, Ca, Fe, Cu, Zn, Ge, Sr, Cd, Sn, Ba). J. Phys. Chem. C 2016, 120, 12819–12830. [Google Scholar] [CrossRef]
- Lahoz, M.F.D.; Calero, S.; Gutiérrez, S.J.J.; Martin, C.A. Adsorptive separation of ethane and ethylene using isoreticular metal-organic frameworks. Microporous Mesoporous Mater. 2017, 248, 40–45. [Google Scholar] [CrossRef]
- Wu, Y.; Chen, H.Y.; Xiao, J.; Liu, D.F.; Liu, Z.W.; Qian, Y.; Xi, H.X. Adsorptive separation of methanol-acetone on isostructural series of metal-organic frameworks M-BTC (M = Ti, Fe, Cu, Co, Ru, Mo): A computational study of adsorption mechanisms and metal-substitution impacts. ACS Appl. Mater. Interfaces 2015, 7, 26930–26940. [Google Scholar] [CrossRef]
- Liu, K.; Li, B.; Li, Y.; Li, X.; Yang, F.; Zeng, G.; Peng, Y.; Zhang, Z.; Li, G.; Shi, Z.; et al. An N-rich metal-organic framework with an rht topology: High CO2 and C2 hydrocarbons uptake and selective capture from CH4. Chem. Commun. 2014, 50, 5031–5033. [Google Scholar] [CrossRef]
- Biovia Software Inc. Materials Studio, v7.0; Biovia Software Inc.: San Diego, CA, USA, 2023.
- Altintas, C.; Acvi, G.; Daglar, H.; Azar, A.N.V.; Erucar, I.; Velioglu, S.; Keskin, S. An extensive comparative analysis of two MOF databases: High-throughput screening of computation-ready MOFs for CH4 and H2 adsorption. J. Mater. Chem. A 2019, 7, 9593–9608. [Google Scholar] [CrossRef]
- Liu, Z.W.; Zhang, K.; Wu, Y.; Xi, H.X. New functionalized IRMOF-10 with strong affinity for methanol: A simulation study. Appl. Surf. Sci. 2018, 440, 351–358. [Google Scholar] [CrossRef]
- Wu, X.; Peng, L.; Xiang, S.; Cai, W. Computational design of tetrazolate-based metal-organic frameworks for CH4 storage. Phys. Chem. Chem. Phys. 2018, 20, 30150–30158. [Google Scholar] [CrossRef]
- Liu, Z.W.; Zhang, K.; Xia, Q.B.; Wang, X.J.; Huang, B.C.; Xi, H.X. Predicting adsorption and separation performance indicators of Xe/Kr in metal-organic frameworks via a precursor-based neural network model. Chem. Eng. Sci. 2021, 243, 116772. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B. GAUSSIAN 09, Rev. D.1; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Dubbeldam, D.; Calero, S.; Ellis, D.E.; Snurr, R.Q. RASPA: Molecular simulation software for adsorption and diffusion in flexible nanoporous materials. Mol. Simul. 2015, 42, 81–101. [Google Scholar] [CrossRef]
- Barker, J.A.; Henderson, D. What is “liquid”? Understanding the states of matter. Rev. Mod. Phys. 1976, 48, 587–671. [Google Scholar] [CrossRef]
- Rappé, A.K.; Casewit, C.J.; Colwell, K.S.; Goddard III, W.A.; Skif, W.M. UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations. J. Am. Chem. Soc. 1992, 114, 10024–10035. [Google Scholar] [CrossRef]
- Stephen, L.M.; Olafson, B.D.; Goddard III, W.A. DREIDING: A generic force field for molecular simulations. J. Phys. Chem. 1990, 94, 8897–8909. [Google Scholar]
- Becker, T.M.; Triguero, A.L.; Luna, J.M.V.; Lin, L.C.; Dubbeldam, D.; Calero, S.; Vlugt, T.J.H. Potential of polarizable force fields for predicting the separation performance of small hydrocarbons in M-MOF-74. Phys. Chem. Chem. Phys. 2018, 20, 28848–28859. [Google Scholar] [CrossRef]
- Düren, T.S.; Snurr, R.Q. Assessment of isoreticular metal–organic frameworks for adsorption separations: A molecular simulation study of methane/n-butane mixtures. J. Phys. Chem. B 2004, 108, 15703–15708. [Google Scholar] [CrossRef]
- Talu, O.; Myers, A.L. Molecular simulation of adsorption: Gibbs dividing surface and comparison with experiment. AIChE J. 2001, 47, 1160–1168. [Google Scholar] [CrossRef]
- Myers, A.L.; Prausnitz, J.M. Thermodynamics of mixed-gas adsorption. AIChE J. 1965, 11, 121–127. [Google Scholar] [CrossRef]
- Pai, S.; Ahmed, R.; Manna, A.; Das, M. Potential of a pH-stable microporous MOF for C2H2/C2H4 and C2H2/CO2 gas separations under ambient conditions. Inorg. Chem. 2022, 61, 18293–18302. [Google Scholar]
- Liu, X.; Tang, Y.; Yang, G.; Wang, Y. Porous functional metal–organic frameworks (MOFs) constructed from different N-heterocyclic carboxylic ligands for gas adsorption/separation. CrystEngComm. 2023, 25, 896–908. [Google Scholar] [CrossRef]
- Esfandiari, K.; Ghoreyshi, A.A.; Jahanshahi, M. Using Artificial neural network and ideal adsorbed solution theory for predicting the CO2/CH4 selectivities of metal–organic frameworks: A comparative study. Ind. Eng. Chem. Res. 2017, 56, 14610–14622. [Google Scholar] [CrossRef]
- Liang, H.; Yang, W.; Peng, F.; Liu, Z.; Liu, J.; Qiao, Z.W. Combining large-scale screening and machine learning to predict the metal-organic frameworks for organosulfurs removal from high-sour natural gas. APL Mater. 2019, 7, 091101. [Google Scholar] [CrossRef]
- Ye, F.; Ma, S.; Tong, L.; Xiao, J.; Bénard, P.; Chahine, R. Artificial neural network based optimization for hydrogen purification performance of pressure swing adsorption. Int. J. Hydrogen Energy 2019, 44, 5334–5344. [Google Scholar] [CrossRef]
- Isiyaka, H.A.; Jumbri, K.; Sambudi, N.S.; Zango, Z.U.; Abdullah, N.A.F.; Saad, B.; Mustapha, A. Adsorption of dicamba and MCPA onto MIL-53(Al) metal–organic framework: Response surface methodology and artificial neural network model studies. RSC Adv. 2020, 10, 43213–43224. [Google Scholar] [CrossRef] [PubMed]
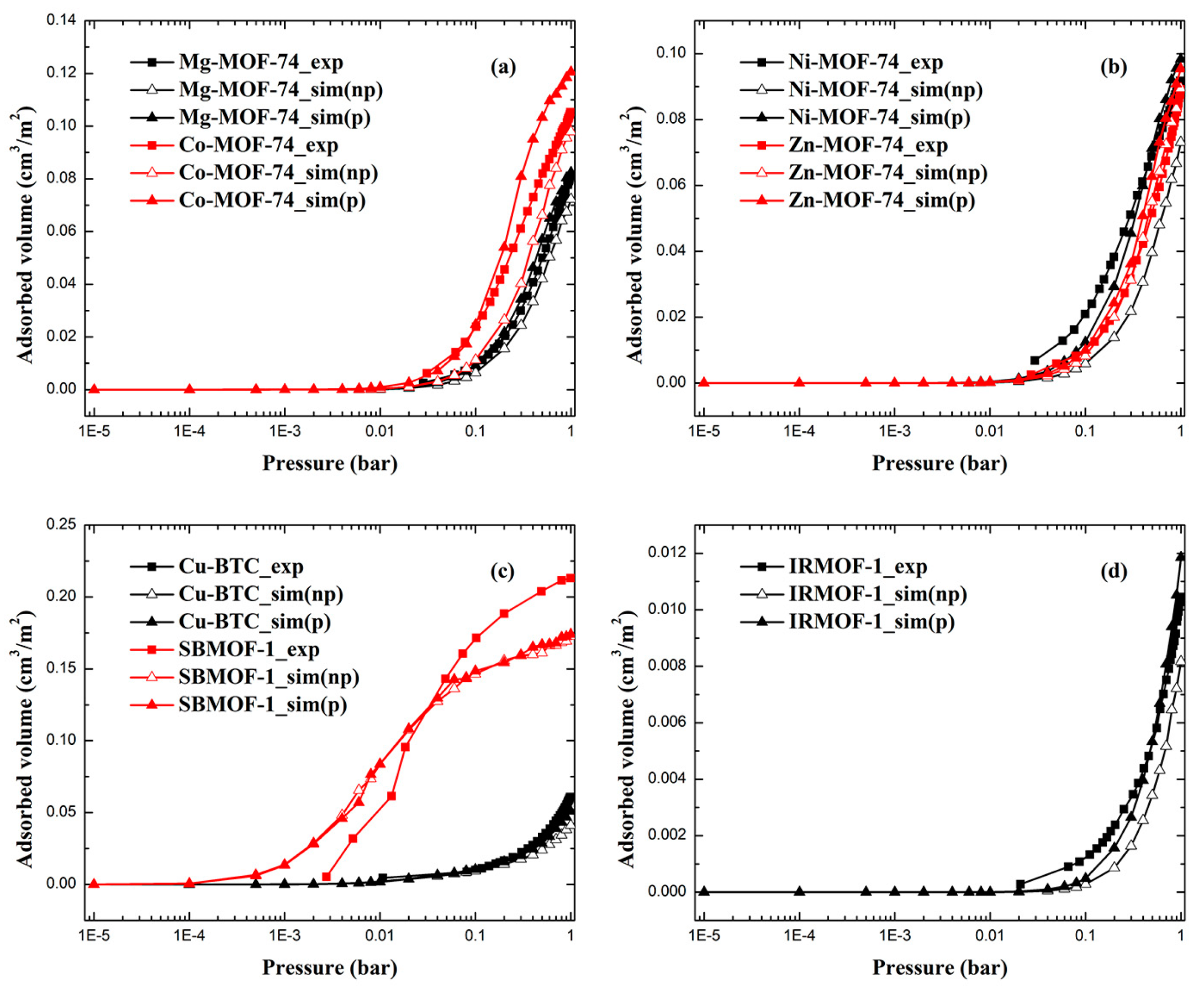


| RMSE-I (cm3/m2) | RMSE-II (%) | |||
|---|---|---|---|---|
| np | p | np | p | |
| Mg-MOF-74 | 0.007 | 0.004 | 18 | 10 |
| Co-MOF-74 | 0.012 | 0.016 | 30 | 18 |
| Ni-MOF-74 | 0.023 | 0.006 | 47 | 24 |
| Zn-MOF-74 | 0.002 | 0.009 | 9 | 14 |
| Cu-BTC | 0.013 | 0.006 | 27 | 13 |
| SBMOF-1 | 0.031 | 0.030 | 23 | 23 |
| IRMOF-1 | 0.002 | 0.001 | 42 | 29 |
| Average | 0.013 | 0.010 | 28 | 19 |
| RMSE-I (cm3/m2) | RMSE-II (%) | |||
|---|---|---|---|---|
| np | p | np | p | |
| Mg-MOF-74 | 0.003 | 0.001 | 37 | 23 |
| Co-MOF-74 | 0.004 | 0.004 | 40 | 24 |
| Ni-MOF-74 | 0.008 | 0.002 | 60 | 29 |
| Zn-MOF-74 | 0.003 | 0.001 | 33 | 22 |
| Cu-BTC | 0.001 | 0.001 | 15 | 19 |
| SBMOF-1 | 0.016 | 0.018 | 14 | 16 |
| IRMOF-1 | 0.001 | 0.001 | 65 | 54 |
| Average | 0.005 | 0.004 | 38 | 27 |
| IAST | np | p | |
|---|---|---|---|
| Co-MOF-74 | 12.44 | 8.09 | 9.53 |
| Mg-MOF-74 | 6.68 | 7.02 | 7.68 |
| Ni-MOF-74 | 10.17 | 6.36 | 7.28 |
| Zn-MOF-74 | 6.25 | 6.99 | 7.07 |
| Cu-BTC | 8.98 | 5.51 | 7.58 |
| IRMOF-1 | 3.14 | 2.58 | 3.01 |
| SBMOF-1 | 14.56 | 12.02 | 11.92 |
| RMSE-I | 2.75 | 1.06 | |
| RMSE-II | 26% | 18% |
| Model | Network Architecture | Error Types (mmol/g) | Regression Coefficient | |||||
|---|---|---|---|---|---|---|---|---|
| MAE | MBE | RMSE | Training | Validation | Testing | All Data | ||
| 1 | 5-1 | 1.277 | 0.249 | 1.813 | 0.975 | 0.966 | 0.971 | 0.973 |
| 2 | 10-1 | 1.034 | 0.008 | 1.594 | 0.979 | 0.978 | 0.977 | 0.979 |
| 3 | 20-1 | 0.643 | −0.055 | 0.966 | 0.995 | 0.985 | 0.987 | 0.992 |
| 4 | 30-1 | 0.568 | −0.059 | 0.905 | 0.996 | 0.988 | 0.985 | 0.993 |
| 5 | 40-1 | 0.697 | −0.018 | 1.100 | 0.992 | 0.986 | 0.983 | 0.990 |
| 6 | 50-1 | 0.623 | −0.008 | 0.997 | 0.995 | 0.984 | 0.984 | 0.992 |
| 7 | 60-1 | 0.656 | 0.085 | 1.193 | 0.994 | 0.976 | 0.974 | 0.988 |
| 8 | 5-2-1 | 1.096 | 0.024 | 1.579 | 0.983 | 0.971 | 0.970 | 0.979 |
| 9 | 5-5-1 | 0.938 | 0.064 | 1.377 | 0.985 | 0.985 | 0.982 | 0.984 |
| 10 | 10-2-1 | 0.812 | −0.029 | 1.195 | 0.990 | 0.987 | 0.977 | 0.988 |
| 11 | 10-5-1 | 0.555 | 0.036 | 0.811 | 0.995 | 0.992 | 0.994 | 0.995 |
| 12 | 10-10-1 | 0.440 | 0.000 | 0.701 | 0.997 | 0.993 | 0.993 | 0.996 |
| 13 | 20-5-1 | 0.499 | 0.041 | 0.768 | 0.997 | 0.992 | 0.992 | 0.995 |
| 14 (BPNN-SP) | 20-10-1 | 0.331 | −0.002 | 0.505 | 0.999 | 0.996 | 0.995 | 0.998 |
| 15 | 20-20-1 | 0.356 | 0.002 | 0.620 | 0.999 | 0.992 | 0.992 | 0.997 |
| 16 | 30-10-1 | 0.345 | 0.003 | 0.648 | 0.999 | 0.990 | 0.992 | 0.997 |
| 17 | 30-20-1 | 0.575 | −0.001 | 0.973 | 0.996 | 0.981 | 0.988 | 0.992 |
| 18 | 30-30-1 | 0.755 | −0.314 | 1.119 | 0.992 | 0.986 | 0.988 | 0.990 |
| 19 | 40-10-1 | 0.432 | 0.039 | 0.812 | 0.999 | 0.986 | 0.983 | 0.995 |
| 20 | 40-20-1 | 0.542 | −0.032 | 0.927 | 0.997 | 0.986 | 0.984 | 0.993 |
| 21 | 40-30-1 | 0.445 | −0.052 | 0.845 | 0.998 | 0.988 | 0.985 | 0.994 |
| 22 | 40-40-1 | 0.597 | 0.007 | 0.961 | 0.996 | 0.986 | 0.982 | 0.992 |
| MOFs | Temperature (K) | Pressure (Bar) | SP_EXP (mmol/g) | SP_BPNN (mmol/g) |
|---|---|---|---|---|
| NOTT-100 | 292 | 0.1 | 0.820 | 1.295 |
| NOTT-100 | 292 | 0.4 | 3.013 | 3.179 |
| NOTT-100 | 292 | 1 | 6.380 | 6.387 |
| NOTT-101 | 292 | 0.1 | 0.388 | 0.460 |
| NOTT-101 | 292 | 0.4 | 1.463 | 1.289 |
| NOTT-101 | 292 | 1 | 3.401 | 3.046 |
| NOTT-102 | 292 | 0.1 | 0.179 | 0.261 |
| NOTT-102 | 292 | 0.4 | 0.632 | 0.517 |
| NOTT-102 | 292 | 1 | 1.403 | 1.522 |
| NOTT-103 | 292 | 0.1 | 0.311 | 0.337 |
| NOTT-103 | 292 | 0.4 | 1.207 | 0.823 |
| NOTT-103 | 292 | 1 | 2.873 | 2.961 |
| PCN-14 | 292 | 0.1 | 0.335 | 0.683 |
| PCN-14 | 292 | 0.4 | 2.366 | 2.158 |
| PCN-14 | 292 | 1 | 5.461 | 5.446 |
| UiO-66 | 298 | 0.1 | 0.345 | 0.884 |
| UiO-66 | 298 | 0.4 | 1.163 | 1.300 |
| UiO-66 | 298 | 1 | 2.227 | 2.069 |
| RMSE | 0.248 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Xia, Q.; Huang, B.; Yi, H.; Yan, J.; Chen, X.; Xu, F.; Xi, H. Prediction of Xe/Kr Separation in Metal-Organic Frameworks by a Precursor-Based Neural Network Synergistic with a Polarizable Adsorbate Model. Molecules 2023, 28, 7367. https://doi.org/10.3390/molecules28217367
Liu Z, Xia Q, Huang B, Yi H, Yan J, Chen X, Xu F, Xi H. Prediction of Xe/Kr Separation in Metal-Organic Frameworks by a Precursor-Based Neural Network Synergistic with a Polarizable Adsorbate Model. Molecules. 2023; 28(21):7367. https://doi.org/10.3390/molecules28217367
Chicago/Turabian StyleLiu, Zewei, Qibin Xia, Bichun Huang, Hao Yi, Jian Yan, Xin Chen, Feng Xu, and Hongxia Xi. 2023. "Prediction of Xe/Kr Separation in Metal-Organic Frameworks by a Precursor-Based Neural Network Synergistic with a Polarizable Adsorbate Model" Molecules 28, no. 21: 7367. https://doi.org/10.3390/molecules28217367
APA StyleLiu, Z., Xia, Q., Huang, B., Yi, H., Yan, J., Chen, X., Xu, F., & Xi, H. (2023). Prediction of Xe/Kr Separation in Metal-Organic Frameworks by a Precursor-Based Neural Network Synergistic with a Polarizable Adsorbate Model. Molecules, 28(21), 7367. https://doi.org/10.3390/molecules28217367






