Theoretical Study on Fluorinated Derivatives of Sulfolane, Cyclopentanone, and Gamma-Butyrolactone
Abstract
:1. Introduction
- ▪
- High redox stability (voltage durability), as the capacity of a double-layer capacitor is proportional to the square of the operating voltage.
- ▪
- Low viscosity, which is a prerequisite for high ionic conductivity [7].
- ▪
- High ion solubilities to produce electrolytes with sufficient ion concentrations (achievable by the high free energy of the solvation of relevant ions and high dielectric constant).
- ▪
- Low enough melting point and high boiling and flash points.
- ▪
- Sufficient thermal stability.
- ▪
- Low protonation/deprotonation ability and low reactivity.
- ▪
- ▪
- ▪
- Higher dielectric constant, if the F atom is placed in the right position to increase the dipole moment of the molecule.
- ▪
- Lower basicity and higher acidity.
- ▪
- ▪
- Electrochemical stability windows (ESWs) were estimated via the calculated oxidation and reduction potentials in gas phase and DMSO, or approximated via the differences of the gas-phase HOMO and LUMO energies [35].
- ▪
- Dielectric constants (εr) and boiling points (BP) were computed with the COSMO-RS method with empirical corrections.
- ▪
- Basicities were characterized via the predicted Gibbs energies of the transfer of a proton from water to the studied solvent (∆trG°(H+)), basicity in acetonitrile (pKaH(MeCN), corresponding to the pKa of the protonated molecule), and gas-phase basicity (GB) of the solvents.
- ▪
- Mutual solubility with water and lipophilicity were computed with the COSMO-RS method.
2. Results
3. Discussion
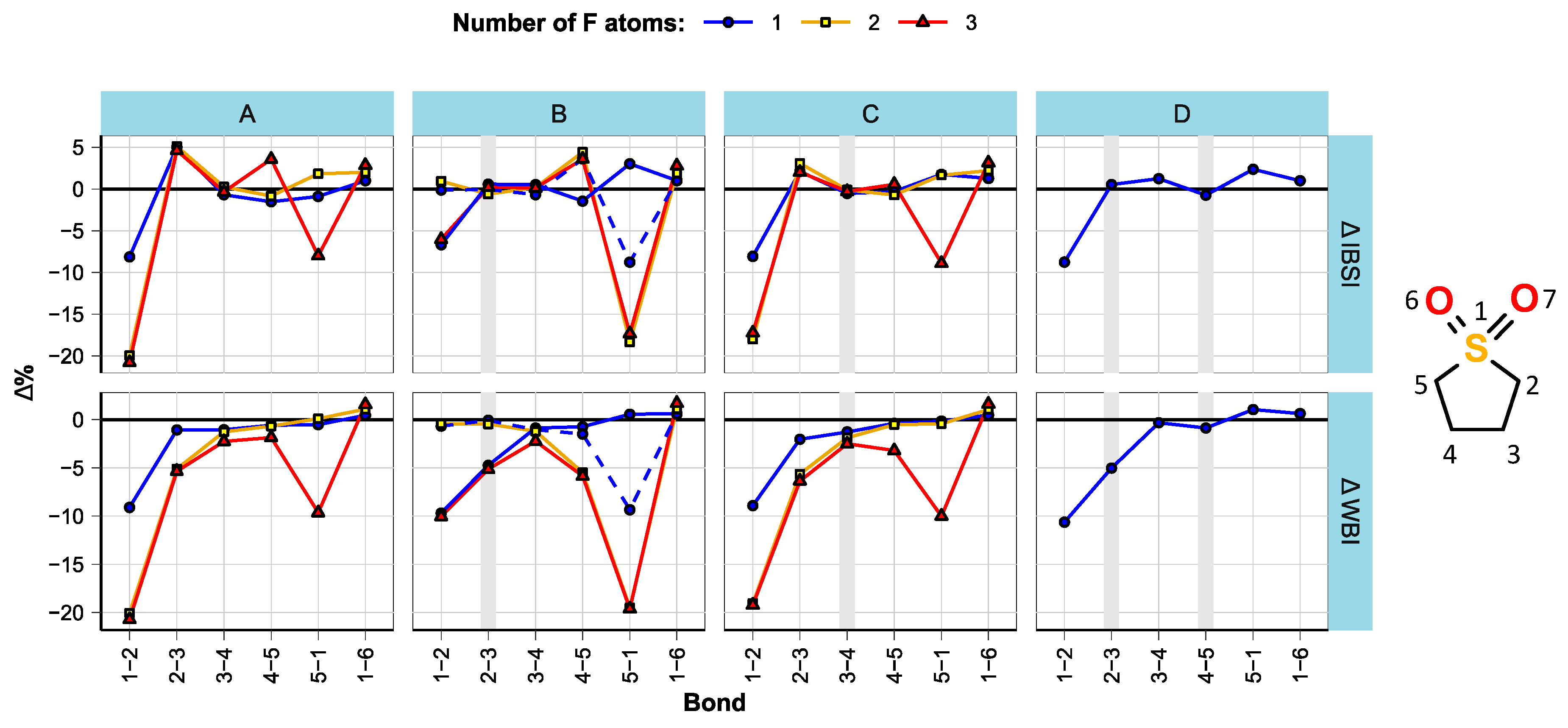
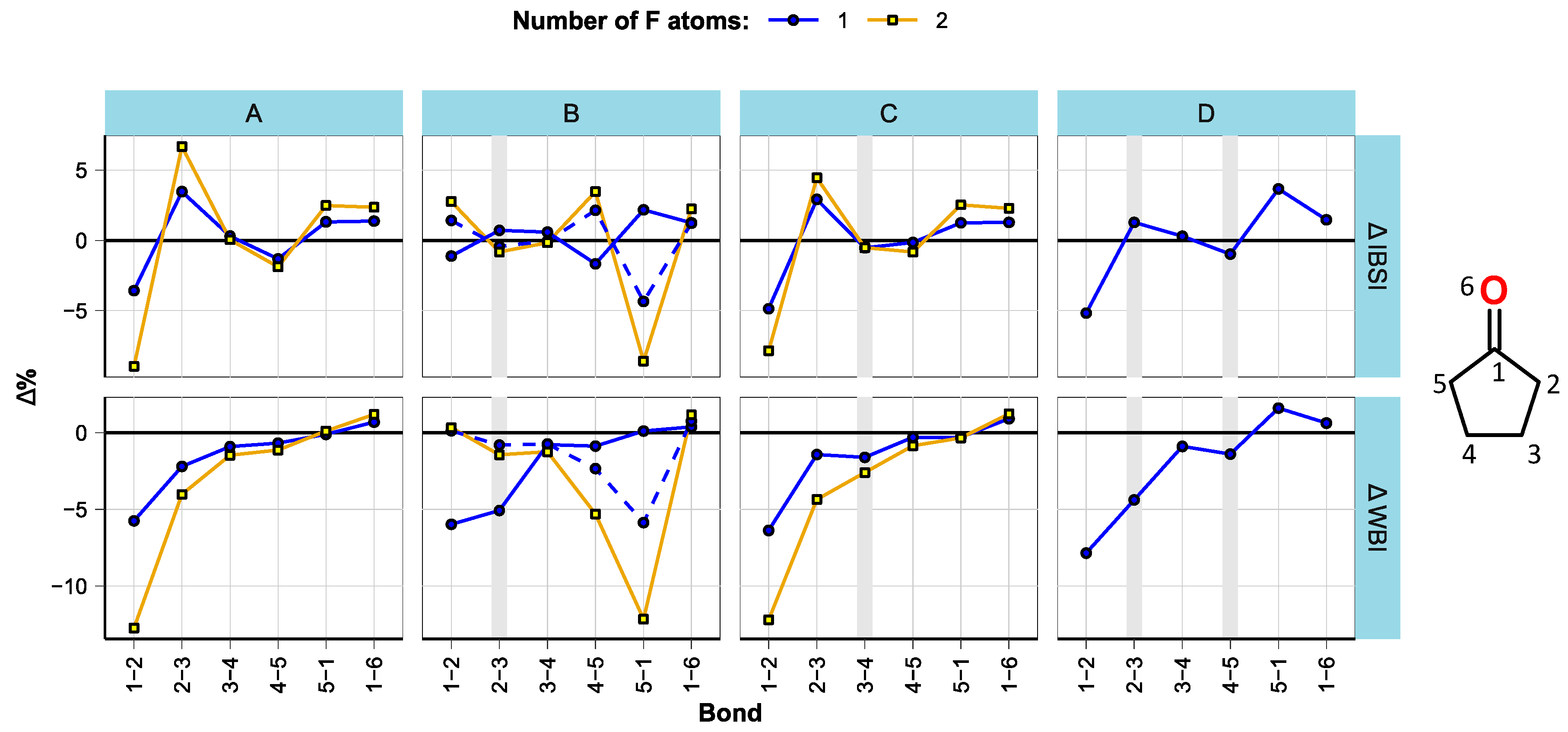
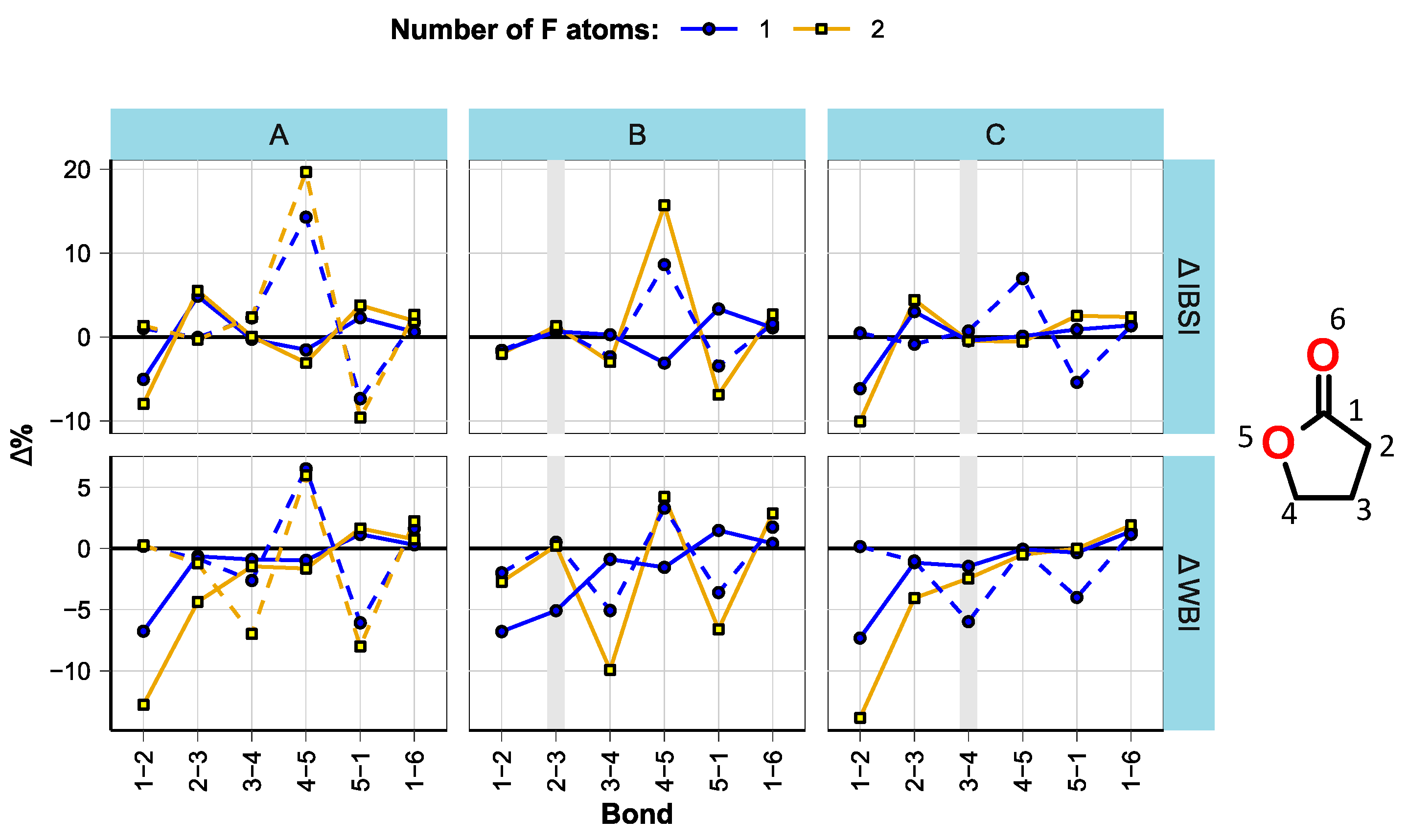
3.1. Effect of Fluorination on Bond Strengths
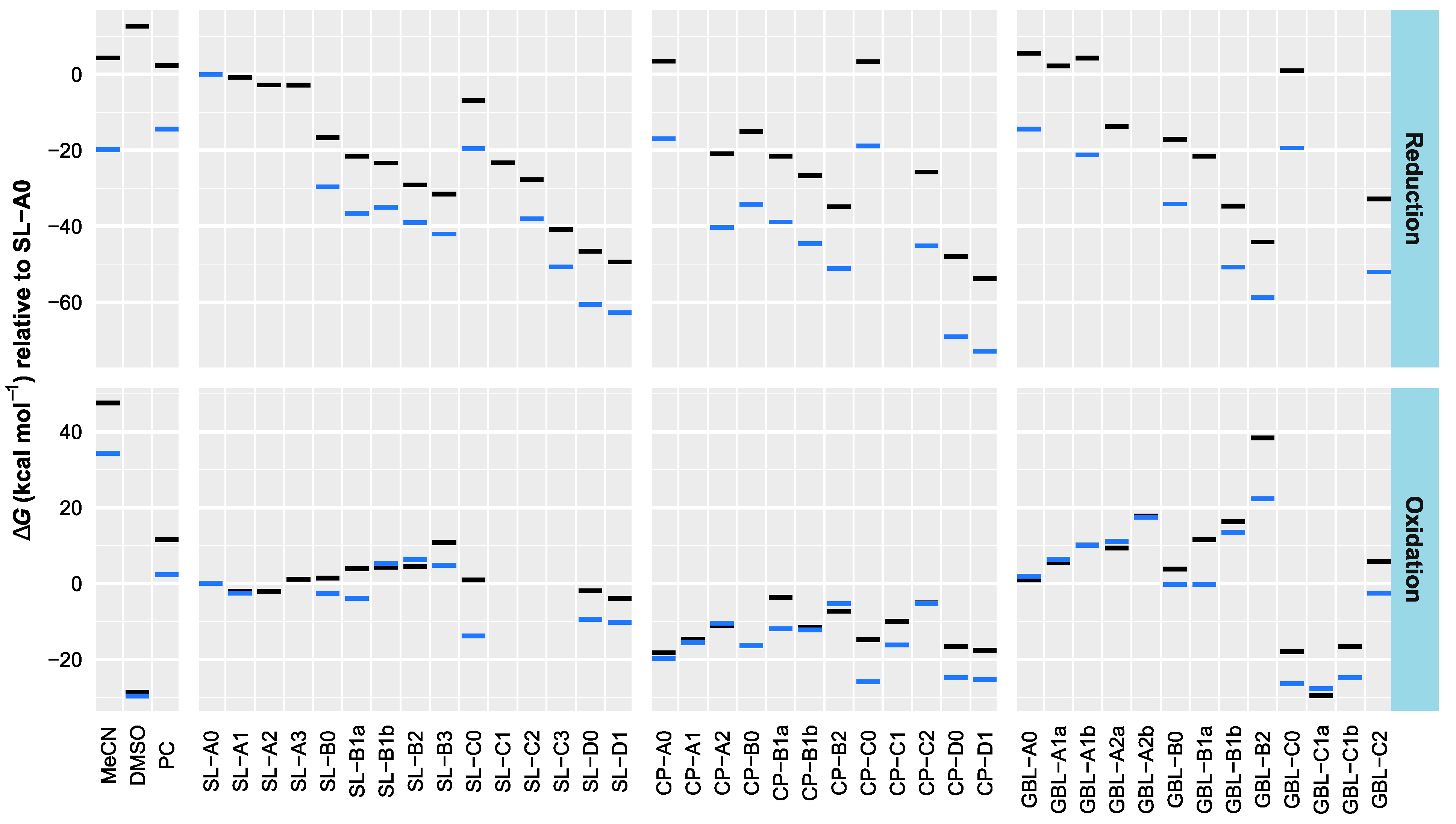
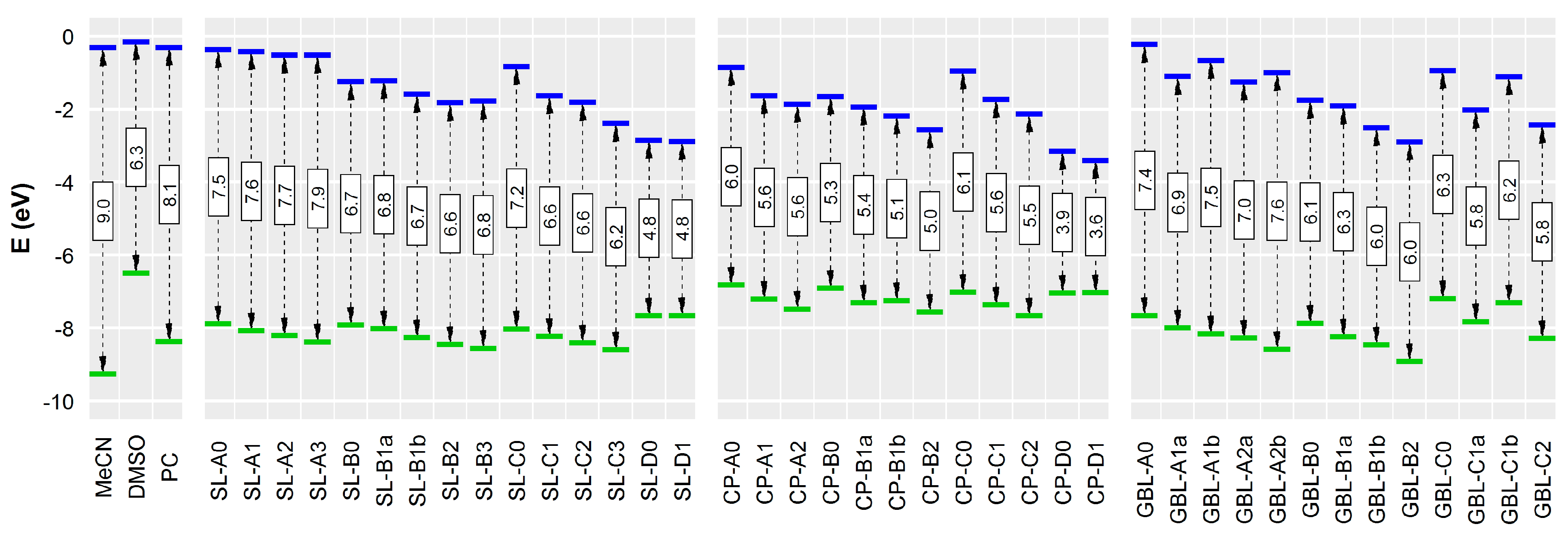
3.2. Effect of Structural Variations on the Electrochemical Stability
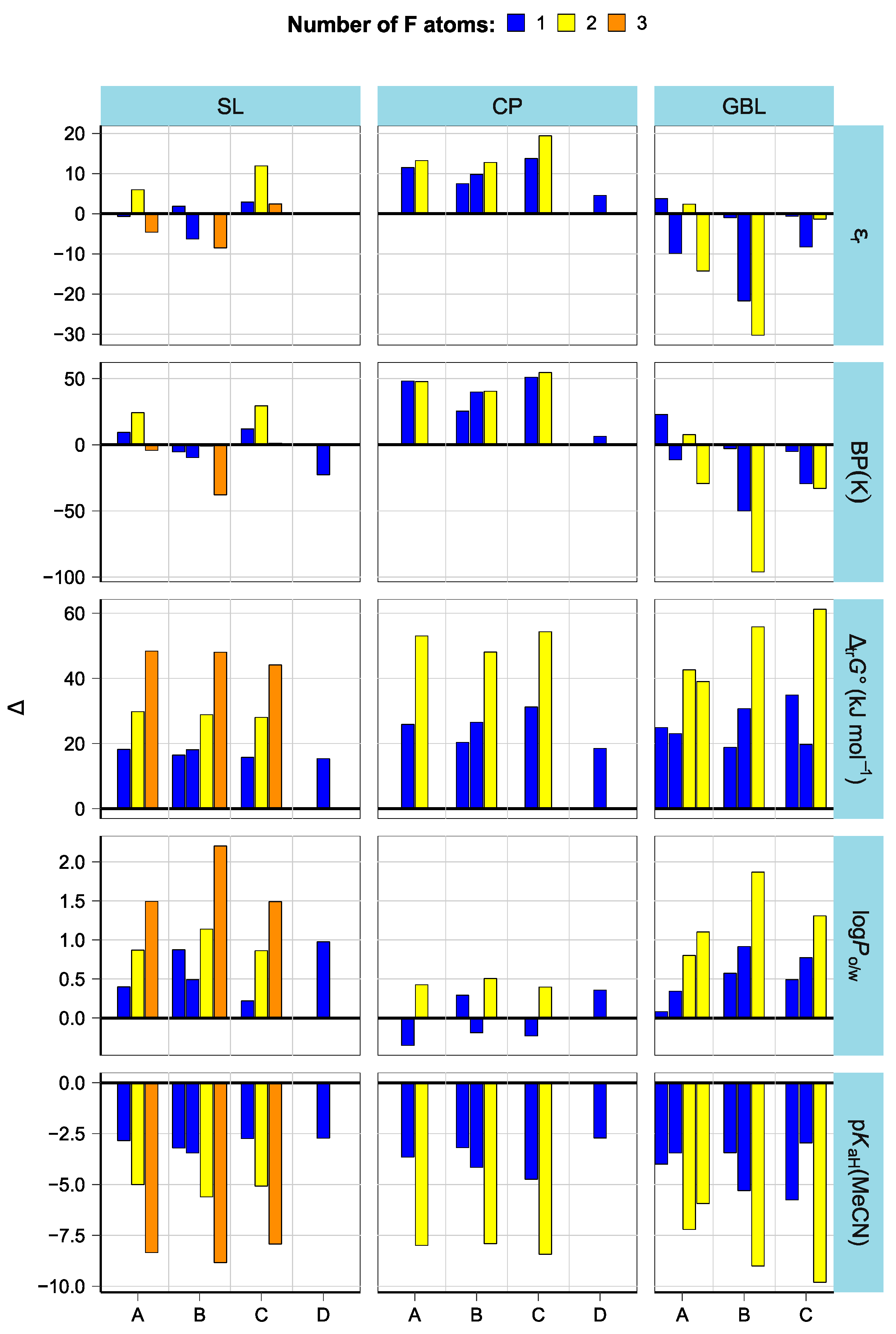
3.3. Effect of Structural Variations on Other Properties
3.4. Solubility Trends
3.5. Synthesis of the Proposed Compounds
4. Conclusions
5. Materials and Methods
5.1. Computational Parameters and Software
5.2. Solvation Models
5.3. Accuracy of the Computed Values and Applied Corrections
N = 6, R2 = 0.89, Sres = 18 kJ mol−1
N = 29, R2 = 0.94, Sres = 18 K
N = 20, R2 = 0.97, Sres = 0.08 log units
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhong, C.; Deng, Y.; Hu, W.; Qiao, J.; Zhang, L.; Zhang, J. A Review of Electrolyte Materials and Compositions for Electrochemical Supercapacitors. Chem. Soc. Rev. 2015, 44, 7484–7539. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Hicks, R.P.; Chen, Z.; Luo, C.; Guo, J.; Wang, C.; Xu, Y. Electrolytes in Organic Batteries. Chem. Rev. 2023, 123, 1712–1773. [Google Scholar] [CrossRef] [PubMed]
- Cheng, L.; Assary, R.S.; Qu, X.; Jain, A.; Ong, S.P.; Rajput, N.N.; Persson, K.; Curtiss, L.A. Accelerating Electrolyte Discovery for Energy Storage with High-Throughput Screening. J. Phys. Chem. Lett. 2015, 6, 283–291. [Google Scholar] [CrossRef] [PubMed]
- Marcou, G.; Flamme, B.; Beck, G.; Chagnes, A.; Mokshyna, O.; Horvath, D.; Varnek, A. In Silico Design, Virtual Screening and Synthesis of Novel Electrolytic Solvents. Mol. Inform. 2019, 38, e1900014. [Google Scholar] [CrossRef] [PubMed]
- Schütter, C.; Husch, T.; Viswanathan, V.; Passerini, S.; Balducci, A.; Korth, M. Rational Design of New Electrolyte Materials for Electrochemical Double Layer Capacitors. J. Power Sources 2016, 326, 541–548. [Google Scholar] [CrossRef]
- Balducci, A. Electrolytes for High Voltage Electrochemical Double Layer Capacitors: A Perspective Article. J. Power Sources 2016, 326, 534–540. [Google Scholar] [CrossRef]
- Gong, K.; Fang, Q.; Gu, S.; Li, S.F.Y.; Yan, Y. Nonaqueous Redox-Flow Batteries: Organic Solvents, Supporting Electrolytes, and Redox Pairs. Energy Environ. Sci. 2015, 8, 3515–3530. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, J.; Liu, T.; Wu, H.; Tian, S.; Zhou, L.; Zhang, B.; Cui, G. Toward Low-Temperature Lithium Batteries: Advances and Prospects of Unconventional Electrolytes. Adv. Energy Sustain. Res. 2021, 2, 2100039. [Google Scholar] [CrossRef]
- Takehaea, M.; Ebara, R.; Nanbu, N.; Ue, M.; Sasaki, Y. Electrochemical Properties of Fluoro-γ-Butyrolactone and Its Application to Lithium Rechargeable Cells. Electrochemistry 2003, 71, 1172–1176. [Google Scholar] [CrossRef]
- Nambu, N.; Matsushita, Y.; Takehara, M.; Sasaki, Y. Physical and Electrochemical Properties of Fluorinated Dialkyl Ethers. Electrochemistry 2016, 84, 776–778. [Google Scholar] [CrossRef]
- Yue, Z.; Dunya, H.; Aryal, S.; Segre, C.U.; Mandal, B. Synthesis and Electrochemical Properties of Partially Fluorinated Ether Solvents for Lithiumsulfur Battery Electrolytes. J. Power Sources 2018, 401, 271–277. [Google Scholar] [CrossRef]
- Lu, H.; He, L.; Yuan, Y.; Zhu, Y.; Zheng, B.; Zheng, X.; Liu, C.; Du, H. Synergistic Effect of Fluorinated Solvents for Improving High Voltage Performance of LiNi0.5Mn1.5O4 Cathode. J. Electrochem. Soc. 2020, 167, 120534. [Google Scholar] [CrossRef]
- Todorov, Y.M.; Aoki, M.; Mimura, H.; Fujii, K.; Yoshimoto, N.; Morita, M. Thermal and Electrochemical Properties of Nonflammable Electrolyte Solutions Containing Fluorinated Alkylphosphates for Lithium-Ion Batteries. J. Power Sources 2016, 332, 322–329. [Google Scholar] [CrossRef]
- Zhang, S.S.; Read, J. Partially Fluorinated Solvent as a Co-Solvent for the Non-Aqueous Electrolyte of Li/Air Battery. J. Power Sources 2011, 196, 2867–2870. [Google Scholar] [CrossRef]
- Du, F.; Ye, T.; Shi, Y.; Zhang, Y.; Qiu, Z.; Liu, W.; Lv, T.; Duan, S.; Liu, J. Deciphering Reduction Stability of Sulfone and Fluorinated Sulfone Electrolytes: Insight from Quantum Chemical Calculations. Chem. Phys. 2023, 568, 111840. [Google Scholar] [CrossRef]
- Khamitov, E.M.; Kuz’mina, E.V.; Karaseva, E.V.; Kolosnitsyn, V.S. Evaluation of Electrochemical Stability of Substituted Sulfolanes Based on Bond Orders. Russ. J. Phys. Chem. A 2021, 95, 730–735. [Google Scholar] [CrossRef]
- Yang, X.; Liu, X.; Han, J.; Liu, Z.; Zhang, X. Tuning Fluorination of Carbonates for Lithium-Ion Batteries: A Theoretical Study. J. Phys. Chem. B 2023, 127, 3026–3040. [Google Scholar] [CrossRef] [PubMed]
- Khetan, A.; Pitsch, H.; Viswanathan, V. Identifying Descriptors for Solvent Stability in Nonaqueous Li–O2 Batteries. J. Phys. Chem. Lett. 2014, 5, 1318–1323. [Google Scholar] [CrossRef] [PubMed]
- Mathieu, O.; Diévart, P.; Turner, M.A.; Mohr, D.J.; Grégoire, C.M.; Alturaifi, S.A.; Catoire, L.; Petersen, E.L. Experimental and Detailed Kinetics Modeling Study of the Fire Suppressant Properties of di(2,2,2trifluoroethyl) Carbonate. Proc. Combust. Inst. 2023, 39, 499–510. [Google Scholar] [CrossRef]
- Yang, A.; Yang, C.; Xie, K.; Xin, S.; Xiong, Z.; Li, K.; Guo, Y.-G.; You, Y. Benchmarking the Safety Performance of Organic Electrolytes for Rechargeable Lithium Batteries: A Thermochemical Perspective. ACS Energy Lett. 2023, 8, 836–843. [Google Scholar] [CrossRef]
- Möller, K.-C.; Hodal, T.; Appel, W.K.; Winter, M.; Besenhard, J.O. Fluorinated Organic Solvents in Electrolytes for Lithium Ion Cells. J. Power Sources 2001, 97–98, 595–597. [Google Scholar] [CrossRef]
- Bryantsev, V.S.; Giordani, V.; Walker, W.; Blanco, M.; Zecevic, S.; Sasaki, K.; Uddin, J.; Addison, D.; Chase, G.V. Predicting Solvent Stability in Aprotic Electrolyte Li–Air Batteries: Nucleophilic Substitution by the Superoxide Anion Radical (O2•–). J. Phys. Chem. A 2011, 115, 12399–12409. [Google Scholar] [CrossRef]
- Ho, J.S.; Borodin, O.A.; Ding, M.S.; Ma, L.; Schroeder, M.A.; Pastel, G.R.; Xu, K. Understanding Lithium-ion Transport in Sulfolane- and Tetraglyme-Based Electrolytes Using Very Low-Frequency Impedance Spectroscopy. Energy Environ. Mater. 2023, 6, e12302. [Google Scholar] [CrossRef]
- Tilstam, U. Sulfolane: A Versatile Dipolar Aprotic Solvent. Org. Process Res. Dev. 2012, 16, 1273–1278. [Google Scholar] [CrossRef]
- Timmermans, J. The Melting Point of Organic Substances. X Bull. Soc. Chim. Belg. 1927, 36, 502–518. [Google Scholar]
- Ding, M.S.; Jow, T.R. Properties of PC-EA Solvent and Its Solution of LiBOB Comparison of Linear Esters to Linear Carbonates for Use in Lithium Batteries. J. Electrochem. Soc. 2005, 152, A1199. [Google Scholar] [CrossRef]
- Krug, R.C.; Tichelaar, G.R.; Didot, F.E. Unsaturated Cyclic Sulfones. III. Some Halogen-Containing Derivatives. J. Org. Chem. 1958, 23, 212–215. [Google Scholar] [CrossRef]
- Clauson-Kaas, N.; Elming, N.; Rottenberg, M.; Stenhagen, E.; Östling, S. 2-Acetoxyfuran. Acta Chem. Scand. 1952, 6, 560–564. [Google Scholar] [CrossRef]
- Kotha, S.; Khedkar, P.; Ghosh, A.K. Synthesis of Symmetrical Sulfones from Rongalite: Expansion to Cyclic Sulfones by Ring-Closing Metathesis. Eur. J. Org. Chem. 2005, 2005, 3581–3585. [Google Scholar] [CrossRef]
- Perrotti, E.; Palladino, N.; Greco, M.; De Malde, M. Reactions of Nitrosyl Salts. I. Reaction of Nitrosyl Sulfate with Succinic-Type Dicarboxylic Acids and 3,4-Dialkylisoxazol-5-Ones. Ann. Chim. 1966, 56, 1358–1372. [Google Scholar]
- Nesmeyanov, A.N.; Sazonova, V.A.; Drosd, V.N. Synthesis of Ferrocene Derivatives by Means of Boron- and Halogen-Substituted Ferrocenes. Chem. Ber. 1960, 93, 2717–2729. [Google Scholar]
- Abe, K.; Miyoshi, K.; Hattori, T.; Ushigoe, Y.; Yoshitake, H. Functional Electrolytes: Synergetic Effect of Electrolyte Additives for Lithium-Ion Battery. J. Power Sources 2008, 184, 449–455. [Google Scholar] [CrossRef]
- Chen, Y.; He, Q.; Mo, Y.; Zhou, W.; Zhao, Y.; Piao, N.; Liu, C.; Xiao, P.; Liu, H.; Li, B.; et al. Engineering an Insoluble Cathode Electrolyte Interphase Enabling High Performance NCM811//Graphite Pouch Cell at 60 °C. Adv. Energy Mater. 2022, 12, 2201631. [Google Scholar] [CrossRef]
- Kubota, T.; Ihara, M.; Katayama, S.; Nakai, H.; Ichikawa, J. 1,1-Difluoro-1-Alkenes as New Electrolyte Additives for Lithium Ion Batteries. J. Power Sources 2012, 207, 141–149. [Google Scholar] [CrossRef]
- Husch, T.; Yilmazer, N.D.; Balducci, A.; Korth, M. Large-Scale Virtual High-Throughput Screening for the Identification of New Battery Electrolyte Solvents: Computing Infrastructure and Collective Properties. Phys. Chem. Chem. Phys. 2015, 17, 3394–3401. [Google Scholar] [CrossRef]
- Abboud, J.-L.M.; Notari, R. Critical Compilation of Scales of Solvent Parameters. Part I. Pure, Non-Hydrogen Bond Donor Solvents. Pure Appl. Chem. 1999, 71, 645–718. [Google Scholar] [CrossRef]
- Yaws, C.L. Thermophysical Properties of Chemicals and Hydrocarbons; William Andrew: Norwich, NY, USA, 2008. [Google Scholar]
- Marcus, Y.; Kamlet, M.J.; Taft, R.W. Linear Solvation Energy Relationships: Standard Molar Gibbs Free Energies and Enthalpies of Transfer of Ions from Water into Nonaqueous Solvents. J. Phys. Chem. 1988, 92, 3613–3622. [Google Scholar] [CrossRef]
- Hansch, C.; Leo, A.; Hoekman, D. Exploring QSAR: Hydrophobic, Electronic, and Steric Constants; ACS professional reference book; American Chemical Society: Washington, DC, USA, 1995. [Google Scholar]
- Linstrom, P.; Mallard, W.G. (Eds.) NIST Chemistry WebBook, NIST Standard Reference Database 69; National Institute of Standards and Testing (NIST): Gaithersburg, MD, USA, 1997. [Google Scholar] [CrossRef]
- Klein, J.; Khartabil, H.; Boisson, J.-C.; Contreras-García, J.; Piquemal, J.-P.; Hénon, E. New Way for Probing Bond Strength. J. Phys. Chem. A 2020, 124, 1850–1860. [Google Scholar] [CrossRef]
- Wiberg, K.B. Application of the Pople-Santry-Segal CNDO Method to the Cyclopropylcarbinyl and Cyclobutyl Cation and to Bicyclobutane. Tetrahedron 1968, 24, 1083–1096. [Google Scholar] [CrossRef]
- Clark, E. Sulfolane and Sulfones. In Kirk-Othmer Encyclopedia of Chemical Technology; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2000. [Google Scholar]
- Liu, J.; Shi, W.; Wang, X. ZnO–POM Cluster Sub-1 nm Nanosheets as Robust Catalysts for the Oxidation of Thioethers at Room Temperature. J. Am. Chem. Soc. 2021, 143, 16217–16225. [Google Scholar] [CrossRef]
- Bresciani, G.; Bortoluzzi, M.; Marchetti, F.; Pampaloni, G. Titanium(IV) Alkoxide-Carbamate Complexes: Synthesis and Catalytic Potential in H2O2-Oxidation of Organic Sulfides. Eur. J. Inorg. Chem. 2022, 2022, e202200402. [Google Scholar] [CrossRef]
- Assis, M.; Gouveia, A.F.; Ribeiro, L.K.; Ponce, M.A.; Churio, M.S.; Oliveira, O.N.; Mascaro, L.H.; Longo, E.; Llusar, R.; Guillamón, E.; et al. Towards an Efficient Selective Oxidation of Sulfides to Sulfones by NiWO4 and α-Ag2WO4. Appl. Catal. Gen. 2023, 652, 119038. [Google Scholar] [CrossRef]
- Kuźnik, N.; Krompiec, S.; Bieg, T.; Baj, S.; Skutil, K.; Chrobok, A. Double Bond Migration in S-allyl Systems Catalysed by [RuClH(CO)(PPh3)3]. J. Organomet. Chem. 2003, 665, 167–175. [Google Scholar] [CrossRef]
- Lim, K.M.-H.; Hayashi, T. Rhodium-Catalyzed Asymmetric Arylation of Allyl Sulfones under the Conditions of Isomerization into Alkenyl Sulfones. J. Am. Chem. Soc. 2015, 137, 3201–3204. [Google Scholar] [CrossRef] [PubMed]
- Jalilian, F.; Yadollahi, B.; Farsani, M.R.; Tangestaninejad, S.; Rudbari, H.A.; Habibi, R. New Perspective to Keplerate Polyoxomolybdates: Green Oxidation of Sulfides with Hydrogen Peroxide in Water. Catal. Commun. 2015, 66, 107–110. [Google Scholar] [CrossRef]
- Sasaki, Y.; Ue, M.; Takehara, M. Monofluorosulfolane. JP2002155074A, 28 May 2002. [Google Scholar]
- Sasaki, Y.; Ebara, R.; Nanbu, N.; Takehara, M.; Ue, M. Direct Fluorination of γ-Butyrolactone. J. Fluor. Chem. 2001, 108, 117–120. [Google Scholar] [CrossRef]
- Nielsen, M.K.; Ahneman, D.T.; Riera, O.; Doyle, A.G. Deoxyfluorination with Sulfonyl Fluorides: Navigating Reaction Space with Machine Learning. J. Am. Chem. Soc. 2018, 140, 5004–5008. [Google Scholar] [CrossRef]
- Deng, L.; Kang, B.; Englert, U.; Klankermayer, J.; Palkovits, R. Direct Hydrogenation of Biobased Carboxylic Acids Mediated by a Nitrogen-centered Tridentate Phosphine Ligand. ChemSusChem 2016, 9, 177–180. [Google Scholar] [CrossRef]
- Risley, J.M.; Kastanis, J.P.; Young, A.M. Determination of the Second-Order 1H NMR Parameters for the Aromatic Protons in 4-Fluoroaniline and Application to the Analysis of the 1H NMR Spectra for the Aromatic Protons in N4-(4′-Fluorophenyl)Succinamic Acid and in N4-(4′-Fluorophenyl)-3,3-Difluorosuccinamic Acid. J. Fluor. Chem. 2011, 132, 269–275. [Google Scholar] [CrossRef]
- Yu, Y.; Guo, Y.; Zhan, W.; Guo, Y.; Wang, Y.; Wang, Y.; Zhang, Z.; Lu, G. Gas-Phase Hydrogenation of Maleic Anhydride to γ-Butyrolactone at Atmospheric Pressure over Cu–CeO2–Al2O3 Catalyst. J. Mol. Catal. Chem. 2011, 337, 77–81. [Google Scholar] [CrossRef]
- Kobayashi, M.; Inoguchi, T.; Iida, T.; Tanioka, T.; Kumase, H.; Fukai, Y. Development of Direct Fluorination Technology for Application to Materials for Lithium Battery. J. Fluor. Chem. 2003, 120, 105–110. [Google Scholar] [CrossRef]
- Kvíala, J.; Plocar, J.; Vlasáková, R.; Paleta, O.; Pelter, A. 2-Fluoro-2-Buten-4-Olide, a New Fluorinated Synthon. Preparation; 1,2-, 1,4- and Tandem Additions. Synlett 1997, 1997, 986–988. [Google Scholar] [CrossRef]
- Ahn, J.A.; Jung, H.M.; Park, J.H.; Lee, C.H.; Lim, Y.M.; Ha, Y.J. Non-Aqueous Electrolyte and Secondary Battery Comprising the Same. KR20080065561A, 14 July 2008. [Google Scholar]
- Vasileff, T.P.; Koster, D.F. Preparation of Maleoyl Fluoride. Nuclear Magnetic Resonance Spectra of Maleoyl Fluoride, Fumaroyl Fluoride, and Fumaroyl Chloride Fluoride. J. Org. Chem. 1970, 35, 2461–2463. [Google Scholar] [CrossRef]
- Cao, R.; Liu, C.; Liu, L. A Convenient Synthesis of 2(5h)-Furanone. Org. Prep. Proced. Int. 1996, 28, 215–216. [Google Scholar] [CrossRef]
- Stavber, S.; Šket, B.; Zajc, B.; Zupan, M. Chemistry of Organo Halogenic Molecules. Part 100. Comparative Behaviour of Xenon Diflouride and Caesium Fluoroxysulphate in the Fluorination of Enol Acetates and Ketones. Tetrahedron 1989, 45, 6003–6010. [Google Scholar] [CrossRef]
- Stavber, S.; Zupan, M. High Yield Direct Fluorofunctionalisation of Ketones Using AccufluorTM-NFTh Fluorinating Reagent. Tetrahedron Lett. 1996, 37, 3591–3594. [Google Scholar] [CrossRef]
- Zajc, B.; Zupan, M. Room Temperature Fluorination of 1,3-Diketones and Enol Acetates with Xenon Difluoride. J. Chem. Soc. Chem. Commun. 1980, 759–760. [Google Scholar] [CrossRef]
- Weng, Z.; Wang, F. Salt and Crystal Form of Ketohexokinase Inhibitor and Use Thereof. WO2022022476A1, 3 February 2022. [Google Scholar]
- Kaneko, C.; Sato, M. Production of Alpha-Fluorocycloalkenones. JPH07242595A, 19 September 1995. [Google Scholar]
- Gharagheizi, F.; Eslamimanesh, A.; Mohammadi, A.H.; Richon, D. Empirical Method for Representing the Flash-Point Temperature of Pure Compounds. Ind. Eng. Chem. Res. 2011, 50, 5877–5880. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision A.03; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Curtiss, L.A.; Redfern, P.C.; Raghavachari, K. Gaussian-4 Theory Using Reduced Order Perturbation Theory. J. Chem. Phys. 2007, 127, 124105. [Google Scholar] [CrossRef] [PubMed]
- BIOVIA COSMOtherm, Release 2023; Dassault Systèmes. Available online: http://www.3ds.com (accessed on 22 November 2023).
- TURBOMOLE V6.5 2013, a Development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007. Available online: http://www.turbomole.com (accessed on 22 November 2023).
- Klamt, A. Conductor-like Screening Model for Real Solvents: A New Approach to the Quantitative Calculation of Solvation Phenomena. J. Phys. Chem. 1995, 99, 2224–2235. [Google Scholar] [CrossRef]
- Klamt, A.; Jonas, V.; Bürger, T.; Lohrenz, J.C.W. Refinement and Parametrization of COSMO-RS. J. Phys. Chem. A 1998, 102, 5074–5085. [Google Scholar] [CrossRef]
- Eckert, F.; Klamt, A. Fast Solvent Screening via Quantum Chemistry: COSMO-RS Approach. AIChE J. 2002, 48, 369–385. [Google Scholar] [CrossRef]
- Klamt, A.; Eckert, F.; Arlt, W. COSMO-RS: An Alternative to Simulation for Calculating Thermodynamic Properties of Liquid Mixtures. Annu. Rev. Chem. Biomol. Eng. 2010, 1, 101–122. [Google Scholar] [CrossRef] [PubMed]
- Marenich, A.V.; Ho, J.; Coote, M.L.; Cramer, C.J.; Truhlar, D.G. Computational Electrochemistry: Prediction of Liquid-Phase Reduction Potentials. Phys. Chem. Chem. Phys. 2014, 16, 15068–15106. [Google Scholar] [CrossRef] [PubMed]
- Korth, M. Large-Scale Virtual High-Throughput Screening for the Identification of New Battery Electrolyte Solvents: Evaluation of Electronic Structure Theory Methods. Phys. Chem. Chem. Phys. 2014, 16, 7919–7926. [Google Scholar] [CrossRef]
- Tshepelevitsh, S.; Hernits, K.; Leito, I. Prediction of Partition and Distribution Coefficients in Various Solvent Pairs with COSMO-RS. J. Comput. Aided Mol. Des. 2018, 32, 711–722. [Google Scholar] [CrossRef]
- Dupeux, T.; Gaudin, T.; Marteau-Roussy, C.; Aubry, J.-M.; Nardello-Rataj, V. COSMO-RS as an Effective Tool for Predicting the Physicochemical Properties of Fragrance Raw Materials. Flavour Fragr. J. 2022, 37, 106–120. [Google Scholar] [CrossRef]
- Klamt, A.; Eckert, F.; Hornig, M.; Beck, M.E.; Bürger, T. Prediction of Aqueous Solubility of Drugs and Pesticides with COSMO-RS. J. Comput. Chem. 2002, 23, 275–281. [Google Scholar] [CrossRef]
- Kholod, Y.A.; Muratov, E.N.; Gorb, L.G.; Hill, F.C.; Artemenko, A.G.; Kuz’min, V.E.; Qasim, M.; Leszczynski, J. Application of Quantum Chemical Approximations to Environmental Problems: Prediction of Water Solubility for Nitro Compounds. Environ. Sci. Technol. 2009, 43, 9208–9215. [Google Scholar] [CrossRef] [PubMed]
- Chang, H.; Zhong, F.; Cao, R.; Liu, Y.; Wang, M.; Pu, X. Prediction of the Solubilities of Water in Hydrocarbons with COSMO-RS and Interpretation of the Solubility Characteristics. J. Solut. Chem. 2020, 49, 365–382. [Google Scholar] [CrossRef]
- Reinisch, J.; Klamt, A. Predicting Flash Points of Pure Compounds and Mixtures with COSMO-RS. Ind. Eng. Chem. Res. 2015, 54, 12974–12980. [Google Scholar] [CrossRef]
- University of Tartu. UT Rocket; share.neic.no. Available online: https://doi.org/10.23673/PH6N-0144 (accessed on 22 November 2023).
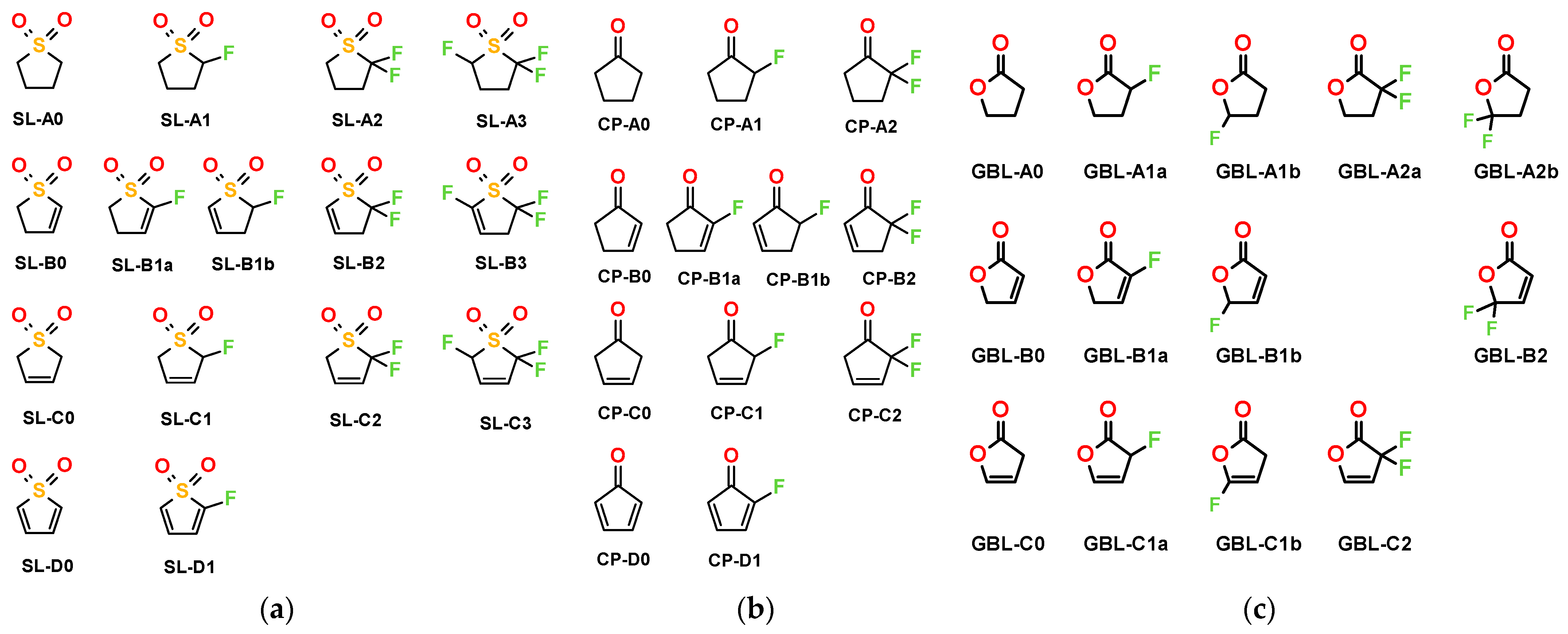
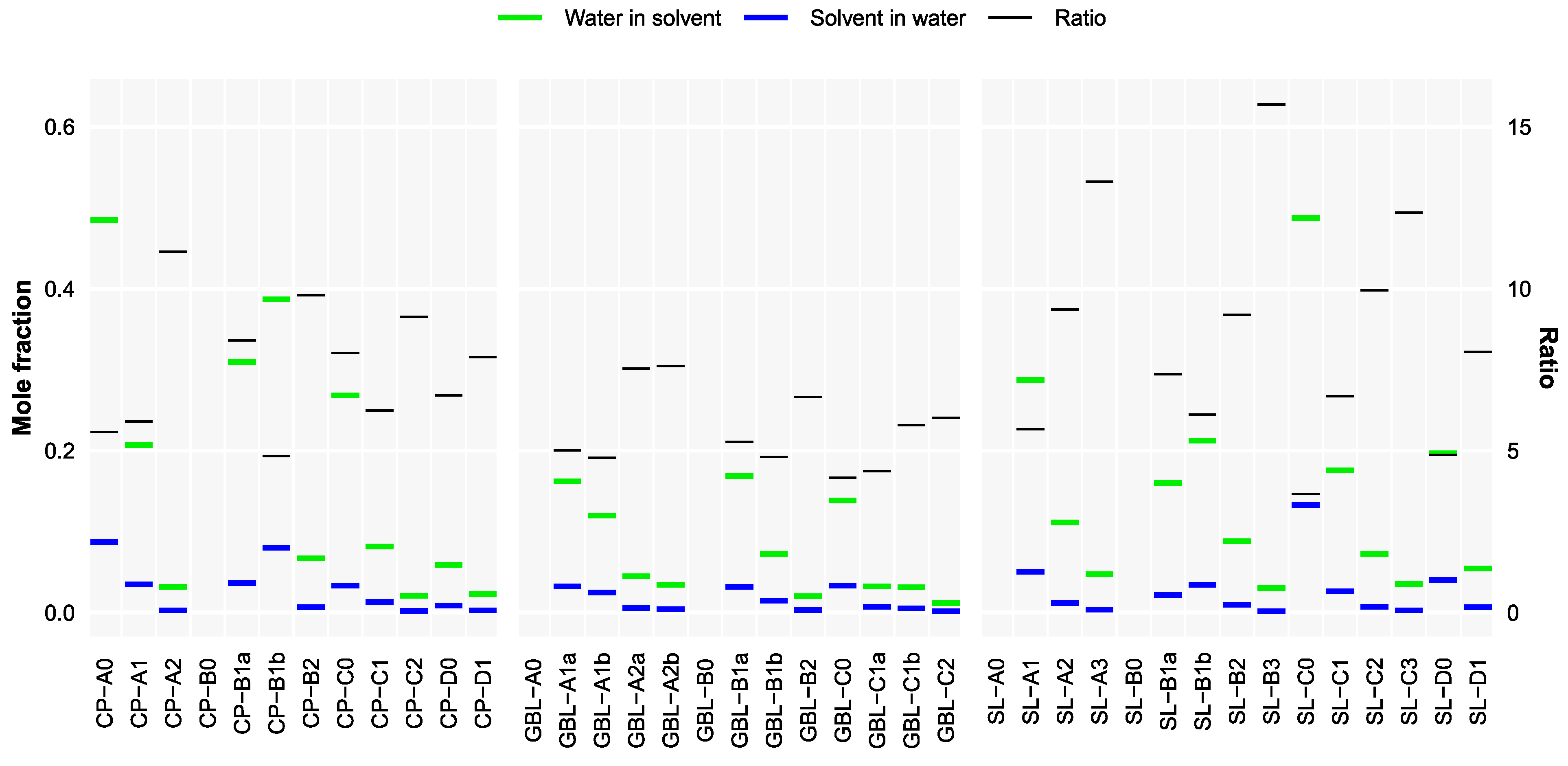
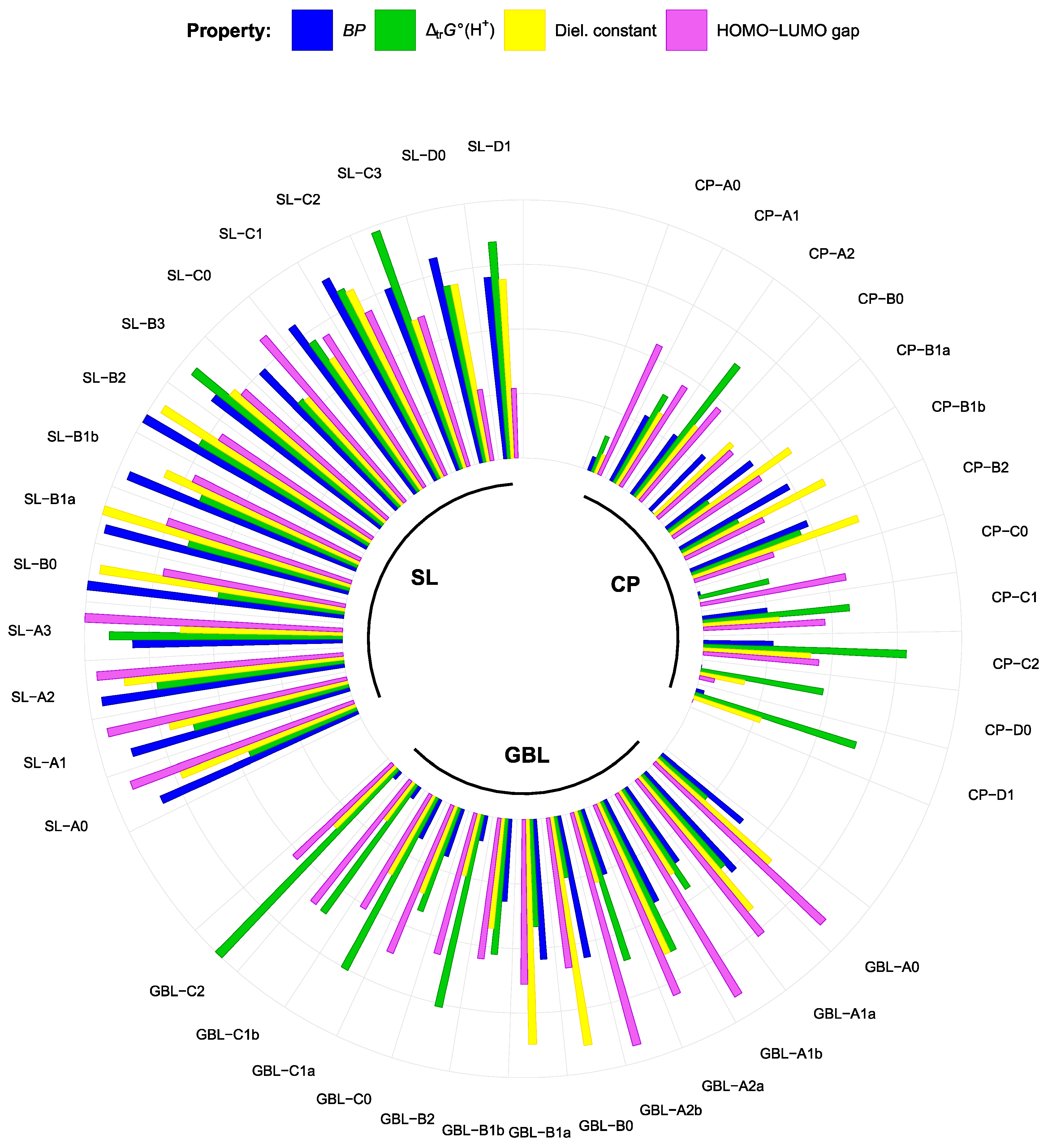
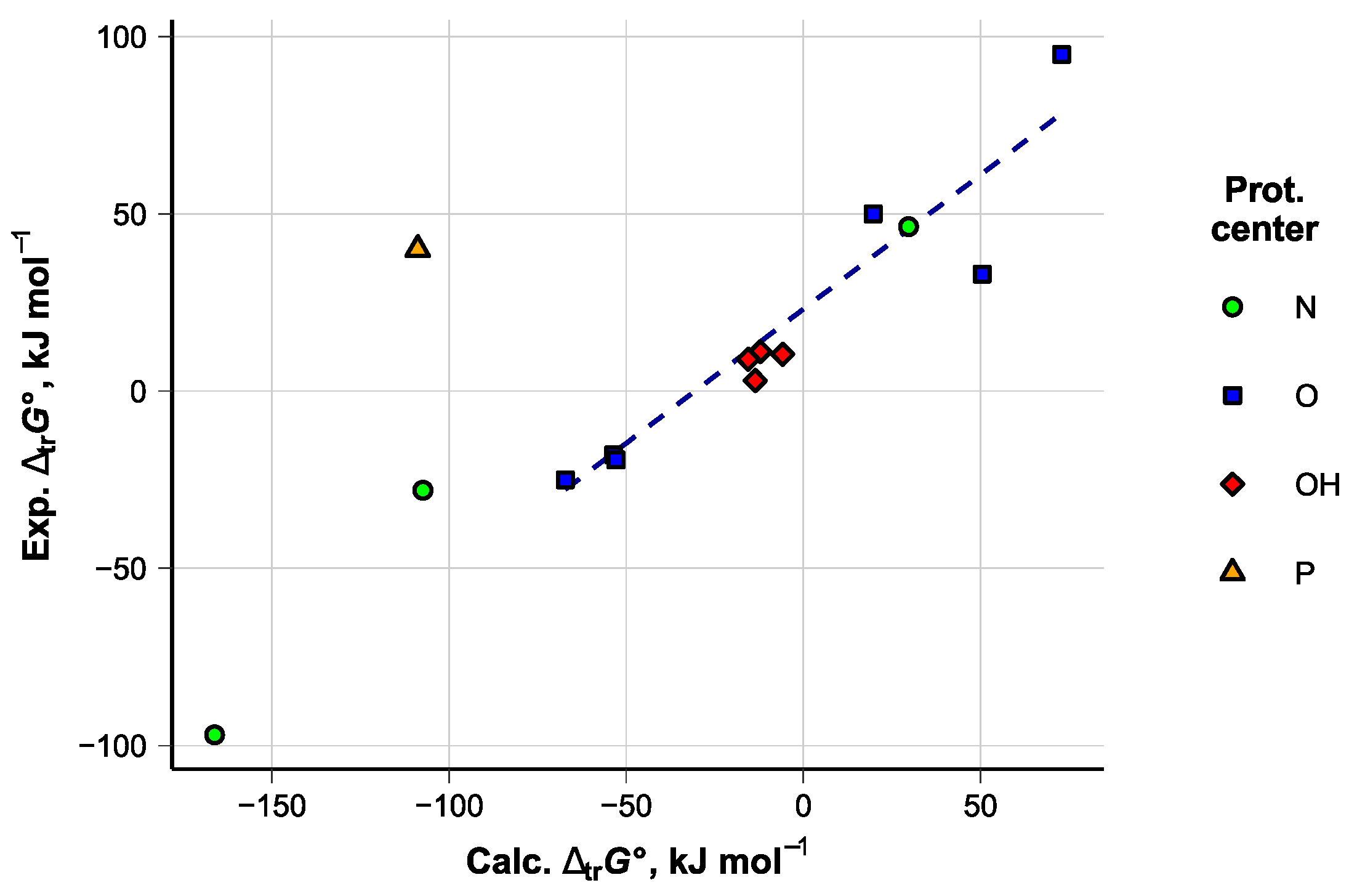
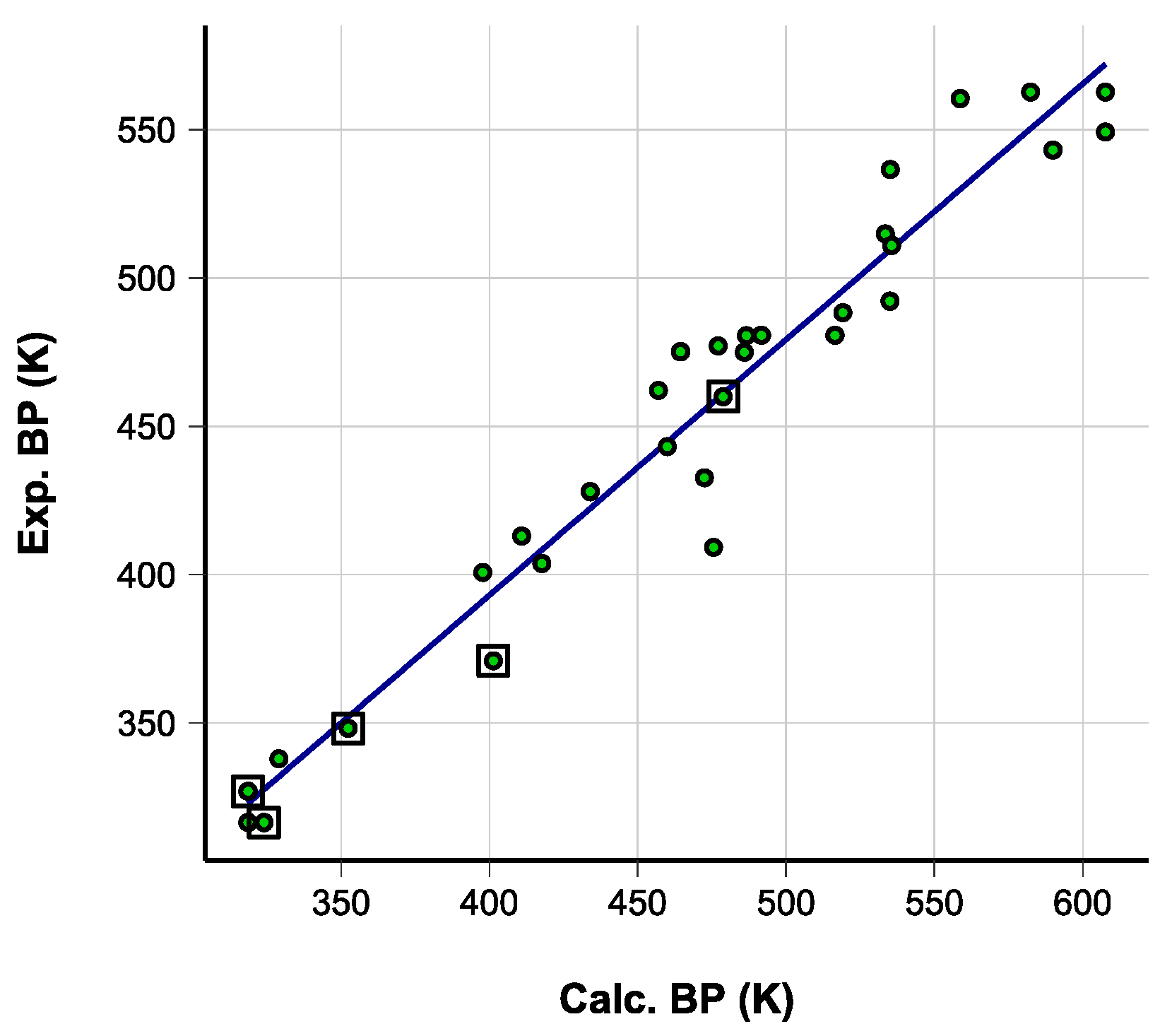
| Double Bonds | Compound | MP | Compound | MP | Compound | MP |
|---|---|---|---|---|---|---|
| 0 | SL-A0 | 28.4 [24] | CP-A0 | −52.8 [25] | GBL-A0 | −43.1 [26] |
| 1 | SL-B0 | 49–50 [27] | GBL-B0 | 4–5 [28] | ||
| 1 | SL-C0 | 63–64 [29] | GBL-C0 | 48–49 [30] | ||
| 2 | CP-D0 | 96–98 [31] |
| Compound | CAS | Relative Red./Ox. Energies (kcal mol−1) | EHOMO (eV) | ELUMO (eV) | εr | BP (K) | ∆trG°(H+) (kJ mol−1) | logPo/w | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ∆oxGgas | ∆redGgas | ∆oxGDMSO | ∆redGDMSO | ||||||||
| MeCN | 75-05-8 | 47.6 | 4.3 | 34.4 | −19.8 | −9.27 | −0.32 | 35.94 [36] | 355 [37] | 46.4 [38] | −0.34 [39] |
| DMSO | 67-68-5 | −28.7 | 12.7 | −29.6 | −6.49 | −0.16 | 46.71 [36] | 464 [37] | −19.4 [38] | −1.35 [39] | |
| PC | 108-32-7 | 11.5 | 2.3 | 2.3 | −14.4 | −8.36 | −0.31 | 62.93 [36] | 515 [37] | 50 [38] | −0.41 [39] |
| SL-A0 | 126-33-0 | 0 | 0 | 0 | 0 | −7.89 | −0.36 | 42.13 [36] | 560 [37] | 44 | −0.77 [39] |
| SL-A1 | 397248-09-8 | −2.0 | −0.8 | −2.6 | −8.07 | −0.42 | 47 | 581 | 62 | −0.91 | |
| SL-A2 | 2413977-86-1 | −2.0 | −2.8 | −8.21 | −0.52 | 54 | 596 | 74 | −0.44 | ||
| SL-A3 | 2413977-87-2 | 1.1 | −2.8 | −8.38 | −0.52 | 43 | 567 | 92 | 0.19 | ||
| SL-B0 | 1192-16-1 | 1.5 | −16.7 | −2.6 | −29.6 | −7.92 | −1.25 | 59 | 606 | 49 | −1.42 |
| SL-B1a | --- | 3.9 | −21.6 | −3.9 | −36.6 | −8.02 | −1.22 | 61 | 601 | 65 | −0.55 |
| SL-B1b | 2851432-77-2 | 4.3 | −23.4 | 5.3 | −35.0 | −8.27 | −1.60 | 52 | 597 | 67 | −0.93 |
| SL-B2 | --- | 4.4 | −29.1 | 6.3 | −39.0 | −8.45 | −1.82 | 58 | 606 | 77 | −0.28 |
| SL-B3 | --- | 10.9 | −31.6 | 4.8 | −42.1 | −8.56 | −1.78 | 50 | 569 | 97 | 0.78 |
| SL-C0 | 77-79-2 | 1.0 | −6.9 | −13.8 | −19.5 | −8.02 | −0.83 | 40 | 553 | 56 | −0.90 |
| SL-C1 | 444334-21-8 | −23.3 | −8.22 | −1.63 | 43 | 565 | 72 | −0.68 | |||
| SL-C2 | --- | −27.7 | −38.0 | −8.41 | −1.81 | 52 | 583 | 84 | −0.03 | ||
| SL-C3 | --- | −40.8 | −50.7 | −8.59 | −2.39 | 42 | 555 | 100 | 0.59 | ||
| SL-D0 | 27092-46-2 | −1.9 | −46.6 | −9.4 | −60.6 | −7.66 | −2.86 | 46 | 568 | 70 | −0.63 |
| SL-D1 | --- | −3.9 | −49.4 | −10.2 | −62.8 | −7.66 | −2.89 | 46 | 545 | 86 | 0.34 |
| CP-A0 | 120-92-3 | −18.3 | 3.5 | −19.7 | −17.0 | −6.83 | −0.86 | 14.45 [36] | 404 [37] | 12 | 0.45 |
| CP-A1 | 1755-12-0 | −14.7 | −15.5 | −7.20 | −1.63 | 29 | 457 | 38 | 0.10 | ||
| CP-A2 | 2167972-33-8 | −11.0 | −20.9 | −10.4 | −40.3 | −7.48 | −1.87 | 31 | 456 | 65 | 0.88 |
| CP-B0 | 930-30-3 | −16.3 | −15.0 | −16.3 | −34.2 | −6.90 | −1.65 | 33 | 409 [40] | −4 | −0.11 |
| CP-B1a | 143998-28-1 | −3.6 | −21.6 | −11.9 | −38.9 | −7.31 | −1.94 | 40 | 484 | 16 | 0.18 |
| CP-B1b | --- | −11.6 | −26.7 | −12.2 | −44.6 | −7.25 | −2.19 | 43 | 499 | 22 | −0.30 |
| CP-B2 | --- | −7.2 | −34.8 | −5.3 | −51.1 | −7.56 | −2.57 | 46 | 499 | 44 | 0.40 |
| CP-C0 | 14320-37-7 | −14.8 | 3.4 | −25.9 | −18.9 | −7.02 | −0.96 | 14 | 399 | 25 | 0.55 |
| CP-C1 | 175544-12-4 (R) | −10.0 | −16.2 | −7.37 | −1.74 | 28 | 450 | 57 | 0.32 | ||
| CP-C2 | --- | −5.1 | −25.7 | −5.3 | −45.1 | −7.67 | −2.14 | 33 | 453 | 80 | 0.94 |
| CP-D0 | 13177-38-3 | −16.6 | −48.0 | −24.8 | −69.1 | −7.04 | −3.16 | 22 | 397 | 47 | 0.86 |
| CP-D1 | --- | −17.6 | −53.8 | −25.3 | −72.9 | −7.03 | −3.40 | 27 | 403 | 66 | 1.22 |
| GBL-A0 | 96-48-0 | 0.9 | 5.6 | 2.0 | −14.4 | −7.66 | −0.23 | 40.96 [36] | 477 [37] | 22 | −0.64 [39] |
| GBL-A1a | 3885-31-2 | 5.6 | 2.2 | 6.4 | −7.99 | −1.11 | 45 | 504 | 46 | −0.39 | |
| GBL-A1b | 2343-90-0 | 10.2 | 4.3 | 10.0 | −21.2 | −8.16 | −0.67 | 32 | 470 | 45 | −0.13 |
| GBL-A2a | 220294-13-3 | 9.4 | −13.7 | 11.2 | −8.27 | −1.26 | 44 | 489 | 64 | 0.33 | |
| GBL-A2b | 1345047-11-1 | 17.8 | 17.5 | −8.58 | −1.00 | 27 | 452 | 61 | 0.63 | ||
| GBL-B0 | 497-23-4 | 3.9 | −17.1 | −0.3 | −34.2 | −7.87 | −1.76 | 56 | 514 | 21 | −0.70 |
| GBL-B1a | 197096-95-0 | 11.6 | −21.5 | −0.2 | −8.24 | −1.92 | 55 | 511 | 40 | −0.12 | |
| GBL-B1b | 1052601-43-0 | 16.3 | −34.7 | 13.5 | −50.8 | −8.46 | −2.51 | 34 | 464 | 52 | 0.22 |
| GBL-B2 | 24647-21-0 | 38.3 | −44.1 | 22.4 | −58.7 | −8.92 | −2.90 | 25 | 418 | 77 | 1.17 |
| GBL-C0 | 20825-71-2 | −17.9 | 0.9 | −26.4 | −19.4 | −7.19 | −0.94 | 31 | 437 | 41 | 0.11 |
| GBL-C1a | --- | −29.6 | −27.6 | −7.83 | −2.03 | 30 | 432 | 76 | 0.60 | ||
| GBL-C1b | 1052601-43-0 | −16.6 | −24.8 | −7.31 | −1.12 | 22 | 408 | 61 | 0.88 | ||
| GBL-C2 | --- | 5.8 | −32.9 | −2.6 | −52.1 | −8.29 | −2.44 | 29 | 404 | 103 | 1.42 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tshepelevitsh, S.; Kütt, A.; Leito, I. Theoretical Study on Fluorinated Derivatives of Sulfolane, Cyclopentanone, and Gamma-Butyrolactone. Molecules 2023, 28, 7770. https://doi.org/10.3390/molecules28237770
Tshepelevitsh S, Kütt A, Leito I. Theoretical Study on Fluorinated Derivatives of Sulfolane, Cyclopentanone, and Gamma-Butyrolactone. Molecules. 2023; 28(23):7770. https://doi.org/10.3390/molecules28237770
Chicago/Turabian StyleTshepelevitsh, Sofja, Agnes Kütt, and Ivo Leito. 2023. "Theoretical Study on Fluorinated Derivatives of Sulfolane, Cyclopentanone, and Gamma-Butyrolactone" Molecules 28, no. 23: 7770. https://doi.org/10.3390/molecules28237770
APA StyleTshepelevitsh, S., Kütt, A., & Leito, I. (2023). Theoretical Study on Fluorinated Derivatives of Sulfolane, Cyclopentanone, and Gamma-Butyrolactone. Molecules, 28(23), 7770. https://doi.org/10.3390/molecules28237770