Stability of the Inclusion Complexes of Dodecanoic Acid with α-Cyclodextrin, β-Cyclodextrin and 2-HP-β-Cyclodextrin
Abstract
:1. Introduction
2. Results
3. Discussion
4. Materials and Methods
4.1. Materials
4.2. Characterization Methods
5. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nishimura, T.; Kometani, T.; Nakae, T.; Takii, H.; Okada, S. Cyclic α-1,4-glucan formation by bacterial α-amylases. J. Ferment. Bioeng. 1996, 81, 26–31. [Google Scholar] [CrossRef]
- Avci, A.; Donmez, S. A novel thermophilic anaerobic bacteria producing cyclodextrin glycosyltransferase. Process Biochem. 2009, 44, 36–42. [Google Scholar] [CrossRef]
- Bouchal, F.; Skiba, M.; Chaffai, N.; Hallouard, F.; Fatmi, S.; Lahiani-Skiba, M. Fast dissolving cyclodextrin complex of piroxicam in solid dispersion Part I: Influence of β-CD and HPβ-CD on the dissolution rate of piroxicam. Int. J. Pharm. 2015, 478, 625–632. [Google Scholar] [CrossRef] [PubMed]
- De Sousa, F.B.; Leite Denadai, A.M.; Lula, I.S.; Lopes, J.F.; Dos Santos, H.F.; De Almeida, W.B.; Sinisterra, R.D. Supramolecular complex of fluoxetine with β-cyclodextrin: An experimental and theoretical study. Int. J. Pharm. 2008, 353, 160–169. [Google Scholar] [CrossRef]
- Tafazzoli, M.; Ghiasi, M. Structure and conformation of α-, β-, γ-cyclodextrin in solution: Theoretical approaches and experimental validation. Carboh. Polym. 2009, 78, 10–15. [Google Scholar] [CrossRef]
- Buranaboripan, W.; Lang, W.; Motomura, E.; Sakairi, N. Preparation and characterization of polymeric host molecules, β-cyclodextrin linked chitosan derivatives having different inkers. Int. J. Biol. Macrom. 2014, 69, 27–34. [Google Scholar] [CrossRef]
- Loftsson, T.; Duchene, D. Cyclodextrins and their pharmaceutical applications. Int. J. Pharm. 2007, 329, 1–11. [Google Scholar] [CrossRef]
- Song, L.X.; Bai, L.; Xu, X.M.; He, J.; Pan, S.Z. Inclusion complexation, encapsulation interaction and inclusion number in cyclodextrin chemistry. Coord. Chem. Rev. 2009, 253, 1276–1284. [Google Scholar] [CrossRef]
- Huskamp, H.A. Pharmaceutical cost management and access to psychotropic drugs: The U.S. context. Int. J. Law Psych. 2008, 28, 484–495. [Google Scholar] [CrossRef]
- Thatiparti, T.R.; Shoffstall, A.J.; Recum, H.A. Cyclodextrin-based device coating for affinity-based of antibiotics. Biomaterials 2010, 31, 2335–2347. [Google Scholar] [CrossRef]
- Schloss, P.; Henn, F.A. New insights into the mechanism of antidepressant therapy. Pharm. Ther. 2004, 102, 47–60. [Google Scholar] [CrossRef] [PubMed]
- Moya-Ortega, M.D.; Alvarez-Lorenzo, C.; Sigurdsson, H.H.; Concheiro, A.; Loftsson, T. γ-Cyclodextrin hydrogels and semi-interpenetrating networks for sustained delivery of dexamethanose. Carboh. Polym. 2010, 80, 900–907. [Google Scholar] [CrossRef]
- Misiuk, W.; Govil, J.N. Cyclodextrins, structures, properties useful for treating diseases and revitalizing body systems. In Recent Progress in Medicinal Plants, Drug Plants III; Govil, J.N., Singh, V.K., Eds.; Studium Press LLC: Houston, TX, USA, 2010; Volume 29, pp. 159–181. [Google Scholar]
- Gibson, R.W.; Rice, A.D.; Pickett, J.A.; Smith, M.C.; Sawicki, R.M. The effects of the repellents dodecanoic acid and polygodial on the acquisition of non-, semi- and persistent plant viruses by the aphid Myzus persicae. Ann. Appl. Biol. 1982, 100, 55–59. [Google Scholar] [CrossRef]
- Desgrosseilliers, L.; Whitman, C.A.; Groulx, D.; White, M.A. Dodecanoic acid as a promising phase-change material for thermal energy storage. Appl. Therm. Eng. 2013, 53, 37–41. [Google Scholar] [CrossRef]
- Warren, E.C.; Kramár, P.; Lloyd-Jones, K.; Williams, R.S.B. Decanoic acid stimulates autophagy in D. discoideum. Cells 2021, 10, 2946. [Google Scholar] [CrossRef] [PubMed]
- Kinart, Z.; Tomaš, R. Studies of the Formation of Inclusion Complexes Derivatives of Cinnamon Acid with α-Cyclodextrin in a Wide Range of Temperatures Using Conductometric Methods. Molecules 2022, 27, 4420. [Google Scholar] [CrossRef]
- Kinart, Z. Conductometric Studies of Formation the Inclusion Complexes of Phenolic Acids with β-Cyclodextrin and 2-HP-β-Cyclodextrin in Aqueous Solutions. Molecules 2023, 28, 292. [Google Scholar] [CrossRef]
- Salomon, M.; Hefter, G.T. Mobilities of cation-macrocyclic ligand complexes. Pure App. Chem. 1993, 65, 1533–1540. [Google Scholar] [CrossRef]
- Salomon, M. Conductometric study of cationic and anionic complexes in propylene carbonate. J. Solut. Chem. 1990, 19, 1225–1236. [Google Scholar] [CrossRef]
- Verrall, R.E.; Wilson, L.D.; Siddall, S.R. A spectral displacement study of the binding constants of cyclodextrin–hydrocarbon and –fluorocarbon surfactant inclusion complexes. Can. J. Chem. 1997, 75, 927–933. [Google Scholar]
- Gadre, A.; Rüdiger, V.; Schneider, H.-J.; Connors, K.A. Binding of cyclodextrins to alicyclic and aromatic substrates: Complex formation of α-, β-, and γ-cyclodextrins with substituted cyclohexanecarboxylic acids and phenylalkanoic acids. J. Pharm. Sci. 1997, 86, 236–243. [Google Scholar] [CrossRef] [PubMed]
- Atwood, J.L.; Davies, J.E.D.; MacNicol, D.D. Inclusion Compounds; Academic Press: London, UK, 1984; Volume 3, pp. 391–443. [Google Scholar]
- Laufer, D.A.; Gelb, R.I.; Schwartz, L.M.; Cardelino, B.; Fuhrman, H.S.; Johnson, R.F. Binding mechanisms in cyclohexaamylose complexes. J. Am. Chem. Soc. 1981, 103, 1750–1757. [Google Scholar]
- Skoulika, S.G.; Georgiou, C.A.; Polissiou, M.G. Interaction of β-cyclodextrin with unsaturated and saturated straight chain fatty acid anions studied by phenolphthalein displacement. J. Incl. Phenom. 1999, 34, 85–96. [Google Scholar] [CrossRef]
- Wilson, L.D.; Verrall, R.E. A 1H NMR study of cyclodextrin-Hydrocarbon surfactant inclusion complexes in aqueous solutions. Can. J. Chem. 1998, 76, 25–34. [Google Scholar]
- Boruń, A.; Bald, A. Conductometric Studies of 1-Ethyl-3-methylimidazolium Tetrafluoroborate and 1 Butyl-3-methylimidazolium Tetrafluoroborate in N,N-Dimethylformamide at Temperatures from (283.15 to 318.15) K. J. Chem. Eng. Data 2012, 57, 475–481. [Google Scholar] [CrossRef]
- Boruń, A.; Bald, A. Ionic association and conductance of [emim][BF4] and [bmim][BF4] in 1-butanol in a wide range of temperature. J. Chem. Thermodyn. 2016, 96, 175–180. [Google Scholar] [CrossRef]
- Boruń, A. Conductance and ionic association of selected imidazolium ionic liquids in various solvents: A review. J. Mol. Liq. 2019, 276, 214–224. [Google Scholar] [CrossRef]
- Matejczyk, M.; Swisłocka, R.; Golonko, A.; Lewandowski, W.; Hawrylik, E. Cytotoxic, genotoxic and antimicrobial activity of caffeic and rosmarinic acids and their lithium, sodium and potassium salts as potential anticancer compounds. Adv. Med. Sci. 2018, 63, 14–21. [Google Scholar] [CrossRef]
- Swisłocka, R. Spectroscopic (FT-IR, FT-Raman, UV absorption, 1H and 13C NMR) and theoretical (in B3LYP/6-311++G** level) studies on alkalimetal salts of caffeic acid. Spectrochim. Acta A 2013, 100, 21–30. [Google Scholar] [CrossRef]
- Kinart, Z.; Tomaš, R. Conductivity properties of selected aliphatic monocarboxylic acid anions in water at 298.15 K. Int. J. Electrochem. Sci. 2020, 15, 10007–10027. [Google Scholar] [CrossRef]
- Bešter-Rogač, M.; Neueder, R.; Barthel, J.; Appeblat, A. Conductivity studies on aqueous solutions of stereoisomers of tartaricacids and tartrates. Part III. Acidic tartrates. J. Solut. Chem. 1998, 27, 299–307. [Google Scholar] [CrossRef]
- Barthel, J.; Feuerlein, F.; Neueder, R.; Wachter, R. Calibration of conductance cells at various temperatures. J. Solut. Chem. 1980, 9, 209–219. [Google Scholar] [CrossRef]
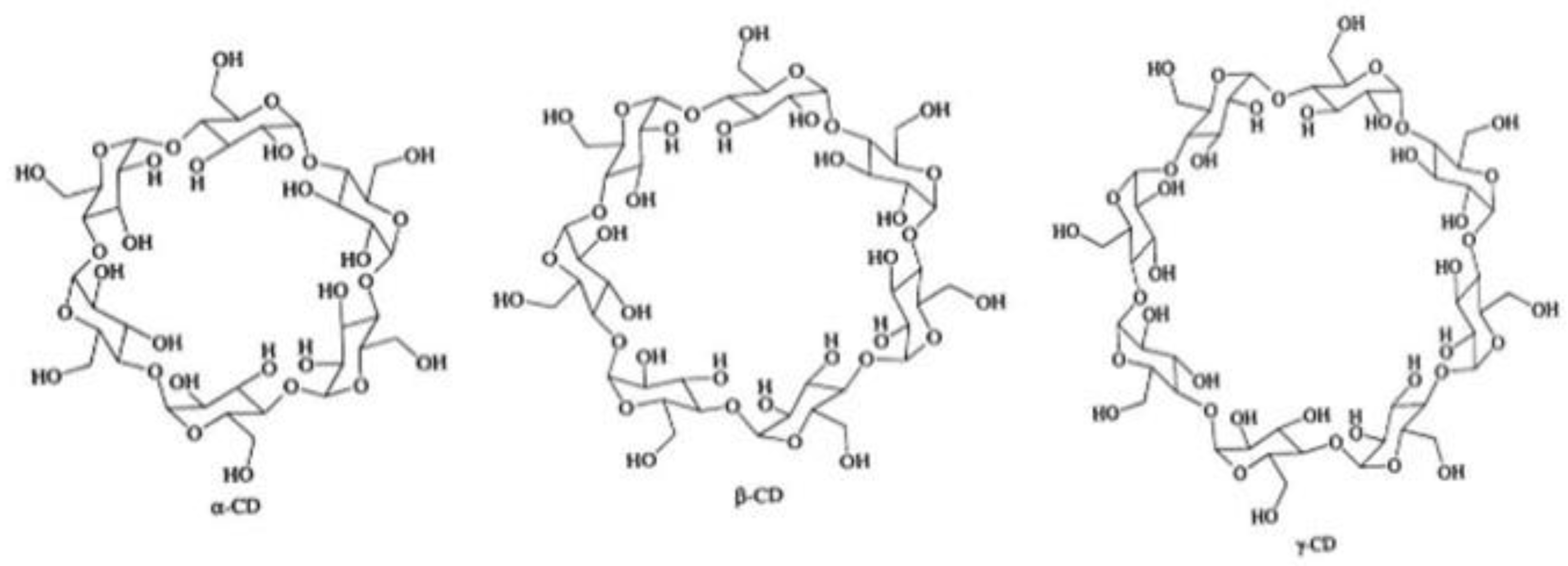
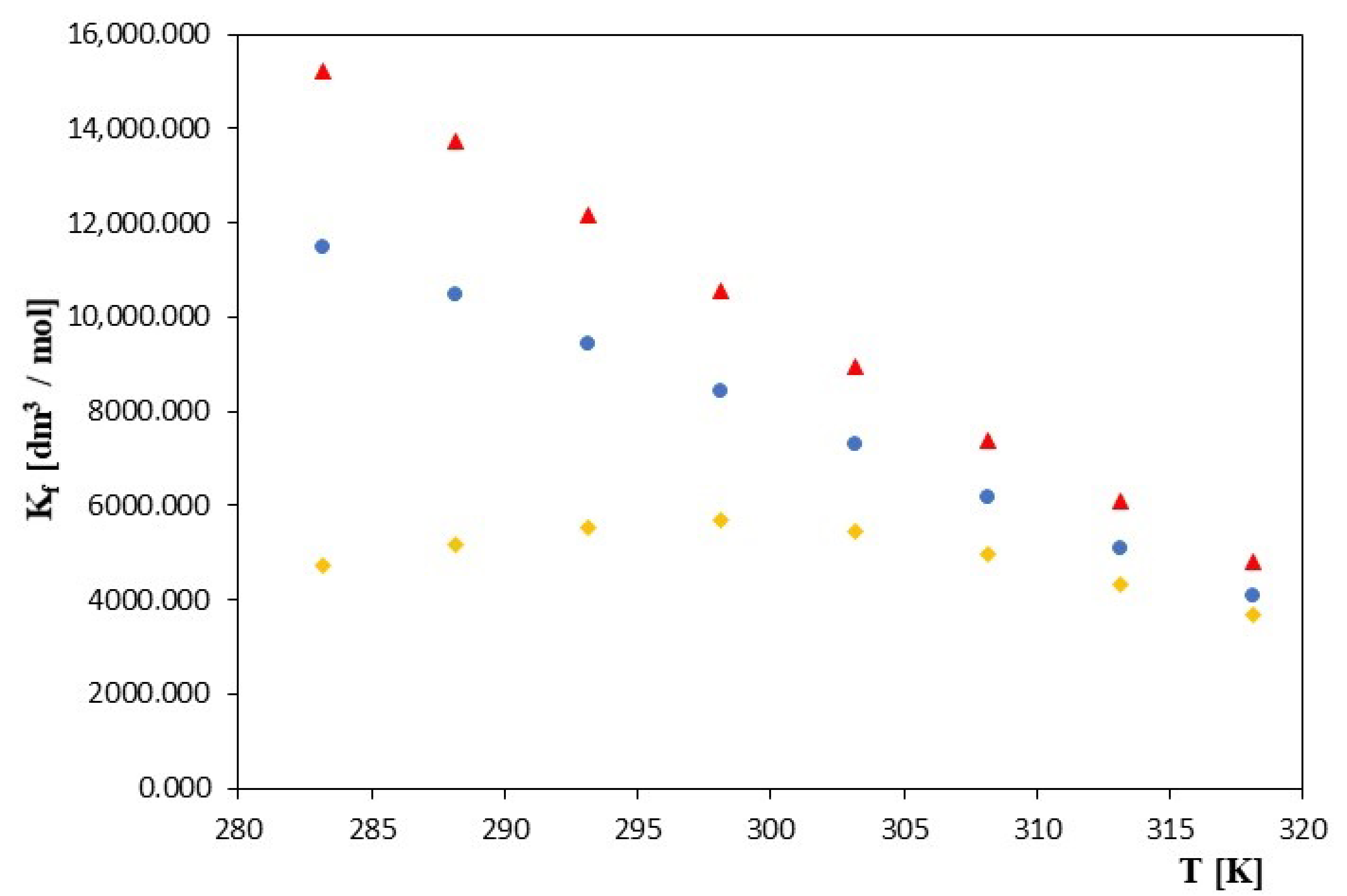
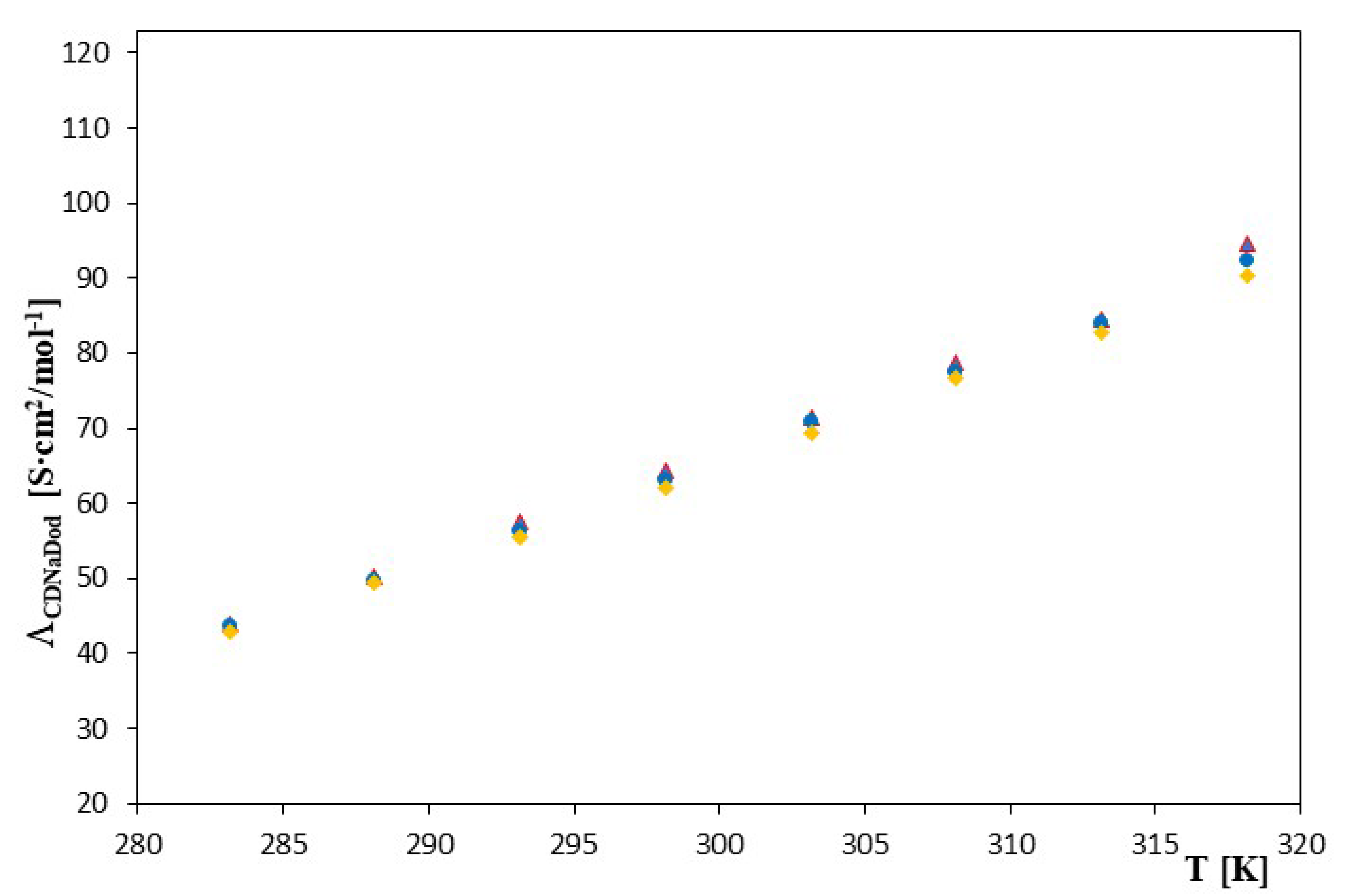


| α-Cyclodextrin | β-Cyclodextrin | |||||||
|---|---|---|---|---|---|---|---|---|
| T [K] | Kf [dm3/mol] | lnKf [dm3/mol] | ΛCDNaDod [S·cm2/mol−1] | σ(Λ) | Kf [dm3/mol] | lnKf [dm3/mol] | ΛCDNaDod [S·cm2/mol−1] | σ(Λ) |
| 283.15 | 15,225 ± 8 | 15,225 | 44.02 ± 0.01 | 0.01 | 11,480 ± 9 | 9.3484 | 43.68 ± 0.02 | 0.01 |
| 288.15 | 13,730 ± 5 | 13,730 | 50.22 ± 0.01 | 0.01 | 10,466 ± 8 | 9.2559 | 49.82 ± 0.01 | 0.01 |
| 293.15 | 12,150 ± 6 | 12,150 | 57.52 ± 0.01 | 0.02 | 9449 ± 6 | 9.1537 | 56.38 ± 0.01 | 0.01 |
| 298.15 | 10,555 ± 3 | 10,555 | 64.31± 0.01 | 0.02 | 8450 ± 4 | 9.0419 | 63.00 ± 0.01 | 0.02 |
| 303.15 | 8940 ± 2 | 8940 | 71.41 ± 0.01 | 0.01 | 7300 ± 2 | 8.8956 | 77.92 ± 0.01 | 0.01 |
| 308.15 | 7385 ± 1 | 7385 | 78.64 ± 0.02 | 0.01 | 6180 ± 1 | 8.7291 | 77.51 ± 0.01 | 0.01 |
| 313.15 | 6110 ± 1 | 6110 | 84.63 ± 0.01 | 0.01 | 5100 ± 1 | 8.5370 | 83.96 ± 0.01 | 0.02 |
| 318.15 | 4825 ± 0.9 | 4825 | 94.74 ± 0.02 | 0.01 | 4085 ± 1 | 8.3151 | 92.25 ± 0.01 | 0.01 |
| 2-HP-β-cyclodextrin | ||||||||
| T [K] | Kf [dm3/mol] | lnKf [dm3/mol] | ΛCDNaDod [S·cm2/mol−1] | σ(Λ) | ||||
| 283.15 | 4719 ± 8 | 8.4594 | 43.01 ± 0.01 | 0.01 | ||||
| 288.15 | 5161 ± 8 | 8.5489 | 49.43 ± 0.01 | 0.01 | ||||
| 293.15 | 5531 ± 7 | 8.6181 | 55.40 ± 0.01 | 0.02 | ||||
| 298.15 | 5697 ± 5 | 8.6477 | 62.03 ± 0.02 | 0.01 | ||||
| 303.15 | 5455 ± 4 | 8.6043 | 69.39 ± 0.01 | 0.01 | ||||
| 308.15 | 4981 ± 2 | 8.5134 | 76.73 ± 0.01 | 0.01 | ||||
| 313.15 | 4335 ± 2 | 8.3745 | 82.87 ± 0.01 | 0.01 | ||||
| 318.15 | 3680 ± 1 | 8.2107 | 90.34 ± 0.01 | 0.02 | ||||
| System | Kf [dm3/mol] |
|---|---|
| βCD–C10 | 8000 ± 20 [26]; 3800 ± 100 [25]; 5100 ± 600 [21] |
| βCD–C8 | 700 ± 290 [26]; 480 ± 50 [25]; 660 ± 80 [21] |
| α-Cyclodextrin | β-Cyclodextrin | |||||
|---|---|---|---|---|---|---|
| T [K] | ∆G0 [J·mol−1] | ∆S0 [J·mol−1K−1] | ∆H0 [J·mol−1] | ∆G0 [J·mol−1] | ∆S0 [J·mol−1‧K−1] | ∆H0 [J·mol−1] |
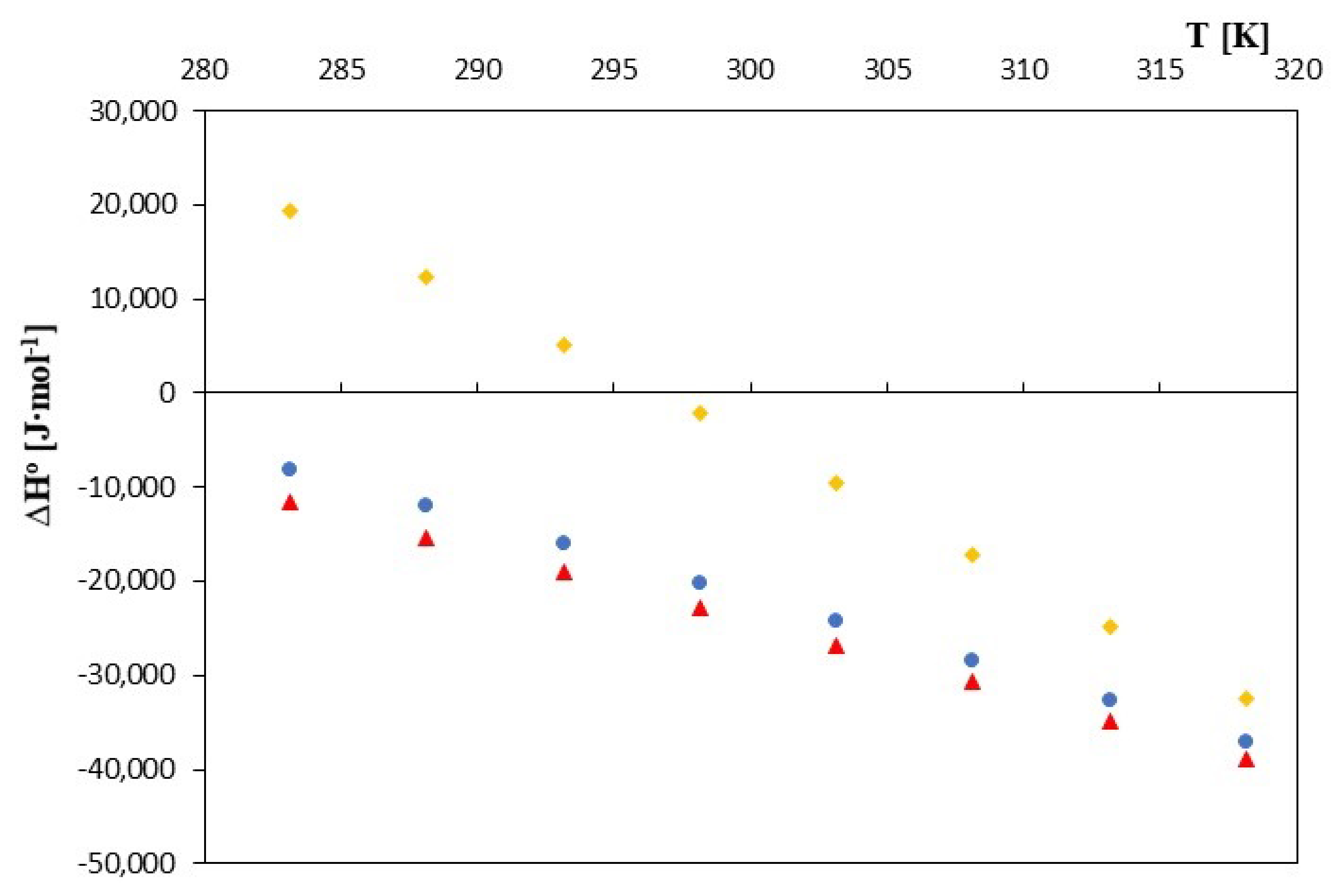
| 283.15 | −22671.705 | 39.072 | −11608.847 | −22007.063 | 48.971 | −8140.868 |
| 288.15 | −22824.446 | 26.116 | −15299.201 | −22174.135 | 35.211 | −12028.028 |
| 293.15 | −22922.534 | 13.160 | −19064.762 | −22309.760 | 21.451 | −16021.341 |
| 298.15 | −22964.660 | 0.204 | −22903.921 | −22413.288 | 7.691 | −20120.157 |
| 303.15 | −22931.233 | −12.752 | −26797.087 | −22420.448 | −6.069 | −24260.205 |
| 308.15 | −22819.898 | −25.708 | −30741.904 | −22363.529 | −19.829 | −28473.774 |
| 313.15 | −22696.739 | −38.664 | −34804.458 | −22226.317 | −33.589 | −32744.650 |
| 318.15 | −22434.583 | −51.620 | −38857.575 | −21994.203 | −47.349 | −37058.223 |
| 2-HP-β-cyclodextrin | ||||||
| T [K] | ∆G0 [J·mol−1] | ∆S0 [J·mol−1‧K−1] | ∆H0 [J·mol−1] | |||
| 283.15 | −19914.238 | 138.450 | 19287.897 | |||
| 288.15 | −20480.387 | 113.812 | 12314.558 | |||
| 293.15 | −21004.515 | 89.174 | 5136.861 | |||
| 298.15 | −21436.072 | 64.536 | −2194.645 | |||
| 303.15 | −21686.153 | 39.898 | −9591.057 | |||
| 308.15 | −21810.947 | 15.260 | −17108.559 | |||
| 313.15 | −21803.194 | −9.378 | −24739.896 | |||
| 318.15 | −21718.031 | −34.016 | −32540.202 | |||
| Chemical Name | Chemical Formula | Chemical Formula | Source | CAS No | Mass Fraction Purity |
|---|---|---|---|---|---|
| Dodecanoic acid (Lauric acid) | C11H21O2 | 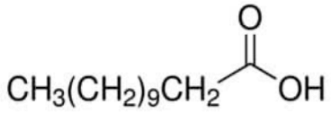 | Merck | 143-07-7 | ≥0.999 |
| α -cyclodextrin | C36H60O30 | 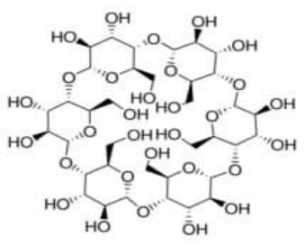 | TCI * | 10016-20-3 | ≥0.998 |
| β -cyclodextrin | C42H70O35 | 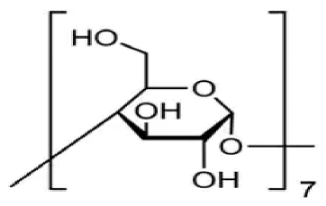 | TCI * | 7585-39-9 | ≥0.998 |
| 2-HP-β-cyclodextrin | C66H112O42 | 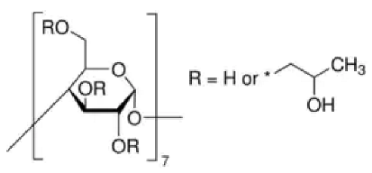 | TCI * | 128446-35-5 | ≥0.998 |
| Sodium hydroxide micropills | NaOH | Avantor | 1310-73-2 | ≥0.998 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kinart, Z. Stability of the Inclusion Complexes of Dodecanoic Acid with α-Cyclodextrin, β-Cyclodextrin and 2-HP-β-Cyclodextrin. Molecules 2023, 28, 3113. https://doi.org/10.3390/molecules28073113
Kinart Z. Stability of the Inclusion Complexes of Dodecanoic Acid with α-Cyclodextrin, β-Cyclodextrin and 2-HP-β-Cyclodextrin. Molecules. 2023; 28(7):3113. https://doi.org/10.3390/molecules28073113
Chicago/Turabian StyleKinart, Zdzisław. 2023. "Stability of the Inclusion Complexes of Dodecanoic Acid with α-Cyclodextrin, β-Cyclodextrin and 2-HP-β-Cyclodextrin" Molecules 28, no. 7: 3113. https://doi.org/10.3390/molecules28073113
APA StyleKinart, Z. (2023). Stability of the Inclusion Complexes of Dodecanoic Acid with α-Cyclodextrin, β-Cyclodextrin and 2-HP-β-Cyclodextrin. Molecules, 28(7), 3113. https://doi.org/10.3390/molecules28073113







