Broadening of the ν2 Raman Band of CH4 by C3H8 and C4H10
Abstract
:1. Introduction
2. Results and Discussion
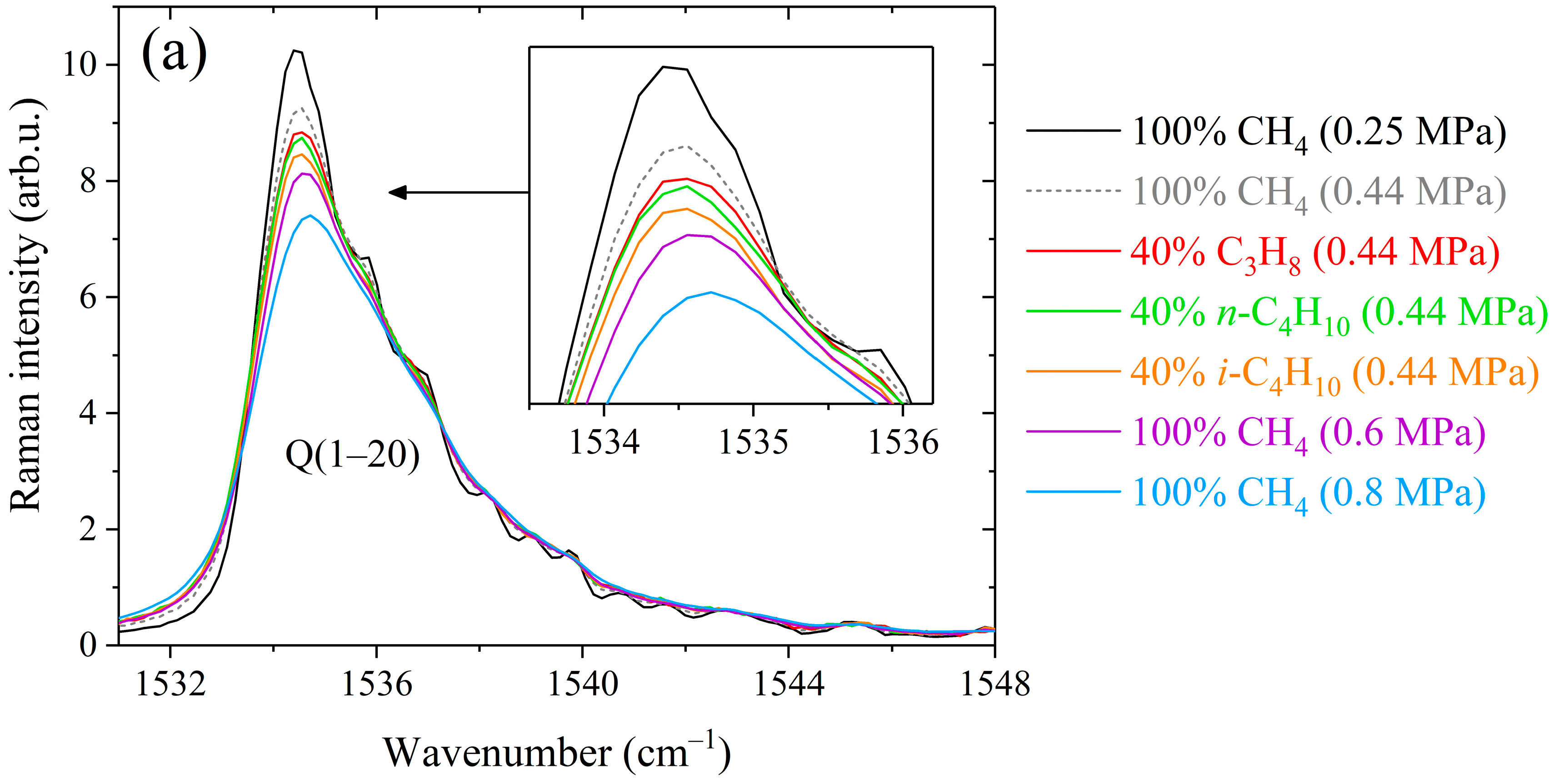
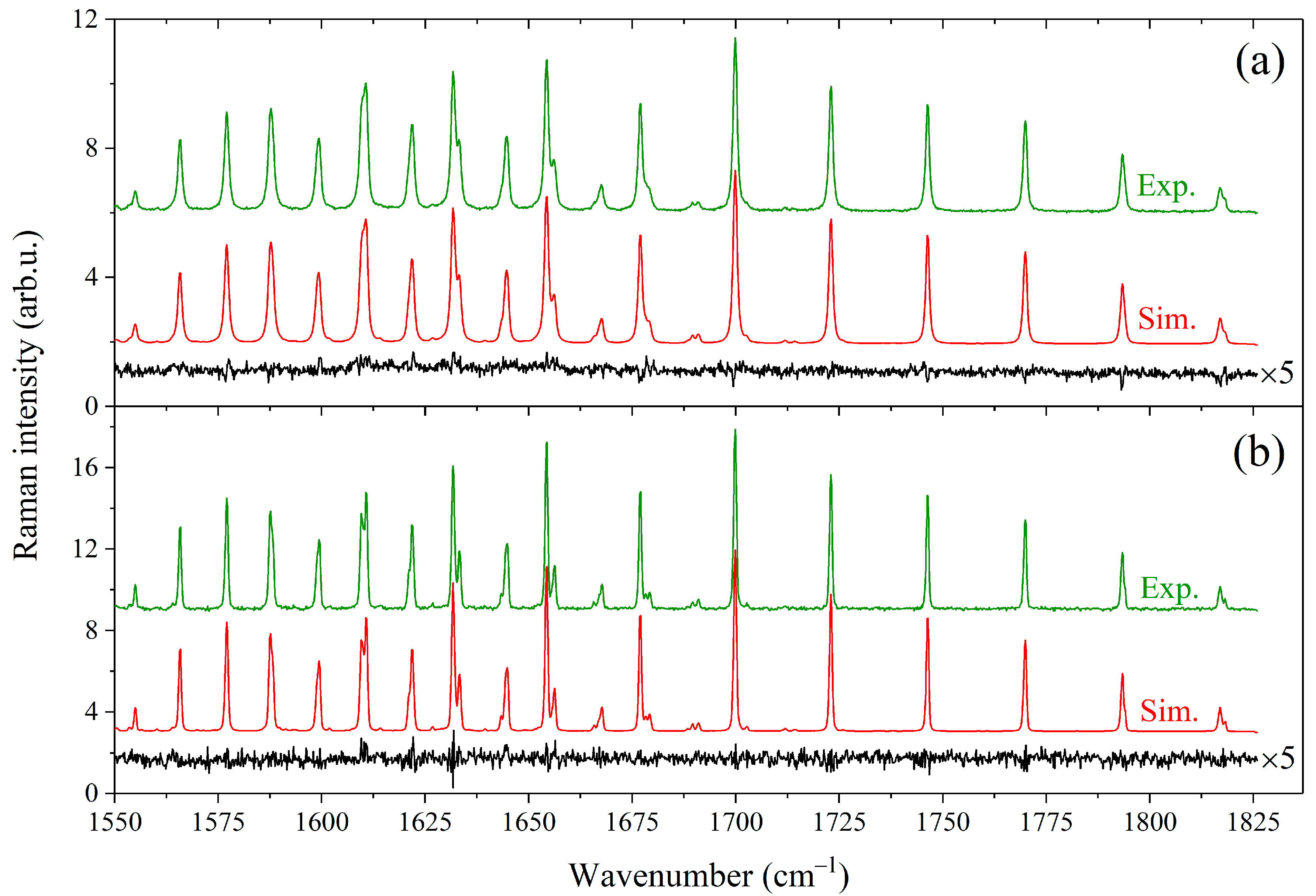
2.1. Methane Lines Broadened by Propane and Butanes
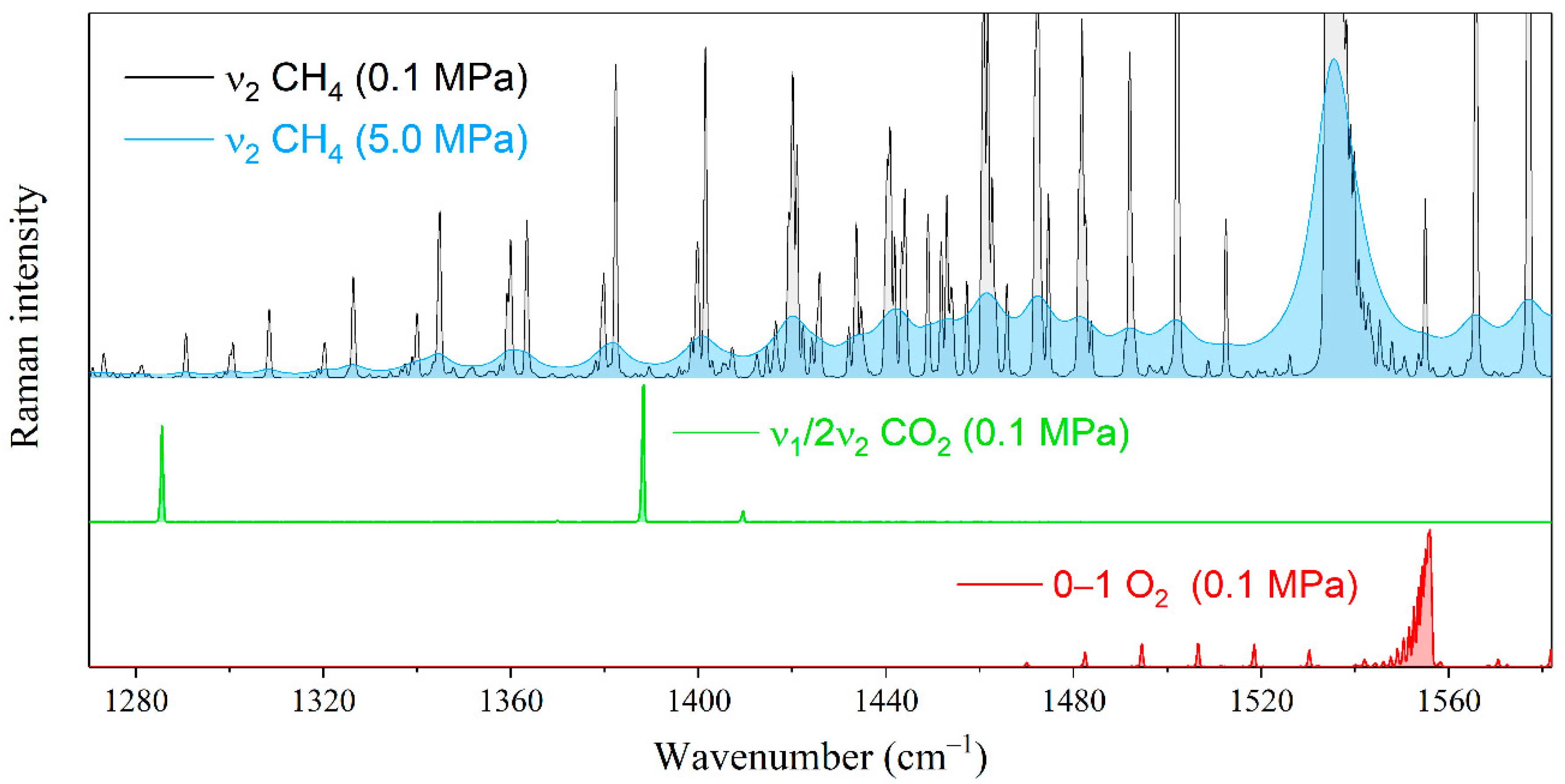
2.2. Evaluation of Broadening Effect by Heavier Alkanes
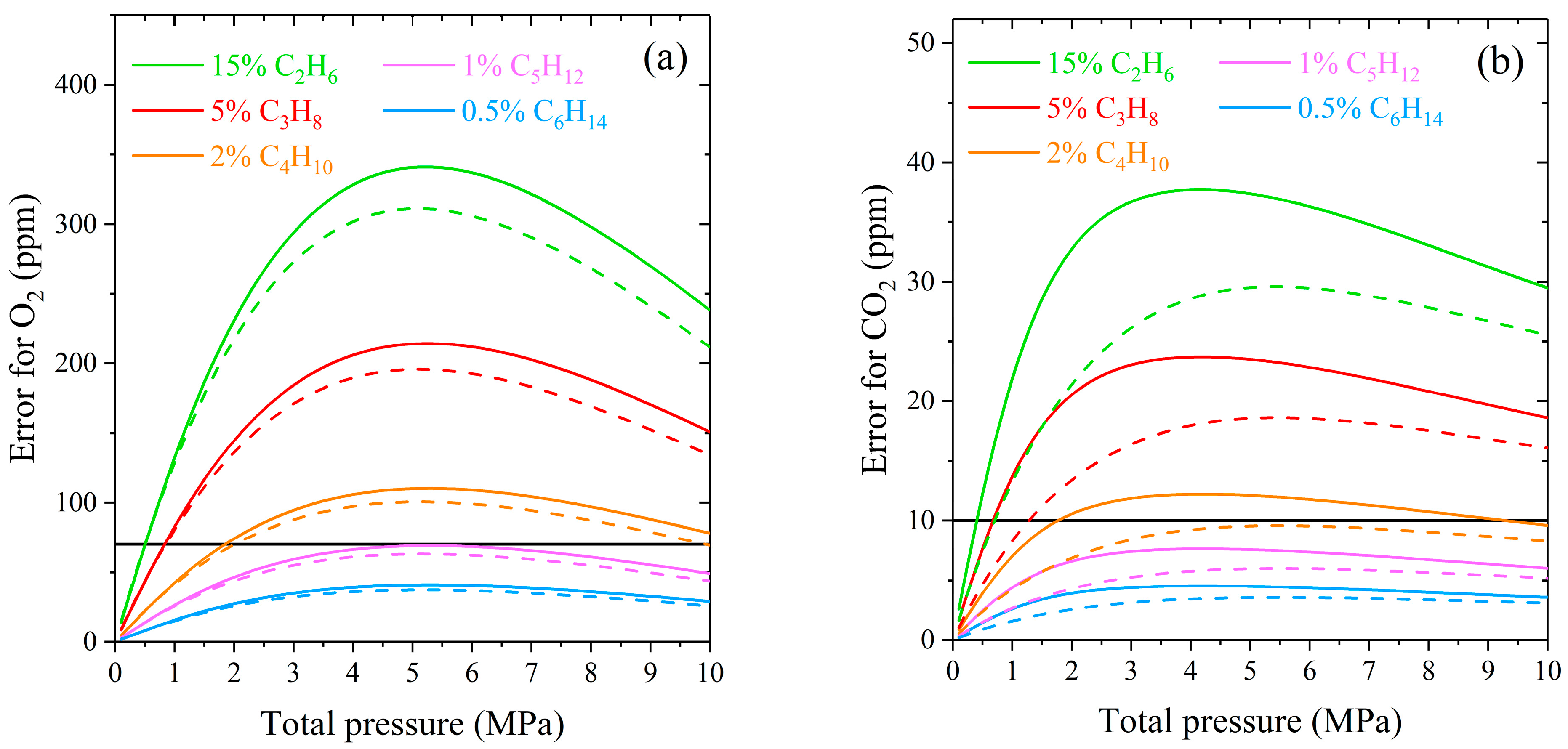
2.3. Influence of Methane Broadening by C2–C6 Alkanes on Measurement Error
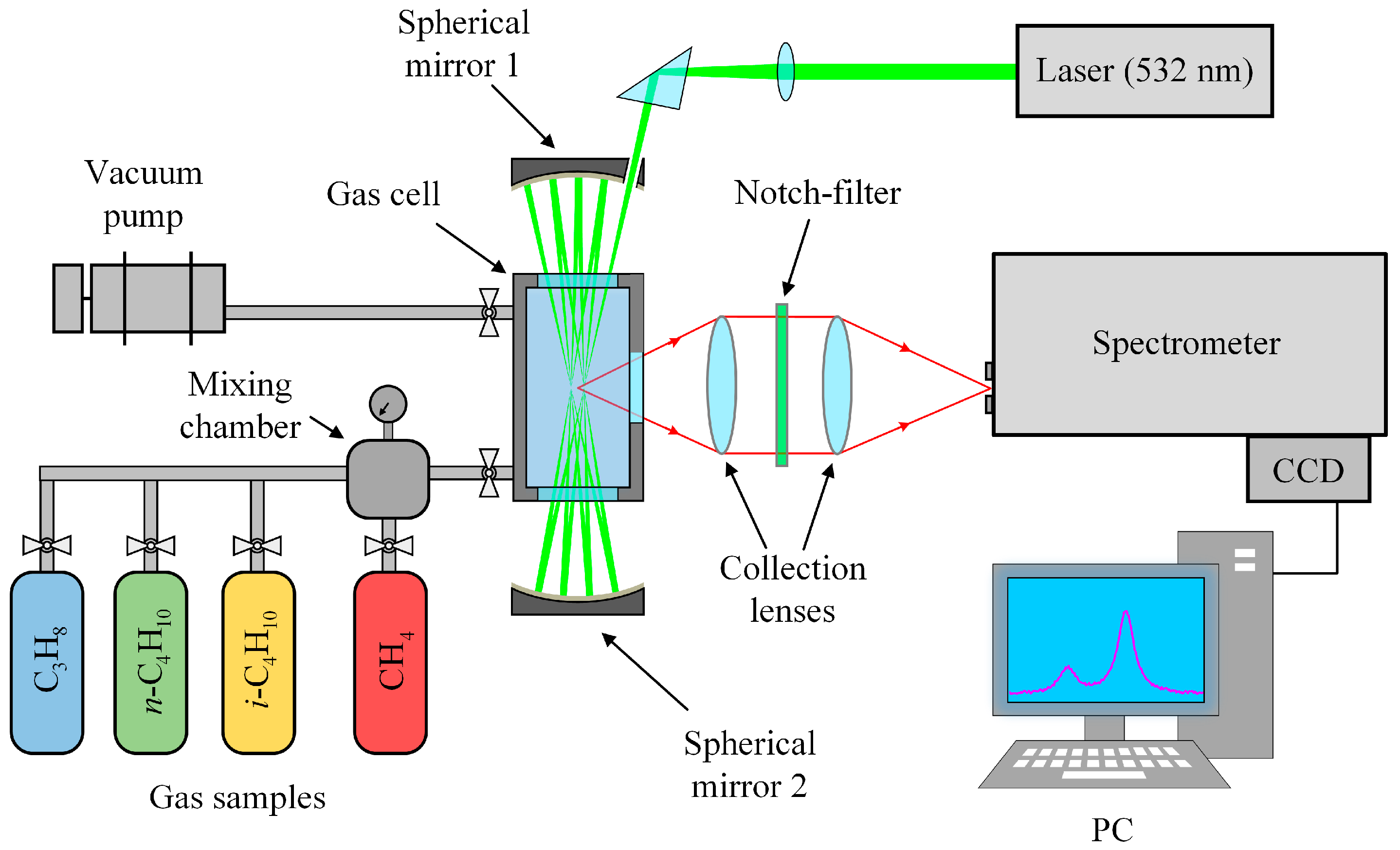
3. Methods
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Kuczyński, S.; Włodek, T.; Smulski, R.; Dąbrowski, K.; Krakowiak, M.; Barbacki, J.; Pawłowski, M. Application of Raman spectroscopy analysis in unconventional natural gas reservoirs—Density and pressure dependence on Raman signal intensity. AGH Drill. Oil Gas 2017, 34, 761–774. [Google Scholar] [CrossRef]
- Sieburg, A.; Knebl, A.; Jacob, J.M.; Frosch, T. Characterization of fuel gases with fiber-enhanced Raman spectroscopy. Anal. Bioanal. Chem. 2019, 411, 7399–7408. [Google Scholar] [CrossRef] [PubMed]
- Han, X.; Huang, Z.X.; Chen, X.D.; Li, Q.F.; Xu, K.X.; Chen, D. On-line multi-component analysis of gases for mud logging industry using data driven Raman spectroscopy. Fuel 2017, 207, 146–153. [Google Scholar] [CrossRef]
- Hippler, M. Cavity-Enhanced Raman Spectroscopy of Natural Gas with Optical Feedback cw-Diode Lasers. Anal. Chem. 2015, 87, 7803–7809. [Google Scholar] [CrossRef]
- Petrov, D.V.; Matrosov, I.I. Raman Gas Analyzer (RGA): Natural Gas Measurements. Appl. Spectrosc. 2016, 70, 1770–1776. [Google Scholar] [CrossRef] [PubMed]
- Petrov, D.V.; Matrosov, I.I.; Tikhomirov, A.A. High-Sensitivity Spontaneous Raman Spectrometer for Gaseous Media. J. Appl. Spectrosc. 2015, 82, 120–124. [Google Scholar] [CrossRef]
- Knebl, A.; Yan, D.; Popp, J.; Frosch, T. Fiber enhanced Raman gas spectroscopy. Trends Anal. Chem. 2018, 103, 230–238. [Google Scholar] [CrossRef]
- Gao, Y.; Dai, L.K.; Zhu, H.D.; Chen, Y.L.; Zhou, L. Quantitative Analysis of Main Components of Natural Gas Based on Raman Spectroscopy. Chin. J. Anal. Chem. 2019, 47, 67–76. [Google Scholar] [CrossRef]
- Buldakov, M.A.; Korolev, B.V.; Matrosov, I.I.; Petrov, D.V.; Tikhomirov, A.A. Raman gas analyzer for determining the composition of natural gas. J. Appl. Spectrosc. 2013, 80, 124–128. [Google Scholar] [CrossRef]
- Hansen, S.B.; Berg, R.W.; Stenby, E.H. High-pressure measuring cell for Raman spectroscopic studies of natural gas. Appl. Spectrosc. 2001, 55, 55–60. [Google Scholar] [CrossRef]
- Dieter, K.; Koschnick, K.; Lill, J.; Magnotti, G.; Weinmann, A.; Dreizler, A.; Geyer, D. Development of a Raman spectrometer for the characterization of gaseous hydrocarbons at high temperatures. J. Quant. Spectrosc. Radiat. Transf. 2022, 277, 107978. [Google Scholar] [CrossRef]
- Guo, J.; Luo, Z.; Liu, Q.; Yang, D.; Dong, H.; Huang, S.; Kong, A.; Wu, L. High-Sensitivity Raman Gas Probe for In Situ Multi-Component Gas Detection. Sensors 2021, 21, 3539. [Google Scholar] [CrossRef]
- Knebl, A.; Domes, C.; Domes, R.; Wolf, S.; Popp, J.; Frosch, T. Hydrogen and C2–C6 Alkane Sensing in Complex Fuel Gas Mixtures with Fiber-Enhanced Raman Spectroscopy. Anal. Chem. 2021, 93, 10546–10552. [Google Scholar] [CrossRef] [PubMed]
- Hanf, S.; Keiner, R.; Yan, D.; Popp, J.; Frosch, T. Fiber-Enhanced Raman Multigas Spectroscopy: A Versatile Tool for Environmental Gas Sensing and Breath Analysis. Anal. Chem. 2014, 86, 5278–5285. [Google Scholar] [CrossRef] [PubMed]
- Petrov, D.V. Features of Measuring Low CO Concentrations in N2-Containing Mixtures at Different Temperatures Using Spontaneous Raman Spectroscopy. Appl. Spectrosc. 2020, 75, 81–86. [Google Scholar] [CrossRef] [PubMed]
- ISO 6974-5:2014; Natural Gas—Determination of Composition and Associated Uncertainty by Gas Chromatography—Part 5: Isothermal Method for Nitrogen, Carbon Dioxide, C1 to C5 Hydrocarbons and C6+ Hydrocarbons. ISO: London, UK, 2014.
- Le, V.H.; Caumon, M.C.; Tarantola, A.; Randi, A.; Robert, P.; Mullis, J. Calibration data for simultaneous determination of P-V-X properties of binary and ternary CO2–CH4–N2 gas mixtures by Raman spectroscopy over 5–600 bar: Application to natural fluid inclusions. Chem. Geol. 2020, 552, 119783. [Google Scholar] [CrossRef]
- Tanichev, A.S.; Petrov, D.V. Pressure broadening in Raman spectra of CH4–N2, CH4–CO2, and CH4–C2H6 gas mixtures. Spectrochim. Acta—Part A Mol. Biomol. Spectrosc. 2023, 291, 122396. [Google Scholar] [CrossRef]
- Seitz, J.C.; Pasteris, J.D. I-Ming Chou Raman spectroscopic characterization of gas mixtures. I. Quantitative composition and pressure determination of CH4, N2, and their mixtures. Am. J. Sci. 1993, 293, 297–321. [Google Scholar] [CrossRef]
- Seitz, J.C.; Pasteris, J.D.; Chou, I.M. Raman spectroscopic characterization of gas mixtures. II. Quantitative composition and pressure determination of the CO2-CH4 system. Am. J. Sci. 1996, 296, 577–600. [Google Scholar] [CrossRef]
- Petrov, D.V.; Matrosov, I.I.; Zaripov, A.R.; Maznoy, A.S. Effects of pressure and composition on Raman spectra of CO-H2-CO2-CH4 mixtures. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2019, 215, 363–370. [Google Scholar] [CrossRef]
- Petrov, D.V. Pressure dependence of peak positions, half widths, and peak intensities of methane Raman bands (ν2, 2ν4, ν1, ν3, and 2ν2). J. Raman Spectrosc. 2017, 48, 1426–1430. [Google Scholar] [CrossRef]
- Sublett, D.M.; Sendula, E.; Lamadrid, H.; Steele-MacInnis, M.; Spiekermann, G.; Burruss, R.C.; Bodnar, R.J. Shift in the Raman symmetric stretching band of N2, CO2, and CH4 as a function of temperature, pressure, and density. J. Raman Spectrosc. 2020, 51, 555–568. [Google Scholar] [CrossRef]
- Petrov, D.V.; Matrosov, I.I.; Zaripov, A.R.; Tanichev, A.S. Raman Natural Gas Analyzer: Effects of Composition on Measurement Precision. Sensors 2022, 22, 3492. [Google Scholar] [CrossRef]
- Petrov, D.V.; Matrosov, I.I.; Zaripov, A.R.; Maznoy, A.S. Application of Raman Spectroscopy for Determination of Syngas Composition. Appl. Spectrosc. 2020, 74, 948–953. [Google Scholar] [CrossRef] [PubMed]
- Wenger, C.; Champion, J.P. Spherical Top Data System (STDS) software for the simulation of spherical top spectra. J. Quant. Spectrosc. Radiat. Transf. 1998, 59, 471–480. [Google Scholar] [CrossRef]
- Wenger, C.; Boudon, V.; Rotger, M.; Sanzharov, M.; Champion, J.P. XTDS and SPVIEW: Graphical tools for the analysis and simulation of high-resolution molecular spectra. J. Mol. Spectrosc. 2008, 251, 102–113. [Google Scholar] [CrossRef]
- Gabard, T.; Champion, J.P. Calculation of collision induced energy transfer rates in tetrahedral molecules. Application to 12CH4 perturbed by argon. J. Quant. Spectrosc. Radiat. Transf. 1994, 52, 303–317. [Google Scholar] [CrossRef]
- Jourdanneau, E.; Gabard, T.; Chaussard, F.; Saint-Loup, R.; Berger, H.; Bertseva, E.; Grisch, F. CARS methane spectra: Experiments and simulations for temperature diagnostic purposes. J. Mol. Spectrosc. 2007, 246, 167–179. [Google Scholar] [CrossRef]
- Jourdanneau, E.; Chaussard, F.; Saint-Loup, R.; Gabard, T.; Berger, H. The methane Raman spectrum from 1200 to 5500 cm−1: A first step toward temperature diagnostic using methane as a probe molecule in combustion systems. J. Mol. Spectrosc. 2005, 233, 219–230. [Google Scholar] [CrossRef]
- Butterworth, T.D.; Amyay, B.; Bekerom, D.V.D.; Steeg, A.V.D.; Minea, T.; Gatti, N.; Ong, Q.; Richard, C.; van Kruijsdijk, C.; Smits, J.T.; et al. Quantifying methane vibrational and rotational temperature with Raman scattering. J. Quant. Spectrosc. Radiat. Transf. 2019, 236, 106562. [Google Scholar] [CrossRef]
- Pieroni, D.; Hartmann, J.M.; Chaussard, F.; Michaut, X.; Gabard, T.; Saint-Loup, R.; Berger, H.; Champion, J.P. Experimental and theoretical study of line mixing in methane spectra. III. The Q branch of the Raman ν1 band. J. Chem. Phys. 2000, 112, 1335–1343. [Google Scholar] [CrossRef]
- Pieroni, D.; Nguyen-Van-Thanh; Brodbeck, C.; Hartmann, J.M.; Gabard, T.; Champion, J.P.; Bermejo, D.; Domenech, J.L.; Claveau, C.; Valentin, A.; et al. Experimental and theoretical study of line mixing in methane spectra. II. Influence of the collision partner (He and Ar) in the ν3 IR band. J. Chem. Phys. 1999, 111, 6850–6863. [Google Scholar] [CrossRef]
- Pieroni, D.; Nguyen-Van-Thanh; Brodbeck, C.; Claveau, C.; Valentin, A.; Hartmann, J.M.; Gabard, T.; Champion, J.P.; Bermejo, D.; Domenech, J.L. Experimental and theoretical study of line mixing in methane spectra. I. The N2-broadened ν3 band at room temperature. J. Chem. Phys. 1999, 110, 7717–7732. [Google Scholar] [CrossRef] [Green Version]
- Pieroni, D.; Nguyen-Van-Thanh; Brodbeck, C.; Claveau, C.; Valentin, A.; Hartmann, J.M.; Gabard, T.; Champion, J.P.; Bermejo, D.; Domenech, J.L. Experimental and theoretical study of line mixing in methane spectra. IV. Influence of the temperature and of the band. J. Chem. Phys. 2000, 113, 5776–5783. [Google Scholar] [CrossRef] [Green Version]
- Tran, H.; Flaud, P.M.; Gabard, T.; Hase, F.; von Clarmann, T.; Camy-Peyret, C.; Payan, S.; Hartmann, J.M. Model, software and database for line-mixing effects in the ν3 and ν4 bands of CH4 and tests using laboratory and planetary measurements-I: N2 (and air) broadenings and the earth atmosphere. J. Quant. Spectrosc. Radiat. Transf. 2006, 101, 284–305. [Google Scholar] [CrossRef]
- Tran, H.; Flaud, P.M.; Fouchet, T.; Gabard, T.; Hartmann, J.M. Model, software and database for line-mixing effects in the ν3 and ν4 bands of CH4 and tests using laboratory and planetary measurements-II: H2 (and He) broadening and the atmospheres of Jupiter and Saturn. J. Quant. Spectrosc. Radiat. Transf. 2006, 101, 306–324. [Google Scholar] [CrossRef]
- Pine, A.S.; Gabard, T. Multispectrum fits for line mixing in the ν3 band Q branch of methane. J. Mol. Spectrosc. 2003, 217, 105–114. [Google Scholar] [CrossRef]
- Pine, A.S. Speed-dependent line mixing in the ν3 band Q branch of methane. J. Quant. Spectrosc. Radiat. Transf. 2019, 224, 62–77. [Google Scholar] [CrossRef]
- Smith, M.A.H.; Benner, D.C.; Predoi-Cross, A.; Malathy Devi, V. Air- and self-broadened half widths, pressure-induced shifts, and line mixing in the ν2 band of 12CH4. J. Quant. Spectrosc. Radiat. Transf. 2014, 133, 217–234. [Google Scholar] [CrossRef]
- Ballard, J.; Johnston, W.B. Self-broadened widths and absolute strengths of 12CH4 lines in the 1310–1370 cm−1 region. J. Quant. Spectrosc. Radiat. Transf. 1986, 36, 365–371. [Google Scholar] [CrossRef]
- Smith, M.A.H.; Chris Benner, D.; Predoi-Cross, A.; Malathy Devi, V. Multispectrum analysis of 12CH4 in the ν4 spectral region: II. Self-broadened half widths, pressure-induced shifts, temperature dependences and line mixing. J. Quant. Spectrosc. Radiat. Transf. 2010, 111, 1152–1166. [Google Scholar] [CrossRef]
- Tanichev, A.S.; Petrov, D.V. Simulation of ν2 Raman band of methane as a function of pressure. J. Raman Spectrosc. 2022, 53, 654–663. [Google Scholar] [CrossRef]
- Millot, G.; Lavorel, B.; Steinfeld, J.I. Collisional broadening, line shifting, and line mixing in the stimulated Raman 2ν2 Q branch of CH4. J. Chem. Phys. 1991, 95, 7938–7946. [Google Scholar] [CrossRef]
- Es-Sebbar, E.T.; Farooq, A. Intensities, broadening and narrowing parameters in the ν3 band of methane. J. Quant. Spectrosc. Radiat. Transf. 2014, 149, 241–252. [Google Scholar] [CrossRef] [Green Version]
- Le, T.; Fissiaux, L.; Lepère, M.; Tran, H. Isolated line shape of methane with various collision partners. J. Quant. Spectrosc. Radiat. Transf. 2016, 185, 27–36. [Google Scholar] [CrossRef]
- Varanasi, P.; Giver, L.P.; Valero, F.P.J. Thermal infrared lines of methane broadened by nitrogen at low temperatures. J. Quant. Spectrosc. Radiat. Transf. 1983, 30, 481–490. [Google Scholar] [CrossRef]
- Varanasi, P.; Chudamani, S. Measurements of collision-broadened line widths in the 7.66-μm band of 12CH4 at temperatures relevant to the atmosphere. J. Geophys. Res. 1989, 94, 73–78. [Google Scholar] [CrossRef]
- Martin, B.; Lepère, M. O2- and air-broadening coefficients in the ν4 band of 12CH4 at room temperature. J. Mol. Spectrosc. 2009, 255, 6–12. [Google Scholar] [CrossRef]
- Pine, A.S. Self-, N2, O2, H2, Ar, and He broadening in the v3 band Q branch of CH4. J. Chem. Phys. 1992, 97, 773–785. [Google Scholar] [CrossRef]
- Manne, J.; Bui, T.Q.; Webster, C.R. Determination of foreign broadening coefficients for Methane Lines Targeted by the Tunable Laser Spectrometer (TLS) on the Mars Curiosity Rover. J. Quant. Spectrosc. Radiat. Transf. 2017, 191, 59–66. [Google Scholar] [CrossRef]
- Fissiaux, L.; Delière, Q.; Blanquet, G.; Robert, S.; Vandaele, A.C.; Lepère, M. CO2-broadening coefficients in the ν4 fundamental band of methane at room temperature and application to CO2-rich planetary atmospheres. J. Mol. Spectrosc. 2014, 297, 35–40. [Google Scholar] [CrossRef]
- Vispoel, B.; Fissiaux, L.; Lepère, M. CO2-broadening coefficients in the ν3 fundamental band of methane. J. Mol. Spectrosc. 2019, 360, 1–6. [Google Scholar] [CrossRef]
- Grigoriev, I.M.; Filippov, N.N.; Tonkov, M.V.; Gabard, T.; Doucen, R. Le Estimation of line parameters under line mixing effects: The v3 band of CH4 in helium. J. Quant. Spectrosc. Radiat. Transf. 2001, 69, 189–204. [Google Scholar] [CrossRef]
- Dufour, G.; Hurtmans, D.; Henry, A.; Valentin, A.; Lepère, M. Line profile study from diode laser spectroscopy in the 12CH4 2v3 band perturbed by N2, O2, Ar, and He. J. Mol. Spectrosc. 2003, 221, 80–92. [Google Scholar] [CrossRef]
- Rinsland, C.P.; Devi, V.M.; Smith, M.A.H.; Benner, D.C. Measurements of argon broadened Lorentz width and pressure-induced line shift coefficients in the ν4 band of 12CH4. Appl. Opt. 1989, 28, 2111. [Google Scholar] [CrossRef] [PubMed]
- Zéninari, V.; Parvitte, B.; Courtois, D.; Kapitanov, V.A.; Ponomarev, Y.N. Measurements of air and noble-gas broadening and shift coefficients of the methane R3 triplet of the 2v3 band. Appl. Phys. B Lasers Opt. 2001, 72, 953–959. [Google Scholar] [CrossRef]
- Varanasi, P. Collision-broadened half-widths and shapes of methane lines. J. Quant. Spectrosc. Radiat. Transf. 1971, 11, 1711–1724. [Google Scholar] [CrossRef]
- Varanasi, P.; Tejwani, G.D.T. Experimental and theoretical studies on collision-broadened lines in the v4-fundamental of methane. J. Quant. Spectrosc. Radiat. Transf. 1972, 12, 849–855. [Google Scholar] [CrossRef]
- Margolis, J.S. Hydrogen and helium broadening and pressure induced line shifts of 13CH4 in the ν4 band. J. Quant. Spectrosc. Radiat. Transf. 1996, 55, 823–836. [Google Scholar] [CrossRef]
- Varanasi, P.; Chudamani, S. The temperature dependence of lineshifts, linewidths and line intensities of methane at low temperatures. J. Quant. Spectrosc. Radiat. Transf. 1990, 43, 1–11. [Google Scholar] [CrossRef]
- Nikitin, A.V.; Mikhailenko, S.; Morino, I.; Yokota, T.; Kumazawa, R.; Watanabe, T. Isotopic substitution shifts in methane and vibrational band assignment in the 5560–6200 cm−1 region. J. Quant. Spectrosc. Radiat. Transf. 2009, 110, 964–973. [Google Scholar] [CrossRef]
- Albert, S.; Bauerecker, S.; Boudon, V.; Brown, L.R.; Champion, J.P.; Loëte, M.; Nikitin, A.; Quack, M. Global analysis of the high resolution infrared spectrum of methane 12CH4 in the region from 0 to 4800 cm−1. Chem. Phys. 2009, 356, 131–146. [Google Scholar] [CrossRef]
- Berger, H. Simultaneous study of the vibrational bands ν2 and ν4 of spherical tops, using the irreducible tensors of O3. J. Mol. Spectrosc. 1975, 55, 48–55. [Google Scholar] [CrossRef]
- Feldman, T.; Romanko, J.; Welsh, H.L. The v2 Raman Band of Methane. Can. J. Phys. 1955, 33, 138–145. [Google Scholar] [CrossRef]
- Gray, D.L.; Robiette, A.G. Simultaneous analysis of the v2 and v4 bands of methane. Mol. Phys. 1976, 32, 1609–1625. [Google Scholar] [CrossRef]
- Ba, Y.A.; Wenger, C.; Surleau, R.; Boudon, V.; Rotger, M.; Daumont, L.; Bonhommeau, D.A.; Tyuterev, V.G.; Dubernet, M.L. MeCaSDa and ECaSDa: Methane and ethene calculated spectroscopic databases for the virtual atomic and molecular data centre. J. Quant. Spectrosc. Radiat. Transf. 2013, 130, 62–68. [Google Scholar] [CrossRef]
- Devi, V.M.; Benner, D.C.; Gamache, R.R.; Tran, H.; Smith, M.A.H.; Sams, R.L. Multispectrum analysis of air-broadened spectra in the ν3 Q branch of 12CH4. J. Quant. Spectrosc. Radiat. Transf. 2018, 206, 409–429. [Google Scholar] [CrossRef]
- Brown, L.R.; Benner, D.C.; Champion, J.P.; Devi, V.M.; Fejard, L.; Gamache, R.R.; Gabard, T.; Hilico, J.C.; Lavorel, B.; Loete, M.; et al. Methane line parameters in HITRAN. J. Quant. Spectrosc. Radiat. Transf. 2003, 82, 219–238. [Google Scholar] [CrossRef]
- Yurchenko, S.N.; Tennyson, J. ExoMol line lists-IV. The rotation-vibration spectrum of methane up to 1500 K. Mon. Not. R. Astron. Soc. 2014, 440, 1649–1661. [Google Scholar] [CrossRef] [Green Version]
- Gabard, T.; Boudon, V. Line broadening coefficient calculations for methane perturbed by nitrogen. J. Quant. Spectrosc. Radiat. Transf. 2010, 111, 1328–1343. [Google Scholar] [CrossRef] [Green Version]
- Leavitt, R.P. Pressure broadening and shifting in microwave and infrared spectra of molecules of arbitrary symmetry: An irreducible tensor approach. J. Chem. Phys. 1980, 73, 5432–5450. [Google Scholar] [CrossRef]
- Zameroski, N.D.; Hager, G.D.; Rudolph, W.; Erickson, C.J.; Hostutler, D.A. Pressure broadening and collisional shift of the Rb D2 absorption line by CH4, C2H6, C3H8, n-C4H10, and He. J. Quant. Spectrosc. Radiat. Transf. 2011, 112, 59–67. [Google Scholar] [CrossRef]
- Yamano, D.; Sakamoto, Y.; Yabushita, A.; Kawasaki, M.; Morino, I.; Inoue, G. Buffer-gas pressure broadening for the 2ν3 band of methane measured with continuous-wave cavity ring-down spectroscopy. Appl. Phys. B Lasers Opt. 2009, 97, 523–528. [Google Scholar] [CrossRef]
- Lübken, F.J.; Eng, R.; Karecki, D.R.; Mackay, G.I.; Nadler, S.; Schiff, H.I. The effect of water vapour broadening on methane eddy correlation flux measurements. J. Atmos. Chem. 1991, 13, 97–108. [Google Scholar] [CrossRef]
- Benner, C.D.; Devi, M.V.; Smith, M.A.H.; Rinsland, C.P. Air-, N2-, and O2-broadening and shift coefficients in the ν3 spectral region of 12CH4. J. Quant. Spectrosc. Radiat. Transf. 1993, 50, 65–89. [Google Scholar] [CrossRef]
- Rinsland, C.P.; Devi, V.M.; Smith, M.A.H.; Benner, D.C. Measurements of air-broadened and nitrogen-broadened Lorentz width coefficients and pressure shift coefficients in the ν4 and ν2 bands of 12CH4. Appl. Opt. 1988, 27, 631–651. [Google Scholar] [CrossRef]
- Gharib-Nezhad, E.; Heays, A.N.; Bechtel, H.A.; Lyons, J.R. H2-induced pressure broadening and pressure shift in the P-branch of the ν3 band of CH4 from 300 to 655 K. J. Quant. Spectrosc. Radiat. Transf. 2019, 239, 106649. [Google Scholar] [CrossRef] [Green Version]
- Gussoni, M.; Rui, M.; Zerbi, G. Electronic and relaxation contribution to linear molecular polarizability. An analysis of the experimental values. J. Mol. Struct. 1998, 447, 163–215. [Google Scholar] [CrossRef]
- Gordon, I.E.; Rothman, L.S.; Hill, C.; Kochanov, R.V.; Tan, Y.; Bernath, P.F.; Birk, M.; Boudon, V.; Campargue, A.; Chance, K.V.; et al. The HITRAN2016 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2017, 203, 3–69. [Google Scholar] [CrossRef]
- Delahaye, T.; Landsheere, X.; Pangui, E.; Huet, F.; Hartmann, J.M.; Tran, H. Measurements of H2O broadening coefficients of infrared methane lines. J. Quant. Spectrosc. Radiat. Transf. 2016, 173, 40–48. [Google Scholar] [CrossRef]
- ISO 6974-3:2000; Natural Gas—Determination of Composition with Defined Uncertainty by Gas Chromatography—Part 3: Determination of Hydrogen, Helium, Oxygen, Nitrogen, Carbon Dioxide and Hydrocarbons up to C8 Using Two Packed Columns. ISO: London, UK, 2014.
- ISO 6974-6:2002; Natural Gas—Determination of Composition with Defined Uncertainty by Gas Chromatography—Part 6: Determination of Hydrogen, Helium, Oxygen, Nitrogen, Carbon Dioxide and C1 to C8 Hydrocarbons Using Three Capillary Columns. ISO: London, UK, 2014.
- Petrov, D.V. Multipass optical system for a Raman gas spectrometer. Appl. Opt. 2016, 55, 9521. [Google Scholar] [CrossRef] [PubMed]
- Kojima, J.; Nguyen, Q.V. Quantitative analysis of spectral interference of spontaneous Raman scattering in high-pressure fuel-rich H2-air combustion. J. Quant. Spectrosc. Radiat. Transf. 2005, 94, 439–466. [Google Scholar] [CrossRef] [Green Version]
- Lii, J.H.; Allinger, N.L. Molecular Mechanics. The MM3 Force Field for Hydrocarbons. 2. Vibrational Frequencies and Thermodynamics. J. Am. Chem. Soc. 1989, 111, 8566–8575. [Google Scholar] [CrossRef]


| J″ | R Branch | S Branch | ||||||
|---|---|---|---|---|---|---|---|---|
| γ(CH4) | γ(C3H8) | γ(n-C4H10) | γ(i-C4H10) | γ(CH4) | γ(C3H8) | γ(n-C4H10) | γ(i-C4H10) | |
| 0 | – | – | – | – | 81 ± 5 | 110 ± 10 | 114 ± 10 | 122 ± 11 |
| 1 | 77 ± 3 | 105 ± 7 | 108 ± 7 | 116 ± 7 | 82 ± 2 | 109 ± 5 | 113 ± 5 | 117 ± 5 |
| 2 | 71 ± 3 | 97 ± 7 | 100 ± 7 | 107 ± 7 | 79 ± 2 | 108 ± 6 | 116 ± 6 | 118 ± 6 |
| 3 | 78 ± 1 | 104 ± 3 | 108 ± 3 | 112 ± 3 | 76 ± 1 | 104 ± 3 | 110 ± 3 | 111 ± 3 |
| 4 | 71 ± 2 | 94 ± 4 | 98 ± 4 | 101 ± 4 | 74 ± 1 | 101 ± 2 | 104 ± 2 | 110 ± 3 |
| 5 | 74 ± 2 | 100 ± 5 | 108 ± 5 | 110 ± 5 | 68 ± 1 | 93 ± 3 | 97 ± 3 | 101 ± 3 |
| 6 | 65 ± 1 | 88 ± 4 | 94 ± 4 | 96 ± 4 | 63 ± 1 | 87 ± 2 | 96 ± 2 | 97 ± 2 |
| 7 | 66 ± 1 | 91 ± 3 | 96 ± 3 | 97 ± 3 | 63 ± 1 | 88 ± 2 | 93 ± 2 | 92 ± 2 |
| 8 | 60 ± 2 | 83 ± 4 | 87 ± 4 | 88 ± 4 | 58 ± 1 | 81 ± 2 | 85 ± 2 | 85 ± 2 |
| 9 | 52 ± 2 | 72 ± 3 | 74 ± 3 | 78 ± 3 | 53 ± 1 | 75 ± 3 | 80 ± 3 | 84 ± 3 |
| 10 | 61 ± 3 | 83 ± 5 | 86 ± 5 | 91 ± 5 | 52 ± 2 | 75 ± 4 | 80 ± 4 | 83 ± 4 |
| 11 | 59 ± 4 | 81 ± 7 | 84 ± 7 | 87 ± 7 | 52 ± 4 | 74 ± 7 | 80 ± 8 | 83 ± 8 |
| 12 | 54 ± 6 | 74 ± 9 | 77 ± 10 | 80 ± 10 | – | – | – | – |
| 13 | 45 ± 6 | 63 ± 9 | 69 ± 10 | 70 ± 10 | – | – | – | – |
| Component | α, 10−3 nm3 | References | ||
|---|---|---|---|---|
| Estimated | Measured | |||
| CH4 | 2.448 | 1.00 | 1.00 | – |
| C2H6 | 4.226 | 1.18 | 1.20 | [18] |
| C3H8 | 5.921 | 1.32 | 1.38 | This work |
| n-C4H10 | 8.020 | 1.48 | 1.45 | This work |
| i-C4H10 | 8.009 | 1.48 | 1.50 | This work |
| C5H12 | 9.879 | 1.60 | – | – |
| C6H14 | 11.630 | 1.71 | – | – |
| N2 | 1.710 | 0.77 | 0.75 | [39,46,48,50,74,75,76,77] |
| O2 | 1.562 | 0.72 | 0.71 | [39,46,48,49,50,74,75,76] |
| H2 | 0.787 | 0.99 | 0.80 | [39,50,75,78] |
| CO2 | 2.507 | 0.88 | 0.91 | [51,52,53] |
| H2O | 1.501 | 0.77 | 0.84 | [75] |
| H2S | 3.631 | 1.08 | – | – |
| CO | 1.953 | 0.82 | – | – |
| Ar | 1.664 | 0.72 | 0.66 | [39,46,50,57,74] |
| He | 0.208 | 0.50 | 0.51 | [39,46,50,51,54,57,74,75] |
| Ne | 0.381 | 0.35 | 0.42 | [57,74] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tanichev, A.S.; Petrov, D.V. Broadening of the ν2 Raman Band of CH4 by C3H8 and C4H10. Molecules 2023, 28, 3365. https://doi.org/10.3390/molecules28083365
Tanichev AS, Petrov DV. Broadening of the ν2 Raman Band of CH4 by C3H8 and C4H10. Molecules. 2023; 28(8):3365. https://doi.org/10.3390/molecules28083365
Chicago/Turabian StyleTanichev, Aleksandr S., and Dmitry V. Petrov. 2023. "Broadening of the ν2 Raman Band of CH4 by C3H8 and C4H10" Molecules 28, no. 8: 3365. https://doi.org/10.3390/molecules28083365
APA StyleTanichev, A. S., & Petrov, D. V. (2023). Broadening of the ν2 Raman Band of CH4 by C3H8 and C4H10. Molecules, 28(8), 3365. https://doi.org/10.3390/molecules28083365







