Computational Insights into Cyclodextrin Inclusion Complexes with the Organophosphorus Flame Retardant DOPO
Abstract
1. Introduction
2. Results and Discussion
2.1. Molecular Docking Prediction
2.2. Molecular Dynamics Simulations of Isolated and Complex Systems
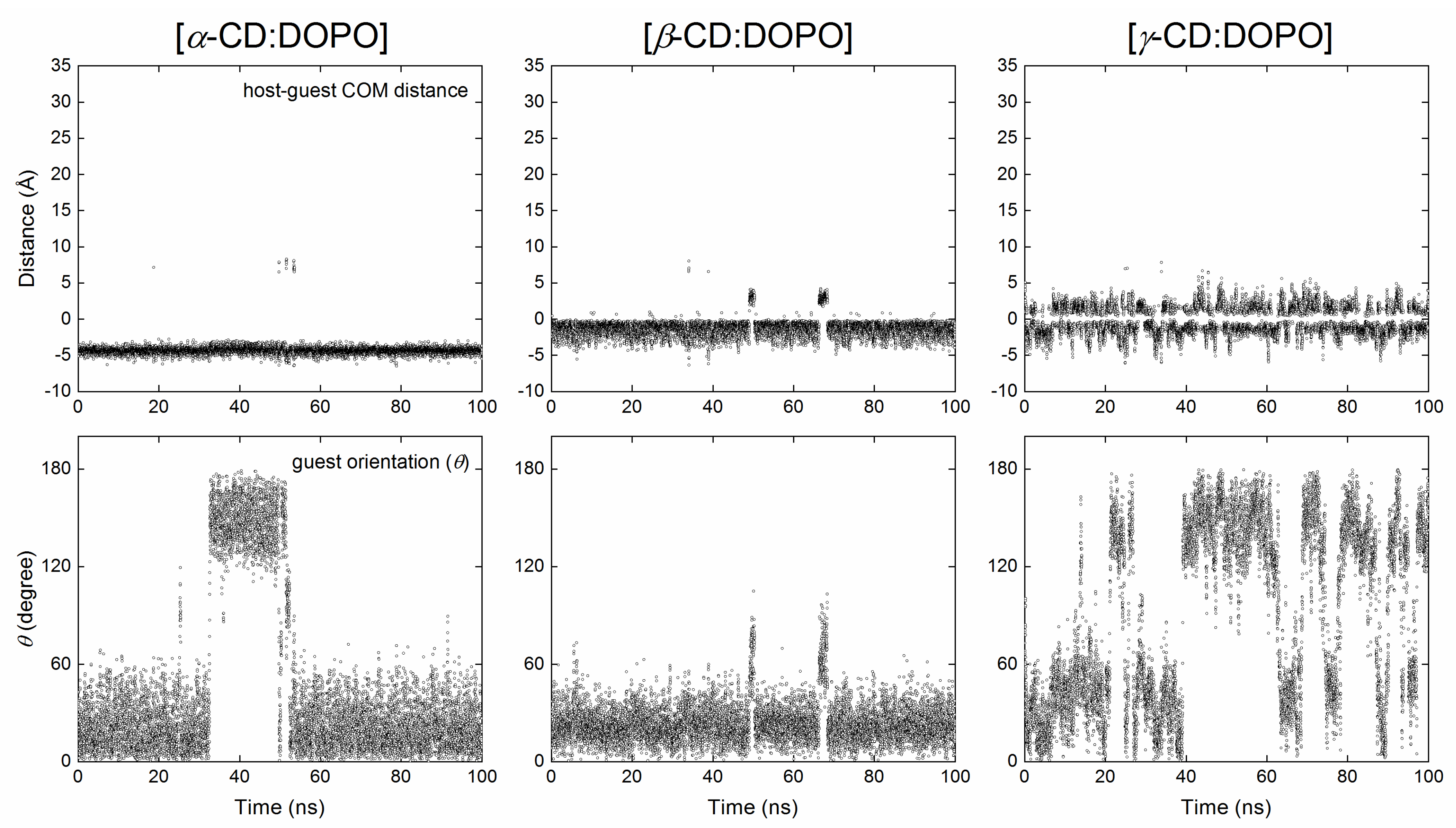
2.2.1. Structural Stability of Inclusion Complexes
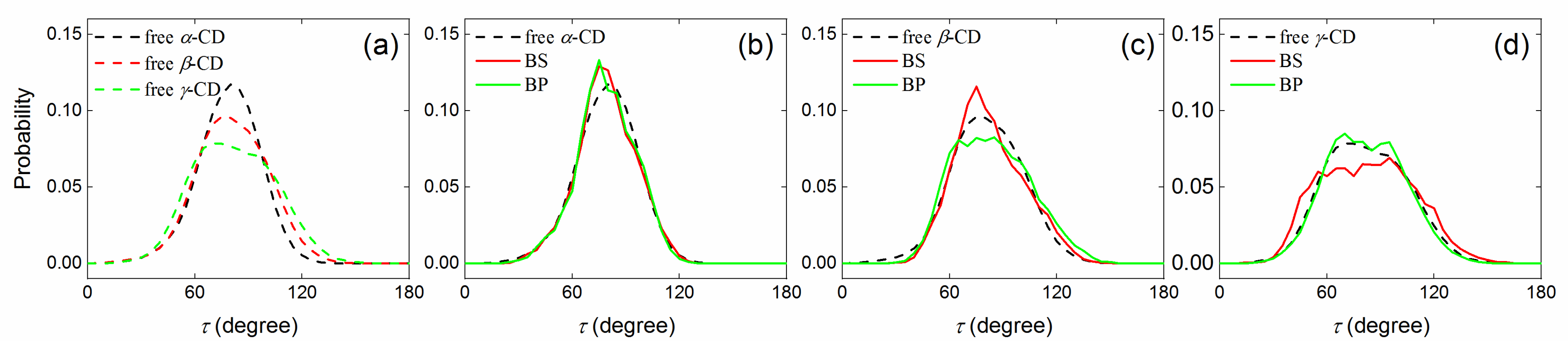
2.2.2. Tilt Angle of Glucose Units with and without Guest inside the CD Cavity
2.3. Binding Free Energy Calculations via MM–PBSA
2.4. QM-Optimized Structures
2.5. Energy Decomposition Analysis (EDA)
2.5.1. EDA-FF
2.5.2. sobEDAw
3. Materials and Methods
3.1. Molecular Docking
3.2. Molecular Dynamics Simulation
3.3. MM–PBSA Analysis
3.4. QM-Optimized Structures of Inclusion Complexes
3.5. Energy Decomposition Analysis (EDA)
3.5.1. EDA-FF
3.5.2. sobEDA
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- van der Veen, I.; de Boer, J. Phosphorus Flame Retardants: Properties, Production, Environmental Occurrence, Toxicity and Analysis. Chemosphere 2012, 88, 1119–1153. [Google Scholar] [CrossRef] [PubMed]
- de Wit, C.A. An Overview of Brominated Flame Retardants in the Environment. Chemosphere 2002, 46, 583–624. [Google Scholar] [CrossRef] [PubMed]
- Venier, M.; Salamova, A.; Hites, R.A. Halogenated Flame Retardants in the Great Lakes Environment. Acc. Chem. Res. 2015, 48, 1853–1861. [Google Scholar] [CrossRef]
- Ezechiáš, M.; Covino, S.; Cajthaml, T. Ecotoxicity and Biodegradability of New Brominated Flame Retardants: A Review. Ecotoxicol. Environ. Saf. 2014, 110, 153–167. [Google Scholar] [CrossRef] [PubMed]
- Domínguez, A.A.; Law, R.J.; Herzke, D.; de Boer, J. Bioaccumulation of Brominated Flame Retardants. In Brominated Flame Retardants; Eljarrat, E., Barceló, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 141–185. [Google Scholar]
- Choo, G.; Lee, I.-S.; Oh, J.-E. Species and Habitat-Dependent Accumulation and Biomagnification of Brominated Flame Retardants and Pbde Metabolites. J. Hazard. Mater. 2019, 371, 175–182. [Google Scholar] [CrossRef] [PubMed]
- Feiteiro, J.; Mariana, M.; Cairrão, E. Health Toxicity Effects of Brominated Flame Retardants: From Environmental to Human Exposure. Environ. Pollut. 2021, 285, 117475. [Google Scholar] [CrossRef]
- Rakotomalala, M.; Wagner, S.; Döring, M. Recent Developments in Halogen Free Flame Retardants for Epoxy Resins for Electrical and Electronic Applications. Materials 2010, 3, 4300–4327. [Google Scholar] [CrossRef] [PubMed]
- Huo, S.Q.; Song, P.A.; Yu, B.; Ran, S.Y.; Chevali, V.S.; Liu, L.; Fang, Z.P.; Wang, H. Phosphorus-Containing Flame Retardant Epoxy Thermosets: Recent Advances and Future Perspectives. Prog. Polym. Sci. 2021, 114, 101366. [Google Scholar] [CrossRef]
- Velencoso, M.M.; Battig, A.; Markwart, J.C.; Schartel, B.; Wurm, F.R. Molecular Firefighting—How Modern Phosphorus Chemistry Can Help Solve the Challenge of Flame Retardancy. Angew. Chem. Int. Ed. 2018, 57, 10450–10467. [Google Scholar] [CrossRef]
- Qiu, Y.; Qian, L.; Chen, Y.; Hao, J. Improving the Fracture Toughness and Flame Retardant Properties of Epoxy Thermosets by Phosphaphenanthrene/Siloxane Cluster-Like Molecules with Multiple Reactive Groups. Compos. Part B Eng. 2019, 178, 107481. [Google Scholar] [CrossRef]
- Levchik, S.V.; Weil, E.D. A Review of Recent Progress in Phosphorus-Based Flame Retardants. J. Fire Sci. 2006, 24, 345–364. [Google Scholar] [CrossRef]
- Mihajlović, I.; Miloradov, M.V.; Fries, E. Application of Twisselmann Extraction, Spme, and Gc-Ms to Assess Input Sources for Organophosphate Esters into Soil. Environ. Sci. Technol. 2011, 45, 2264–2269. [Google Scholar] [CrossRef] [PubMed]
- Yadav, I.C.; Devi, N.L.; Li, J.; Zhang, G.; Breivik, K. Possible Emissions of Pops in Plain and Hilly Areas of Nepal: Implications for Source Apportionment and Health Risk Assessment. Environ. Pollut. 2017, 220, 1289–1300. [Google Scholar] [CrossRef] [PubMed]
- Chokwe, T.B.; Abafe, O.A.; Mbelu, S.P.; Okonkwo, J.O.; Sibali, L.L. A Review of Sources, Fate, Levels, Toxicity, Exposure and Transformations of Organophosphorus Flame-Retardants and Plasticizers in the Environment. Emerg. Contam. 2020, 6, 345–366. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, H.W.; Zhu, H.K.; Yao, Y.M.; Chen, H.; Ren, C.; Wu, F.C.; Kannan, K. Occurrence and Distribution of Organophosphate Flame Retardants (Opfrs) in Soil and Outdoor Settled Dust from a Multi-Waste Recycling Area in China. Sci. Total Environ. 2018, 625, 1056–1064. [Google Scholar] [CrossRef] [PubMed]
- Abafe, O.A.; Martincigh, B.S. Concentrations, Sources and Human Exposure Implications of Organophosphate Esters in Indoor Dust from South Africa. Chemosphere 2019, 230, 239–247. [Google Scholar] [CrossRef] [PubMed]
- Araki, A.; Saito, I.; Kanazawa, A.; Morimoto, K.; Nakayama, K.; Shibata, E.; Tanaka, M.; Takigawa, T.; Yoshimura, T.; Chikara, H.; et al. Phosphorus Flame Retardants in Indoor Dust and Their Relation to Asthma and Allergies of Inhabitants. Indoor Air 2014, 24, 3–15. [Google Scholar] [CrossRef] [PubMed]
- Stapleton, H.M.; Klosterhaus, S.; Eagle, S.; Fuh, J.; Meeker, J.D.; Blum, A.; Webster, T.F. Detection of Organophosphate Flame Retardants in Furniture Foam and U. S. House Dust. Environ. Sci. Technol. 2009, 43, 7490–7495. [Google Scholar] [CrossRef] [PubMed]
- Chokwe, T.B.; Mporetji, S.M. Organophosphorus Flame Retardants in Surface and Effluent Water Samples from the Vaal River Catchment, South Africa: Levels and Risk to Aquatic Life. Water SA 2019, 45, 469–476. [Google Scholar] [CrossRef]
- Meyer, J.; Bester, K. Organophosphate Flame Retardants and Plasticisers in Wastewater Treatment Plants. J. Environ. Monit. 2004, 6, 599–605. [Google Scholar] [CrossRef]
- He, M.-J.; Yang, T.; Yang, Z.-H.; Li, Q.; Wei, S.-Q. Occurrence and Distribution of Organophosphate Esters in Surface Soil and Street Dust from Chongqing, China: Implications for Human Exposure. Arch. Environ. Contam. Toxicol. 2017, 73, 349–361. [Google Scholar] [CrossRef] [PubMed]
- Luo, Q.; Shan, Y.; Muhammad, A.; Wang, S.; Sun, L.; Wang, H. Levels, Distribution, and Sources of Organophosphate Flame Retardants and Plasticizers in Urban Soils of Shenyang, China. Environ. Sci. Pollut. Res. 2018, 25, 31752–31761. [Google Scholar] [CrossRef]
- Giulivo, M.; Capri, E.; Kalogianni, E.; Milacic, R.; Majone, B.; Ferrari, F.; Eljarrat, E.; Barceló, D. Occurrence of Halogenated and Organophosphate Flame Retardants in Sediment and Fish Samples from Three European River Basins. Sci. Total Environ. 2017, 586, 782–791. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.-W.; Isobe, T.; Chang, K.-H.; Amano, A.; Maneja, R.H.; Zamora, P.B.; Siringan, F.P.; Tanabe, S. Levels and Distribution of Organophosphorus Flame Retardants and Plasticizers in Fishes from Manila Bay, the Philippines. Environ. Pollut. 2011, 159, 3653–3659. [Google Scholar] [CrossRef]
- Luda, M.P.; Zanetti, M. Cyclodextrins and Cyclodextrin Derivatives as Green Char Promoters in Flame Retardants Formulations for Polymeric Materials. A Review. Polymers 2019, 11, 664. [Google Scholar] [CrossRef] [PubMed]
- Zhang, N.; Yildirim, E.; Zane, C.P.; Shen, J.; Vinueza, N.; Hinks, D.; Tonelli, A.E.; Pasquinelli, M.A. Improved Eco-Friendliness of a Common Flame Retardant through Inclusion Complexation with Cyclodextrins. ACS Appl. Polym. Mater. 2019, 1, 2768–2777. [Google Scholar] [CrossRef]
- Shan, X.; Jiang, K.; Li, J.; Song, Y.; Han, J.; Hu, Y. Preparation of Beta-Cyclodextrin Inclusion Complex and Its Application as an Intumescent Flame Retardant for Epoxy. Polymers 2019, 11, 71. [Google Scholar] [CrossRef]
- Zhao, X.; Xiao, D.; Alonso, J.P.; Wang, D.-Y. Inclusion Complex between Beta-Cyclodextrin and Phenylphosphonicdiamide as Novel Bio-Based Flame Retardant to Epoxy: Inclusion Behavior, Characterization and Flammability. Mater. Des. 2017, 114, 623–632. [Google Scholar] [CrossRef]
- Zhang, N.; Shen, J.; Pasquinelli, M.A.; Hinks, D.; Tonelli, A.E. Formation and Characterization of an Inclusion Complex of Triphenyl Phosphate and Β-Cyclodextrin and Its Use as a Flame Retardant for Polyethylene Terephthalate. Polym. Degrad. Stab. 2015, 120, 244–250. [Google Scholar] [CrossRef]
- Huang, L.; Gerber, M.; Lu, J.; Tonelli, A.E. Formation of a Flame Retardant-Cyclodextrin Inclusion Compound and Its Application as a Flame Retardant for Poly(Ethylene Terephthalate). Polym. Degrad. Stab. 2001, 71, 279–284. [Google Scholar] [CrossRef]
- Park, Y.; Banerjee, D.; Jin, S.A.; Li, S.; Beck, S.; Purser, L.; Ford, E. Organophosphate-Cyclodextrin Inclusion Complex for Flame Retardancy in Doped Cellulose Acetate Butyrate Melt-Spun Fibers. Ind. Eng. Chem. Res. 2023, 62, 11595–11605. [Google Scholar] [CrossRef]
- Szejtli, J. Introduction and General Overview of Cyclodextrin Chemistry. Chem. Rev. 1998, 98, 1743–1754. [Google Scholar] [CrossRef]
- Villiers, A. Sur La Fermentation De La Fécule Par L’action Du Ferment Butyrique. Compt. Rend. Acad. Sci. 1891, 112, 536–538. [Google Scholar]
- Li, S.; Purdy, W.C. Cyclodextrins and Their Applications in Analytical Chemistry. Chem. Rev. 1992, 92, 1457–1470. [Google Scholar] [CrossRef]
- Del Valle, E.M.M. Cyclodextrins and Their Uses: A Review. Process Biochem. 2004, 39, 1033–1046. [Google Scholar] [CrossRef]
- Lezcano, M.; Al-Soufi, W.; Novo, M.; Rodriguez-Nunez, E.; Tato, J.V. Complexation of Several Benzimidazole-Type Fungicides with Alpha- and Beta-Cyclodextrins. J. Agric. Food. Chem. 2002, 50, 108–112. [Google Scholar] [CrossRef] [PubMed]
- Bhardwaj, R.; Dorr, R.T.; Blanchard, J. Approaches to Reducing Toxicity of Parenteral Anticancer Drug Formulations Using Cyclodextrins. PDA J. Pharm. Sci. Technol. 2000, 54, 233–239. [Google Scholar]
- Trotta, F.; Zanetti, M.; Camino, G. Thermal Degradation of Cyclodextrins. Polym. Degrad. Stab. 2000, 69, 373–379. [Google Scholar] [CrossRef]
- Zhang, N.; Zane, C.P.; Chen, Y.; Yildirim, E.; Hinks, D.; Tonelli, A.E.; Vinueza, N.R.; Pasquinelli, M.A. Physical Characterization of Inclusion Complexes of Triphenyl Phosphate and Cyclodextrins in Solution. J. Phys. Chem. B 2020, 124, 404–412. [Google Scholar] [CrossRef]
- Shan, X.; Han, J.; Song, Y.; Xing, Z.; Li, J. Flame Retardancy of Epoxy Resin/Β-Cyclodextrin@Resorcinol Bisdiphenylphosphate Inclusion Composites. J. Wuhan Univ. Technol. Mater. Sci. Ed. 2020, 35, 455–463. [Google Scholar] [CrossRef]
- Schäfer, A.; Seibold, S.; Lohstroh, W.; Walter, O.; Döring, M. Synthesis and Properties of Flame-Retardant Epoxy Resins Based on Dopo and One of Its Analog Dppo. J. Appl. Polym. Sci. 2007, 105, 685–696. [Google Scholar] [CrossRef]
- Artner, J.; Ciesielski, M.; Walter, O.; Döring, M.; Perez, R.M.; Sandler, J.K.W.; Altstädt, V.; Schartel, B. A Novel Dopo-Based Diamine as Hardener and Flame Retardant for Epoxy Resin Systems. Macromol. Mater. Eng. 2008, 293, 503–514. [Google Scholar] [CrossRef]
- Zhang, W.; Li, X.; Yang, R. Novel Flame Retardancy Effects of Dopo-Poss on Epoxy Resins. Polym. Degrad. Stab. 2011, 96, 2167–2173. [Google Scholar] [CrossRef]
- Zhang, Y.-C.; Xu, G.-L.; Liang, Y.; Yang, J.; Hu, J. Preparation of Flame Retarded Epoxy Resins Containing Dopo Group. Thermochim. Acta 2016, 643, 33–40. [Google Scholar] [CrossRef]
- Zhao, J.; Dong, X.; Huang, S.; Tian, X.; Song, L.; Yu, Q.; Wang, Z. Performance Comparison of Flame Retardant Epoxy Resins Modified by DPO–PHE and DOPO–PHE. Polym. Degrad. Stab. 2018, 156, 89–99. [Google Scholar] [CrossRef]
- Hussain, M.; Varley, R.J.; Zenka, M.; Simon, G.P. Synthesis, Thermal Behavior, and Cone Calorimetry of Organophosphorus Epoxy Materials. J. Appl. Polym. Sci. 2003, 90, 3696–3707. [Google Scholar] [CrossRef]
- Saenger, W.; Jacob, J.; Gessler, K.; Steiner, T.; Hoffmann, D.; Sanbe, H.; Koizumi, K.; Smith, S.M.; Takaha, T. Structures of the Common Cyclodextrins and Their Larger Analogues Beyond the Doughnut. Chem. Rev. 1998, 98, 1787–1802. [Google Scholar] [CrossRef] [PubMed]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High Performance Molecular Simulations through Multi-Level Parallelism from Laptops to Supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef]
- Saenger, W.; Noltemeyer, M.; Manor, P.C.; Hingerty, B.; Klar, B. “Induced-Fit”-Type Complex Formation of the Model Enzyme A-Cyclodextrin. Bioorg. Chem. 1976, 5, 187–195. [Google Scholar] [CrossRef]
- Valdés-Tresanco, M.S.; Valdés-Tresanco, M.E.; Valiente, P.A.; Moreno, E. Gmx_Mmpbsa: A New Tool to Perform End-State Free Energy Calculations with GROMACS. J. Chem. Theory Comput. 2021, 17, 6281–6291. [Google Scholar] [CrossRef]
- Chen, W.; Chang, C.-E.; Gilson, M.K. Calculation of Cyclodextrin Binding Affinities: Energy, Entropy, and Implications for Drug Design. Biophys. J. 2004, 87, 3035–3049. [Google Scholar] [CrossRef] [PubMed]
- Yong, C.W.; Washington, C.; Smith, W. Structural Behaviour of 2-Hydroxypropyl-Β-Cyclodextrin in Water: Molecular Dynamics Simulation Studies. Pharm. Res. 2007, 25, 1092–1099. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Feng, W.; Li, C.; Tan, T. Investigation of the Inclusions of Puerarin and Daidzin with Β-Cyclodextrin by Molecular Dynamics Simulation. J. Phys. Chem. B 2010, 114, 4876–4883. [Google Scholar] [CrossRef] [PubMed]
- Lu, T.; Liu, Z.; Chen, Q. Comment on “18 and 12—Member Carbon Rings (Cyclo[N]Carbons)—A Density Functional Study”. Mater. Sci. Eng. B 2021, 273, 115425. [Google Scholar] [CrossRef]
- Schauperl, M.; Nerenberg, P.S.; Jang, H.; Wang, L.-P.; Bayly, C.I.; Mobley, D.L.; Gilson, M.K. Non-Bonded Force Field Model with Advanced Restrained Electrostatic Potential Charges (RESP2). Commun. Chem. 2020, 3, 44. [Google Scholar] [CrossRef]
- Lu, T.; Chen, Q. Simple, Efficient, and Universal Energy Decomposition Analysis Method Based on Dispersion-Corrected Density Functional Theory. J. Phys. Chem. A 2023, 127, 7023–7035. [Google Scholar] [CrossRef]
- Szalewicz, K. Symmetry-Adapted Perturbation Theory of Intermolecular Forces. WIRES Comput. Mol. Sci. 2012, 2, 254–272. [Google Scholar] [CrossRef]
- Knegtel, R.M.A.; Strokopytov, B.; Penninga, D.; Faber, O.G.; Rozeboom, H.J.; Kalk, K.H.; Dijkhuizen, L.; Dijkstra, B.W. Crystallographic Studies of the Interaction of Cyclodextrin Glycosyltransferase from Bacillus Circulans Strain 251 with Natural Substrates and Products (*). J. Biol. Chem. 1995, 270, 29256–29264. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, A.K.; Cottaz, S.; Driguez, H.; Schulz, G.E. Structure of Cyclodextrin Glycosyltransferase Complexed with a Derivative of Its Main Product Β-Cyclodextrin. Biochemistry 1998, 37, 5909–5915. [Google Scholar] [CrossRef]
- Uitdehaag, J.C.M.; Kalk, K.H.; van der Veen, B.A.; Dijkhuizen, L.; Dijkstra, B.W. The Cyclization Mechanism of Cyclodextrin Glycosyltransferase (Cgtase) as Revealed by a Γ-Cyclodextrin-Cgtase Complex at 1. 8-Resolution*. J. Biol. Chem. 1999, 274, 34868–34876. [Google Scholar] [CrossRef]
- Kim, S.; Thiessen, P.A.; Bolton, E.E.; Chen, J.; Fu, G.; Gindulyte, A.; Han, L.; He, J.; He, S.; Shoemaker, B.A.; et al. Pubchem Substance and Compound Databases. Nucleic Acids Res. 2016, 44, D1202–D1213. [Google Scholar] [CrossRef] [PubMed]
- Trott, O.; Olson, A.J. Autodock Vina: Improving the Speed and Accuracy of Docking with a New Scoring Function, Efficient Optimization, and Multithreading. J. Comput. Chem. 2010, 31, 455–461. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Fang, X.; Lu, Y.; Wang, S. The Pdbbind Database: Collection of Binding Affinities for Protein−Ligand Complexes with Known Three-Dimensional Structures. J. Med. Chem. 2004, 47, 2977–2980. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Fang, X.; Lu, Y.; Yang, C.-Y.; Wang, S. The Pdbbind Database: Methodologies and Updates. J. Med. Chem. 2005, 48, 4111–4119. [Google Scholar] [CrossRef] [PubMed]
- Cézard, C.; Trivelli, X.; Aubry, F.; Djedaïni-Pilard, F.; Dupradeau, F.-Y. Molecular Dynamics Studies of Native and Substituted Cyclodextrins in Different Media: 1. Charge Derivation and Force Field Performances. Phys. Chem. Chem. Phys. 2011, 13, 15103–15121. [Google Scholar] [PubMed]
- Kirschner, K.N.; Woods, R.J. Solvent Interactions Determine Carbohydrate Conformation. Proc. Natl. Acad. Sci. USA 2001, 98, 10541–10545. [Google Scholar] [CrossRef] [PubMed]
- Basma, M.; Sundara, S.; Çalgan, D.; Vernali, T.; Woods, R.J. Solvated Ensemble Averaging in the Calculation of Partial Atomic Charges. J. Comput. Chem. 2001, 22, 1125–1137. [Google Scholar] [CrossRef] [PubMed]
- Kirschner, K.N.; Woods, R.J. Quantum Mechanical Study of the Nonbonded Forces in Water−Methanol Complexes. J. Phys. Chem. A 2001, 105, 4150–4155. [Google Scholar] [CrossRef][Green Version]
- Hornak, V.; Abel, R.; Okur, A.; Strockbine, B.; Roitberg, A.; Simmerling, C. Comparison of Multiple Amber Force Fields and Development of Improved Protein Backbone Parameters. Proteins 2006, 65, 712–725. [Google Scholar] [CrossRef]
- Zhang, H.; Tan, T.; Feng, W.; van der Spoel, D. Molecular Recognition in Different Environments: Beta-Cyclodextrin Dimer Formation in Organic Solvents. J. Phys. Chem. B 2012, 116, 12684–12693. [Google Scholar] [CrossRef]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and Testing of a General Amber Force Field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision A.03; Gaussian, Inc: Wallingford, CT, USA, 2016. [Google Scholar]
- Yin, C.; Cui, Z.; Jiang, Y.; van der Spoel, D.; Zhang, H. Role of [host:guest] Charge Transfer in Cyclodextrin Complexation: A Computational Study. J. Phys. Chem. C 2019, 123, 17745–17756. [Google Scholar] [CrossRef]
- Zhang, H.; Tan, T.; Hetényi, C.; Lv, Y.; van der Spoel, D. Cooperative Binding of Cyclodextrin Dimers to Isoflavone Analogues Elucidated by Free Energy Calculations. J. Phys. Chem. C 2014, 118, 7163–7173. [Google Scholar] [CrossRef]
- Zhang, H.; Tan, T.; Hetényi, C.; van der Spoel, D. Quantification of Solvent Contribution to the Stability of Noncovalent Complexes. J. Chem. Theory Comput. 2013, 9, 4542–4551. [Google Scholar] [CrossRef]
- Miller, B.R., 3rd; McGee, T.D., Jr.; Swails, J.M.; Homeyer, N.; Gohlke, H.; Roitberg, A.E. Mmpbsa. Py: An Efficient Program for End-State Free Energy Calculations. J. Chem. Theory Comput. 2012, 8, 3314–3321. [Google Scholar]
- van der Spoel, D.; Zhang, J.; Zhang, H. Quantitative Predictions from Molecular Simulations Using Explicit or Implicit Interactions. WIRES Comput. Mol. Sci. 2022, 12, e1560. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105, 2999–3094. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Wang, J.; Cieplak, P.; Kollman, P.A. How Well Does a Restrained Electrostatic Potential (Resp) Model Perform in Calculating Conformational Energies of Organic and Biological Molecules? J. Comput. Chem. 2000, 21, 1049–1074. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F.-W. Comparison of Computational Methods for Atomic Charges. Acta Phys.-Chim. Sin. 2012, 28, 1–18. [Google Scholar]
- Sigfridsson, E.; Ryde, U. Comparison of Methods for Deriving Atomic Charges from the Electrostatic Potential and Moments. J. Comput. Chem. 1998, 19, 377–395. [Google Scholar] [CrossRef]
- Zhang, J.; Lu, T. Efficient Evaluation of Electrostatic Potential with Computerized Optimized Code. Phys. Chem. Chem. Phys. 2021, 23, 20323–20328. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
- Lu, T.; Chen, Q. Shermo: A General Code for Calculating Molecular Thermochemistry Properties. Comput. Theor. Chem. 2021, 1200, 113249. [Google Scholar] [CrossRef]
- Merrick, J.P.; Moran, D.; Radom, L. An Evaluation of Harmonic Vibrational Frequency Scale Factors. J. Phys. Chem. A 2007, 111, 11683–11700. [Google Scholar] [CrossRef]





| Cyclodextrin | Interval of Center Z (Å) a | ∆Edock (kcal/mol) b | θ (degree) c | COM Distance (Å) d | Binding Mode e |
|---|---|---|---|---|---|
| α-CD | [−11, 3] | −4.5 | 27.3 ± 1.0 | −4.3 ± 0.0 | BS |
| α-CD | [4, 10] | −4.2 | 153.4 ± 0.3 | 4.3 ± 0.0 | BP |
| β-CD | [−9, 6] | −5.3 | 28.1 ± 3.4 | −1.5 ± 0.5 | BS |
| γ-CD | −7 | −5.0 | 32.7 | −0.7 | BS |
| γ-CD | [−6, 8] | −5.0 | 151.8 ± 6.5 | 1.2 ± 0.0 | BP |
| Energy | [α-CD:DOPO] | [β-CD:DOPO] | [γ-CD:DOPO] | ||||
|---|---|---|---|---|---|---|---|
| BS | BP | BS | BP | BS | BP | ||
| MM | ΔEbonded | 2.3 ± 0.3 | 2.8 ± 0.3 | 2.0 ± 0.3 | 1.9 ± 0.4 | 1.8 ± 0.3 | 1.3 ± 0.4 |
| ΔEbonded,H | 2.0 ± 0.3 | 2.6 ± 0.3 | 1.8 ± 0.3 | 1.7 ± 0.3 | 1.6 ± 0.3 | 1.1 ± 0.3 | |
| ΔEbonded,G | 0.3 ± 0.1 | 0.3 ± 0.1 | 0.2 ± 0.1 | 0.2 ± 0.1 | 0.2 ± 0.1 | 0.2 ± 0.1 | |
| ΔEvdW | −19.1 ± 0.1 | −19.6 ± 0.1 | −26.9 ± 0.2 | −24.4 ± 0.1 | −23.3 ± 0.9 | −22.2 ± 0.4 | |
| ΔEelec | −3.0 ± 0.4 | −6.8 ± 0.2 | −5.2 ± 0.3 | −9.0 ± 0.5 | −5.1 ± 1.0 | −4.2 ± 0.5 | |
| ΔEnonbonded | −22.1 ± 0.3 | −26.4 ± 0.4 | −32.1 ± 0.4 | −33.4 ± 0.5 | −28.3 ± 1.6 | −26.4 ± 0.3 | |
| ΔEMM | −19.9 ± 0.4 | −23.5 ± 0.4 | −30.1 ± 0.4 | −31.5 ± 0.6 | −26.6 ± 2.8 | −25.1 ± 0.4 | |
| solvation | ΔGpolar | 12.4 ± 0.3 | 15.4 ± 0.2 | 18.6 ± 0.3 | 20.4 ± 0.4 | 17.1 ± 1.2 | 14.9 ± 0.2 |
| ΔGnonpolar | −1.7 ± 0.0 | −1.8 ± 0.0 | −2.3 ± 0.0 | −2.2 ± 0.0 | −2.3 ± 0.1 | −2.3 ± 0.0 | |
| ΔGsol | 10.7 ± 0.3 | 13.6 ± 0.2 | 16.3 ± 0.3 | 18.1 ± 0.4 | 14.8 ± 1.1 | 12.7 ± 0.2 | |
| total | ΔEbind | −9.2 ± 0.4 | −10.0 ± 0.3 | −13.8 ± 0.3 | −13.4 ± 0.4 | −11.7 ± 0.4 | −12.5 ± 0.4 |
| Host | State | Gas Phase | Water Phase | ||||||
|---|---|---|---|---|---|---|---|---|---|
| τ (Degree) | Circularity | θ (Degree) | COM Distance (Å) | τ (Degree) | Circularity | θ (Degree) | COM Distance (Å) | ||
| α-CD | crystal | 85.2 | 0.950 | 85.2 | 0.950 | ||||
| free | 78.8 | 0.949 | 78.4 | 0.938 | |||||
| BS | 77.5 | 0.958 | 57.1 | −5.2 | 77.7 | 0.933 | 31.1 | −5.8 | |
| BP | 87.6 | 0.961 | 169.5 | 4.5 | 88.3 | 0.956 | 171.9 | 4.3 | |
| β-CD | crystal | 84.5 | 0.935 | 84.5 | 0.935 | ||||
| free | 81.7 | 0.955 | 80.9 | 0.941 | |||||
| BS | 83.6 | 0.932 | 24.6 | 1.5 | 83.7 | 0.923 | 24.5 | 1.7 | |
| BP | 80.7 | 0.964 | 171.6 | 3.8 | 83.1 | 0.960 | 160.6 | 2.5 | |
| γ-CD | crystal | 83.8 | 0.964 | 83.8 | 0.964 | ||||
| free | 79.5 | 0.954 | 78.4 | 0.942 | |||||
| BS | 81.8 | 0.912 | 23.1 | −0.1 | 79.8 | 0.908 | 25.4 | 0.6 | |
| BP | 79.0 | 0.952 | 147.4 | 1.6 | 78.3 | 0.939 | 148.9 | 1.5 | |
| Host | Charge Method | Optimized Complexes in Gas | Optimized Complexes in Water | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ΔEelec | ΔErep | ΔEdisp | ΔEFF | ΔEelec | ΔErep | ΔEdisp | ΔEFF | ||||||||||
| BS | BP | BS | BP | BS | BP | BS | BP | BS | BP | BS | BP | BS | BP | BS | BP | ||
| α-CD | MK | −9.4 | −3.4 | 8.4 | 16.3 | −23.1 | −32.7 | −24.1 | −19.8 | −8.3 | −3.0 | 6.6 | 14.4 | −20.0 | −31.6 | −21.7 | −20.2 |
| CHELPG | −9.4 | −3.0 | −24.1 | −19.3 | −8.4 | −2.5 | −21.8 | −19.8 | |||||||||
| RESP | −9.6 | −3.7 | −24.2 | −20.1 | −8.5 | −3.0 | −21.9 | −20.2 | |||||||||
| RESP2 | −10.8 | −4.4 | −25.5 | −20.8 | −9.5 | −3.6 | −22.9 | −20.8 | |||||||||
| FFMD | −9.9 | −2.8 | −24.5 | −19.2 | −8.4 | −1.8 | −21.8 | −19.1 | |||||||||
| β-CD | MK | −4.2 | −10.7 | 19.8 | 10.6 | −41.7 | −27.1 | −26.0 | −27.3 | −3.3 | −10.6 | 17.8 | 9.8 | −40.0 | −26.4 | −25.5 | −27.1 |
| CHELPG | −3.6 | −10.5 | −25.5 | −27.0 | −2.8 | −10.4 | −25.1 | −26.9 | |||||||||
| RESP | −4.7 | −10.4 | −26.5 | −26.9 | −4.0 | −10.2 | −26.2 | −26.8 | |||||||||
| RESP2 | −6.0 | −12.9 | −27.8 | −29.4 | −5.1 | −12.6 | −27.4 | −29.2 | |||||||||
| FFMD | −3.9 | −11.4 | −25.7 | −27.9 | −2.9 | −11.3 | −25.2 | −27.9 | |||||||||
| γ-CD | MK | −4.5 | −4.3 | 9.1 | 6.3 | −27.8 | −23.8 | −23.2 | −21.8 | −3.2 | −3.5 | 9.8 | 7.1 | −26.4 | −25.4 | −21.6 | −20.9 |
| CHELPG | −4.1 | −4.1 | −22.8 | −21.6 | −3.0 | −3.4 | −21.4 | −20.7 | |||||||||
| RESP | −4.0 | −4.2 | −22.7 | −21.7 | −3.3 | −3.3 | −21.7 | −20.7 | |||||||||
| RESP2 | −5.5 | −5.5 | −24.2 | −22.9 | −4.6 | −4.5 | −23.0 | −21.8 | |||||||||
| FFMD | −6.2 | −5.3 | −24.9 | −22.7 | −3.8 | −4.3 | −22.2 | −21.7 | |||||||||
| Energies | Optimized Complexes in Gas | Optimized Complexes in Water | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [α-CD:DOPO] | [β-CD:DOPO] | [γ-CD:DOPO] | [α-CD:DOPO] | [β-CD:DOPO] | [γ-CD:DOPO] | ||||||||
| BS | BP | BS | BP | BS | BP | BS | BP | BS | BP | BS | BP | ||
| interaction energy | ΔEels | −17.3 | −14.7 | −19.6 | −22.8 | −12.9 | −10.2 | −14.3 | −12.9 | −17.3 | −18.7 | −9.9 | −9.4 |
| ΔEx | −7.9 | −10.4 | −13.1 | −9.9 | −5.3 | −2.4 | −7.6 | −8.8 | −11.4 | −8.4 | −3.5 | −2.5 | |
| ΔErep | 40.1 | 51.4 | 64.1 | 47.2 | 33.0 | 22.4 | 33.9 | 46.4 | 58.7 | 45.1 | 26.3 | 22.9 | |
| ΔExrep | 27.8 | 34.7 | 43.2 | 32.4 | 22.9 | 16.3 | 23.2 | 31.7 | 39.8 | 31.6 | 18.8 | 16.7 | |
| ΔEorb | −9.2 | −6.7 | −8.7 | −9.6 | −5.3 | −4.1 | −7.5 | −6.3 | −8.1 | −9.3 | −4.5 | −4.1 | |
| ΔEDFTc | −11.1 | −15.0 | −18.8 | −12.7 | −11.4 | −8.7 | −8.1 | −14.1 | −17.8 | −12.6 | −9.6 | −8.8 | |
| ΔEdc | −19.2 | −25.6 | −32.5 | −22.1 | −22.5 | −19.7 | −13.7 | −25.1 | −31.8 | −24.7 | −21.3 | −20.0 | |
| ΔEc | −30.3 | −40.6 | −51.3 | −34.8 | −33.8 | −28.4 | −21.7 | −39.2 | −49.6 | −37.3 | −31.0 | −28.8 | |
| ΔEdisp | −25.9 | −34.3 | −43.4 | −29.9 | −29.1 | −24.7 | −18.7 | −33.3 | −42.1 | −32.1 | −26.9 | −25.1 | |
| ΔEint | −24.7 | −21.0 | −28.5 | −29.8 | −24.4 | −22.7 | −17.3 | −20.7 | −27.8 | −28.5 | −22.5 | −21.9 | |
| deformation effect | ΔEdef,H | 1.9 | 12.1 | 3.8 | −0.3 | 3.8 | 0.5 | 1.3 | 14.0 | 3.7 | 5.5 | 0.7 | 0.0 |
| ΔEdef,G | 0.2 | 0.2 | 0.6 | 0.6 | 0.2 | 0.1 | 0.4 | 0.2 | 0.7 | 0.4 | 0.2 | 0.1 | |
| ΔEdef | 2.1 | 12.3 | 4.4 | 0.3 | 3.9 | 0.6 | 1.8 | 14.2 | 4.4 | 5.9 | 0.9 | 0.1 | |
| solvation effect | ΔEpolar | 8.9 | 5.8 | 8.7 | 12.3 | 7.6 | 7.2 | 9.1 | 5.0 | 7.7 | 16.7 | 6.1 | 6.0 |
| ΔEnonpolar | −2.4 | −2.4 | −3.5 | −2.6 | −2.4 | −1.9 | −2.6 | −2.3 | −3.4 | −3.9 | −2.1 | −1.8 | |
| ΔEsol | 6.5 | 3.4 | 5.2 | 9.7 | 5.2 | 5.3 | 6.5 | 2.7 | 4.3 | 12.8 | 4.0 | 4.2 | |
| thermodynamic correction | ΔGcorr | 17.6 | 15.0 | 19.2 | 20.8 | 16.9 | 16.7 | 16.9 | 14.3 | 18.6 | 19.8 | 16.8 | 16.4 |
| total | ΔGbind | 1.5 | 9.7 | 0.2 | 1.0 | 1.6 | 0.0 | 7.9 | 10.5 | −0.6 | 10.0 | −0.9 | −1.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, L.; Zhang, Y.; Zhang, P.; Zhang, H. Computational Insights into Cyclodextrin Inclusion Complexes with the Organophosphorus Flame Retardant DOPO. Molecules 2024, 29, 2244. https://doi.org/10.3390/molecules29102244
Ma L, Zhang Y, Zhang P, Zhang H. Computational Insights into Cyclodextrin Inclusion Complexes with the Organophosphorus Flame Retardant DOPO. Molecules. 2024; 29(10):2244. https://doi.org/10.3390/molecules29102244
Chicago/Turabian StyleMa, Le, Yongguang Zhang, Puyu Zhang, and Haiyang Zhang. 2024. "Computational Insights into Cyclodextrin Inclusion Complexes with the Organophosphorus Flame Retardant DOPO" Molecules 29, no. 10: 2244. https://doi.org/10.3390/molecules29102244
APA StyleMa, L., Zhang, Y., Zhang, P., & Zhang, H. (2024). Computational Insights into Cyclodextrin Inclusion Complexes with the Organophosphorus Flame Retardant DOPO. Molecules, 29(10), 2244. https://doi.org/10.3390/molecules29102244







