Ferroelectric and Relaxor-Ferroelectric Phases Coexisting Boosts Energy Storage Performance in (Bi0.5Na0.5)TiO3-Based Ceramics
Abstract
:1. Introduction
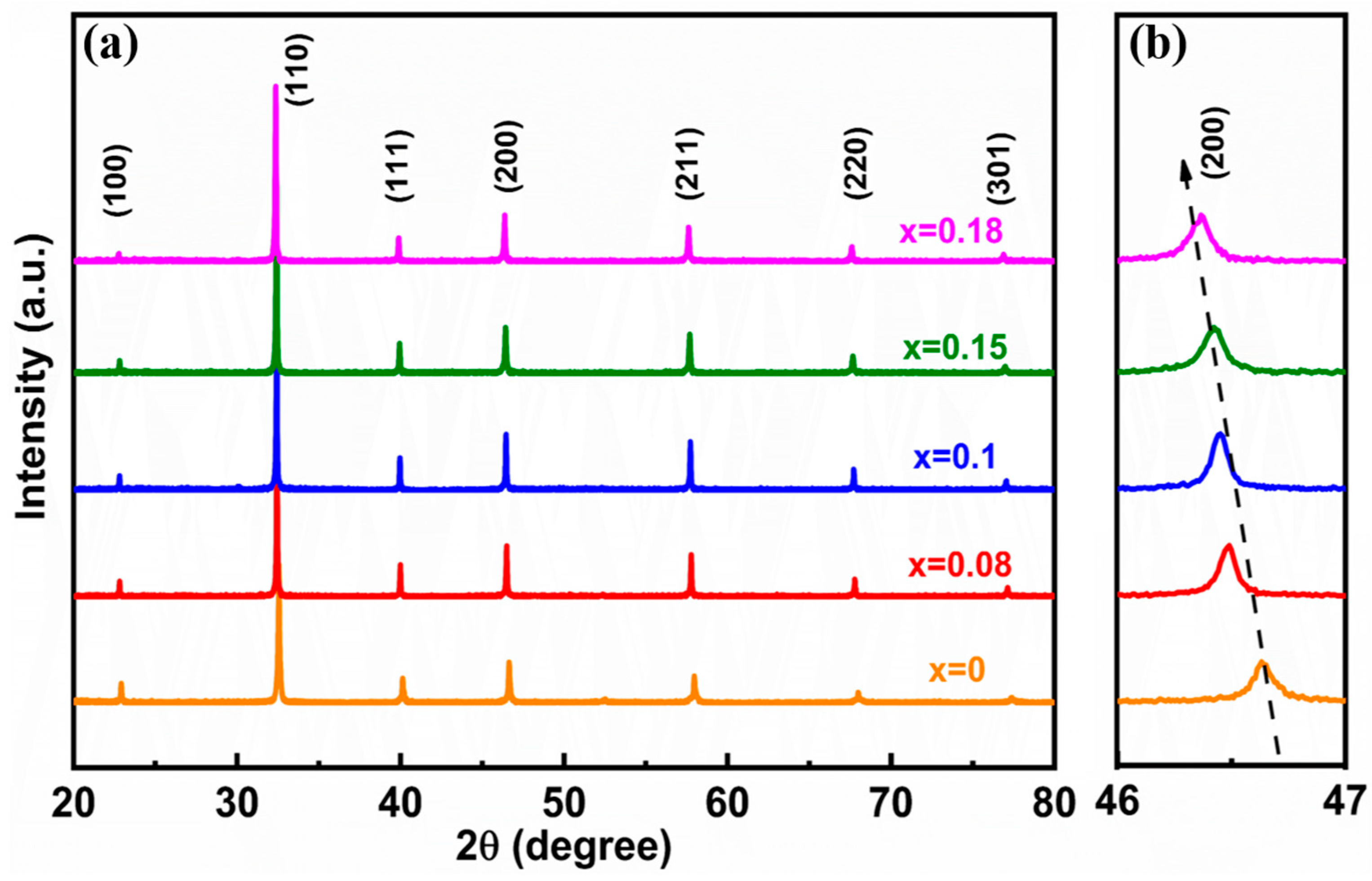
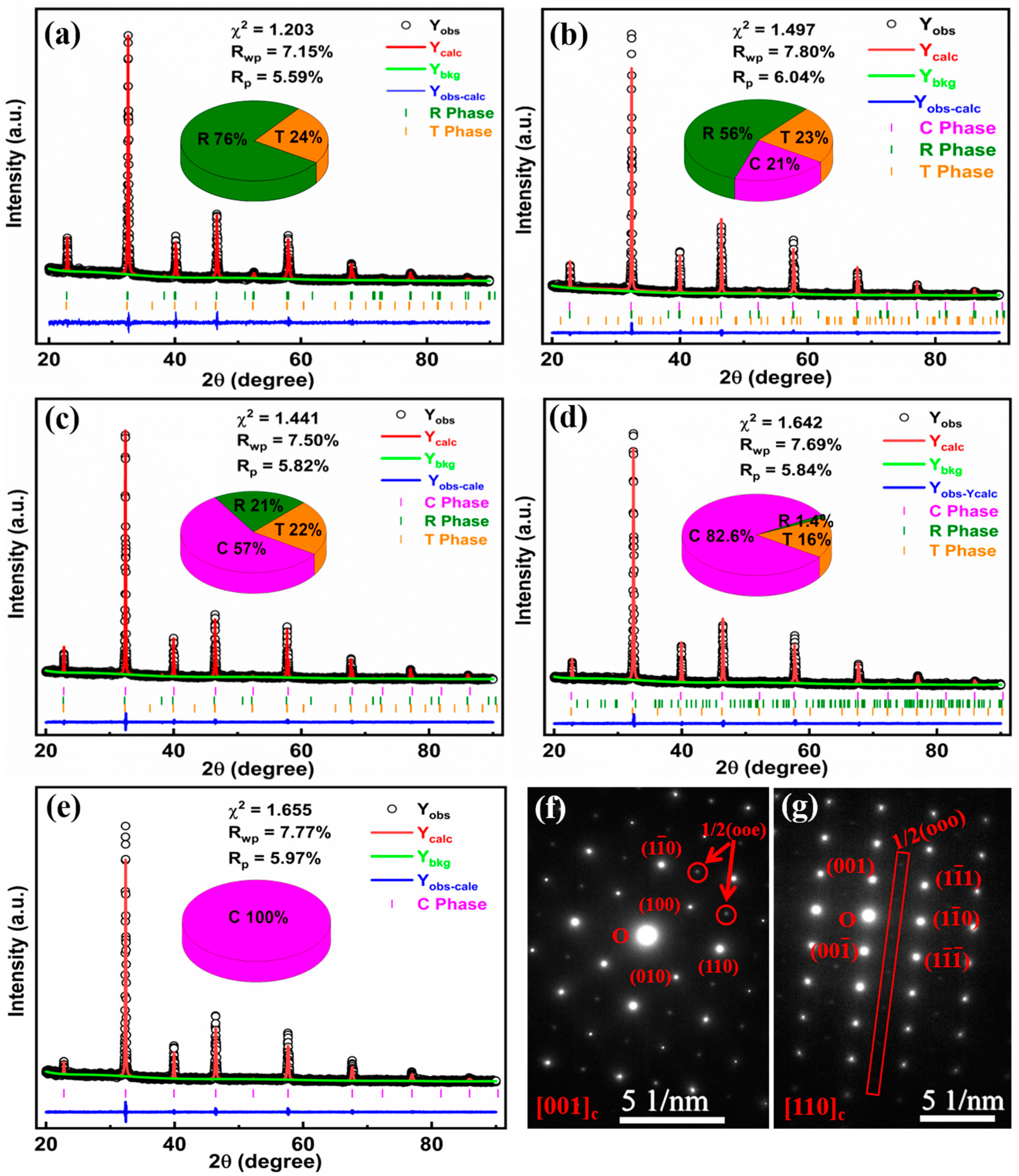
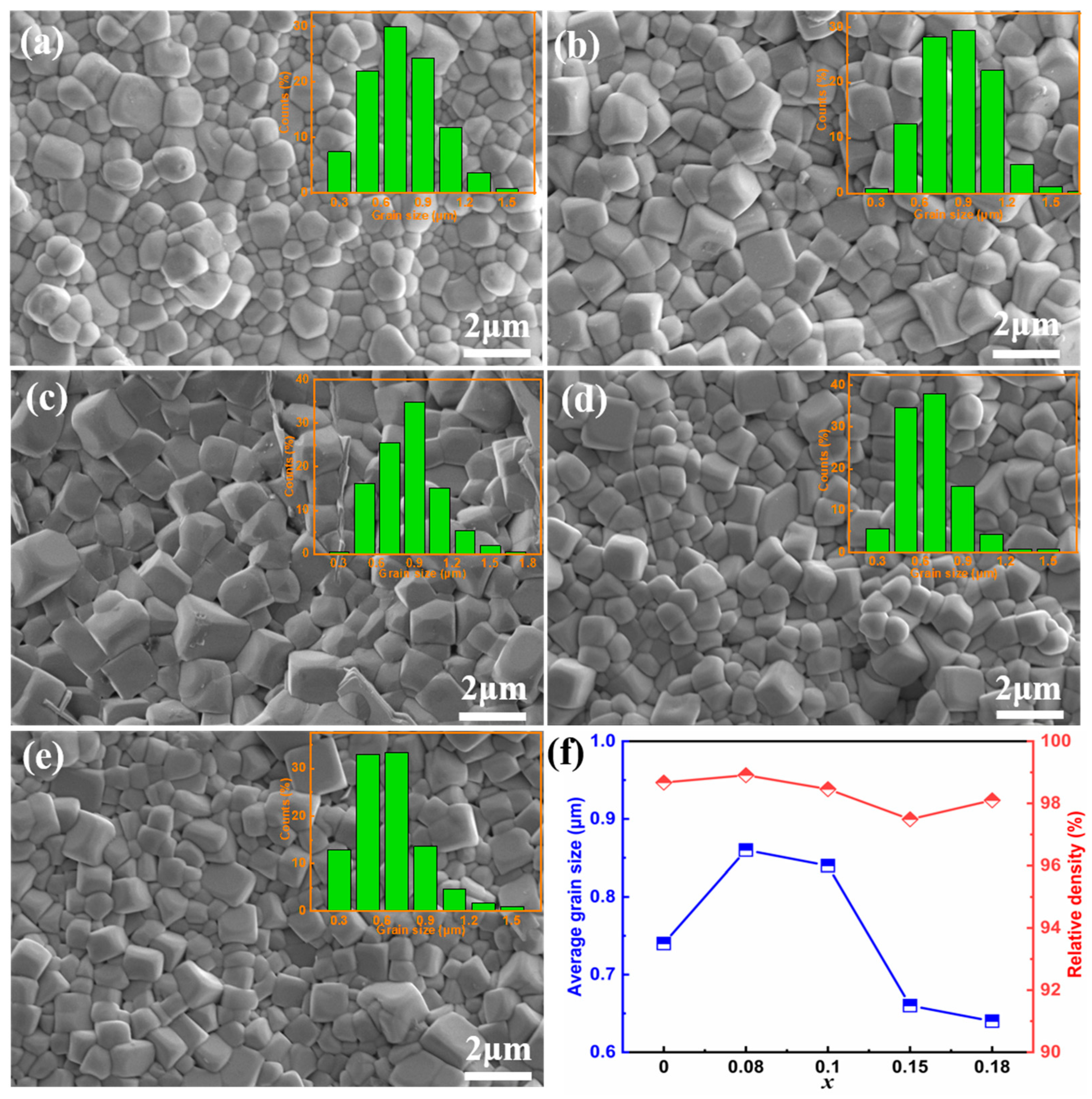
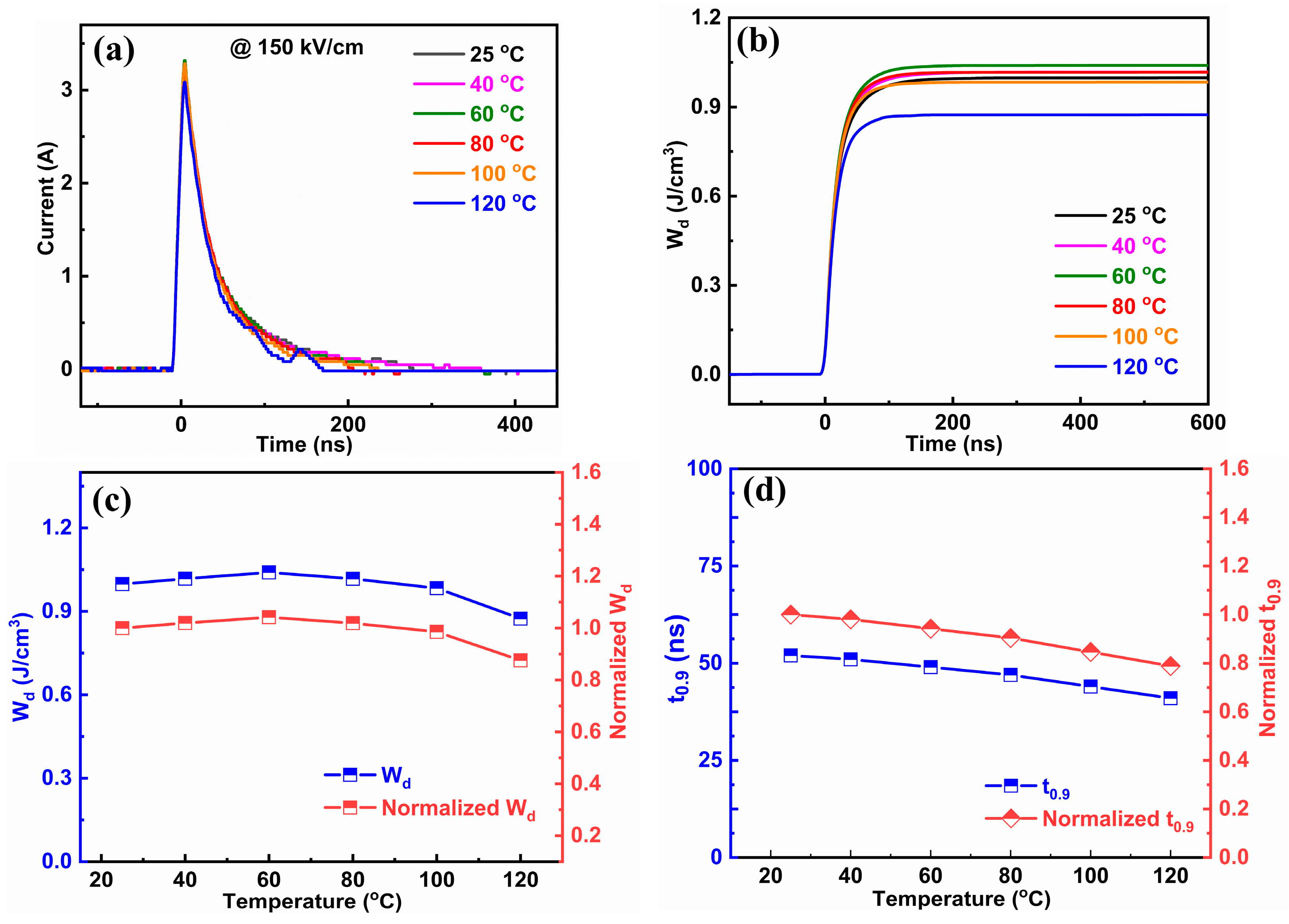
2. Results and Discussion
3. Materials and Methods
3.1. Materials and Synthesis
3.2. Characterization
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Feng, M.G.; Feng, Y.; Zhang, T.D.; Li, J.L.; Chen, Q.G.; Chi, Q.G.; Lei, Q.Q. Recent advances in multilayer-structure dielectrics for energy storage application. Adv. Sci. 2021, 8, 2102221. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Lu, Z.L.; Li, Y.; Li, L.H.; Ji, H.F.; Feteira, A.; Zhou, D.; Wang, D.W.; Zhang, S.J.; Reaney, I.M. Electroceramics for high-energy density capacitors: Current status and future perspectives. Chem. Rev. 2021, 121, 6124–6172. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.T.; Du, H.L.; Jin, L.; Poelman, D. High-performance lead-free bulk ceramics for electrical energy storage applications: Design strategies and challenges. J. Mater. Chem. A 2021, 9, 18026–18085. [Google Scholar] [CrossRef]
- Luo, H.; Wang, F.; Guo, R.; Zhang, D.; He, G.H.; Chen, S.; Wang, Q. Progress on polymer dielectrics for electrostatic capacitors application. Adv. Sci. 2022, 9, 2202438. [Google Scholar] [CrossRef] [PubMed]
- Pan, H.; Lan, S.; Xu, S.Q.; Zhang, Q.H.; Yao, H.B.; Liu, Y.Q.; Meng, F.Q.; Guo, E.J.; Gu, L.; Yi, D. Ultrahigh energy storage in superparaelectric relaxor ferroelectrics. Science 2021, 374, 100–104. [Google Scholar] [CrossRef] [PubMed]
- Pan, H.; Li, F.; Liu, Y.; Zhang, Q.H.; Wang, M.; Lan, S.; Zheng, Y.P.; Ma, J.; Gu, L.; Shen, Y. Ultrahigh–energy density lead-free dielectric films via polymorphic nanodomain design. Science 2019, 365, 578–582. [Google Scholar] [CrossRef] [PubMed]
- Che, Z.Y.; Ma, L.; Luo, G.G.; Xu, C.; Cen, Z.Y.; Feng, Q.; Chen, X.Y.; Ren, K.L.; Luo, N.N. Phase structure and defect engineering in (Bi0.5Na0.5)TiO3-based relaxor antiferroelectrics toward excellent energy storage performance. Nano Energy 2022, 100, 107484. [Google Scholar] [CrossRef]
- Gao, P.; Liu, Z.H.; Zhang, N.; Wu, H.; Bokov, A.A.; Ren, W.; Ye, Z.G. New antiferroelectric perovskite system with ultrahigh energy-storage performance at low electric field. Chem. Mater. 2019, 31, 979–990. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, L.Y.; Shi, W.J.; Yang, Y.L.; Alikin, D.; Shur, V.; Lou, Z.H.; Wang, D.; Zhang, A.M.; Gao, J.H. Enhanced energy storage properties in lead-free (Na0.5Bi0.5)0.7Sr0.3TiO3-based relaxor ferroelectric ceramics through a cooperative optimization strategy. ACS Appl. Mater. Interfaces 2023, 15, 6990–7001. [Google Scholar] [CrossRef]
- Shi, W.J.; Zhang, L.Y.; Jing, R.Y.; Hu, Q.Y.; Zeng, X.Y.; Alikin, D.; Shur, V.Y.; Wei, X.Y.; Gao, J.H.; Liu, G. Relaxor antiferroelectric-like characteristic boosting enhanced energy storage performance in eco-friendly (Bi0.5Na0.5)TiO3-based ceramics. J. Eur. Ceram. Soc. 2022, 42, 4528–4538. [Google Scholar] [CrossRef]
- Chen, L.; Deng, S.Q.; Liu, H.; Wu, J.; Qi, H.; Chen, J. Giant energy-storage density with ultrahigh efficiency in lead-free relaxors via high-entropy design. Nat. Commun. 2022, 13, 3089. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, L.Y.; Yang, Y.L.; Shi, W.J.; Huang, Y.Y.; Alikin, D.; Shur, V.Y.; Lou, Z.H.; Zhang, A.M.; Wei, X.Y. Enhancing energy storage performance in Na0.5Bi0.5TiO3-based lead-free relaxor ferroelectric ceramics along a stepwise optimization route. J. Mater. Chem. A 2023, 11, 2641–2651. [Google Scholar] [CrossRef]
- Cao, W.J.; Lin, R.J.; Hou, X.; Li, L.; Li, F.; Bo, D.F.; Ge, B.H.; Song, D.S.; Zhang, J.; Cheng, Z.X. Interfacial polarization restriction for ultrahigh energy-storage density in lead-free ceramics. Adv. Funct. Mater. 2023, 33, 2301027. [Google Scholar] [CrossRef]
- Yan, F.; Bai, H.R.; Ge, G.L.; Lin, J.F.; Zhu, K.; Li, G.H.; Qian, J.; Shen, B.; Zhai, J.W.; Liu, Z.F. Boosting Energy Storage Performance of Lead-Free Ceramics via Layered Structure Optimization Strategy. Small 2022, 18, 2202575. [Google Scholar] [CrossRef] [PubMed]
- Ji, H.F.; Wang, D.W.; Bao, W.C.; Lu, Z.L.; Wang, G.; Yang, H.J.; Mostaed, A.; Li, L.H.; Feteira, A.; Sun, S.K. Ultrahigh energy density in short-range tilted NBT-based lead-free multilayer ceramic capacitors by nanodomain percolation. Energy Storage Mater. 2021, 38, 113–120. [Google Scholar] [CrossRef]
- Li, D.; Zhou, D.; Wang, D.; Zhao, W.C.; Guo, Y.; Shi, Z.Q.; Zhou, T.; Sun, S.K.; Singh, C.; Trukhanov, S. Lead-free relaxor ferroelectric ceramics with ultrahigh energy storage densities via polymorphic polar nanoregions design. Small 2023, 19, 2206958. [Google Scholar] [CrossRef] [PubMed]
- Zhu, C.Q.; Cai, Z.M.; Luo, B.C.; Cheng, X.; Guo, L.M.; Jiang, Y.; Cao, X.H.; Fu, Z.X.; Li, L.T.; Wang, X.H. Multiphase engineered BNT-based ceramics with simultaneous high polarization and superior breakdown strength for energy storage applications. ACS Appl. Mater. Interfaces 2021, 13, 28484–28492. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.P.; Gao, Y.F.; Shi, P.; Kang, R.R.; Kang, F.; Qiao, W.J.; Zhao, J.Y.; Wang, Z.; Yuan, Y.; Lou, X.J. Ultrahigh energy storage density in (Bi0.5Na0.5)0.65Sr0.35TiO3-based lead-free relaxor ceramics with excellent temperature stability. Nano Energy 2022, 98, 107276. [Google Scholar] [CrossRef]
- Chen, L.; Wang, N.; Zhang, Z.F.; Yu, H.F.; Wu, J.; Deng, S.Q.; Liu, H.; Qi, H.; Chen, J. Local Diverse Polarization Optimized Comprehensive Energy-Storage Performance in Lead-Free Superparaelectrics. Adv. Mater. 2022, 34, 2205787. [Google Scholar] [CrossRef]
- Bokov, A.; Ye, Z.G. Recent progress in relaxor ferroelectrics with perovskite structure. J. Mater. Sci. 2006, 41, 31–52. [Google Scholar] [CrossRef]
- Burns, G.; Dacol, F. Glassy polarization behavior in ferroelectric compounds Pb(Mg1/3Nb2/3)O3 and Pb(Zn1/3Nb2/3)O3. Solid State Commun. 1983, 48, 853–856. [Google Scholar] [CrossRef]
- Hu, Q.Y.; Tian, Y.; Zhu, Q.S.; Bian, J.H.; Jin, L.; Du, H.L.; Alikin, D.; Shur, V.Y.; Feng, Y.J.; Xu, Z. Achieve ultrahigh energy storage performance in BaTiO3–Bi(Mg1/2Ti1/2)O3 relaxor ferroelectric ceramics via nano-scale polarization mismatch and reconstruction. Nano Energy 2020, 67, 104264. [Google Scholar] [CrossRef]
- Liu, H.; Sun, Z.; Zhang, J.; Luo, H.J.; Zhang, Q.H.; Yao, Y.H.; Deng, S.H.; Qi, H.; Liu, J.; Gallington, L.C. Chemical design of Pb-free relaxors for giant capacitive energy storage. J. Am. Chem. Soc. 2023, 145, 11764–11772. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.K.; Li, P.; Li, C.Y.; Bai, W.F.; Wu, S.T.; Zheng, P.; Zhang, J.G.; Zhai, J.W. Synergy of a stabilized antiferroelectric phase and domain engineering boosting the energy storage performance of NaNbO3-based relaxor antiferroelectric ceramics. ACS Appl. Mater. Interfaces 2022, 14, 17662–17673. [Google Scholar] [CrossRef] [PubMed]
- Qi, H.; Xie, A.W.; Tian, A.; Zuo, R.Z. Superior Energy-Storage Capacitors with Simultaneously Giant Energy Density and Efficiency Using Nanodomain Engineered BiFeO3-BaTiO3-NaNbO3 Lead-Free Bulk Ferroelectrics. Adv. Energy Mater. 2020, 10, 1903338. [Google Scholar] [CrossRef]
- Waser, R. TrI4: The role of grain boundaries in conduction and breakdown of perovskite-type titanates. Ferroelectrics 1992, 133, 109–114. [Google Scholar] [CrossRef]
- Shannon, R.D.J. Revised Effective Ionic Radii and Systematic Study of Inter Atomic Distances in Halides and Chalcogenides. Acta Crystallogra A 1976, 32, 751–767. [Google Scholar] [CrossRef]
- Boonlakhorn, J.; Thongbai, P.; Putasaeng, B.; Yamwong, T.; Maensiri, S. Very high-performance dielectric properties of Ca1-3x/2YbxCu3Ti4O12 ceramics. J. Alloys Compd. 2014, 612, 103–109. [Google Scholar] [CrossRef]
- Yang, L.T.; Kong, X.; Li, F.; Hao, H.; Cheng, Z.X.; Liu, H.X.; Li, J.F.; Zhang, S.J. Perovskite lead-free dielectrics for energy storage applications. Prog. Mater. Sci. 2019, 102, 72–108. [Google Scholar] [CrossRef]
- Kang, R.R.; Wang, Z.P.; Yang, W.J.; Zhu, X.P.; He, L.Q.; Gao, Y.F.; Zhao, J.T.; Shi, P.; Zhao, Y.Y.; Mao, P. Enhanced energy storage performance in Sr0.7La0.2Zr0.15Ti0.85O3-modified Bi0.5Na0.5TiO3 ceramics via constructing local phase coexistence. Chem. Eng. J. 2022, 446, 137105. [Google Scholar] [CrossRef]
- Hiruma, Y.J.; Nagata, H.M.; Takenaka, T. Thermal depoling process and piezoelectric properties of bismuth sodium titanate ceramics. J. Appl. Phys. 2009, 105, 084112. [Google Scholar] [CrossRef]
- Dai, Z.H.; Xie, J.L.; Chen, Z.B.; Zhou, S.; Liu, J.J.; Liu, W.G.; Xi, Z.Z.; Ren, X.B. Improved energy storage density and efficiency of (1 − x)Ba0.85Ca0.15Zr0.1Ti0.9O3-xBiMg2/3Nb1/3O3 lead-free ceramics. Chem. Eng. J. 2021, 410, 128341. [Google Scholar] [CrossRef]
- Li, D.; Lin, Y.; Zhang, M.; Yang, H.B. Achieved ultrahigh energy storage properties and outstanding charge–discharge performances in (Na0.5Bi0.5)0.7Sr0.3TiO3-based ceramics by introducing a linear additive. Chem. Eng. J. 2020, 392, 123729. [Google Scholar] [CrossRef]
- Li, D.; Xu, D.; Zhao, W.; Avdeev, M.; Jing, H.; Guo, Y.; Zhou, T.; Liu, W.; Wang, D.; Zhou, D. A high-temperature performing and near-zero energy loss lead-free ceramic capacitor. Energy Environ. Sci. 2023, 16, 4511–4521. [Google Scholar] [CrossRef]
- Qiao, X.S.; Zhang, F.D.; Wu, D.; Chen, B.; Zhao, X.M.; Peng, Z.H.; Ren, X.D.; Liang, P.F.; Chao, X.L.; Yang, Z.P. Superior comprehensive energy storage properties in Bi0.5Na0.5TiO3-based relaxor ferroelectric ceramics. Chem. Eng. J. 2020, 388, 124158. [Google Scholar] [CrossRef]
- Uchino, K.; Nomura, S. Critical exponents of the dielectric constants in diffused-phase-transition crystals. Ferroelectrics 1982, 44, 55–61. [Google Scholar] [CrossRef]
- Qi, H.; Zuo, R.Z. Linear-like lead-free relaxor antiferroelectric (Bi0.5Na0.5)TiO3–NaNbO3 with giant energy-storage density/efficiency and super stability against temperature and frequency. J. Mater. Chem. A 2019, 7, 3971–3978. [Google Scholar] [CrossRef]
- Dissado, L.A.; Fothergill, J.C.; Wolfe, S.V.; Hill, R.M. Weibull Statistics in Dielectric Breakdown; Theoretical Basis, Applications and Implications. IEEE Trans. Electr. Insul. 1984, 3, 227–233. [Google Scholar] [CrossRef]
- Fabiani, D.; Simoni, L. Discussion on application of the Weibull distribution to electrical breakdown of insulating materials. IEEE Trans. Dielectr. Electr. Insul. 2005, 12, 11–16. [Google Scholar] [CrossRef]
- Ma, W.G.; Zhu, Y.W.; Marwat, M.A.; Fan, P.Y.; Xie, B.; Salamon, D.; Ye, Z.G.; Zhang, H.B. Enhanced energy-storage performance with excellent stability under low electric fields in BNT–ST relaxor ferroelectric ceramics. J. Mater. Chem. C 2019, 7, 281–288. [Google Scholar] [CrossRef]
- Chu, B.K.; Hao, J.G.; Li, P.; Li, Y.C.; Li, W.; Zheng, L.M.; Zeng, H.R. High-energy storage properties over a broad temperature range in La-modified BNT-based lead-free ceramics. ACS Appl. Mater. Interfaces 2022, 14, 19683–19696. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.C.; Lu, Y.; Li, P.; Du, J.; Fu, P.; Hao, J.G.; Li, W. Achieving High Energy Storage Performance under a Low Electric Field in KNbO3-Doped BNT-Based Ceramics. Inorg. Chem. 2024, 63, 7080–7088. [Google Scholar] [CrossRef] [PubMed]
- Pan, Z.B.; Hu, D.; Zhang, Y.; Liu, J.J.; Shen, B.; Zhai, J.W. Achieving high discharge energy density and efficiency with NBT-based ceramics for application in capacitors. J. Mater. Chem. C 2019, 7, 4072–4078. [Google Scholar] [CrossRef]
- Zhang, Y.S.; Li, W.H.; Tang, X.G.; Meng, K.; Zhang, S.Y.; Xiao, X.Z.; Guo, X.B.; Jiang, Y.P.; Tang, Z.H. Energy storage and charge-discharge performance of B-site doped NBT-based lead-free ceramics. J. Alloys Compd. 2022, 911, 165074. [Google Scholar] [CrossRef]
- Yang, H.B.; Yan, F.; Lin, Y.; Wang, T.; He, L.; Wang, F. A lead free relaxation and high energy storage efficiency ceramics for energy storage applications. J. Alloys Compd. 2017, 710, 436–445. [Google Scholar] [CrossRef]
- Yan, F.; Yang, H.B.; Lin, Y.; Wang, T. Dielectric and ferroelectric properties of SrTiO3–Bi0.5Na0.5TiO3–BaAl0.5Nb0.5O3 lead-free ceramics for high-energy-storage applications. Inorg. Chem. 2017, 56, 13510–13516. [Google Scholar] [CrossRef] [PubMed]
- Yan, Y.X.; Qin, W.J.; Wang, X.Y.; Li, Z.M.; Zhang, D.Y.; Zhang, M.L.; Xu, Y.H.; Jin, L. Enhanced energy storage in temperature stable Bi0.5Na0.5TiO3-modified BaTiO3-Bi (Zn2/3Nb1/3)O3 ceramics. Ceram. Int. 2022, 48, 36478–36489. [Google Scholar] [CrossRef]
- Zhou, M.G.; Liang, R.H.; Zhou, Z.Y.; Dong, X.L. Superior energy storage properties and excellent stability of novel NaNbO3-based lead-free ceramics with A-site vacancy obtained via a Bi2O3 substitution strategy. J. Mater. Chem. A 2018, 6, 17896–17904. [Google Scholar] [CrossRef]
- Zhang, F.B.; Dai, Z.H.; Chen, Y.; Liu, J.J.; Liu, W.G.; Karaki, T. Enhanced energy storage properties of Sr(Ti0.5Zr0.5)O3 modified (Na0.5Bi0.5)TiO3 ceramics. Int. J. Energy Res. 2022, 46, 11492–11500. [Google Scholar] [CrossRef]
- Dai, Z.H.; Zhang, F.B.; Wang, S.B.; Lei, Y.; Liu, Y.; Chen, H.; Pan, Y.; Ding, X.D. High energy storage properties for BiMg0.5Ti0.5O3-modified KNN ceramics under low electric fields. J. Mater. Sci. 2022, 57, 15919–15928. [Google Scholar] [CrossRef]
- Ma, C.; Tan, X.L.; Kin, E.D.; Roth, M. Domain structure-dielectric property relationship in lead-free (1 − x)(Bi1/2Na1/2)TiO3-xBaTiO3 ceramics. J. Appl. Phys. 2010, 108, 104105. [Google Scholar] [CrossRef]
- Liu, L.L.; Liu, Y.; Hao, J.G.; Chen, J.W.; Li, P.; Chen, S.; Fu, P.; Li, W.; Zhai, J.W. Multi-scale collaborative optimization of SrTiO3-based energy storage ceramics with high performance and excellent stability. Nano Energy 2023, 109, 108275. [Google Scholar] [CrossRef]
- Liu, X.; Zhai, J.W.; Shen, B. Novel bismuth ferrite-based lead-free incipient piezoceramics with high electromechanical response. J. Mater. Chem. C 2019, 7, 5122–5130. [Google Scholar] [CrossRef]
- Shvartsman, V.V.; Lupascu, D.C. Lead-free relaxor ferroelectrics. J. Am. Ceram. Soc. 2012, 95, 1–26. [Google Scholar] [CrossRef]
- Li, F.; Zhang, S.J.; Damjanovic, D.; Chen, L.Q.; Shrout, T.R. Local structural heterogeneity and electromechanical responses of ferroelectrics: Learning from relaxor ferroelectrics. Adv. Funct. Mater. 2018, 28, 1801504. [Google Scholar] [CrossRef]

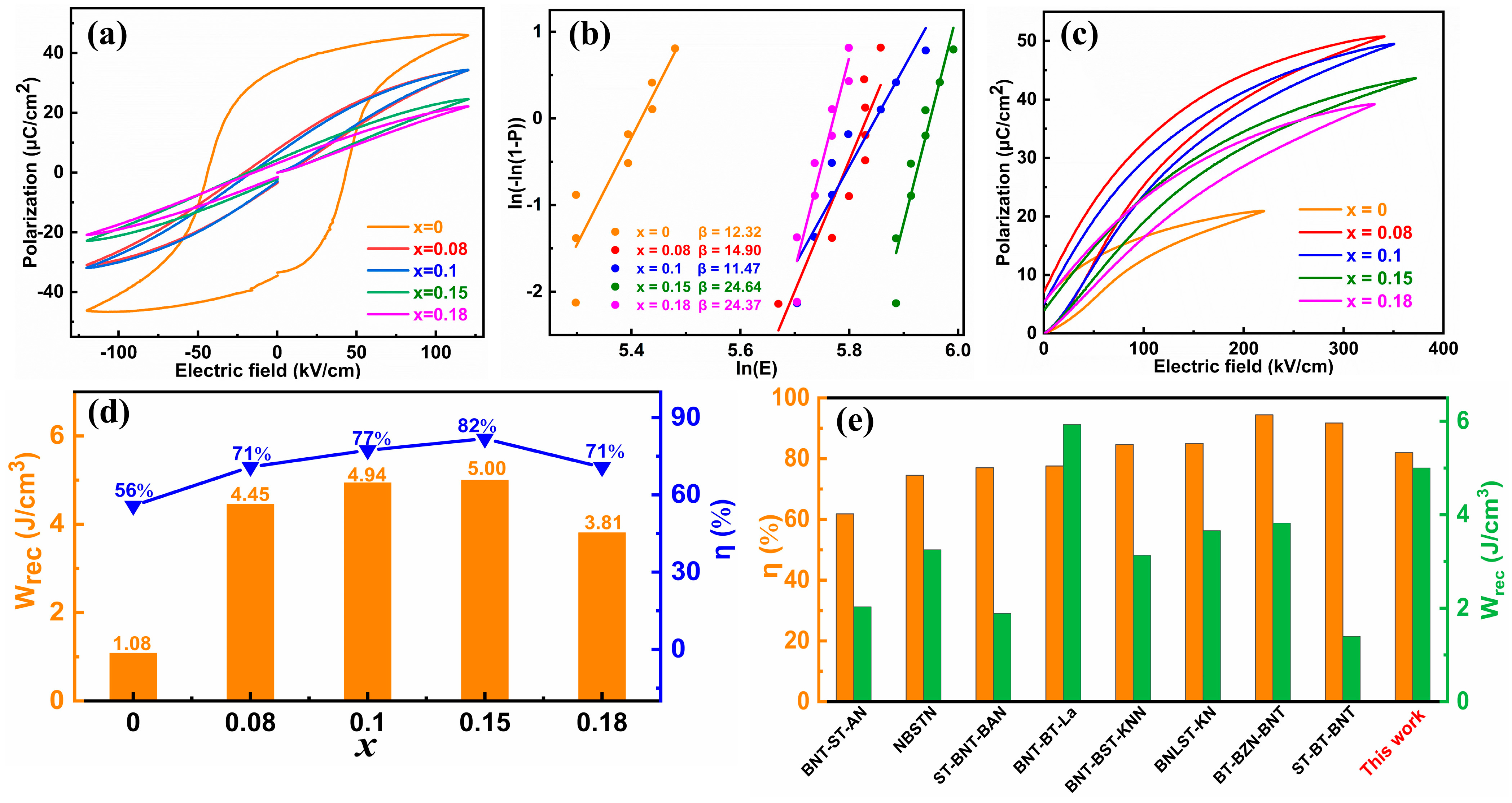


| x | Pr (μC/cm2) | Pmax (μC/cm2) | Ec (kV/cm) | Eb (kV/cm) | Wrec (J/cm3) | η |
|---|---|---|---|---|---|---|
| 0 | 5.37 | 20.92 | 43.30 | 226 | 1.08 | 56% |
| 0.08 | 7.25 | 50.77 | 20.57 | 342 | 4.45 | 71% |
| 0.10 | 5.21 | 49.46 | 16.22 | 347 | 4.94 | 77% |
| 0.15 | 3.96 | 43.42 | 17.75 | 383 | 5.00 | 82% |
| 0.18 | 5.44 | 39.15 | 14.43 | 321 | 3.81 | 71% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Lu, G.; Zhao, Y.; Zhao, R.; Zhao, J.; Hao, J.; Bai, W.; Li, P.; Li, W. Ferroelectric and Relaxor-Ferroelectric Phases Coexisting Boosts Energy Storage Performance in (Bi0.5Na0.5)TiO3-Based Ceramics. Molecules 2024, 29, 3187. https://doi.org/10.3390/molecules29133187
Li Y, Lu G, Zhao Y, Zhao R, Zhao J, Hao J, Bai W, Li P, Li W. Ferroelectric and Relaxor-Ferroelectric Phases Coexisting Boosts Energy Storage Performance in (Bi0.5Na0.5)TiO3-Based Ceramics. Molecules. 2024; 29(13):3187. https://doi.org/10.3390/molecules29133187
Chicago/Turabian StyleLi, Yunting, Guangrui Lu, Yan Zhao, Rui Zhao, Jiaqi Zhao, Jigong Hao, Wangfeng Bai, Peng Li, and Wei Li. 2024. "Ferroelectric and Relaxor-Ferroelectric Phases Coexisting Boosts Energy Storage Performance in (Bi0.5Na0.5)TiO3-Based Ceramics" Molecules 29, no. 13: 3187. https://doi.org/10.3390/molecules29133187
APA StyleLi, Y., Lu, G., Zhao, Y., Zhao, R., Zhao, J., Hao, J., Bai, W., Li, P., & Li, W. (2024). Ferroelectric and Relaxor-Ferroelectric Phases Coexisting Boosts Energy Storage Performance in (Bi0.5Na0.5)TiO3-Based Ceramics. Molecules, 29(13), 3187. https://doi.org/10.3390/molecules29133187





