Quantum Mechanics Characterization of Non-Covalent Interaction in Nucleotide Fragments
Abstract
:1. Introduction
2. Results
2.1. Small Molecule Benchmarking
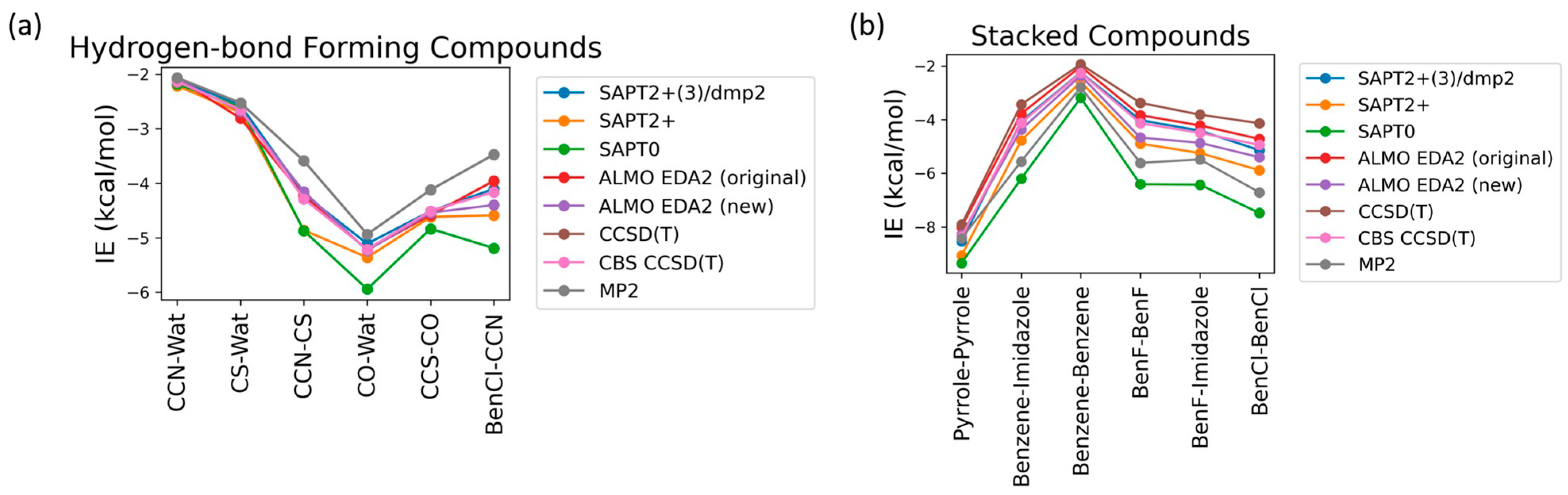
2.1.1. Various Theoretical Methods
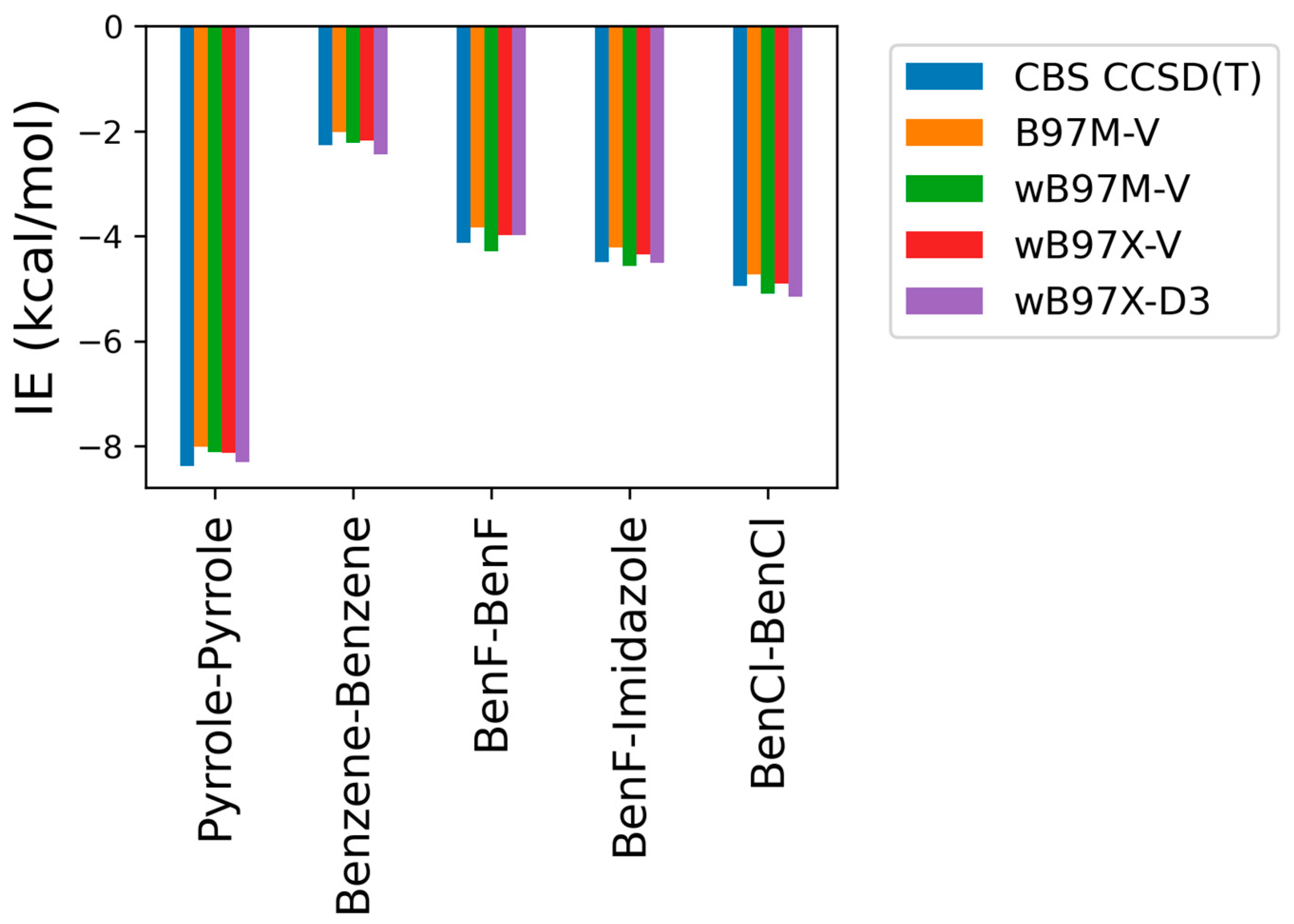
2.1.2. Comparison of DFT Methods
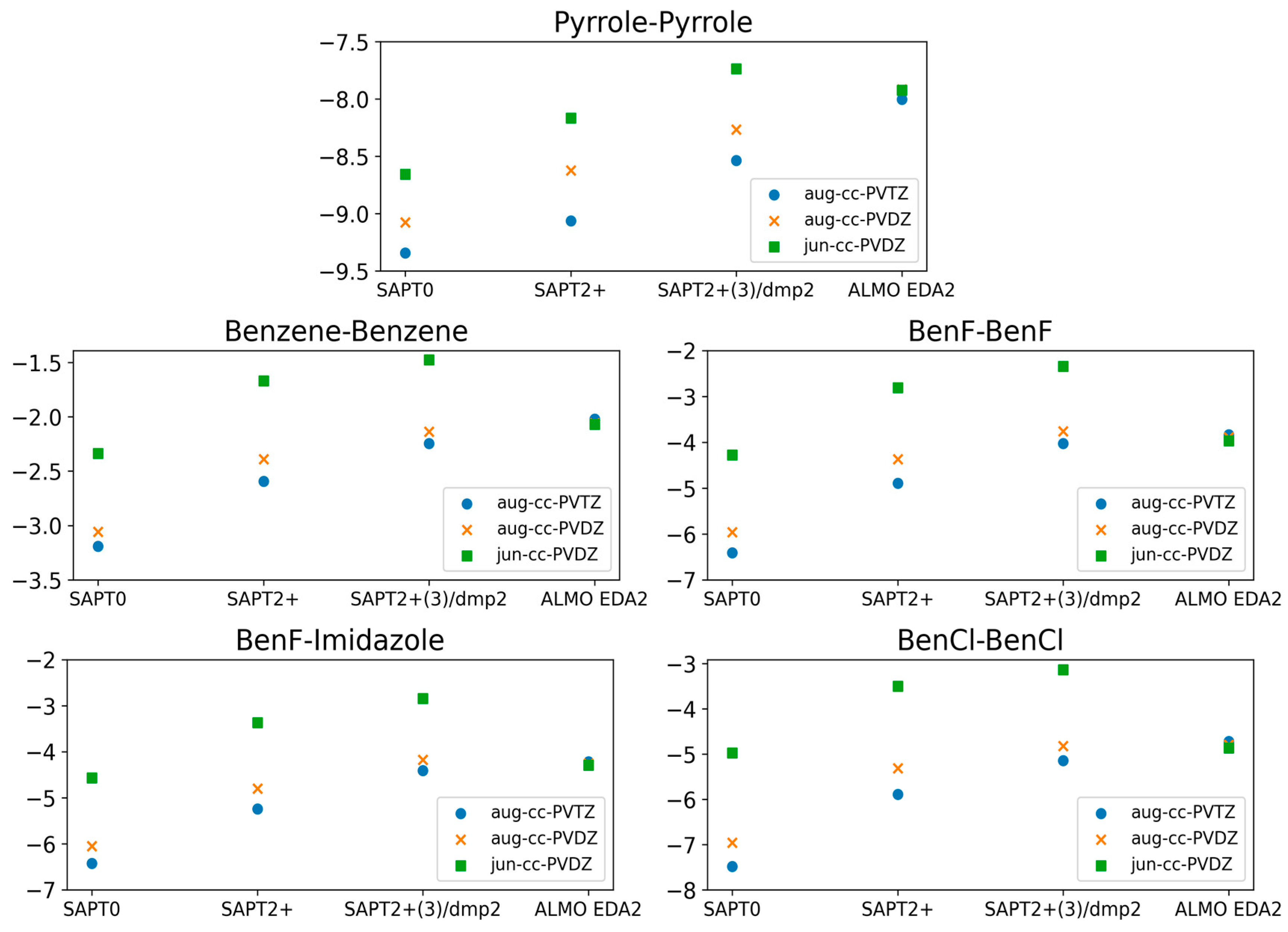
2.1.3. Basis Set Dependence
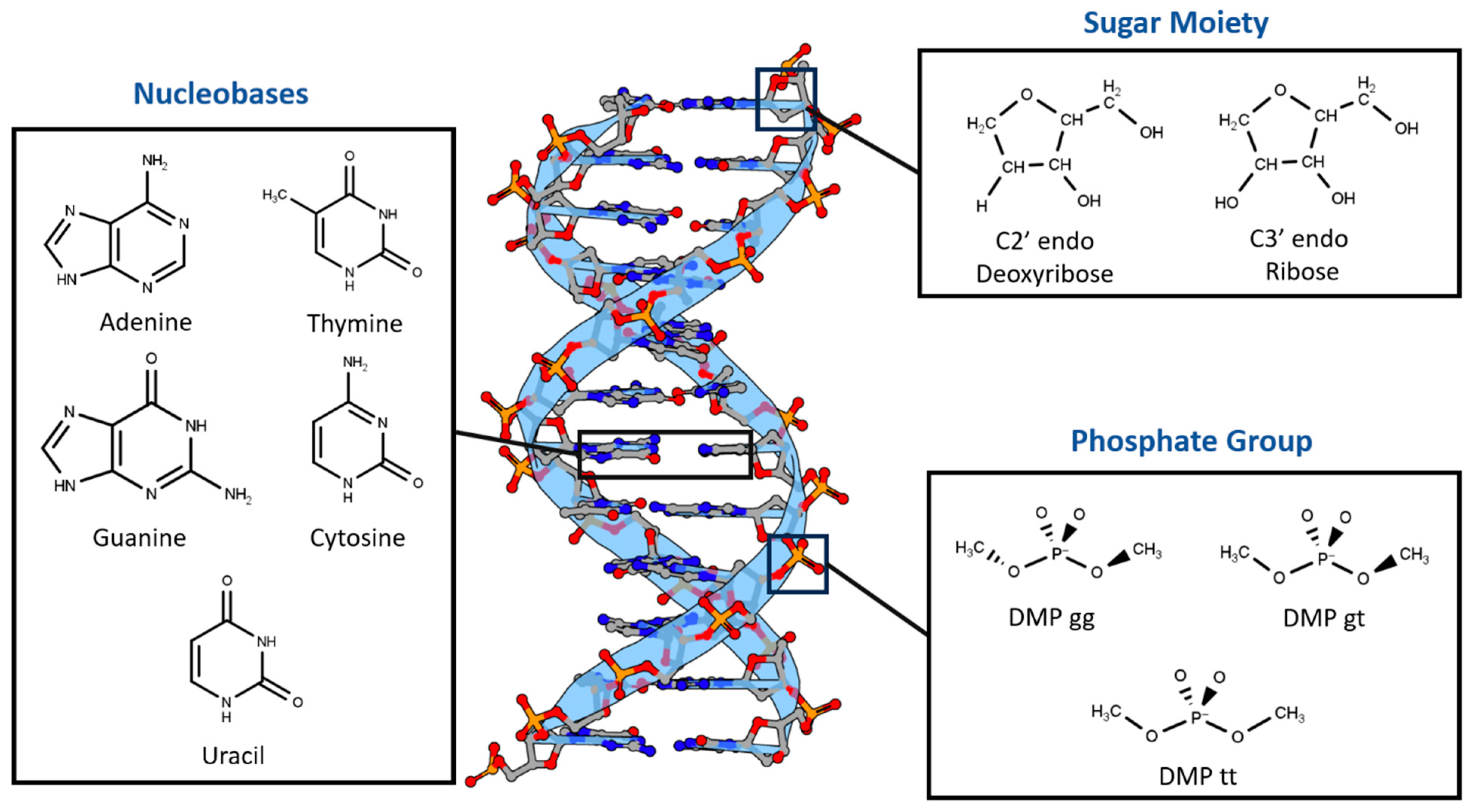
2.2. Total Interaction Energies of the Main Three Nucleotide Constituents
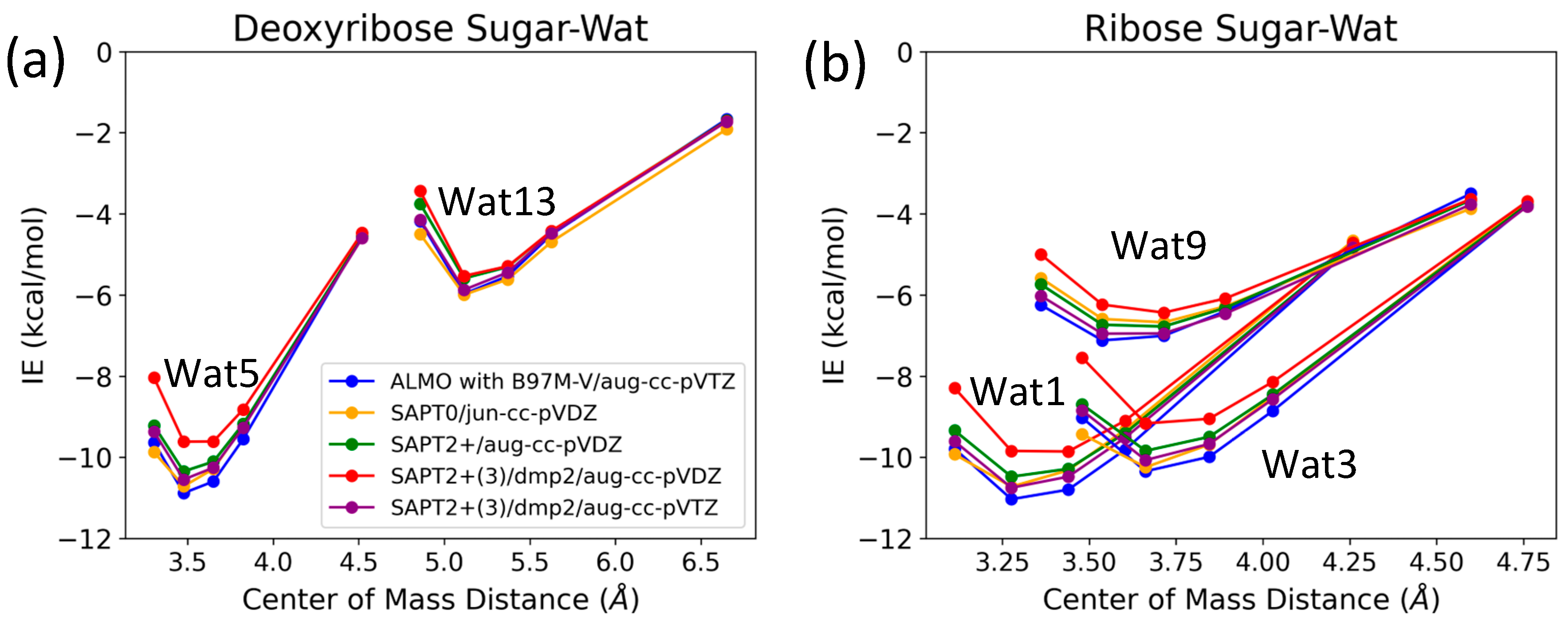
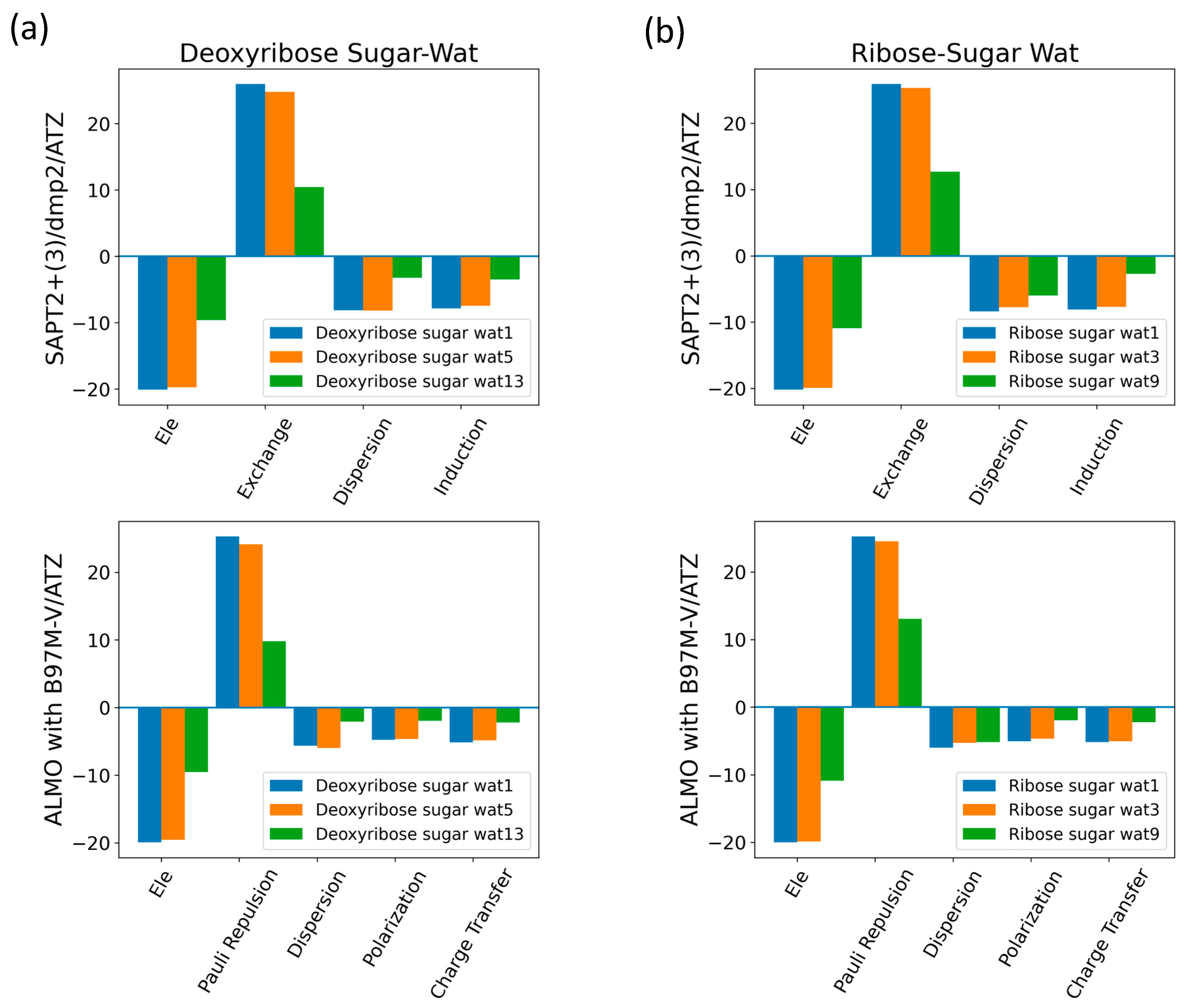
2.2.1. Sugar Moiety
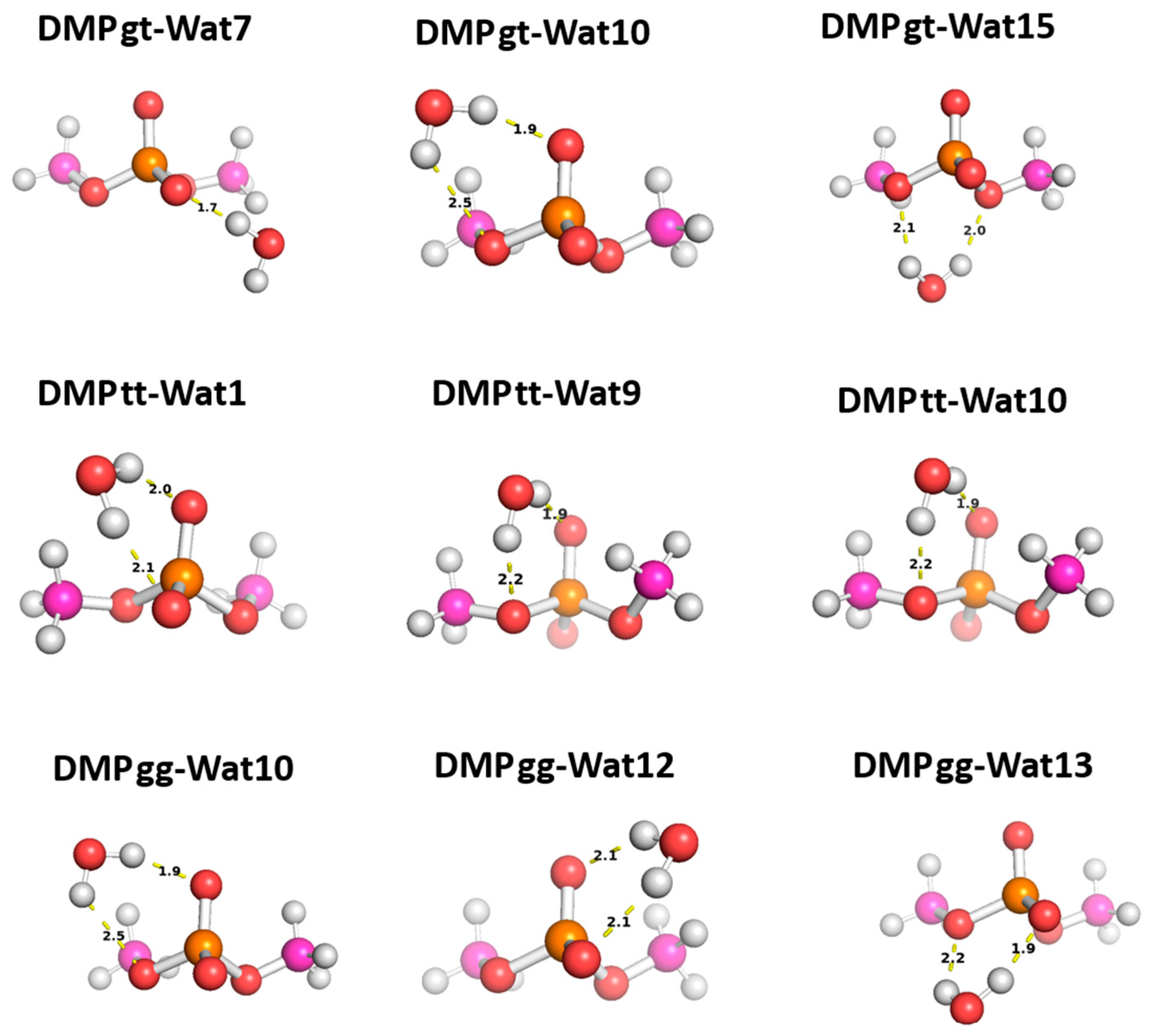
2.2.2. DMP
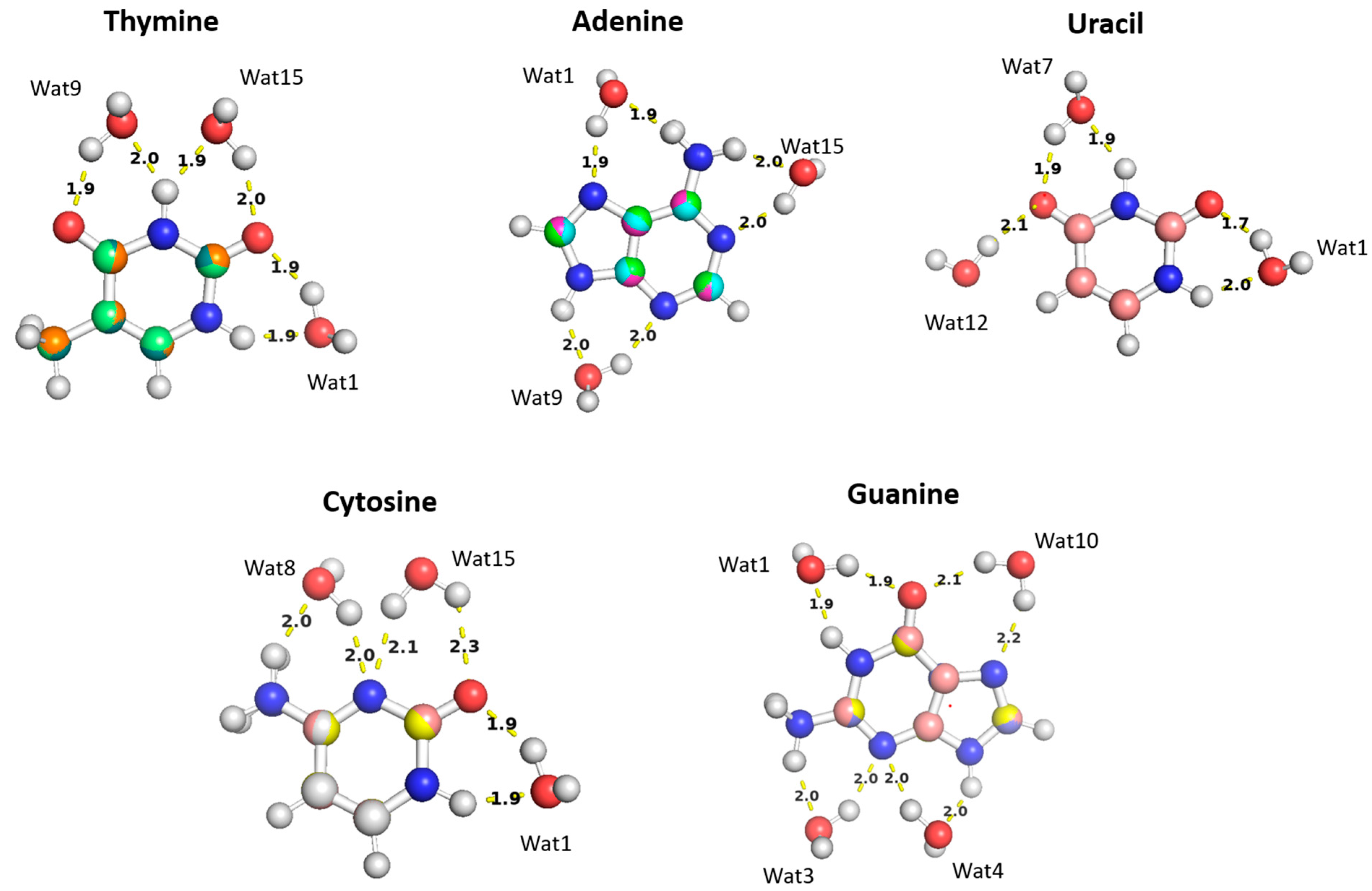
2.2.3. Nucleobases
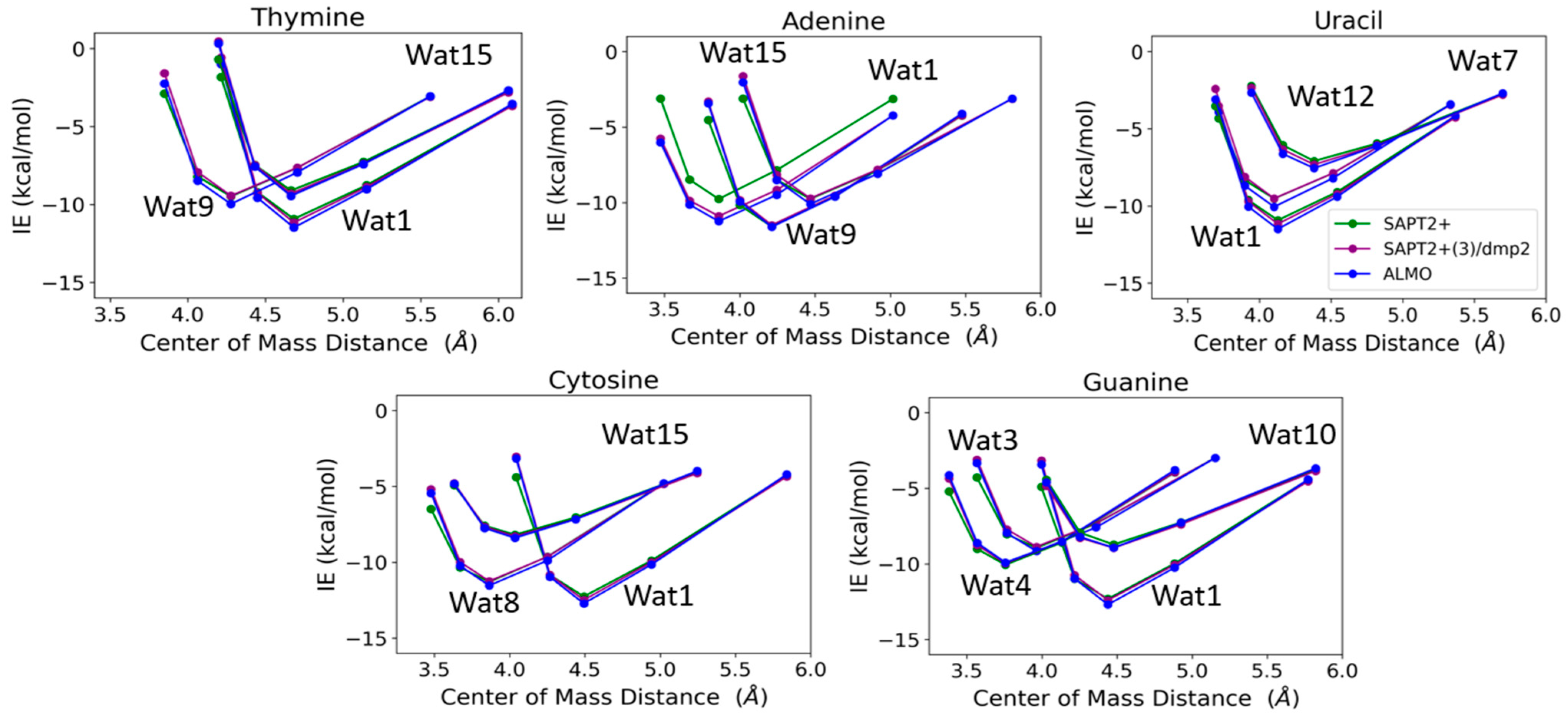
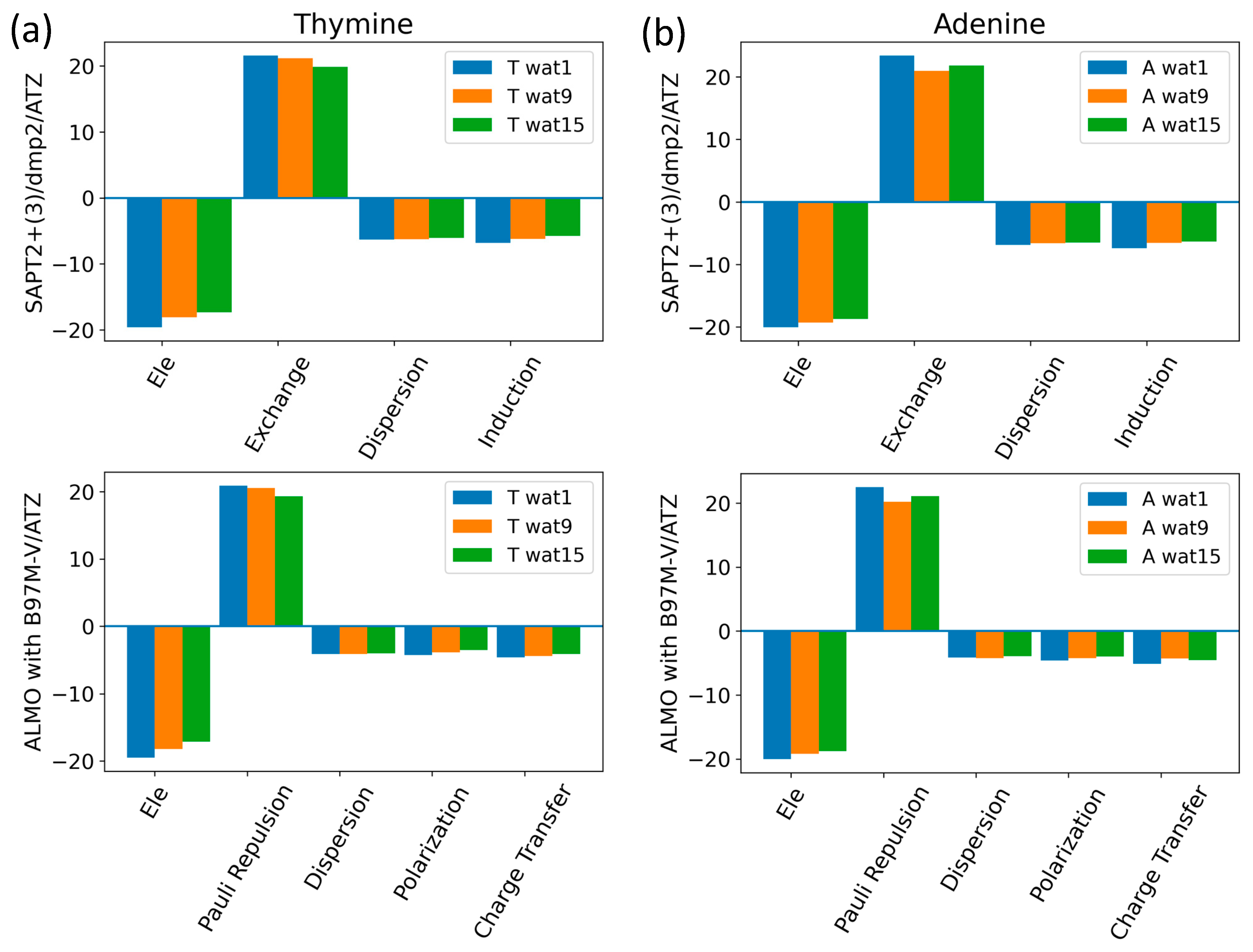
Nucleobase-Water Interactions
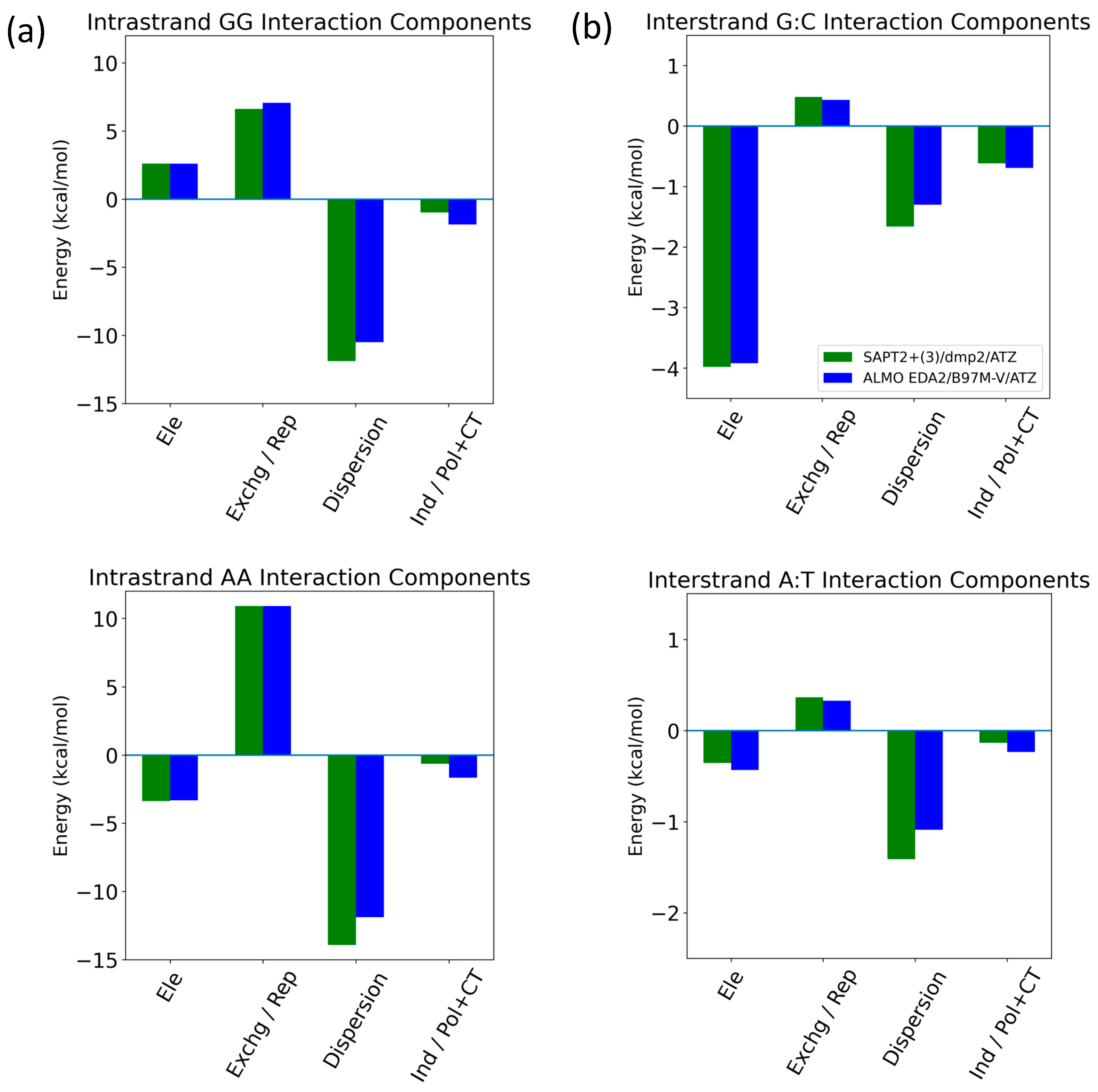
Intrastrand and Interstrand Nucleobases
3. Discussion
4. Materials and Methods
4.1. Preparation of Structures
4.2. Ab Initio Calculations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rudolph, F.B. The Biochemistry and Physiology of Nucleotides123. J. Nutr. 1994, 124, 124S–127S. [Google Scholar] [CrossRef] [PubMed]
- Breaker, R.R.; Joyce, G.F. The expanding view of RNA and DNA function. Chem. Biol. 2014, 21, 1059–1065. [Google Scholar] [CrossRef]
- Hudson, W.H.; Ortlund, E.A. The structure, function and evolution of proteins that bind DNA and RNA. Nat. Rev. Mol. Cell Biol. 2014, 15, 749–760. [Google Scholar] [CrossRef] [PubMed]
- Varshney, D.; Spiegel, J.; Zyner, K.; Tannahill, D.; Balasubramanian, S. The regulation and functions of DNA and RNA G-quadruplexes. Nat. Rev. Mol. Cell Biol. 2020, 21, 459–474. [Google Scholar] [CrossRef] [PubMed]
- Carthew, R.W.; Sontheimer, E.J. Origins and mechanisms of miRNAs and siRNAs. Cell 2009, 136, 642–655. [Google Scholar] [CrossRef]
- Hays, F.A.; Teegarden, A.; Jones, Z.J.; Harms, M.; Raup, D.; Watson, J.; Cavaliere, E.; Ho, P.S. How sequence defines structure: A crystallographic map of DNA structure and conformation. Proc. Natl. Acad. Sci. USA 2005, 102, 7157–7162. [Google Scholar] [CrossRef]
- Svozil, D.; Kalina, J.; Omelka, M.; Schneider, B. DNA conformations and their sequence preferences. Nucleic Acids Res. 2008, 36, 3690–3706. [Google Scholar] [CrossRef]
- Minchenkova, L.E.; Schyolkina, A.K.; Chernov, B.K.; Ivanov, V.I. CC/GG contacts facilitate the B to A transition of DMA in solution. J. Biomol. Struct. Dyn. 1986, 4, 463–476. [Google Scholar] [CrossRef]
- Jose, D.; Porschke, D. The dynamics of the B-A transition of natural DNA double helices. J. Am. Chem. Soc. 2005, 127, 16120–16128. [Google Scholar] [CrossRef]
- Whelan, D.R.; Hiscox, T.J.; Rood, J.I.; Bambery, K.R.; McNaughton, D.; Wood, B.R. Detection of an en masse and reversible B-to A-DNA conformational transition in prokaryotes in response to desiccation. J. R. Soc. Interface 2014, 11, 20140454. [Google Scholar] [CrossRef]
- Zhang, C.; Lu, C.; Jing, Z.; Wu, C.; Piquemal, J.P.; Ponder, J.W.; Ren, P. AMOEBA polarizable atomic multipole force field for nucleic acids. J. Chem. Theory Comput. 2018, 14, 2084–2108. [Google Scholar] [CrossRef] [PubMed]
- Herbert, A.; Rich, A. The Biology of Left-handed Z-DNA (∗). J. Biol. Chem. 1996, 271, 11595–11598. [Google Scholar] [CrossRef] [PubMed]
- Gessner, R.V.; Frederick, C.A.; Quigley, G.J.; Rich, A.; Wang, A.H.J. The molecular structure of the left-handed Z-DNA double helix at 1.0-Å atomic resolution: Geometry, conformation, and ionic interactions of d (CGCGCG). J. Biol. Chem. 1989, 264, 7921–7935. [Google Scholar] [CrossRef]
- Leontis, N.; Westhof, E. RNA 3D Structure Analysis and Prediction; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 27. [Google Scholar]
- Rao, S.N.; Kollman, P. On the role of uniform and mixed sugar puckers in DNA double-helical structures. J. Am. Chem. Soc. 1985, 107, 1611–1617. [Google Scholar] [CrossRef]
- Galindo-Murillo, R.; Robertson, J.C.; Zgarbova, M.; Sponer, J.; Otyepka, M.; Jurecka, P.; Cheatham, T.E., III. Assessing the current state of amber force field modifications for DNA. J. Chem. Theory Comput. 2016, 12, 4114–4127. [Google Scholar] [CrossRef]
- Zhang, C.; Lu, C.; Wang, Q.; Ponder, J.W.; Ren, P. Polarizable multipole-based force field for dimethyl and trimethyl phosphate. J. Chem. Theory Comput. 2015, 11, 5326–5339. [Google Scholar] [CrossRef]
- Zhang, C.; Bell, D.; Harger, M.; Ren, P. Polarizable multipole-based force field for aromatic molecules and nucleobases. J. Chem. Theory Comput. 2017, 13, 666–678. [Google Scholar] [CrossRef] [PubMed]
- Lemkul, J.A.; MacKerell, A.D., Jr. Polarizable force field for DNA based on the classical Drude oscillator: II. Microsecond molecular dynamics simulations of duplex DNA. J. Chem. Theory Comput. 2017, 13, 2072–2085. [Google Scholar] [CrossRef] [PubMed]
- Lemkul, J.A.; MacKerell, A.D., Jr. Polarizable force field for DNA based on the classical Drude oscillator: I. Refinement using quantum mechanical base stacking and conformational energetics. J. Chem. Theory Comput. 2017, 13, 2053–2071. [Google Scholar] [CrossRef]
- Lemkul, J.A.; MacKerell, A.D., Jr. Polarizable force field for RNA based on the classical drude oscillator. J. Comput. Chem. 2018, 39, 2624–2646. [Google Scholar] [CrossRef]
- Sherrill, C.D.; Sumpter, B.G.; Sinnokrot, M.O.; Marshall, M.S.; Hohenstein, E.G.; Walker, R.C.; Gould, I.R. Assessment of standard force field models against high-quality ab initio potential curves for prototypes of π–π, CH/π, and SH/π interactions. J. Comput. Chem. 2009, 30, 2187–2193. [Google Scholar] [CrossRef] [PubMed]
- Hohenstein, E.G.; Duan, J.; Sherrill, C.D. Origin of the surprising enhancement of electrostatic energies by electron-donating substituents in substituted sandwich benzene dimers. J. Am. Chem. Soc. 2011, 133, 13244–13247. [Google Scholar] [CrossRef] [PubMed]
- Stone, A. The Theory of Intermolecular Forces; oUP Oxford: Oxford, UK, 2013. [Google Scholar]
- Parker, T.M.; Sherrill, C.D. Assessment of empirical models versus high-accuracy ab initio methods for nucleobase stacking: Evaluating the importance of charge penetration. J. Chem. Theory Comput. 2015, 11, 4197–4204. [Google Scholar] [CrossRef] [PubMed]
- Hohenstein, E.G.; Sherrill, C.D. Efficient evaluation of triple excitations in symmetry-adapted perturbation theory via second-order Møller–Plesset perturbation theory natural orbitals. J. Chem. Phys. 2010, 133, 104107. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.G.; Burns, L.A.; Simmonett, A.C.; Parrish, R.M.; Schieber, M.C.; Galvelis, R.; Kraus, P.; Kruse, H.; Di Remigio, R.; Alenaizan, A.; et al. PSI4 1.4: Open-source software for high-throughput quantum chemistry. J. Chem. Phys. 2020, 152, 184108. [Google Scholar] [CrossRef] [PubMed]
- Horn, P.R.; Head-Gordon, M. Polarization contributions to intermolecular interactions revisited with fragment electric-field response functions. J. Chem. Phys. 2015, 143, 114111. [Google Scholar] [CrossRef] [PubMed]
- Horn, P.R.; Mao, Y.; Head-Gordon, M. Probing non-covalent interactions with a second generation energy decomposition analysis using absolutely localized molecular orbitals. Phys. Chem. Chem. Phys. 2016, 18, 23067–23079. [Google Scholar] [CrossRef] [PubMed]
- Horn, P.R.; Mao, Y.; Head-Gordon, M. Defining the contributions of permanent electrostatics, Pauli repulsion, and dispersion in density functional theory calculations of intermolecular interaction energies. J. Chem. Phys. 2016, 144, 114107. [Google Scholar] [CrossRef] [PubMed]
- Rosenberger, D.; Smith, J.S.; Garcia, A.E. Modeling of Peptides with Classical and Novel Machine Learning Force Fields: A Comparison. J. Phys. Chem. B 2021, 125, 3598–3612. [Google Scholar] [CrossRef]
- Montavon, G.; Rupp, M.; Gobre, V.; Vazquez-Mayagoitia, A.; Hansen, K.; Tkatchenko, A.; Müller, K.R.; Von Lilienfeld, O.A. Machine learning of molecular electronic properties in chemical compound space. New J. Phys. 2013, 15, 095003. [Google Scholar] [CrossRef]
- Ramakrishnan, R.; Dral, P.O.; Rupp, M.; von Lilienfeld, O.A. Big Data Meets Quantum Chemistry Approximations: The Δ-Machine Learning Approach. J. Chem. Theory Comput. 2015, 11, 2087. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.S.; Nebgen, B.T.; Zubatyuk, R.; Lubbers, N.; Devereux, C.; Barros, K.; Tretiak, S.; Isayev, O.; Roitberg, A.E. Approaching coupled cluster accuracy with a general-purpose neural network potential through transfer learning. Nat. Commun. 2019, 10, 2903. [Google Scholar] [CrossRef] [PubMed]
- Mezei, P.D.; von Lilienfeld, O.A. Non-covalent quantum machine learning corrections to density functionals. J. Chem. Theory Comput. 2020, 16, 2647. [Google Scholar] [CrossRef] [PubMed]
- Chmiela, S.; Sauceda, H.E.; Müller, K.-R.; Tkatchenko, A. Towards exact molecular dynamics simulations with machine-learned force fields. Nat. Commun. 2018, 9, 3887. [Google Scholar] [CrossRef] [PubMed]
- Nudejima, T.; Ikabata, Y.; Seino, J.; Yoshikawa, T.; Nakai, H. Machine-learned electron correlation model based on correlation energy density at complete basis set limit. J. Chem. Phys. 2019, 151, 024104. [Google Scholar] [CrossRef] [PubMed]
- Eastman, P.; Behara, P.K.; Dotson, D.L.; Galvelis, R.; Herr, J.E.; Horton, J.T.; Mao, Y.; Chodera, J.D.; Pritchard, B.P.; Wang, Y.; et al. SPICE, A Dataset of Drug-like Molecules and Peptides for Training Machine Learning Potentials. Sci. Data 2023, 10, 11. [Google Scholar] [CrossRef] [PubMed]
- Gyevi-Nagy, L.; Kállay, M.; Nagy, P.R. Accurate Reduced-Cost CCSD(T) Energies: Parallel Implementation, Benchmarks, and Large-Scale Applications. J. Chem. Theory Comput. 2021, 17, 860–878. [Google Scholar] [CrossRef] [PubMed]
- Helgaker, T.; Jørgensen, P.; Olsen, J. Molecular Electronic Structure Theory; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- Shavitt, I.; Bartlett, R.J. Many-Body Methods in Chemistry and Physics: MBPT and Coupled-Cluster Theory; Cambridge Molecular Science; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Bartlett, R.J.; Musiał, M. Coupled-cluster theory in quantum chemistry. Rev. Mod. Phys. 2007, 79, 291. [Google Scholar] [CrossRef]
- Crawford, T.D.; Schaefer, H.F., III. An Introduction to Coupled Cluster Theory for Computational Chemists. Rev. Comput. Chem. 2000, 14, 33–136. [Google Scholar] [CrossRef]
- Donchev, A.G.; Taube, A.G.; Decolvenaere, E.; Hargus, C.; McGibbon, R.T.; Law, K.H.; Gregersen, B.A.; Li, J.L.; Palmo, K.; Siva, K.; et al. Quantum chemical benchmark databases of gold-standard dimer interaction energies. Sci. Data 2021, 8, 55. [Google Scholar] [CrossRef]
- Řezáč, J.; Jurečka, P.; Riley, K.E.; Černý, J.; Valdes, H.; Pluháčková, K.; Berka, K.; Řezáč, T.; Pitoňák, M.; Vondrášek, J.; et al. Quantum chemical benchmark energy and geometry database for molecular clusters and complex molecular systems (www.begdb.com): A users manual and examples. Collect. Czechoslov. Chem. Commun. 2008, 73, 1261–1270. [Google Scholar] [CrossRef]
- Marek, P.H.; Szatylowicz, H.; Krygowski, T.M. Stacking of nucleic acid bases: Optimization of the computational approach—The case of adenine dimers. Struct. Chem. 2019, 30, 351–359. [Google Scholar] [CrossRef]
- Parker, T.M.; Hohenstein, E.G.; Parrish, R.M.; Hud, N.V.; Sherrill, C.D. Quantum-mechanical analysis of the energetic contributions to π stacking in nucleic acids versus rise, twist, and slide. J. Am. Chem. Soc. 2013, 135, 1306–1316. [Google Scholar] [CrossRef] [PubMed]
- Kruse, H.; Havrila, M.; Šponer, J. QM computations on complete nucleic acids building blocks: Analysis of the Sarcin-Ricin RNA motif using DFT-D3, HF-3c, PM6-D3H, and MM approaches. J. Chem. Theory Comput. 2014, 10, 2615–2629. [Google Scholar] [CrossRef]
- Sladek, V.; Fedorov, D.G. The Importance of Charge Transfer and Solvent Screening in the Interactions of Backbones and Functional Groups in Amino Acid Residues and Nucleotides. Int. J. Mol. Sci. 2022, 23, 3514. [Google Scholar] [CrossRef]
- Kumawat, R.L.; Sherrill, C.D. High-Order Quantum-Mechanical Analysis of Hydrogen Bonding in Hachimoji and Natural DNA Base Pairs. J. Chem. Inf. Model. 2023, 63, 3150–3157. [Google Scholar] [CrossRef] [PubMed]
- Riley, K.E.; Hobza, P. Noncovalent interactions in biochemistry. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 3–17. [Google Scholar] [CrossRef]
- Lee, A.J.; Rackers, J.A.; Pathak, S.; Bricker, W.P. Building an ab initio solvated DNA model using Euclidean neural networks. PLoS ONE 2024, 19, e0297502. [Google Scholar] [CrossRef]
- Tomasello, G.; Armenia, I.; Molla, G. The Protein Imager: A full-featured online molecular viewer interface with server-side HQ-rendering capabilities. Bioinformatics 2020, 36, 2909–2911. [Google Scholar] [CrossRef]
- Khaliullin, R.Z.; Cobar, E.A.; Lochan, R.C.; Bell, A.T.; Head-Gordon, M. Unravelling the origin of intermolecular interactions using absolutely localized molecular orbitals. J. Phys. Chem. A 2007, 111, 8753–8765. [Google Scholar] [CrossRef]
- McDaniel, J.G.; Schmidt, J.R. Next-generation force fields from symmetry-adapted perturbation theory. Annu. Rev. Phys. Chem. 2016, 67, 467–488. [Google Scholar] [CrossRef] [PubMed]
- Hohenstein, E.G.; Sherrill, C.D. Density fitting and Cholesky decomposition approximations in symmetry-adapted perturbation theory: Implementation and application to probe the nature of π-π interactions in linear acenes. J. Chem. Phys. 2010, 132, 184111. [Google Scholar] [CrossRef]
- Hohenstein, E.G.; Sherrill, C.D. Density fitting of intramonomer correlation effects in symmetry-adapted perturbation theory. J. Chem. Phys. 2010, 133, 014101. [Google Scholar] [CrossRef] [PubMed]
- Plett, C.; Grimme, S. Automated and efficient generation of general molecular aggregate structures. Angew. Chem. Int. Ed. 2023, 62, e202214477. [Google Scholar] [CrossRef] [PubMed]
- Ponder, J.W. TINKER: Software Tools for Molecular Design; Washington University School of Medicine: Saint Louis, MO, USA, 2004; Volume 3, p. 116. [Google Scholar]
- Rackers, J.A.; Wang, Z.; Lu, C.; Laury, M.L.; Lagardère, L.; Schnieders, M.J.; Piquemal, J.P.; Ren, P.; Ponder, J.W. Tinker 8: Software tools for molecular design. J. Chem. Theory Comput. 2018, 14, 5273–5289. [Google Scholar] [CrossRef] [PubMed]
- Bannwarth, C.; Caldeweyher, E.; Ehlert, S.; Hansen, A.; Pracht, P.; Seibert, J.; Spicher, S.; Grimme, S. Extended tight-binding quantum chemistry methods. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2021, 11, e1493. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical Extended Tight-Binding Program Package. 2019. Available online: https://github.com/grimme-lab/xtb (accessed on 1 July 2024).
- Grimme, S.; Bannwarth, C.; Caldeweyher, E.; Pisarek, J.; Hansen, A. A general intermolecular force field based on tight-binding quantum chemical calculations. J. Chem. Phys. 2017, 147, 161708. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Hohenstein, E.G.; Parrish, R.M.; Sherrill, C.D.; Turney, J.M.; Schaefer, H.F. Large-scale symmetry-adapted perturbation theory computations via density fitting and Laplace transformation techniques: Investigating the fundamental forces of DNA-intercalator interactions. J. Chem. Phys. 2011, 135, 174107. [Google Scholar] [CrossRef]
- Jeziorski, B.; Moszynski, R.; Szalewicz, K. Perturbation theory approach to intermolecular potential energy surfaces of van der Waals complexes. Chem. Rev. 1994, 94, 1887–1930. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tarek Ibrahim, M.; Wait, E.; Ren, P. Quantum Mechanics Characterization of Non-Covalent Interaction in Nucleotide Fragments. Molecules 2024, 29, 3258. https://doi.org/10.3390/molecules29143258
Tarek Ibrahim M, Wait E, Ren P. Quantum Mechanics Characterization of Non-Covalent Interaction in Nucleotide Fragments. Molecules. 2024; 29(14):3258. https://doi.org/10.3390/molecules29143258
Chicago/Turabian StyleTarek Ibrahim, Mayar, Elizabeth Wait, and Pengyu Ren. 2024. "Quantum Mechanics Characterization of Non-Covalent Interaction in Nucleotide Fragments" Molecules 29, no. 14: 3258. https://doi.org/10.3390/molecules29143258
APA StyleTarek Ibrahim, M., Wait, E., & Ren, P. (2024). Quantum Mechanics Characterization of Non-Covalent Interaction in Nucleotide Fragments. Molecules, 29(14), 3258. https://doi.org/10.3390/molecules29143258






