Is Passynski’s Approach to Hydration Numbers Consistent with Thermodynamics?
Abstract
:1. Introduction
2. Two-State Model of the Binary Aqueous Solution
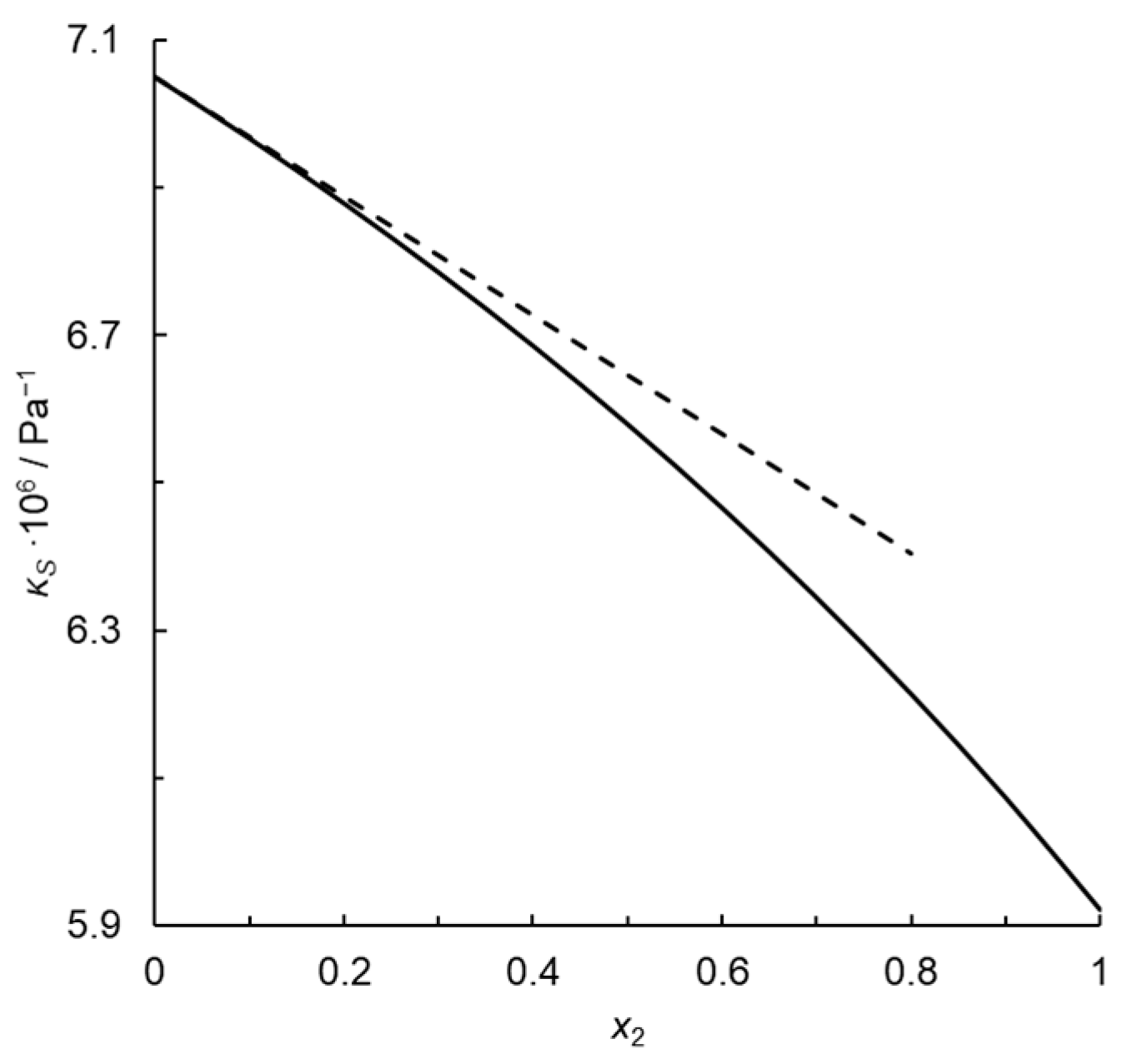
3. Discussion
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Franks, F. Water: 2nd Edition—A Matrix of Life. The Royal Society of Chemistry: Cambridge, UK, 2000. [Google Scholar]
- Passynski, A. Compressibility and solvation of solutions of electrolytes. Acta Physicochim. URSS 1938, 8, 385–418. [Google Scholar]
- Burakowski, A.; Gliński, J. Hydration Numbers of Nonelectrolytes from Acoustic Methods. Chem. Rev. 2012, 112, 2059–2081. [Google Scholar] [CrossRef] [PubMed]
- Burakowski, A.; Gliński, J. Hydration of the Zwitterionic Forms of Amino Acids from the Acoustic Passynski Method. Acta Phys. Pol. A 2008, 114, A39–A44. [Google Scholar] [CrossRef]
- Burakowski, A.; Gliński, J. Hydration of urea and its derivatives from acoustic and volumetric methods. Chem. Phys. Lett. 2015, 641, 40–43. [Google Scholar] [CrossRef]
- Chakraborty, N.; Juglan, K.C.; Kumar, H. Temperature-dependent thermodynamic and physicochemical studies of glycols in aqueous biotin solutions. J. Mol. Liq. 2021, 337, 116605. [Google Scholar] [CrossRef]
- Clavijo-Penagos, J.A.; Gracia-Fadrique, J.; Romero, C.M. Effect of temperature on the volumetric and thermoacoustic properties of polyoxyethylene (10) cetyl ether: C16E10 and polyoxyethylene (20) cetyl ether: C16E20 in aqueous solution. J. Mol. Liq. 2024, 398, 124225. [Google Scholar] [CrossRef]
- Cruz, Y.P.; Esteso, M.A.; Romero, C.M. Effect of temperature on the partial molar volumes and the partial molar compressibilities of amino alcohols in aqueous solution. J. Chem. Thermodyn. 2021, 160, 106521. [Google Scholar] [CrossRef]
- Dagade, D.H.; Shinde, S.P.; Madkar, K.R.; Barge, S.S. Density and sound speed study of hydration of 1-butyl-3-methylimidazolium based amino acid ionic liquids in aqueous solutions. J. Chem. Thermodyn. 2014, 79, 192–204. [Google Scholar] [CrossRef]
- Gliński, J.; Burakowski, A. Is the hydration number of a non-electrolyte additive with length and constituents of the solute molecule? Eur. Phys. J. Spec. Top. 2008, 154, 275–279. [Google Scholar] [CrossRef]
- Jóźwiak, M.; Burakowski, A.; Tyczyńska, M.; Komudzińska, M. Compression of selected glymes in N,N-dimethylformamide plus water. The hydration numbers and hydrophobic hydration process of glymes. J. Mol. Liq. 2022, 362, 119722. [Google Scholar] [CrossRef]
- Krakowiak, J.; Wawer, J. Hydration of urea and its derivatives—Volumetric and compressibility studies. J. Chem. Thermodyn. 2014, 79, 109–117. [Google Scholar] [CrossRef]
- Musale, S.P.; Patil, K.R.; Gavhane, R.J.; Dagade, D.H. Density and Speed-of-Sound Measurements for Dilute Binary Mixtures of Diethylammonium-Based Protic Ionic Liquids with Water. J. Chem. Eng. Data 2018, 63, 1859–1876. [Google Scholar] [CrossRef]
- Warmińska, D.; Kloskowski, A. Influence of temperature and anion type on thermophysical properties of aqueous solutions of morpholine based amino acid ionic liquids. J. Chem. Thermodyn. 2023, 187, 107148. [Google Scholar] [CrossRef]
- Kiełek, K.; Marczak, W. Hydration of Non-electrolytes in H2O and D2O Investigated by Passynski’s Method. Int. J. Thermophys. 2010, 31, 77–84. [Google Scholar] [CrossRef]
- Density and Sound Velocity Meter: DSA 5000 M, Anton Paar. Available online: https://www.anton-paar.com/uk-en/products/details/density-and-sound-velocity-meter-dsa-5000-m/ (accessed on 26 July 2024).
- Onori, G. Ionic hydration in sodium chloride solutions. J. Chem. Phys. 1988, 89, 510–516. [Google Scholar] [CrossRef]
- Reis, J.C.R.; Blandamer, M.J.; Davis, M.I.; Douhéret, G. The concepts of non-Gibbsian and non-Lewisian properties in chemical thermodynamics. Phys. Chem. Chem. Phys. 2001, 3, 1465–1470. [Google Scholar] [CrossRef]
- Douhéret, G.; Davis, M.I.; Reis, J.C.R.; Blandamer, M.J. Isentropic Compressibilities—Experimental Origin and the Quest for their Rigorous Estimation in Thermodynamically Ideal Liquid Mixtures. ChemPhysChem 2001, 2, 148–161. [Google Scholar] [CrossRef] [PubMed]
- Marczak, W.; Łężniak, M.; Zorębski, M.; Lodowski, P.; Przybyła, A.; Truszkowska, D.; Almásy, L. Water-induced aggregation and hydrophobic hydration in aqueous solutions of N-methylpiperidine. RSC Adv. 2013, 3, 22053–22064. [Google Scholar] [CrossRef]
- Shiio, H.; Ogawa, T.; Yoshihashi, H. Measurement of the Amount of Bound Water by Ultrasonic Interferometer. J. Am. Chem. Soc. 1955, 77, 4980–4982. [Google Scholar] [CrossRef]
- Shiio, H.; Yoshihashi, H. Measurement of the Amount of Bound Water by Ultrasonic Interferometer. II. Polyvinyl Alcohol and its Partially Substituted Acetates. J. Phys. Chem. 1956, 60, 1049–1061. [Google Scholar] [CrossRef]
- Shiio, H. Ultrasonic Interferometer Measurements of the Amount of Bound Water. Saccharides. J. Am. Chem. Soc. 1958, 80, 70–73. [Google Scholar] [CrossRef]
- Yasunaga, T.; Hirata, Y.; Kawano, Y.; Miura, M. Ultrasonic Studies of the Hydration of Various Compounds in an Ethanol-Water Mixed Solvent. I. Hydration of Inorganic Compounds. Bull. Chem. Soc. Jpn. 1964, 37, 867–871. [Google Scholar] [CrossRef]
- Yasunaga, T.; Usui, I.; Iwata, K.; Miura, M. Ultrasonic Studies of the Hydration of Various Compounds in an Ethanol- Water Mixed Solvent. II. The Hydration of Organic Compounds. Bull. Chem. Soc. Jpn. 1964, 37, 1658–1660. [Google Scholar] [CrossRef]
- Isemura, T.; Goto, S. Studies of the Hydration and the Structure of Water and Their Roles in Protein Structure. II. The Hydration of Electrolytes by Ultrasonic Interferometry and Its Temperature Dependence. Bull. Chem. Soc. Jpn. 1964, 37, 1690–1693. [Google Scholar] [CrossRef]
- Goto, S.; Isemura, T. Studies of the Hydration and the Structure of Water and Their Roles in Protein Structure. IV. The Hydration of Amino Acids and Oligopeptides. Bull. Chem. Soc. Jpn. 1964, 37, 1697–1701. [Google Scholar] [CrossRef]
- Millero, F.J.; Ward, G.K.; Lepple, F.K.; Hoff, E.V. Isothermal Compressibility of Aqueous Sodium Chloride, Magnesium Chloride, Sodium Sulfate, and Magnesium Sulfate Solutions from 0 to 45° at 1 Atm. J. Phys. Chem. 1974, 78, 1636–1643. [Google Scholar] [CrossRef]
- Millero, F.J.; Lo Surdo, A.; Shin, C.J. The Apparent Molal Volumes and Adiabatic Compressibilities of Aqueous Amino Acids at 25 °C. J. Phys. Chem. 1978, 82, 784–792. [Google Scholar] [CrossRef]
- Muller, N. Is There a Region of Highly Structured Water Around a Nonpolar Solute Molecule? J. Solut. Chem. 1988, 17, 661–672. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marczak, W. Is Passynski’s Approach to Hydration Numbers Consistent with Thermodynamics? Molecules 2024, 29, 4214. https://doi.org/10.3390/molecules29174214
Marczak W. Is Passynski’s Approach to Hydration Numbers Consistent with Thermodynamics? Molecules. 2024; 29(17):4214. https://doi.org/10.3390/molecules29174214
Chicago/Turabian StyleMarczak, Wojciech. 2024. "Is Passynski’s Approach to Hydration Numbers Consistent with Thermodynamics?" Molecules 29, no. 17: 4214. https://doi.org/10.3390/molecules29174214




