Modeling UV/Vis Absorption Spectra of Food Colorants in Solution: Anthocyanins and Curcumin as Case Studies
Abstract
1. Introduction
2. Results and Discussion
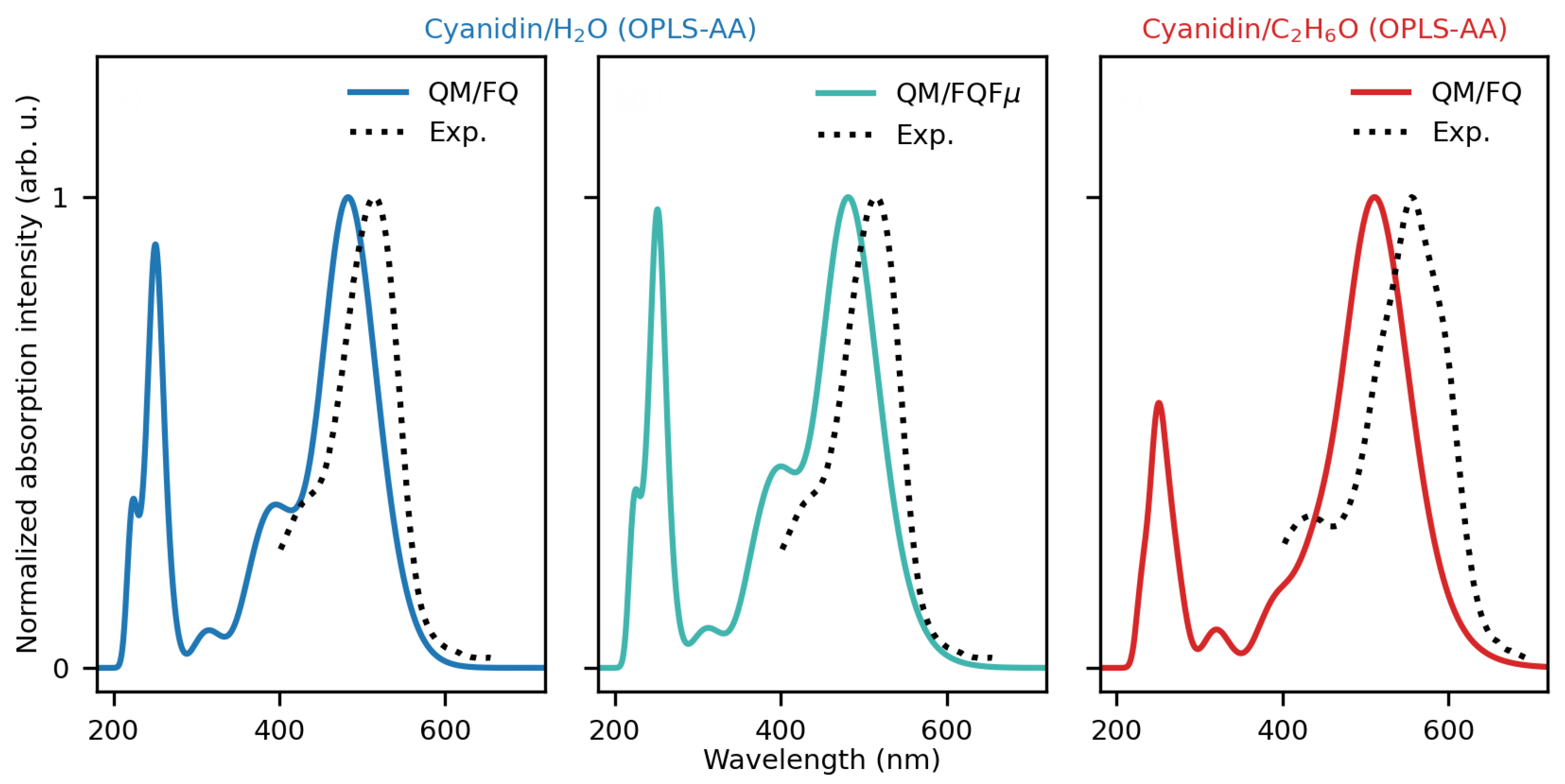
2.1. Cyanidin Dissolved in Water and Ethanol
2.1.1. MD Analysis and Hydrogen Bonding Patterns
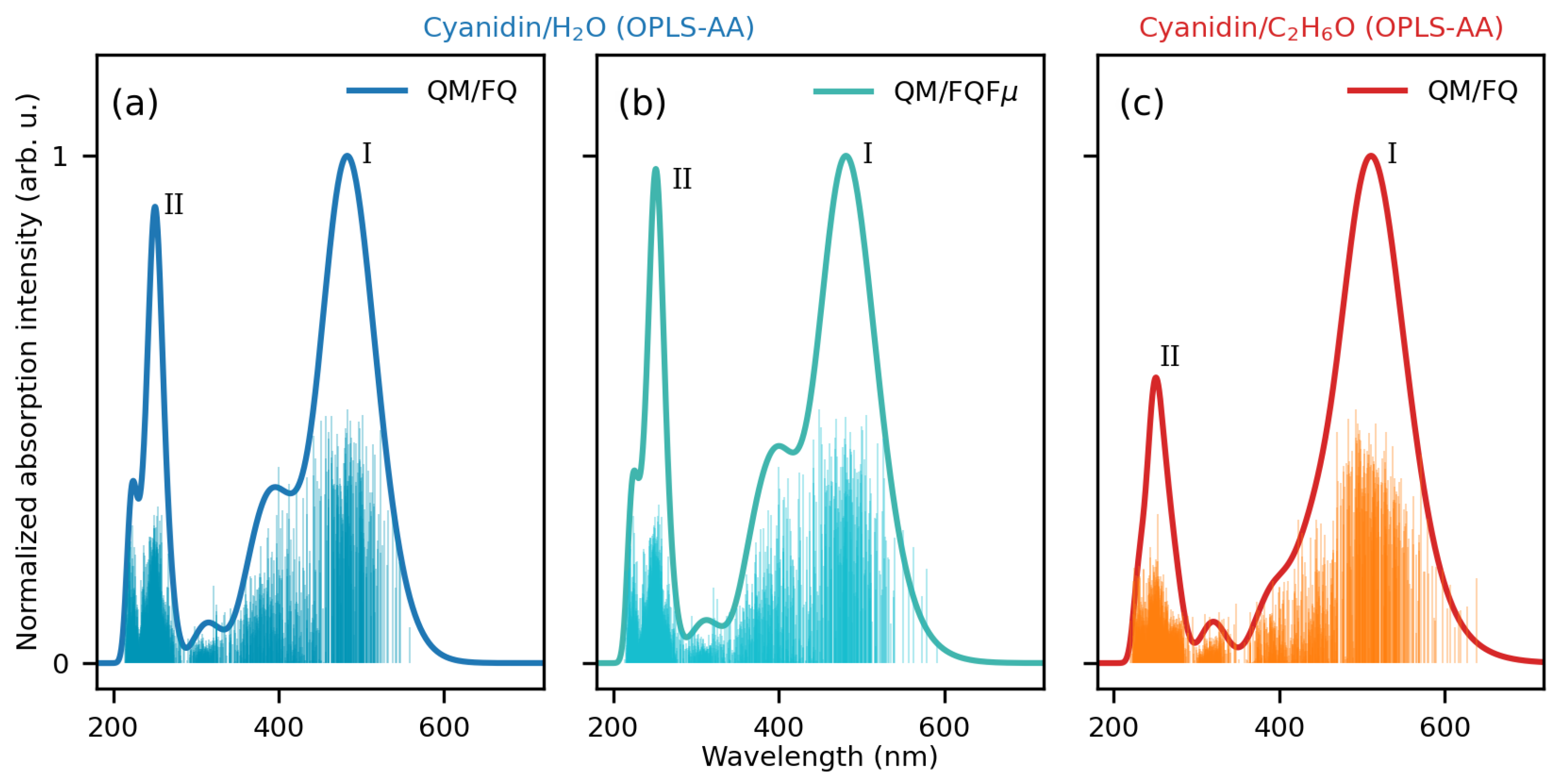
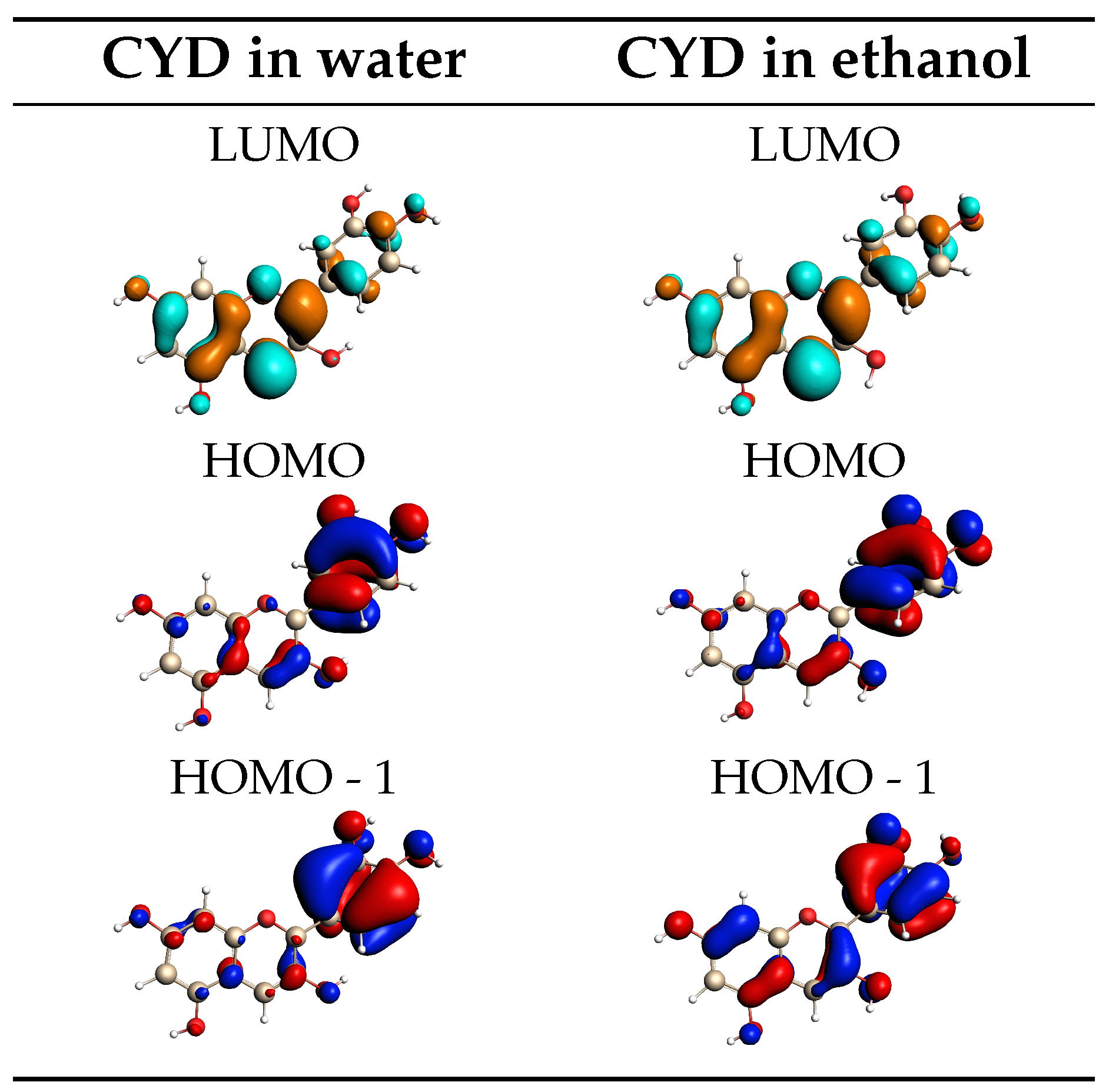
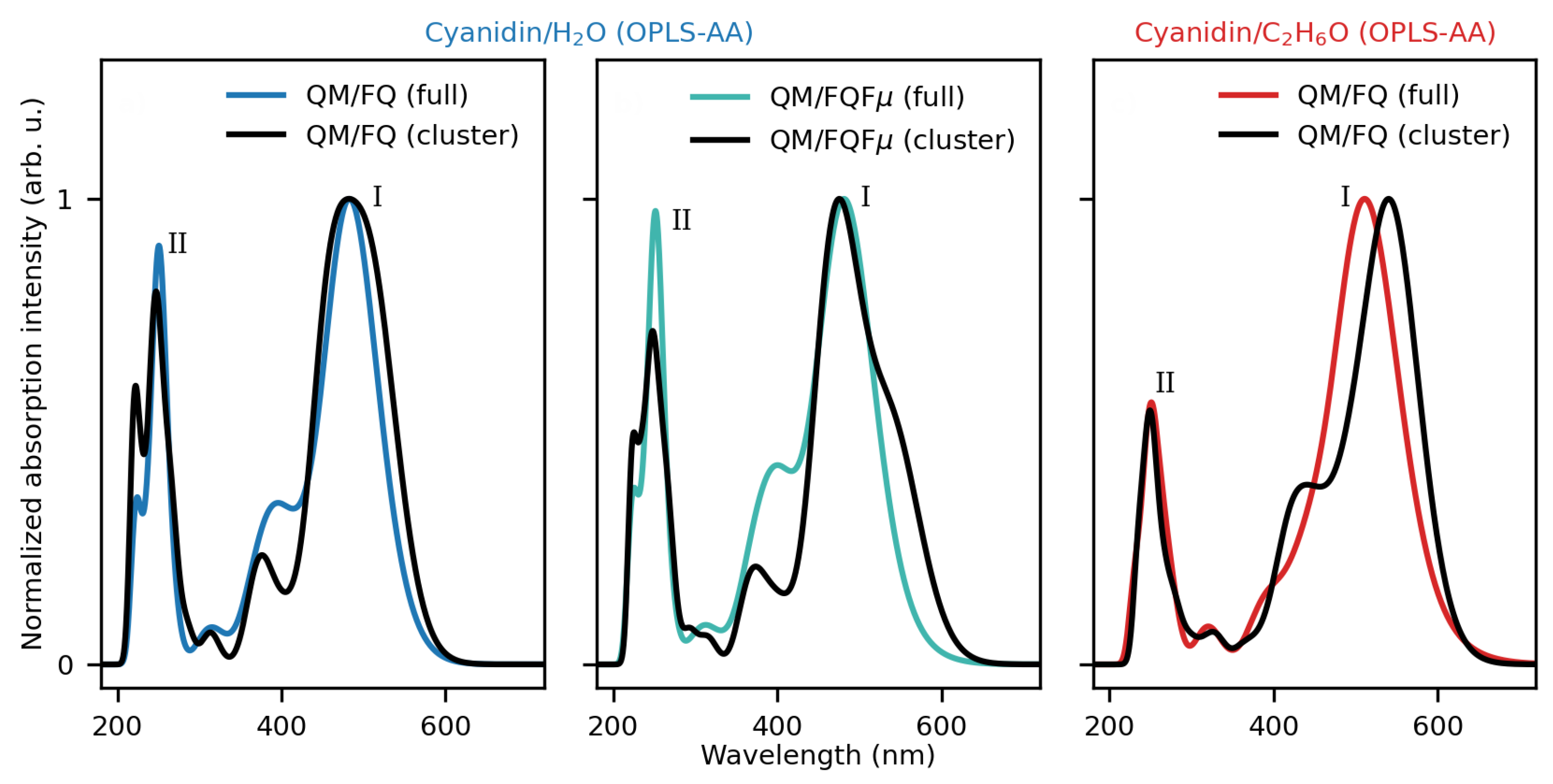
2.1.2. Absorption Spectra
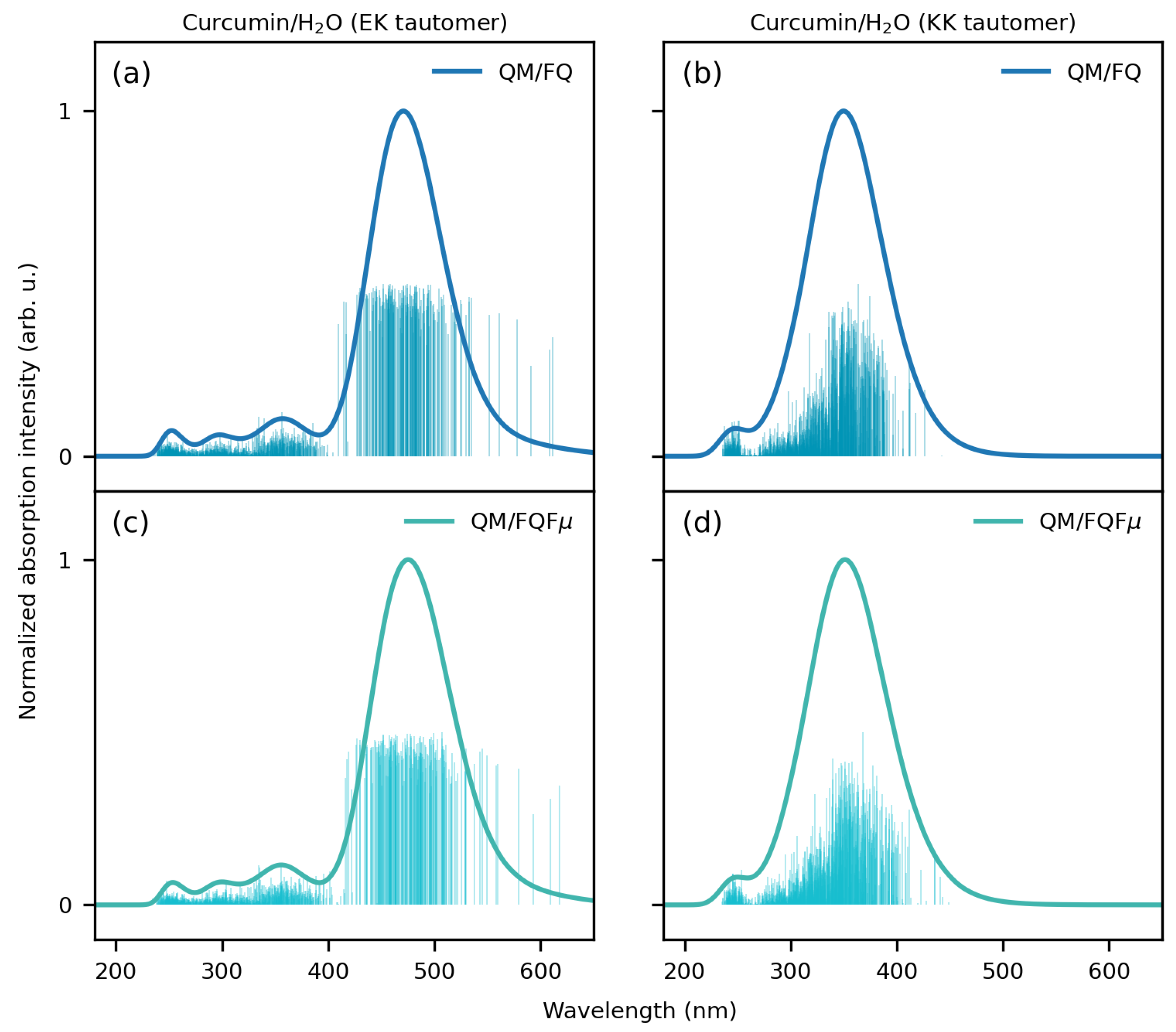
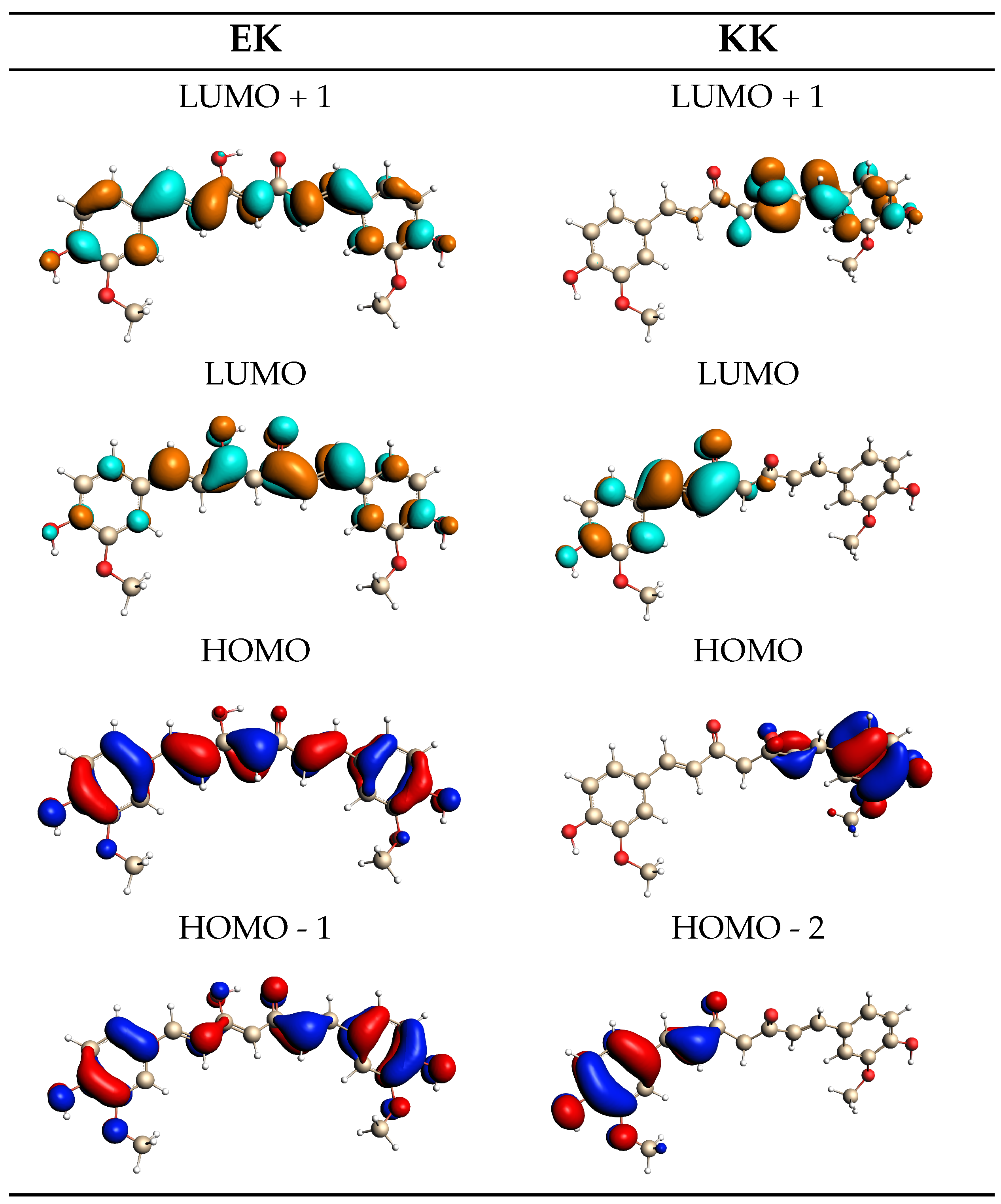
2.2. Curcumin Tautomers in Aqueous Solution
3. Materials and Methods
- Definition of QM/MM boundaries: The parts of the system to be treated as the “solute” and as the “solvent” need to be delineated. For a solution, the solute is described at the QM level, while the solvent is treated at the MM level. The boundary between these two regions (i.e., the QM/MM boundary) is thus defined accordingly.
- Dynamical sampling: To account for the dynamical aspects of the solvation phenomenon, the solute-solvent phase space must be sampled. In this work, we resort to classical non-polarizable MD simulations, which have been shown to be particularly reliable when combined with QM/MM calculations for computational spectroscopy [41]. For curcumin tautomers in aqueous solution, we borrow the trajectories obtained in ref. [98], where two 10 ns classical MD simulations were performed by treating each curcumin tautomer with the GAFF force field while describing water molecules by means of the TIP3P force field.We then study CYD dissolved in water and ethanol. CYD is the sugar-free counterpart of the cyanidin-3-glucoside pigment. In this study, we do not consider the sugar portion as it does not directly participate in the optical transitions on the conjugated core [60,65]. CYD is known to present different behaviors depending on the pH range. Here, we study it in the flavylium-charged state, which is the most stable under acidic conditions (pH < 3) and perform MD simulations of CYD in solution, namely, water and ethanol, plus a Cl− counterion to neutralize the system. To parametrize the chromophore, we first analyze its main conformers. Initial CYD structures are generated using the AMS Conformers tool [99], then optimize it at the density functional tight-binding (DFTB) level [100] to be finally scored by employing the CAMY-B3LYP/TZP level in the ADF engine [99,101]. The best-ranked conformer (planar) is used to obtain parameters using two force fields, namely OPLS-AA and GAFF, exploiting the LigParGen [102,103,104] and acpype web servers [105,106], respectively. In conjunction with TIP3P parameters, GAFF was used in ref. [65], while OPLS-AA was used in ref. [64]. Electrostatics are refined using the CM5 atomic charges [107] computed at the CAMY-B3LYP/TZP level.CYN is fully solvated in TIP3P water [108] and separately in ethanol, using cubic cells of 62 Å edge accommodating 7500 and 2500 solvent molecules, respectively, in periodic boundary conditions. Initial velocities are assigned according to the Boltzmann distribution at 300 K. For both charge–charge and van der Waals terms, a cutoff of 11 Å is used, while the particle mesh Ewald method is employed to account for long-range electrostatics. MDs are run in an NPT ensemble after NVT and NPT equilibration stages, which last for 1 and 2 ns, respectively, with a V-rescale [109] thermostat and Berendsen barostat [110]. In the NPT production stage, keeping temperature (300 K) and pressure (1 atm) constant, an integration time step of 2 fs is employed for a total simulation time of 30 ns. All MD simulations are performed using the GROMACS 2020.4 software [111]. The analyses of the trajectories are performed with the TRAVIS package [112,113].
- Extraction of structures: Two hundred uncorrelated snapshots are extracted from each MD run and employed for the subsequent QM/MM calculations. The snapshots are shaped as spherical “droplets” with a radius of 20 Å for curcumin tautomers, and 18 Å for CYD (see Table 2 for a graphical depiction). The total number of snapshots is chosen to guarantee the convergence of the final computed spectrum.
- Polarizable QM/MM calculations: On each extracted snapshot, the absorption spectrum is calculated at the fully polarizable QM/FQ and QM/FQF levels. In a QM/MM approach, the total energy of the system can therefore be written as follows [29]:where and are the energies of the QM and MM portions, while defines the interaction energy between the two layers. In the QM/FQ and QM/FQF approaches, the MM atoms are endowed with a fluctuating charge (FQ) and dipole (FQF), which can dynamically respond to the QM density (). Therefore, the QM/MM interaction can be specified in terms of the Coulomb law between the two portions as follows [41,42,46]:where and are the charge and dipole of the i-th atom, while and are the electric potential and field due to the QM density calculated on the same MM atom. The charges and dipoles are polarized by the QM density and are obtained by solving the following linear equation [46]:where contains the Lagrangian () blocks used to ensure that the total charge of each MM molecule is kept fixed to . , , and are the charge–charge, charge–dipole, and dipole–dipole interaction kernels defining the interactions between the polarization sources. Such kernels are defined in terms of atomic chemical hardnesses and polarizabilities , which, together with the atomic electronegativities are the parameters defining FQ () and FQF () force fields. Note that the FQ linear system is obtained by discarding rows/columns involving dipoles in Equation (4).In this work, the QM region is defined at the density functional level (DFT) level. The Kohn–Sham matrix is thus modified by considering the external embedding potential () generated by the MM polarization sources (charges and dipoles) as follows [114]:By using Equation (5) in combination with Equation (4), mutual solute–solvent polarization effects are consistently introduced.To calculate the absorption spectra of solvated systems, we exploit the linear response time-dependent DFT (TDDFT) [115] extension of the QM/FQ and QM/FQF methods (see ref. [44,46]). Within this approach, the polarization sources of the MM portion dynamically respond to the transition density of the QM portion, consistently accounting for polarization effects in the linear response regime.All QM/MM calculations are performed using the ADF [101] engine within the Amsterdam Modeling Suite (AMS) v. 2024.1 [99]. The QM part is treated by exploiting the CAMY-B3LYP density functional [116,117] combined with the TZP basis set [118]. TDDFT calculations are performed requesting 10 excited states. Solvent molecules within the MM region are described at the FQ and FQF force field using the parameters reported in ref. [97] (FQ: water and ethanol) and [42] (FQF: water).
- Extraction of spectra and comparison with experiments: The spectra obtained for each snapshot are extracted and averaged to produce final spectra. In particular, each spectrum is convoluted using a Gaussian-type function with a full width at half maximum (FWHM) of 0.3 eV for CYD and EK tautomer, while 0.6 eV is used for the KK tautomer in agreement with ref. [98]. The final computed spectra are compared with the available experimental data. For the sake of comparison, implicit QM/COSMO [119] calculations have also been performed (see Sections S1 and S2 in the Supplementary Materials for further details).
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Reichardt, C.; Welton, T. Solvents and Solvent Effects in Organic Chemistry; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Reichardt, C. Solvatochromic dyes as solvent polarity indicators. Chem. Rev. 1994, 94, 2319–2358. [Google Scholar] [CrossRef]
- Reichardt, C. Solvatochromism, thermochromism, piezochromism, halochromism, and chiro-solvatochromism of pyridinium N-phenoxide betaine dyes. Chem. Soc. Rev. 1992, 21, 147–153. [Google Scholar] [CrossRef]
- Perkampus, H.H. UV-VIS Spectroscopy and Its Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Antonov, L.; Nedeltcheva, D. Resolution of overlapping UV–Vis absorption bands and quantitative analysis. Chem. Soc. Rev. 2000, 29, 217–227. [Google Scholar] [CrossRef]
- Power, A.; Chapman, J.; Chandra, S.; Cozzolino, D. Ultraviolet-visible spectroscopy for food quality analysis. Eval. Technol. Food Qual. 2019, 6, 91–104. [Google Scholar]
- Antonov, L. Tautomerism: Methods and Theories; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Antonov, L.; Gergov, G.; Petrov, V.; Kubista, M.; Nygren, J. UV–Vis spectroscopic and chemometric study on the aggregation of ionic dyes in water. Talanta 1999, 49, 99–106. [Google Scholar] [CrossRef]
- Manolova, Y.; Deneva, V.; Antonov, L.; Drakalska, E.; Momekova, D.; Lambov, N. The effect of the water on the curcumin tautomerism: A quantitative approach. Spectrochim. Acta A 2014, 132, 815–820. [Google Scholar] [CrossRef]
- Morzan, U.N.; Alonso de Armino, D.J.; Foglia, N.O.; Ramirez, F.; Gonzalez Lebrero, M.C.; Scherlis, D.A.; Estrin, D.A. Spectroscopy in complex environments from QM–MM simulations. Chem. Rev. 2018, 118, 4071–4113. [Google Scholar] [CrossRef]
- Ma, H.; Ma, Y. Solvent effect on electronic absorption, fluorescence, and phosphorescence of acetone in water: Revisited by quantum mechanics/molecular mechanics (QM/MM) simulations. J. Chem. Phys. 2013, 138, 224505. [Google Scholar] [CrossRef]
- Zuehlsdorff, T.J.; Isborn, C.M. Modeling absorption spectra of molecules in solution. Int. J. Quantum Chem. 2019, 119, e25719. [Google Scholar] [CrossRef]
- Parac, M.; Doerr, M.; Marian, C.M.; Thiel, W. QM/MM calculation of solvent effects on absorption spectra of guanine. J. Comput. Chem. 2010, 31, 90–106. [Google Scholar] [CrossRef]
- Giovannini, T.; Ambrosetti, M.; Cappelli, C. Quantum Confinement Effects on Solvatochromic Shifts of Molecular Solutes. J. Phys. Chem. Lett. 2019, 10, 5823–5829. [Google Scholar] [CrossRef] [PubMed]
- Aidas, K.; Møgelhøj, A.; Nilsson, E.J.; Johnson, M.S.; Mikkelsen, K.V.; Christiansen, O.; Söderhjelm, P.; Kongsted, J. On the performance of quantum chemical methods to predict solvatochromic effects: The case of acrolein in aqueous solution. J. Chem. Phys. 2008, 128, 194503. [Google Scholar] [CrossRef] [PubMed]
- Söderhjelm, P.; Husberg, C.; Strambi, A.; Olivucci, M.; Ryde, U. Protein influence on electronic spectra modeled by multipoles and polarizabilities. J. Chem. Theory Comput. 2009, 5, 649–658. [Google Scholar] [CrossRef] [PubMed]
- Isborn, C.M.; Gotz, A.W.; Clark, M.A.; Walker, R.C.; Martínez, T.J. Electronic absorption spectra from MM and ab initio QM/MM molecular dynamics: Environmental effects on the absorption spectrum of photoactive yellow protein. J. Chem. Theory Comput. 2012, 8, 5092–5106. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum mechanical continuum solvation models. Chem. Rev. 2005, 105, 2999–3094. [Google Scholar] [CrossRef]
- Giovannini, T.; Cappelli, C. Continuum vs. atomistic approaches to computational spectroscopy of solvated systems. Chem. Commun. 2023, 59, 5644–5660. [Google Scholar] [CrossRef]
- Marrazzini, G.; Giovannini, T.; Scavino, M.; Egidi, F.; Cappelli, C.; Koch, H. Multilevel density functional theory. J. Chem. Theory Comput. 2021, 17, 791–803. [Google Scholar] [CrossRef]
- Giovannini, T.; Marrazzini, G.; Scavino, M.; Koch, H.; Cappelli, C. Integrated multiscale multilevel approach to open shell molecular systems. J. Chem. Theory Comput. 2023, 19, 1446–1456. [Google Scholar] [CrossRef] [PubMed]
- Wesolowski, T.A.; Warshel, A. Frozen density functional approach for ab initio calculations of solvated molecules. J. Phys. Chem. 1993, 97, 8050–8053. [Google Scholar] [CrossRef]
- Jacob, C.R.; Neugebauer, J.; Visscher, L. A flexible implementation of frozen-density embedding for use in multilevel simulations. J. Comput. Chem. 2008, 29, 1011–1018. [Google Scholar] [CrossRef]
- Vidal, L.N.; Giovannini, T.; Cappelli, C. Can the Resonance Raman Optical Activity Spectrum Display Sign Alternation? J. Phys. Chem. Lett. 2016, 7, 3585–3590. [Google Scholar] [CrossRef] [PubMed]
- Warshel, A.; Levitt, M. Theoretical studies of enzymic reactions: Dielectric, electrostatic and steric stabilization of the carbonium ion in the reaction of lysozyme. J. Mol. Biol. 1976, 103, 227–249. [Google Scholar] [CrossRef] [PubMed]
- Field, M.J.; Bash, P.A.; Karplus, M. A combined quantum mechanical and molecular mechanical potential for molecular dynamics simulations. J. Comput. Chem. 1990, 11, 700–733. [Google Scholar] [CrossRef]
- Gao, J. Hybrid quantum and molecular mechanical simulations: An alternative avenue to solvent effects in organic chemistry. Acc. Chem. Res. 1996, 29, 298–305. [Google Scholar] [CrossRef]
- Lin, H.; Truhlar, D.G. QM/MM: What have we learned, where are we, and where do we go from here? Theor. Chem. Acc. 2007, 117, 185–199. [Google Scholar] [CrossRef]
- Senn, H.M.; Thiel, W. QM/MM methods for biomolecular systems. Angew. Chem. Int. Ed. 2009, 48, 1198–1229. [Google Scholar] [CrossRef]
- Boulanger, E.; Harvey, J.N. QM/MM methods for free energies and photochemistry. Curr. Opin. Struc. Biol. 2018, 49, 72–76. [Google Scholar] [CrossRef]
- Monari, A.; Rivail, J.L.; Assfeld, X. Theoretical modeling of large molecular systems. Advances in the local self consistent field method for mixed quantum mechanics/molecular mechanics calculations. Acc. Chem. Res. 2012, 46, 596–603. [Google Scholar] [CrossRef] [PubMed]
- Gokcan, H.; Kratz, E.G.; Darden, T.A.; Piquemal, J.P.; Cisneros, G.A. QM/MM Simulations with the Gaussian Electrostatic Model, A Density-Based Polarizable Potential. J. Phys. Chem. Lett. 2018, 9, 3062–3067. [Google Scholar] [CrossRef]
- Kratz, E.G.; Walker, A.R.; Lagardère, L.; Lipparini, F.; Piquemal, J.P.; Andrés Cisneros, G. LICHEM: A QM/MM program for simulations with multipolar and polarizable force fields. J. Comput. Chem. 2016, 37, 1019–1029. [Google Scholar] [CrossRef]
- Cappelli, C. Integrated QM/Polarizable MM/Continuum Approaches to Model Chiroptical Properties of Strongly Interacting Solute-Solvent Systems. Int. J. Quantum Chem. 2016, 116, 1532–1542. [Google Scholar] [CrossRef]
- Bondanza, M.; Nottoli, M.; Cupellini, L.; Lipparini, F.; Mennucci, B. Polarizable embedding QM/MM: The future gold standard for complex (bio) systems? Phys. Chem. Chem. Phys. 2020, 22, 14433–14448. [Google Scholar] [CrossRef] [PubMed]
- Olsen, J.M.H.; Kongsted, J. Molecular properties through polarizable embedding. Adv. Quantum Chem. 2011, 61, 107–143. [Google Scholar]
- Olsen, J.M.H.; Steinmann, C.; Ruud, K.; Kongsted, J. Polarizable density embedding: A new QM/QM/MM-based computational strategy. J. Phys. Chem. A 2015, 119, 5344–5355. [Google Scholar] [CrossRef]
- Boulanger, E.; Thiel, W. Solvent boundary potentials for hybrid QM/MM computations using classical drude oscillators: A fully polarizable model. J. Chem. Theory Comput. 2012, 8, 4527–4538. [Google Scholar] [CrossRef]
- Kvedaraviciute, S.; Carrasco-Busturia, D.; Møller, K.B.; Olsen, J.M.H. Polarizable Embedding without Artificial Boundary Polarization. J. Chem. Theory Comput. 2023, 19, 5122–5141. [Google Scholar] [CrossRef]
- Nottoli, M.; Bondanza, M.; Mazzeo, P.; Cupellini, L.; Curutchet, C.; Loco, D.; Lagardère, L.; Piquemal, J.P.; Mennucci, B.; Lipparini, F. QM/AMOEBA description of properties and dynamics of embedded molecules. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2023, 13, e1674. [Google Scholar] [CrossRef]
- Giovannini, T.; Egidi, F.; Cappelli, C. Molecular spectroscopy of aqueous solutions: A theoretical perspective. Chem. Soc. Rev. 2020, 49, 5664–5677. [Google Scholar] [CrossRef] [PubMed]
- Giovannini, T.; Puglisi, A.; Ambrosetti, M.; Cappelli, C. Polarizable QM/MM approach with fluctuating charges and fluctuating dipoles: The QM/FQFμ model. J. Chem. Theory Comput. 2019, 15, 2233–2245. [Google Scholar] [CrossRef]
- Giovannini, T.; Egidi, F.; Cappelli, C. Theory and algorithms for chiroptical properties and spectroscopies of aqueous systems. Phys. Chem. Chem. Phys. 2020, 22, 22864–22879. [Google Scholar] [CrossRef]
- Giovannini, T.; Riso, R.R.; Ambrosetti, M.; Puglisi, A.; Cappelli, C. Electronic Transitions for a Fully Polarizable QM/MM Approach Based on Fluctuating Charges and Fluctuating Dipoles: Linear and Corrected Linear Response Regimes. J. Chem. Phys. 2019, 151, 174104. [Google Scholar] [CrossRef] [PubMed]
- Di Remigio, R.; Giovannini, T.; Ambrosetti, M.; Cappelli, C.; Frediani, L. Fully polarizable QM/fluctuating charge approach to two-photon absorption of aqueous solutions. J. Chem. Theory Comput. 2019, 15, 4056–4068. [Google Scholar] [CrossRef] [PubMed]
- Gómez, S.; Giovannini, T.; Cappelli, C. Multiple facets of modeling electronic absorption spectra of systems in solution. ACS Phys. Chem. Au 2023, 3, 1–16. [Google Scholar] [CrossRef]
- Lafiosca, P.; Gómez, S.; Giovannini, T.; Cappelli, C. Absorption properties of large complex molecular systems: The DFTB/fluctuating charge approach. J. Chem. Theory Comput. 2022, 18, 1765–1779. [Google Scholar] [CrossRef]
- Gómez, S.; Giovannini, T.; Cappelli, C. Absorption spectra of xanthines in aqueous solution: A computational study. Phys. Chem. Chem. Phys. 2020, 22, 5929–5941. [Google Scholar] [CrossRef] [PubMed]
- Skoko, S.; Ambrosetti, M.; Giovannini, T.; Cappelli, C. Simulating Absorption Spectra of Flavonoids in Aqueous Solution: A Polarizable QM/MM Study. Molecules 2020, 25, 5853. [Google Scholar] [CrossRef]
- Sigurdson, G.T.; Tang, P.; Giusti, M.M. Natural colorants: Food colorants from natural sources. Annu. Rev. Food Sci. Technol. 2017, 8, 261–280. [Google Scholar] [CrossRef] [PubMed]
- Coultate, T.; Blackburn, R.S. Food colorants: Their past, present and future. Color. Technol. 2018, 134, 165–186. [Google Scholar] [CrossRef]
- Sinopoli, A.; Calogero, G.; Bartolotta, A. Computational aspects of anthocyanidins and anthocyanins: A review. Food Chem. 2019, 297, 124898. [Google Scholar] [CrossRef]
- Ge, X.; Calzolari, A.; Baroni, S. Optical properties of anthocyanins in the gas phase. Chem. Phys. Lett. 2015, 618, 24–29. [Google Scholar] [CrossRef]
- Ekanayake, P.; Kooh, M.R.R.; Kumara, N.; Lim, A.; Petra, M.I.; Voo, N.Y.; Lim, C.M. Combined experimental and DFT–TDDFT study of photo-active constituents of Canarium odontophyllum for DSSC application. Chem. Phys. Lett. 2013, 585, 121–127. [Google Scholar] [CrossRef]
- Soto-Rojo, R.; Baldenebro-López, J.; Flores-Holguín, N.; Glossman-Mitnik, D. Comparison of several protocols for the computational prediction of the maximum absorption wavelength of chrysanthemin. J. Mol. Model. 2014, 20, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Trouillas, P.; Di Meo, F.; Gierschner, J.; Linares, M.; Sancho-García, J.C.; Otyepka, M. Optical properties of wine pigments: Theoretical guidelines with new methodological perspectives. Tetrahedron 2015, 71, 3079–3088. [Google Scholar] [CrossRef]
- Barraza-Jiménez, D.; la Cruz, A.M.D.; Saucedo-Mendiola, L.; Torres-Herrera, S.I.; Mendiola, A.P.; Quiñones, E.M.C.; Corral, R.A.O.; Frías-Zepeda, M.E.; Flores-Hidalgo, M.A. Solvent Effects on Dye Sensitizers Derived from Anthocyanidins for Applications in Photocatalysis. In Solvents, Ionic Liquids and Solvent Effects; Glossman-Mitnik, D., Maciejewska, M., Eds.; IntechOpen: Rijeka, Croatia, 2019; Chapter 10. [Google Scholar] [CrossRef]
- Barraza-Jiménez, D.; Flores-Hidalgo, H.I.; Torres-Herrera, S.I.; Olvera-Corral, R.A.; Flores-Hidalgo, M.A. Excited States of Six Anthocyanidin Variants with Different Solvents as Dye Sensitizers for Photocatalysis. In Photocatalysts; Awwad, N.S., Alarfaji, S.S., Alomary, A., Eds.; IntechOpen: Rijeka, Croatia, 2022; Chapter 11. [Google Scholar] [CrossRef]
- Torskangerpoll, K.; Børve, K.J.; Andersen, Ø.M.; Sæthre, L.J. Color and substitution pattern in anthocyanidins. A combined quantum chemical–chemometrical study. Spectrochim. Acta A 1999, 55, 761–771. [Google Scholar] [CrossRef]
- Malcıoǧlu, O.B.; Calzolari, A.; Gebauer, R.; Varsano, D.; Baroni, S. Dielectric and thermal effects on the optical properties of natural dyes: A case study on solvated cyanin. J. Am. Chem. Soc. 2011, 133, 15425–15433. [Google Scholar] [CrossRef] [PubMed]
- Rustioni, L.; Di Meo, F.; Guillaume, M.; Failla, O.; Trouillas, P. Tuning color variation in grape anthocyanins at the molecular scale. Food Chem. 2013, 141, 4349–4357. [Google Scholar] [CrossRef] [PubMed]
- Ge, X.; Timrov, I.; Binnie, S.; Biancardi, A.; Calzolari, A.; Baroni, S. Accurate and inexpensive prediction of the color optical properties of anthocyanins in solution. J. Phys. Chem. A 2015, 119, 3816–3822. [Google Scholar] [CrossRef]
- Timrov, I.; Micciarelli, M.; Rosa, M.; Calzolari, A.; Baroni, S. Multimodel approach to the optical properties of molecular dyes in solution. J. Chem. Theory Comput. 2016, 12, 4423–4429. [Google Scholar] [CrossRef]
- Cacelli, I.; Ferretti, A.; Prampolini, G. Predicting light absorption properties of anthocyanidins in solution: A multi-level computational approach. Theor. Chem. Acc. 2016, 135, 1–17. [Google Scholar] [CrossRef]
- Rusishvili, M.; Grisanti, L.; Laporte, S.; Micciarelli, M.; Rosa, M.; Robbins, R.J.; Collins, T.; Magistrato, A.; Baroni, S. Unraveling the molecular mechanisms of color expression in anthocyanins. Phys. Chem. Chem. Phys. 2019, 21, 8757–8766. [Google Scholar] [CrossRef]
- Gould, K.; Davies, K.; Winefield, C. Anthocyanins: Biosynthesis, Functions, and Applications; Springer: New York, NY, USA, 2008. [Google Scholar]
- Pina, F.; Melo, M.J.; Laia, C.A.; Parola, A.J.; Lima, J.C. Chemistry and applications of flavylium compounds: A handful of colours. Chem. Soc. Rev. 2012, 41, 869–908. [Google Scholar] [CrossRef] [PubMed]
- Trouillas, P.; Sancho-García, J.C.; De Freitas, V.; Gierschner, J.; Otyepka, M.; Dangles, O. Stabilizing and modulating color by copigmentation: Insights from theory and experiment. Chem. Rev. 2016, 116, 4937–4982. [Google Scholar] [CrossRef]
- MacDougall, D.; MacDougall, D.B. Colour in Food: Improving Quality; Woodhead Publishing: Sawston, UK, 2002. [Google Scholar]
- Novais, C.; Molina, A.K.; Abreu, R.M.; Santo-Buelga, C.; Ferreira, I.C.; Pereira, C.; Barros, L. Natural food colorants and preservatives: A review, a demand, and a challenge. J. Agric. Food Chem. 2022, 70, 2789–2805. [Google Scholar] [CrossRef]
- Echegaray, N.; Guzel, N.; Kumar, M.; Guzel, M.; Hassoun, A.; Lorenzo, J.M. Recent advancements in natural colorants and their application as coloring in food and in intelligent food packaging. Food Chem. 2023, 404, 134453. [Google Scholar] [CrossRef] [PubMed]
- Llano, S.; Gómez, S.; Londoño, J.; Restrepo, A. Antioxidant activity of curcuminoids. Phys. Chem. Chem. Phys. 2019, 21, 3752–3760. [Google Scholar] [CrossRef]
- Shen, L.; Ji, H.F. Theoretical study on physicochemical properties of curcumin. Spectrochim. Acta A 2007, 67, 619–623. [Google Scholar] [CrossRef] [PubMed]
- Benassi, E.; Spagnolo, F. A theoretical study about the structural, electronic and spectroscopic properties of the ground and singlet excited states of curcuminoidic core. Theor. Chem. Acc. 2009, 124, 235–250. [Google Scholar] [CrossRef]
- Benassi, R.; Ferrari, E.; Lazzari, S.; Spagnolo, F.; Saladini, M. Theoretical study on Curcumin: A comparison of calculated spectroscopic properties with NMR, UV–vis and IR experimental data. J. Mol. Struct. 2008, 892, 168–176. [Google Scholar] [CrossRef]
- Santin, L.G.; Toledo, E.M.; Carvalho-Silva, V.H.; Camargo, A.J.; Gargano, R.; Oliveira, S.S. Methanol solvation effect on the proton rearrangement of curcumin’s enol forms: An ab initio molecular dynamics and electronic structure viewpoint. J. Phys. Chem. C 2016, 120, 19923–19931. [Google Scholar] [CrossRef]
- Anjomshoa, S.; Namazian, M.; Noorbala, M.R. The effect of solvent on tautomerism, acidity and radical stability of curcumin and its derivatives based on thermodynamic quantities. J. Solution Chem. 2016, 45, 1021–1030. [Google Scholar] [CrossRef]
- Kolev, T.M.; Velcheva, E.A.; Stamboliyska, B.A.; Spiteller, M. DFT and experimental studies of the structure and vibrational spectra of curcumin. Int. J. Quantum Chem. 2005, 102, 1069–1079. [Google Scholar] [CrossRef]
- Tonnesen, H.; Karlsen, J.; Mostad, A. Structural studies of curcuminoids. I. The crystal structure of curcumin. Acta Chem. Scand. Ser. B 1982, 36, 475–479. [Google Scholar] [CrossRef]
- Andreev, G.; Schrader, B.; Schulz, H.; Fuchs, R.; Popov, S.; Handjieva, N. Non-destructive NIR-FT-Raman analyses in practice. Part 1. Analyses of plants and historic textiles. Fresenius J. Anal. Chem. 2001, 371, 1009–1017. [Google Scholar]
- Osifová, Z.; Reiberger, R.; Cisarova, I.; Machara, A.; Dracinsky, M. Diketo–ketoenol tautomers in curcuminoids: Synthesis, separation of tautomers, and kinetic and structural studies. J. Org. Chem. 2022, 87, 10309–10318. [Google Scholar] [CrossRef]
- de França, B.M.; Oliveira, S.S.; Souza, L.O.; Mello, T.P.; Santos, A.L.; Forero, J.S.B. Synthesis and photophysical properties of metal complexes of curcumin dyes: Solvatochromism, acidochromism, and photoactivity. Dyes Pigm. 2022, 198, 110011. [Google Scholar] [CrossRef]
- Rastelli, G.; Costantino, L.; Albasini, A. Physico-chemical properties of anthocyanidins. Part 1. Theoretical evaluation of the stability of the neutral and anionic tautomeric forms. J. Mol. Struct. 1993, 279, 157–166. [Google Scholar] [CrossRef]
- Merlin, J.C.; Statoua, A.; Cornard, J.P.; Saidi-Idrissi, M.; Brouillard, R. Resonance Raman spectroscopic studies of anthocyanins and anthocyanidins in aqueous solutions. Phytochemistry 1993, 35, 227–232. [Google Scholar] [CrossRef]
- Pereira, G.K.; Donate, P.M.; Galembeck, S.E. Effects of substitution for hydroxyl in the B-ring of the flavylium cation. J. Mol. Struct. 1997, 392, 169–179. [Google Scholar] [CrossRef]
- Sakata, K.; Saito, N.; Honda, T. Ab initio study of molecular structures and excited states in anthocyanidins. Tetrahedron 2006, 62, 3721–3731. [Google Scholar] [CrossRef]
- Calzolari, A.; Varsano, D.; Ruini, A.; Catellani, A.; Tel-Vered, R.; Yildiz, H.; Ovits, O.; Willner, I. Optoelectronic properties of natural cyanin dyes. J. Phys. Chem. A 2009, 113, 8801–8810. [Google Scholar] [CrossRef]
- Barone, V.; Ferretti, A.; Pino, I. Absorption spectra of natural pigments as sensitizers in solar cells by TD-DFT and MRPT2: Protonated cyanidin. Phys. Chem. Chem. Phys. 2012, 14, 16130–16137. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Zhao, B.; Li, Y.; Gao, H.; Xia, Q.; Fang, Z. Investigation of the difference in color enhancement effect on cyanidin-3-O-glucoside by phenolic acids and the interaction mechanism. Food Chem. 2023, 411, 135409. [Google Scholar] [CrossRef] [PubMed]
- Ueno, K.; Saito, N. Cyanidin bromide monohydrate (3, 5, 7, 3′, 4′-pentahydroxyflavylium bromide monohydrate). Acta Crystallogr. B 1977, 33, 114–116. [Google Scholar] [CrossRef]
- Daura, X.; Gademann, K.; Jaun, B.; Seebach, D.; Van Gunsteren, W.F.; Mark, A.E. Peptide folding: When simulation meets experiment. Angew. Chem. Int. Ed. 1999, 38, 236–240. [Google Scholar] [CrossRef]
- Del Galdo, S.; Fusè, M.; Barone, V. The ONIOM/PMM model for effective yet accurate simulation of optical and chiroptical spectra in solution: Camphorquinone in methanol as a case study. J. Chem. Theory Comput. 2020, 16, 3294–3306. [Google Scholar] [CrossRef]
- Del Galdo, S.; Chandramouli, B.; Mancini, G.; Barone, V. Assessment of multi-scale approaches for computing UV–Vis spectra in condensed phases: Toward an effective yet reliable integration of variational and perturbative QM/MM approaches. J. Chem. Theory Comput. 2019, 15, 3170–3184. [Google Scholar] [CrossRef]
- Kiataki, M.; Varella, M.d.N.; Coutinho, K. New approach to instantaneous polarizable electrostatic embedding of the solvent. J. Mol. Liq. 2023, 389, 122861. [Google Scholar] [CrossRef]
- Kiataki, M.B.; Varella, M.T.d.N.; Coutinho, K.; Rabilloud, F. Novel Approach for Predicting Vertical Electron Attachment Energies in Bulk-Solvated Molecules. J. Chem. Theory Comput. 2024, 20, 4893–4900. [Google Scholar] [CrossRef]
- Dai, Q.; Rabani, J. Photosensitization of nanocrystalline TiO2 films by anthocyanin dyes. J. Photochem. Photobiol. A 2002, 148, 17–24. [Google Scholar] [CrossRef]
- Ambrosetti, M.; Skoko, S.; Giovannini, T.; Cappelli, C. Quantum mechanics/fluctuating charge protocol to compute solvatochromic shifts. J. Chem. Theory Comput. 2021, 17, 7146–7156. [Google Scholar] [CrossRef]
- Puglisi, A.; Giovannini, T.; Antonov, L.; Cappelli, C. Interplay between conformational and solvent effects in UV-visible absorption spectra: Curcumin tautomers as a case study. Phys. Chem. Chem. Phys. 2019, 21, 15504–15514. [Google Scholar] [CrossRef] [PubMed]
- AMS 2024.1, SCM, Theoretical Chemistry; Vrije Universiteit: Amsterdam, The Netherlands, 2024.
- Elstner, M.; Porezag, D.; Jungnickel, G.; Elsner, J.; Haugk, M.; Frauenheim, T.; Suhai, S.; Seifert, G. Self-consistent-charge density-functional tight-binding method for simulations of complex materials properties. Phys. Rev. B 1998, 58, 7260. [Google Scholar] [CrossRef]
- Te Velde, G.t.; Bickelhaupt, F.M.; Baerends, E.J.; Fonseca Guerra, C.; van Gisbergen, S.J.; Snijders, J.G.; Ziegler, T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931–967. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Tirado-Rives, J. Potential energy functions for atomic-level simulations of water and organic and biomolecular systems. Proc. Natl. Acad. Sci. USA 2005, 102, 6665–6670. [Google Scholar] [CrossRef]
- Dodda, L.S.; Vilseck, J.Z.; Tirado-Rives, J.; Jorgensen, W.L. 1.14* CM1A-LBCC: Localized bond-charge corrected CM1A charges for condensed-phase simulations. J. Phys. Chem. B 2017, 121, 3864–3870. [Google Scholar] [CrossRef] [PubMed]
- Dodda, L.S.; Cabeza de Vaca, I.; Tirado-Rives, J.; Jorgensen, W.L. LigParGen web server: An automatic OPLS-AA parameter generator for organic ligands. Nucleic Acids Res. 2017, 45, W331–W336. [Google Scholar] [CrossRef]
- Sousa da Silva, A.W.; Vranken, W.F. ACPYPE-Antechamber python parser interface. BMC Res. Notes 2012, 5, 1–8. [Google Scholar] [CrossRef]
- Kagami, L.; Wilter, A.; Diaz, A.; Vranken, W. The ACPYPE web server for small-molecule MD topology generation. Bioinformatics 2023, 39, btad350. [Google Scholar] [CrossRef] [PubMed]
- Marenich, A.V.; Jerome, S.V.; Cramer, C.J.; Truhlar, D.G. Charge model 5: An extension of Hirshfeld population analysis for the accurate description of molecular interactions in gaseous and condensed phases. J. Chem. Theory Comput. 2012, 8, 527–541. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef] [PubMed]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1, 19–25. [Google Scholar] [CrossRef]
- Brehm, M.; Kirchner, B. TRAVIS—A Free Analyzer and Visualizer for Monte Carlo and Molecular Dynamics Trajectories. J. Chem. Inf. Model. 2011, 51, 2007–2023. [Google Scholar] [CrossRef] [PubMed]
- Brehm, M.; Thomas, M.; Gehrke, S.; Kirchner, B. TRAVIS—A free analyzer for trajectories from molecular simulation. J. Chem. Phys. 2020, 152, 164105. [Google Scholar] [CrossRef] [PubMed]
- Nicoli, L.; Giovannini, T.; Cappelli, C. Assessing the quality of QM/MM approaches to describe vacuo-to-water solvatochromic shifts. J. Chem. Phys. 2022, 157, 214101. [Google Scholar] [CrossRef]
- Casida, M.E. Time-Dependent Density Functional Response Theory for Molecules. In Recent Advances in Density Functional Methods Part I; Chong, D.P., Ed.; World Scientific: Singapore, 1995; pp. 155–192. [Google Scholar]
- Akinaga, Y.; Ten-no, S. Range-separation by the Yukawa potential in long-range corrected density functional theory with Gaussian-type basis functions. Chem. Phys. Lett. 2008, 462, 348–351. [Google Scholar] [CrossRef]
- Seth, M.; Ziegler, T. Range-separated exchange functionals with Slater-type functions. J. Chem. Theory Comput. 2012, 8, 901–907. [Google Scholar] [CrossRef]
- Van Lenthe, E.; Baerends, E.J. Optimized Slater-type basis sets for the elements 1–118. J. Comput. Chem. 2003, 24, 1142–1156. [Google Scholar] [CrossRef]
- Klamt, A.; Schüürmann, G. COSMO: A new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient. J. Chem. Soc. Perkin Trans. 2 1993, 2, 799–805. [Google Scholar] [CrossRef]
- Mazza, G.; Brouillard, R. The mechanism of co-pigmentation of anthocyanins in aqueous solutions. Phytochemistry 1990, 29, 1097–1102. [Google Scholar] [CrossRef]
- Harborne, J. Spectral methods of characterizing anthocyanins. Biochem. J. 1958, 70, 22. [Google Scholar] [CrossRef] [PubMed]
- Ferreira da Silva, P.; Paulo, L.; Barbafina, A.; Elisei, F.; Quina, F.H.; Ma¸canita, A.L. Photoprotection and the photophysics of acylated anthocyanins. Chem.—Eur. J. 2012, 18, 3736–3744. [Google Scholar] [CrossRef] [PubMed]

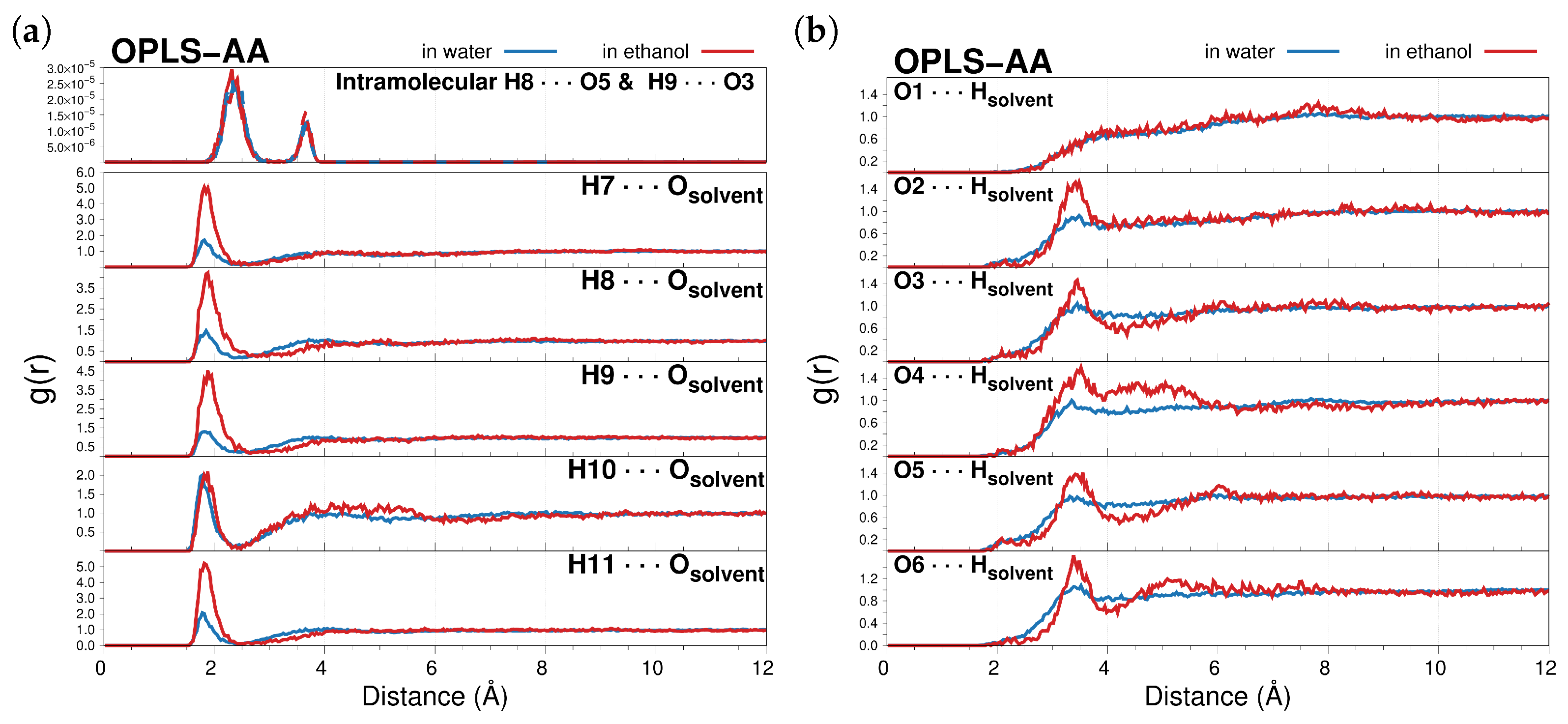


| In Water | In Ethanol | |||
|---|---|---|---|---|
| Max at (Å) | RCN | Max at (Å) | RCN | |
| H7⋯Osolvent | 1.82 | 0.99 | 1.82 | 0.87 |
| H8⋯Osolvent | 1.85 | 0.87 | 1.88 | 0.94 |
| H9⋯Osolvent | 1.82 | 1.02 | 1.88 | 0.94 |
| H10⋯Osolvent | 1.78 | 0.97 | 1.88 | 0.34 |
| H11⋯Osolvent | 1.78 | 1.02 | 1.82 | 0.86 |
| CYD in Water | CYD in Ethanol | KK in Water | EK in Water |
|---|---|---|---|
 |  |  |  |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gómez, S.; Lafiosca, P.; Giovannini, T. Modeling UV/Vis Absorption Spectra of Food Colorants in Solution: Anthocyanins and Curcumin as Case Studies. Molecules 2024, 29, 4378. https://doi.org/10.3390/molecules29184378
Gómez S, Lafiosca P, Giovannini T. Modeling UV/Vis Absorption Spectra of Food Colorants in Solution: Anthocyanins and Curcumin as Case Studies. Molecules. 2024; 29(18):4378. https://doi.org/10.3390/molecules29184378
Chicago/Turabian StyleGómez, Sara, Piero Lafiosca, and Tommaso Giovannini. 2024. "Modeling UV/Vis Absorption Spectra of Food Colorants in Solution: Anthocyanins and Curcumin as Case Studies" Molecules 29, no. 18: 4378. https://doi.org/10.3390/molecules29184378
APA StyleGómez, S., Lafiosca, P., & Giovannini, T. (2024). Modeling UV/Vis Absorption Spectra of Food Colorants in Solution: Anthocyanins and Curcumin as Case Studies. Molecules, 29(18), 4378. https://doi.org/10.3390/molecules29184378






