Optoelectronic Properties of Triply Twisted Möbius Carbon Nanobelt and the Design of Its Isomeric Nanomaterials
Abstract
:1. Introduction
2. Results and Discussion
2.1. The Physical Mechanism of the Photoelectric Properties of TMCNB
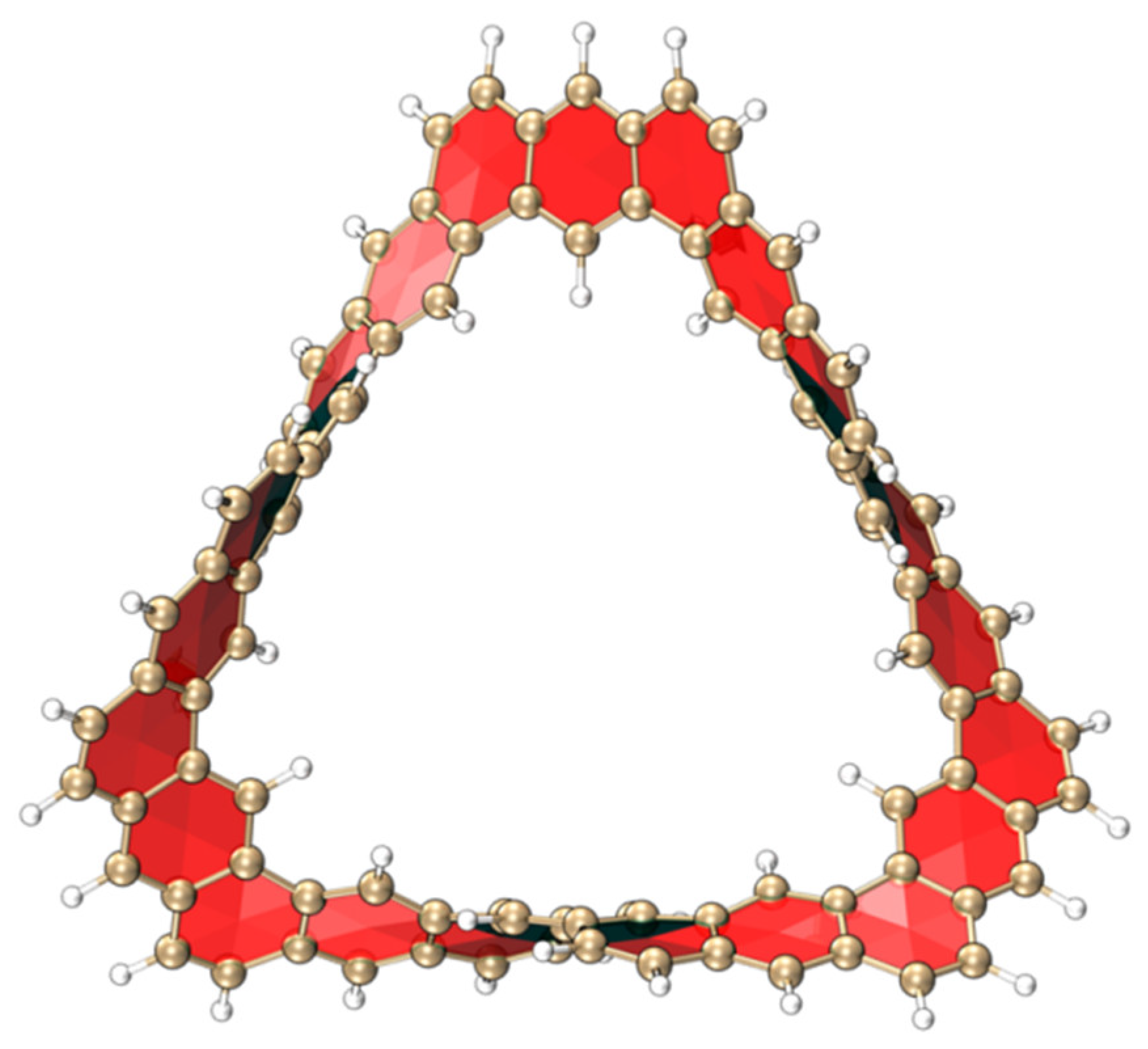
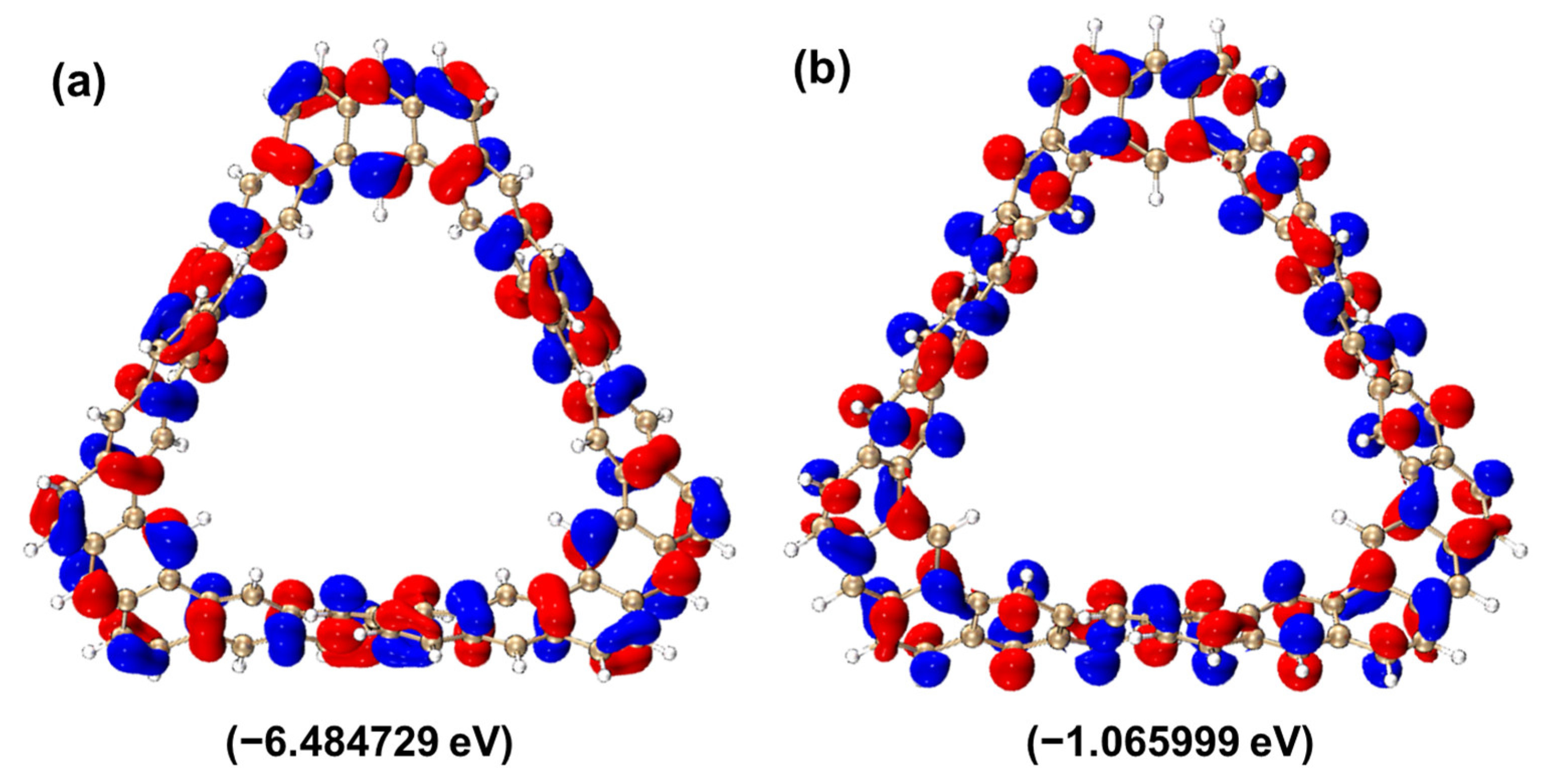
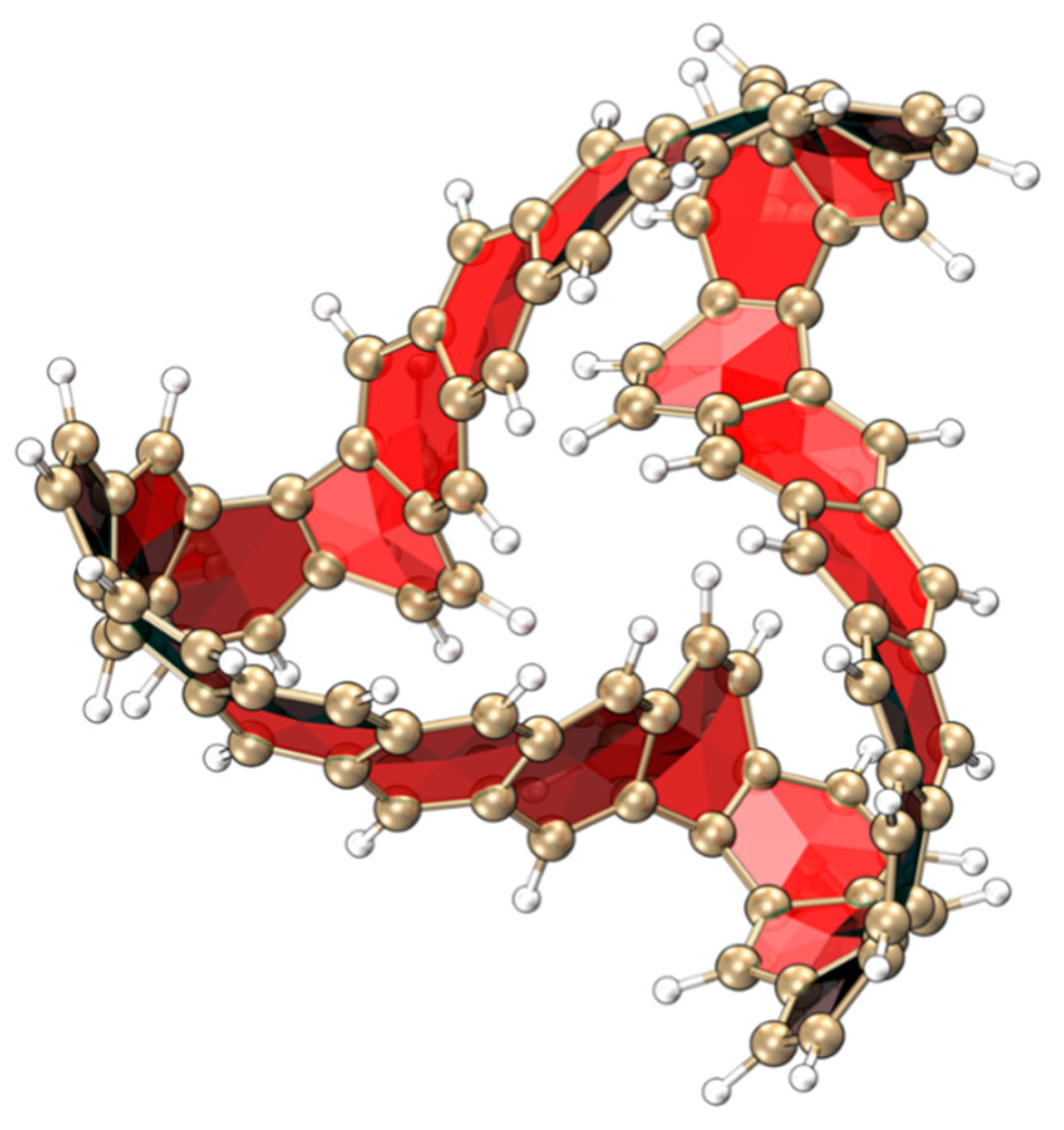
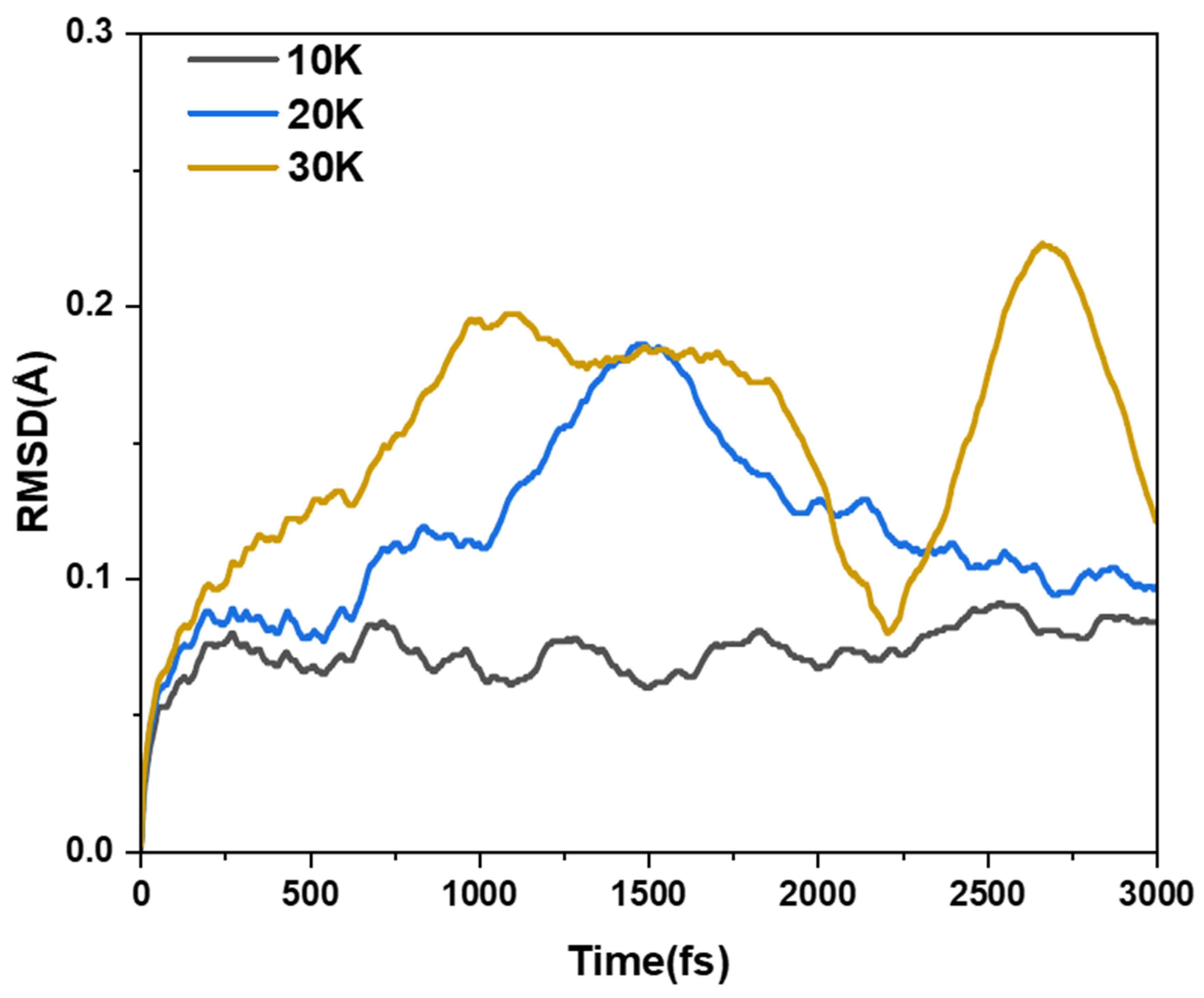
2.1.1. Structure and Properties of TMCNB
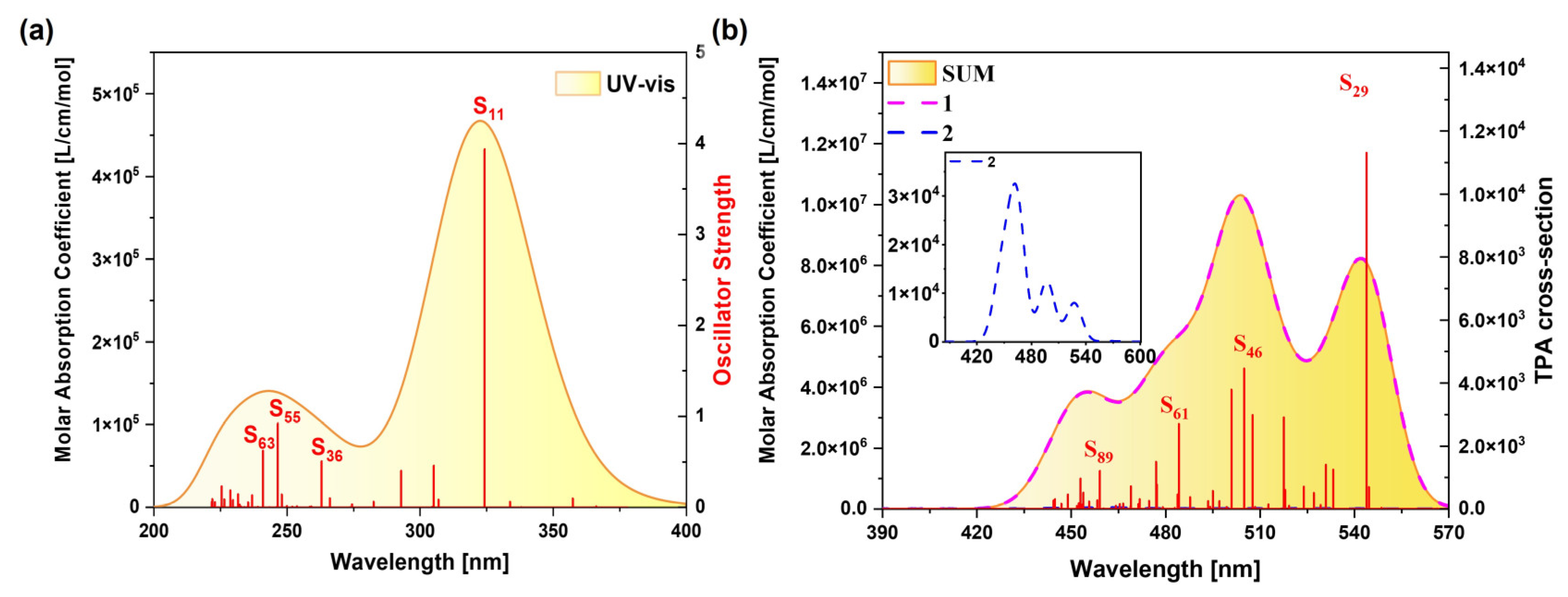
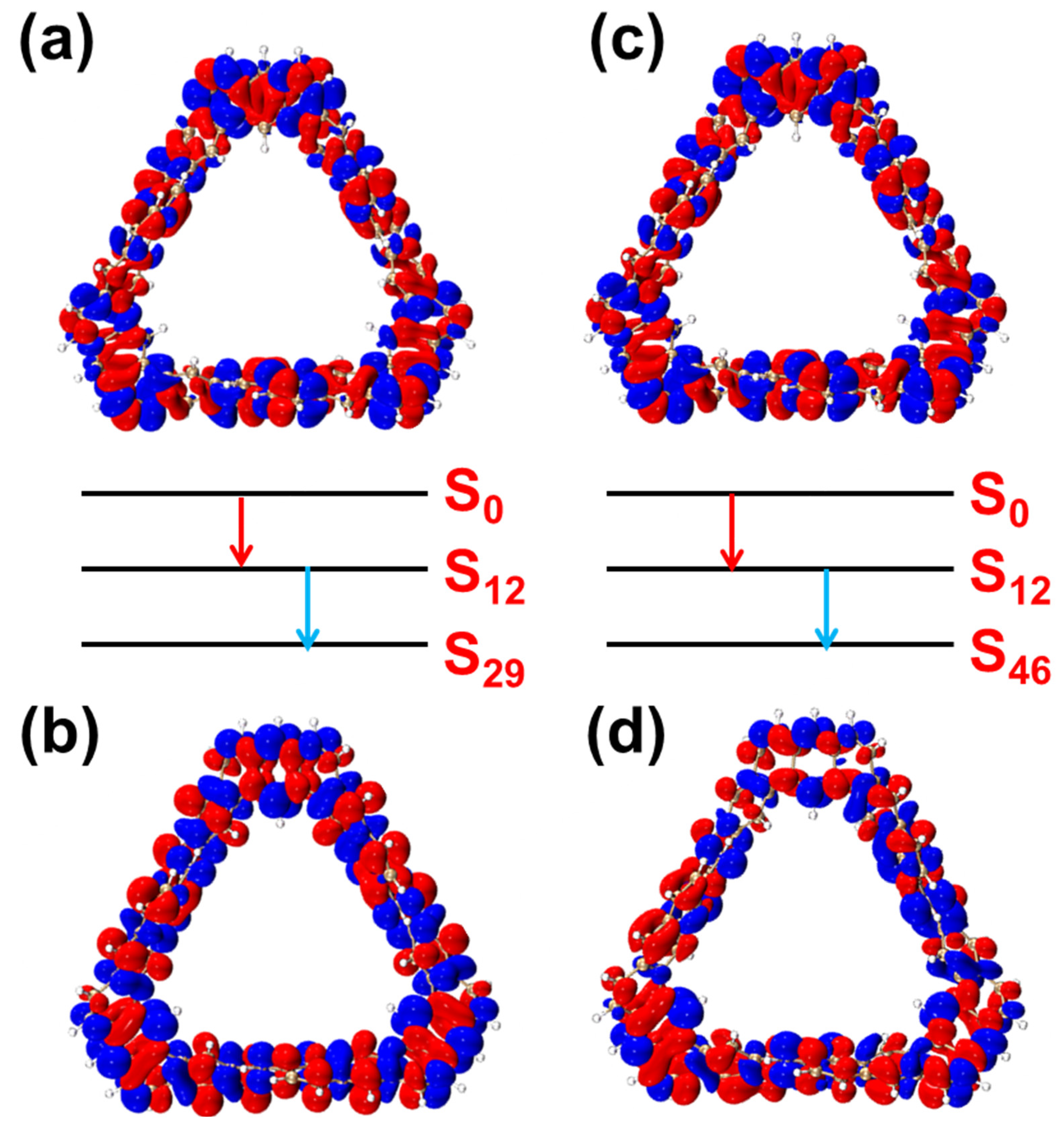
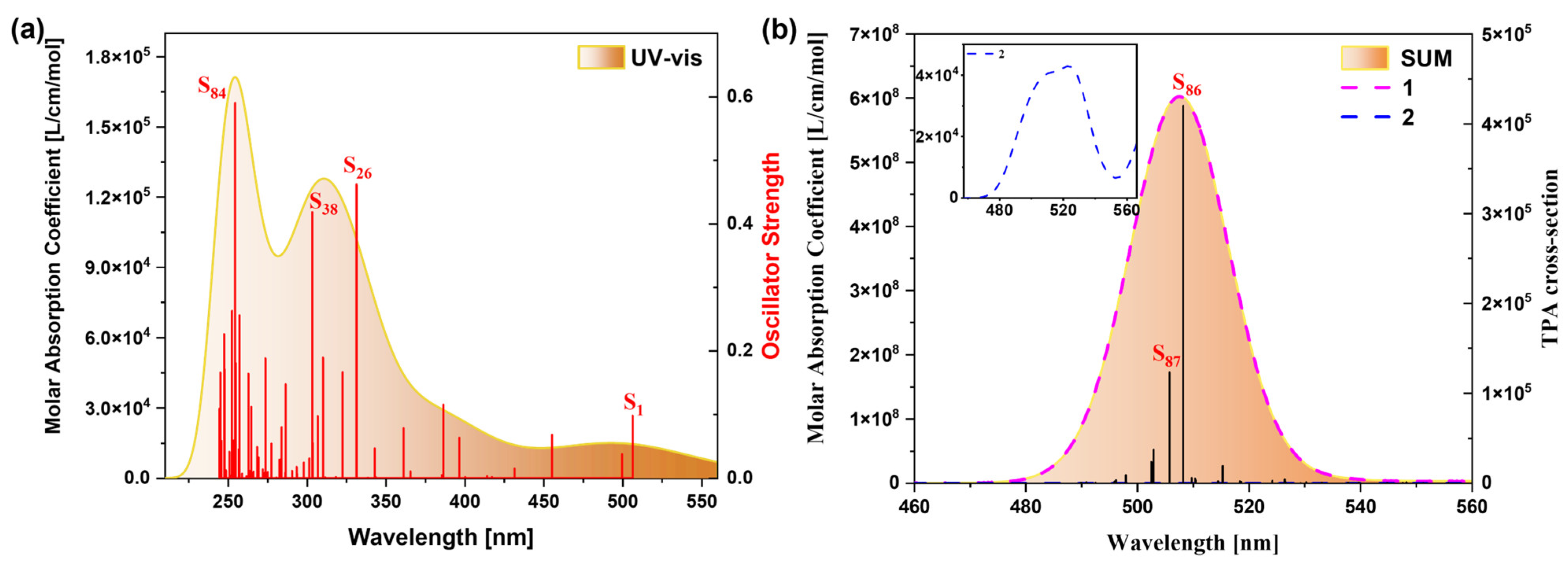
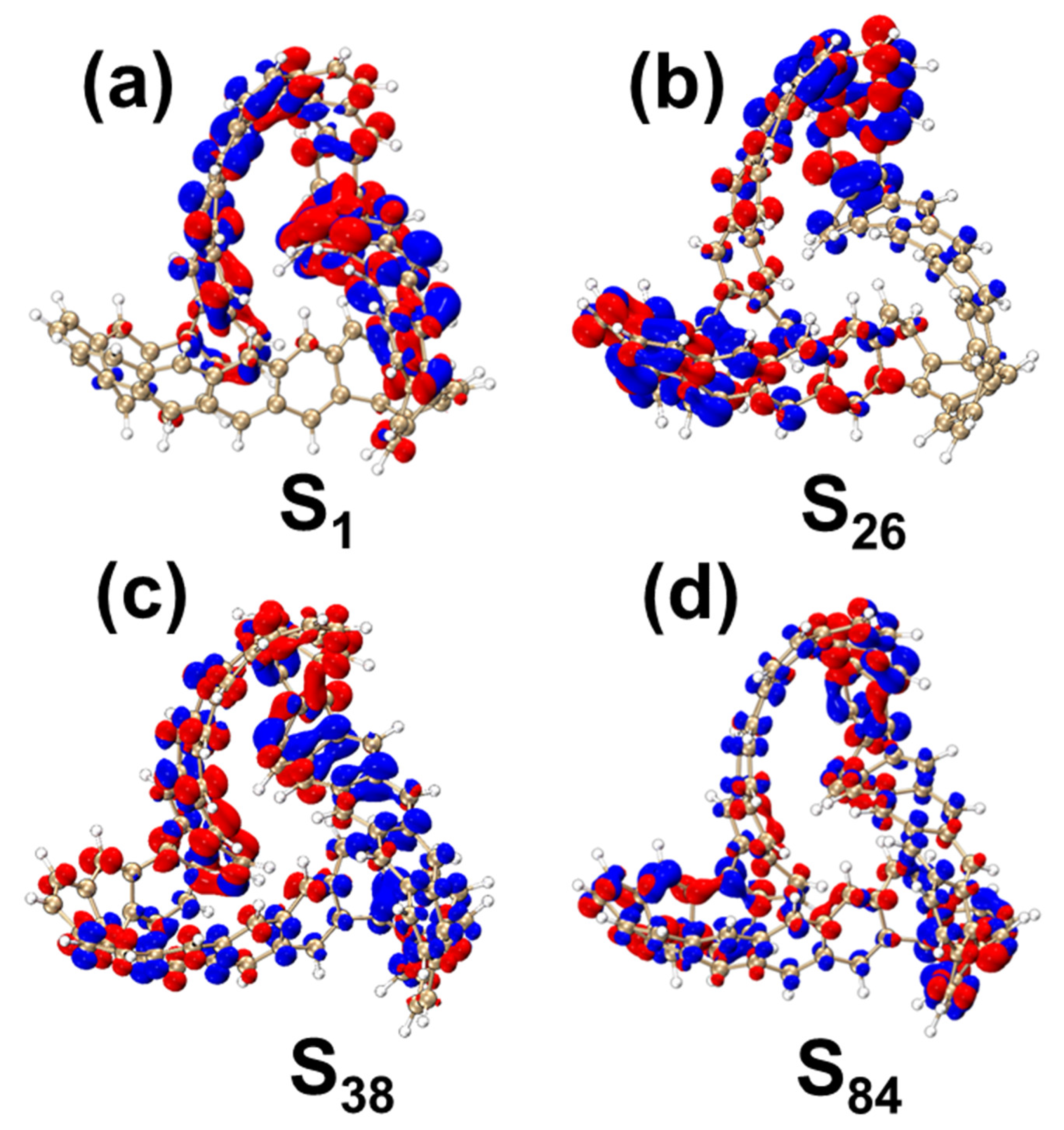
2.1.2. OPA and TPA Spectral Analysis
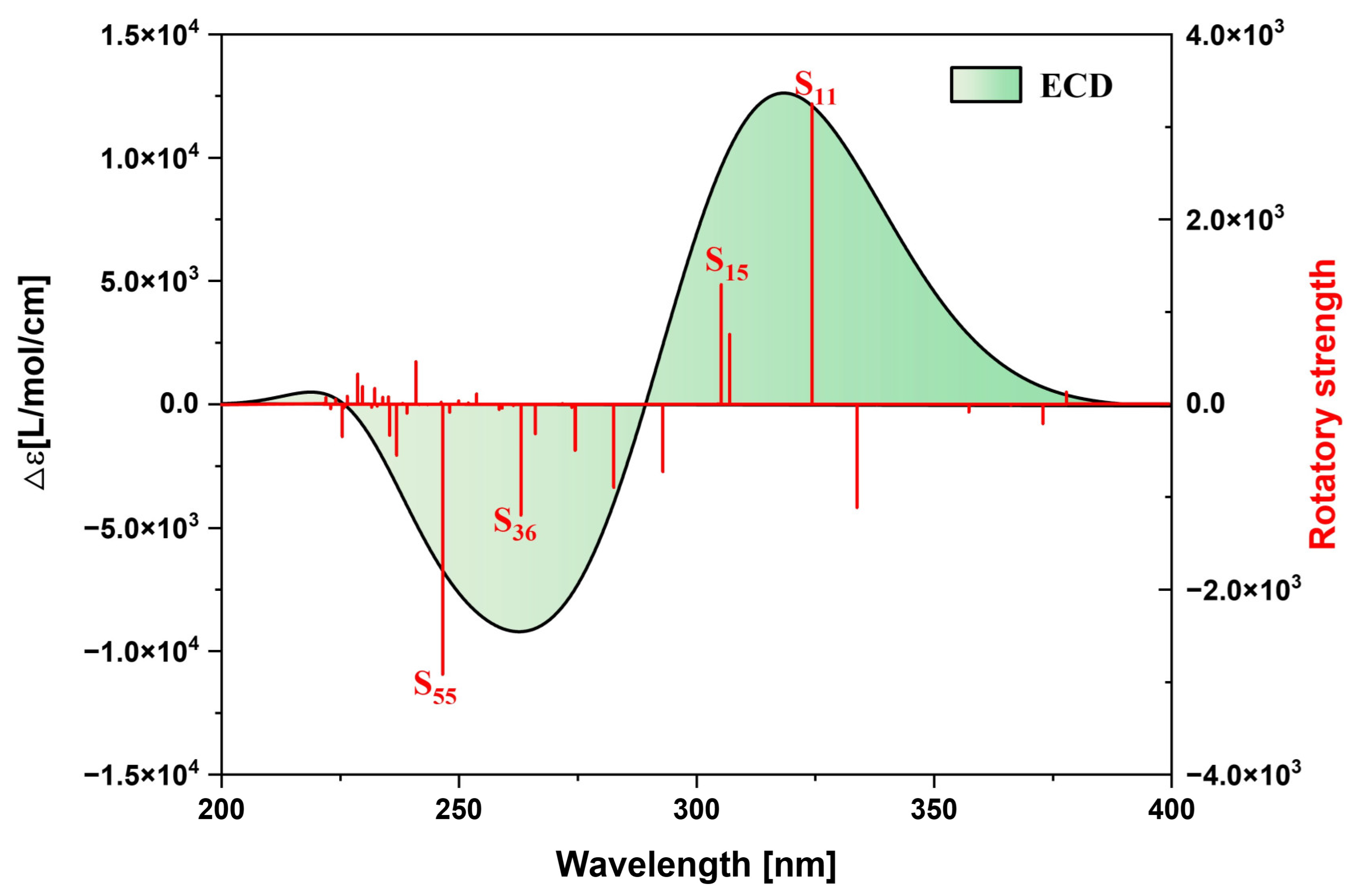
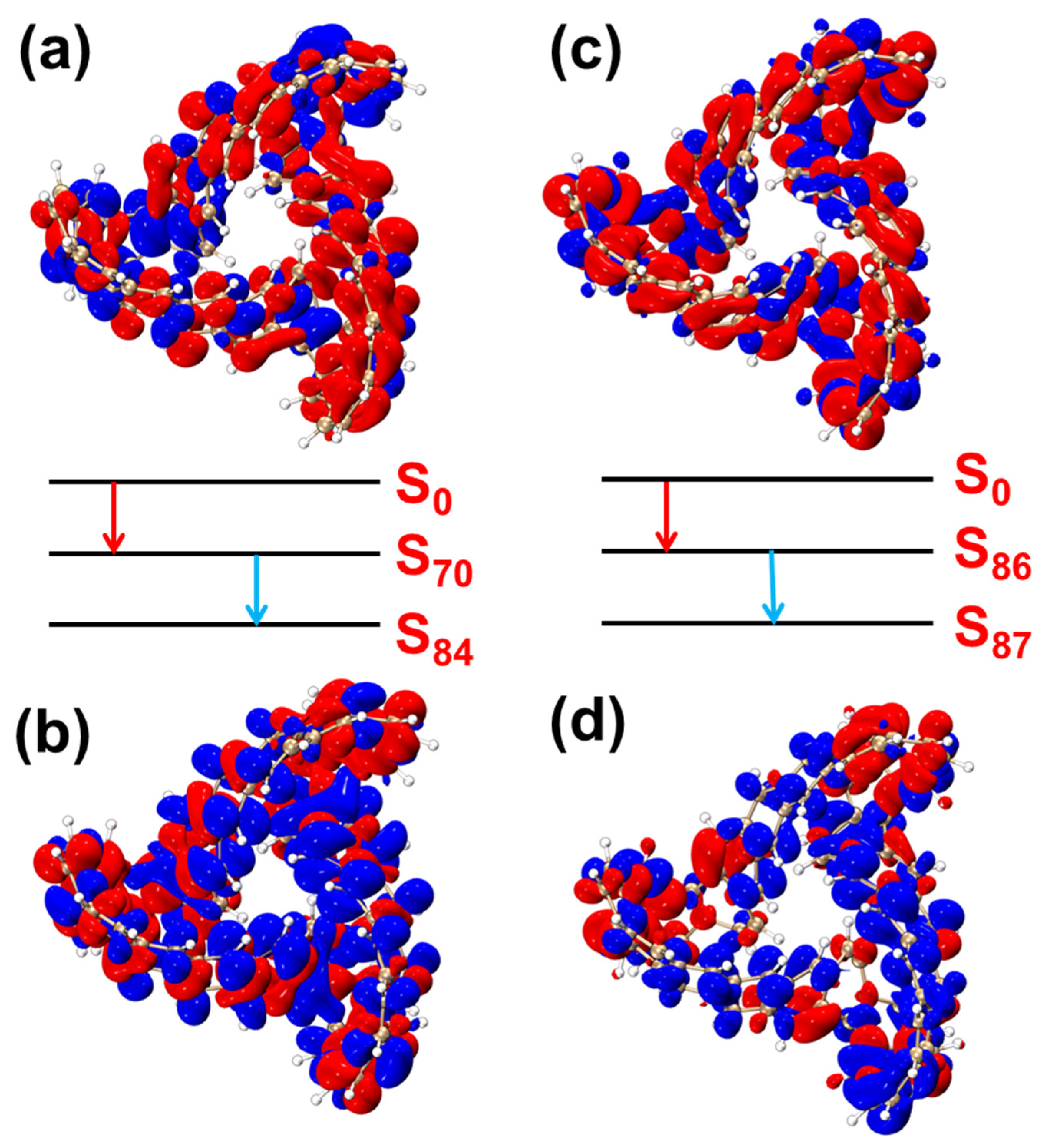
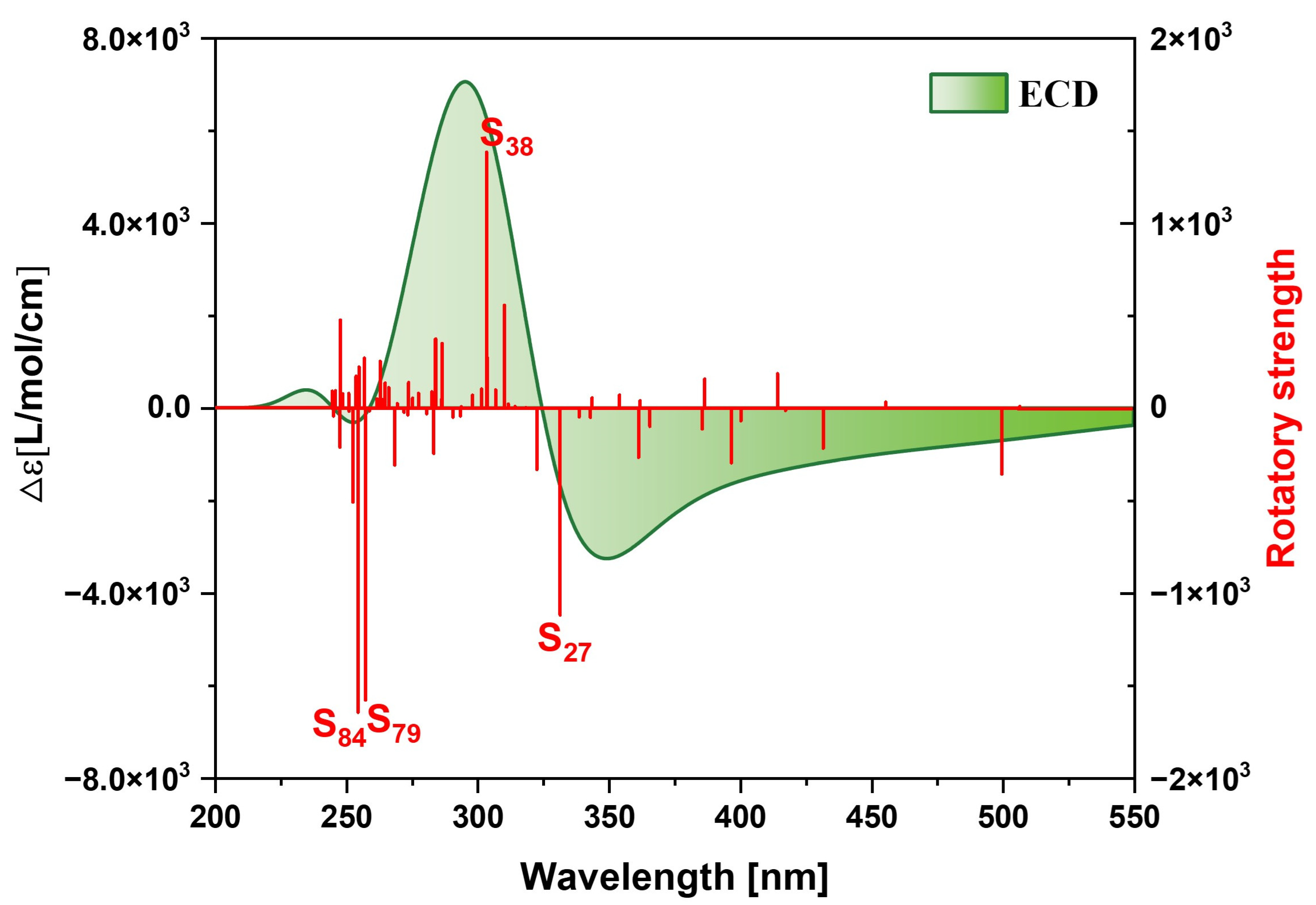
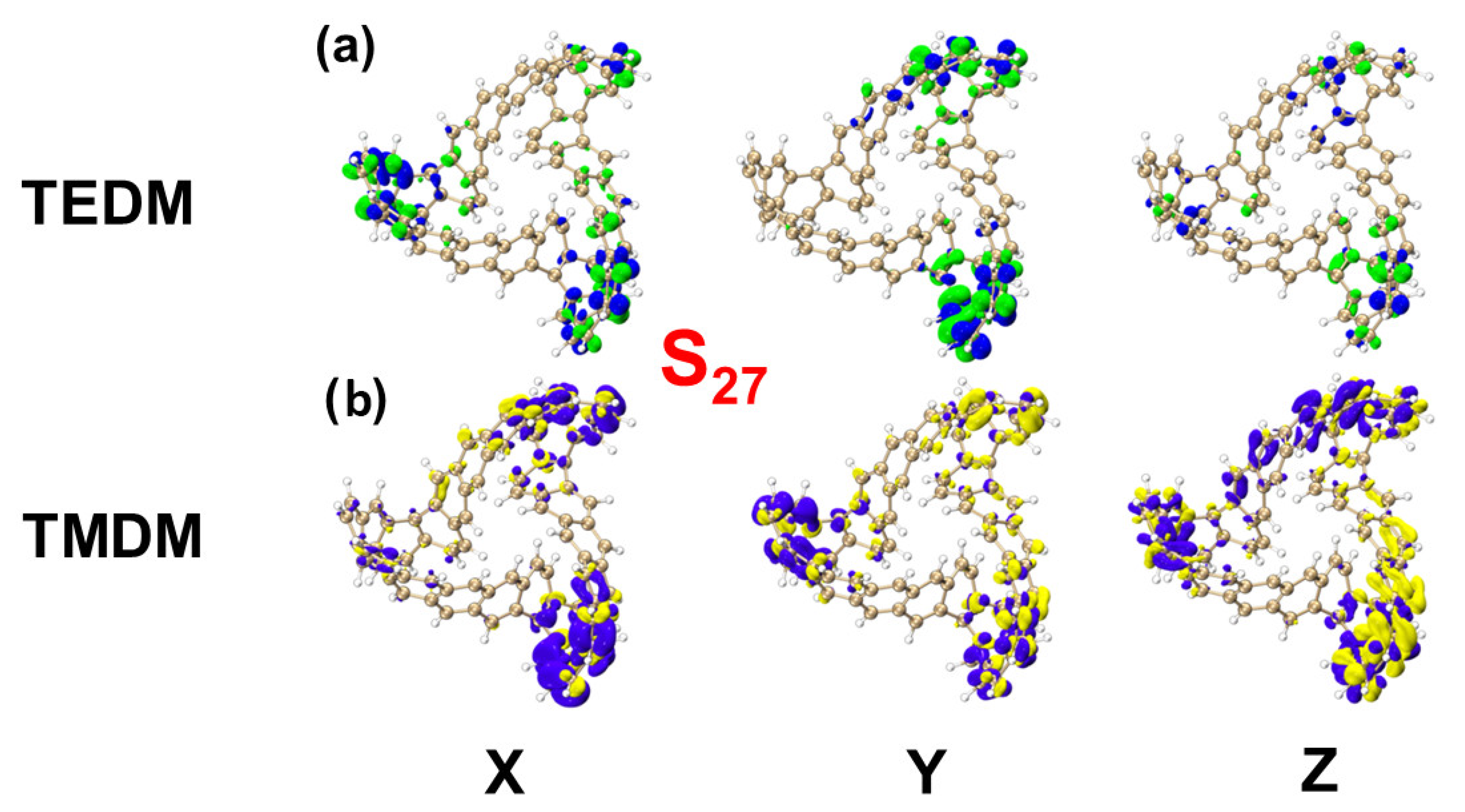
2.1.3. Chiral Physical Mechanism of Electronic Circular Dichroism
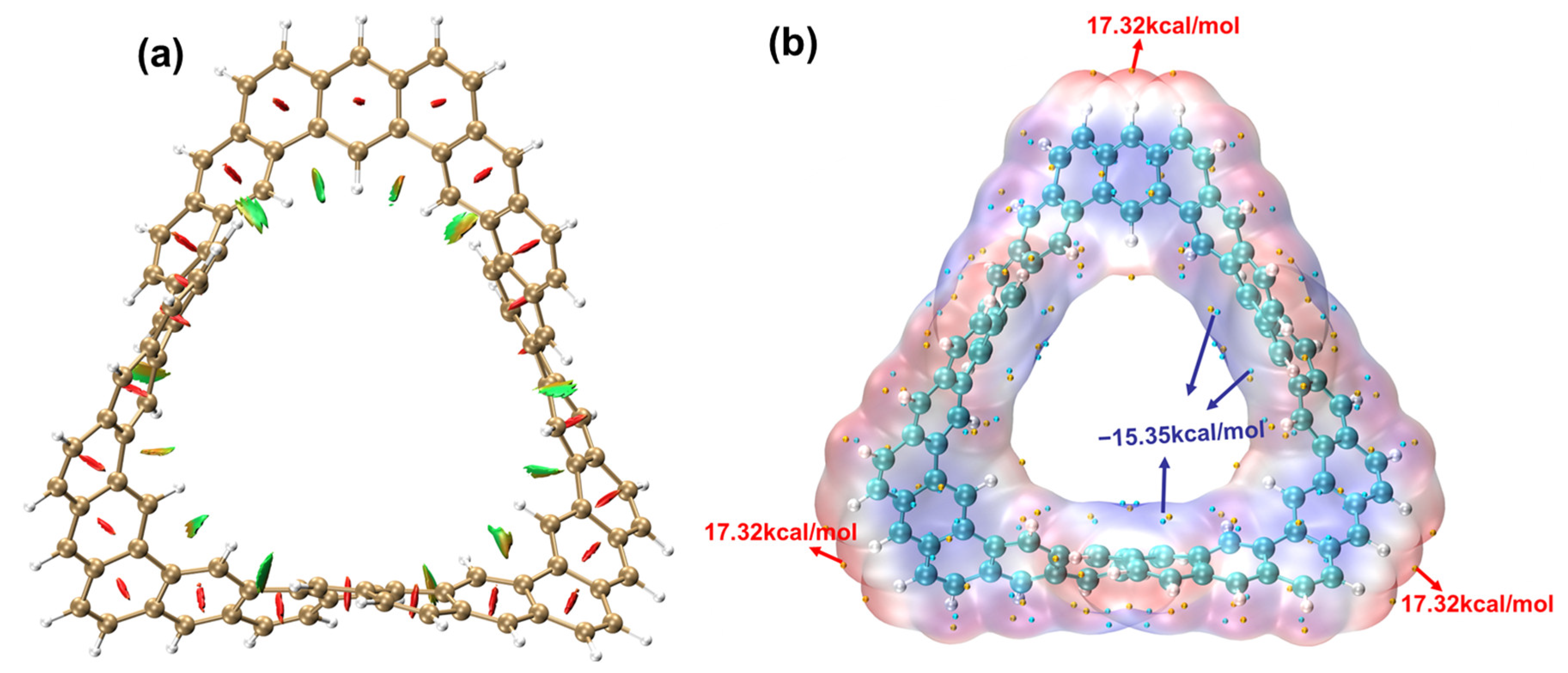
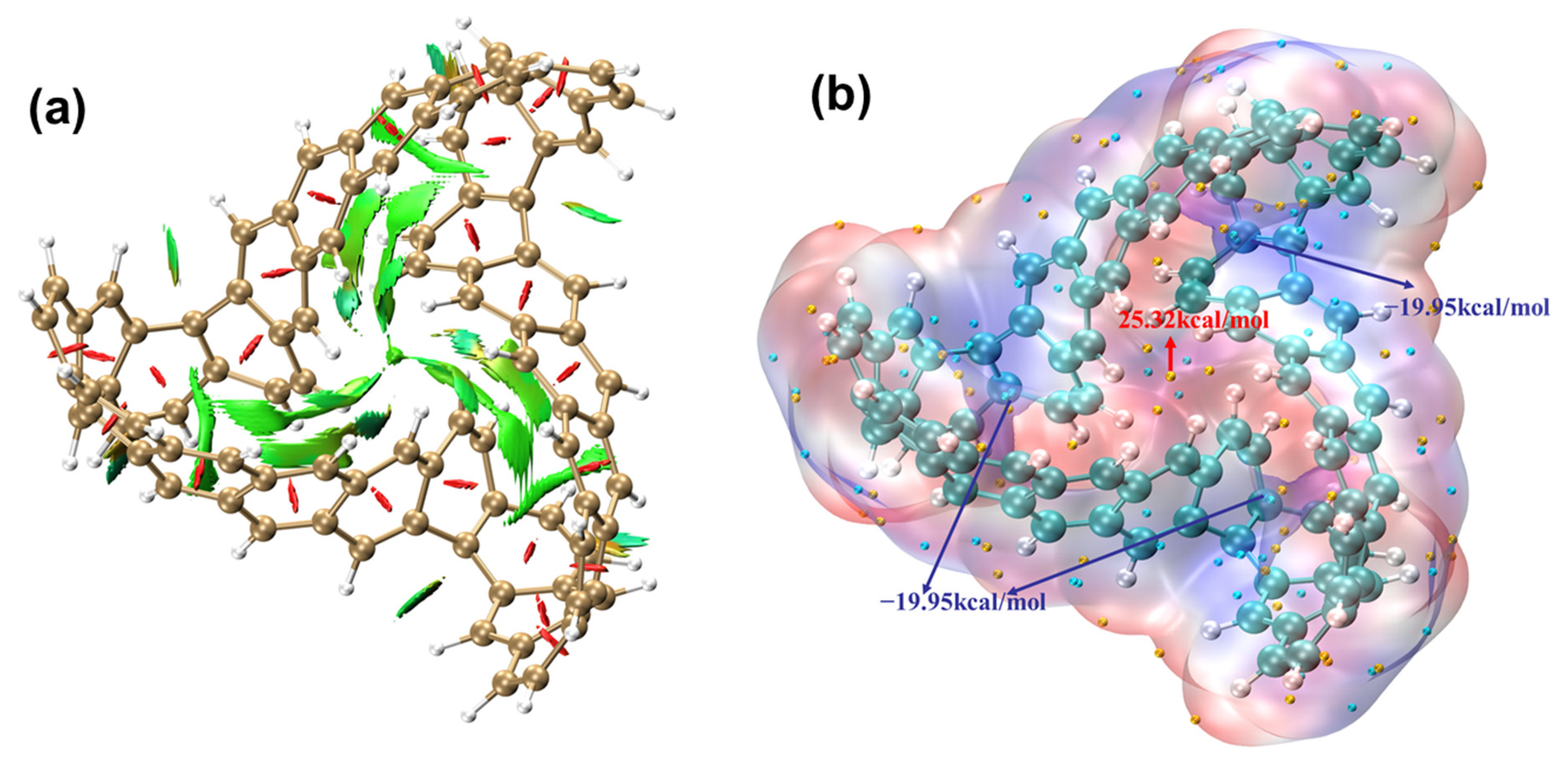
2.1.4. Electrostatic Potential and Weak Interaction
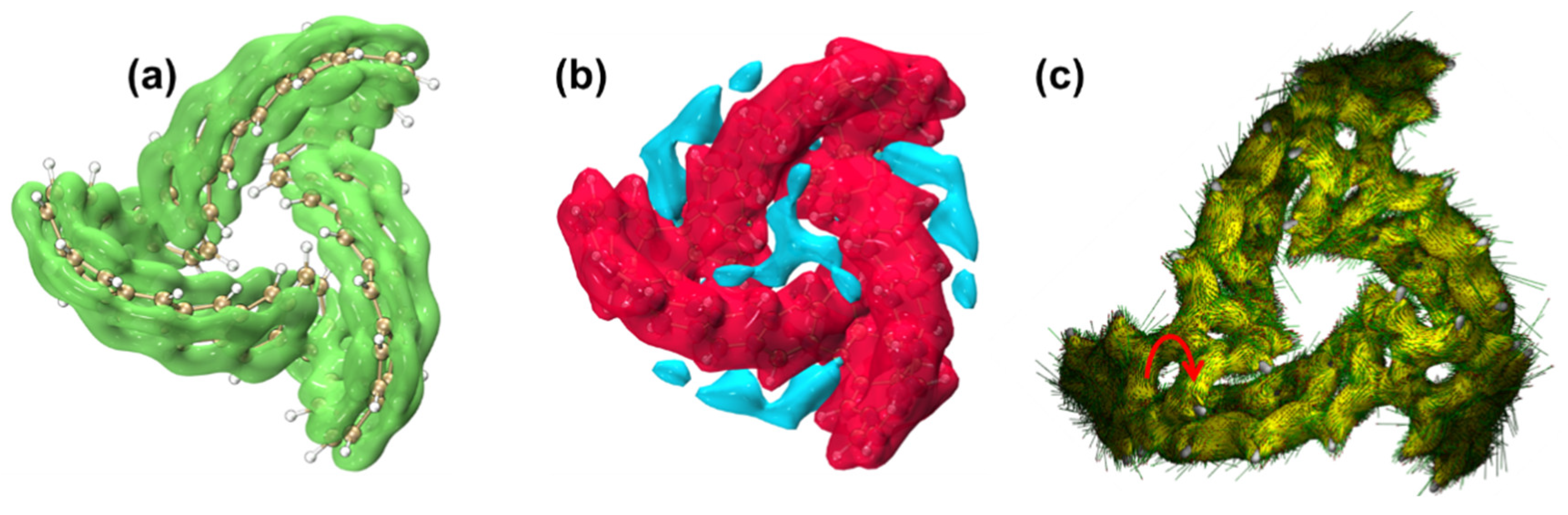
2.1.5. Study on Electronic Delocalization and Aromaticity of TMCNB
2.2. Photoelectric Properties and Physical Mechanism of MCNB2—A Designed Isomer of TMCNB
2.2.1. Structure and Properties of MSNB2
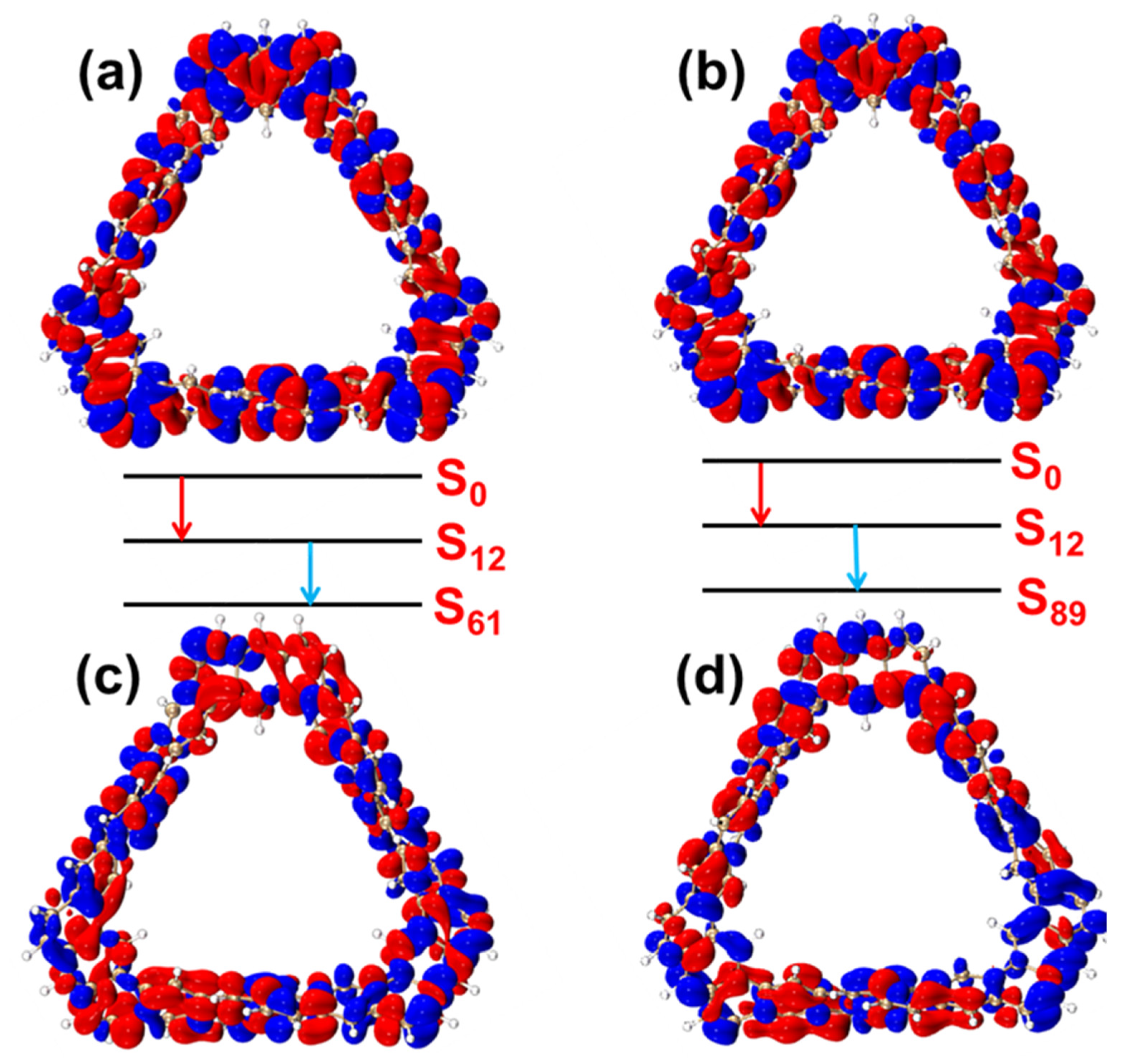
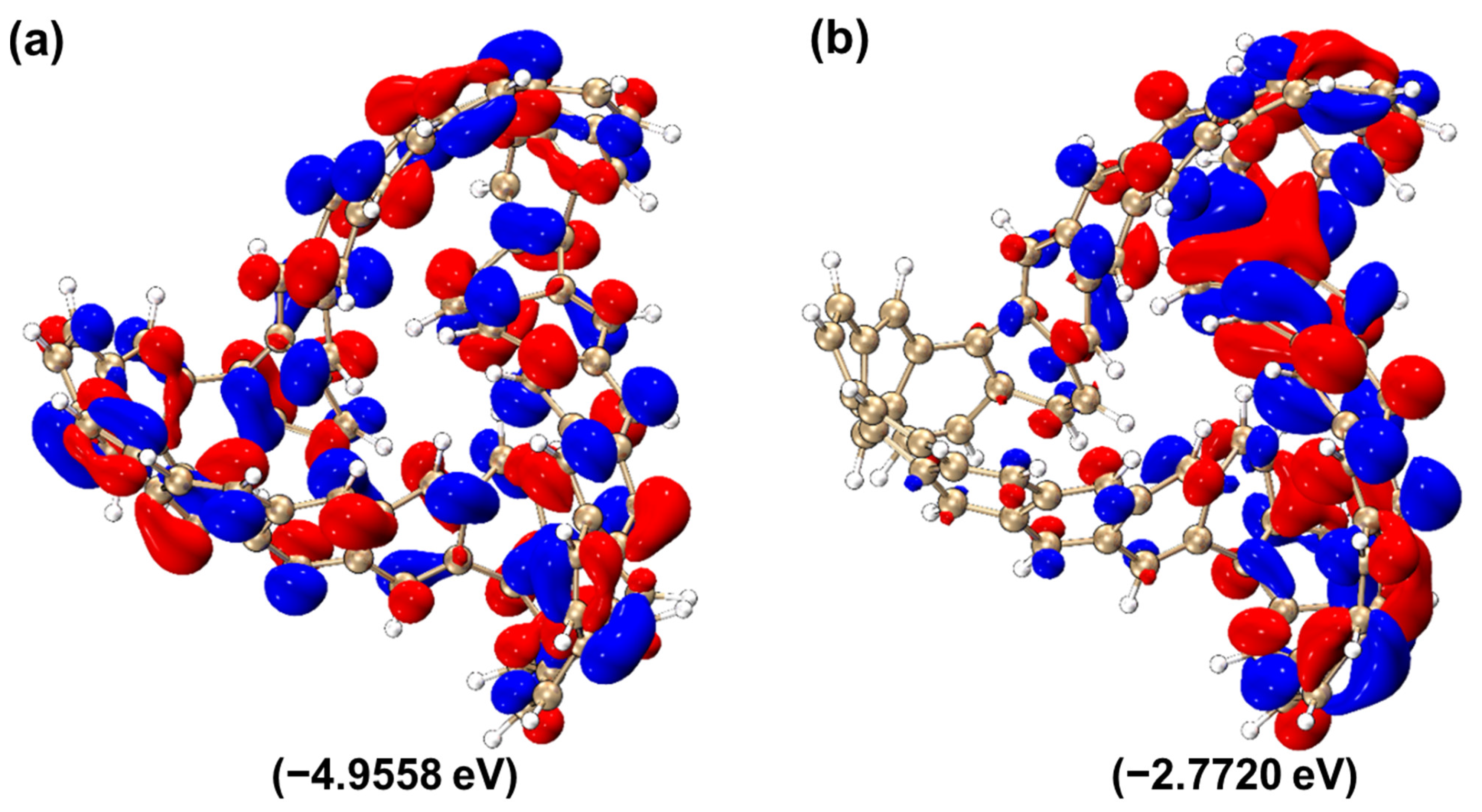
2.2.2. HOMO–LUMO Molecular Orbital Analysis
2.2.3. OPA and TPA Characteristics
2.2.4. The Chiral Physical Mechanism of the Electronic Circular Dichroism of MCNB2
2.2.5. Study on Electronic Delocalization and Aromaticity of MCNB2
3. Computational Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Buyalo, S. Möbius and Sub-Möbius Structures. St. Petersburg Math. J. 2017, 28, 555–568. [Google Scholar] [CrossRef]
- Ajami, D.; Hess, K.; Köhler, F.; Näther, C.; Oeckler, O.; Simon, A.; Yamamoto, C.; Okamoto, Y.; Herges, R. Synthesis and Properties of the First Möbius Annulenes. Chem. Eur. J. 2006, 12, 5434–5445. [Google Scholar] [CrossRef] [PubMed]
- Berger, C.; Bresler, C.; Dilger, U.; Geuenich, D.; Herges, R.; Röttele, H.; Schröder, G. A Spontaneous Fragmentation: From the Criegee Zwitterion to Coarctate Möbius Aromaticity. Angew. Chem. Int. Ed. 1998, 37, 1850–1853. [Google Scholar] [CrossRef]
- Karadakov, P.B.; Cooper, D.L. Does the Electronic Structure of Möbius Annulenes Follow Heilbronner’s Ideas? ChemPhysChem 2018, 19, 3186–3190. [Google Scholar] [CrossRef]
- Ajami, D.; Oeckler, O.; Simon, A.; Herges, R. Synthesis of a Möbius Aromatic Hydrocarbon. Nature 2003, 426, 819–821. [Google Scholar] [CrossRef]
- Schaller, G.; Topić, F.; Rissanen, K. Design and Synthesis of the First Triply Twisted Möbius Annulene. Nat. Chem. 2014, 6, 608–613. [Google Scholar] [CrossRef]
- Tanaka, Y.; Saito, S.; Mori, S.; Aratani, N.; Shinokubo, H.; Shibata, N.; Higuchi, Y.; Yoon, Z.; Kim, K.; Noh, S.; et al. Metalation of Expanded Porphyrins: A Chemical Trigger Used to Produce Molecular Twisting and Möbius Aromaticity. Angew. Chem. Int. Ed. 2008, 47, 681–684. [Google Scholar] [CrossRef]
- Naulet, G.; Sturm, L.; Robert, A. Cyclic Tris-[5] Helicenes with Single and Triple Twisted Möbius Topologies and Möbius Aromaticity. Chem. Sci. 2018, 9, 8930–8936. [Google Scholar] [CrossRef]
- Fan, W.; Fukunaga, T.M.; Wu, S. Synthesis and Chiral Resolution of a Triply Twisted Möbius Carbon Nanobelt. Nat. Synth. 2023, 2, 880–887. [Google Scholar] [CrossRef]
- Kang, D.; Zhu, S.; Liu, D.; Cao, S.; Sun, M. One- and Two-Photon Absorption: Physical Principle and Applications. Chem. Rec. 2020, 20, 894–906. [Google Scholar] [CrossRef]
- Gai, X.; Sheng, H.; Wang, J. Physical Mechanism on the Linear Spectrum and Nonlinear Spectrum in a Twist Bilayer Graphdiyne Nanodisk. Phys. Chem. Chem. Phys. 2023, 25, 20049–20065. [Google Scholar] [CrossRef] [PubMed]
- Xue, Y.; Tian, J.; Tian, W. Spiropyran-Based Recognitions of Amines: UV–Vis Spectra and Mechanisms. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2021, 250, 119385. [Google Scholar] [CrossRef] [PubMed]
- Mu, X.; Wang, J.; Sun, M. Visualization of Photoinduced Charge Transfer and Electron–Hole Coherence in Two-Photon Absorption. J. Phys. Chem. C 2019, 123, 14132–14143. [Google Scholar] [CrossRef]
- Rumi, M.; Ehrlich, J.E.; Heikal, A.A.; Perry, J.W.; Barlow, S.; Hu, Z.; McCord-Maughon, D.; Parker, T.C.; Röckel, H.; Thayumanavan, S.; et al. Structure–Property Relationships for Two-Photon Absorbing Chromophores: Bis-Donor Diphenylpolyene and Bis(styryl)benzene Derivatives. J. Am. Chem. Soc. 2000, 122, 9500–9510. [Google Scholar] [CrossRef]
- Walters, G.; Sutherland, B.R.; Hoogland, S.; Shi, D.; Comin, R.; Sellan, D.P.; Bakr, O.M.; Sargent, E.H. Two-Photon Absorption in Organometallic Bromide Perovskites. ACS Nano 2015, 9, 9340–9346. [Google Scholar] [CrossRef]
- Lu, C.; Li, N.; Jin, Y. Physical Mechanisms of Intermolecular Interactions and Cross-Space Charge Transfer in Two-Photon BDBT-TCNB Co-Crystals. Nanomaterials 2022, 12, 2757. [Google Scholar] [CrossRef]
- Ding, S.S.; Zhang, C.C.; Shi, W.S. Absolute Configuration of Two Novel Compounds from the Talaromyces aculeatus Using Optical Rotation, Electronic Circular Dichroism and Vibrational Circular Dichroism. Tetrahedron Lett. 2016, 57, 75–79. [Google Scholar] [CrossRef]
- Bruhn, T.; Schaumlöffel, A.N.U.; Hemberger, Y. SpecDis: Quantifying the Comparison of Calculated and Experimental Electronic Circular Dichroism Spectra. Chirality 2013, 25, 243–249. [Google Scholar] [CrossRef]
- Furche, F.; Ahlrichs, R.; Wachsmann, C.; Weber, E.; Sobanski, A.; Vögtle, F.; Grimme, S. Circular Dichroism of Helicenes Investigated by Time-Dependent Density Functional Theory. J. Am. Chem. Soc. 2000, 122, 1717–1724. [Google Scholar] [CrossRef]
- Albano, G.; Pescitelli, G.; Di Bari, L. Chiroptical Properties in Thin Films of π-Conjugated Systems. Chem. Rev. 2020, 120, 10145–10243. [Google Scholar] [CrossRef]
- Schleyer, P.v.R. Introduction: Aromaticity. Chem. Rev. 2001, 101, 1115–1118. [Google Scholar] [CrossRef]
- Liu, Z.; Lu, T.; Chen, Q. An sp-Hybridized All-Carboatomic Ring, Cyclo [18]carbon: Bonding Character, Electron Delocalization, and Aromaticity. Carbon 2020, 165, 468–475. [Google Scholar] [CrossRef]
- Krygowski, T.M.; Cyrański, M.K. Structural Aspects of Aromaticity. Chem. Rev. 2001, 101, 1385–1420. [Google Scholar] [CrossRef] [PubMed]
- Geuenich, D.; Hess, K.; Kohler, F.; Herges, R. Anisotropy of the Induced Current Density (ACID), a General Method to Quantify and Visualize Electronic Delocalization. Chem. Rev. 2005, 105, 3758–3772. [Google Scholar] [CrossRef] [PubMed]
- Klod, S.; Kleinpeter, E. Ab Initio Calculation of the Anisotropy Effect of Multiple Bonds and the Ring Current Effect of Arenes—Application in Conformational and Configurational Analysis. J. Chem. Soc. Perkin Trans. 2 2001, 10, 1893–1898. [Google Scholar]
- Tsirelson, V.G.; Stash, A. Analyzing Experimental Electron Density with the Localized-Orbital Locator. Acta Crystallogr. Sect. B Struct. Sci. 2002, 58, 780–785. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Lu, T.; Chen, Q. A Simple Real Space Function Clearly Revealing Both Chemical Bonds and Weak Interactions. Chem. Methods 2021, 1, 231–239. [Google Scholar] [CrossRef]
- Tirado-Rives, J.; Jorgensen, W.L. Performance of B3LYP Density Functional Methods for a Large Set of Organic Molecules. J. Chem. Theory Comput. 2008, 4, 297–306. [Google Scholar] [CrossRef]
- Becke, A.D. Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Grimme, S. Density Functional Theory with London Dispersion Corrections. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 211–228. [Google Scholar] [CrossRef]
- Frisch, M.; Trucks, G.; Schlegel, H.; Scuseria, G.; Robb, M.; Cheeseman, J.; Scalmani, G.; Barone, V.; Petersson, G.; Nakatsuji, H. Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Yanai, T.; Tew, D.P.; Handy, N.C. A New Hybrid Exchange–Correlation Functional Using the Coulomb-Attenuating Method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
- Mu, X.; Chen, X.; Wang, J.; Sun, M. Visualizations of Electric and Magnetic Interactions in Electronic Circular Dichroism and Raman Optical Activity. J. Phys. Chem. A 2019, 123, 8071–8081. [Google Scholar] [CrossRef]
- Mu, X.; Sun, M. The Linear and Non-Linear Optical Absorption and Asymmetrical Electromagnetic Interaction in Chiral Twisted Bilayer Graphene with Hybrid Edges. Mater. Today Phys. 2020, 14, 100222. [Google Scholar] [CrossRef]
- Sergio, M.; Lu, T. The Geometry and Electronic Structure of Aristolochic Acid: Possible Implications for a Frozen Resonance. J. Phys. Org. Chem. 2013, 26, 473–483. [Google Scholar]
- Li, N.; Sheng, H.; Sun, Y. Spectroscopic Study on Size-Dependent Optoelectronics of N-Type Ultra-High Conductive Polymer PBFDO. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2023, 298, 122744. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Kühne, T.D.; Iannuzzi, M.; Del Ben, M.; Rybkin, V.V.; Seewald, P.; Stein, F.; Laino, T.; Khaliullin, R.Z.; Schütt, O.; Schiffmann, F.; et al. CP2K: An Electronic Structure and Molecular Dynamics Software Package—Quickstep: Efficient and Accurate Electronic Structure Calculations. J. Chem. Phys. 2020, 152, 194103. [Google Scholar] [CrossRef]

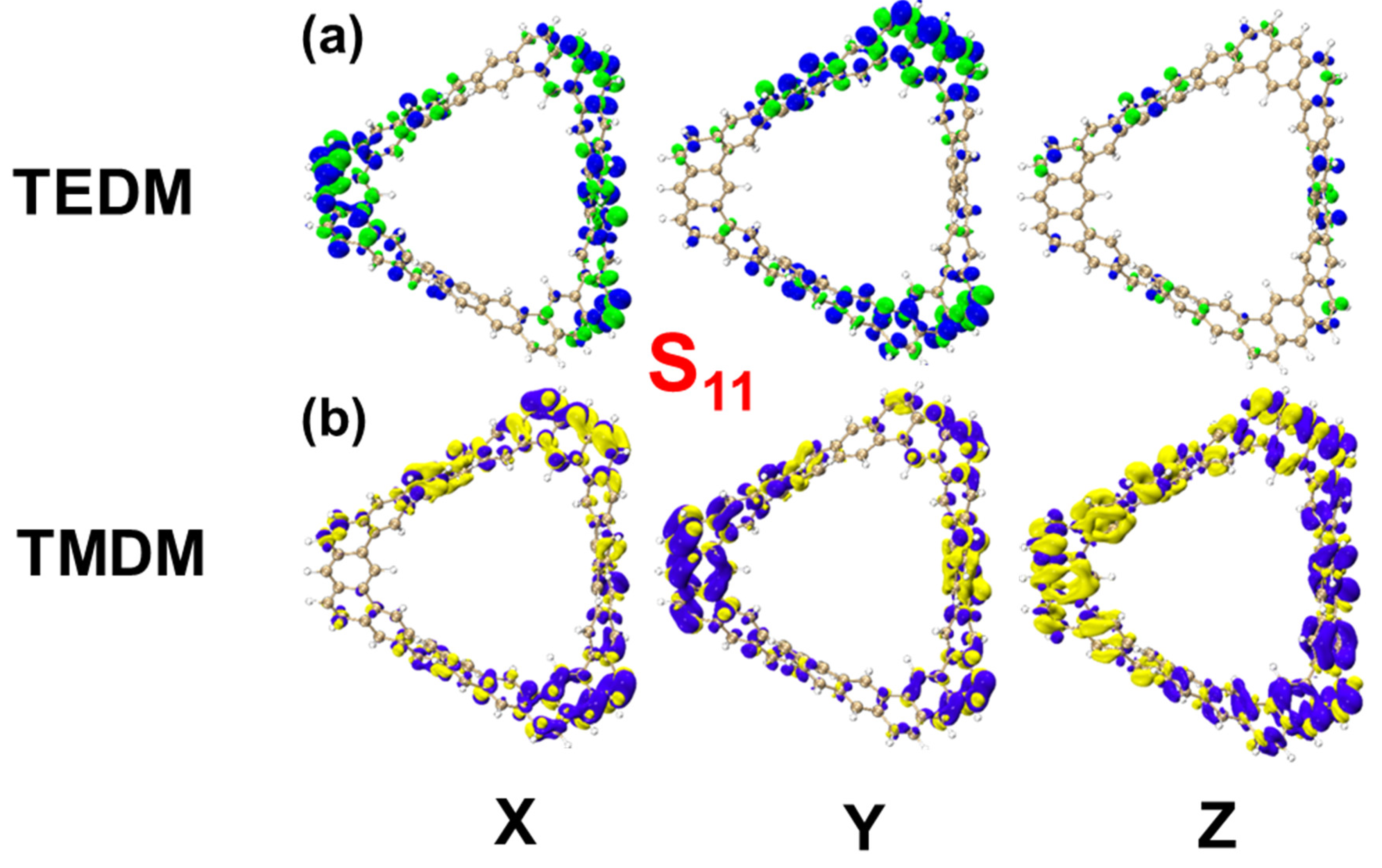

| X | Y | Z | Eigenvalue | ||
|---|---|---|---|---|---|
| S11 | TEDM | 2.6963 | 5.8930 | 0.0002 | 13.82759357 |
| TMDM | −0.8881 | −1.9401 | −0.0012 | ||
| S15 | TEDM | −0.0177 | 0.0323 | −0.0001 | 0.00170296 |
| TMDM | 0.0203 | −0.0416 | −0.0003 | ||
| S36 | TEDM | 1.6935 | −1.2341 | −0.0006 | −5.15281076 |
| TMDM | 1.9867 | −1.4491 | 0.0000 | ||
| S55 | TEDM | 0.0017 | 0.0005 | 2.7348 | −12.73021732 |
| TMDM | −0.0020 | 0.0004 | 4.6549 |
| X | Y | Z | Eigenvalue | ||
|---|---|---|---|---|---|
| S27 | TEDM | −1.0245 | −1.9976 | 0.0010 | −4.69866582 |
| TMDM | −4.3178 | −0.1377 | 0.0102 | ||
| S38 | TEDM | 1.1735 | 1.6742 | 0.0127 | 5.95234577 |
| TMDM | −2.7698 | −1.6137 | −0.0259 | ||
| S79 | TEDM | −0.0053 | −0.0070 | −1.4730 | −6.71631021 |
| TMDM | 0.0063 | 0.0135 | −4.5597 | ||
| S84 | TEDM | 0.0121 | 0.0223 | −2.2231 | −6.98005882 |
| TMDM | −0.0225 | −0.0091 | −3.1400 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, C.; Wang, T. Optoelectronic Properties of Triply Twisted Möbius Carbon Nanobelt and the Design of Its Isomeric Nanomaterials. Molecules 2024, 29, 4621. https://doi.org/10.3390/molecules29194621
Yao C, Wang T. Optoelectronic Properties of Triply Twisted Möbius Carbon Nanobelt and the Design of Its Isomeric Nanomaterials. Molecules. 2024; 29(19):4621. https://doi.org/10.3390/molecules29194621
Chicago/Turabian StyleYao, Cailian, and Tao Wang. 2024. "Optoelectronic Properties of Triply Twisted Möbius Carbon Nanobelt and the Design of Its Isomeric Nanomaterials" Molecules 29, no. 19: 4621. https://doi.org/10.3390/molecules29194621
APA StyleYao, C., & Wang, T. (2024). Optoelectronic Properties of Triply Twisted Möbius Carbon Nanobelt and the Design of Its Isomeric Nanomaterials. Molecules, 29(19), 4621. https://doi.org/10.3390/molecules29194621





