A Machine Learning Model for Predicting the Propagation Rate Coefficient in Free-Radical Polymerization
Abstract
1. Introduction
2. Results and Discussion
2.1. Comparison of Four Regression Models on the Training Dataset
2.2. Construction of the External Test Dataset
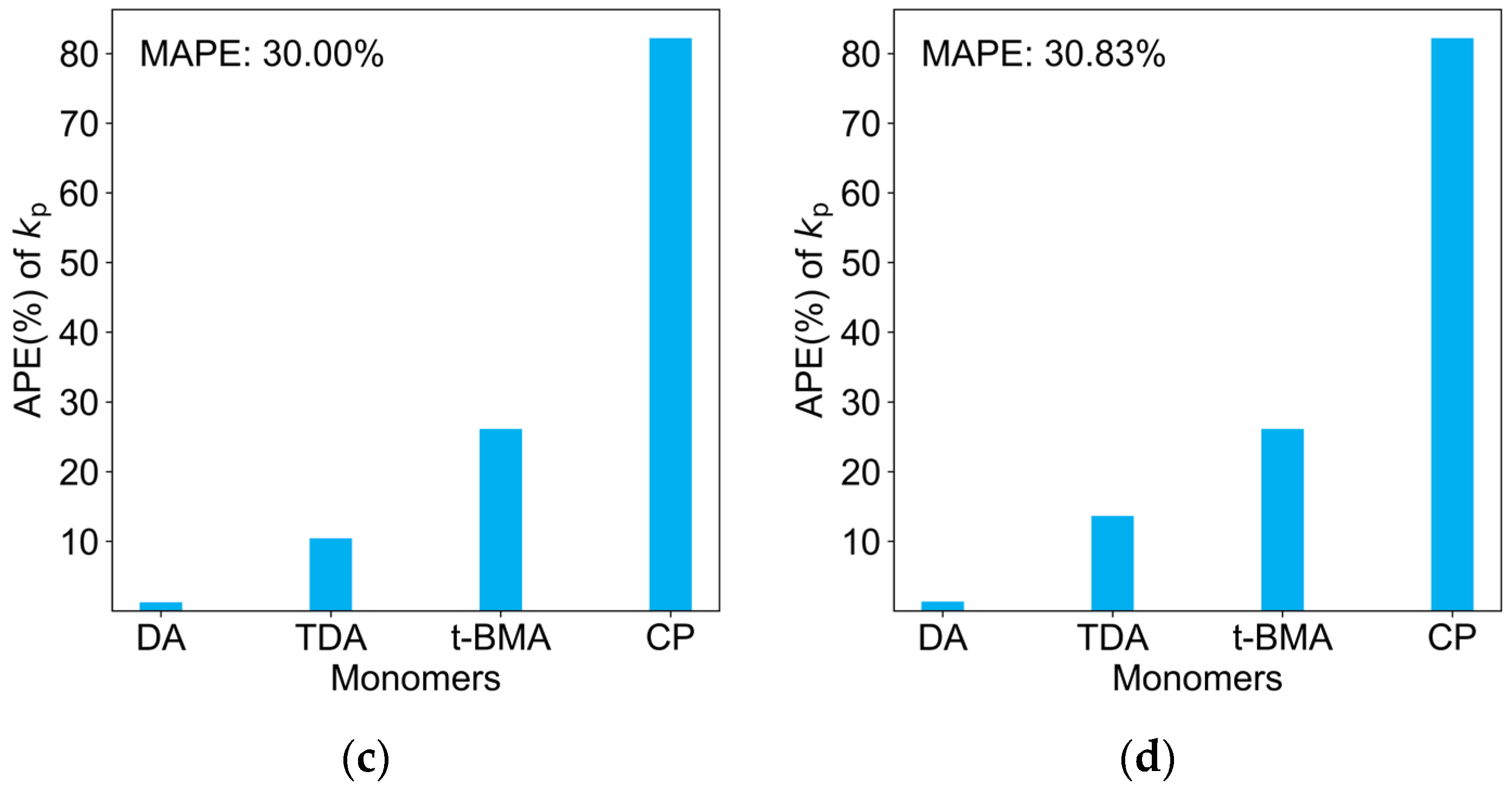
2.3. Comparison of Four Regression Models on the Test Dataset
2.4. Reflection of Scientific Principles
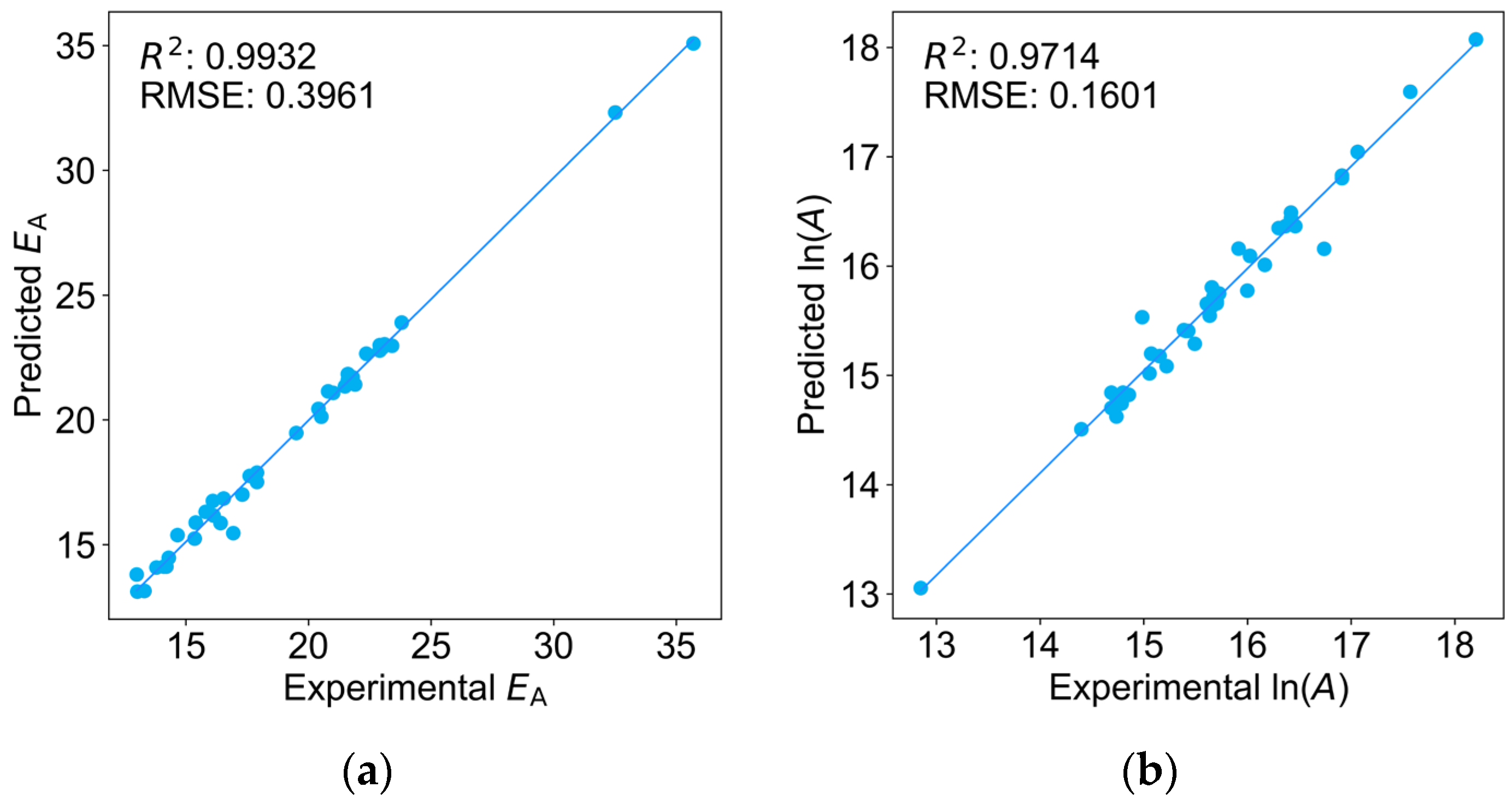
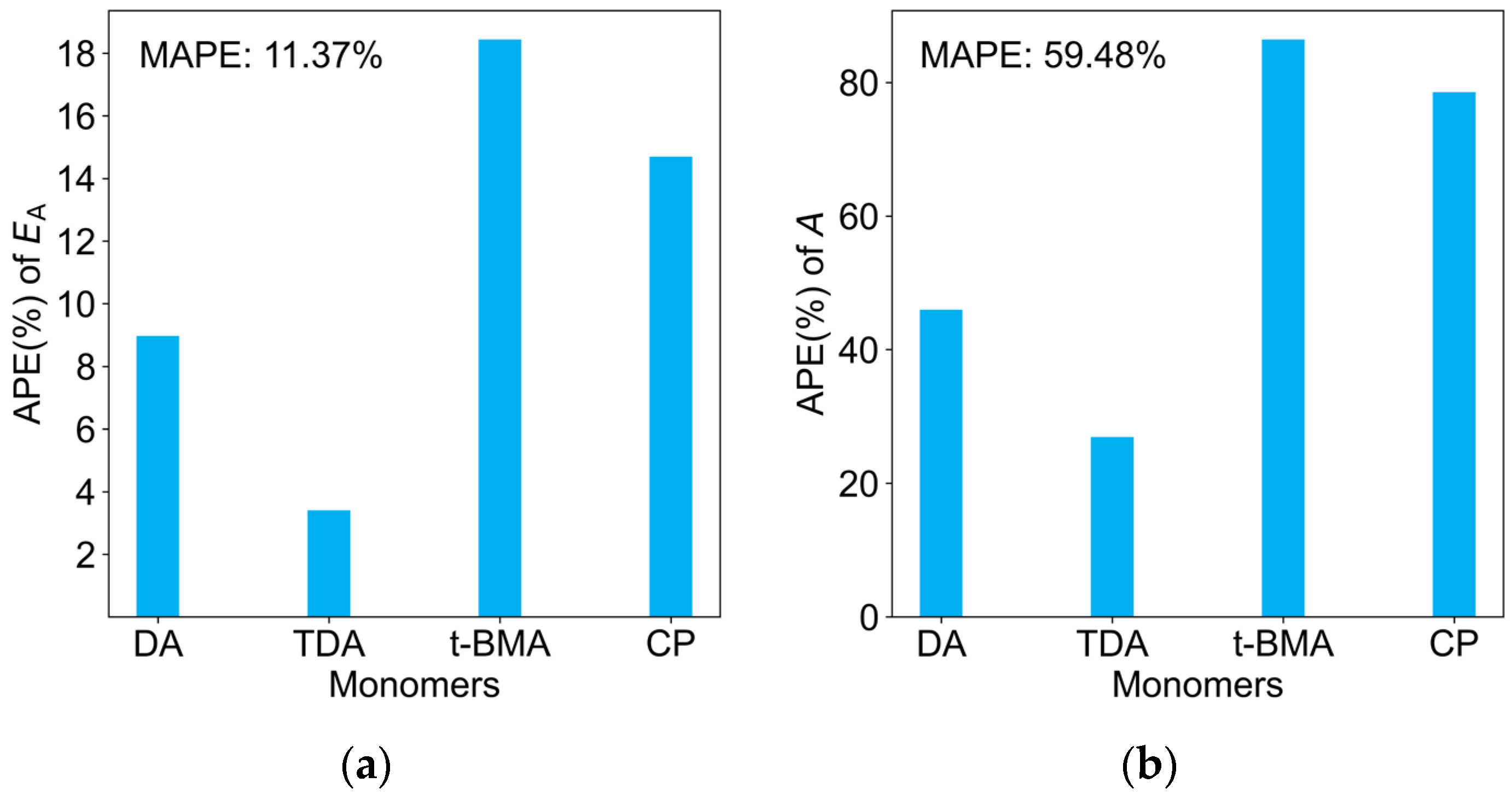
2.5. Predictions of kp at Multiple Temperatures, A, and EA
3. Methods
3.1. Construction of the Training Dataset
3.2. Feature Representation
3.2.1. Scientific Understanding
3.2.2. SMILES and MACCS Fingerprints
3.2.3. Molecular Transformer Embeddings
3.3. Algorithms of Regression Models
3.3.1. Multivariate Linear Regression
3.3.2. Ridge Regression and Lasso Regression
3.3.3. Bayesian Ridge Regression
3.4. Validation Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Beuermann, S.; Buback, M. Rate coefficients of free-radical polymerization deduced from pulsed laser experiments. Prog. Polym. Sci. 2002, 27, 191–254. [Google Scholar]
- Nikitin, A.N.; Lacík, I.; Hutchinson, R.A. A 3D simulation investigation of the influence of temperature increases on the accuracy of propagation rate coefficients determined by Pulsed-Laser Polymerization. Macromolecules 2016, 49, 9320–9335. [Google Scholar] [CrossRef]
- Heuts, J.P.; Gilbert, R.G.; Radom, L. A priori prediction of propagation rate coefficients in free-radical polymerizations: Propagation of ethylene. Macromolecules 1995, 28, 8771–8781. [Google Scholar] [CrossRef]
- Kockler, K.B.; Haehnel, A.P.; Junkers, T.; Barner-Kowollik, C. Determining Free-Radical Propagation Rate Coefficients with High-Frequency Lasers: Current Status and Future Perspectives. Macromol. Rapid Commun. 2016, 37, 123–134. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.-N.; Luo, Z.-H. Copper (0)-mediated reversible-deactivation radical polymerization: Kinetics insight and experimental study. Macromolecules 2014, 47, 6218–6229. [Google Scholar] [CrossRef]
- Barner-Kowollik, C.; Günzler, F.; Junkers, T. Pushing the limit: Pulsed laser polymerization of n-butyl acrylate at 500 Hz. Macromolecules 2008, 41, 8971–8973. [Google Scholar] [CrossRef]
- Buback, M.; Gilbert, R.G.; Hutchinson, R.A.; Klumperman, B.; Kuchta, F.D.; Manders, B.G.; O’Driscoll, K.F.; Russell, G.T.; Schweer, J. Critically evaluated rate coefficients for free-radical polymerization, 1. Propagation rate coefficient for styrene. Macromol. Chem. Phys. 1995, 196, 3267–3280. [Google Scholar] [CrossRef]
- Marien, Y.W.; Van Steenberge, P.H.; Barner-Kowollik, C.; Reyniers, M.-F.o.; Marin, G.B.; D’hooge, D.R. Kinetic Monte Carlo modeling extracts information on chain initiation and termination from complete PLP-SEC traces. Macromolecules 2017, 50, 1371–1385. [Google Scholar] [CrossRef]
- Beuermann, S.; Harrisson, S.; Hutchinson, R.A.; Junkers, T.; Russell, G.T. Update and critical reanalysis of IUPAC benchmark propagation rate coefficient data. Polym. Chem. 2022, 13, 1891–1900. [Google Scholar] [CrossRef]
- Beuermann, S.; Buback, M.; Davis, T.P.; Gilbert, R.G.; Hutchinson, R.A.; Kajiwara, A.; Klumperman, B.; Russell, G.T. Critically evaluated rate coefficients for free-radical polymerization, 3. Propagation rate coefficients for alkyl methacrylates. Macromol. Chem. Phys. 2000, 201, 1355–1364. [Google Scholar] [CrossRef]
- Beuermann, S.; Buback, M.; Davis, T.P.; Gilbert, R.G.; Hutchinson, R.A.; Olaj, O.F.; Russell, G.T.; Schweer, J.; Van Herk, A.M. Critically evaluated rate coefficients for free-radical polymerization, 2. Propagation rate coefficients for methyl methacrylate. Macromol. Chem. Phys. 1997, 198, 1545–1560. [Google Scholar] [CrossRef]
- Huang, D.M.; Monteiro, M.J.; Gilbert, R.G. A theoretical study of propagation rate coefficients for methacrylonitrile and acrylonitrile. Macromolecules 1998, 31, 5175–5187. [Google Scholar]
- Van de Reydt, E.; Marom, N.; Saunderson, J.; Boley, M.; Junkers, T. A Predictive machine-learning model for propagation rate coefficients in radical polymerization. Polym. Chem. 2023, 14, 1622–1629. [Google Scholar] [CrossRef]
- Shi, Y.; Yu, M.; Liu, J.; Yan, F.; Luo, Z.-H.; Zhou, Y.-N. Quantitative structure–property relationship model for predicting the propagation rate coefficient in free-radical polymerization. Macromolecules 2022, 55, 9397–9410. [Google Scholar] [CrossRef]
- Weininger, D. SMILES, a chemical language and information system. 1. Introduction to methodology and encoding rules. J. Chem. Inf. Comput. Sci. 1988, 28, 31–36. [Google Scholar] [CrossRef]
- Morris, P.; St. Clair, R.; Hahn, W.E.; Barenholtz, E. Predicting binding from screening assays with transformer network embeddings. J. Chem. Inf. Model. 2020, 60, 4191–4199. [Google Scholar]
- Durant, J.L.; Leland, B.A.; Henry, D.R.; Nourse, J.G. Reoptimization of MDL keys for use in drug discovery. J. Chem. Inf. Comput. Sci. 2002, 42, 1273–1280. [Google Scholar] [CrossRef]
- Ranstam, J.; Cook, J.A. LASSO regression. J. Br. Surg. 2018, 105, 1348. [Google Scholar] [CrossRef]
- Buback, M.; Kurz, C.H.; Schmaltz, C. Pressure dependence of propagation rate coefficients in free-radical homopolymerizations of methyl acrylate and dodecyl acrylate. Macromol. Chem. Phys. 1998, 199, 1721–1727. [Google Scholar] [CrossRef]
- Haehnel, A.P.; Schneider-Baumann, M.; Arens, L.; Misske, A.M.; Fleischhaker, F.; Barner-Kowollik, C. Global trends for kp? The influence of ester side chain topography in alkyl (meth) acrylates−completing the data base. Macromolecules 2014, 47, 3483–3496. [Google Scholar] [CrossRef]
- Hutchinson, R.; Aronson, M.; Richards, J. Analysis of pulsed-laser-generated molecular weight distributions for the determination of propagation rate coefficients. Macromolecules 1993, 26, 6410–6415. [Google Scholar] [CrossRef]
- Pascal, P.; Winnik, M.A.; Napper, D.H.; Gilbert, R.G. Pulsed laser study of the propagation kinetics of tert-butyl methacrylate. Die Makromol. Chem. Rapid Commun. 1993, 14, 213–215. [Google Scholar] [CrossRef]
- Hutchinson, R.A.; Beuermann, S. Critically evaluated propagation rate coefficients for radical polymerizations: Acrylates and vinyl acetate in bulk (IUPAC Technical Report). Pure Appl. Chem. 2019, 91, 1883–1888. [Google Scholar] [CrossRef]
- Luong, K.-D.; Singh, A. Application of Transformers in Cheminformatics. J. Chem. Inf. Model. 2024, 64, 4392–4409. [Google Scholar] [CrossRef] [PubMed]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. Lightgbm: A highly efficient gradient boosting decision tree. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Tipping, M.E. Sparse Bayesian learning and the relevance vector machine. J. Mach. Learn. Res. 2001, 1, 211–244. [Google Scholar]
- Cha, G.-W.; Moon, H.J.; Kim, Y.-M.; Hong, W.-H.; Hwang, J.-H.; Park, W.-J.; Kim, Y.-C. Development of a prediction model for demolition waste generation using a random forest algorithm based on small datasets. Int. J. Environ. Res. Public Health 2020, 17, 6997. [Google Scholar] [CrossRef]
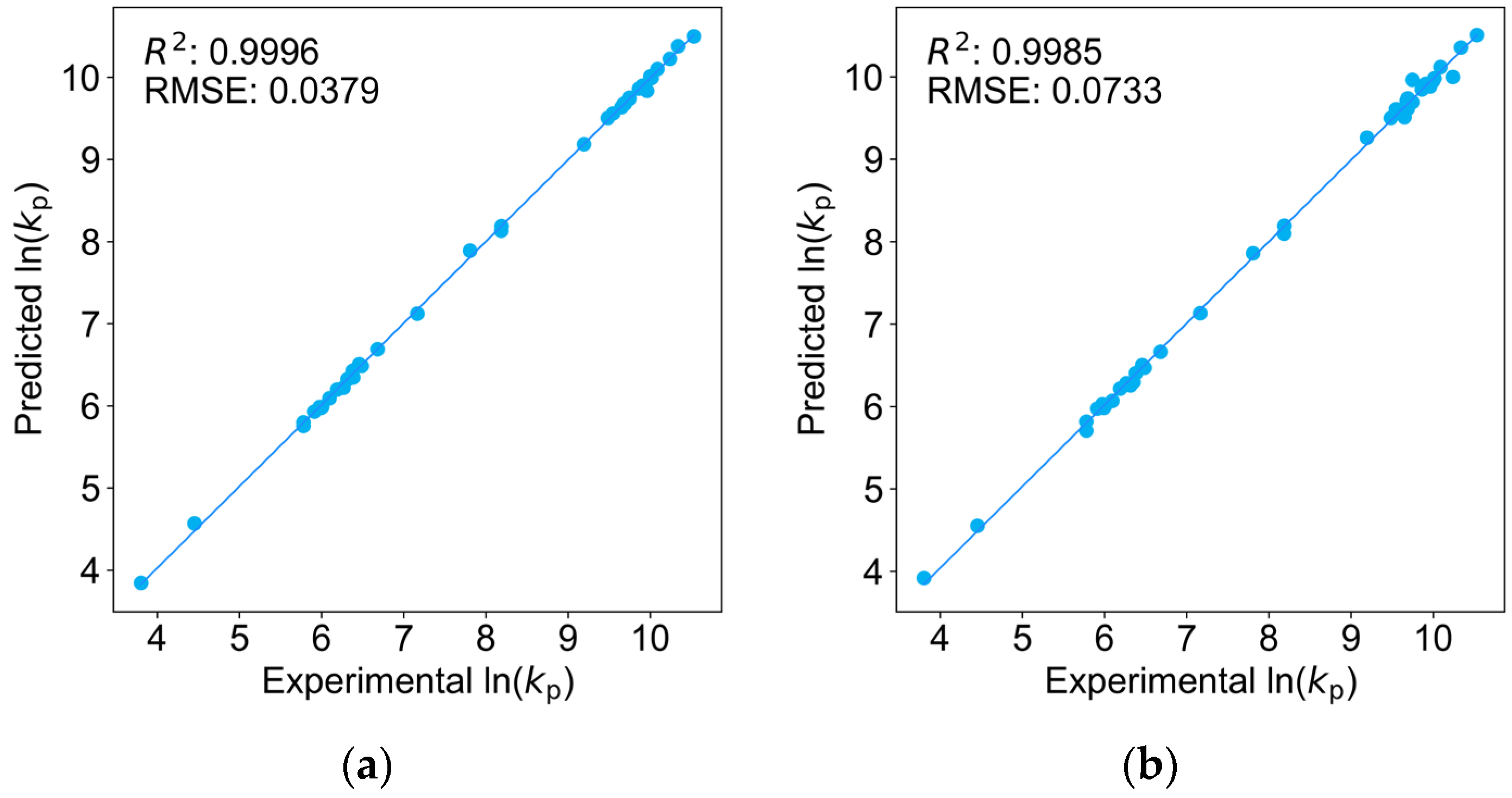
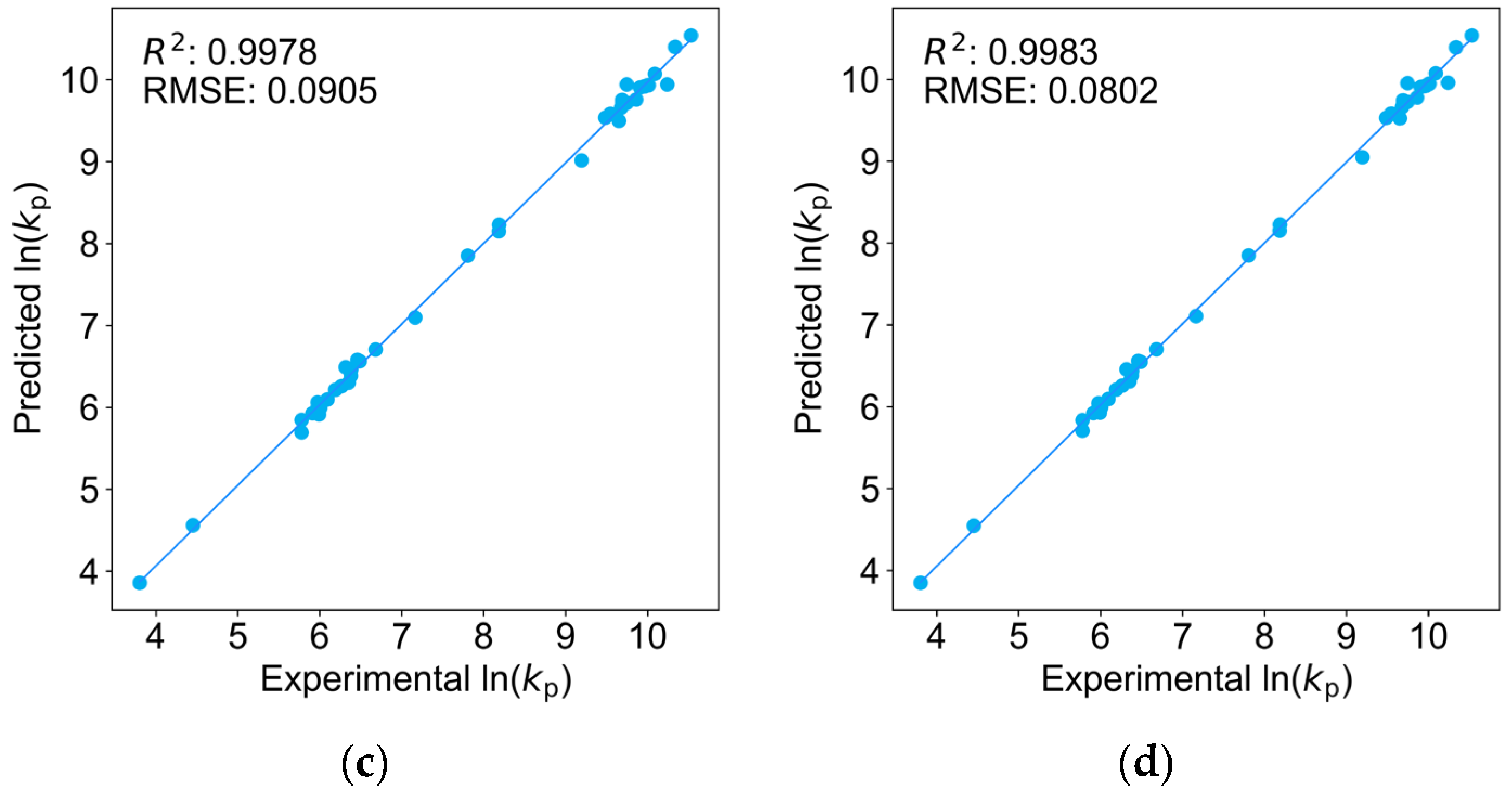
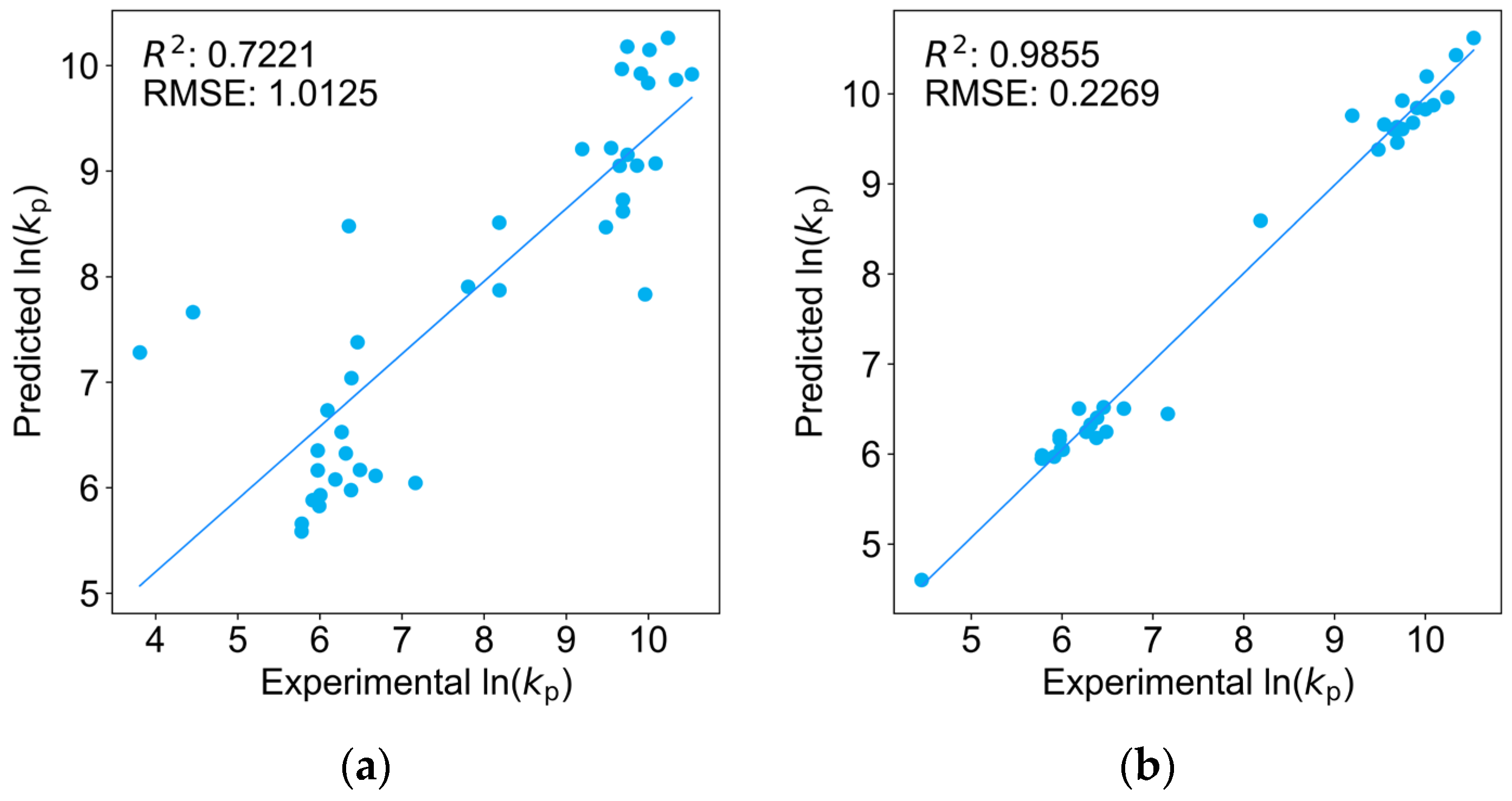

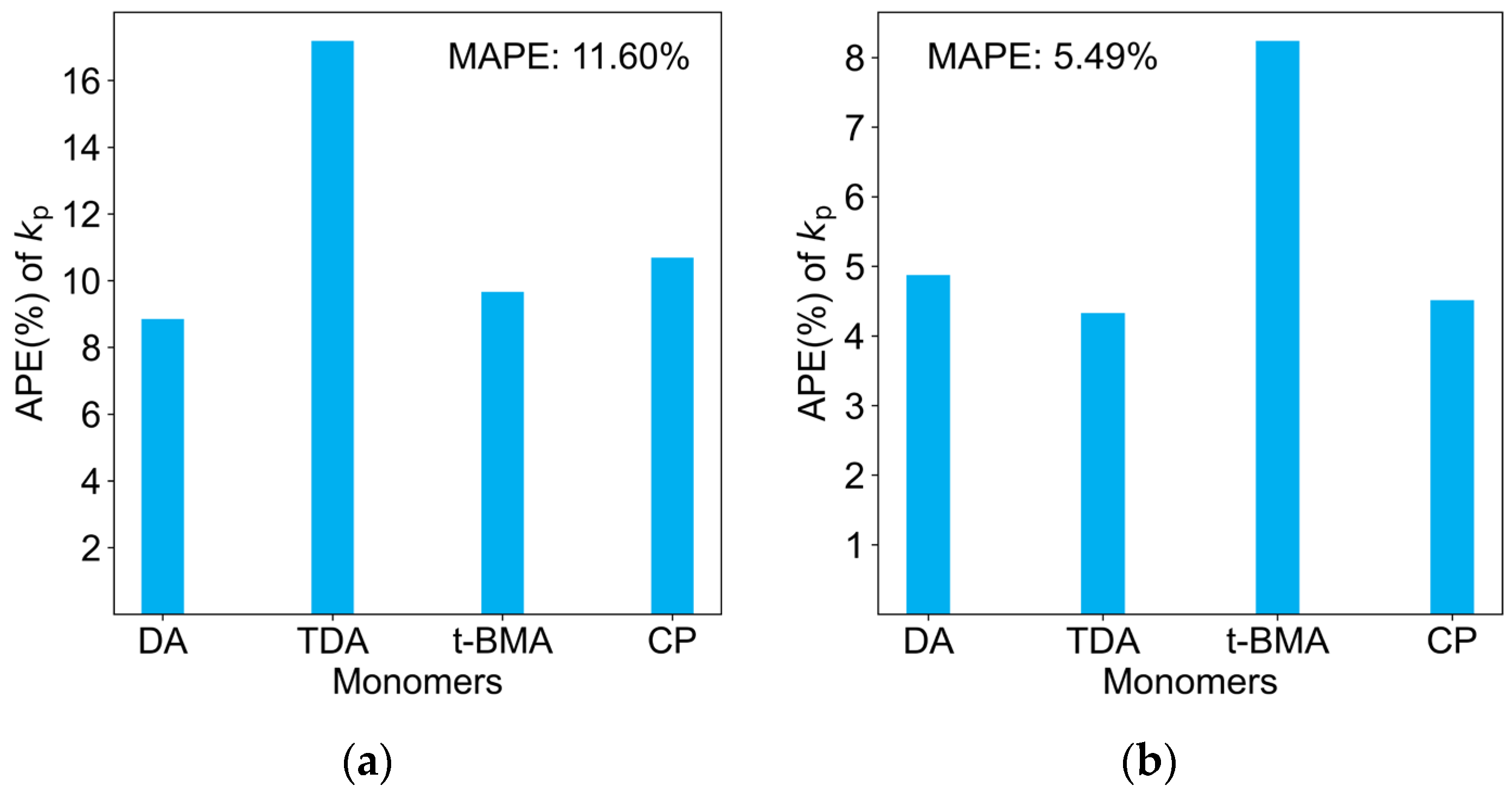
| Monomers | Abbr. | A [L mol−1 s−1] | EA [KJ mol−1] | kp25 °C [L mol−1 s−1] |
|---|---|---|---|---|
| Dodecyl acrylate [19] | DA | 10,900,000 | 15.80 | 18,588 |
| Tridecyl acrylate [20] | TDA | 5,710,000 | 14.08 | 19,489 |
| Tert-butyl methacrylate [22] | t-BMA | 25,100,000 | 27.70 | 352 |
| Chloroprene [21] | CP | 19,500,000 | 26.63 | 421 |
| Monomers | kp 25 °C [L mol−1 s−1] |
|---|---|
| Dodecyl acrylate | 17,682 |
| Tridecyl acrylate | 20,333 |
| Tetradecyl acrylate | 22,034 |
| Pentadecyl acrylate | 22,635 |
| Tetradecy methacrylate | 611 |
| Monomers | Abbr. | T [°C] | Predicted kp [L mol−1 s−1] | Predicted A [L mol−1 s−1] | Predicted EA [KJ mol−1] |
|---|---|---|---|---|---|
| Dodecyl acrylate | DA | 15 | 14,621 | 5,887,746 | 14.38 |
| Dodecyl acrylate | DA | 25 | 17,682 | ||
| Dodecyl acrylate | DA | 35 | 21,396 | ||
| Dodecyl acrylate | DA | 45 | 25,672 | ||
| Dodecyl acrylate | DA | 55 | 30,192 | ||
| Dodecyl acrylate | DA | 65 | 35,402 | ||
| Tridecyl acrylate | TDA | 15 | 16,627 | 7,247,982 | 14.56 |
| Tridecyl acrylate | TDA | 25 | 20,333 | ||
| Tridecyl acrylate | TDA | 35 | 24,705 | ||
| Tridecyl acrylate | TDA | 45 | 29,663 | ||
| Tridecyl acrylate | TDA | 55 | 34,847 | ||
| Tridecyl acrylate | TDA | 65 | 40,749 | ||
| Tert-butyl methacrylate | t-BMA | 15 | 270 | 3,407,435 | 22.59 |
| Tert-butyl methacrylate | t-BMA | 25 | 381 | ||
| Tert-butyl methacrylate | t-BMA | 35 | 505 | ||
| Tert-butyl methacrylate | t-BMA | 45 | 664 | ||
| Tert-butyl methacrylate | t-BMA | 55 | 857 | ||
| Tert-butyl methacrylate | t-BMA | 65 | 1105 | ||
| Chloroprene | CP | 15 | 317 | 4,181,175 | 22.71 |
| Chloroprene | CP | 25 | 440 | ||
| Chloroprene | CP | 35 | 589 | ||
| Chloroprene | CP | 45 | 780 | ||
| Chloroprene | CP | 55 | 1019 | ||
| Chloroprene | CP | 65 | 1284 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Fang, Y.; Zhou, H.; Gao, H. A Machine Learning Model for Predicting the Propagation Rate Coefficient in Free-Radical Polymerization. Molecules 2024, 29, 4694. https://doi.org/10.3390/molecules29194694
Wang Y, Fang Y, Zhou H, Gao H. A Machine Learning Model for Predicting the Propagation Rate Coefficient in Free-Radical Polymerization. Molecules. 2024; 29(19):4694. https://doi.org/10.3390/molecules29194694
Chicago/Turabian StyleWang, Yiming, Yue Fang, Haifan Zhou, and Hanyu Gao. 2024. "A Machine Learning Model for Predicting the Propagation Rate Coefficient in Free-Radical Polymerization" Molecules 29, no. 19: 4694. https://doi.org/10.3390/molecules29194694
APA StyleWang, Y., Fang, Y., Zhou, H., & Gao, H. (2024). A Machine Learning Model for Predicting the Propagation Rate Coefficient in Free-Radical Polymerization. Molecules, 29(19), 4694. https://doi.org/10.3390/molecules29194694







