Simulation Studies of the Dynamics and the Connectivity Patterns of Hydrogen Bonds in Water from Ambient to Supercritical Conditions
Abstract
:1. Introduction
2. Results
2.1. Time Correlation Functions
2.2. Lifetime of Hydrogen Bonds
2.3. Persistence of Monomers
3. Discussion
4. Materials and Methods
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| T, K | Pressure, MPa | <τc>, fs | <τint>, fs |
|---|---|---|---|
| 573 | 10 | 23.9 ± 0.7 | 325 ± 14 |
| 623 | 22.5 | 22.1 ± 0.7 | 241 ± 9 |
| 653 | 25 | 21.2 ± 1.2 | 215 ± 11 |
| 673 | 25 | 24.5 ± 1.6 | 204 ± 10 |
References
- Maréchal, Y. The Hydrogen Bond and the Water Molecule; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Sun, C.Q.; Huang, Y.; Zhang, X.; Ma, Z.; Wang, B. The physics behind water irregularity. Phys. Rep. 2023, 998, 1–68. [Google Scholar] [CrossRef]
- Swiatla-Wojcik, D. Role of water in radical reactions: Molecular simulation and modelling. In Reaction Rate Constant Computations: Theories and Applications; Han, K., Chu, T., Eds.; Theoretical and Computational Chemistry Series No. 6; RSC Publishing: London, UK, 2014; pp. 352–378. [Google Scholar]
- Palmer, D.A.; Fernandez-Prini, R.; Harvey, A.H. (Eds.) Aqueous Systems at Elevated Temperatures, 3rd ed.; Elsevier Academic Press: London, UK, 2004. [Google Scholar]
- Kiran, E.; Debenedetti, P.G.; Peters, C.J. (Eds.) Supercritical Fluids. Fundamentals and Applications; NATO Science Series E: Applied Science; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2000. [Google Scholar]
- Clarke, C.J.; Tu, W.-C.; Levers, O.; Bröhl, A.; Hallett, J.P. Green and Sustainable Solvents in Chemical Processes. Chem. Rev. 2018, 118, 747–800. [Google Scholar] [CrossRef] [PubMed]
- Swiatla-Wojcik, D.; Pabis, A.; Szala, J. Density and Temperature Effect on Hydrogen-Bonded Clusters in Water–MD Simulation Study. Centr. Eur. J. Chem. 2008, 6, 555–564. [Google Scholar]
- Swiatla-Wojcik, D.; Szala-Bilnik, J. Transition from Patchlike to Clusterlike Inhomogeneity Arising from Hydrogen Bonding in Water. J. Chem. Phys. 2011, 134, 054121-1–054121-10. [Google Scholar] [CrossRef]
- Bopp, P.; Jancsó, G.; Heinzinger, K. An Improved Potential for Non-rigid Water Molecules in the Liquid Phase. Chem. Phys. Lett. 1983, 98, 129–133. [Google Scholar] [CrossRef]
- Swiatla-Wojcik, D. Evaluation of the Criteria of Hydrogen Bonding in Highly Associated Liquids. Chem. Phys. 2007, 342, 260–266. [Google Scholar] [CrossRef]
- Walrafen, G.E.; Chu, G.C.; Piermarini, G.J. Low-Frequency Raman Scattering from Water at High Pressures and High Temperatures. J. Phys. Chem. 1996, 100, 10363–10372. [Google Scholar] [CrossRef]
- Vöhringer-Martinez, E.; Link, O.; Lugovoy, E.; Siefermann, K.R.; Wiederschein, F.; Grubmüller, H.; Abel, B. Hydrogen Bond Dynamics of Superheated Water and Methanol by Ultrafast IR-pump and EUV-photoelectron Probe Spectroscopy. Phys. Chem. Chem. Phys. 2014, 16, 19365–19375. [Google Scholar] [CrossRef]
- Perakis, F.; De Marco, L.; Shalit, A.; Tang, F.; Kann, Z.R.; Kühne, T.D.; Torre, R.; Bonn, M.; Nagata, Y. Vibrational Spectroscopy and Dynamics of Water. Chem. Rev. 2016, 116, 7590–7607. [Google Scholar] [CrossRef]
- Yang, J.; Dettori, R.; Nunes, J.P.; List, N.H.; Biasin, E.; Centurion, M.; Chen, Z.; Cordones, A.A.; Deponte, D.P.; Heinz, T.F.; et al. Direct Observation of Ultrafast Hydrogen Bond Strengthening in Liquid Water. Nature 2021, 596, 531–535. [Google Scholar] [CrossRef]
- Rapaport, D.C. Hydrogen Bonds in Water: Network Organization and Lifetimes. Mol. Phys. 1983, 50, 1151–1162. [Google Scholar] [CrossRef]
- Luzar, A.; Chandler, D. Hydrogen-bond Kinetics in Liquid Water. Nature 1996, 379, 55–57. [Google Scholar] [CrossRef]
- Mizan, T.I.; Savage, P.E.; Ziff, R.M. Temperature Dependence of Hydrogen Bonding in Supercritical Water. J. Phys. Chem. 1996, 100, 403–408. [Google Scholar] [CrossRef]
- Martı́, J.; Padro, J.A.; Guàrdia, E. Molecular Dynamics Simulation of Liquid Water Along the Coexistence Curve: Hydrogen Bonds and Vibrational Spectra. J. Chem. Phys. 1996, 105, 639–649. [Google Scholar] [CrossRef]
- Martı́, J. Analysis of the Hydrogen Bonding and Vibrational Spectra of Supercritical Model Water by Molecular Dynamics Simulations. J. Chem. Phys. 1999, 110, 6876–6886. [Google Scholar] [CrossRef]
- Sutmann, G.; Vallauri, R. Dynamics of the Hydrogen Bond Network in Liquid Water. J. Mol. Liq. 2002, 98–99, 215–226. [Google Scholar] [CrossRef]
- Stubbs, J.M. Molecular Simulations of Supercritical Fluid Systems. J. Supercrit. Fluids 2016, 108, 104–122. [Google Scholar] [CrossRef]
- Luzar, A. Resolving the Hydrogen Bond Conundrum. J. Chem. Phys. 2000, 113, 10663–10675. [Google Scholar] [CrossRef]
- Bellissent-Funel, M.-C. Structure of Supercritical Water. J. Mol. Liq. 2001, 90, 313–322. [Google Scholar] [CrossRef]
- Matubayasi, N.; Wakai, C.; Nakahara, M. Structural Study of Supercritical Water. I. Nuclear Magnetic Resonance Spectroscopy. J. Chem. Phys. 1997, 107, 9133–9140. [Google Scholar] [CrossRef]
- Martiniano, H.F.M.C.; Galamba, N. Insights on Hydrogen-Bond Lifetimes in Liquid and Supercooled Water. J. Phys. Chem. B 2013, 117, 16188–16195. [Google Scholar] [CrossRef] [PubMed]
- Teixeira, J.; Bellissent-Funel, M.-C.; Chen, S.H.; Dianoux, A.J. Experimental Determination of the Nature of Diffusive Motions of Water Molecules at Low Temperatures. Phys. Rev. A 1985, 31, 1913–1917. [Google Scholar] [CrossRef] [PubMed]
- Skarmoutsos, I.; Guardia, E. Effect of the Local Hydrogen Bonding Network on the Reorientational and Translational Dynamics in Supercritical Water. J. Chem. Phys. 2010, 132, 074502-1–074502-10. [Google Scholar] [CrossRef] [PubMed]
- Conde, O.; Teixeira, J. Depolarized Light-Scattering of Heavy-Water, and Hydrogen-Bond Dynamics. Mol. Phys. 1984, 53, 951–959. [Google Scholar] [CrossRef]
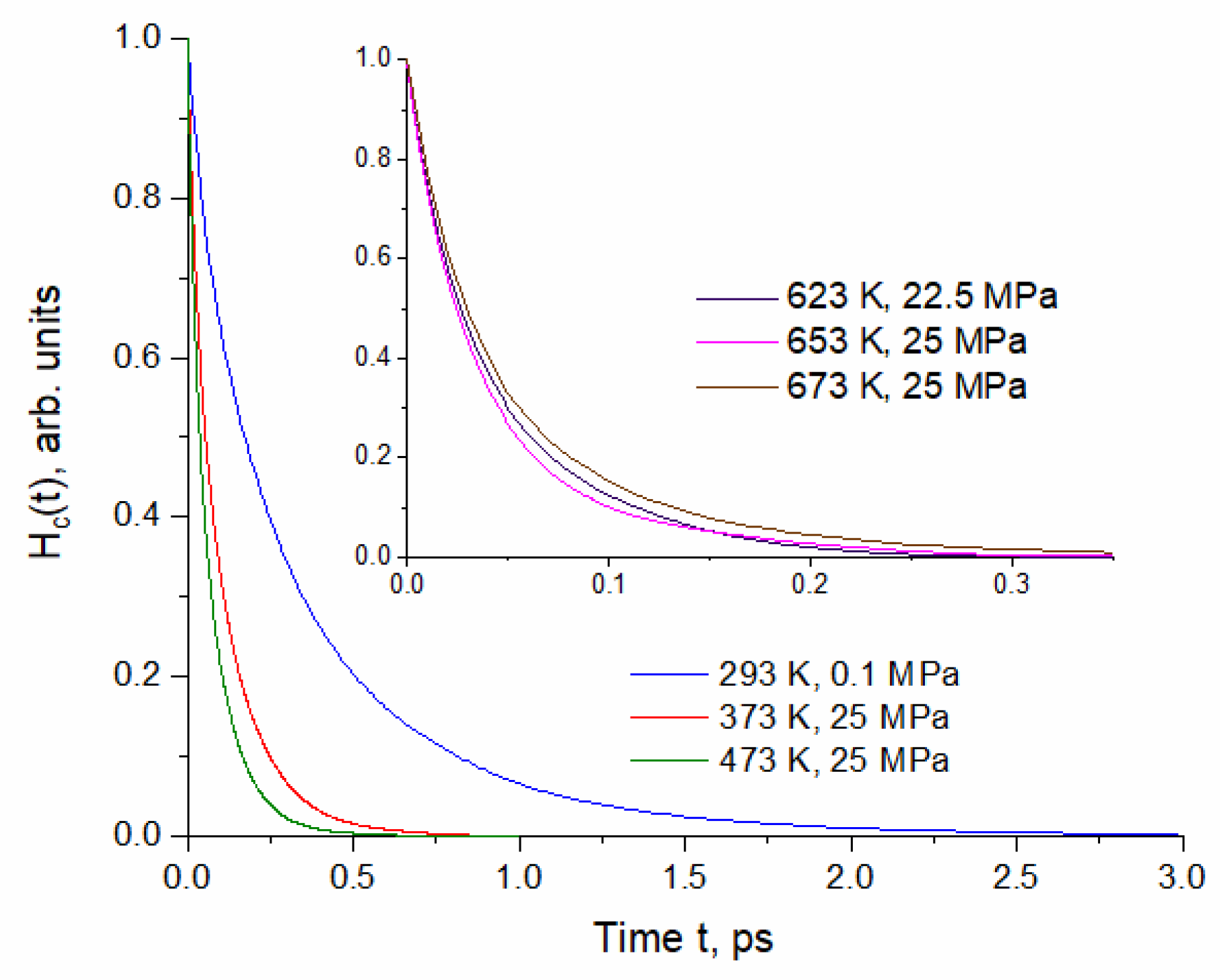


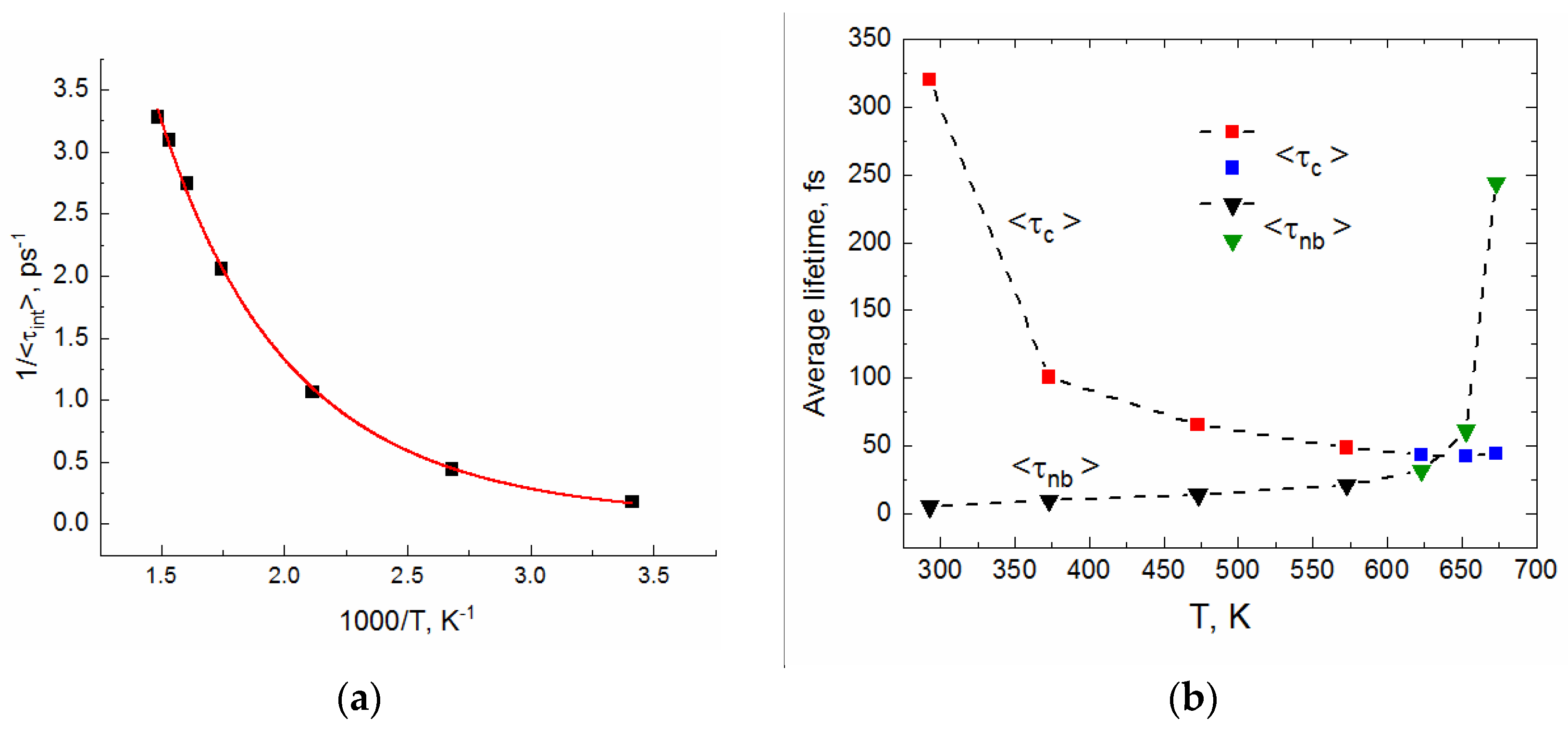
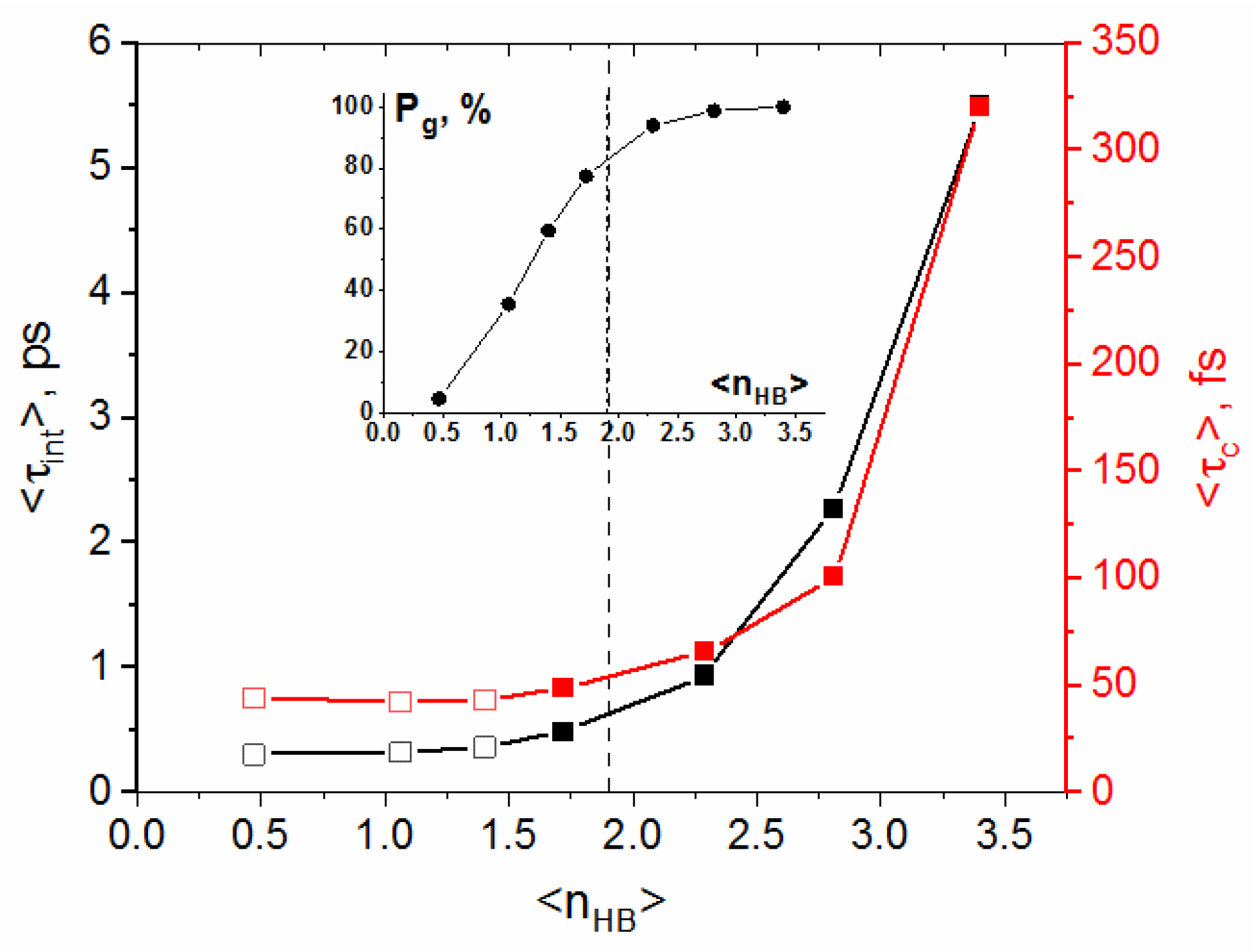
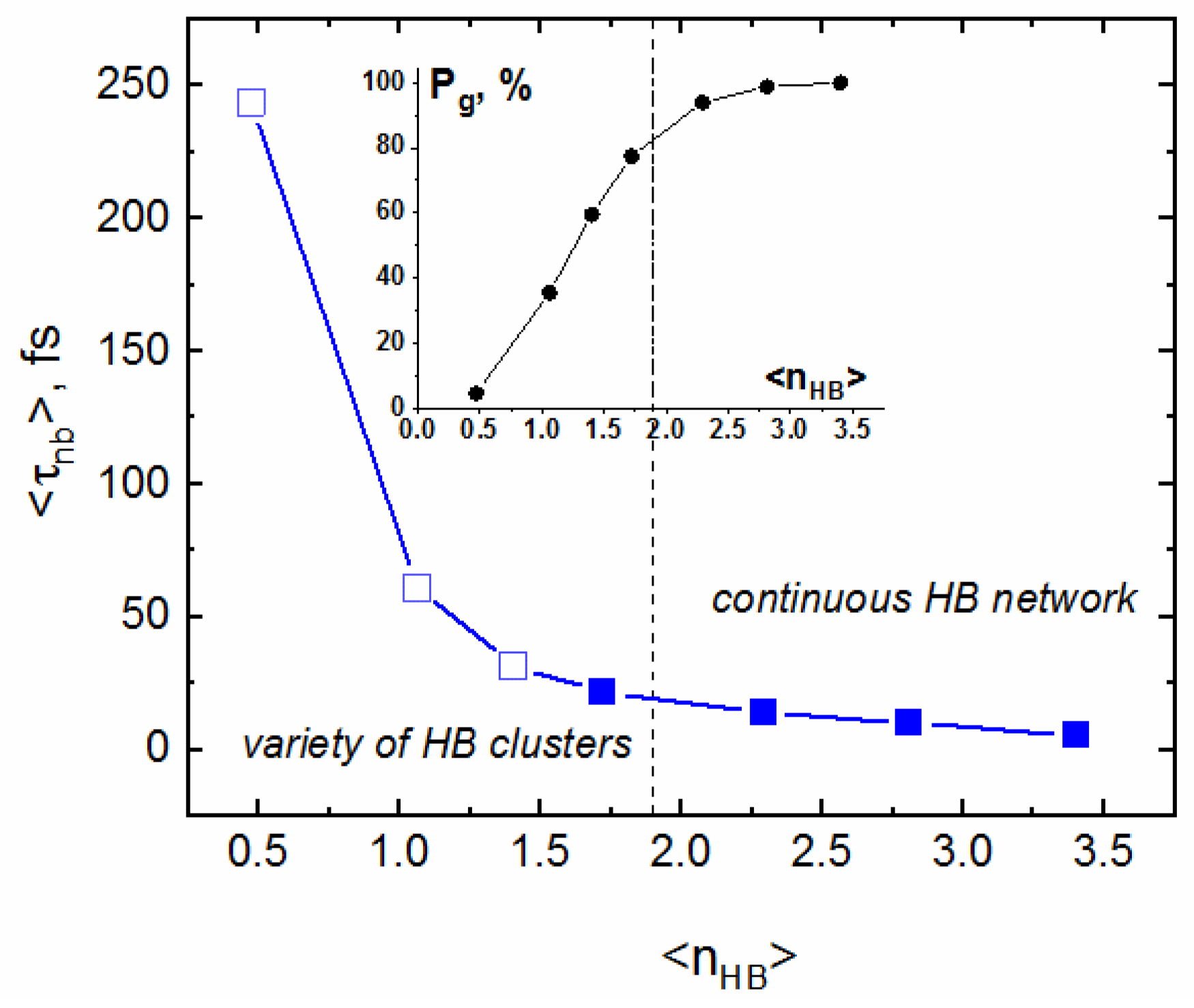
| Temperature T, K | Density ρ, kg/L | Pressure, MPa |
|---|---|---|
| 293 (288.3 ± 5.6) | 0.997 | 0.1 |
| 373 (376.3 ± 6.8) | 0.969 | 25 |
| 473 (474.2 ± 8.3) | 0.881 | 25 |
| 573 (571.1 ± 9.8) | 0.720 | 10 b |
| 623 (619.4 ± 10.0) | 0.610 | 22.5 |
| 653 (649.5 ± 10.4) | 0.451 | 25 |
| 673 (676.3 ± 10.2) | 0.167 | 25 |
| T, K | Pressure, MPa | <τc>, fs | <τint>, fs | <τnb>, fs |
|---|---|---|---|---|
| 293 | 0.1 | 320 ± 2 | 5500 ± 150 | 5.4 ± 1.7 |
| 373 | 25 | 100.7 ± 1.4 | 2269 ± 111 | 10.0 ± 2.7 |
| 473 | 25 | 65.7 ± 1.1 | 937 ± 17 | 13.9 ± 2.3 |
| 573 | 10 | 48.7 ± 2.4 | 486 ± 16 | 21.4 ± 2.1 |
| 623 | 22.5 | 43.3 ± 1.7 | 364 ± 23 | 31.8 ± 3.8 |
| 653 | 25 | 42.5 ± 1.8 | 323 ± 15 | 61.3 ± 6.9 |
| 673 | 25 | 44.1 ± 4.9 | 305 ± 13 | 244 ± 21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Swiatla-Wojcik, D. Simulation Studies of the Dynamics and the Connectivity Patterns of Hydrogen Bonds in Water from Ambient to Supercritical Conditions. Molecules 2024, 29, 5513. https://doi.org/10.3390/molecules29235513
Swiatla-Wojcik D. Simulation Studies of the Dynamics and the Connectivity Patterns of Hydrogen Bonds in Water from Ambient to Supercritical Conditions. Molecules. 2024; 29(23):5513. https://doi.org/10.3390/molecules29235513
Chicago/Turabian StyleSwiatla-Wojcik, Dorota. 2024. "Simulation Studies of the Dynamics and the Connectivity Patterns of Hydrogen Bonds in Water from Ambient to Supercritical Conditions" Molecules 29, no. 23: 5513. https://doi.org/10.3390/molecules29235513
APA StyleSwiatla-Wojcik, D. (2024). Simulation Studies of the Dynamics and the Connectivity Patterns of Hydrogen Bonds in Water from Ambient to Supercritical Conditions. Molecules, 29(23), 5513. https://doi.org/10.3390/molecules29235513







