Temperature Dependence of the Polar and Lewis Acid–Base Properties of Poly Methyl Methacrylate Adsorbed on Silica via Inverse Gas Chromatography
Abstract
:1. Introduction
2. Experimental Results
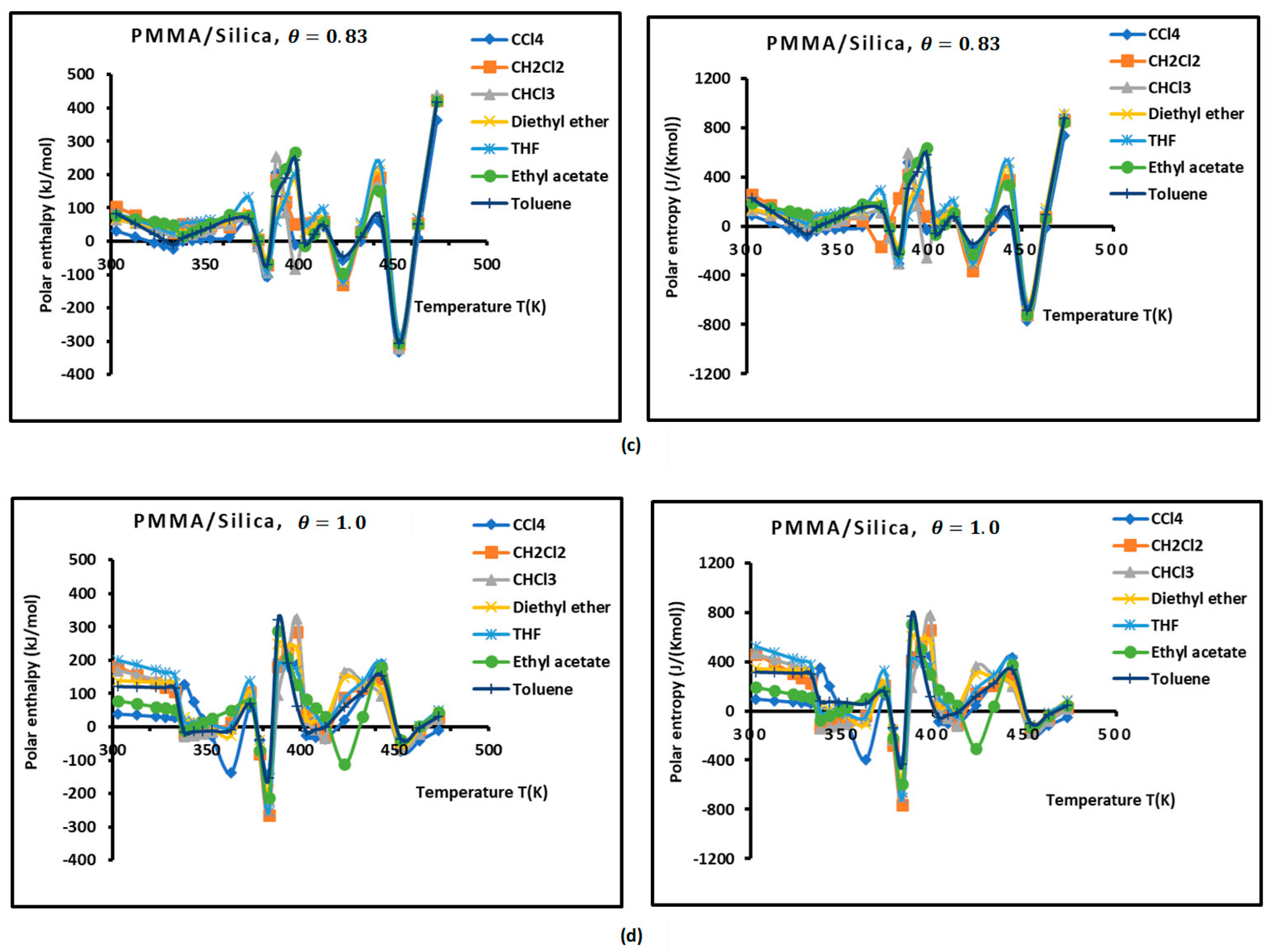
2.1. Polar Surface Interactions between PMMA/Silica and Solvents
2.2. Enthalpic and Entropic Lewis’s Acid–Base Parameters
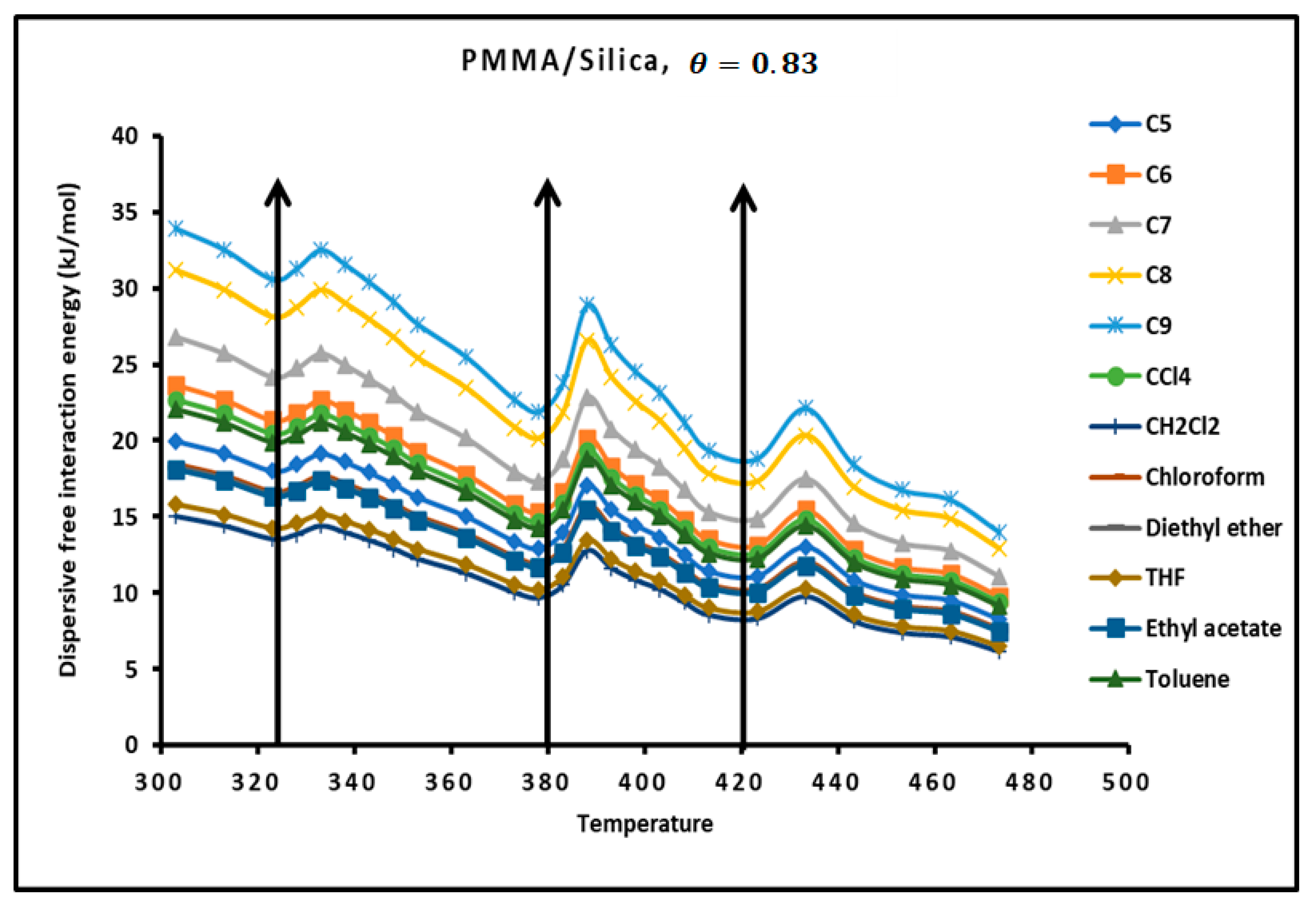
2.3. London Dispersive Free Interaction Energies of PMMA/Silica
2.4. Determination of the Separation Distance between Solid Particles and Solvents
3. Chromatographic Methods and Materials
- -
- The n-alkanes, such as n-pentane, n-hexane, n-heptane, n-octane, and n-nonane.
- -
- The polar molecules, divided into three groups:
- ➢
- Lewis’s acid solvents such as dichloromethane, chloroform, and carbon tetrachloride;
- ➢
- Basic solvents such as ethyl acetate, diethyl ether, and tetrahydrofuran;
- ➢
- Amphoterics such as toluene.
4. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mathur, S.; Moudgil, B.M. Mechanisms of nonionic polymer adsorption on oxide surfaces. Min. Metall. Explor. 1998, 15, 24–28. [Google Scholar] [CrossRef]
- Jimenez, A.M.; Zhao, D.; Misquitta, K.; Jestin, J.; Kumar, S.K. Exchange lifetimes of the bound polymer layer on silica nanoparticles. ACS Macro Lett. 2019, 8, 166–171. [Google Scholar] [CrossRef] [PubMed]
- Cui, W.; You, W.; Sun, Z.; Yu, W. Decoupled polymer dynamics in weakly attractive poly(methyl methacrylate)/silica nanocomposites. Macromolecules 2021, 54, 5484–5497. [Google Scholar] [CrossRef]
- Boucher, V.M.; Cangialosi, D.; Alegría, A.; Colmenero, J. Enthalpy recovery of PMMA/silica nanocomposites. Macromolecules 2010, 43, 7594–7603. [Google Scholar] [CrossRef]
- Priestley, R.D.; Rittigstein, P.; Broadbelt, L.J.; Fukao, K.; Torkelson, J.M. Evidence for the molecular-scale origin of the suppression of physical ageing in confined polymer: Fluorescence and dielectric spectroscopy studies of polymer–silica nanocomposites. J. Phys. Condens. Matter. 2007, 19, 205120. [Google Scholar] [CrossRef]
- González-Benito, J.; González-Gaitano, G. Interfacial conformations and molecular structure of PMMA in PMMA/silica nanocomposites. Effect of high-energy ball milling. Macromolecules 2008, 41, 4777–4785. [Google Scholar] [CrossRef]
- Lin, Y.; Liu, L.; Xu, G.; Zhang, D.; Guan, A.; Wu, G. Interfacial interactions and segmental dynamics of poly(vinyl acetate)/silica nanocomposites. J. Phys. Chem. C 2015, 119, 12956–12966. [Google Scholar] [CrossRef]
- Ma, M.; Cui, W.; Guo, Y.; Yu, W. Adsorption-desorption effect on physical aging in PMMA-silica nanocomposites. Polymer 2022, 255, 125124. [Google Scholar] [CrossRef]
- Rochat, S.; Polak-Kraśna, K.; Tian, M.; Mays, T.J.; Bowen, C.R.; Burrows, A.D. Assessment of the long-term stability of the polymer of intrinsic microporosity PIM-1 for hydrogen storage applications. Int. J. Hydrogen Energy 2019, 44, 332–337. [Google Scholar] [CrossRef]
- Õige, K.; Avarmaa, T.; Suisalu, A.; Jaaniso, R. Effect of long-term aging on oxygen sensitivity of luminescent Pd-tetraphenylporphyrin/PMMA films. Sens. Actuators B Chem. 2005, 106, 424–430. [Google Scholar] [CrossRef]
- Gallino, I.; Cangialosi, D.; Evenson, Z.; Schmitt, L.; Hechler, S.; Stolpe, M.; Ruta, B. Hierarchical aging pathways and reversible fragile-to-strong transition upon annealing of a metallic glass former. Acta Mater. 2018, 144, 400–410. [Google Scholar] [CrossRef]
- Mandal, L.; Verma, B.; Patel, P.K. Review on polymer nanocomposite for ballistic & aerospace applications. Mater. Today Proc. 2020, 26 Pt 2, 3161–3166. [Google Scholar] [CrossRef]
- Wypych, A.; Duval, E.; Boiteux, G.; Ulanski, J.; David, L.; Mermet, A. Effect of physical aging on nano- and macroscopic properties of poly(methyl methacrylate) glass. Polymer 2005, 46, 12523–12531. [Google Scholar] [CrossRef]
- Huang, C.-C.; Liu, C.-Y. Peculiar α-β relaxations of Syndiotactic-Poly(methyl methacrylate). Polymer 2021, 225, 123760. [Google Scholar] [CrossRef]
- Liu, B.; Yu, W. On-demand direct design of polymeric thermal actuator by machine learning algorithm. Chin. J. Polym. Sci. 2020, 38, 908–914. [Google Scholar] [CrossRef]
- Njuguna, J.; Pielichowski, K. Polymer nanocomposites for aerospace applications: Fabrication. Adv. Eng. Mater. 2004, 6, 193–203. [Google Scholar] [CrossRef]
- Beiner, M.; Schröter, K.; Hempel, E.; Reissig, S.; Donth, E. Multiple glass transition and nanophase separation in poly(n-alkyl methacrylate) homopolymers. Macromolecules 1999, 32, 6278–6282. [Google Scholar] [CrossRef]
- Balasubramanian, K.B.N.; Ramesh, T. Role, effect, and influences of micro and nano-fillers on various properties of polymer matrix composites for microelectronics: A review. Polym. Adv. Technol. 2018, 29, 1568–1585. [Google Scholar] [CrossRef]
- Cheng, S.; Bocharova, V.; Belianinov, A.; Xiong, S.; Kisliuk, A.M.; Somnath, S.; Holt, A.P.; Ovchinnikova, O.S.; Jesse, S.; Martin, H.; et al. Unraveling the mechanism of nanoscale mechanical reinforcement in glassy polymer nanocomposites. Nano Lett. 2016, 16, 3630–3637. [Google Scholar] [CrossRef] [PubMed]
- Moll, J.; Kumar, S.K. Glass transitions in highly attractive highly filled polymer nanocomposites. Macromolecules 2012, 45, 1131–1135. [Google Scholar] [CrossRef]
- Napolitano, S. Irreversible adsorption of polymer melts and nanoconfinement effects. Soft Matter. 2020, 16, 5348–5365. [Google Scholar] [CrossRef] [PubMed]
- Ryan, H.M.; Douglas, J.G. Rupert Wimmer, Inverse Gas Chromatography for Determining the Dispersive Surface Free Energy and Acid–Base Interactions of Sheet Molding Compound-Part II Ligno-Cellulosic Fiber Types for Possible Composite Reinforcement. J. Appl. Polym. Sci. 2008, 110, 3880–3888. [Google Scholar]
- Gamble, J.F.; Dave, R.N.; Kiang, S.; Leane, M.M.; Tobyn, M.; Wang, S.S.Y. Investigating the applicability of inverse gas chromatography to binary powdered systems: An application of surface heterogeneity profiles to understanding preferential probe-surface interactions. Int. J. Pharm. 2013, 445, 39–46. [Google Scholar] [CrossRef] [PubMed]
- Balard, H.; Maafa, D.; Santini, A.; Donnet, J.B. Study by inverse gas chromatography of the surface properties of milled graphites. J. Chromatogr. A 2008, 1198–1199, 173–180. [Google Scholar] [CrossRef]
- Bogillo, V.I.; Shkilev, V.P.; Voelkel, A. Determination of surface free energy components for heterogeneous solids by means of inverse gas chromatography at finite concentrations. J. Mater. Chem. 1998, 8, 1953–1961. [Google Scholar] [CrossRef]
- Das, S.C.; Zhou, Q.; Morton, D.A.V.; Larson, I.; Stewart, P.J. Use of surface energy distributions by Inverse gas chromatography to understand mechanofusion processing and functionality of lactose coated with magnesium stearate. Eur. J. Pharm. Sci. 2011, 43, 325–333. [Google Scholar] [CrossRef] [PubMed]
- Das, S.C.; Stewart, P.J. Characterising surface energy of pharmaceutical powders by inverse gas chromatography at finite dilution. J. Pharm. Pharmacol. 2012, 64, 1337–1348. [Google Scholar] [CrossRef] [PubMed]
- Stella, K.P.; Costas, P. Assessment of the thermodynamic properties of poly(2,2,2-trifluoroethyl methacrylate) by inverse gas chromatography. J. Chromatogr. A 2014, 1324, 207–214. [Google Scholar] [CrossRef]
- Saint-Flour, C.; Papirer, E. Gas-solid chromatography. A method of measuring surface free energy characteristics of short carbon fibers. 1. Through adsorption isotherms. Ind. Eng. Chem. Prod. Res. Dev. 1982, 21, 337–341. [Google Scholar] [CrossRef]
- Saint-Flour, C.; Papirer, E. Gas-solid chromatography: Method of measuring surface free energy characteristics of short fibers. 2. Through retention volumes measured near zero surface coverage. Ind. Eng. Chem. Prod. Res. Dev. 1982, 21, 666–669. [Google Scholar] [CrossRef]
- Saint-Flour, C.; Papirer, E. Gas-solid chromatography: A quick method of estimating surface free energy variations induced by the treatment of short glass fibers. J. Colloid Interface Sci. 1983, 91, 69–75. [Google Scholar] [CrossRef]
- Schultz, J.; Lavielle, L.; Martin, C. The role of the interface in carbon fibre-epoxy composites. J. Adhes. 1987, 23, 45–60. [Google Scholar] [CrossRef]
- Donnet, J.-B.; Park, S.; Balard, H. Evaluation of specific interactions of solid surfaces by inverse gas chromatography. Chromatographia 1991, 31, 434–440. [Google Scholar] [CrossRef]
- Brendlé, E.; Papirer, E. A New Topological Index for Molecular Probes Used in Inverse Gas Chromatography. J. Colloid Interface Sci. 1997, 194, 217–224. [Google Scholar] [CrossRef] [PubMed]
- Brendlé, E.; Papirer, E. A New Topological Index for Molecular Probes Used in Inverse Gas Chromatography for the Surface Nanorugosity Evaluation. J. Colloid Interface Sci. 1997, 194, 207–216. [Google Scholar] [CrossRef]
- Sawyer, D.T.; Brookman, D.J. Thermodynamically based gas chromatographic retention index for organic molecules using salt-modified aluminas and porous silica beads. Anal. Chem. 1968, 40, 1847–1850. [Google Scholar] [CrossRef]
- Chehimi, M.M.; Pigois-Landureau, E. Determination of acid–base properties of solid materials by inverse gas chromatography at infinite dilution. A novel empirical method based on the dispersive contribution to the heat of vaporization of probes. J. Mater. Chem. 1994, 4, 741–745. [Google Scholar] [CrossRef]
- Hamieh, T. New methodology to study the dispersive component of the surface energy and acid–base properties of silica particles by inverse gas chromatography at infinite dilution. J. Chromatogr. Sci. 2022, 60, 126–142. [Google Scholar] [CrossRef]
- Hamieh, T.; Schultz, J. New approach to characterize physicochemical properties of solid substrates by inverse gas chromatography at infinite dilution. Some new methods to determine the surface areas of some molecules adsorbed on solid surfaces. J. Chromatogr. A 2002, 969, 17–47. [Google Scholar] [CrossRef]
- Voelkel, A. Inverse gas chromatography: Characterization of polymers, fibers, modified silicas, and surfactants. Crit. Rev. Anal. Chem. 1991, 22, 411–439. [Google Scholar] [CrossRef]
- Hamieh, T.; Ahmad, A.A.; Roques-Carmes, T.; Toufaily, J. New approach to determine the surface and interface thermodynamic properties of H-β-zeolite/rhodium catalysts by inverse gas chromatography at infinite dilution. Sci. Rep. 2020, 10, 20894. [Google Scholar] [CrossRef] [PubMed]
- Hamieh, T. Some Irregularities in the Evaluation of Surface Parameters of Solid Materials by Inverse Gas Chromatography. Langmuir 2023, 39, 17059–17070. [Google Scholar] [CrossRef]
- Hamieh, T. New physicochemical methodology for the determination of the surface thermodynamic properties of solid particles. Appl. Chem. 2023, 3, 229–255. [Google Scholar] [CrossRef]
- Hamieh, T. New Progress on London Dispersive Energy, Polar Surface Interactions, and Lewis’s Acid–Base Properties of Solid Surfaces. Molecules 2024, 29, 949. [Google Scholar] [CrossRef] [PubMed]
- Hamieh, T. London Dispersive and Lewis Acid-Base Surface Energy of 2D Single-Crystalline and Polycrystalline Covalent Organic Frameworks. Crystals 2024, 14, 148. [Google Scholar] [CrossRef]
- Hamieh, T. Inverse Gas Chromatography to Characterize the Surface Properties of Solid Materials. Chem. Mater. 2024, 36, 2231–2244. [Google Scholar] [CrossRef]
- Hamieh, T. Study of the temperature effect on the surface area of model organic molecules, the dispersive surface energy and the surface properties of solids by inverse gas chromatography. J. Chromatogr. A 2020, 1627, 461372. [Google Scholar] [CrossRef] [PubMed]
- Dritsas, G.S.; Karatasos, K.; Panayiotou, C. Investigation of thermodynamic properties of hyperbranched aliphatic polyesters by inverse gas chromatography. J. Chromatogr. A 2009, 1216, 8979–8985. [Google Scholar] [CrossRef] [PubMed]
- Papadopoulou, S.K.; Panayiotou, C. Thermodynamic characterization of poly(1,1,1,3,3,3-hexafluoroisopropyl methacrylate) by inverse gas chromatography. J. Chromatogr. A 2012, 1229, 230–236. [Google Scholar] [CrossRef] [PubMed]
- Davis, P.K.; Danner, R.P.; Duda, J.L.; Hadj Romdhane, I. Use of Inverse Gas Chromatography To Study Binary Polymer−Solvent Systems near the Glass Transition Temperature. Macromolecules 2004, 37, 9201–9210. [Google Scholar] [CrossRef]
- Kołodziejek, J.; Voelkel, A.; Heberger, K. Characterization of hybrid materials by means of inverse gas chromatography and chemometrics. J. Pharm. Sci. 2013, 102, 15241531. [Google Scholar] [CrossRef] [PubMed]
- Lazar, P.; Karlický, F.; Jurečka, P.; Kocman, M.; Otyepková, E.; Šafářová, K.; Otyepka, M. Adsorption of small organic molecules on graphene. J. Am. Chem. Soc. 2013, 135, 6372. [Google Scholar] [CrossRef] [PubMed]
- Belgacem, M.N.; Czeremuszkin, G.; Sapieha, S.; Gandini, A. Surface by XPS characterization and inverse gas of cellulose fibres chromatography. Cellulose 1995, 2, 145157. [Google Scholar] [CrossRef]
- Papadopoulou, S.; Tsioptsias, C.; Pavlou, A.; Kaderides, K.; Sotiriou, S.; Panayiotou, C. Superhydrophobic surfaces from hydrophobic or hydrophilic polymers via nanophase separation or electrospinning/electrospraying. Colloids Surf. A Physicochem. Eng. Asp. 2011, 387, 71–78. [Google Scholar] [CrossRef]
- Hamieh, T.; Rezzaki, M.; Schultz, J. Study of the second order transitions and acid-base properties of polymers adsorbed on oxides, by using inverse gas chromatography at infinite dilution, I and II. J. Colloid Interface Sci. 2001, 233, 339–347. [Google Scholar] [CrossRef] [PubMed]
- Hamieh, T. Study of the Specific Entropy of Poly (α-n-alkyl) Methacrylates Adsorbed on Alumina or Silica by Inverse Gas Chromatography (IGC). Soft Mater. 2010, 9, 15–31. [Google Scholar] [CrossRef]
- Hamieh, T. Determination of Lewis Acid Base Properties of Poly(α-n-alkyl) Methacrylates Adsorbed on Silica by Inverse GC. Chromatographia 2011, 73, 709–719. [Google Scholar] [CrossRef]
- Hamieh, T.; Toufaily, J.; Mouneimné, A.B. Effect of the Tacticity of PMMA Adsorbed on Alumina and Silica on the Specific Entropy Change of Polymer by Inverse G. Chromatographia 2011, 73, 99–107. [Google Scholar] [CrossRef]
- Papirer, E.; Perrin, J.-M.; Siffert, B.; Philipponneau, G. Surface characteristics of aluminas in relation with polymer adsorption. J. Colloid Interface Sci. 1991, 144, 263–270. [Google Scholar] [CrossRef]
- Hamieh, T.; Rezzaki, M.; Schultz, J. Study of the transition temperatures and acid-base properties of poly (methyl methacrylate) adsorbed on alumina and silica, by using inverse gas chromatography technique. Colloids Surf. A Physicochem. Eng. Asp. 2001, 189, 279–291. [Google Scholar] [CrossRef]
- David, R.L. (Ed.) CRC Handbook of Chemistry and Physics, Internet Version 2007, 87th ed.; Taylor and Francis: Boca Raton, FL, USA, 2007. [Google Scholar]
- Gutmann, V. The Donor-Acceptor Approach to Molecular Interactions; Plenum: New York, NY, USA, 1978. [Google Scholar]
- Riddle, F.L.; Fowkes, F.M. Spectral shifts in acid-base chemistry. Van der Waals contributions to acceptor numbers, Spectral shifts in acid-base chemistry. 1. van der Waals contributions to acceptor numbers. J. Am. Chem. Soc. 1990, 112, 3259–3264. [Google Scholar] [CrossRef]
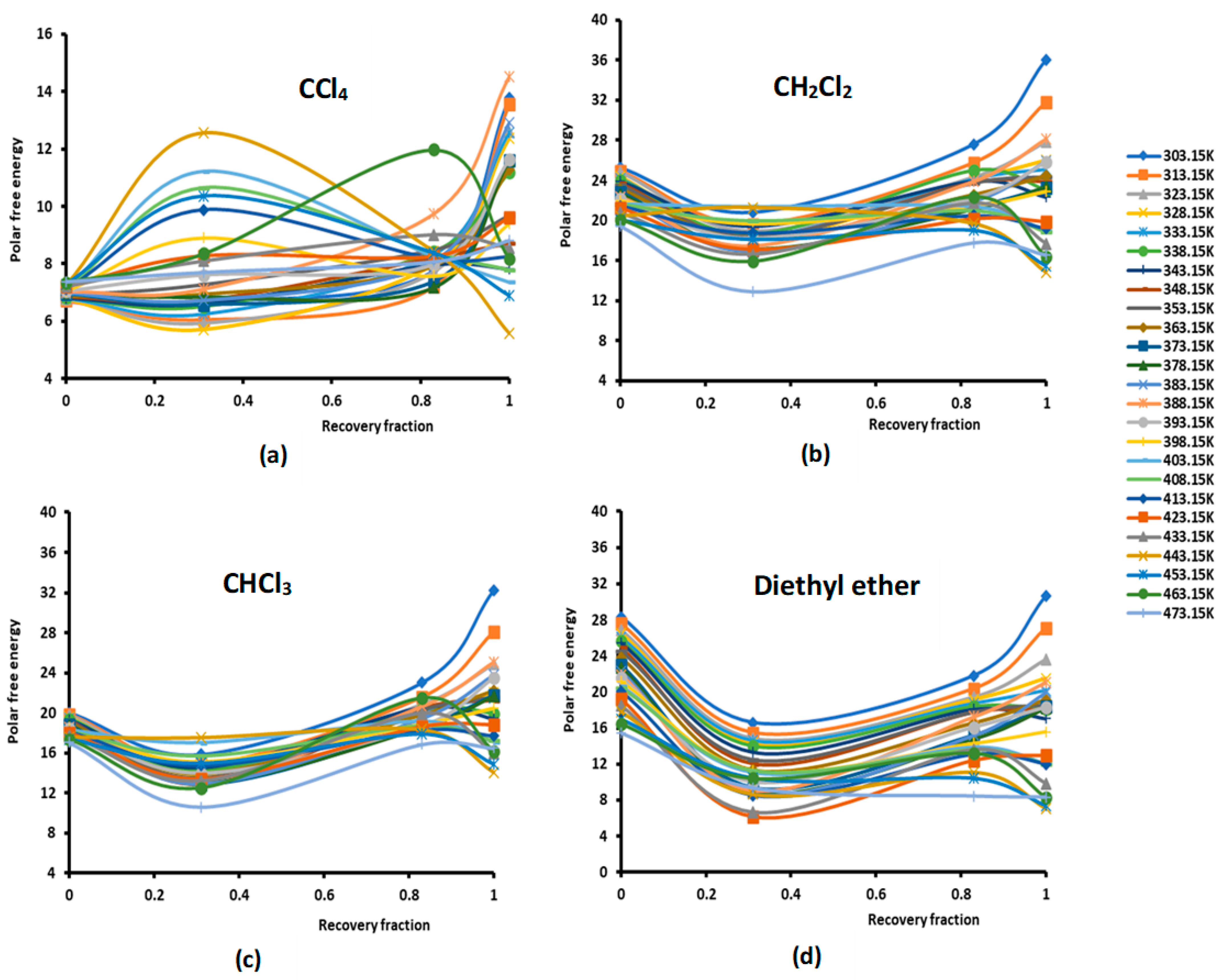
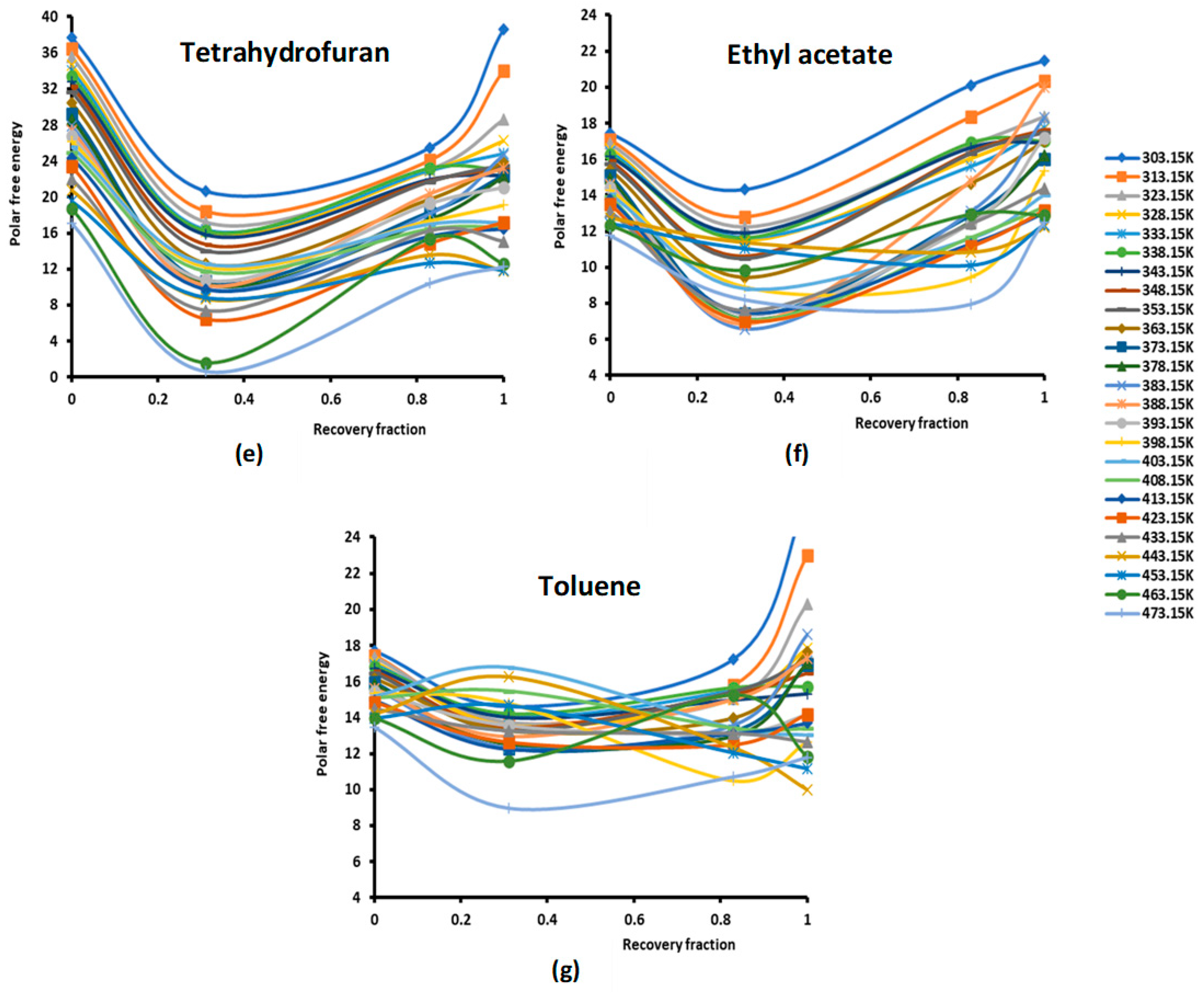
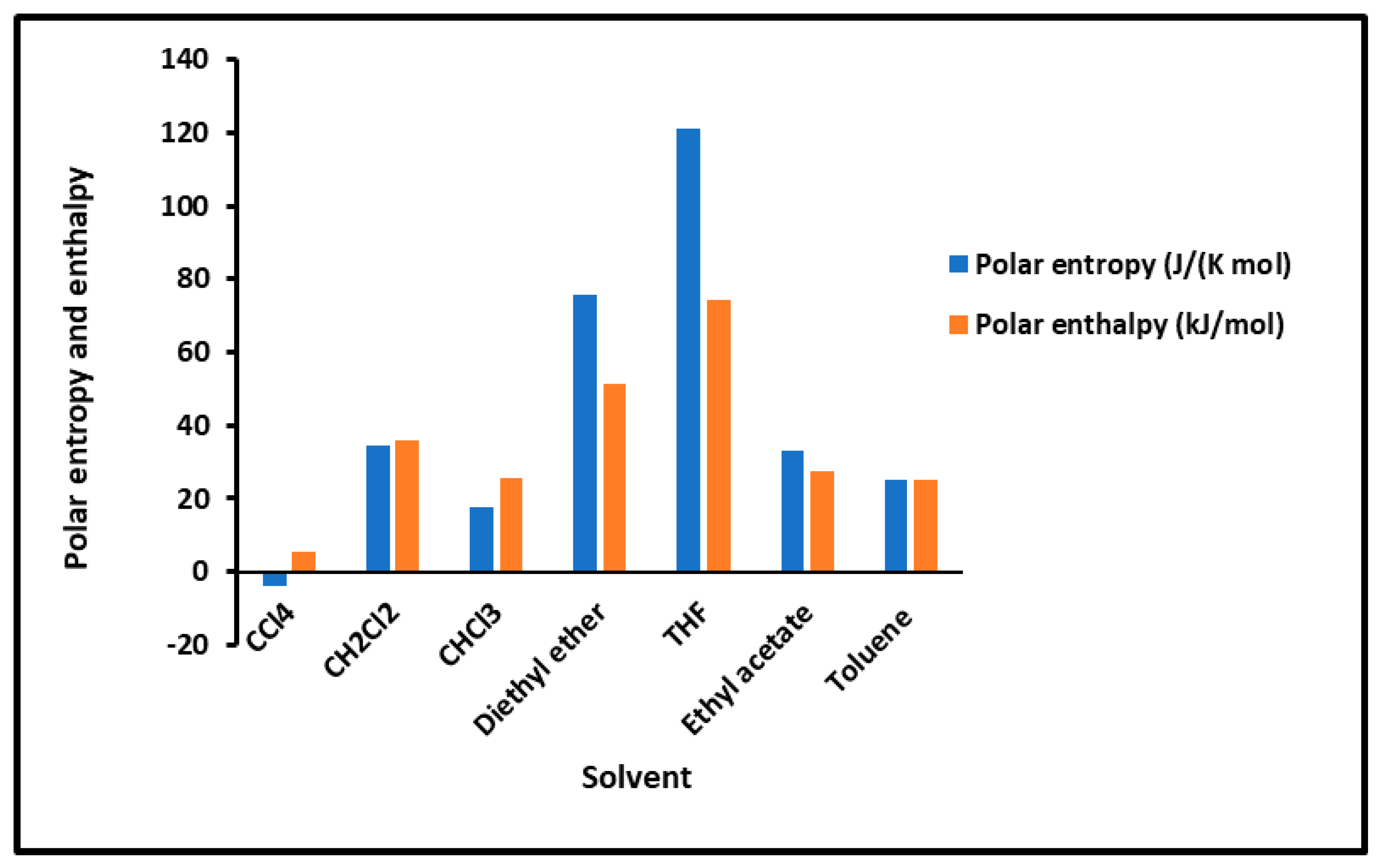
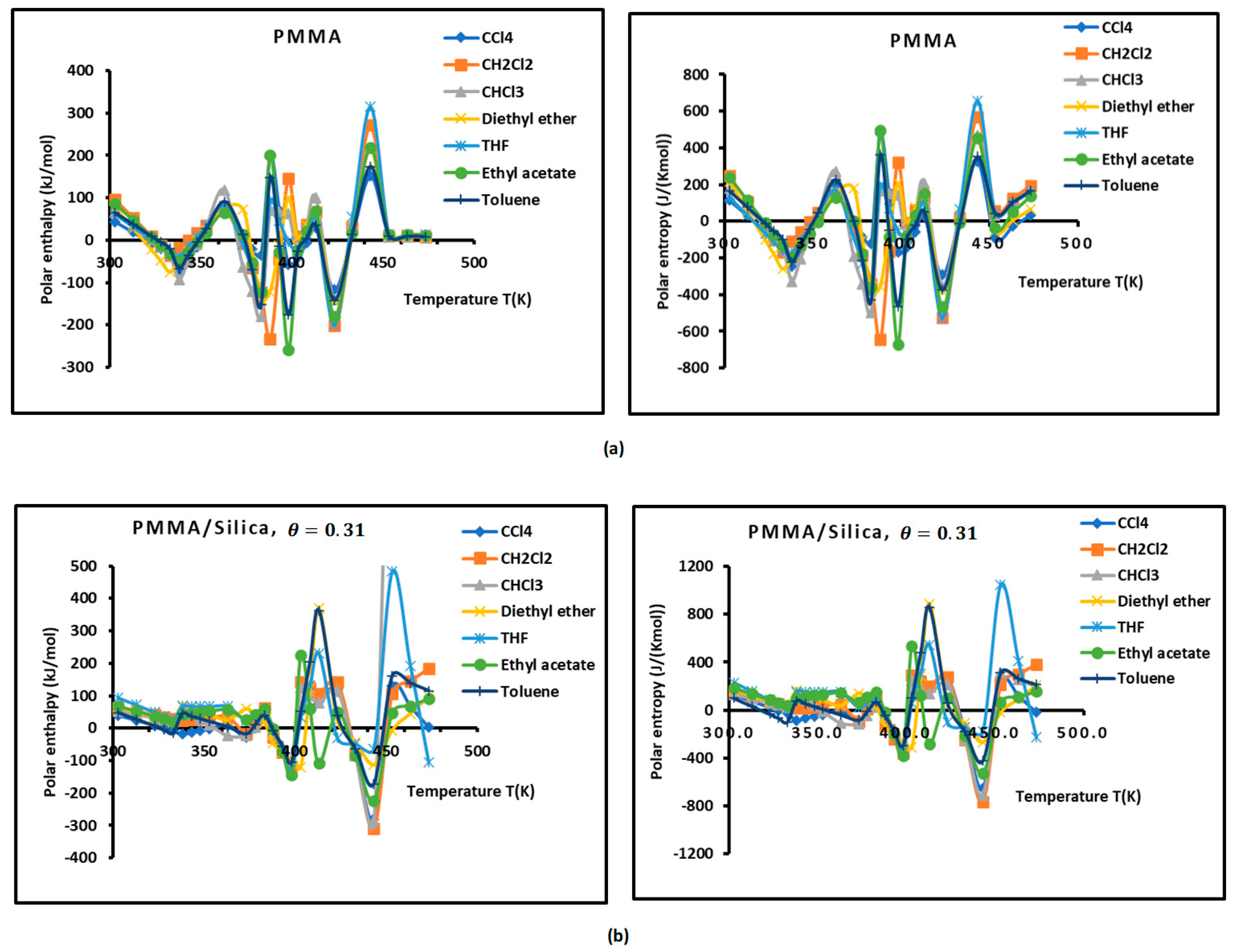



| PMMA | ||||||||
| T(K) | ||||||||
| 303.15 | 0.478 | 3.881 | 4.358 | 8.120 | 0.90 | 18.20 | 19.10 | 20.15 |
| 313.15 | 0.317 | 2.523 | 2.840 | 7.953 | 0.56 | 7.52 | 8.08 | 13.40 |
| 323.15 | 0.090 | 0.664 | 0.754 | 7.413 | −0.62 | −3.15 | −3.77 | 5.12 |
| 328.15 | −0.122 | −0.522 | −0.644 | 4.293 | −1.00 | −4.91 | −5.90 | 4.93 |
| 333.15 | −0.153 | −0.636 | −0.789 | 4.160 | −1.38 | −6.06 | −7.44 | 4.41 |
| 338.15 | −0.144 | −0.658 | −0.802 | 4.568 | −0.88 | −7.59 | −8.47 | 8.63 |
| 343.15 | 0.152 | −0.695 | −0.543 | −4.565 | −0.59 | −8.31 | −8.91 | 14.04 |
| 348.15 | 0.170 | −0.529 | −0.358 | −3.103 | −0.16 | −1.87 | −2.03 | 11.61 |
| 353.15 | 0.278 | 1.826 | 2.105 | 6.560 | 0.20 | 2.78 | 2.98 | 14.04 |
| 363.15 | 0.536 | 3.122 | 3.658 | 5.828 | 0.92 | 15.67 | 16.59 | 17.10 |
| 373.15 | 0.433 | 3.955 | 4.388 | 9.135 | 0.90 | 7.40 | 8.30 | 8.24 |
| 378.15 | 0.398 | 3.739 | 4.138 | 9.385 | −1.99 | −8.98 | −10.97 | 4.52 |
| 383.15 | 0.186 | 1.527 | 1.713 | 8.217 | −0.66 | −6.52 | −7.19 | 9.84 |
| 388.15 | 0.521 | 5.841 | 6.362 | 11.213 | 0.91 | 12.80 | 13.71 | 14.05 |
| 393.15 | 0.274 | 1.750 | 2.024 | 6.389 | 0.29 | 2.47 | 2.76 | 8.42 |
| 398.15 | 0.266 | 0.560 | 0.826 | 2.106 | 0.27 | −1.89 | −1.62 | −6.93 |
| 403.15 | 0.220 | −0.630 | −0.410 | −2.864 | −0.45 | −1.32 | −1.77 | 2.92 |
| 408.15 | 0.174 | 0.800 | 0.975 | 4.595 | 0.22 | −0.66 | −0.44 | −2.95 |
| 413.15 | 0.433 | 3.358 | 3.791 | 7.755 | 0.90 | 6.21 | 7.10 | 6.91 |
| 423.15 | 0.488 | 2.131 | 2.619 | 4.366 | −4.56 | −14.72 | −19.27 | 3.23 |
| 433.15 | 0.543 | 0.904 | 1.447 | 1.665 | 0.66 | −0.40 | 0.26 | −0.61 |
| 443.15 | 1.755 | 7.262 | 9.016 | 4.138 | 5.88 | 19.88 | 25.76 | 3.38 |
| 453.15 | 0.111 | 1.044 | 1.155 | 9.419 | 0.60 | −1.83 | −1.22 | −3.04 |
| 463.15 | 0.107 | 1.047 | 1.154 | 9.766 | 1.00 | 1.60 | 2.61 | 1.60 |
| 473.15 | 0.100 | 0.980 | 1.080 | 9.832 | 1.40 | 6.23 | 7.63 | 4.44 |
| T(K) | ||||||||
| 303.15 | 0.884 | 3.819 | 4.704 | 4.318 | 2.11 | 10.71 | 12.82 | 5.06 |
| 313.15 | 0.704 | 2.319 | 3.023 | 3.291 | 1.53 | 5.84 | 7.37 | 3.81 |
| 323.15 | 0.519 | 0.770 | 1.288 | 1.484 | 0.95 | 0.97 | 1.91 | 1.02 |
| 328.15 | 0.424 | −0.023 | 0.400 | −0.055 | 0.65 | −0.52 | 0.14 | −0.79 |
| 333.15 | 0.327 | −0.828 | −0.501 | −2.532 | 0.36 | −0.73 | −0.37 | −2.02 |
| 338.15 | 0.789 | 0.508 | 1.298 | 0.644 | 1.97 | −0.94 | 1.03 | −0.48 |
| 343.15 | 0.781 | 0.387 | 1.168 | 0.495 | 1.95 | −1.19 | 0.76 | −0.61 |
| 348.15 | 0.773 | 0.264 | 1.037 | 0.341 | 1.92 | −1.20 | 0.72 | −0.63 |
| 353.15 | 0.764 | 0.139 | 0.903 | 0.181 | 1.90 | −1.34 | 0.56 | −0.71 |
| 363.15 | 0.747 | −0.117 | 0.630 | −0.157 | 1.85 | −1.67 | 0.19 | −0.90 |
| 373.15 | 2.013 | 2.013 | 4.026 | 1.000 | 4.85 | 15.21 | 20.05 | 3.14 |
| 378.15 | 0.425 | 0.594 | 1.020 | 1.397 | 0.84 | −0.56 | 0.28 | −0.67 |
| 383.15 | 0.781 | 0.387 | 1.168 | 0.495 | 1.95 | −0.73 | 1.21 | −0.38 |
| 388.15 | −0.530 | −1.038 | −1.568 | 1.959 | −0.57 | −2.05 | −2.62 | 3.61 |
| 393.15 | −0.717 | −1.493 | −2.210 | 2.083 | −1.54 | −3.12 | −4.66 | 2.03 |
| 398.15 | −0.917 | -2.588 | −3.505 | 2.821 | −2.39 | −3.21 | −5.60 | 1.34 |
| 403.15 | 0.584 | 7.647 | 8.231 | 13.084 | −3.52 | 12.57 | 9.05 | −3.58 |
| 408.15 | 1.006 | 11.211 | 12.216 | 11.149 | 2.39 | 18.37 | 20.76 | 7.67 |
| 413.15 | 2.013 | 14.818 | 16.831 | 7.362 | 4.85 | 21.18 | 26.03 | 4.37 |
| 423.15 | −2.076 | 9.053 | 6.977 | −4.361 | −3.51 | 13.30 | 9.79 | −3.79 |
| 433.15 | −0.729 | −2.522 | −3.250 | 3.460 | −1.26 | −1.61 | −2.87 | 1.27 |
| 443.15 | 0.550 | −1.493 | −0.944 | −2.718 | 0.99 | −1.72 | −0.73 | −1.74 |
| 453.15 | 4.266 | 9.254 | 13.520 | 2.169 | 10.38 | −1.11 | 9.27 | −0.11 |
| 463.15 | 1.213 | 15.550 | 16.763 | 12.821 | 3.76 | 10.71 | 14.47 | 2.84 |
| 473.15 | −1.907 | 14.815 | 12.908 | −7.768 | −2.85 | 10.46 | 7.61 | −3.67 |
| T(K) | ||||||||
| 303.15 | 0.736 | 5.459 | 6.195 | 7.421 | 1.73 | 14.24 | 15.97 | 8.23 |
| 313.15 | 0.621 | 3.385 | 4.006 | 5.448 | 1.36 | 7.51 | 8.86 | 5.52 |
| 323.15 | 0.503 | 1.243 | 1.747 | 2.471 | 0.99 | 0.77 | 1.76 | 0.78 |
| 328.15 | 0.443 | 0.147 | 0.590 | 0.333 | 0.80 | −1.40 | −0.60 | −1.74 |
| 333.15 | 0.381 | −0.966 | −0.584 | −2.531 | 0.62 | −1.92 | −1.31 | −3.12 |
| 338.15 | 0.579 | −0.169 | 0.410 | −0.292 | 1.07 | −2.54 | −1.47 | −2.37 |
| 343.15 | 0.605 | 0.520 | 1.125 | 0.860 | 1.15 | −1.89 | −0.74 | −1.64 |
| 348.15 | 0.632 | 1.220 | 1.851 | 1.931 | 1.23 | −0.28 | 0.94 | −0.23 |
| 353.15 | 0.659 | 1.929 | 2.588 | 2.929 | 1.30 | 1.74 | 3.04 | 1.33 |
| 363.15 | 0.714 | 3.379 | 4.093 | 4.732 | 1.46 | 5.79 | 7.24 | 3.97 |
| 373.15 | 0.893 | 3.854 | 4.747 | 4.316 | 1.91 | 0.69 | 2.60 | 0.36 |
| 378.15 | 0.315 | −1.651 | −1.336 | −5.240 | 0.30 | −0.70 | −0.40 | −2.34 |
| 383.15 | 0.605 | 0.520 | 1.125 | 0.860 | 1.15 | 2.31 | 3.46 | 2.01 |
| 388.15 | 0.778 | 22.143 | 22.921 | 28.465 | −2.56 | 13.14 | 10.57 | −5.12 |
| 393.15 | 0.962 | 14.877 | 15.839 | 15.464 | 1.76 | 12.13 | 13.89 | 6.90 |
| 398.15 | 2.200 | 7.518 | 9.718 | 3.417 | 4.89 | 11.61 | 16.50 | 2.38 |
| 403.15 | 0.595 | −1.252 | −0.657 | −2.105 | 1.18 | −2.16 | −0.99 | −1.84 |
| 408.15 | 0.743 | 1.285 | 2.028 | 1.730 | 1.54 | 0.41 | 1.95 | 0.27 |
| 413.15 | 0.893 | 3.854 | 4.747 | 4.316 | 1.91 | 6.66 | 8.57 | 3.50 |
| 423.15 | −1.125 | −1.531 | −2.656 | 1.361 | −1.46 | −2.53 | −3.99 | 1.74 |
| 433.15 | 0.602 | 0.223 | 0.824 | 0.370 | 1.38 | −1.26 | 0.12 | −0.91 |
| 443.15 | 2.369 | 6.543 | 8.912 | 2.762 | 5.41 | 10.87 | 16.28 | 2.01 |
| 453.15 | −1.704 | −4.480 | −6.185 | 2.629 | −2.26 | −4.54 | −6.80 | 2.01 |
| 463.15 | 0.679 | 2.897 | 3.577 | 4.264 | 1.26 | 2.74 | 4.00 | 2.18 |
| 473.15 | 4.310 | 23.213 | 27.523 | 5.386 | 2.06 | 2.73 | 4.80 | 1.33 |
| T(K) | ||||||||
| 303.15 | 2.135 | 6.006 | 8.141 | 2.813 | 5.06 | 14.99 | 20.06 | 2.96 |
| 313.15 | 1.805 | 5.719 | 7.524 | 3.169 | 4.61 | 14.06 | 18.67 | 3.05 |
| 323.15 | 1.661 | 5.423 | 7.084 | 3.266 | 4.16 | 13.13 | 17.29 | 3.16 |
| 328.15 | 1.587 | 5.272 | 6.859 | 3.322 | 3.93 | 12.67 | 16.60 | 3.22 |
| 333.15 | 1.512 | 5.118 | 6.630 | 3.385 | 3.70 | 12.20 | 15.90 | 3.30 |
| 338.15 | 2.177 | 6.179 | 8.357 | 2.838 | −2.30 | 15.92 | 13.62 | −6.92 |
| 343.15 | 0.385 | 3.423 | 3.808 | 8.884 | −3.19 | 12.37 | 9.19 | −3.88 |
| 348.15 | 0.452 | 0.627 | 1.078 | 1.388 | −2.59 | 4.01 | 1.42 | −1.55 |
| 353.15 | 0.510 | −1.015 | −0.506 | −1.992 | 0.51 | 4.36 | 4.87 | 8.54 |
| 363.15 | 0.611 | −1.645 | −-1.035 | −2.695 | 0.75 | 13.22 | 13.96 | 17.68 |
| 373.15 | 0.385 | −0.996 | −0.611 | −2.585 | 0.45 | 6.65 | 7.10 | 14.73 |
| 378.15 | −0.439 | −0.731 | −1.169 | 1.666 | −2.86 | 11.09 | 8.23 | −3.88 |
| 383.15 | −0.735 | 3.423 | 2.688 | −4.659 | −2.31 | 9.21 | 6.90 | −3.99 |
| 388.15 | 1.235 | 21.076 | 22.312 | 17.060 | 2.59 | 19.86 | 22.46 | 7.66 |
| 393.15 | 1.188 | 18.884 | 20.072 | 15.892 | 2.47 | 21.30 | 23.78 | 8.61 |
| 398.15 | 1.141 | 13.057 | 14.197 | 11.448 | 2.35 | 18.65 | 21.01 | 7.93 |
| 403.15 | 0.887 | −1.004 | −0.117 | −1.132 | 1.64 | −1.93 | −0.29 | −1.17 |
| 408.15 | 0.558 | −0.941 | −0.383 | −1.687 | 0.83 | −1.86 | −1.03 | −2.25 |
| 413.15 | 0.224 | −0.452 | −0.228 | −2.017 | 0.73 | −1.81 | −1.08 | −2.49 |
| 423.15 | 0.786 | 2.985 | 3.771 | 3.798 | 1.57 | 4.81 | 6.38 | 3.08 |
| 433.15 | 1.060 | 9.697 | 10.756 | 9.149 | 2.21 | 13.41 | 15.62 | 6.08 |
| 443.15 | 1.340 | 13.578 | 14.918 | 10.131 | 2.85 | 15.73 | 18.58 | 5.53 |
| 453.15 | −1.978 | 6.298 | 4.320 | −3.184 | −1.53 | −1.92 | −3.46 | 1.26 |
| 463.15 | 0.188 | -0.611 | −0.422 | −3.242 | 0.23 | −0.74 | −0.51 | −3.25 |
| 473.15 | 0.571 | 1.133 | 1.703 | 1.985 | 1.04 | −0.74 | 0.31 | −0.71 |
| Solid Surface | ||||||||
|---|---|---|---|---|---|---|---|---|
| Silica | 0.807 | 0.412 | 1.219 | 0.510 | 1.39 | −1.32 | 0.07 | −0.95 |
| T(K) | PMMA | ||||
|---|---|---|---|---|---|
| 303.15 | 378.20 | 395.51 | 354.74 | 337.33 | 297.06 |
| 313.15 | 367.18 | 371.55 | 340.26 | 319.84 | 276.45 |
| 323.15 | 356.15 | 353.99 | 319.89 | 299.94 | 268.35 |
| 328.15 | 350.64 | 348.49 | 327.15 | 308.07 | 274.64 |
| 333.15 | 345.13 | 353.01 | 340 | 322.86 | 296.16 |
| 338.15 | 339.62 | 357.02 | 330.02 | 310.12 | 272.62 |
| 343.15 | 334.11 | 361.76 | 317.89 | 297.17 | 257.28 |
| 348.15 | 328.60 | 341.88 | 304.58 | 284.75 | 245.91 |
| 353.15 | 323.09 | 322.53 | 289.18 | 272.25 | 237.62 |
| 363.15 | 312.07 | 296.06 | 266.8 | 250.08 | 227 |
| 373.15 | 301.04 | 271.64 | 237.43 | 219.87 | 231.39 |
| 378.15 | 295.53 | 266.5 | 229.4 | 215.81 | 262.31 |
| 383.15 | 290.02 | 263.87 | 248.84 | 267.22 | 307.3 |
| 388.15 | 284.51 | 271.09 | 302.26 | 317.52 | 252.09 |
| 393.15 | 279.00 | 290.69 | 274.76 | 296.44 | 221.75 |
| 398.15 | 273.49 | 311.45 | 256.56 | 272.99 | 209.51 |
| 403.15 | 267.98 | 291.54 | 242.31 | 238.62 | 199.78 |
| 408.15 | 262.47 | 268.3 | 222.02 | 215.57 | 196.16 |
| 413.15 | 256.96 | 247.67 | 202.81 | 198.03 | 193.27 |
| 423.15 | 245.93 | 233.94 | 196.97 | 194.06 | 215.82 |
| 433.15 | 234.91 | 238.92 | 231.59 | 226.19 | 258.37 |
| 443.15 | 223.89 | 241.02 | 192.79 | 180.85 | 195.77 |
| 453.15 | 212.87 | 214.66 | 175.48 | 156.95 | 166.58 |
| 463.15 | 201.85 | 206.05 | 168.88 | 150.69 | 158.53 |
| 473.15 | 190.82 | 180.38 | 146.81 | 131.75 | 136.51 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamieh, T. Temperature Dependence of the Polar and Lewis Acid–Base Properties of Poly Methyl Methacrylate Adsorbed on Silica via Inverse Gas Chromatography. Molecules 2024, 29, 1688. https://doi.org/10.3390/molecules29081688
Hamieh T. Temperature Dependence of the Polar and Lewis Acid–Base Properties of Poly Methyl Methacrylate Adsorbed on Silica via Inverse Gas Chromatography. Molecules. 2024; 29(8):1688. https://doi.org/10.3390/molecules29081688
Chicago/Turabian StyleHamieh, Tayssir. 2024. "Temperature Dependence of the Polar and Lewis Acid–Base Properties of Poly Methyl Methacrylate Adsorbed on Silica via Inverse Gas Chromatography" Molecules 29, no. 8: 1688. https://doi.org/10.3390/molecules29081688
APA StyleHamieh, T. (2024). Temperature Dependence of the Polar and Lewis Acid–Base Properties of Poly Methyl Methacrylate Adsorbed on Silica via Inverse Gas Chromatography. Molecules, 29(8), 1688. https://doi.org/10.3390/molecules29081688







