Vibronic Effects Analysis of the Substituent Effect on the Spectral Properties of the EMI and CPL of Three [7]Helicene Derivatives
Abstract
:1. Introduction
2. Results and Discussion
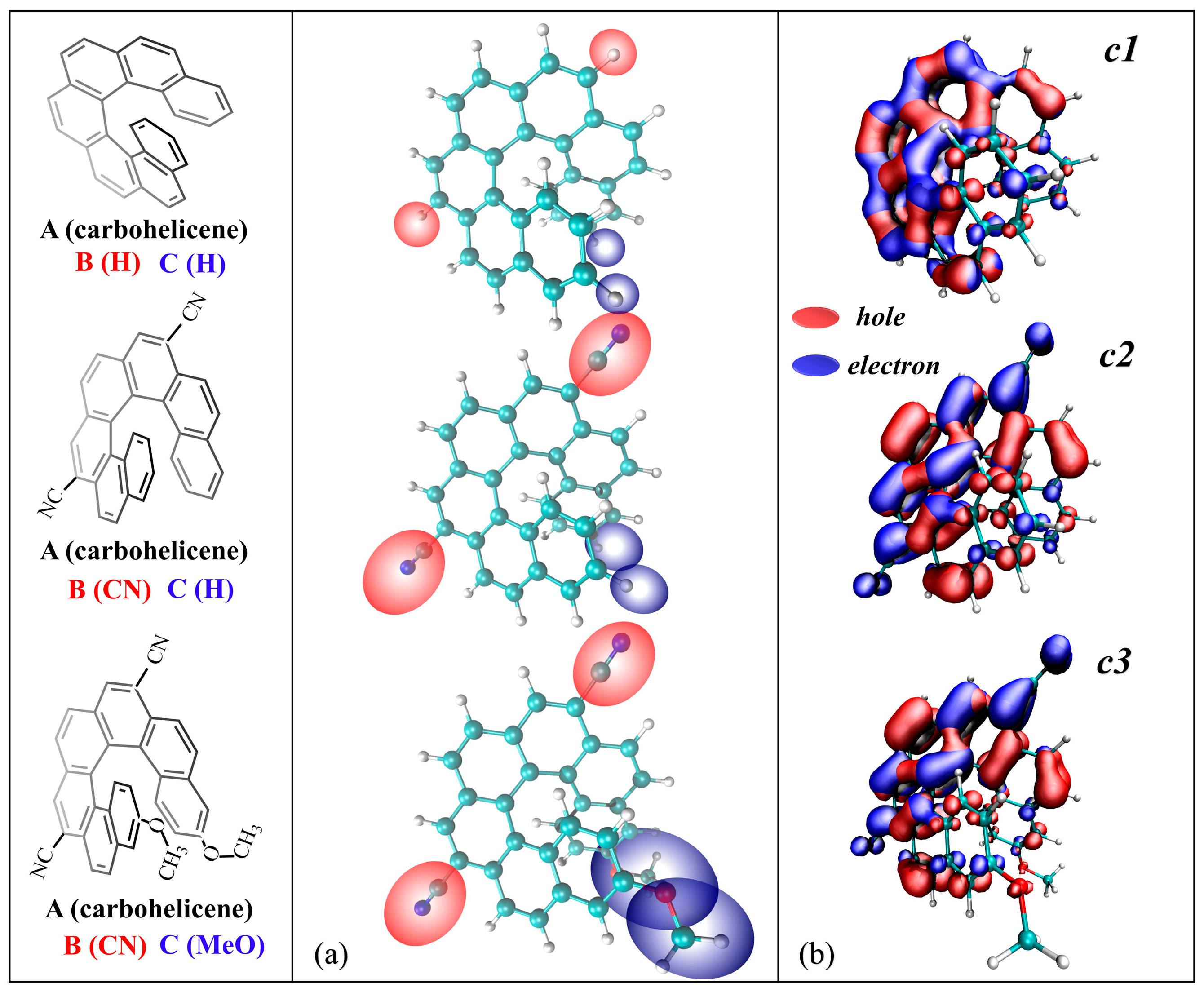
2.1. Transition Nature
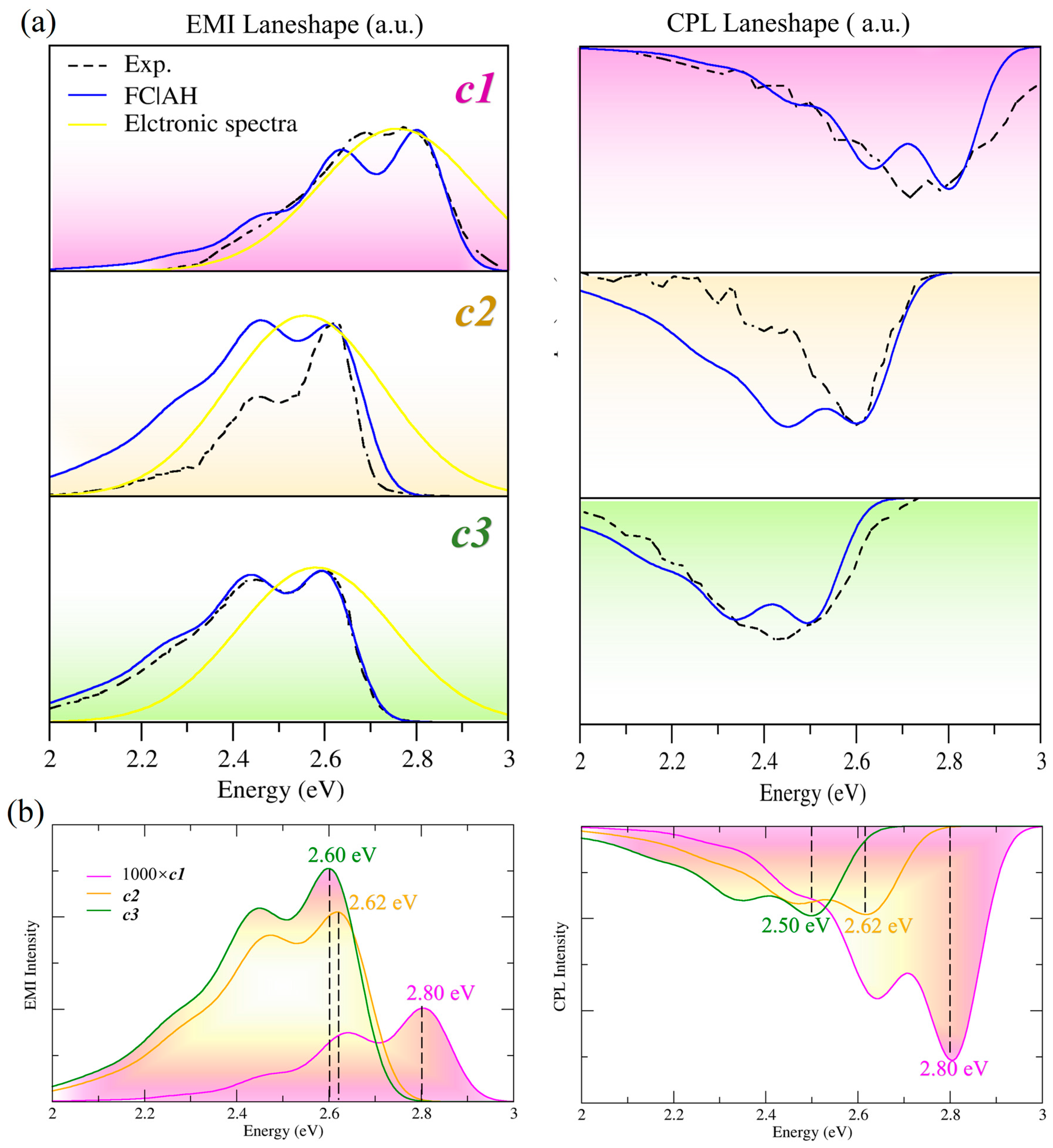
2.2. Calculated Spectra
2.3. Substituent Effect
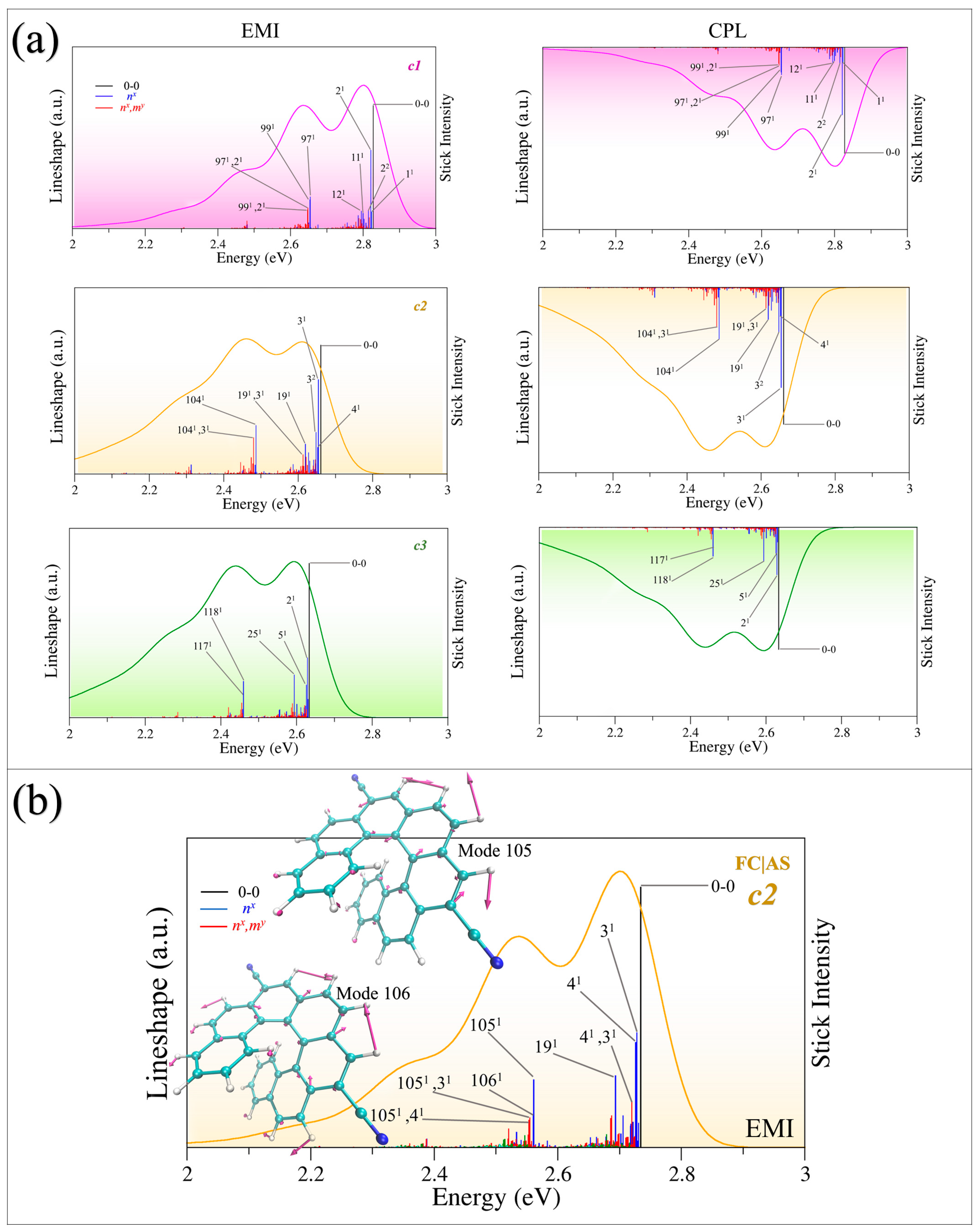
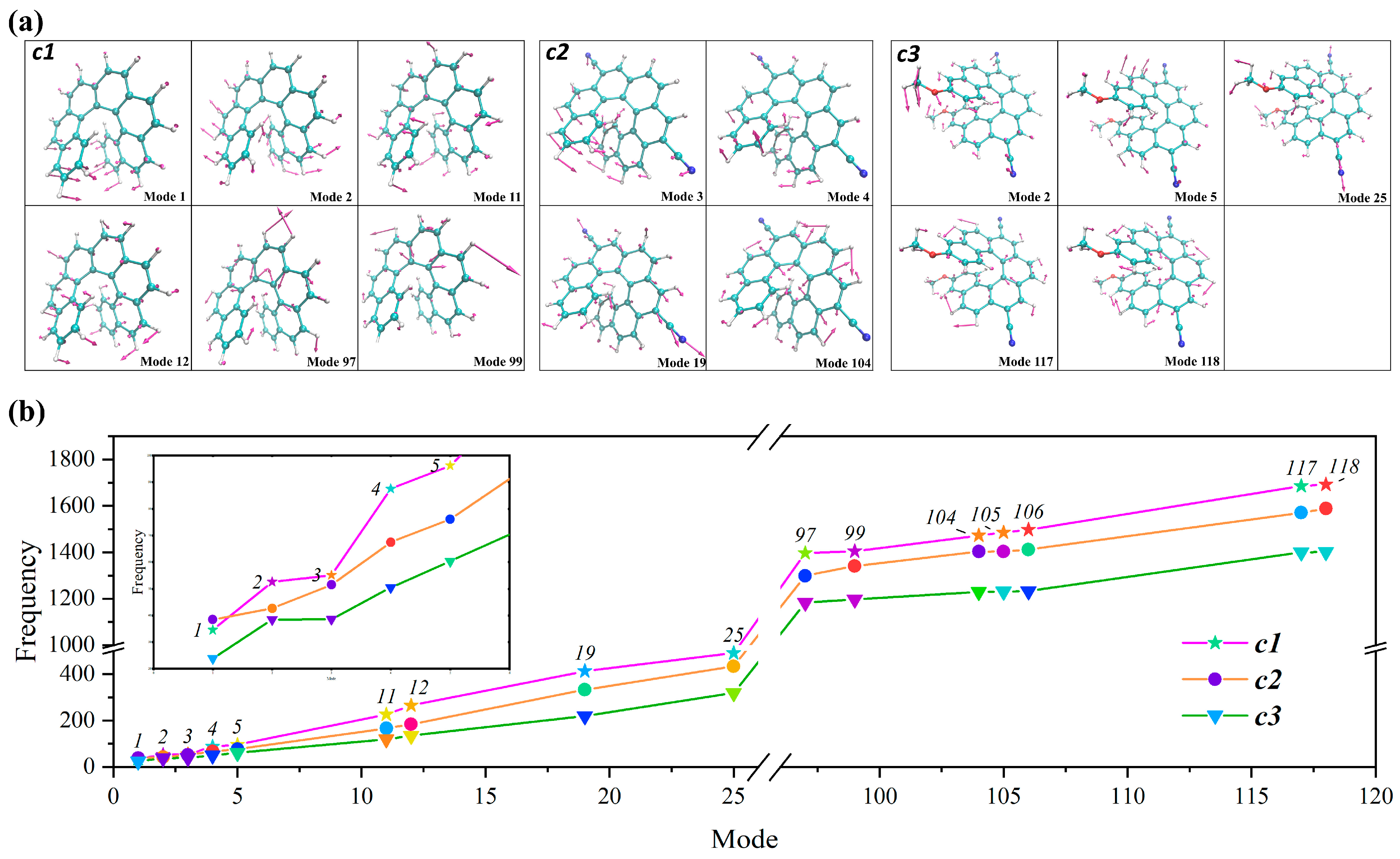
2.4. The Assignment of the Main Vibronic Bands
3. Conclusions
4. Computational Details
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shahamirian, M.; Wieczorkiewicz, P.A.; Krygowski, T.M.; Szatylowicz, H. Substituent Effects from the Point of View of Energetics and Molecular Geometry in Acene, Polyene, and Polyyne Derivatives. J. Org. Chem. 2023, 88, 7940–7952. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, C.; Burešová, Z.; Bureš, F.; Liu, J. Cyano-capped molecules: Versatile organic materials. J. Mater. Chem. A 2023, 11, 3753–3770. [Google Scholar] [CrossRef]
- Chen, J.; Yang, J.; Ma, L.; Li, J.; Shahzad, N.; Kim, C.K. Structure-antioxidant activity relationship of methoxy, phenolic hydroxyl, and carboxylic acid groups of phenolic acids. Sci. Rep. 2020, 10, 2611. [Google Scholar]
- Cei, M.; Di Bari, L.; Zinna, F. Circularly polarized luminescence of helicenes: A data-informed insight. Chirality 2023, 35, 192–210. [Google Scholar] [CrossRef] [PubMed]
- dos Santos, J.M.; Sun, D.; Moreno-Naranjo, J.M.; Hall, D.; Zinna, F.; Ryan, S.T.; Shi, W.; Matulaitis, T.; Cordes, D.B.; Slawin, A.M. An S-shaped double helicene showing both multi-resonance thermally activated delayed fluorescence and circularly polarized luminescence. J. Mater. Chem. C 2022, 10, 4861–4870. [Google Scholar] [CrossRef]
- Shinohara, K.-i.; Sannohe, Y.; Kaieda, S.; Tanaka, K.-i.; Osuga, H.; Tahara, H.; Xu, Y.; Kawase, T.; Bando, T.; Sugiyama, H. A chiral wedge molecule inhibits telomerase activity. J. Am. Chem. Soc. 2010, 132, 3778–3782. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Zhang, Y.X.; Sugiyama, H.; Umano, T.; Osuga, H.; Tanaka, K. (P)-helicene displays chiral selection in binding to Z-DNA. J. Am. Chem. Soc. 2004, 126, 6566–6567. [Google Scholar] [CrossRef]
- Wigglesworth, T.J.; Sud, D.; Norsten, T.B.; Lekhi, V.S.; Branda, N.R. Chiral discrimination in photochromic helicenes. J. Am. Chem. Soc. 2005, 127, 7272–7273. [Google Scholar] [CrossRef] [PubMed]
- Kelly, T.R.; Cai, X.; Damkaci, F.; Panicker, S.B.; Tu, B.; Bushell, S.M.; Cornella, I.; Piggott, M.J.; Salives, R.; Cavero, M. Progress toward a rationally designed, chemically powered rotary molecular motor. J. Am. Chem. Soc. 2007, 129, 376–386. [Google Scholar] [CrossRef]
- Sahasithiwat, S.; Mophuang, T.; Menbangpung, L.; Kamtonwong, S.; Sooksimuang, T. 3, 12-Dimethoxy-7, 8-dicyano-[5]helicene as a novel emissive material for organic light-emitting diode. Synth. Met. 2010, 160, 1148–1152. [Google Scholar] [CrossRef]
- Shi, L.; Liu, Z.; Dong, G.; Duan, L.; Qiu, Y.; Jia, J.; Guo, W.; Zhao, D.; Cui, D.; Tao, X. Synthesis, Structure, Properties, and application of a carbazole-based diaza [7]helicene in a deep-blue-emitting OLED. Chem-Eur. J. 2012, 18, 8092–8099. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Rauch, F.; Swain, A.; Marder, T.B.; Ravat, P. Efficient Narrowband Circularly Polarized Light Emitters Based on 1, 4-B, N-embedded Rigid Donor–Acceptor Helicenes. Angew. Chem. 2023, 135, e202218965. [Google Scholar] [CrossRef]
- Birks, J.; Birch, D.; Cordemans, E.; Vander Donckt, E. Fluorescence of the higher helicenes. Chem. Phys. Lett. 1976, 43, 33–36. [Google Scholar] [CrossRef]
- Sapir, M.; Vander Donckt, E. Intersystem crossing in the helicenes. Chem. Phys. Lett. 1975, 36, 108–110. [Google Scholar] [CrossRef]
- Kubo, H.; Hirose, T.; Nakashima, T.; Kawai, T.; Hasegawa, J.-y.; Matsuda, K. Tuning transition electric and magnetic dipole moments: [7]helicenes showing intense circularly polarized luminescence. J. Phys. Chem. Lett. 2021, 12, 686–695. [Google Scholar] [CrossRef] [PubMed]
- Crassous, J.; Fuchter, M.J.; Freedman, D.E.; Kotov, N.A.; Moon, J.; Beard, M.C.; Feldmann, S. Materials for chiral light control. Nat. Rev. Mater. 2023, 8, 365–371. [Google Scholar] [CrossRef]
- Hübener, H.; De Giovannini, U.; Schäfer, C.; Andberger, J.; Ruggenthaler, M.; Faist, J.; Rubio, A. Engineering quantum materials with chiral optical cavities. Nature. Mat. 2021, 20, 438–442. [Google Scholar] [CrossRef]
- Qian, Q.; Ren, H.; Zhou, J.; Wan, Z.; Zhou, J.; Yan, X.; Cai, J.; Wang, P.; Li, B.; Sofer, Z. Chiral molecular intercalation superlattices. Nature 2022, 606, 902–908. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Xu, Q.; Sun, J.; Wang, L.; He, D.; Wang, M.; Yang, C. Insights for vibronic effects on spectral shapes of electronic circular dichroism and circularly polarized luminescence of aza [7]helicene. Spectroc. Acta Pt. A-Molec. Biomolec. Spectr. 2020, 239, 118475. [Google Scholar] [CrossRef]
- Mori, T. Significance of Vibronic Coupling that Shapes Circularly Polarized Luminescence of Double Helicenes. Angew. Chem. 2024, 136, e202319702. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, Q.; Wang, L.; Gao, A.; Li, Q.; Chen, S.; Zhao, Y.; Wang, M.; Jiang, J.; Jia, C. Rational Control of Maximum EMI/CPL Intensity and Wavelength of Bora [6]helicene via Polarity and Vibronic Effects. J. Phys. Chem. Lett. 2024, 15, 10818–10825. [Google Scholar] [CrossRef]
- Xu, Q.; Liu, Y.; Lin, N.; Zhao, X.; He, D.; Wang, L.; Xu, Y.; Wang, M. Theoretical study on some carbohelicenes dyes with tunable emission wavelength: Optical properties, vibronic effect, quantum yield. Dye. Pigm. 2022, 204, 110407. [Google Scholar] [CrossRef]
- Xu, Q.; Chi, L.; Liu, Y.; Li, Q.; Chen, S.; Wang, M. Vibronic effect explains ECD spectral shape and tunability of CPL wavelength of two triarylborane-based [5]helicenes derivatives. J. Lumin. 2021, 239, 118374. [Google Scholar] [CrossRef]
- Santoro, F.; Lami, A.; Improta, R.; Bloino, J.; Barone, V. Effective method for the computation of optical spectra of large molecules at finite temperature including the Duschinsky and Herzberg–Teller effect: The Q x band of porphyrin as a case study. J. Chem. Phys. 2008, 128, 224311. [Google Scholar] [CrossRef] [PubMed]
- Santoro, F.; Lami, A.; Improta, R.; Barone, V. Effective method to compute vibrationally resolved optical spectra of large molecules at finite temperature in the gas phase and in solution. J. Chem. Phys. 2007, 126, 184102. [Google Scholar] [CrossRef]
- Santoro, F.; Improta, R.; Lami, A.; Bloino, J.; Barone, V. Effective method to compute Franck-Condon integrals for optical spectra of large molecules in solution. J. Chem. Phys. 2007, 126, 084509. [Google Scholar] [CrossRef]
- Santoro, F.; Barone, V. Computational approach to the study of the lineshape of absorption and electronic circular dichroism spectra. Int. J. Quantum Chem 2010, 110, 476–486. [Google Scholar] [CrossRef]
- Aranda, D.; Santoro, F. Vibronic spectra of π-conjugated systems with a multitude of coupled states: A protocol based on linear vibronic coupling models and quantum dynamics tested on hexahelicene. J. Chem. Theory Comput. 2021, 17, 1691–1700. [Google Scholar] [CrossRef] [PubMed]
- Cerezo, J.; Santoro, F. FCclasses3: Vibrationally-resolved spectra simulated at the edge of the harmonic approximation. J. Comput. Chem. 2023, 44, 626–643. [Google Scholar] [CrossRef]
- Cerezo, J.; Mazzeo, G.; Longhi, G.; Abbate, S.; Santoro, F. Quantum-classical calculation of vibronic spectra along a reaction path: The case of the ECD of easily interconvertible conformers with opposite chiral responses. J. Phys. Chem. Lett. 2016, 7, 4891–4897. [Google Scholar] [CrossRef] [PubMed]
- Ferrer, F.J.A.; Cerezo, J.; Soto, J.; Improta, R.; Santoro, F. First-principle computation of absorption and fluorescence spectra in solution accounting for vibronic structure, temperature effects and solvent inhomogenous broadening. Comput. Theo. Chem. 2014, 1040, 328–337. [Google Scholar] [CrossRef]
- Herzberg, G.; Teller, E. Schwingungsstruktur der Elektronenübergänge bei mehratomigen Molekülen. Z. Phys. Chem. 1933, 21, 410–446. [Google Scholar] [CrossRef]
- Duschinsky, F. The importance of the electron spectrum in multi atomic molecules. Concerning the Franck-Condon principle. Acta Physicochim. URSS 1937, 7, 551–566. [Google Scholar]
- Xu, Q.; Liu, Y.; Zhao, X.; Chen, S.; Li, Q.; Wang, M.; Yang, C. Vibrationally resolved electronic circular dichroism and circularly polarized luminescence spectra of a boron-fused double helicene: A theoretical study. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2020, 231, 118132. [Google Scholar] [CrossRef] [PubMed]
- Humeniuk, A.; Bužančić, M.; Hoche, J.; Cerezo, J.; Mitrić, R.; Santoro, F.; Bonačić-Koutecký, V. Predicting fluorescence quantum yields for molecules in solution: A critical assessment of the harmonic approximation and the choice of the lineshape function. J. Chem. Phys. 2020, 152, 054107. [Google Scholar] [CrossRef]
- Liu, Z.; Lu, T.; Chen, Q. An sp-hybridized all-carboatomic ring, cyclo [18]carbon: Electronic structure, electronic spectrum, and optical nonlinearity. Carbon 2020, 165, 461–467. [Google Scholar] [CrossRef]
- Zhou, Q.; Guo, Y.; Zhu, Y. Photocatalytic sacrificial H2 evolution dominated by micropore-confined exciton transfer in hydrogen-bonded organic frameworks. Nat. Catal. 2023, 6, 574–584. [Google Scholar] [CrossRef]
- Lu, T. A comprehensive electron wavefunction analysis toolbox for chemists, Multiwfn. J. Chem. Phys. 2024, 161, 082503. [Google Scholar] [CrossRef] [PubMed]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Wei, M.; Zhang, L.; Tian, G.; Hua, W. Vibronic fine structure in the nitrogen 1 s photoelectron spectra from Franck-Condon simulation. II. Indoles. Phys. Rev. A 2023, 108, 022816. [Google Scholar] [CrossRef]
- Wei, M.; Cheng, X.; Zhang, L.; Zhang, J.-R.; Wang, S.-Y.; Ge, G.; Tian, G.; Hua, W. Vibronic fine structure in the nitrogen 1 s photoelectron spectra of molecules from Franck-Condon simulations: Azines. Phys. Rev. A 2022, 106, 022811. [Google Scholar] [CrossRef]
- Wei, M.; Zuo, J.; Tian, G.; Hua, W. Vibronic fine structure in the nitrogen 1 s photoelectron spectra from Franck-Condon simulations. III. Rules for amine and imine N atoms in small N-heterocycles. Phys. Rev. A 2024, 109, 022820. [Google Scholar] [CrossRef]
- Kong, F.-F.; Tian, X.-J.; Zhang, Y.; Yu, Y.-J.; Jing, S.-H.; Zhang, Y.; Tian, G.-J.; Luo, Y.; Yang, J.-L.; Dong, Z.-C. Probing intramolecular vibronic coupling through vibronic-state imaging. Nat. Commun. 2021, 12, 1280. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.; Schlegel, H.; Scuseria, G.; Robb, M.; Cheeseman, J.; Scalmani, G.; Barone, V.; Petersson, G.; Nakatsuji, H.; et al. Gaussian, 16; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum mechanical continuum solvation models. Chem. Rev. 2005, 105, 2999–3094. [Google Scholar] [CrossRef]
- Begam, K.; Bhandari, S.; Maiti, B.; Dunietz, B.D. Screened range-separated hybrid functional with polarizable continuum model overcomes challenges in describing triplet excitations in the condensed phase using TDDFT. J. Chem. Theory. Comput. 2020, 16, 3287–3293. [Google Scholar] [CrossRef]
- Herbert, J.M. Dielectric continuum methods for quantum chemistry. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2021, 11, e1519. [Google Scholar] [CrossRef]
- Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Schäfer, A.; Horn, H.; Ahlrichs, R. Fully optimized contracted Gaussian basis sets for atoms Li to Kr. J. Chem. Phys. 1992, 97, 2571–2577. [Google Scholar] [CrossRef]
- Liu, Y.; Aranda, D.; Santoro, F. A computational study of the vibronic effects on the electronic spectra and the photophysics of aza [7]helicene. Phys. Chem. Chem. Phys. 2021, 23, 16551–16563. [Google Scholar] [CrossRef]
- Santoro, F.; Cerezo, J. FCclasses 3, a Code for Vibronic Calculations. Available online: http://www.iccom.cnr.it/en/fcclasses/ (accessed on 23 November 2022).
- Avila Ferrer, F.J.; Cerezo, J.; Stendardo, E.; Improta, R.; Santoro, F. Insights for an accurate comparison of computational data to experimental absorption and emission spectra: Beyond the vertical transition approximation. J. Chem. Theory. Comput. 2013, 9, 2072–2082. [Google Scholar] [CrossRef] [PubMed]
- Karunakaran, V.; Senyushkina, T.; Saroja, G.; Liebscher, J.; Ernsting, N.P. 2-Amino-7-nitro-fluorenes in Neat and Mixed Solvents Optical Band Shapes and Solvatochromism. J. Phys. Chem. A 2007, 111, 10944–10952. [Google Scholar] [CrossRef] [PubMed]
- Valeur, B. Molecular Fluorescence Principles and Applications; Wiley-VCH: Weinheim, Germany, 2001; p. 51. [Google Scholar]
| Molecules | |m| | EAH | E0→0 | |||
|---|---|---|---|---|---|---|
| c1 | 0.03 | 0.05 | 3.36 | 0.001 | 3.27 | 3.39 × 10−3 |
| c2 | 0.89 | 0.31 | 3.08 | 1.13 | 3.01 | 1.38 |
| c3 | 0.99 | 0.28 | 3.11 | 1.43 | 3.00 | 2.44 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Q.; Wang, M.; Liu, Y. Vibronic Effects Analysis of the Substituent Effect on the Spectral Properties of the EMI and CPL of Three [7]Helicene Derivatives. Molecules 2025, 30, 44. https://doi.org/10.3390/molecules30010044
Xu Q, Wang M, Liu Y. Vibronic Effects Analysis of the Substituent Effect on the Spectral Properties of the EMI and CPL of Three [7]Helicene Derivatives. Molecules. 2025; 30(1):44. https://doi.org/10.3390/molecules30010044
Chicago/Turabian StyleXu, Qiushuang, Meishan Wang, and Yanli Liu. 2025. "Vibronic Effects Analysis of the Substituent Effect on the Spectral Properties of the EMI and CPL of Three [7]Helicene Derivatives" Molecules 30, no. 1: 44. https://doi.org/10.3390/molecules30010044
APA StyleXu, Q., Wang, M., & Liu, Y. (2025). Vibronic Effects Analysis of the Substituent Effect on the Spectral Properties of the EMI and CPL of Three [7]Helicene Derivatives. Molecules, 30(1), 44. https://doi.org/10.3390/molecules30010044







