NMR and MD Simulations of Non-Ionic Surfactants
Abstract
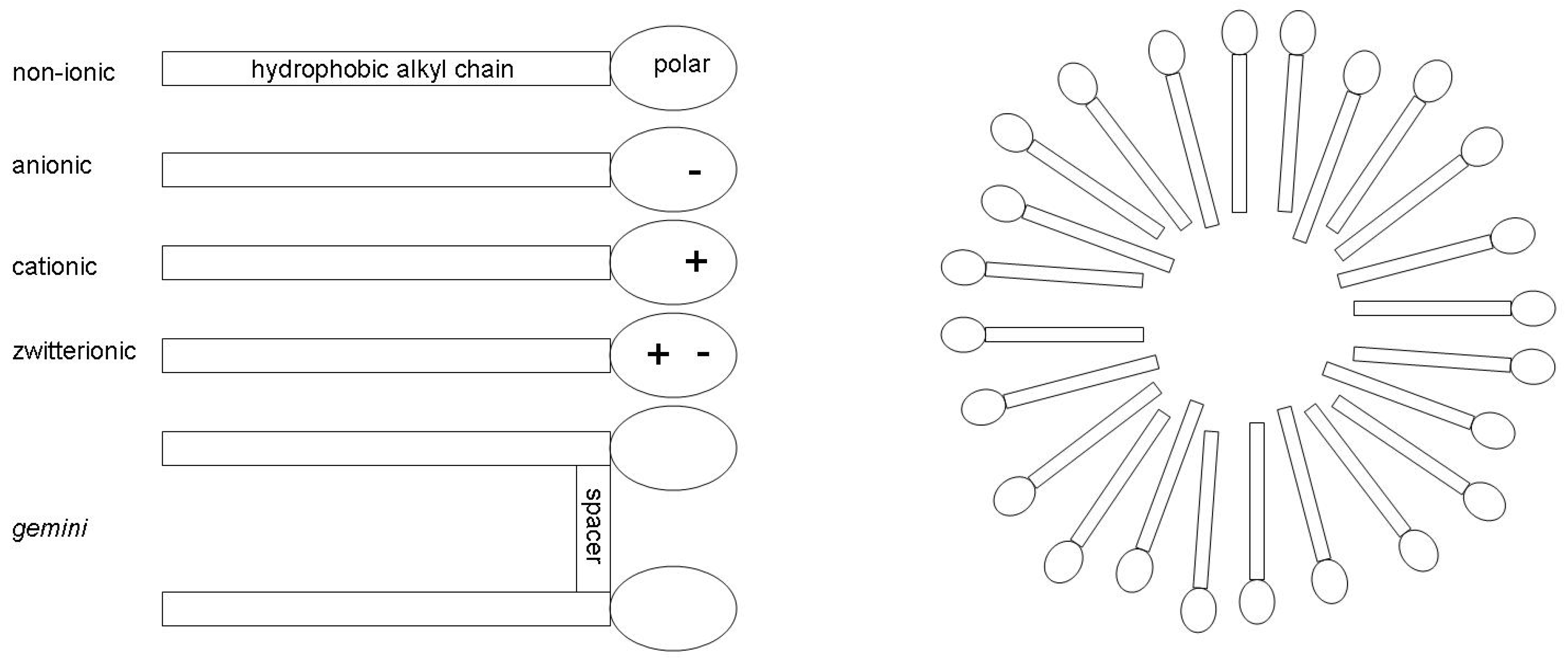
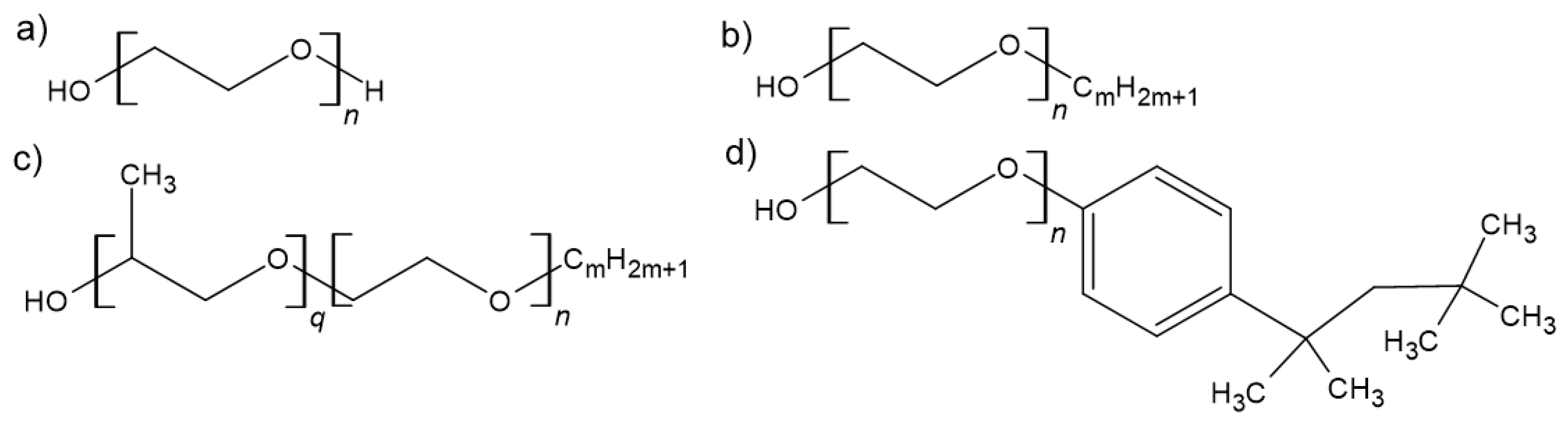
1. Introduction
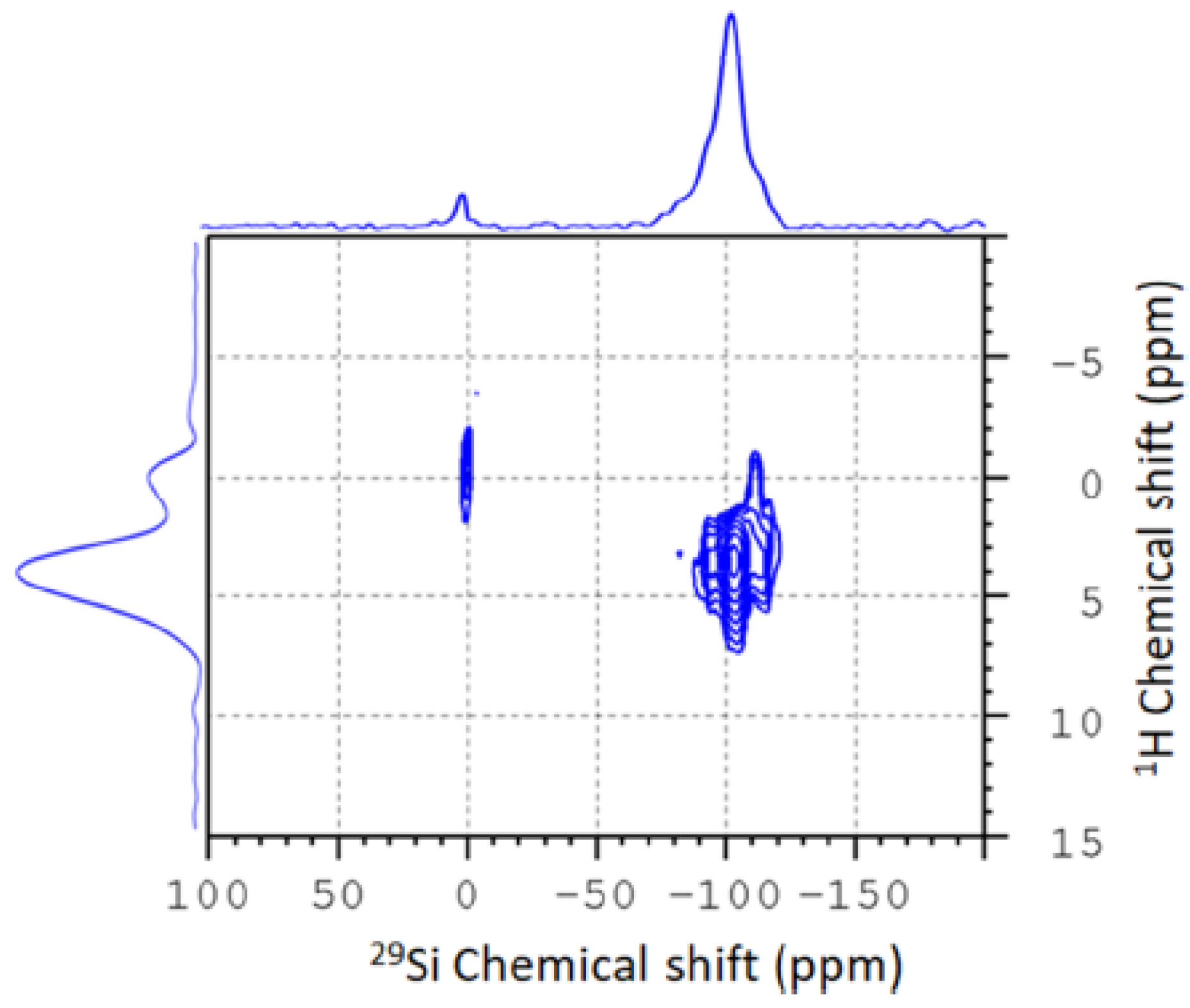
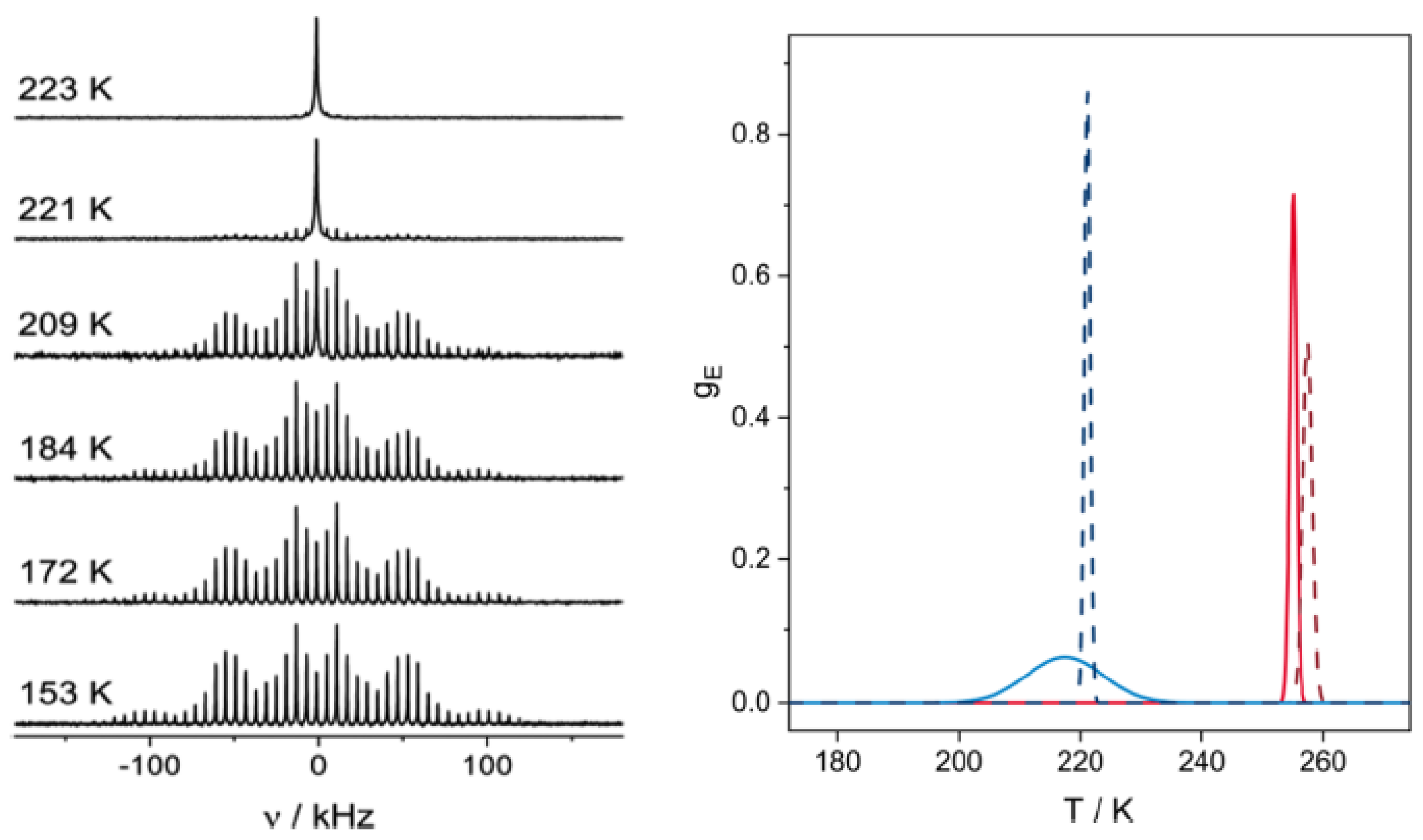
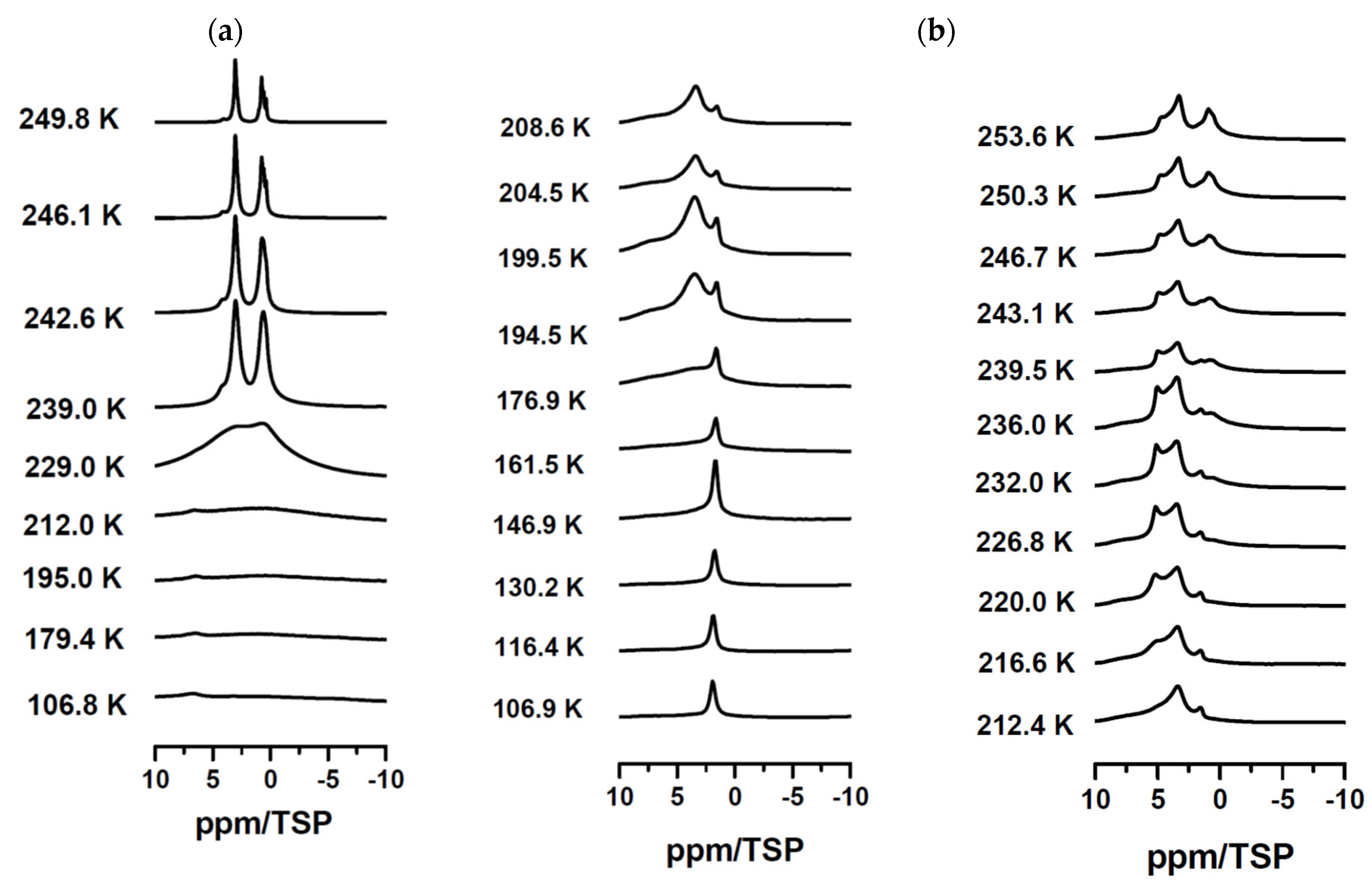
2. Typical Results
3. Small Molecules as Models for Confined Surfactants
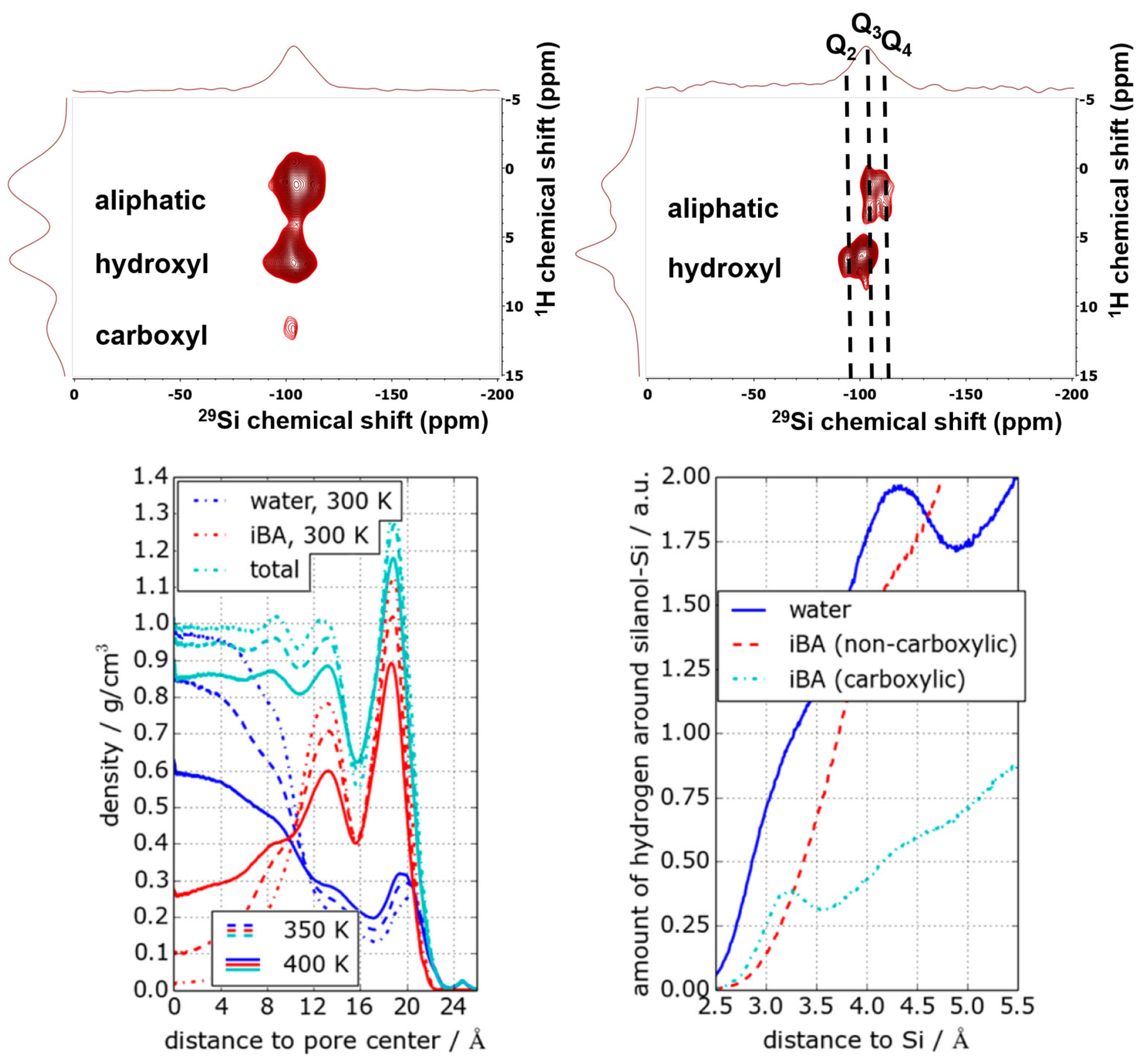
3.1. Water–Octanol Mixtures
3.2. Water–Isobutyric Acid Mixtures
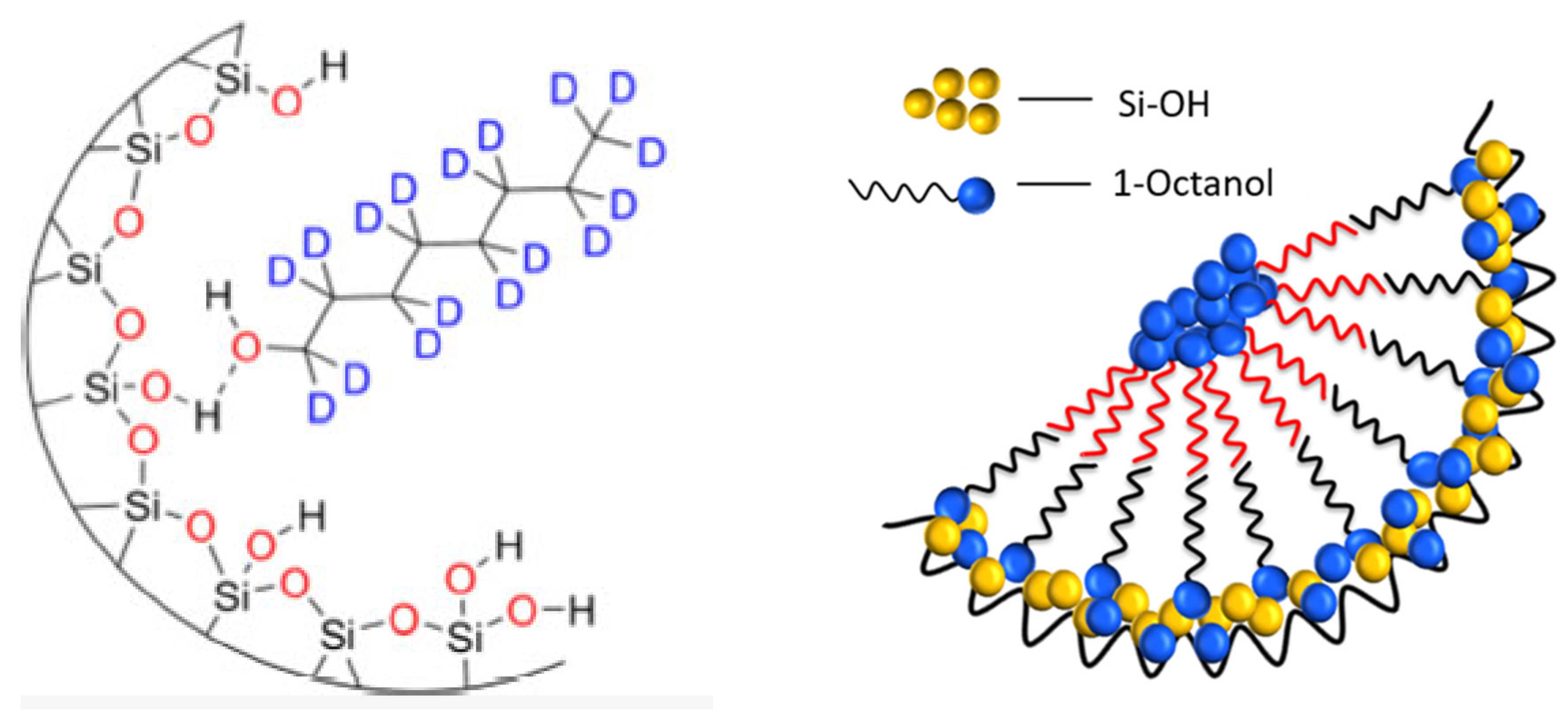
3.3. Confined Surfactants
4. Surfactants and MD Simulations
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Anastas, P.T.; Warner, J.C. Green Chemistry: Theory and Practice; Oxford University Press: Oxford, UK, 1998; ISBN 0198502346. [Google Scholar]
- Turowski, A.; Skrypzak, W.; Reng, A.; Juerges, P. Characterization of mild surfactants for hair and skin-cleansing products. Parfümerie Kosmet. 1995, 76, 16–18+21–22+24+26–27. [Google Scholar]
- Pletnev, M.Y. Green and natural surfactants: Recent developments. SOFW J. 2006, 132, 2–8+10–12. [Google Scholar]
- Hauthal, H.G. Progress in surfactants-innovations of the last five years. SOFW J. 2008, 134, 10+12–16+18–20+22–32+34–35. [Google Scholar]
- Judd, C.S. News from online: Cleaning up-soap, detergent, and more. J. Chem. Ed. 2002, 79, 1179–1181. [Google Scholar] [CrossRef]
- Kesting, W.; Bach, E.; Tummuscheit, M.; Schollmeyer, E. Surfactants in textile finishing. Mechanisms and trends. Tenside Surfactants Deterg. 1994, 31, 362–371. [Google Scholar] [CrossRef]
- Dodgson, D.V. Surfactants and emulsion polymerisation: An industrial perspective. In Surfactants in Polymers, Coatings, Inks, and Adhesives; Applied Surfactant Series; Blackwell: Hoboken, NJ, USA, 2003; Volume 1, pp. 1–31. [Google Scholar]
- Boyde, S. Green lubricants. Environmental benefits and impacts of lubrication. Green Chem. 2002, 4, 293–307. [Google Scholar] [CrossRef]
- Howick, C. New developments in emulsion-PVC polymerisation to produce polymers with the potential of reduced or zero VOC requirements when used in plastisol applications. Green Chem. 2007, 9, 243–246. [Google Scholar] [CrossRef]
- Mitcham, E.J. Innovations in quarantine. In Environmentally Friendly Technologies for Agricultural Produce Quality; CRC Press: Boca Raton, FL, USA, 2005; pp. 113–131. [Google Scholar]
- Ruiz-Angel, M.J.; Garcia-Alvarez-Coque, M.C.; Berthod, A. New Insights and recent developments in micellar liquid chromatography. Sep. Purif. Rev 2009, 38, 45–96. [Google Scholar] [CrossRef]
- Mohammad, A.; Haq, N. Green eluents in chromatography. In Green Chemistry for Environmental Sustainability; CRC Press: Boca Raton, FL, USA, 2011; pp. 285–302. [Google Scholar]
- Morales-Munoz, S.; Luque-Garcia, J.L.; Luque de Castro, M.D. Pure and modified water assisted by auxiliary energies: An environmental friendly extractant for sample preparation. Anal. Chim. Acta 2006, 557, 278–286. [Google Scholar] [CrossRef]
- Canselier, J.P. Surfactants in pollution removal and environmental protection. Comun. Present. A Jorn. Com. Esp. Deterg. 2007, 37, 221–233. [Google Scholar]
- Surfactants Market Size—Industry Report on Share, Growth Trends & Forecasts Analysis (2024–2029). Available online: https://www.mordorintelligence.com/industry-reports/surfactants-market (accessed on 22 November 2024).
- McCoy, M. Goodbye, phosphates. Chem. Eng. News 2011, 24, 12–17. [Google Scholar] [CrossRef]
- Toernvall, U.; Hatti-Kaul, R. Specialty chemicals from vegetable oils: Achievements within the greenchem research program. Lipid Techn. 2007, 19, 84–87. [Google Scholar] [CrossRef]
- Nakamura, M. Fatty acid methyl ester and its relative products from palm oil. J. Oleo Sci. 2001, 50, 445–452. [Google Scholar] [CrossRef]
- Hill, K. Industrial development and application of biobased oleochemicals. Pure Appl. Chem. 2007, 79, 1999–2011. [Google Scholar] [CrossRef]
- Hill, K. Fats and oils as oleochemical raw materials. J. Oleo Sci. 2001, 50, 433–444. [Google Scholar] [CrossRef][Green Version]
- Hill, K. Fats and oils as oleochemical raw materials. Pure Appl. Chem. 2000, 72, 1255–1264. [Google Scholar] [CrossRef]
- Hill, K. Fats and oils as oleochemical raw materials. Recent developments and perspectives. Agro Food Ind. Hi Tech 1998, 9, 9–15. [Google Scholar]
- Moran, M.C.; Pinazo, A.; Perez, L.; Clapes, P.; Angelet, M.; Garcia, M.T.; Vinardell, M.P.; Infante, M.R. “Green” amino acid-based surfactants. Green Chem. 2004, 6, 233–240. [Google Scholar] [CrossRef]
- Hoefer, R.; Bigorra, J. Green chemistry—A sustainable solution for industrial specialties applications. Green Chem. 2007, 9, 203–212. [Google Scholar] [CrossRef]
- Behr, A.; Eilting, J.; Irawandi, K.; Leschinski, J.; Lindner, F. Improved utilisation of renewable resources: New important derivates of glycerol. Green Chem. 2008, 10, 13–30. [Google Scholar] [CrossRef]
- Nakamura, M.; Oba, K. Recent developments and future trends in oleochemistry. Nihon Yukagakkaishi 1997, 46, 957–967. [Google Scholar] [CrossRef]
- Hill, K. Alkyl polyglycosides—Where green meets performance. SOFW J. 2009, 135, 6+8–12+14. [Google Scholar]
- Maier, R.M. Biosurfactants: Evolution and diversity in bacteria. Adv. Appl. Microbiol. 2003, 52, 101–121. [Google Scholar]
- Desai, J.D.; Banat, I.M. Microbial Production of Surfactants and Their Commercial Potential. Microbiol. Mol. Biol. Rev. 1997, 61, 47–64. [Google Scholar]
- Boethling, R.S.; Sommer, E.; Di Fiore, D. Designing Small Molecules for Biodegradability. Chem. Rev. 2007, 107, 2207–2227. [Google Scholar] [CrossRef]
- Hayes, D.G. Enzyme-catalyzed modification of oilseed materials to produce eco-friendly products. J. Am. Oil Chem. Soc. 2004, 81, 1077–1103. [Google Scholar] [CrossRef]
- Dwars, T.; Paetzold, E.; Oehme, G. Reactions in micellar systems. Angew. Chem. Int. Ed. Engl. 2005, 44, 7174–7199. [Google Scholar] [CrossRef]
- Fendler, J.H. Membrane Mimetic Chemistry; Wiley: New York, NY, USA, 1982. [Google Scholar]
- Israelachvili, J. Thermodynamic and Geometric Aspects of Amphiphile Aggregation into Micelles, Vesicles, and Bilayers, and the Interaction Between Them. In Physics of Amphiphiles: Micelles, Vesicles and Microemulsions; Corso, Ed.; Società Italiana di Fisica: Bologna, Italy, 1985; pp. 24–58. [Google Scholar]
- Kunitake, T. Synthetic Bilayer Membranes: Molecular Design, Self-organization, and Application. Angew. Chem. Int. Ed. Engl. 1992, 104, 709–726. [Google Scholar] [CrossRef]
- Laughlin, R.G. The Aqueous Phase Behavior of Surfactants, 1st ed.; Academic Press: London, UK, 1996. [Google Scholar]
- Rideout, D.C.; Breslow, R. Hydrophobic acceleration of Diels-Alder reactions. J. Am. Chem. Soc. 1980, 102, 7816–7817. [Google Scholar] [CrossRef]
- Serrano-Luginbühl, S.; Ruiz-Mirazo, K.; Ostaszewski, R.; Gallou, F.; Walde, P. Soft and dispersed interface-rich aqueous systems that promote and guide chemical reactions. Nat. Rev. Chem. 2018, 2, 306–327. [Google Scholar] [CrossRef]
- Cortes-Clerget, M.; Yu, J.; Kincaid, J.R.A.; Walde, P.; Gallou, F.; Lipshutz, B.H. Water as the reaction medium in organic chemistry: From our worst enemy to our best friend. Chem. Sci. 2021, 12, 4237–4266. [Google Scholar] [CrossRef] [PubMed]
- Barhoum, S.; Palit, S.; Yethiraj, A. Diffusion NMR studies of macromolecular complex formation, crowding and confinement in soft materials. Prog. Nucl. Magn. Reson. Spectrosc. 2016, 94–95, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Yan, N.; Song, Y.; Zhu, Y. Confined self-assembly of block copolymers in emulsion droplets: Preparation, shape and internal structure, and applications. J. Polym. Sci. 2023, 61, 3211–3227. [Google Scholar] [CrossRef]
- Vendel, K.J.A.; Alkemade, C.; Andrea, N.; Koenderink, G.H.; Dogterom, M. In Vitro Reconstitution of Dynamic Co-organization of Microtubules and Actin Filaments in Emulsion Droplets. Methods Mol. Biol. 2020, 2101, 53–75. [Google Scholar] [CrossRef]
- Ma, M.-C.; Guo, Y.-L. Physical Properties of Polymers Under Soft and Hard Nanoconfinement: A Review. Chin. J. Polym. Sci. 2020, 38, 565–578. [Google Scholar] [CrossRef]
- Pagis, C.; Morgado Prates, A.R.; Farrusseng, D.; Bats, N.; Tuel, A. Hollow Zeolite Structures: An Overview of Synthesis Methods. Chem. Mater. 2016, 28, 5205–5223. [Google Scholar] [CrossRef]
- Meldrum, F.C.; O’Shaughnessy, C. Crystallization in Confinement. Adv. Mater. 2020, 32, 2001068. [Google Scholar] [CrossRef] [PubMed]
- Serrano, D.P.; Escola, J.M.; Pizarro, P. Synthesis strategies in the search for hierarchical zeolites. Chem. Soc. Rev. 2013, 42, 4004–4035. [Google Scholar] [CrossRef] [PubMed]
- Petkovich, N.D.; Stein, A. Controlling macro- and mesostructures with hierarchical porosity through combined hard and soft templating. Chem. Soc. Rev. 2013, 42, 3721–3739. [Google Scholar] [CrossRef]
- Hoffmann, M.M. Polyethylene glycol as a green chemical solvent. Curr. Opin. Colloid Interface Sci. 2022, 57, 101537. [Google Scholar] [CrossRef]
- Soni, J.; Sahiba, N.; Sethiya, A.; Agarwal, S. Polyethylene glycol: A promising approach for sustainable organic synthesis. J. Mol. Liq. 2020, 315, 113766. [Google Scholar] [CrossRef]
- Campos, J.F.; Berteina-Raboin, S. Greener synthesis of nitrogen-containing heterocycles in water, PEG, and bio-based solvents. Catalysts 2020, 10, 429. [Google Scholar] [CrossRef]
- Kardooni, R.; Kiasat, A.R. Polyethylene glycol as a green and biocompatible reaction media for the catalyst free synthesis of organic compounds. Curr. Org. Chem. 2020, 24, 1275–1314. [Google Scholar] [CrossRef]
- Kumari, B.; Brodrecht, M.; Breitzke, H.; Werner, M.; Grünberg, B.; Limbach, H.-H.; Forg, S.; Sanjon, E.P.; Drossel, B.; Gutmann, T.; et al. Mixtures of Alcohols and Water confined in Mesoporous Silica: A Combined Solid-State NMR and Molecular Dynamics Simulation Study. J. Phys. Chem. C 2018, 122, 19540–19550. [Google Scholar] [CrossRef]
- Vafaeezadeh, M.; Hashemi, M.M. Polyethylene glycol (PEG) as a green solvent for carbon–carbon bond formation reactions. J. Mol. Liq. 2015, 207, 73–79. [Google Scholar] [CrossRef]
- Carvalho, G.; Paul, E.; Novais, J.M.; Pinheiro, H.M. Studies on activated sludge response to variations in the composition of a synthetic surfactant-containing feed effluent. Water Sci. Technol. 2000, 42, 135–143. [Google Scholar] [CrossRef]
- Rother, G.; Müter, D.; Bock, H.; Schoen, M.; Findenegg, G. From aggregative adsorption to surface depletion: Aqueous systems of Cn Em amphiphiles at hydrophilic surfaces. Mol. Phys. 2017, 115, 1408–1416. [Google Scholar] [CrossRef]
- Müter, D.; Rother, G.; Bock, H.; Schoen, M.; Findenegg, G. Adsorption and Depletion Regimes of a Nonionic Surfactant in Hydrophilic Mesopores: An Experimental and Simulation Study. Langmuir 2017, 33, 11406–11416. [Google Scholar] [CrossRef]
- Dietsch, O.; Eltekov, A.; Bock, H.; Gubbins, K.E.; Findenegg, G. Crossover from Normal to Inverse Temperature Dependence in the Adsorption of Nonionic Surfactants at Hydrophilic Surfaces and Pore Walls. J. Phys. Chem. C 2007, 111, 16045–16054. [Google Scholar] [CrossRef]
- Ma, Y.; Wu, Y.; Lee, J.G.; He, L.; Rother, G.; Fameau, A.-L.; Shelton, W.A.; Bharti, B. Adsorption of Fatty Acid Molecules on Amine-Functionalized Silica Nanoparticles: Surface Organization and Foam Stability. Langmuir 2020, 36, 3703–3712. [Google Scholar] [CrossRef]
- Wu, Y.; Ma, Y.; He, L.; Rother, G.; Shelton, W.A.; Bharti, B. Directed Pore Uptake and Phase Separation of Surfactant Solutions under Confinement. J. Phys. Chem. C 2019, 123, 9957–9966. [Google Scholar] [CrossRef]
- Biffis, A.; Centomo, P.; Del Zotto, A.; Zecca, M. Pd Metal Catalysts for Cross-Couplings and Related Reactions in the 21st Century: A Critical Review. Chem. Rev. 2018, 118, 2249–2295. [Google Scholar] [CrossRef]
- Wall, V.M.; Eisenstadt, A.; Ager, D.J.; Laneman, S.A. The Heck Reaction and Cinnamic Acid Synthesis by Heterogeneous Catalysis. Platin. Met. Rev. 1999, 43, 138–145. [Google Scholar] [CrossRef]
- Paul, S.; Islam, M.M.; Islam, S.M. Suzuki–Miyaura reaction by heterogeneously supported Pd in water: Recent studies. RSC Adv. 2015, 5, 42193–42221. [Google Scholar] [CrossRef]
- Haro Mares, N.; Logrado, M.; Kergassner, J.; Zhang, B.; Gutmann, T.; Buntkowsky, G. Solid-State NMR of Heterogeneous Catalysts. ChemCatChem 2024, 16, e202401159. [Google Scholar] [CrossRef]
- Jana, S.; Dutta, B.; Bera, R.; Koner, S. Anchoring of copper complex in MCM-41 matrix: A highly efficient catalyst for epoxidation of olefins by tert-BuOOH. Langmuir 2007, 23, 2492–2496. [Google Scholar] [CrossRef] [PubMed]
- Vogt, C.G.; Grätz, S.; Lukin, S.; Halasz, I.; Etter, M.; Evans, J.D.; Borchardt, L. Direct Mechanocatalysis: Palladium as Milling Media and Catalyst in the Mechanochemical Suzuki Polymerization. Angew. Chem. Int. Ed. Engl. 2019, 58, 18942–18947. [Google Scholar] [CrossRef]
- Han, W.; Liu, C.; Jin, Z.-L. In situ generation of palladium nanoparticles: A simple and highly active protocol for oxygen-promoted ligand-free suzuki coupling reaction of aryl chlorides. Org. Lett. 2007, 9, 4005–4007. [Google Scholar] [CrossRef]
- Khanmoradi, M.; Nikoorazm, M.; Ghorbani-Choghamarani, A. Synthesis and Characterization of Pd Schiff Base Complex Immobilized onto Functionalized Nanoporous MCM-41 and its Catalytic Efficacy in the Suzuki, Heck and Stille Coupling Reactions. Catal. Lett. 2017, 147, 1114–1126. [Google Scholar] [CrossRef]
- Werner, M.; Rothermel, N.; Breitzke, H.; Gutmann, T.; Buntkowsky, G. Recent Advances in Solid State NMR of Small Molecules in Confinement. Isr. J. Chem. 2014, 54, 60–73. [Google Scholar] [CrossRef]
- Fumagalli, L.; Esfandiar, A.; Fabregas, R.; Hu, S.; Ares, P.; Janardanan, A.; Yang, Q.; Radha, B.; Taniguchi, T.; Watanabe, K.; et al. Anomalously low dielectric constant of confined water. Science 2018, 360, 1339–1342. [Google Scholar] [CrossRef]
- Haro Mares, N.; Döller, S.; Wissel, T.; Hoffmann, M.M.; Vogel, M.; Buntkowsky, G. Structures and Dynamics of Complex Guest Molecules in Confinement, Revealed by Solid-State NMR, Molecular Dynamics, and Calorimetry. Molecules 2024, 29, 1669. [Google Scholar] [CrossRef] [PubMed]
- Buntkowsky, G.; Vogel, M. Small Molecules, Non-Covalent Interactions, and Confinement. Molecules 2020, 25, 3311. [Google Scholar] [CrossRef] [PubMed]
- Becher, M.; Lichtinger, A.; Minikejew, R.; Vogel, M.; Roessler, E. NMR Relaxometry Accessing the Relaxation Spectrum in Molecular Glass Formers. Int. J. Mol. Sci. 2022, 23, 5118. [Google Scholar] [CrossRef]
- Horstmann, R.; Hecht, L.; Kloth, S.; Vogel, M. Structural and Dynamical Properties of Liquids in Confinements: A Review of Molecular Dynamics Simulation Studies. Langmuir 2022, 38, 6506–6522. [Google Scholar] [CrossRef] [PubMed]
- Buntkowsky, G.; Vogel, M.; Winter, R. Properties of Hydrogen-Bonded Liquids at Interfaces. Z. Phys. Chem. 2018, 232, 937–972. [Google Scholar] [CrossRef]
- Gutmann, T.; Groszewicz, P.B.; Buntkowsky, G. Solid-state NMR of nanocrystals. In Annual Reports on NMR Spectroscopy; Elsevier: Amsterdam, The Netherlands, 2019; Volume 97, pp. 1–82. ISBN 9780081028582. [Google Scholar]
- Gutmann, T.; Grünberg, A.; Rothermel, N.; Werner, M.; Srour, M.; Abdulhussain, S.; Tan, S.L.; Xu, Y.; Breitzke, H.; Buntkowsky, G. Solid-state NMR concepts for the investigation of supported transition metal catalysts and nanoparticles. Solid State Nucl. Mag. 2013, 55–56, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Haouas, M.; Martineau, C.; Taulelle, F. Quadrupolar NMR of Nanoporous Materials. In NMR of Quadrupolar Nuclei in Solid Materials; eMagRes; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Gołowicz, D.; Kasprzak, P.; Orekhov, V.; Kazimierczuk, K. Fast time-resolved NMR with non-uniform sampling. Prog. NMR Spec. 2020, 116, 40–55. [Google Scholar] [CrossRef]
- Araki, H.; Brézin, E.; Ehlers, J.; Frisch, U.; Hepp, K.; Jaffe, R.L.; Kippenhahn, R.; Weidenmüller, H.A.; Wess, J.; Zittartz, J.; et al. Computer Simulation of Condensed Phases in Complex Geometries; Springer: Berlin/Heidelberg, Germany, 1993; ISBN 978-3-540-56564-2. [Google Scholar]
- Rapaport, D.C. The Art of Molecular Dynamics Simulation; Cambridge University Press: Cambridge, UK, 2011; ISBN 9780521825689. [Google Scholar]
- Andrew, E.R.; Bradbury, A.; Eades, R.G. NMR Spectra from a Crystal rotated at High Speed. Nature 1958, 182, 1659. [Google Scholar] [CrossRef]
- Lowe, I.J. Free Induction Decay in Rotating Solids. Phys. Rev. Lett. 1959, 2, 285–287. [Google Scholar] [CrossRef]
- Schaefer, J.; Stejskal, E.O. 13C NMR of Polymers Spinning at the Magic Angle. J. Am. Chem. Soc. 1976, 98, 1031–1032. [Google Scholar] [CrossRef]
- Schaefer, J.; Stejskal, E.O.; Buchdahl, R. High-Resolution Carbon-13 Nuclear Magnetic Resonance Study of Some Solid, Glassy Polymers. Macromolecules 1975, 8, 291–296. [Google Scholar] [CrossRef]
- Bennett, A.E.; Griffin, R.G.; Vega, S. Recoupling of Homo- and Heteronuclear Dipolar Interactions in Rotation Solids. In Solid-State NMR IV Methods and Applications of Solid-State NMR; Springer Series in NMR; Springer: Berlin/Heidelberg, Germany, 1994; Volume 33, pp. 1–77. [Google Scholar]
- Gullion, T.; Schaefer, J. Rotational Echo Double Resonance NMR. J. Magn. Reson. 1989, 81, 196–200. [Google Scholar] [CrossRef]
- Gullion, T.; Schaefer, J. Detection of Weak Heteronuclear Dipolar Coupling by Rotational Echo Double Resonance Nuclear Magnetic Resonance. Adv. Magn. Opt. Reson. 1989, 13, 57–83. [Google Scholar]
- Bax, A.; Szeverenyi, N.M.; Maciel, G.E. Chemical Shift Anisotropy in Powders Studied by 2D FT NMR with Flipping of Spinning Axis. J. Magn. Reson. 1983, 55, 494–497. [Google Scholar]
- Becerra, L.R.; Gerfen, G.J.; Temkin, R.J.; Singel, D.J.; Griffin, R.G. Dynamic Nuclear Polarization with a Cyclotron Resonance Maser at 5 T. Phys. Rev. Lett. 1993, 71, 3561–3564. [Google Scholar] [CrossRef]
- Maly, T.; Debelouchina, G.T.; Bajaj, V.S.; Hu, K.; Joo, C.; Mak-Jurkauskas, M.L.; Sirigiri, J.R.; van der Wel, P.; Herzfeld, J.; Temkin, R.J.; et al. Dynamic Nuclear Polarization at High Magnetic Fields. J. Chem. Phys. 2008, 128, 52211. [Google Scholar] [CrossRef]
- Thankamony, A.S.L.; Wittmann, J.J.; Kaushik, M.; Corzilius, B. Dynamic nuclear polarization for sensitivity enhancement in modern solid-state NMR. Prog. Nucl. Magn. Reson. Spectrosc. 2017, 102, 120–195. [Google Scholar] [CrossRef]
- Harrach, M.F.; Drossel, B.; Winschel, W.; Gutmann, T.; Buntkowsky, G. Mixtures of Isobutyric Acid and Water Confined in Cylindrical Silica Nanopores Revisited: A Combined Solid-State NMR and Molecular Dynamics Simulation Study. J. Phys. Chem. C 2015, 119, 28961–28969. [Google Scholar] [CrossRef]
- Buntkowsky, G.; Döller, S.; Haro Mares, N.; Gutmann, T.; Hoffmann, M.M. Solid-state NMR studies of non-ionic surfactants confined in mesoporous silica. Z. Phys. Chem. 2022, 236, 939–960. [Google Scholar] [CrossRef]
- Sun, Y.; Xu, C.; Li, Y. Intrusion of polyethylene glycol into solid-state nanopores. RSC Adv. 2018, 8, 9070–9073. [Google Scholar] [CrossRef] [PubMed]
- Grefe, A.-K.; Kuttich, B.; Stühn, L.; Stark, R.; Stühn, B. Oriented crystallization of PEG induced by confinement in cylindrical nanopores: Structural and thermal properties. Soft Matter 2019, 15, 3149–3159. [Google Scholar] [CrossRef]
- Guo, X.-Y.; Watermann, T.; Sebastiani, D. Local Microphase Separation of a Binary Liquid under Nanoscale Confinement. J. Phys. Chem. B 2014, 118, 10207–10213. [Google Scholar] [CrossRef]
- Hermens, J.L.; de Bruijn, J.H.; Brooke, D.N. The octanol–water partition coefficient: Strengths and limitations. Environ. Toxicol. Chem. 2013, 32, 732–733. [Google Scholar] [CrossRef]
- Leo, A.; Hansch, C.; Elkins, D. Partition coefficients and their uses. Chem. Rev. 1971, 71, 525–616. [Google Scholar] [CrossRef]
- Kumari, B.; Brodrecht, M.; Gutmann, T.; Breitzke, H.; Buntkowsky, G. Efficient Referencing of FSLG CPMAS HETCOR Spectra Using 2D H-1-H-1 MAS FSLG. Appl. Magn. Reson. 2019, 50, 1399–1407. [Google Scholar] [CrossRef]
- Döller, S.; Brodrecht, M.; Haro Mares, N.; Breitzke, H.; Gutmann, T.; Hoffmann, M.M.; Buntkowsky, G. Deuterium NMR Studies of the Solid–Liquid Phase Transition of Octanol- d17 Confined in SBA-15. J. Phys. Chem. C 2021, 125, 25155–25164. [Google Scholar] [CrossRef]
- Grünberg, B.; Emmler, T.; Gedat, E.; Shenderovich, I.; Findenegg, G.H.; Limbach, H.H.; Buntkowsky, G. Hydrogen bonding of water confined in mesoporous silica MCM-41 and SBA-15 studied by H-1 solid-state NMR. Chem. Eur. J. 2004, 10, 5689–5696. [Google Scholar] [CrossRef]
- Weigler, M.; Brodrecht, M.; Breitzke, H.; Dietrich, F.; Sattig, M.; Buntkowsky, G.; Vogel, M. 2H NMR studies on water dynamics in functionalized mesoporous silica. Z. Phys. Chem. 2018, 232, 1041–1058. [Google Scholar] [CrossRef]
- Weigler, M.; Winter, E.; Kresse, B.; Brodrecht, M.; Buntkowsky, G.; Vogel, M. Static field gradient NMR studies of water diffusion in mesoporous silica. Phys. Chem. Chem. Phys. 2020, 22, 13989–13998. [Google Scholar] [CrossRef] [PubMed]
- Steinrücken, E.; Wissel, T.; Brodrecht, M.; Breitzke, H.; Regentin, J.; Buntkowsky, G.; Vogel, M. 2H NMR study on temperature-dependent water dynamics in amino-acid functionalized silica nanopores. J. Chem. Phys. 2021, 154, 114702. [Google Scholar] [CrossRef]
- Weigler, M.; Brodrecht, M.; Buntkowsky, G.; Vogel, M. Reorientation of Deeply Cooled Water in Mesoporous Silica: NMR Studies of the Pore-Size Dependence. J. Phys. Chem. B 2019, 123, 2123–2134. [Google Scholar] [CrossRef] [PubMed]
- Gedat, E.; Schreiber, A.; Albrecht, J.; Shenderovich, I.; Findenegg, G.; Limbach, H.-H.; Buntkowsky, G. 2H- Solid State NMR Study of Benzene-d6 confined in mesoporous Silica SBA-15. J. Phys. Chem. B 2002, 106, 1977. [Google Scholar] [CrossRef]
- Masierak, W.; Emmler, T.; Gedat, E.; Schreiber, A.; Findenegg, G.; Buntkowsky, G. Microcrystallization of Benzene- d6 in Mesoporous Silica Revealed by 2 H Solid-State Nuclear Magnetic Resonance. J. Phys. Chem. B 2004, 108, 18890–18896. [Google Scholar] [CrossRef]
- Haro Mares, N.; Brodrecht, M.; Wissel, T.; Döller, S.; Rösler, L.; Breitzke, H.; Hoffmann, M.M.; Gutmann, T.; Buntkowsky, G. Influence of APTES-Decorated Mesoporous Silica on the Dynamics of Ethylene Glycol Molecules–Insights from Variable Temperature 2 H Solid-State NMR. J. Phys. Chem. C 2023, 127, 19735–19746. [Google Scholar] [CrossRef]
- Reuhl, M.; Weigler, M.; Brodrecht, M.; Buntkowsky, G.; Vogel, M. Nuclear Magnetic Resonance and Broadband Dielectric Spectroscopy Studies on the Dynamics of Ethylene Glycol in Mesoporous Silica. J. Phys. Chem. C 2020, 124, 20998–21012. [Google Scholar] [CrossRef]
- Vyalikh, A.; Emmler, T.; Gedat, E.; Shenderovich, I.; Findenegg, G.; Limbach, H.-H.; Buntkowsky, G. Evidence of microphase separation in controlled pore glasses. Solid State Nucl. Mag. 2005, 28, 117–124. [Google Scholar] [CrossRef] [PubMed]
- Buntkowsky, G.; Breitzke, H.; Adamczyk, A.; Roelofs, F.; Emmler, T.; Gedat, E.; Grünberg, B.; Xu, Y.; Limbach, H.-H.; Shenderovich, I.; et al. Structural and Dynamical Properties of Guest Molecules confined in mesoporous Silica Materials revealed by NMR. Phys. Chem. Chem. Phys. 2007, 9, 4843–4853. [Google Scholar] [CrossRef]
- Vyalikh, A.; Emmler, T.; Shenderovich, I.; Zeng, Y.; Findenegg, G.; Buntkowsky, G. 2H-solid state NMR and DSC study of isobutyric acid in mesoporous silica materials. Phys. Chem. Chem. Phys. 2007, 9, 2249–2257. [Google Scholar] [CrossRef]
- Hoffmann, M.M.; Bothe, S.; Brodrecht, M.; Klimavičius, V.; Haro Mares, N.; Gutmann, T.; Buntkowsky, G. Direct and Indirect Dynamic Nuclear Polarization Transfer Observed in Mesoporous Materials Impregnated with Nonionic Surfactant Solutions of Polar Polarizing Agents. J. Phys. Chem. C 2020, 124, 5145–5156. [Google Scholar] [CrossRef]
- Lesage, A.; Lelli, M.; Gajan, D.; Caporini, M.A.; Vitzthum, V.; Mieville, P.; Alauzun, J.; Roussey, A.; Thieuleux, C.; Mehdi, A.; et al. Surface Enhanced NMR Spectroscopy by Dynamic Nuclear Polarization. J. Am. Chem. Soc. 2010, 132, 15459–15461. [Google Scholar] [CrossRef] [PubMed]
- Lelli, M.; Gajan, D.; Lesage, A.; Caporini, M.A.; Vitzthum, V.; Mieville, P.; Heroguel, F.; Rascon, F.; Roussey, A.; Thieuleux, C.; et al. Fast Characterization of Functionalized Silica Materials by Silicon-29 Surface-Enhanced NMR Spectroscopy Using Dynamic Nuclear Polarization. J. Am. Chem. Soc. 2011, 133, 2104–2107. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, M.M.; Bothe, S.; Gutmann, T.; Buntkowsky, G. Combining Freezing Point Depression and Self-Diffusion Data for Characterizing Aggregation. J. Phys. Chem. B 2018, 122, 4913–4921. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, M.M.; Too, M.D.; Vogel, M.; Gutmann, T.; Buntkowsky, G. Breakdown of the Stokes-Einstein Equation for Solutions of Water in Oil Reverse Micelles. J. Phys. Chem. B 2020, 124, 9115–9125. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, M.M.; Horowitz, R.H.; Gutmann, T.; Buntkowsky, G. Densities, Viscosities, and Self-Diffusion Coefficients of Ethylene Glycol Oligomers. J. Chem. Eng. Data 2021, 66, 2480–2500. [Google Scholar] [CrossRef]
- Hoffmann, M.M.; Bothe, S.; Gutmann, T.; Hartmann, F.-F.; Reggelin, M.; Buntkowsky, G. Directly vs Indirectly Enhanced 13 C in Dynamic Nuclear Polarization Magic Angle Spinning NMR Experiments of Nonionic Surfactant Systems. J. Phys. Chem. C 2017, 121, 2418–2427. [Google Scholar] [CrossRef]
- Daube, D.; Aladin, V.; Heiliger, J.; Wittmann, J.J.; Barthelmes, D.; Bengs, C.; Schwalbe, H.; Corzilius, B. Heteronuclear Cross-Relaxation under Solid-State Dynamic Nuclear Polarization. J. Am. Chem. Soc. 2016, 138, 16572–16575. [Google Scholar] [CrossRef]
- Bothe, S.; Hoffmann, M.M.; Gutmann, T.; Buntkowsky, G. Comparative Study of the Magnetic Field Dependent Signal Enhancement in Solid-State Dynamic Nuclear Polarization Experiments. J. Phys. Chem. C 2017, 121, 27089–27097. [Google Scholar] [CrossRef]
- Hoffmann, M.M.; Bothe, S.; Gutmann, T.; Buntkowsky, G. Unusual Local Molecular Motions in the Solid State Detected by Dynamic Nuclear Polarization Enhanced NMR Spectroscopy. J. Phys. Chem. C 2017, 121, 22948–22957. [Google Scholar] [CrossRef]
- Döller, S.; Gutmann, T.; Hoffmann, M.M.; Buntkowsky, G. A case study on the influence of hydrophilicity on the signal enhancement by dynamic nuclear polarization. Solid State Nucl. Mag. 2022, 122, 101829. [Google Scholar] [CrossRef]
- Döller, S.; Brodrecht, M.; Gutmann, T.; Hoffmann, M.M.; Buntkowsky, G. Direct and Indirect DNP NMR Uncovers the Interplay of Surfactants with Their Mesoporous Host Material. J. Phys. Chem. C 2023, 127, 12125–12134. [Google Scholar] [CrossRef]
- Tarek, M.; Bandyopadhyay, S.; Klein, M.L. Molecular dynamics studies of aqueous surfactants systems. J. Mol. Liq. 1998, 78, 1–6. [Google Scholar] [CrossRef]
- Bandyopadhyay, S.; Tarek, M.; Klein, M.L. Computer simulation studies of amphiphilic interfaces. Curr. Opin. Colloid Interface Sci. 1998, 3, 242–246. [Google Scholar] [CrossRef]
- Guruge, A.G.; Warren, D.B.; Pouton, C.W.; Chalmers, D.K. Molecular Dynamics Simulation Studies of Bile, Bile Salts, Lipid-Based Drug Formulations, and mRNA-Lipid Nanoparticles: A Review. Mol. Pharm. 2023, 20, 2781–2800. [Google Scholar] [CrossRef]
- Kepczynski, M.; Rog, T. Functionalized lipids and surfactants for specific applications. Biochim. Biophys. Acta Biomembr. 2016, 1858, 2362–2379. [Google Scholar] [CrossRef] [PubMed]
- Ganesan, V.; Priya, M.H. Revealing the Key Packing Features Determining the Stability of Peptide Bilayer Membrane. ACS Appl. Bio Mater. 2024, 7, 564–578. [Google Scholar] [CrossRef] [PubMed]
- Sharma, V.K.; Mitra, S.; Mukhopadhyay, R. Dynamic Landscape in Self-Assembled Surfactant Aggregates. Langmuir 2019, 35, 14151–14172. [Google Scholar] [CrossRef]
- Ahmadi, M.; Aliabadian, E.; Liu, B.; Lei, X.; Khalilpoorkordi, P.; Hou, Q.; Wang, Y.; Chen, Z. Comprehensive review of the interfacial behavior of water/oil/surfactant systems using dissipative particle dynamics simulation. Adv. Colloid Interface Sci. 2022, 309, 102774. [Google Scholar] [CrossRef] [PubMed]
- Padding, J.T.; Briels, W.J.; Stukan, M.R.; Boek, E.S. Review of multi-scale particulate simulation of the rheology of wormlike micellar fluids. Soft Matter 2009, 5, 4367–4375. [Google Scholar] [CrossRef]
- Tsianou, M.; Bedrov, D.; Alexandridis, P. Surfactants in the Environment: Self-Assembly of PFAS Pollutants in Solution and at Interfaces. ACS Symp. Ser. 2023, 1457, 443–462. [Google Scholar] [CrossRef]
- McHedlov-Petrossyan, N.O.; Farafonov, V.S.; Lebed, A.V. Solvatochromic and Acid-Base Molecular Probes in Surfactant Micelles: Comparison of Molecular Dynamics Simulation with the Experiment. Liquids 2023, 3, 314–370. [Google Scholar] [CrossRef]
- Iscen, A.; Schatz, G.C. Peptide amphiphile self-assembly. EPL 2017, 119, 38002/1. [Google Scholar] [CrossRef]
- Jusufi, A. Molecular simulations of self-assembly processes of amphiphiles in dilute solutions: The challenge for quantitative modelling. Mol. Phys. 2013, 111, 3182–3192. [Google Scholar] [CrossRef]
- Dhasaiyan, P.; Prasad, B.L.V. Self-Assembly of Bolaamphiphilic Molecules. Chem. Rec. 2017, 17, 597–610. [Google Scholar] [CrossRef] [PubMed]
- Ivanova, A.A.; Koltsov, I.N.; Groman, A.A.; Cheremisin, A.N. Molecular Dynamics Simulations for Surfactant Research (A Review). Pet. Chem. 2023, 63, 867–885. [Google Scholar] [CrossRef]
- Ranatunga, R.J.K.U.; Nguyen, C.T.; Chiu, C.; Shinoda, W.; Nielsen, S.O. Molecular dynamics simulations of nanoparticles and surfactants at oil/water interfaces. A qualitative overview. ACS Symp. Ser. 2011, 1070, 294–314. [Google Scholar] [CrossRef]
- Liang, S.; Luo, W.; Luo, Z.; Wang, W.; Xue, X.; Dong, B. Research of CO2-Soluble Surfactants for Enhanced Oil Recovery: Review and Outlook. Molecules 2023, 28, 8042. [Google Scholar] [CrossRef]
- Sohrabi, B.; Poorsargol, M.; Ingram, S.; Roudsari, G. Surfactants-emerging amphiphiles in liquid phase exfoliation method for dispersing carbon nanotubes and graphene: Experimental and molecular dynamics simulation studies. J. Mol. Liq. 2024, 409, 125493. [Google Scholar] [CrossRef]
- Ghoufi, A.; Emile, J.; Malfreyt, P. Recent advances in Many Body Dissipative Particles Dynamics simulations of liquid-vapor interfaces. Eur. Phys. J. E Soft Matter Biol. Phys. 2013, 36, 10. [Google Scholar] [CrossRef]
- Lekhlifi, A.; Antoni, M. Simulation of interfacial properties and droplet hydrodynamics. Prog. Colloid Interface Sci. 2014, 4, 221–253. [Google Scholar]
- Braun, E.; Gilmer, J.; Mayes, H.B.; Mobley, D.L.; Monroe, J.I.; Prasad, S.; Zuckerman, D.M. Best Practices for Foundations in Molecular Simulations [Article v1.0]. Living J. Comput. Mol. Sci. 2019, 1, 5957. [Google Scholar] [CrossRef]
- Lemkul, J. From Proteins to Perturbed Hamiltonians: A Suite of Tutorials for the GROMACS-2018 Molecular Simulation Package [Article v1.0]. Living J. Comput. Mol. Sci. 2019, 1, 5068. [Google Scholar] [CrossRef]
- Jämbeck, J.P.M.; Lyubartsev, A.P. Update to the General Amber Force Field for Small Solutes with an Emphasis on Free Energies of Hydration. J. Phys. Chem. B 2014, 118, 3793–3804. [Google Scholar] [CrossRef]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general amber force field. J. Comp. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Soteras Gutiérrez, I.; Lin, F.-Y.; Vanommeslaeghe, K.; Lemkul, J.; Armacost, K.A.; Brooks, C.L.; MacKerell, A.D. Parametrization of halogen bonds in the CHARMM general force field: Improved treatment of ligand–protein interactions. Bioorg. Med. Chem. 2016, 24, 4812–4825. [Google Scholar] [CrossRef] [PubMed]
- Vanommeslaeghe, K.; Hatcher, E.; Acharya, C.; Kundu, S.; Zhong, S.; Shim, J.; Darian, E.; Guvench, O.; Lopes, P.; Vorobyov, I.; et al. CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J. Comp. Chem. 2010, 31, 671–690. [Google Scholar] [CrossRef]
- Horta, B.A.; Merz, P.T.; Fuchs, P.F.; Dolenc, J.; Riniker, S.; Hunenberger, P.H. A GROMOS-Compatible Force Field for Small Organic Molecules in the Condensed Phase: The 2016H66 Parameter Set. J. Chem. Theory Comput. 2016, 12, 3825–3850. [Google Scholar] [CrossRef]
- Paquet, E.; Viktor, H.L. Computational Methods for Ab Initio Molecular Dynamics. Adv. Chem. 2018, 2018, 1–14. [Google Scholar] [CrossRef]
- Serva, A.; Pezzotti, S.; Bougueroua, S.; Galimberti, D.R.; Gaigeot, M. Combining ab-initio and classical molecular dynamics simulations to unravel the structure of the 2D-HB-network at the air-water interface. J. Mol. Struct. 2018, 1165, 71–78. [Google Scholar] [CrossRef]
- Li, P.; Rangadurai, A.; Al-Hashimi, H.; Hammes-Schiffer, S. Environmental Effects on Guanine-Thymine Mispair Tautomerization Explored with Quantum Mechanical/Molecular Mechanical Free Energy Simulations. J. Am. Chem. Soc. 2020, 142, 11183–11191. [Google Scholar] [CrossRef] [PubMed]
- Grunewald, F.; Rossi, G.; de Vries, A.H.; Marrink, S.J.; Monticelli, L. Transferable MARTINI Model of Poly(ethylene Oxide). J. Phys. Chem. B 2018, 122, 7436–7449. [Google Scholar] [CrossRef]
- Dodda, L.S.; Cabeza de Vaca, I.; Tirado-Rives, J.; Jorgensen, W.L. LigParGen web server: An automatic OPLS-AA parameter generator for organic ligands. Nucleic Acids Res. 2017, 45, W331–W336. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, M.M.; Kealy, J.D.; Gutmann, T.; Buntkowsky, G. Densities, viscosities, and self-diffusion coefficients of several polyethylene glycols. J. Chem. Eng. Data 2021, 67, 88–103. [Google Scholar] [CrossRef]
- Hoffmann, M.M.; Too, M.D.; Paddock, N.A.; Horstmann, R.; Kloth, S.; Vogel, M.; Buntkowsky, G. On the Behavior of the Ethylene Glycol Components of Polydisperse Polyethylene Glycol PEG200. J. Phys. Chem. B 2023, 127, 1178–1196. [Google Scholar] [CrossRef] [PubMed]
- Yeh, I.-C.; Hummer, G. System-Size Dependence of Diffusion Coefficients and Viscosities from Molecular Dynamics Simulations with Periodic Boundary Conditions. J. Phys. Chem. B 2004, 108, 15873–15879. [Google Scholar] [CrossRef]
- Maginn, E.J.; Messerly, R.A.; Carlson, D.J.; Roe, D.R.; Elliott, J.R. Best Practices for Computing Transport Properties 1. Self-Diffusivity and Viscosity from Equilibrium Molecular Dynamics [Article v1.0]. Living J. Comput. Mol. Sci. 2019, 1, 6324. [Google Scholar] [CrossRef]
- Caleman, C.; van Maaren, P.J.; Hong, M.; Hub, J.S.; Costa, L.T.; van der Spoel, D. Force Field Benchmark of Organic Liquids: Density, Enthalpy of Vaporization, Heat Capacities, Surface Tension, Isothermal Compressibility, Volumetric Expansion Coefficient, and Dielectric Constant. J. Chem. Theory Comput. 2012, 8, 61–74. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, M.M.; Gonzalez, A.A.; Huynh, M.T.; Miller, K.K.; Gutmann, T.; Buntkowsky, G. Densities, Viscosities, and Self-Diffusion Coefficients of Octan-1-ol and Related Ether-Alcohols. J. Chem. Eng. Data 2024, 69, 2688–2699. [Google Scholar] [CrossRef]
- Hoffmann, M.M.; Gutmann, T.; Buntkowsky, G. Thermal Behavior of n-Octanol and Related Ether Alcohols. J. Chem. Eng. Data, 2024; accepted. [Google Scholar] [CrossRef]
- Hoffmann, M.M.; Too, M.D.; Paddock, N.A.; Horstmann, R.; Kloth, S.; Vogel, M.; Buntkowsky, G. Molecular Dynamics Study of the Green Solvent Polyethylene Glycol with Water Impurities. Molecules 2024, 29, 2070. [Google Scholar] [CrossRef]
- Ahmadi, M.; Chen, Z. Molecular dynamics simulation of oil detachment from hydrophobic quartz surfaces during steam-surfactant Co-injection. Energy 2022, 254, 124434. [Google Scholar] [CrossRef]
- Pu, W.; Wu, T.; Zhao, J.; Gao, H.; He, M.; He, Y.; Chen, Y.; Zhu, Y. Nano-structure of hydrolyzed polyacrylamide strengthened ultra stable nitrogen foam: Lab experiments and molecular dynamics simulation. J. Mol. Liq. 2024, 396, 124103. [Google Scholar] [CrossRef]
- Ranjkesh Rashteh Roudi, M.; Hosseini, A.; Ranjkesh, M.; Pan, Z.; Habibnejad Korayem, A. Dispersion Stability and the Reaction Mechanism of Boron Nitride Nanosheets in a Cementitious Alkaline Environment: An Experimental and Computational Study. ACS Appl. Nano Mater. 2024, 7, 12592–12604. [Google Scholar] [CrossRef]
- Zhang, K.; Zhou, G.; Fang, T.; Tang, X.; Liu, X. Surface-active ionic liquids near the electrode surface: Development and influence on molecular dynamics simulations. Appl. Surf. Sci. 2023, 614, 156200. [Google Scholar] [CrossRef]
- Zhang, M.; Bradford, S.A.; Klumpp, E.; Simunek, J.; Jin, C.; Qiu, R. Non-monotonic contribution of nonionic surfactant on the retention of functionalized multi-walled carbon nanotubes in porous media. J. Hazard. Mater. 2021, 407, 124874. [Google Scholar] [CrossRef]
- Simmons, B.A.; Irvin, G.C.; Agarwal, V.; Bose, A.; John, V.T.; McPherson, G.L.; Balsara, N.P. Small Angle Neutron Scattering Study of Microstructural Transitions in a Surfactant-Based Gel Mesophase. Langmuir 2002, 18, 624–632. [Google Scholar] [CrossRef]
- Angelikopoulos, P.; Bock, H. Directed Self-Assembly of Surfactants in Carbon Nanotube Materials. J. Phys. Chem. B 2008, 112, 13793–13801. [Google Scholar] [CrossRef]
- Bharti, B.; Meissner, J.; Gasser, U.; Findenegg, G. Surfactant adsorption and aggregate structure at silica nanoparticles: Effects of particle size and surface modification. Soft Matter 2012, 8, 6573. [Google Scholar] [CrossRef]
- Bharti, B.; Xue, M.; Meissner, J.; Cristiglio, V.; Findenegg, G. Assembling Wormlike Micelles in Tubular Nanopores by Tuning Surfactant–Wall Interactions. J. Am. Chem. Soc. 2012, 134, 14756–14759. [Google Scholar] [CrossRef]
- Lugo, D.; Oberdisse, J.; Karg, M.; Schweins, R.; Findenegg, G. Surface aggregate structure of nonionic surfactants on silica nanoparticles. Soft Matter 2009, 5, 2928. [Google Scholar] [CrossRef]
- Müter, D.; Angelikopoulos, P.; Bock, H. Angular Dependence of Surfactant-Mediated Forces Between Carbon Nanotubes. J. Phys. Chem. B 2012, 116, 14869–14875. [Google Scholar] [CrossRef] [PubMed]
- Müter, D.; Widmann, M.A.; Bock, H. Surfactant Self-Assembly in Cylindrical Pores: Insights from Mesoscale Simulations. J. Phys. Chem. Lett. 2013, 4, 2153–2157. [Google Scholar] [CrossRef]
- Shin, T.G.; Müter, D.; Meissner, J.; Paris, O.; Findenegg, G. Structural Characterization of Surfactant Aggregates Adsorbed in Cylindrical Silica Nanopores. Langmuir 2011, 27, 5252–5263. [Google Scholar] [CrossRef] [PubMed]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buntkowsky, G.; Hoffmann, M. NMR and MD Simulations of Non-Ionic Surfactants. Molecules 2025, 30, 309. https://doi.org/10.3390/molecules30020309
Buntkowsky G, Hoffmann M. NMR and MD Simulations of Non-Ionic Surfactants. Molecules. 2025; 30(2):309. https://doi.org/10.3390/molecules30020309
Chicago/Turabian StyleBuntkowsky, Gerd, and Markus Hoffmann. 2025. "NMR and MD Simulations of Non-Ionic Surfactants" Molecules 30, no. 2: 309. https://doi.org/10.3390/molecules30020309
APA StyleBuntkowsky, G., & Hoffmann, M. (2025). NMR and MD Simulations of Non-Ionic Surfactants. Molecules, 30(2), 309. https://doi.org/10.3390/molecules30020309








