Two Coupled Low-Barrier Large Amplitude Motions in 3,5-Dimethylanisole Studied by Microwave Spectroscopy
Abstract
1. Introduction
2. Quantum Chemical Calculations
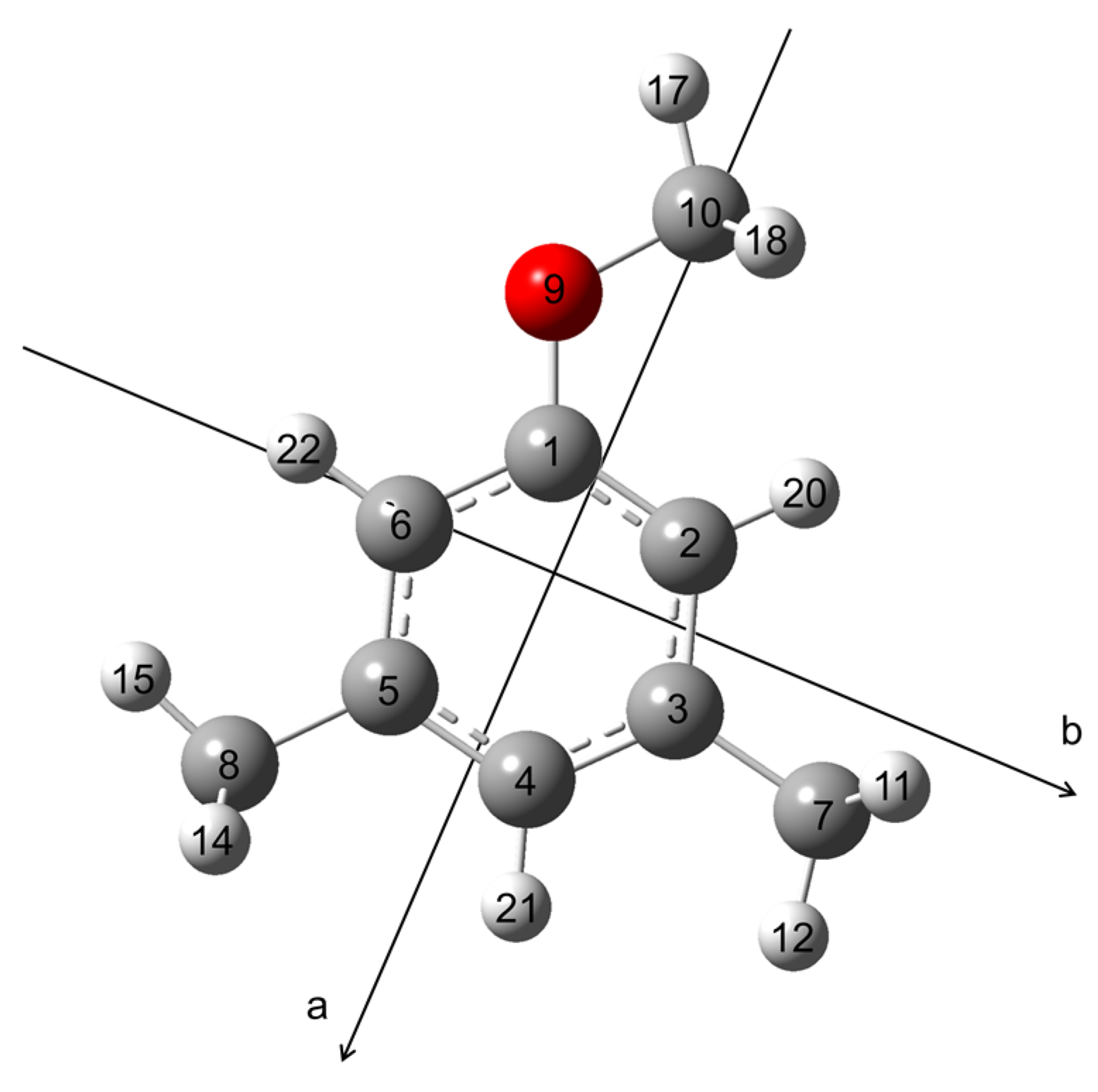
2.1. Conformational Analysis
2.2. Basis Set Variation
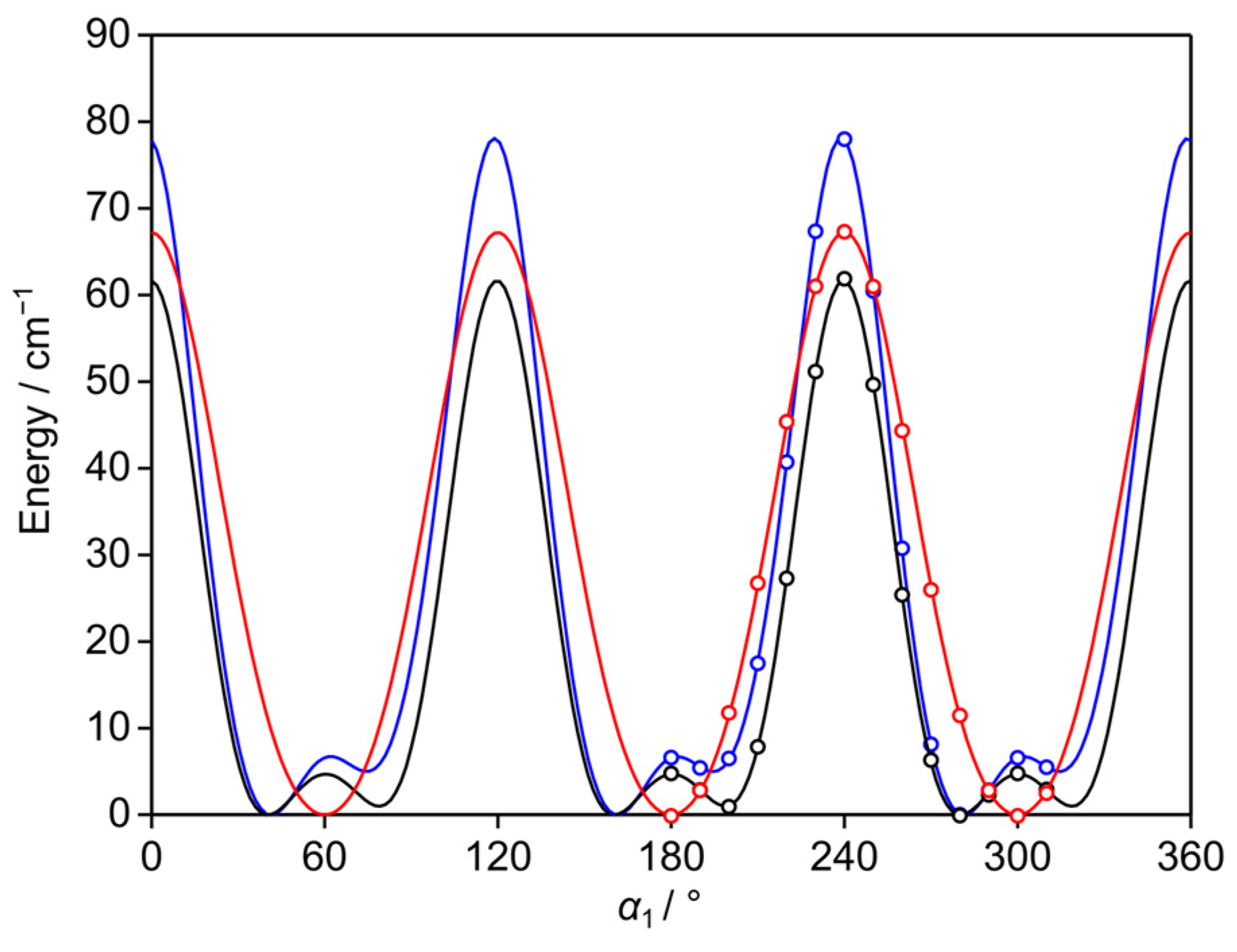
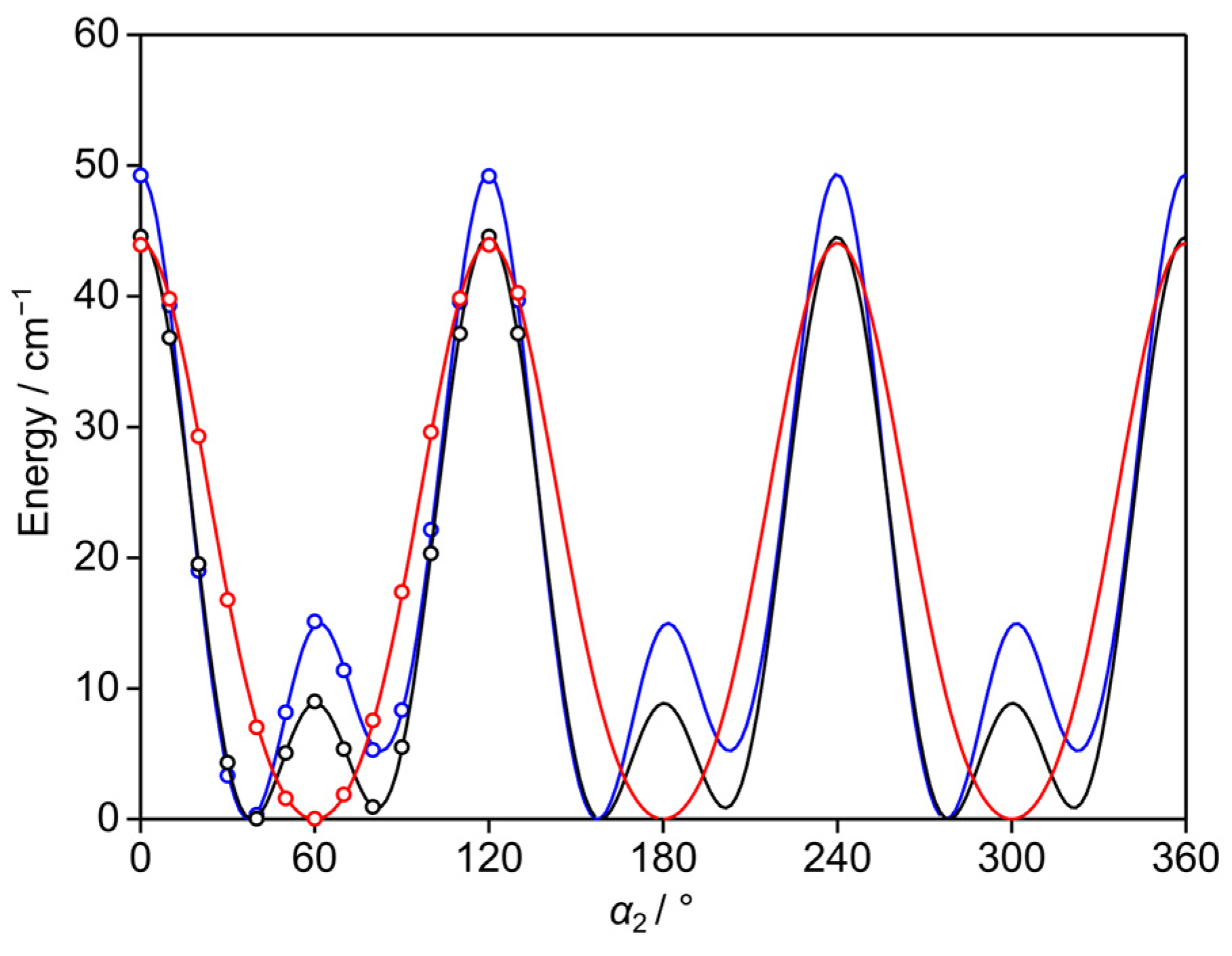
2.3. Methyl Internal Rotations
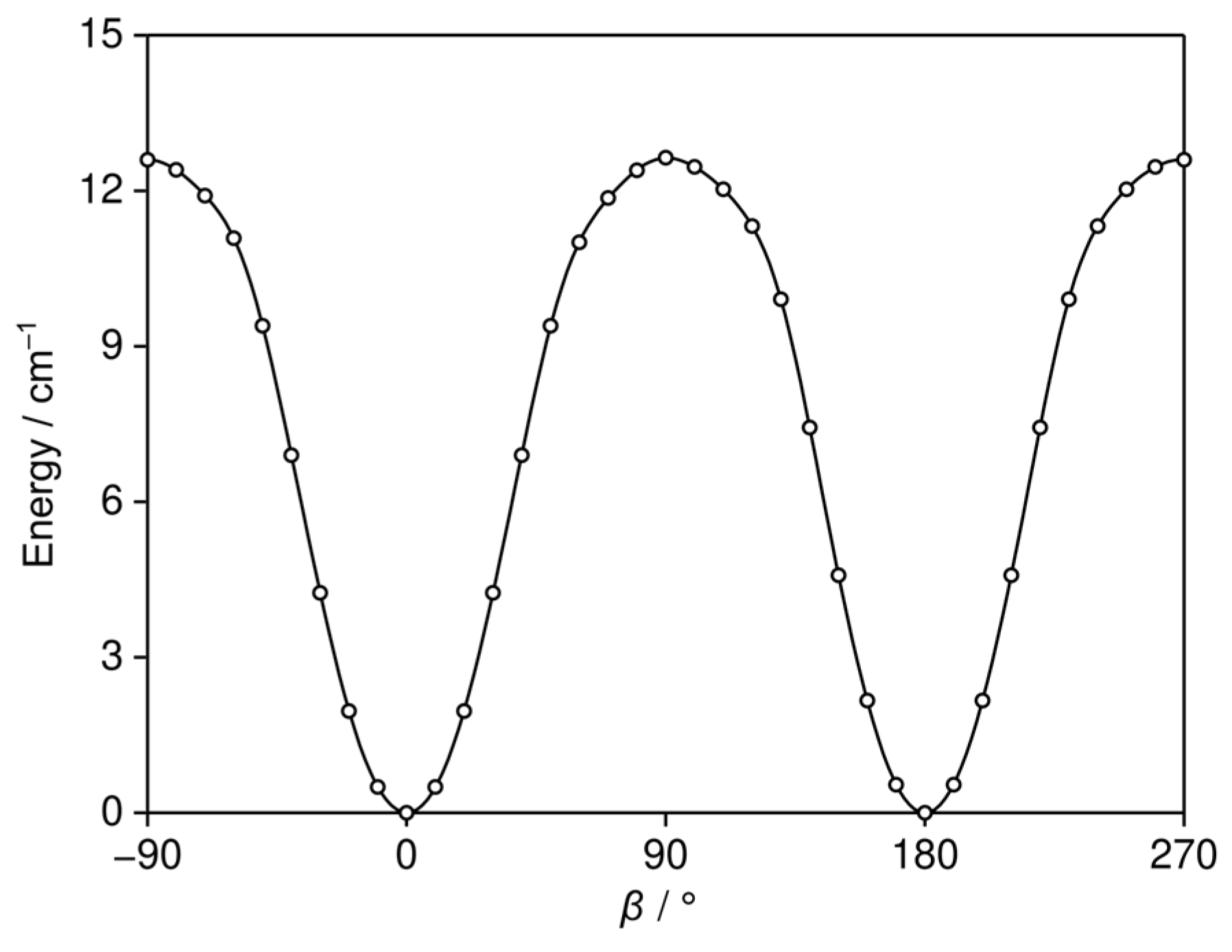
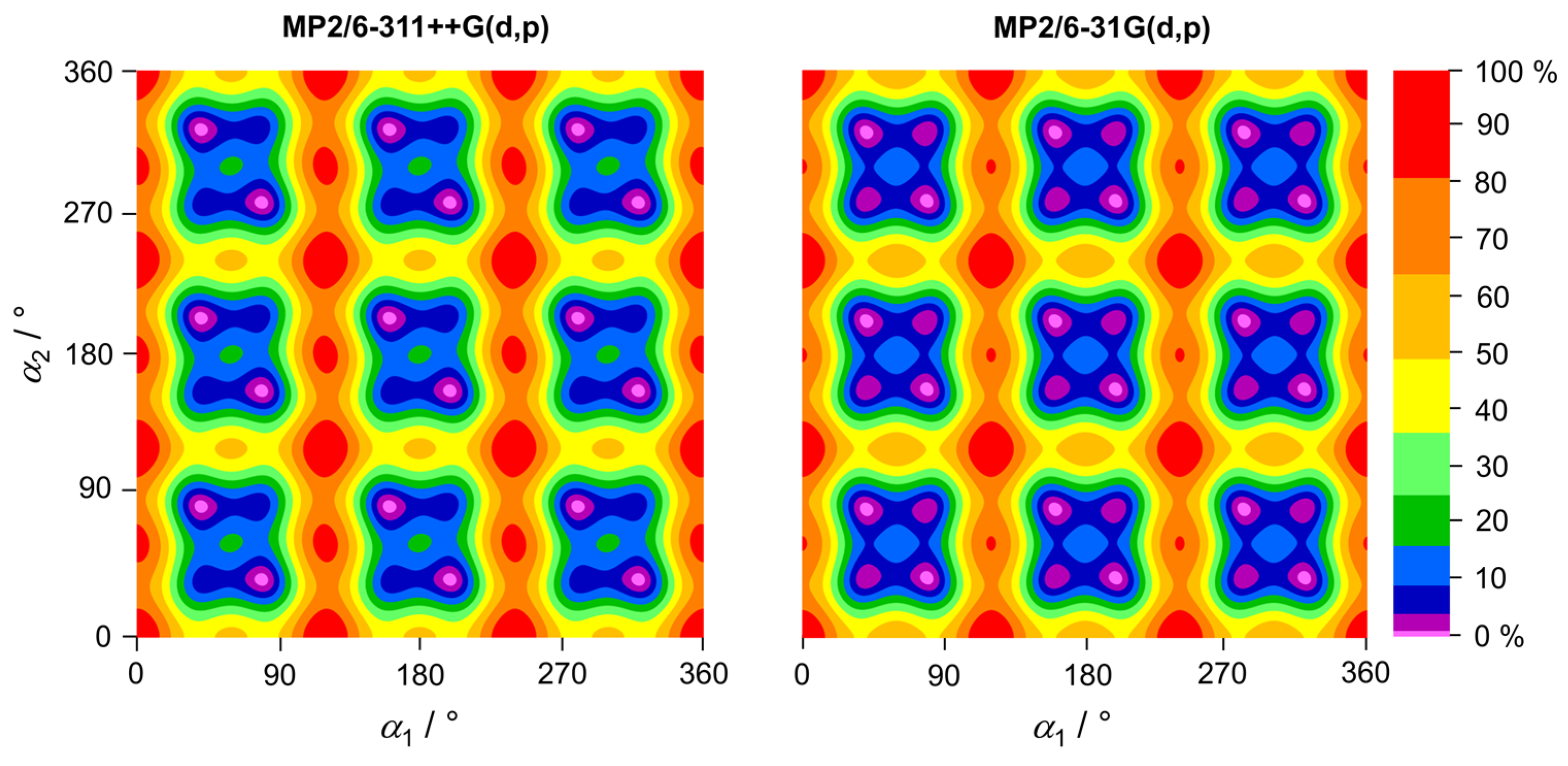
2.4. Potential Energy Surfaces
3. Microwave Spectroscopy
3.1. Measurements
3.2. Spectral Assignments
4. Results of the Global Fits and Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nguyen, H.V.L.; Caminati, W.; Grabow, J.-U. The LAM of the Rings: Large Amplitude Motions in Aromatic Molecules Studied by Microwave Spectroscopy. Molecules 2022, 27, 3948. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.V.L.; Kleiner, I. Understanding (Coupled) Large Amplitude Motions: The Interplay of Microwave Spectroscopy, Spectral Modeling, and Quantum Chemistry. Phys. Sci. Rev. 2022, 7, 679–726. [Google Scholar] [CrossRef]
- Schnitzler, E.G.; Seifert, N.A.; Kusuma, I.; Jäger, W. Rotational Spectroscopy of p-Toluic Acid and Its 1:1 Complex with Water. J. Phys. Chem. A 2017, 121, 8625–8631. [Google Scholar] [CrossRef]
- Bruhn, T.; Mäder, H. The Microwave Spectrum of m-Tolunitrile: Methyl Internal Rotation and 14N Nuclear Quadrupole Coupling. J. Mol. Spectrosc. 2000, 200, 151–161. [Google Scholar] [CrossRef] [PubMed]
- Roucou, A.; Kleiner, I.; Goubet, M.; Bteich, S.; Mouret, G.; Bocquet, R.; Hindle, F.; Meerts, W.L.; Cuisset, A. Towards the Detection of Explosive Taggants: Microwave and Millimeter-Wave Gas-Phase Spectroscopies of 3-Nitrotoluene. ChemPhysChem 2018, 19, 1056–1067. [Google Scholar] [CrossRef]
- Saal, H.; Grabow, J.-U.; Walker, A.H.; Hougen, J.; Kleiner, I.; Caminati, W. Microwave Study of Internal Rotation in para-ToluAldehyde: Local versus Global Symmetry Effects at the Methyl-Rotor Site. J. Mol. Spectrosc. 2018, 351, 55–61. [Google Scholar] [CrossRef]
- Nguyen, T.; Van, V.; Gutlé, C.; Stahl, W.; Schwell, M.; Kleiner, I.; Nguyen, H.V.L. The Microwave Spectrum of 2-Methylthiazole: 14N Nuclear Quadrupole Coupling and Methyl Internal Rotation. J. Chem. Phys. 2020, 152, 134306. [Google Scholar] [CrossRef]
- Obenchain, D.A.; Pinacho, P.; Zinn, S.; Schnell, M. The Low-Barrier Methyl Internal Rotation in the Rotational Spectrum of 3-Methylphenylacetylene. J. Mol. Struct. 2020, 1213, 128109. [Google Scholar] [CrossRef]
- Tudorie, M.; Kleiner, I.; Jahn, M.; Grabow, J.-U.; Goubet, M.; Pirali, O. Coupled Large Amplitude Motions: A Case Study of the Dimethylbenzaldehyde Isomers. J. Phys. Chem. A 2013, 117, 13636–13647. [Google Scholar] [CrossRef]
- Sun, H.; Khemissi, S.; Kleiner, I.; Nguyen, H.V.L. Low Barriers to Internal Rotation in the Microwave Spectrum of 2,5-Dimethylfluorobenzene. J. Chem. Phys. 2024, 160, 094302. [Google Scholar] [CrossRef]
- Sun, H.; Ferres, L.; Kleiner, I.; Nguyen, H.V.L. Coupled Methyl Internal Rotations with Intermediate and Low Torsional Barriers in 2,5-Dimethylanisole Investigated by Microwave Spectroscopy. J. Chem. Phys. 2024, 161, 224304. [Google Scholar] [CrossRef] [PubMed]
- Khemissi, S.; Van, V.; Schwell, M.; Kleiner, I.; Nguyen, H.V.L. Low Barrier Methyl Internal Rotations and 14N Quadrupole Coupling in the Microwave Spectrum of 2,4-Dimethylthiazole. J. Phys. Chem. A 2023, 127, 5779–5789. [Google Scholar] [CrossRef] [PubMed]
- Ferres, L.; Truong, K.-N.; Stahl, W.; Nguyen, H.V.L. Interplay Between Microwave Spectroscopy and X-ray Diffraction: The Molecular Structure and Large Amplitude Motions of 2,3-Dimethylanisole. ChemPhysChem 2018, 19, 1781–1788. [Google Scholar] [CrossRef]
- Thomsen, C.; Dreizler, H. The Microwave Spectra of m-Xylene and m-Xylene-d10. Determination of the Low Methyl Internal Rotation Barrier. Z. Naturforsch. A 2001, 56, 635–640. [Google Scholar] [CrossRef]
- Hartwig, H.; Dreizler, H. The Microwave Spectrum of trans-2,3-Dimethyloxirane in Torsional Excited States. Z. Naturforsch. A 1996, 51, 923–932. [Google Scholar] [CrossRef]
- Welzel, A.; Hellweg, A.; Merke, I.; Stahl, W. Structural and Torsional Properties of o-Cresol and o-Cresol-OD as Obtained from Microwave Spectroscopy and ab Initio Calculations. J. Mol. Spectrosc. 2002, 215, 58–65. [Google Scholar] [CrossRef]
- Schmitz, D.; Shubert, V.A.; Giuliano, B.M.; Schnell, M. The Broadband Microwave Spectra of the Monoterpenoids Thymol and Carvacrol: Conformational Landscape and Internal Dynamics. J. Chem. Phys. 2014, 141, 034304. [Google Scholar] [CrossRef]
- Écija, P.; Evangelisti, L.; Vallejo, M.; Basterretxea, F.J.; Lesarri, A.; Castanño, F.; Caminati, W.; Cocinero, E.J. Conformational Flexibility of Mephenesin. J. Phys. Chem. B 2014, 118, 5357–5364. [Google Scholar] [CrossRef]
- Schnitzler, E.G.; Zenchyzen, B.L.M.; Jäger, W. High-Resolution Fourier-Transform Microwave Spectroscopy of Methyl-and Dimethylnapthalenes. Astrophys. J. 2015, 805, 141. [Google Scholar] [CrossRef]
- Schnitzler, E.G.; Zenchyzen, B.L.M.; Jäger, W. Rotational Spectroscopy of the Atmospheric Photo-Oxidation Product o-Toluic Acid and its Monohydrate. Phys. Chem. Chem. Phys. 2016, 18, 448–457. [Google Scholar] [CrossRef]
- Gurusinghe, R.M.; Tubergen, M.J. Probing the Electronic Environment of Methylindoles using Internal Rotation and 14N Nuclear Quadrupole Coupling. J. Phys. Chem. A 2016, 120, 3491–3496. [Google Scholar] [CrossRef] [PubMed]
- Tudorie, M.; Kleiner, I.; Hougen, J.T.; Melandri, S.; Sutikdja, L.W.; Stahl, W. A Fitting Program for Molecules with Two Inequivalent Methyl Tops and a Plane of Symmetry at Equilibrium: Application to New Microwave and Millimeter-Wave Measurements of Methyl Acetate. J. Mol. Spectrosc. 2011, 269, 211–225. [Google Scholar] [CrossRef]
- Ilyushin, V.V.; Hougen, J. A Fitting Program for Molecules with Two Equivalent Methyl Tops and C2v Point-Group Symmetry at Equilibrium: Application to Existing Microwave, Millimeter, and Sub-millimeter Wave Measurements of Acetone. J. Mol. Spectrosc. 2013, 289, 41–49. [Google Scholar] [CrossRef]
- Groner, P. Effective Rotational Hamiltonian for Molecules with Two Periodic Large-Amplitude Motions. J. Chem. Phys. 1997, 107, 4483–4498. [Google Scholar] [CrossRef]
- Nguyen, H.V.L.; Stahl, W. The Microwave Spectrum of Isopropenyl Acetate—An Asymmetric Molecule with Two Internal Rotors. J. Mol. Spectrosc. 2010, 264, 120–124. [Google Scholar] [CrossRef]
- Ferres, L.; Stahl, W.; Kleiner, I.; Nguyen, H.V.L. The Effect of Internal Rotation in p-Methyl Anisole Studied by Microwave Spectroscopy. J. Mol. Spectrosc. 2018, 343, 44–49. [Google Scholar] [CrossRef]
- Ferres, L.; Stahl, W.; Nguyen, H.V.L. Low Torsional Barrier Challenges in the Microwave Spectrum of 2,4-Dimethylanisole. J. Chem. Phys. 2019, 151, 104310. [Google Scholar] [CrossRef]
- Herbers, S.; Fritz, S.M.; Mishra, P.; Nguyen, H.V.L.; Zwier, T.S. Local and Global Approaches to Treat the Torsional Barriers of 4-Methylacetophenone Using Microwave Spectroscopy. J. Chem. Phys. 2020, 152, 074301. [Google Scholar] [CrossRef]
- Herbers, S.; Zingsheim, O.; Nguyen, H.V.L.; Bonah, L.; Heyne, B.; Wehres, N.; Schlemmer, S. Internal Rotation Arena: Program Performances on the Low Barrier Problem of 4-Methylacetophenone. J. Chem. Phys. 2021, 155, 224302. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian16, Revision B.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Becke, A.D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H.A. Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Pople, J.A.; Binkley, J.S. Self-Consistent Molecular Orbital Methods 25. Supplementary Functions for Gaussian Basis Sets. J. Chem. Phys. 1984, 80, 3265–3269. [Google Scholar] [CrossRef]
- Møller, C.; Plesset, M.S. Note on an Approximation Treatment for Many-Electron Systems. Phys. Rev. 1934, 46, 618–622. [Google Scholar] [CrossRef]
- Khemissi, S.; Schwell, M.; Kleiner, I.; Nguyen, H.V.L. Approaching the Free Rotor Limit: Extremely Low Methyl Torsional Barrier Observed in the Microwave Spectrum of 2,4-Dimethylfluorobenzene. Phys. Chem. Chem. Phys. 2024, 26, 402–411. [Google Scholar] [CrossRef]
- Mélan, J.; Khemissi, S.; Nguyen, H.V.L. Steric Effects on Two Inequivalent Methyl Internal Rotations of 3,4-Dimethylfluorobenzene. Spectrochim. Acta A 2021, 253, 119564. [Google Scholar] [CrossRef] [PubMed]
- Khemissi, S.; Pérez Salvador, A.; Nguyen, H.V.L. Large Amplitude Motions in 2,3-Dimethylfluorobenzene: Steric Effects Failing to Interpret Hindered Methyl Torsion. J. Phys. Chem. A 2021, 125, 8542–8548. [Google Scholar] [CrossRef]
- Khemissi, S.; Nguyen, H.V.L. Two Equivalent Internal Rotations in the Microwave Spectrum of 2,6-Dimethylfluorobenzene. ChemPhysChem 2020, 21, 1682–1687. [Google Scholar] [CrossRef]
- Ferres, L.; Cheung, J.; Stahl, W.; Nguyen, H.V.L. Conformational Effect on the Large Amplitude Motions of 3,4-Dimethylanisole Explored by Microwave Spectroscopy. J. Phys. Chem. A 2019, 123, 3497–3503. [Google Scholar] [CrossRef]
- Yanai, T.; Tew, D.P.; Handy, N.C. A New Hybrid Exchange–Correlation Functional using the Coulomb-Attenuating Method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 Other Functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef]
- Chai, J.-D.; Head-Gordon, M. Long-Range Corrected Hybrid Density Functionals with Damped Atom-Atom Dispersion Corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.S.; He, X.; Li, S.L.; Truhlar, D.G. MN15: A Kohn–Sham Global-Hybrid Exchange–Correlation Density Functional with Broad Accuracy for Multi-Reference and Single-Reference Systems and Noncovalent Interactions. Chem. Sci. 2016, 7, 5032–5051. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0 Model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Bartlett, R.J.; Musiał, M. Coupled-Cluster Theory in Quantum Chemistry. Rev. Mod. Phys. 2007, 79, 291–352. [Google Scholar] [CrossRef]
- Dunning, T.H. Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron through Neon and Hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Reinhold, B.; Finneran, I.A.; Shipman, S.T. Room Temperature Chirped-Pulse Fourier Transform Microwave Spectroscopy of Anisole. J. Mol. Spectrosc. 2011, 270, 89. [Google Scholar] [CrossRef]
- Grabow, J.-U.; Stahl, W.; Dreizler, H.A. Multioctave Coaxially Oriented Beam-resonator Arrangement Fourier-Transform Microwave Spectrometer. Rev. Sci. Instrum. 1996, 67, 4072–4084. [Google Scholar] [CrossRef]
- Zhao, Y.; Nguyen, H.V.L.; Stahl, W.; Hougen, J.T. Unusual Internal Rotation Coupling in the Microwave Spectrum of Pinacolone. J. Mol. Spectrosc. 2015, 318, 91–100. [Google Scholar] [CrossRef]
- Herbers, S.; Nguyen, H.V.L. Next Level Achievement of The XIAM Code in Modeling the Microwave Spectrum of m-Methylanisole. J. Mol. Spectrosc. 2020, 370, 111289. [Google Scholar] [CrossRef]
- Ferres, L.; Stahl, W.; Nguyen, H.V.L. Conformational Effects on the Torsional Barriers in m-Methylanisole Studied by Microwave Spectroscopy. J. Chem. Phys. 2018, 148, 124304. [Google Scholar] [CrossRef] [PubMed]
- Ferres, L.; Mouhib, H.; Stahl, W.; Nguyen, H.V.L. Methyl Internal Rotation in the Microwave Spectrum of o-Methyl Anisole. ChemPhysChem 2017, 18, 1860–1865. [Google Scholar] [CrossRef] [PubMed]
- Shirar, A.J.; Wilcox, D.S.; Hotopp, K.M.; Storck, G.L.; Kleiner, I.; Dian, B.C. Impact of Molecular Conformation on Barriers to Internal Methyl Rotation: The Rotational Spectrum of m-Methylbenzaldehyde. J. Phys. Chem. A 2010, 114, 12187–12194. [Google Scholar] [CrossRef]

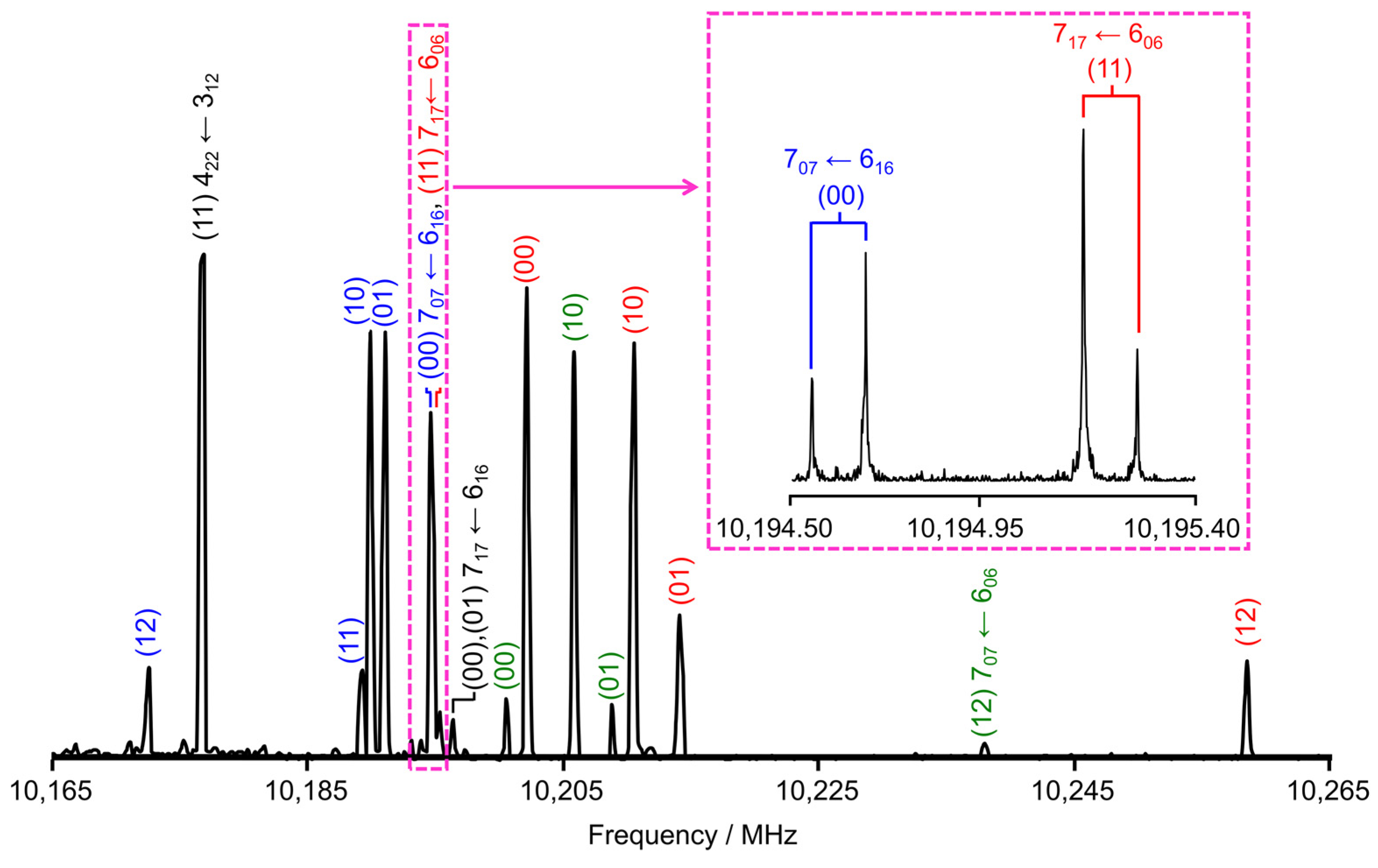
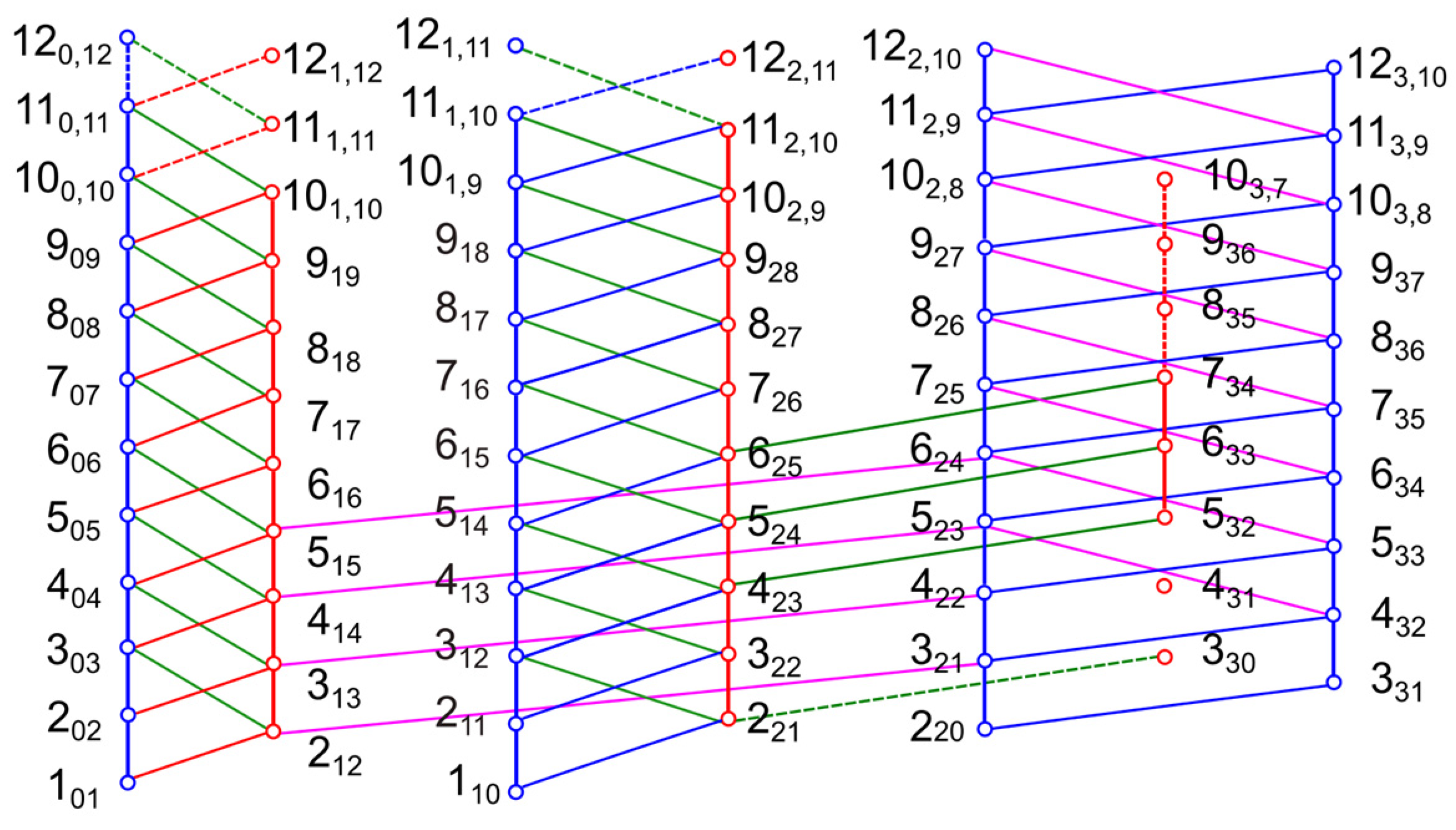

| Par. | Unit | MP2/6-31G(d,p) | MP2/6-311++G(d,p) | B3LYP-D3BJ |
|---|---|---|---|---|
| Ae | MHz | 1736.4 | 1728.6 | 1740.3 |
| Be | MHz | 1095.5 | 1094.0 | 1092.6 |
| Ce | MHz | 680.3 | 678.6 | 679.7 |
| A0 | MHz | 1724.2 | 1717.8 | 1726.9 |
| B0 | MHz | 1085.8 | 1084.5 | 1084.0 |
| C0 | MHz | 674.9 | 673.3 | 674.6 |
| DJ | kHz | 0.073437 | 0.074241 | 0.074614 |
| DJK | kHz | −0.104737 | −0.105306 | −0.097750 |
| DK | kHz | 0.037086 | 0.036934 | 0.029037 |
| d1 | kHz | −0.016684 | −0.016884 | −0.016691 |
| d2 | kHz | 0.001187 | 0.001205 | 0.002070 |
| |µa| | D | 0.5 | 0.5 | 0.5 |
| |µb| | D | 1.1 | 1.2 | 1.2 |
| |µc| | D | 0.1 | 0.0 | 0.0 |
| V3,syn-m | cm−1 | 55.2 | 69.2 | 67.2 |
| V3,anti-m | cm−1 | 36.8 | 34.6 | 44.0 |
| Par. a | Unit | Fit (00) | Fit (10) | Fit (01) | Fit (11) | Fit (12) |
|---|---|---|---|---|---|---|
| A | MHz | 1744.77418(29) | 1744.00056(64) | 1735.59250(52) | 1734.7419(13) | 1735.1469(14) |
| B | MHz | 1101.19864(18) | 1096.03548(24) | 1097.88093(18) | 1093.31277(46) | 1092.68724(31) |
| C | MHz | 680.562851(68) | 680.563975(88) | 680.531514(74) | 680.55101(12) | 680.53608(16) |
| DJ | kHz | 0.0286(14) | 0.0203(30) | 0.0288(24) | 0.0278(76) | 0.0326(35) |
| DJK | kHz | 0.1740(66) | 0.170(26) | 0.330(22) | 0.285(60) | 0.153(27) |
| d1 | kHz | −0.01947(87) | −0.0124(14) | −0.0235(11) | −0.0204(39) | −0.0181(19) |
| d2 | kHz | −0.00821(35) | −0.00525(53) | −0.01183(43) | −0.0092(16) | −0.00443(74) |
| q | MHz | 1817.842(14) | 1104.1998(14) | 1237.8649(25) | 881.224(36) | |
| r | MHz | 563.3230(16) | 630.8680(12) | 70.043(10) | 1127.8147(20) | |
| qJ | kHz | −14.844(99) | −44.003(69) | −55.39(13) | ||
| qK | kHz | 13.52(25) | −21.05(13) | −7.81(17) | ||
| rJ | kHz | −23.138(55) | −15.644(43) | 8.18(42) | −34.871(83) | |
| rK | kHz | −23.90(31) | −120.59(22) | −94.1(22) | −137.82(54) | |
| N b | 141 | 148 | 144 | 100 | 89 | |
| rms c | kHz | 3.6 | 4.8 | 3.3 | 4.8 | 3.0 |
| Par. a | Unit | Fit XIAM | Fit ntop | Calc. b |
|---|---|---|---|---|
| A | MHz | 1737.126(11) | 1742.502(62) | 1740.3 |
| B | MHz | 1095.3062(52) | 1094.343(15) | 1092.6 |
| C | MHz | 680.5538(17) | 680.688(11) | 679.7 |
| DJ | kHz | 0.01311(38) | 0.074614 | |
| DJK | kHz | 0.1113(29) | −0.097750 | |
| d1 | kHz | −0.00679(22) | −0.016691 | |
| d2 | kHz | −0.003364(96) | 0.002070 | |
| Vcc | cm−1 | −7.7494(50) | −9.803586(86) | −7.8 |
| Vss | cm−1 | 0.78428(51) | 0.6 | |
| V3,1 | cm−1 | 60.1207(56) | 58.62367(53) | 67.2 |
| V3,2 | 37.5936(64) | 36.28449(69) | 44.0 | |
| MHz | 4.41(71) | |||
| MHz | −0.060(11) | |||
| MHz | 0.0261(22) | |||
| MHz | 0.02403(75) | |||
| MHz | 0.3687(78) | −0.5658(79) | ||
| DmK,2 | MHz | 0.4228(64) | ||
| dm,2 | MHz | 0.0636(16) | ||
| VJ,1 | MHz | −44.7(72) | −0.46049(65) | |
| VK,1 | MHz | 2.0337(70) | ||
| V−,1 | MHz | −0.31988(69) | ||
| VJ,2 | MHz | 1.076(14) | ||
| VK,2 | MHz | −10.36(11) | ||
| V−,2 | MHz | 1.155(15) | ||
| QzJ,1 | kHz | −3.360(26) | ||
| QzK,1 | kHz | 8.806(88) | ||
| Qz−,1 | kHz | 4.014(79) | ||
| ∠(i1,a) | ° | 78.0849(22) | 78.15036(51) | 78.6 |
| ∠(i1,b) | ° | 11.9151(22) | 11.84964(51) | 11.4 |
| ∠(i1,c) | ° | 90.0 c | 90.0 c | 90.0 |
| ∠(i2,a) | ° | 41.7799(22) | 41.9409(13) | 41.5 |
| ∠(i2,b) | ° | 131.7799(22) | 131.9409(13) | 131.5 |
| ∠(i2,c) | ° | 90.0 c | 90.0 c | 90.0 |
| N d | 622 | 622 | ||
| rms e | kHz | 347.5 | 5.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khemissi, S.; Ferres, L.; Nguyen, H.V.L. Two Coupled Low-Barrier Large Amplitude Motions in 3,5-Dimethylanisole Studied by Microwave Spectroscopy. Molecules 2025, 30, 1195. https://doi.org/10.3390/molecules30061195
Khemissi S, Ferres L, Nguyen HVL. Two Coupled Low-Barrier Large Amplitude Motions in 3,5-Dimethylanisole Studied by Microwave Spectroscopy. Molecules. 2025; 30(6):1195. https://doi.org/10.3390/molecules30061195
Chicago/Turabian StyleKhemissi, Safa, Lynn Ferres, and Ha Vinh Lam Nguyen. 2025. "Two Coupled Low-Barrier Large Amplitude Motions in 3,5-Dimethylanisole Studied by Microwave Spectroscopy" Molecules 30, no. 6: 1195. https://doi.org/10.3390/molecules30061195
APA StyleKhemissi, S., Ferres, L., & Nguyen, H. V. L. (2025). Two Coupled Low-Barrier Large Amplitude Motions in 3,5-Dimethylanisole Studied by Microwave Spectroscopy. Molecules, 30(6), 1195. https://doi.org/10.3390/molecules30061195







