A Non-Autonomous Amphoteric Metal Hydroxide Oscillations and Pattern Formation in Hydrogels
Abstract
:1. Introduction
2. Results
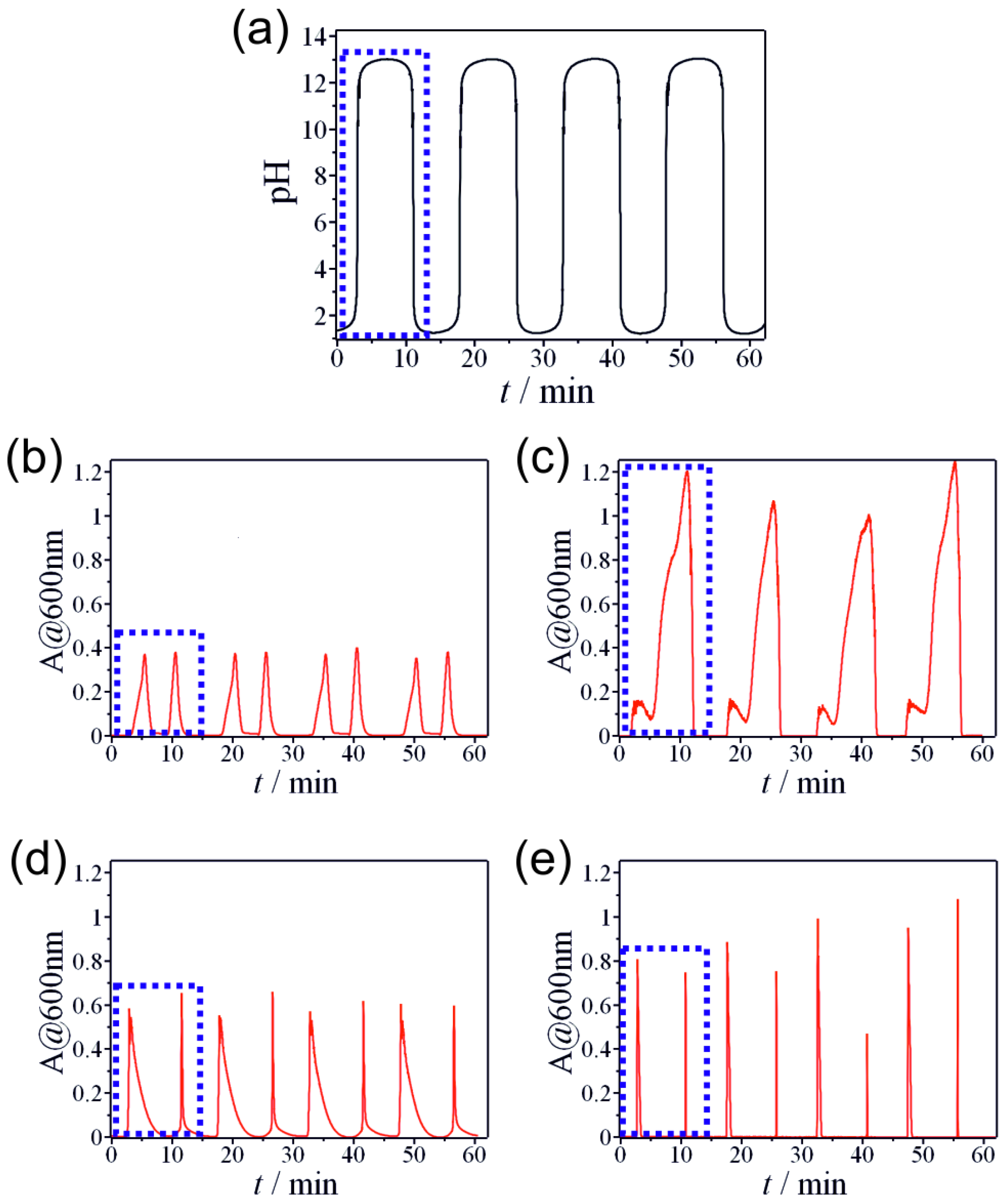
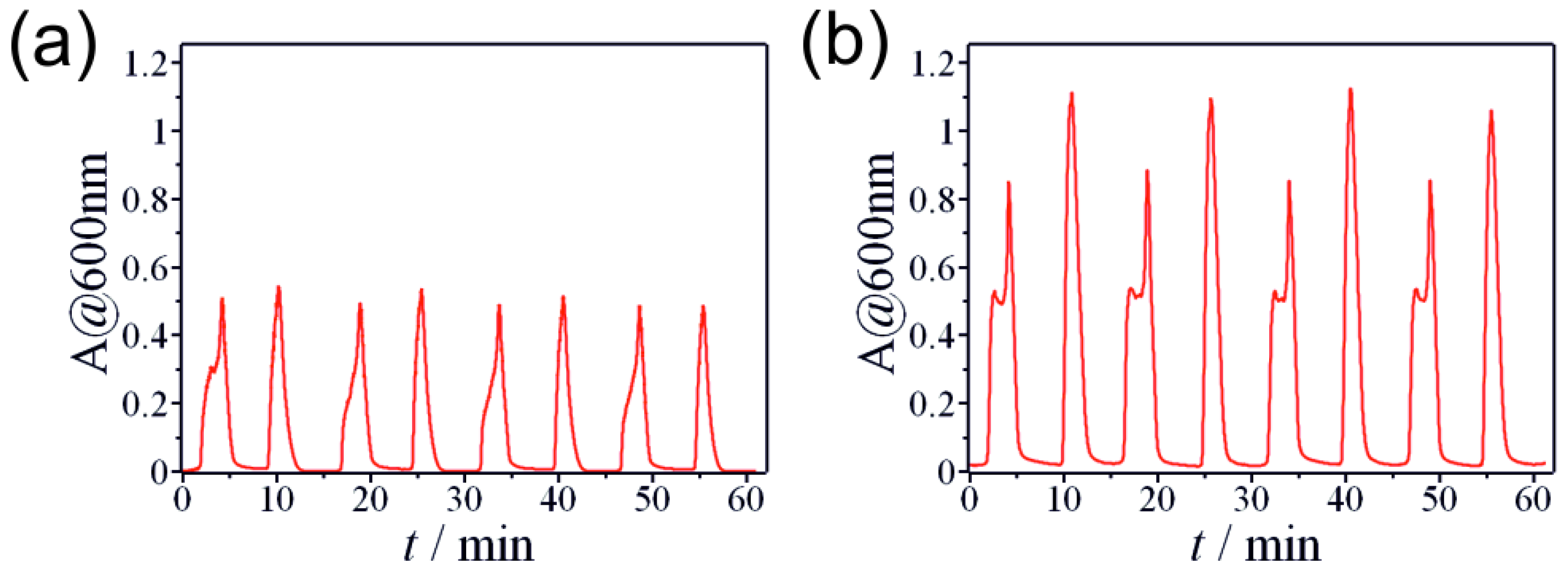
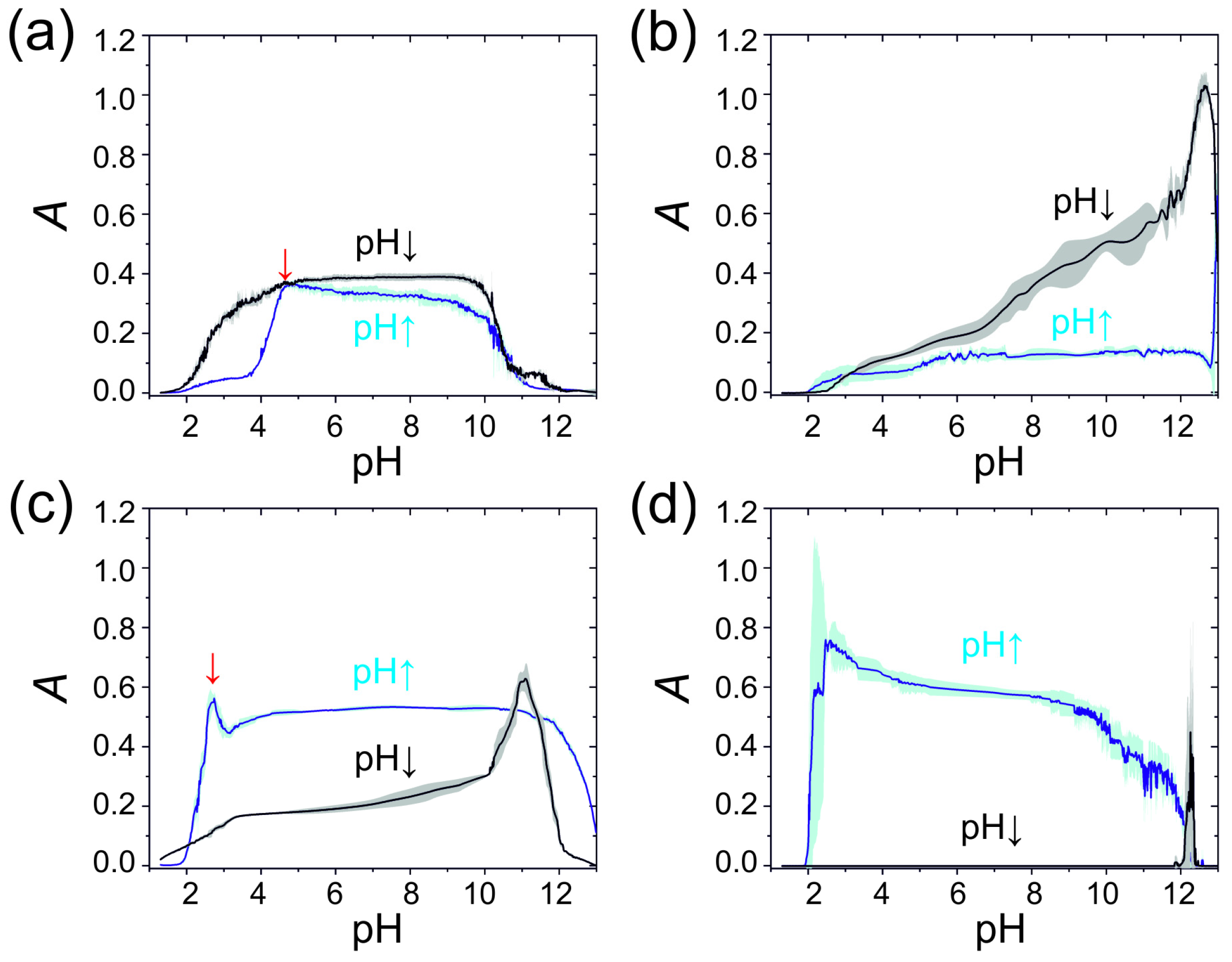
2.1. Non-Autonomous Oscillations of Amphoteric Hydroxides (Al3+, Zn2+, Sn2+, and Pb2+)
2.2. Pattern Formation in a Hydrogel Column
2.3. Propagation of a Precipitation Front in a Thin Layer of Tin (II) Hydroxide Precipitate
3. Methods
3.1. Reagents
3.2. Non-Autonomous Metal Hydroxide Oscillators
3.3. Formation of Layered Metal Hydroxide in a Hydrogel
3.4. Front Propagation in Tin (II) Chloride System
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- De Kepper, P.; Epstein, I.R. Mechanistic Study of Oscillations and Bistability in the Briggs-Rauscher Reaction. J. Am. Chem. Soc. 1982, 104, 49–55. [Google Scholar] [CrossRef]
- Furrow, S.D.; Cervellati, R.; Amadori, G. New Substrates for the Oscillating Briggs–Rauscher Reaction. J. Phys. Chem. A 2002, 106, 5841–5850. [Google Scholar] [CrossRef]
- Noyes, R.M.; Furrow, S.D. The Oscillatory Briggs-Rauscher Reaction. 3. A Skeleton Mechanism for Oscillations. J. Am. Chem. Soc. 1982, 104, 45–48. [Google Scholar] [CrossRef]
- Cassani, A.; Monteverde, A.; Piumetti, M. Belousov-Zhabotinsky Type Reactions: The Non-Linear Behavior of Chemical Systems. J. Math. Chem. 2021, 59, 792–826. [Google Scholar] [CrossRef]
- Frerichs, G.A.; Yengi, D. Complex Oscillations in the Belousov–Zhabotinsky Batch Reaction with Methylmalonic Acid and Manganese(II). RSC Adv. 2021, 11, 16435–16444. [Google Scholar] [CrossRef]
- Petrov, V.; Gáspár, V.; Masere, J.; Showalter, K. Controlling Chaos in the Belousov—Zhabotinsky Reaction. Nature 1993, 361, 240–243. [Google Scholar] [CrossRef]
- Kovacs, K.; McIlwaine, R.; Gannon, K.; Taylor, A.F.; Scott, S.K. Complex Behavior in the Formaldehyde–Sulfite Reaction. J. Phys. Chem. A 2005, 109, 283–288. [Google Scholar] [CrossRef] [PubMed]
- Lawson, H.S.; Holló, G.; Horvath, R.; Kitahata, H.; Lagzi, I. Chemical Resonance, Beats, and Frequency Locking in Forced Chemical Oscillatory Systems. J. Phys. Chem. Lett. 2020, 11, 3014–3019. [Google Scholar] [CrossRef]
- Dateo, C.E.; Orban, M.; De Kepper, P.; Epstein, I.R. Systematic Design of Chemical Oscillators. 5. Bistability and Oscillations in the Autocatalytic Chlorite-Iodide Reaction in a Stirred-Flow Reactor. J. Am. Chem. Soc. 1982, 104, 504–509. [Google Scholar] [CrossRef]
- Orban, M.; Epstein, I.R. Systematic Design of Chemical Oscillators. Part 13. Complex Periodic and Aperiodic Oscillation in the Chlorite-Thiosulfate Reaction. J. Phys. Chem. 1982, 86, 3907–3910. [Google Scholar] [CrossRef]
- Rabai, G.; Orban, M.; Epstein, I.R. Systematic Design of Chemical Oscillators. 64. Design of pH-Regulated Oscillators. Acc. Chem. Res. 1990, 23, 258–263. [Google Scholar] [CrossRef]
- McIlwaine, R.; Kovacs, K.; Scott, S.K.; Taylor, A.F. A Novel Route to pH Oscillators. Chem. Phys. Lett. 2006, 417, 39–42. [Google Scholar] [CrossRef]
- Bubanja, I.N.; Ivanović-Šašić, A.; Čupić, Ž.; Anić, S.; Kolar-Anić, L. Intermittent Chaos in the CSTR Bray–Liebhafsky Oscillator-Specific Flow Rate Dependence. Front. Chem. 2020, 8, 560274. [Google Scholar] [CrossRef]
- Peng, B.; Petrov, V.; Showalter, K. Controlling Chemical Chaos. J. Phys. Chem. 1991, 95, 4957–4959. [Google Scholar] [CrossRef]
- Galanics, C.; Szalai, I. Dynamics of pH Oscillators in Continuous Stirred Tanks in Series. ChemPhysChem 2024, 25, e202400610. [Google Scholar] [CrossRef]
- Epstein, I.R.; Showalter, K. Nonlinear Chemical Dynamics: Oscillations, Patterns, and Chaos. J. Phys. Chem. 1996, 100, 13132–13147. [Google Scholar] [CrossRef]
- Budroni, M.A.; Rossi, F. Transport-Driven Chemical Oscillations: A Review. Phys. Chem. Chem. Phys. 2024, 26, 29185–29226. [Google Scholar] [CrossRef] [PubMed]
- Zaikin, A.N.; Zhabotinsky, A.M. Concentration Wave Propagation in Two-Dimensional Liquid-Phase Self-Oscillating System. Nature 1970, 225, 535–537. [Google Scholar] [CrossRef]
- Castets, V.; Dulos, E.; Boissonade, J.; De Kepper, P. Experimental Evidence of a Sustained Standing Turing-Type Nonequilibrium Chemical Pattern. Phys. Rev. Lett. 1990, 64, 2953–2956. [Google Scholar] [CrossRef]
- De Kepper, P.; Castets, V.; Dulos, E.; Boissonade, J. Turing-Type Chemical Patterns in the Chlorite-Iodide-Malonic Acid Reaction. Phys. D Nonlinear Phenom. 1991, 49, 161–169. [Google Scholar] [CrossRef]
- Horváth, J.; Szalai, I.; De Kepper, P. An Experimental Design Method Leading to Chemical Turing Patterns. Science 2009, 324, 772–775. [Google Scholar] [CrossRef] [PubMed]
- Nakouzi, E.; Steinbock, O. Self-Organization in Precipitation Reactions Far from the Equilibrium. Sci. Adv. 2016, 2, e1601144. [Google Scholar] [CrossRef]
- Barge, L.M.; Cardoso, S.S.S.; Cartwright, J.H.E.; Cooper, G.J.T.; Cronin, L.; De Wit, A.; Doloboff, I.J.; Escribano, B.; Goldstein, R.E.; Haudin, F.; et al. From Chemical Gardens to Chemobrionics. Chem. Rev. 2015, 115, 8652–8703. [Google Scholar] [CrossRef] [PubMed]
- Siev, E.A.; Batista, B.C.; Steinbock, O. Coiling of Secondary Tubes Formed from the Colloidal Exhaust of Primary Chemical Gardens. J. Phys. Chem. B 2024, 128, 2028–2036. [Google Scholar] [CrossRef]
- Lawson, H.S.; Holló, G.; Német, N.; Teraji, S.; Nakanishi, H.; Horvath, R.; Lagzi, I. Design of Non-Autonomous pH Oscillators and the Existence of Chemical Beat Phenomenon in a Neutralization Reaction. Sci. Rep. 2021, 11, 11011. [Google Scholar] [CrossRef] [PubMed]
- Német, N.; Lawson, H.S.; Holló, G.; Valletti, N.; Rossi, F.; Schuszter, G.; Lagzi, I. Non-Autonomous Zinc–Methylimidazole Oscillator and the Formation of Layered Precipitation Structures in a Hydrogel. Sci. Rep. 2023, 13, 11029. [Google Scholar] [CrossRef]
- Ten Elshof, J.E.; Yuan, H.; Gonzalez Rodriguez, P. Two-Dimensional Metal Oxide and Metal Hydroxide Nanosheets: Synthesis, Controlled Assembly and Applications in Energy Conversion and Storage. Adv. Energy Mater. 2016, 6, 1600355. [Google Scholar] [CrossRef]
- Lee, G.; Jun, S.E.; Kim, Y.; Park, I.-H.; Jang, H.W.; Park, S.H.; Kwon, K.C. Multicomponent Metal Oxide- and Metal Hydroxide-Based Electrocatalysts for Alkaline Water Splitting. Materials 2023, 16, 3280. [Google Scholar] [CrossRef]
- Tokudome, Y. Aqueous Synthesis of Metal Hydroxides with Controllable Nano/Macro Architectures. J. Ceram. Soc. Jpn. 2017, 125, 597–602. [Google Scholar] [CrossRef]
- Hall, D.S.; Lockwood, D.J.; Bock, C.; MacDougall, B.R. Nickel Hydroxides and Related Materials: A Review of Their Structures, Synthesis and Properties. Proc. R. Soc. A Math. Phys. Eng. Sci. 2015, 471, 20140792. [Google Scholar] [CrossRef]
- Wood, J.K. XXXVIII.—Amphoteric Metallic Hydroxides. Part I. J. Chem. Soc. Trans. 1908, 93, 411–423. [Google Scholar] [CrossRef]
- Wood, J.K. LXIII.—Amphoteric Metallic Hydroxides. Part II. J. Chem. Soc. Trans. 1910, 97, 878–890. [Google Scholar] [CrossRef]
- Honnick, W.D.; Zuckerman, J.J. Tin(II) Hydroxide. Inorg. Chem. 1976, 15, 3034–3037. [Google Scholar] [CrossRef]
- Perera, W.N.; Hefter, G.; Sipos, P.M. An Investigation of the Lead(II)−Hydroxide System. Inorg. Chem. 2001, 40, 3974–3978. [Google Scholar] [CrossRef]
- Yoshida, R. Self-Oscillating Gels Driven by the Belousov–Zhabotinsky Reaction as Novel Smart Materials. Adv. Mater. 2010, 22, 3463–3483. [Google Scholar] [CrossRef] [PubMed]
- Nakata, S.; Yoshii, M.; Suzuki, S.; Yoshida, R. Periodic Reciprocating Motion of a Polymer Gel on an Aqueous Phase Synchronized with the Belousov–Zhabotinsky Reaction. Langmuir 2014, 30, 517–521. [Google Scholar] [CrossRef] [PubMed]
- Geher-Herczegh, T.; Wang, Z.; Masuda, T.; Yoshida, R.; Vasudevan, N.; Hayashi, Y. Delayed Mechanical Response to Chemical Kinetics in Self-Oscillating Hydrogels Driven by the Belousov–Zhabotinsky Reaction. Macromolecules 2021, 54, 6430–6439. [Google Scholar] [CrossRef]
- Srivastava, R.; Srivastava, P.K. Self-Organized Nanostructured Spherulitic Crystal Pattern Formation in Belousov–Zhabotinsky Type Reaction System. Chem. Phys. 2013, 426, 59–73. [Google Scholar] [CrossRef]
- Pojman, J.A.; Leard, D.C.; West, W. Periodic Polymerization of Acrylonitrile in the Cerium-Catalyzed Belousov-Zhabotinskii Reaction. J. Am. Chem. Soc. 1992, 114, 8298–8299. [Google Scholar] [CrossRef]
- Furue, Y.; Okano, K.; Banno, T.; Asakura, K. Controlled Polymerization of Acrylonitrile Proceeded along with the Belousov–Zhabotinsky Oscillator by Changing Its Stirring Conditions. Chem. Phys. Lett. 2016, 645, 210–214. [Google Scholar] [CrossRef]
- Bastakoti, B.P.; Perez-Mercader, J. Facile One-Pot Synthesis of Functional Giant Polymeric Vesicles Controlled by Oscillatory Chemistry. Angew. Chem. Int. Edit. 2017, 56, 12086–12091. [Google Scholar] [CrossRef]
- Prabhu, G.R.D.; Witek, H.A.; Urban, P.L. Chemical Clocks, Oscillations, and Other Temporal Effects in Analytical Chemistry: Oddity or Viable Approach? Analyst 2018, 143, 3514–3525. [Google Scholar] [CrossRef]
- Al-Ghoul, M.; Ammar, M. Polymorphic and Morphological Transformation during the Transition from a Propagating Band to Static Bands in the Nickel Hydroxide/Ammonia Liesegang System. Deffect Diffus. Forum 2011, 312–315, 800–805. [Google Scholar] [CrossRef]
- Karam, T.; El-Rassy, H.; Zaknoun, F.; Moussa, Z.; Sultan, R. Liesegang Banding and Multiple Precipitate Formation in Cobalt Phosphate Systems. Chem. Phys. Lett. 2012, 525–526, 54–59. [Google Scholar] [CrossRef]
- Ammar, M.; Al-Ghoul, M. Band Propagation, Scaling Laws, and Phase Transition in a Precipitate System III: Effect of the Anions of Precursors. J. Phys. Chem. A 2020, 124, 39–45. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Nakouzi, E. Reaction–Diffusion Coupling Facilitates the Sequential Precipitation of Metal Ions from Battery Feedstock Solutions. Environ. Sci. Technol. Lett. 2023, 10, 1188–1194. [Google Scholar] [CrossRef]
- Wang, Q.; Fu, Y.; Miller, E.A.; Song, D.; Brahana, P.J.; Ritchhart, A.; Xu, Z.; Johnson, G.E.; Bharti, B.; Sushko, M.L.; et al. Selective Recovery of Critical Minerals from Simulated Electronic Wastes Via Reaction-Diffusion Coupling. ChemSusChem 2025, e202402372. [Google Scholar] [CrossRef]
- Nabika, H.; Itatani, M.; Lagzi, I. Pattern Formation in Precipitation Reactions: The Liesegang Phenomenon. Langmuir 2020, 36, 481–497. [Google Scholar] [CrossRef]
- Volford, A.; Izsák, F.; Ripszám, M.; Lagzi, I. Pattern Formation and Self-Organization in a Simple Precipitation System. Langmuir 2007, 23, 961–964. [Google Scholar] [CrossRef]
- Ban, T.; Nagatsu, Y.; Tokuyama, H. Propagation Properties of the Precipitation Band in an AlCl3/NaOH System. Langmuir 2016, 32, 604–610. [Google Scholar] [CrossRef]
- Tinsley, M.R.; Collison, D.; Showalter, K. Propagating Precipitation Waves: Experiments and Modeling. J. Phys. Chem. A 2013, 117, 12719–12725. [Google Scholar] [CrossRef]
- Ayass, M.M.; Al-Ghoul, M.; Lagzi, I. Chemical Waves in Heterogeneous Media. J. Phys. Chem. A 2014, 118, 11678–11682. [Google Scholar] [CrossRef] [PubMed]
- Ayass, M.M.; Lagzi, I.; Al-Ghoul, M. Targets, Ripples and Spirals in a Precipitation System with Anomalous Dispersion. Phys. Chem. Chem. Phys. 2015, 17, 19806–19814. [Google Scholar] [CrossRef]
- Bin Ahmad, M.; Lim, J.J.; Shameli, K.; Ibrahim, N.A.; Tay, M.Y. Synthesis of Silver Nanoparticles in Chitosan, Gelatin and Chitosan/Gelatin Bionanocomposites by a Chemical Reducing Agent and Their Characterization. Molecules 2011, 16, 7237–7248. [Google Scholar] [CrossRef] [PubMed]
- Bradford, S.C. The Liesegang Phenomenon and Concretionary Structure in Rocks. Nature 1916, 97, 80–81. [Google Scholar] [CrossRef]
- Müller, S.C.; Ross, J. Spatial Structure Formation in Precipitation Reactions. J. Phys. Chem. A 2003, 107, 7997–8008. [Google Scholar] [CrossRef]
- Nabika, H. Liesegang Phenomena: Spontaneous Pattern Formation Engineered by Chemical Reactions. Curr. Phys. Chem. 2015, 5, 5–20. [Google Scholar] [CrossRef]
- Narita, K.; Matsumoto, K.; Igawa, M. Application of Liesegang Ring Formation on a Gelatin Film to the Determination of Sulfate Concentration in Individual Rain Droplets. Anal. Sci. 2006, 22, 1559–1563. [Google Scholar] [CrossRef]
- Zhang, H.; Zhan, K.; Chen, Y.; Chen, G.; Zhou, X.; Liu, J.; Wu, M.; Ni, H. Three Dimension Liesegang Rings of Calcium Hydrophosphate in Gelatin. J. Sol-Gel Sci. Technol. 2014, 71, 597–605. [Google Scholar] [CrossRef]
- Ni, H.; Pan, M.; Shi, K.; Zhou, J.; Wu, M. Preparation of Isometric Liesegang Patterns and Application in Multi-Pulsed Drug Release System. J. Sol-Gel Sci. Technol. 2019, 91, 216–224. [Google Scholar] [CrossRef]
- Ibrahim, H.; El-Rassy, H.; Sultan, R. Liesegang Bands versus Random Crystallites in Ag2Cr2O7—Single and Mixed Gelled Media. Chem. Phys. Lett. 2018, 693, 198–201. [Google Scholar] [CrossRef]
- Shimizu, Y.; Matsui, J.; Unoura, K.; Nabika, H. Liesegang Mechanism with a Gradual Phase Transition. J. Phys. Chem. B 2017, 121, 2495–2501. [Google Scholar] [CrossRef] [PubMed]
- Eltantawy, M.M.; Belokon, M.A.; Belogub, E.V.; Ledovich, O.I.; Skorb, E.V.; Ulasevich, S.A. Self-Assembled Liesegang Rings of Hydroxyapatite for Cell Culturing. Adv. NanoBiomed Res. 2021, 1, 2000048. [Google Scholar] [CrossRef]
- Hayashi, H.; Abe, H. X-Ray Spectroscopic Analysis of Liesegang Patterns in Mn–Fe-Based Prussian Blue Analogs. J. Anal. At. Spectrom. 2016, 31, 1658–1672. [Google Scholar] [CrossRef]
- Hayashi, H.; Aoki, S.; Suzuki, T. Spontaneous Precipitation Pattern Formation by Crystallites of Mn–Fe-Based Prussian Blue Analogues in Agarose Gel. RSC Adv. 2019, 9, 36240–36247. [Google Scholar] [CrossRef]
- Morsali, M.; Khan, M.T.A.; Ashirov, R.; Holló, G.; Baytekin, H.T.; Lagzi, I.; Baytekin, B. Mechanical Control of Periodic Precipitation in Stretchable Gels to Retrieve Information on Elastic Deformation and for the Complex Patterning of Matter. Adv. Mater. 2020, 32, 1905779. [Google Scholar] [CrossRef] [PubMed]
- Hayashi, H.; Yamada, K. Transient Submillimeter-Scale Periodic Banding of Ag2O Precipitate through Reaction–Transport–Reaction Processes. Front. Phys. 2024, 12, 1365863. [Google Scholar] [CrossRef]
- Itatani, M.; Onishi, Y.; Suematsu, N.J.; Lagzi, I. Periodic Precipitation in a Confined Liquid Layer. J. Phys. Chem. Lett. 2024, 15, 4948–4957. [Google Scholar] [CrossRef]
- Schuszter, G.; Bogya, E.-S.; Horváth, D.; Tóth, Á.; Haspel, H.; Kukovecz, Á. Liquid Droplet Evaporation from Buckypaper: On the Fundamental Properties of the Evaporation Profile. Microporous Mesoporous Mater. 2015, 209, 105–112. [Google Scholar] [CrossRef]
- Cardoso Rial, R. AI in Analytical Chemistry: Advancements, Challenges, and Future Directions. Talanta 2024, 274, 125949. [Google Scholar] [CrossRef]





| Agarose 1%; [NaOH]0 = 25 mM; [HCl]0 = 30 mM; t = 5 Days | |||
|---|---|---|---|
| Vial | [Al3+]0/mM | [Sn2+]0/mM | Ratio |
| 1 | 20.0 | - | - |
| 2 | 40.0 | - | - |
| 3 | - | 4.0 | - |
| 4 | - | 8.0 | - |
| 5 | 20.0 | 8.0 | 5:2 |
| 6 | 40.0 | 4.0 | 10:1 |
| Agarose 1%; [NaOH]0 = 25 mM; [HCl]0 = 30 mM; t = 7 Days | |||||
|---|---|---|---|---|---|
| Vial | [Al3+]0/mM | [Zn2+]0/mM | [Sn2+]0/mM | [Pb2+]0/mM | Ratio |
| 1 | 10.0 | - | - | - | - |
| 2 | - | 2.0 | - | - | - |
| 3 | - | - | 4.0 | - | - |
| 4 | - | - | - | 0.5 | - |
| 5 | 10.0 | 2.0 | 4.0 | 0.5 | 20:4:8:1 |
| 6 | 10.0 | 4.0 | 4.0 | 0.5 | 20:8:8:1 |
| 7 | 20.0 | 4.0 | 8.0 | 1.0 | 20:4:8:1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Német, N.; Lawson, H.S.; Itatani, M.; Rossi, F.; Suematsu, N.J.; Kitahata, H.; Lagzi, I. A Non-Autonomous Amphoteric Metal Hydroxide Oscillations and Pattern Formation in Hydrogels. Molecules 2025, 30, 1323. https://doi.org/10.3390/molecules30061323
Német N, Lawson HS, Itatani M, Rossi F, Suematsu NJ, Kitahata H, Lagzi I. A Non-Autonomous Amphoteric Metal Hydroxide Oscillations and Pattern Formation in Hydrogels. Molecules. 2025; 30(6):1323. https://doi.org/10.3390/molecules30061323
Chicago/Turabian StyleNémet, Norbert, Hugh Shearer Lawson, Masaki Itatani, Federico Rossi, Nobuhiko J. Suematsu, Hiroyuki Kitahata, and István Lagzi. 2025. "A Non-Autonomous Amphoteric Metal Hydroxide Oscillations and Pattern Formation in Hydrogels" Molecules 30, no. 6: 1323. https://doi.org/10.3390/molecules30061323
APA StyleNémet, N., Lawson, H. S., Itatani, M., Rossi, F., Suematsu, N. J., Kitahata, H., & Lagzi, I. (2025). A Non-Autonomous Amphoteric Metal Hydroxide Oscillations and Pattern Formation in Hydrogels. Molecules, 30(6), 1323. https://doi.org/10.3390/molecules30061323







