Transient-Absorption Pump-Probe Spectra as Information-Rich Observables: Case Study of Fulvene
Abstract
1. Introduction
2. Theoretical Methods and Computational Details
2.1. SQC/MMST Approach
2.2. DW Representation of TA PP Signals
2.3. Computational Details
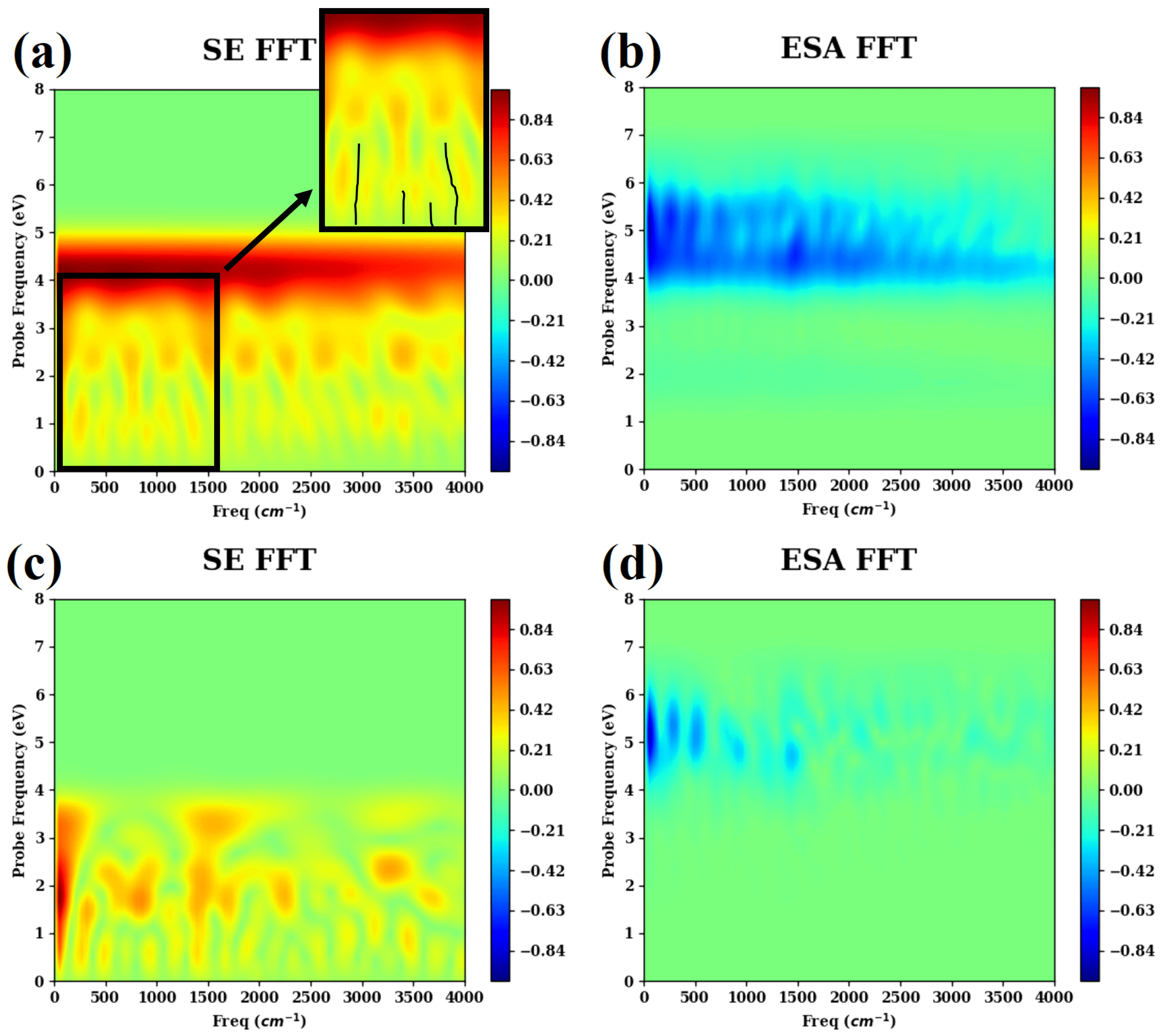
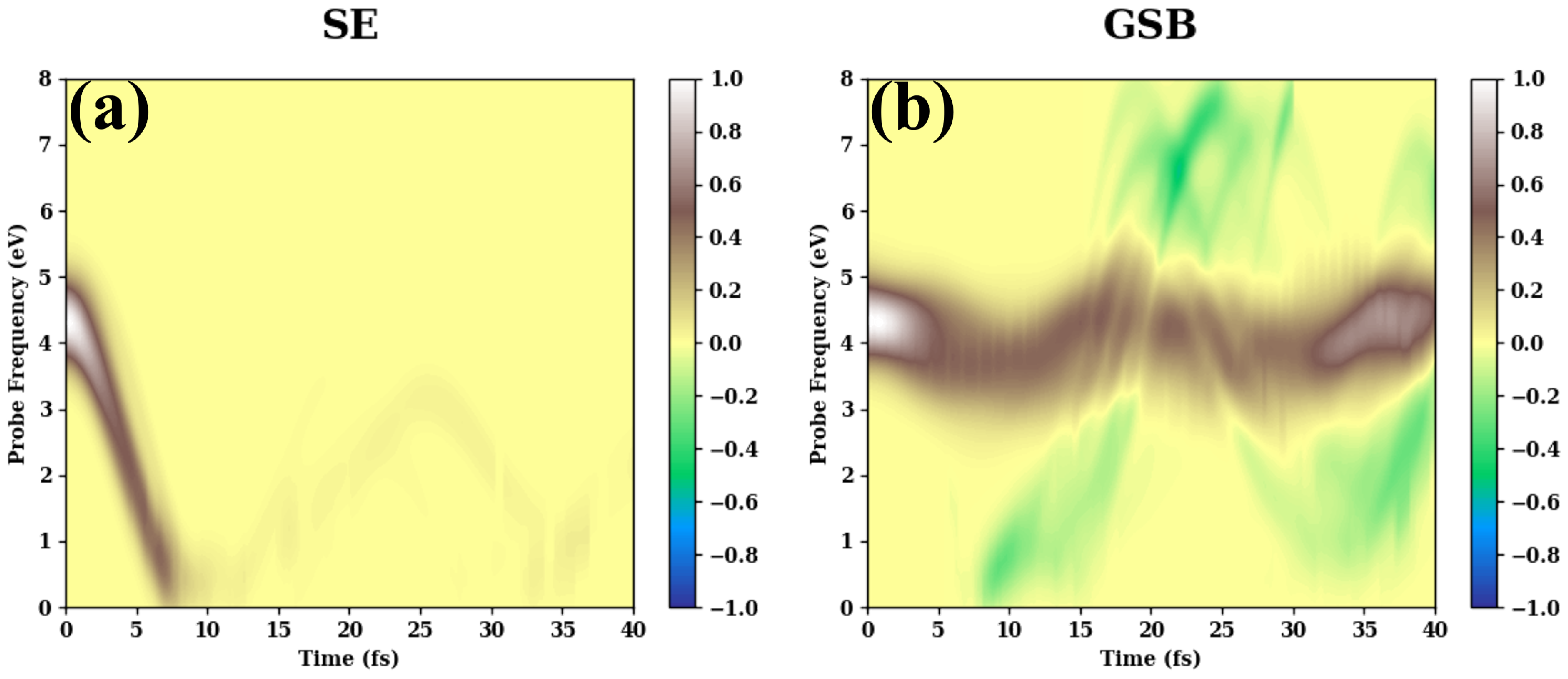
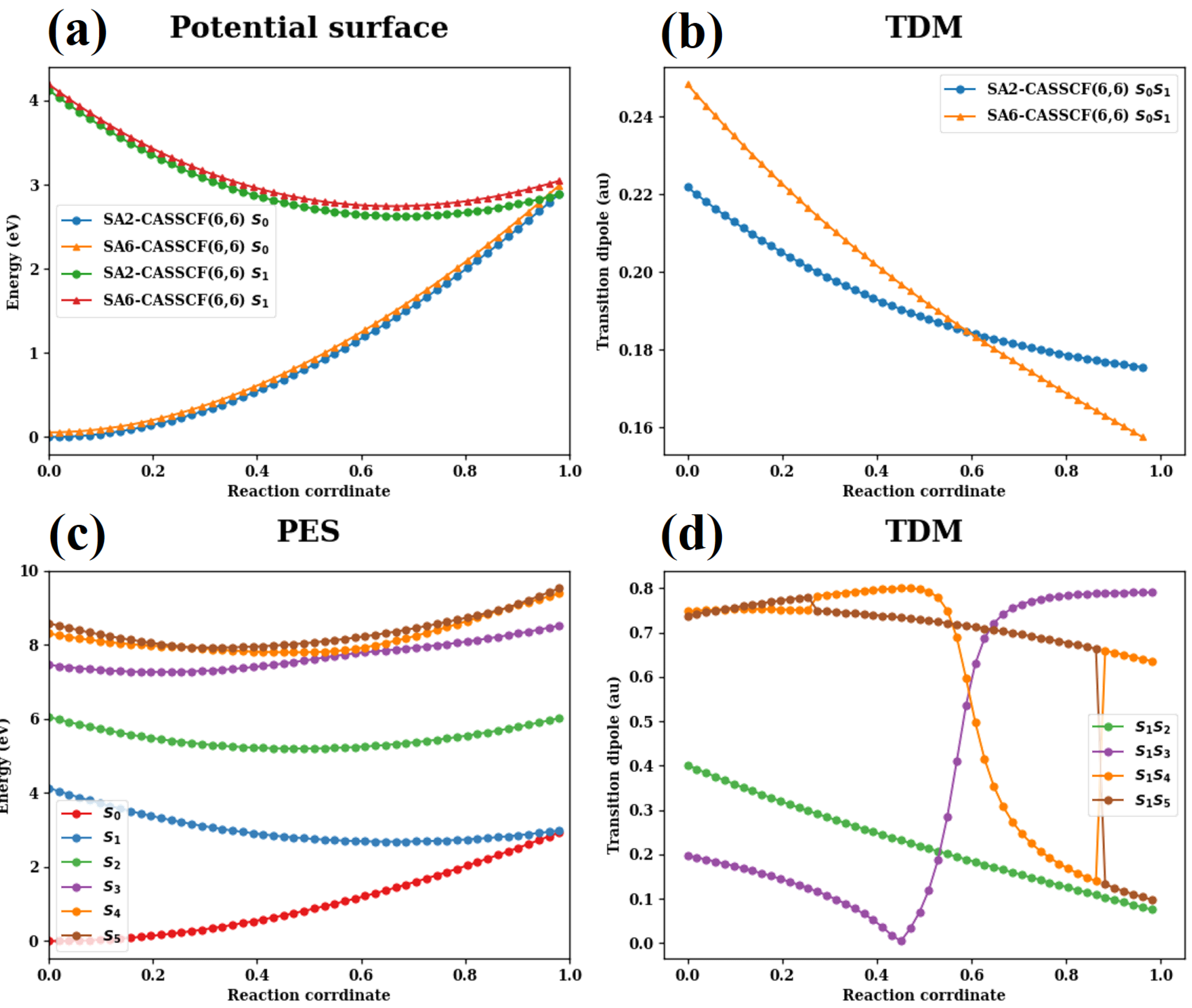
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
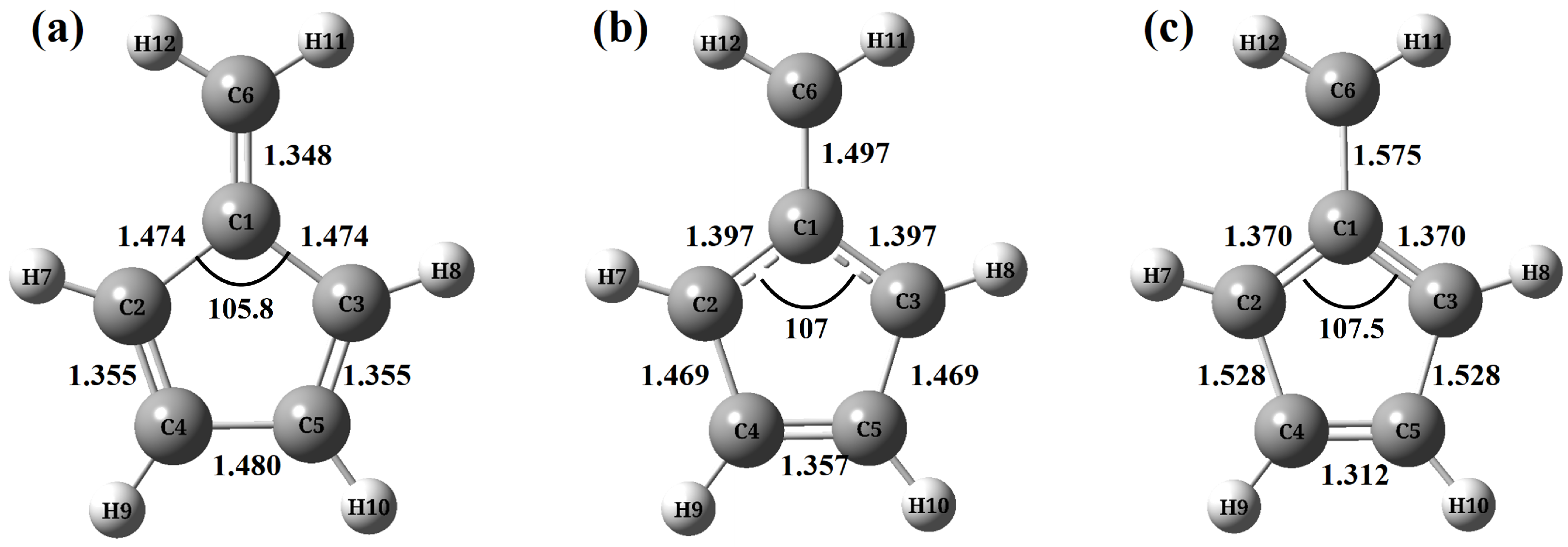
- CASSCF(6,6) level are shown in Figure A1.
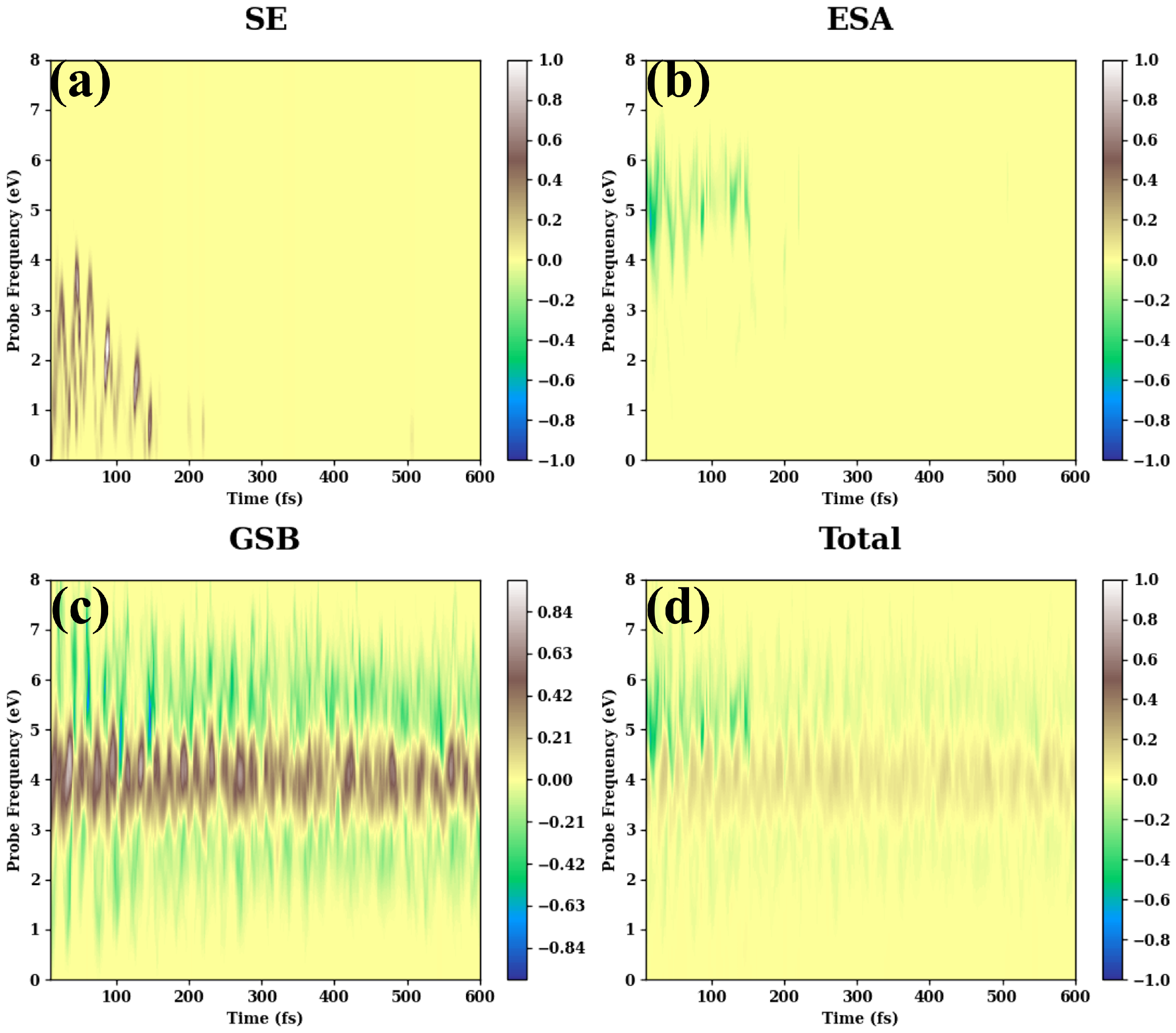
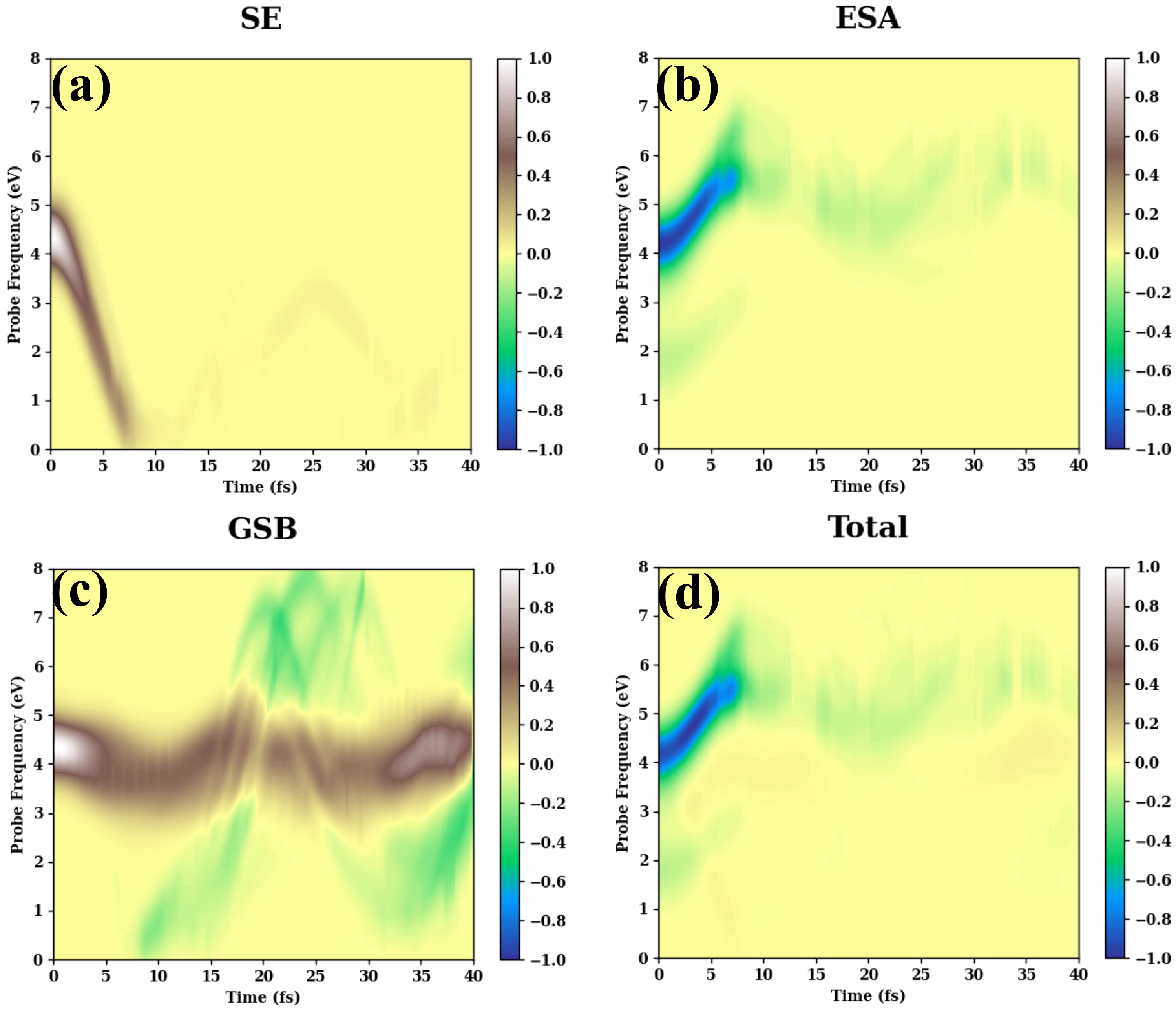
- The long-time TA PP signals are given in Figure A2.
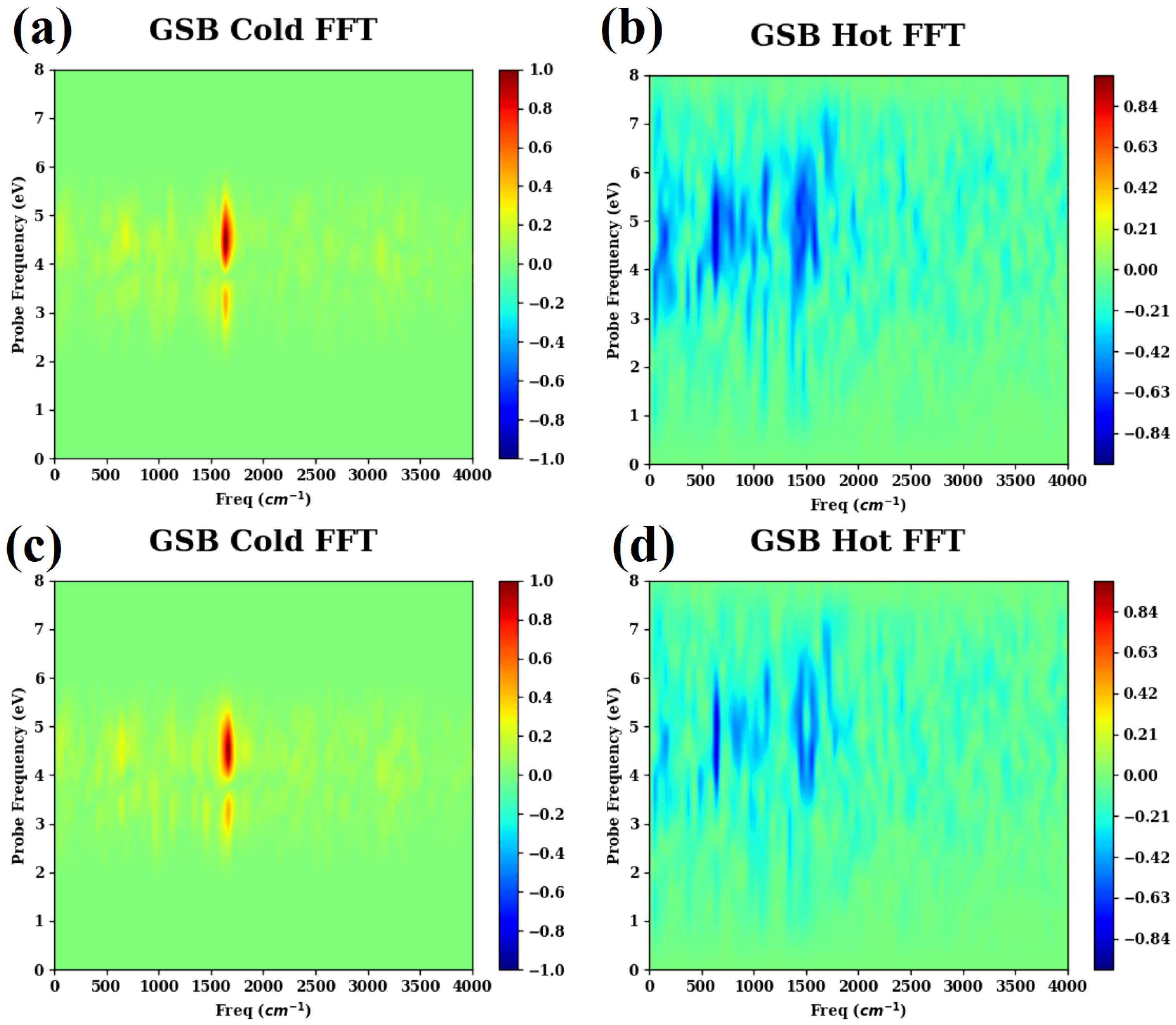
- The Fourier transforms of the cold and hot GSB signals are presented in Figure A3.
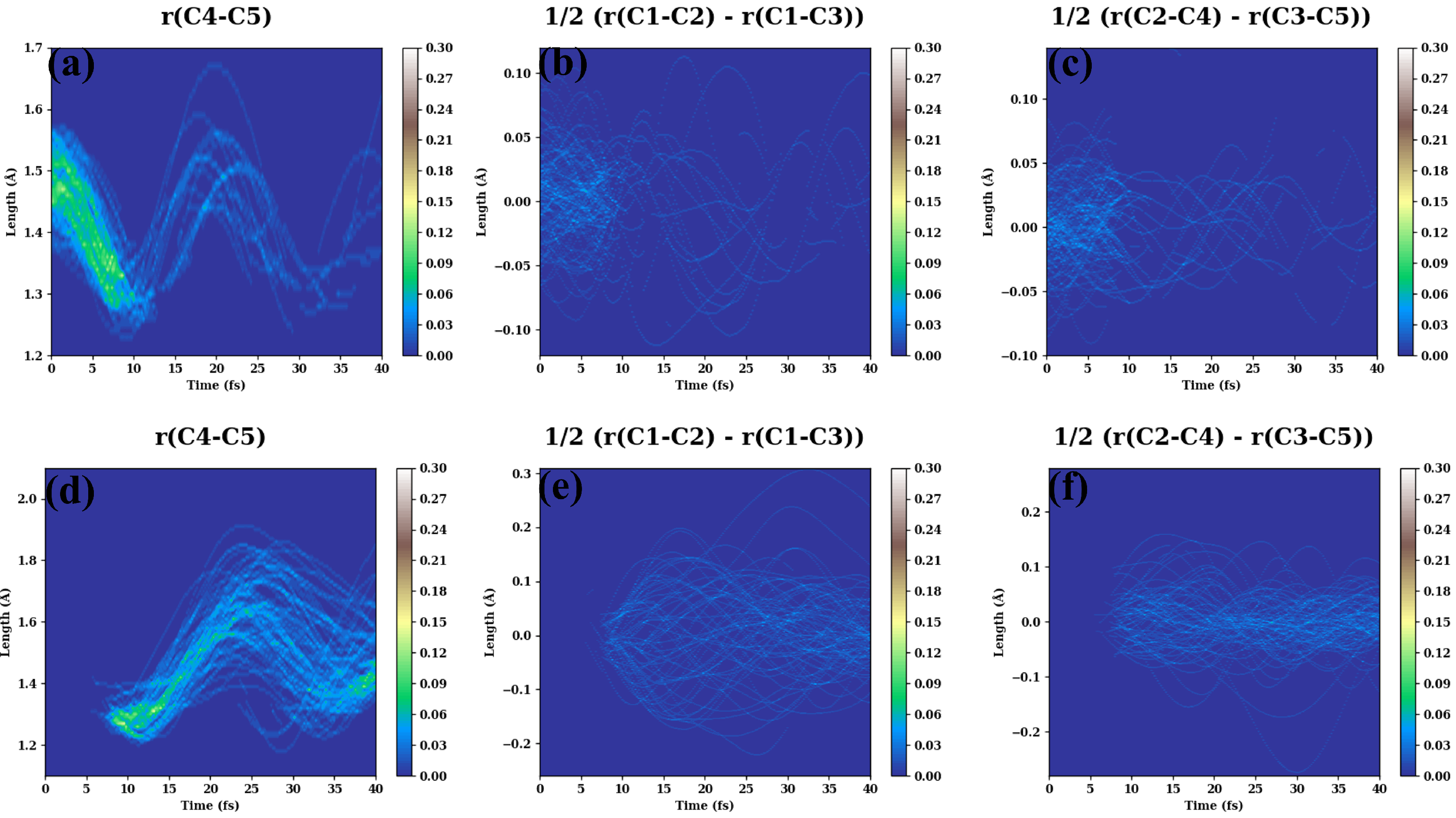
- The evolutions of several additional internal coordinates are displayed in Figure A4.
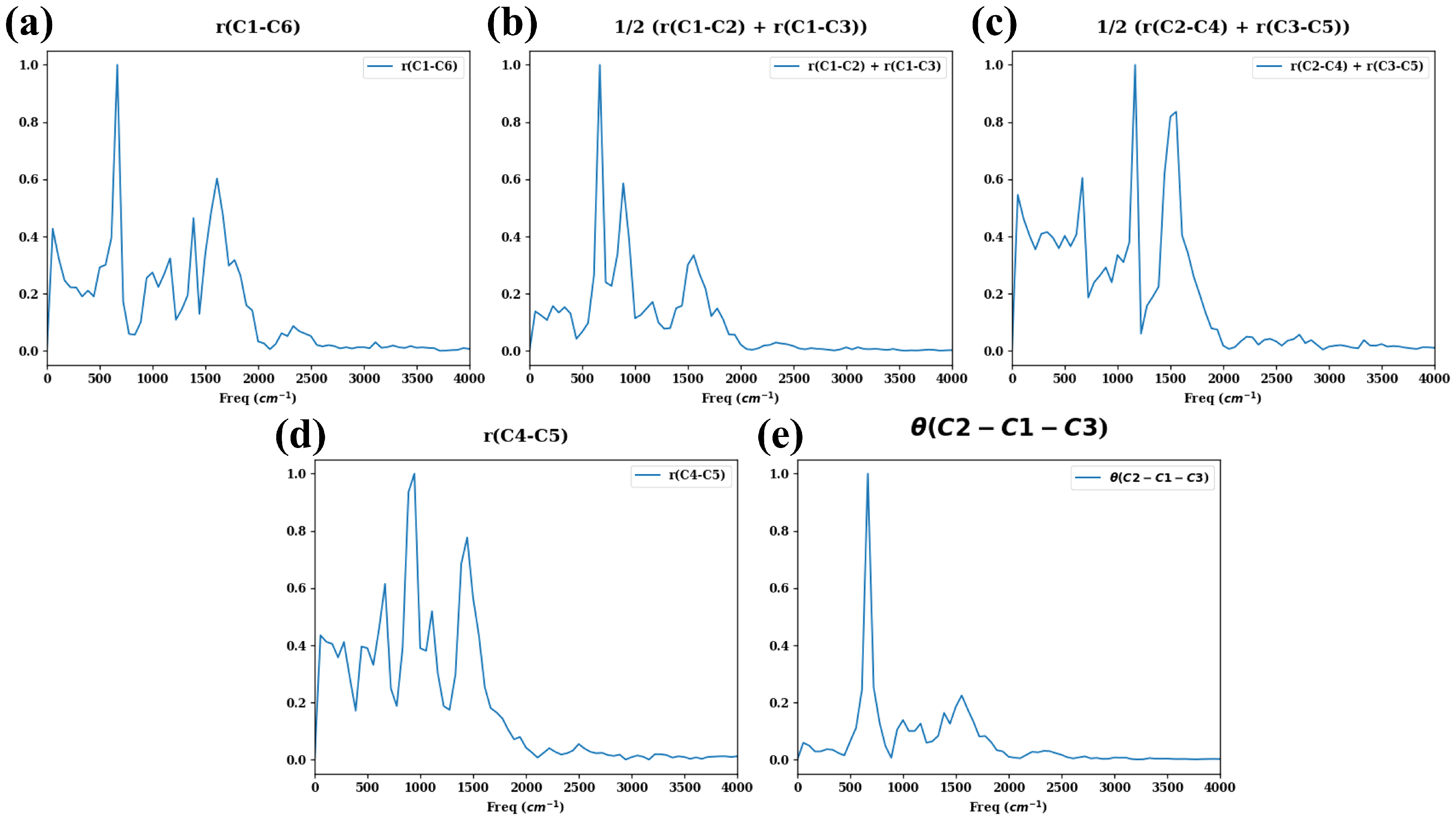
- Fourier transform of some critical nuclear motions is presented in Figure A5.
- The excitation energies and TDMs between different electronic states are collected in Table A1.
| Energy Gap (eV) | TDM (a.u.) | |
|---|---|---|
| 4.39 | 0.27 | |
| 1.79 | 0.41 | |
| 3.22 | 0.21 | |
| 4.03 | 0.75 | |
| 4.36 | 0.77 |
| Frequency cm−1 (Ranking) | Description | |
|---|---|---|
| A1 | 1781.04 (24) | C=C, CH2 sciss. |
| 1637.5 (22) | C=C(r) CH2 sciss., | |
| 1563.95 (21) | C=C(r), CH2 sciss., C=C | |
| 1483.03 (20) | CCH, C=C(r), C-C | |
| 1194.15 (17) | CCH | |
| 1048.43 (15) | C-C | |
| 957.18 (13) | C-C | |
| 706.37 (5) | CCC | |
| A2 | 929.85 (12) | CH wag |
| 797.32 (8) | CCH2 tors, CH wag | |
| 715.91 (6) | CCH2 tors, CH wag | |
| 512.82 (3) | CCCC(r) def | |
| B1 | 925.66 (11) | CH wag |
| 906.37 (10) | CH2 wag | |
| 790.47 (7) | CH wag | |
| 641.15 (4) | CCCC(r) def | |
| 221.89 (1) | CCCC def | |
| B2 | 1690.56 (23) | C=C(r) |
| 1461.33 (19) | C=C, CCH | |
| 1368.43 (18) | C=C, CCH | |
| 1187.5 (16) | CCH | |
| 1037.95 (14) | CH2 rock | |
| 856.37 (9) | CCC(r) | |
| 369.08 (2) | CCC |
| Frequency cm−1 (Ranking) | Description | |
|---|---|---|
| A1 | 1705.61 (23) | C=C, CH2 sciss. |
| 1646.85 (22) | C=C(r) CH2 sciss., | |
| 1590.15 (21) | C=C(r), CH2 sciss., C=C | |
| 1326.29 (18) | CCH, C=C(r), C-C | |
| 1210.35 (17) | CCH | |
| 1101.13 (16) | C-C | |
| 1008.5 (14) | C-C | |
| 679.71 (7) | CCC | |
| A2 | 903.59 (11) | CH wag |
| 806.51 (10) | CCH2 tors, CH wag | |
| 549.89 (6) | CCCC(r) def | |
| B1 | 802.96 (9) | CH wag |
| 701.58 (8) | CH wag | |
| 532.6 (5) | CCCC(r) def | |
| 270.14 (3) | CCCC def | |
| B2 | 1873.28 (24) | C=C(r) |
| 1485.52 (20) | C=C, CCH | |
| 1388.54 (19) | C=C, CCH | |
| 1088.25 (15) | CCH | |
| 996.15 (13) | CH2 rock | |
| 926.05 (12) | CCC(r) | |
| 322.72 (4) | CCC |
References
- Domcke, W.; Yarkony, D.; Köppel, H. Conical Intersections: Electronic Structure, Dynamics & Spectroscopy; World Scientific: Singapore, 2004; Volume 15. [Google Scholar]
- Domcke, W.; Yarkony, D.R.; Köppel, H. Conical Intersections: Theory, Computation and Experiment; World Scientific: Singapore, 2011; Volume 17. [Google Scholar]
- Yarkony, D.R. Nonadiabatic Quantum Chemistry Past, Present, and Future. Chem. Rev. 2012, 112, 481–498. [Google Scholar] [PubMed]
- Jasper, A.W.; Zhu, C.; Nangia, S.; Truhlar, D.G. Introductory lecture: Nonadiabatic effects in chemical dynamics. Faraday Discuss. 2004, 127, 1–22. [Google Scholar] [PubMed]
- Worth, G.A.; Cederbaum, L.S. Beyond Born-Oppenheimer: Molecular dynamics through a conical intersection. Annu. Rev. Phys. Chem. 2004, 55, 127–158. [Google Scholar]
- Schuurman, M.S.; Stolow, A. Dynamics at conical intersections. Annu. Rev. Phys. Chem. 2018, 69, 427–450. [Google Scholar]
- Matsika, S.; Krause, P. Nonadiabatic events and conical intersections. Annu. Rev. Phys. Chem. 2011, 62, 621–643. [Google Scholar]
- Domcke, W.; Yarkony, D.R. Role of conical intersections in molecular spectroscopy and photoinduced chemical dynamics. Annu. Rev. Phys. Chem. 2012, 63, 325–352. [Google Scholar] [PubMed]
- Zewail, A.H. Femtochemistry: Atomic-scale dynamics of the chemical bond. J. Phys. Chem. A 2000, 104, 5660–5694. [Google Scholar]
- Stolow, A. Femtosecond time-resolved photoelectron spectroscopy of polyatomic molecules. Annu. Rev. Phys. Chem. 2003, 54, 89–119. [Google Scholar]
- Stolow, A.; Bragg, A.E.; Neumark, D.M. Femtosecond time-resolved photoelectron spectroscopy. Chem. Rev. 2004, 104, 1719–1758. [Google Scholar]
- Dietze, D.R.; Mathies, R.A. Femtosecond stimulated Raman spectroscopy. ChemPhysChem 2016, 17, 1224–1251. [Google Scholar]
- Bressler, C.; Chergui, M. Ultrafast X-ray absorption spectroscopy. Chem. Rev. 2004, 104, 1781–1812. [Google Scholar] [PubMed]
- Milne, C.; Penfold, T.; Chergui, M. Recent experimental and theoretical developments in time-resolved X-ray spectroscopies. Coord. Chem. Rev. 2014, 277, 44–68. [Google Scholar]
- Fushitani, M. Applications of pump-probe spectroscopy. Annu. Rep. Sect. C Phys. Chem. 2008, 104, 272–297. [Google Scholar] [CrossRef]
- Ruckebusch, C.; Sliwa, M.; Pernot, P.d.; De Juan, A.; Tauler, R. Comprehensive data analysis of femtosecond transient absorption spectra: A review. J. Photochem. Photobiol. C 2012, 13, 1–27. [Google Scholar] [CrossRef]
- Braem, O.; Penfold, T.J.; Cannizzo, A.; Chergui, M. A femtosecond fluorescence study of vibrational relaxation and cooling dynamics of UV dyes. Phys. Chem. Chem. Phys. 2012, 14, 3513–3519. [Google Scholar] [CrossRef]
- Hall, G.E.; North, S.W. Transient laser frequency modulation spectroscopy. Annu. Rev. Phys. Chem. 2000, 51, 243–274. [Google Scholar] [CrossRef] [PubMed]
- Crespo-Hernández, C.E.; Cohen, B.; Hare, P.M.; Kohler, B. Ultrafast excited-state dynamics in nucleic acids. Chem. Rev. 2004, 104, 1977–2020. [Google Scholar] [CrossRef]
- Rulliere, C. Femtosecond Laser Pulses; Springer: New York, NY, USA, 2005. [Google Scholar]
- Diels, J.C.; Rudolph, W. Ultrashort Laser Pulse Phenomena; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Wei, Z.; Nakamura, T.; Takeuchi, S.; Tahara, T. Tracking of the nuclear wavepacket motion in cyanine photoisomerization by ultrafast pump–dump–probe spectroscopy. J. Am. Chem. Soc. 2011, 133, 8205–8210. [Google Scholar] [CrossRef]
- Auböck, G.; Consani, C.; van Mourik, F.; Chergui, M. Ultrabroadband femtosecond two-dimensional ultraviolet transient absorption. Opt. Lett. 2012, 37, 2337–2339. [Google Scholar] [CrossRef]
- Davydova, D.; de la Cadena, A.; Akimov, D.; Dietzek, B. Transient absorption microscopy: Advances in chemical imaging of photoinduced dynamics. Laser Photonics Rev. 2016, 10, 62–81. [Google Scholar]
- Gelin, M.F.; Huang, X.; Xie, W.; Chen, L.; Došlić, N.; Domcke, W. Ab initio surface-hopping simulation of femtosecond transient-absorption pump–probe signals of nonadiabatic excited-state dynamics using the doorway–window representation. J. Chem. Theory Comput. 2021, 17, 2394–2408. [Google Scholar] [PubMed]
- Mukamel, S. Principles of Nonlinear Optical Spectroscopy; Oxford Series in Optical and Imaging Sciences; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Egorova, D. Detection of electronic and vibrational coherences in molecular systems by 2D electronic photon echo spectroscopy. Chem. Phys. 2008, 347, 166–176. [Google Scholar]
- Kowalewski, M.; Bennett, K.; Dorfman, K.E.; Mukamel, S. Catching conical intersections in the act: Monitoring transient electronic coherences by attosecond stimulated X-ray Raman signals. Phys. Rev. Lett. 2015, 115, 193003. [Google Scholar]
- Kowalewski, M.; Bennett, K.; Mukamel, S. Monitoring nonadiabatic avoided crossing dynamics in molecules by ultrafast X-ray diffraction. Struct. Dyn. 2017, 4, 054101. [Google Scholar]
- Bennett, K.; Kowalewski, M.; Rouxel, J.R.; Mukamel, S. Monitoring molecular nonadiabatic dynamics with femtosecond X-ray diffraction. Proc. Natl. Acad. Sci. USA 2018, 115, 6538–6547. [Google Scholar]
- Segatta, F.; Nenov, A.; Orlandi, S.; Arcioni, A.; Mukamel, S.; Garavelli, M. Exploring the capabilities of optical pump X-ray probe NEXAFS spectroscopy to track photo-induced dynamics mediated by conical intersections. Faraday Discuss. 2020, 221, 245–264. [Google Scholar]
- Liu, Y.; Martínez-Fernández, L.; Cerezo, J.; Prampolini, G.; Improta, R.; Santoro, F. Multistate coupled quantum dynamics of photoexcited cytosine in gas-phase: Nonadiabatic absorption spectrum and ultrafast internal conversions. Chem. Phys. 2018, 515, 452–463. [Google Scholar]
- Wang, H.; Thoss, M. Nonperturbative quantum simulation of time-resolved nonlinear spectra: Methodology and application to electron transfer reactions in the condensed phase. Chem. Phys. 2008, 347, 139–151. [Google Scholar]
- Kramer, T.; Noack, M.; Reinefeld, A.; Rodríguez, M.; Zelinskyy, Y. Efficient calculation of open quantum system dynamics and time-resolved spectroscopy with distributed memory HEOM (DM-HEOM). J. Comput. Chem. 2018, 39, 1779–1794. [Google Scholar]
- Toutounji, M. Electronic dephasing of polyatomic molecules interacting with mixed quantum-classical media. Phys. Chem. Chem. Phys. 2021, 23, 21981–21994. [Google Scholar]
- Toutounji, M. Mixed Quantum-Classical Liouville Equation Treatment of Electronic Spectroscopy of Condensed Systems: Harmonic and Anharmonic Electron–Phonon Coupling. J. Chem. Theory Comput. 2023, 19, 3779–3797. [Google Scholar] [PubMed]
- Petit, A.S.; Subotnik, J.E. Calculating time-resolved differential absorbance spectra for ultrafast pump-probe experiments with surface hopping trajectories. J. Chem. Phys. 2014, 141, 154108. [Google Scholar]
- Petit, A.S.; Subotnik, J.E. How to calculate linear absorption spectra with lifetime broadening using fewest switches surface hopping trajectories: A simple generalization of ground-state Kubo theory. J. Chem. Phys. 2014, 141, 014107. [Google Scholar] [PubMed]
- Tempelaar, R.; Van Der Vegte, C.P.; Knoester, J.; Jansen, T.L. Surface hopping modeling of two-dimensional spectra. J. Chem. Phys. 2013, 138, 164106. [Google Scholar]
- Humeniuk, A.; Wohlgemuth, M.; Suzuki, T.; Mitrić, R. Time-resolved photoelectron imaging spectra from non-adiabatic molecular dynamics simulations. J. Chem. Phys. 2013, 139, 134104. [Google Scholar] [PubMed]
- Van Der Vegte, C.; Dijkstra, A.; Knoester, J.; Jansen, T. Calculating two-dimensional spectra with the mixed quantum-classical ehrenfest method. J. Phys. Chem. A 2013, 117, 5970–5980. [Google Scholar]
- Heller, E.J. The Semiclassical Way to Dynamics and Spectroscopy; Princeton University Press: Princeton, NJ, USA, 2018. [Google Scholar]
- Kowalewski, M.; Fingerhut, B.P.; Dorfman, K.E.; Bennett, K.; Mukamel, S. Simulating coherent multidimensional spectroscopy of nonadiabatic molecular processes: From the infrared to the x-ray regime. Chem. Rev. 2017, 117, 12165–12226. [Google Scholar]
- Crespo-Otero, R.; Barbatti, M. Recent advances and perspectives on nonadiabatic mixed quantum–classical dynamics. Chem. Rev. 2018, 118, 7026–7068. [Google Scholar]
- Mai, S.; González, L. Molecular photochemistry: Recent developments in theory. Angew. Chem. Int. Ed. 2020, 59, 16832–16846. [Google Scholar]
- Conti, I.; Cerullo, G.; Nenov, A.; Garavelli, M. Ultrafast spectroscopy of photoactive molecular systems from first principles: Where we stand today and where we are going. J. Am. Chem. Soc. 2020, 142, 16117–16139. [Google Scholar]
- Loring, R.F. Calculating multidimensional optical spectra from classical trajectories. Annu. Rev. Phys. Chem. 2022, 73, 273–297. [Google Scholar] [PubMed]
- Yan, Y.; Liu, Y.; Xing, T.; Shi, Q. Theoretical Study of Excitation Energy Transfer and Nonlinear Spectroscopy of Photosynthetic Light- Harvesting Complexes Using the Nonperturbative Reduced Dynamics Method. WIREs Comput. Mol. Sci. 2021, 11, e1498. [Google Scholar]
- Gelin, M.F.; Chen, L.; Domcke, W. Equation-of-motion methods for the calculation of femtosecond time-resolved 4-wave-mixing and N-wave-mixing signals. Chem. Rev. 2022, 122, 17339–17396. [Google Scholar]
- Jansen, T.L.C. Computational spectroscopy of complex systems. J. Chem. Phys. 2021, 155, 170901. [Google Scholar] [PubMed]
- Krumland, J.; Guerrini, M.; De Sio, A.; Lienau, C.; Cocchi, C. Two-dimensional electronic spectroscopy from first principles. Appl. Phys. Rev. 2024, 11, 011305. [Google Scholar]
- Faraji, S.; Picconi, D.; Palacino-González, E. Advanced quantum and semiclassical methods for simulating photoinduced molecular dynamics and spectroscopy. WIREs Comput. Mol. Sci. 2024, 14, e1731. [Google Scholar]
- Richter, M.; Fingerhut, B.P. Simulation of multi-dimensional signals in the optical domain: Quantum-classical feedback in nonlinear exciton propagation. J. Chem. Theory Comput. 2016, 12, 3284–3294. [Google Scholar]
- Šulc, M.; Hernández, H.; Martínez, T.J.; Vaníček, J. Relation of exact Gaussian basis methods to the dephasing representation: Theory and application to time-resolved electronic spectra. J. Chem. Phys. 2013, 139, 034112. [Google Scholar]
- Zimmermann, T.; Vaníček, J. Efficient on-the-fly ab initio semiclassical method for computing time-resolved nonadiabatic electronic spectra with surface hopping or Ehrenfest dynamics. J. Chem. Phys. 2014, 141, 134102. [Google Scholar]
- Begušić, T.; Roulet, J.; Vaníček, J. On-the-fly ab initio semiclassical evaluation of time-resolved electronic spectra. J. Chem. Phys. 2018, 149, 244115. [Google Scholar]
- Begušić, T.; Vaníček, J. On-the-fly ab initio semiclassical evaluation of third-order response functions for two-dimensional electronic spectroscopy. J. Chem. Phys. 2020, 153, 184110. [Google Scholar]
- Nguyen, T.S.; Koh, J.H.; Lefelhocz, S.; Parkhill, J. Black-box, real-time simulations of transient absorption spectroscopy. J. Phys. Chem. Lett. 2016, 7, 1590–1595. [Google Scholar] [PubMed]
- Meyer, H.D.; Miller, W.H. A classical analog for electronic degrees of freedom in nonadiabatic collision processes. J. Chem. Phys. 1979, 70, 3214–3223. [Google Scholar]
- Stock, G.; Thoss, M. Semiclassical description of nonadiabatic quantum dynamics. Phys. Rev. Lett. 1997, 78, 578. [Google Scholar]
- Thoss, M.; Stock, G. Mapping approach to the semiclassical description of nonadiabatic quantum dynamics. Phys. Rev. A 1999, 59, 64. [Google Scholar]
- Huo, P.; Coker, D.F. Communication: Partial linearized density matrix dynamics for dissipative, non-adiabatic quantum evolution. J. Chem. Phys. 2011, 135, 201101. [Google Scholar]
- Lee, M.K.; Huo, P.; Coker, D.F. Semiclassical path integral dynamics: Photosynthetic energy transfer with realistic environment interactions. Annu. Rev. Phys. Chem. 2016, 67, 639–668. [Google Scholar] [CrossRef]
- Hsieh, C.Y.; Schofield, J.; Kapral, R. Forward–backward solution of quantum-classical Liouville equation in the adiabatic mapping basis. Mol. Phys. 2013, 111, 3546–3554. [Google Scholar] [CrossRef]
- Liu, J.; He, X.; Wu, B. Unified formulation of phase space mapping approaches for nonadiabatic quantum dynamics. Acc. Chem. Res. 2021, 54, 4215–4228. [Google Scholar] [CrossRef]
- He, X.; Wu, B.; Shang, Y.; Li, B.; Cheng, X.; Liu, J. New phase space formulations and quantum dynamics approaches. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2022, 12, e1619. [Google Scholar]
- Wu, B.; He, X.; Liu, J. Nonadiabatic Field on Quantum Phase Space: A Century after Ehrenfest. J. Phys. Chem. Lett. 2024, 15, 644–658. [Google Scholar]
- Miller, W.H.; Cotton, S.J. Classical molecular dynamics simulation of electronically non-adiabatic processes. Faraday Discuss. 2016, 195, 9–30. [Google Scholar] [PubMed]
- Mandal, A.; Yamijala, S.S.; Huo, P. Quasi-diabatic representation for nonadiabatic dynamics propagation. J. Chem. Theory Comput. 2018, 14, 1828–1840. [Google Scholar] [PubMed]
- Zhou, W.; Mandal, A.; Huo, P. Quasi-diabatic scheme for nonadiabatic on-the-fly simulations. J. Phys. Chem. Lett. 2019, 10, 7062–7070. [Google Scholar]
- Hu, D.; Mandal, A.; Weight, B.M.; Huo, P. Quasi-diabatic propagation scheme for simulating polariton chemistry. J. Chem. Phys. 2022, 157, 194109. [Google Scholar] [PubMed]
- Church, M.S.; Hele, T.J.; Ezra, G.S.; Ananth, N. Nonadiabatic semiclassical dynamics in the mixed quantum-classical initial value representation. J. Chem. Phys. 2018, 148, 102326. [Google Scholar]
- Conte, R.; Aieta, C.; Cazzaniga, M.; Ceotto, M. A perspective on the investigation of spectroscopy and kinetics of complex molecular systems with semiclassical approaches. J. Phys. Chem. Lett. 2024, 15, 7566–7576. [Google Scholar]
- Stock, G.; Miller, W.H. A classical model for time-and frequency-resolved spectroscopy of nonadiabatic excited-state dynamics. Chem. Phys. Lett. 1992, 197, 396–404. [Google Scholar]
- Uspenskiy, I.; Strodel, B.; Stock, G. Classical calculation of transient absorption spectra monitoring ultrafast electron transfer processes. J. Chem. Theory Comput. 2006, 2, 1605–1617. [Google Scholar]
- Uspenskiy, I.; Strodel, B.; Stock, G. Classical description of the dynamics and time-resolved spectroscopy of nonadiabatic cis–trans photoisomerization. Chem. Phys. 2006, 329, 109–117. [Google Scholar]
- Loring, R.F. Mean-trajectory approximation for electronic and vibrational-electronic nonlinear spectroscopy. J. Chem. Phys. 2017, 146, 144106. [Google Scholar]
- Polley, K.; Loring, R.F. Two-dimensional vibronic spectra from classical trajectories. J. Chem. Phys. 2019, 150, 164114. [Google Scholar] [PubMed]
- Kwac, K.; Geva, E. A mixed quantum-classical molecular dynamics study of the hydroxyl stretch in methanol/carbon tetrachloride mixtures III: Nonequilibrium hydrogen-bond dynamics and infrared pump–probe spectra. J. Phys. Chem. B 2013, 117, 7737–7749. [Google Scholar]
- Gao, X.; Lai, Y.; Geva, E. Simulating absorption spectra of multiexcitonic systems via quasiclassical mapping Hamiltonian methods. J. Chem. Theory Comput. 2020, 16, 6465–6480. [Google Scholar] [PubMed]
- Gao, X.; Geva, E. A nonperturbative methodology for simulating multidimensional spectra of multiexcitonic molecular systems via quasiclassical mapping Hamiltonian methods. J. Chem. Theory Comput. 2020, 16, 6491–6502. [Google Scholar]
- McRobbie, P.L.; Hanna, G.; Shi, Q.; Geva, E. Signatures of nonequilibrium solvation dynamics on multidimensional spectra. Acc. Chem. Res. 2009, 42, 1299–1309. [Google Scholar] [PubMed]
- Bai, S.; Xie, W.; Zhu, L.; Shi, Q. Calculation of absorption spectra involving multiple excited states: Approximate methods based on the mixed quantum classical Liouville equation. J. Chem. Phys. 2014, 140, 084105. [Google Scholar]
- Provazza, J.; Segatta, F.; Garavelli, M.; Coker, D.F. Semiclassical path integral calculation of nonlinear optical spectroscopy. J. Chem. Theory Comput. 2018, 14, 856–866. [Google Scholar]
- Provazza, J.; Coker, D.F. Communication: Symmetrical quasi-classical analysis of linear optical spectroscopy. J. Chem. Phys. 2018, 148, 181102. [Google Scholar]
- Provazza, J.; Segatta, F.; Coker, D.F. Modeling nonperturbative field-driven vibronic dynamics: Selective state preparation and nonlinear spectroscopy. J. Chem. Theory Comput. 2020, 17, 29–39. [Google Scholar]
- Sun, X. Hybrid equilibrium-nonequilibrium molecular dynamics approach for two-dimensional solute-pump/solvent-probe spectroscopy. J. Chem. Phys. 2019, 151, 194507. [Google Scholar] [CrossRef]
- Karsten, S.; Ivanov, S.D.; Bokarev, S.I.; Kühn, O. Quasi-classical approaches to vibronic spectra revisited. J. Chem. Phys. 2018, 148, 102337. [Google Scholar] [CrossRef] [PubMed]
- Mannouch, J.R.; Richardson, J.O. A partially linearized spin-mapping approach for simulating nonlinear optical spectra. J. Chem. Phys. 2022, 156, 024108. [Google Scholar] [CrossRef] [PubMed]
- Polley, K.; Loring, R.F. Spectroscopic response theory with classical mapping Hamiltonians. J. Chem. Phys. 2020, 153, 204103. [Google Scholar] [CrossRef]
- Seidner, L.; Stock, G.; Domcke, W. Nonperturbative approach to femtosecond spectroscopy: General theory and application to multidimensional nonadiabatic photoisomerization processes. J. Chem. Phys. 1995, 103, 3998–4011. [Google Scholar] [CrossRef]
- Gelin, M.F.; Egorova, D.; Domcke, W. Efficient method for the calculation of time-and frequency-resolved four-wave mixing signals and its application to photon-echo spectroscopy. J. Chem. Phys. 2005, 123, 164112. [Google Scholar] [CrossRef]
- Mančal, T.; Pisliakov, A.V.; Fleming, G.R. Two-dimensional optical three-pulse photon echo spectroscopy. I. Nonperturbative approach to the calculation of spectra. J. Chem. Phys. 2006, 124, 234504. [Google Scholar] [CrossRef]
- Ka, B.J.; Geva, E. A nonperturbative calculation of nonlinear spectroscopic signals in liquid solution. J. Chem. Phys. 2006, 125, 214501. [Google Scholar] [CrossRef]
- Yan, Y.J.; Fried, L.E.; Mukamel, S. Ultrafast pump-probe spectroscopy: Femtosecond dynamics in Liouville space. J. Phys. Chem. 1989, 93, 8149–8162. [Google Scholar] [CrossRef]
- Yan, Y.J.; Mukamel, S. Femtosecond pump-probe spectroscopy of polyatomic molecules in condensed phases. Phys. Rev. A 1990, 41, 6485. [Google Scholar] [CrossRef]
- Bosma, W.B.; Yan, Y.J.; Mukamel, S. Intramolecular and solvent dynamics in femtosecond pump–probe spectroscopy. J. Chem. Phys. 1990, 93, 3863–3873. [Google Scholar] [CrossRef]
- Pollard, W.T.; Lee, S.Y.; Mathies, R.A. Wave packet theory of dynamic absorption spectra in femtosecond pump–probe experiments. J. Chem. Phys. 1990, 92, 4012–4029. [Google Scholar]
- Pollard, W.T.; Mathies, R.A. Analysis of femtosecond dynamic absorption spectra of nonstationary states. Annu. Rev. Phys. Chem. 1992, 43, 497–523. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Lin, C.; Peng, J.; Zhang, J.; Lin, S.; Gu, F.L.; Gelin, M.F.; Lan, Z. On-the-fly simulation of time-resolved fluorescence spectra and anisotropy. J. Chem. Phys. 2024, 160, 104109. [Google Scholar]
- Xu, C.; Lin, K.; Hu, D.; Gu, F.L.; Gelin, M.F.; Lan, Z. Ultrafast internal conversion dynamics through the on-the-Fly simulation of transient absorption pump–probe spectra with different electronic structure methods. J. Phys. Chem. Lett. 2022, 13, 661–668. [Google Scholar]
- Hu, D.; Peng, J.; Chen, L.; Gelin, M.F.; Lan, Z. Spectral fingerprint of excited-state energy transfer in dendrimers through polarization-sensitive transient-absorption pump–probe signals: On-the-fly nonadiabatic dynamics simulations. J. Phys. Chem. Lett. 2021, 12, 9710–9719. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Xie, W.; Došlić, N.; Gelin, M.F.; Domcke, W. Ab initio quasiclassical simulation of femtosecond time-resolved two-dimensional electronic spectra of pyrazine. J. Phys. Chem. Lett. 2021, 12, 11736–11744. [Google Scholar] [CrossRef] [PubMed]
- Pios, S.V.; Gelin, M.F.; Ullah, A.; Dral, P.O.; Chen, L. Artificial-Intelligence-Enhanced On-the-Fly Simulation of Nonlinear Time-Resolved Spectra. J. Phys. Chem. Lett. 2024, 15, 2325–2331. [Google Scholar] [CrossRef]
- Perez-Castillo, R.; Freixas, V.M.; Mukamel, S.; Martinez-Mesa, A.; Uranga-Pina, L.; Tretiak, S.; Gelin, M.F.; Fernandez-Alberti, S. Transient-absorption spectroscopy of dendrimers via nonadiabatic excited-state dynamics simulations. Chem. Sci. 2024, 15, 13250–13261. [Google Scholar] [CrossRef]
- Li, Z.; Peng, J.; Zhu, Y.; Xu, C.; Gelin, M.F.; Gu, F.L.; Lan, Z. On-the-fly simulations of transient absorption pump-probe spectra: Combining mapping dynamics with doorway-window protocol. ChemRxiv, 2024; preprint. [Google Scholar]
- Cotton, S.J.; Miller, W.H. Symmetrical windowing for quantum states in quasi-classical trajectory simulations. J. Phys. Chem. A 2013, 117, 7190–7194. [Google Scholar] [CrossRef]
- Cotton, S.J.; Miller, W.H. Symmetrical windowing for quantum states in quasi-classical trajectory simulations: Application to electronically non-adiabatic processes. J. Chem. Phys. 2013, 139, 234112. [Google Scholar] [PubMed]
- Xie, Y.; Zheng, J.; Lan, Z. Performance evaluation of the symmetrical quasi-classical dynamics method based on Meyer-Miller mapping Hamiltonian in the treatment of site-exciton models. J. Chem. Phys. 2018, 149, 174105. [Google Scholar] [PubMed]
- He, X.; Cheng, X.; Wu, B.; Liu, J. Nonadiabatic Field with Triangle Window Functions on Quantum Phase Space. J. Phys. Chem. Lett. 2024, 15, 5452–5466. [Google Scholar]
- Gao, X.; Saller, M.A.; Liu, Y.; Kelly, A.; Richardson, J.O.; Geva, E. Benchmarking quasiclassical mapping Hamiltonian methods for simulating electronically nonadiabatic molecular dynamics. J. Chem. Theory Comput. 2020, 16, 2883–2895. [Google Scholar] [PubMed]
- Jain, A.; Subotnik, J.E. Vibrational energy relaxation: A benchmark for mixed quantum–classical methods. J. Phys. Chem. A 2018, 122, 16–27. [Google Scholar]
- Cotton, S.J.; Liang, R.; Miller, W.H. On the adiabatic representation of Meyer-Miller electronic-nuclear dynamics. J. Chem. Phys. 2017, 147, 064112. [Google Scholar]
- Tang, D.; Fang, W.H.; Shen, L.; Cui, G. Combining Meyer–Miller Hamiltonian with electronic structure methods for on-the-fly nonadiabatic dynamics simulations: Implementation and application. Phys. Chem. Chem. Phys. 2019, 21, 17109–17117. [Google Scholar]
- Hu, D.; Xie, Y.; Peng, J.; Lan, Z. On-the-fly symmetrical quasi-classical dynamics with Meyer–Miller mapping Hamiltonian for the treatment of nonadiabatic dynamics at conical intersections. J. Chem. Theory Comput. 2021, 17, 3267–3279. [Google Scholar]
- Talbot, J.J.; Head-Gordon, M.; Cotton, S.J. The symmetric quasi-classical model using on-the-fly time-dependent density functional theory within the Tamm–Dancoff approximation. Mol. Phys. 2023, 121, e2153761. [Google Scholar]
- Tully, J.C. Molecular dynamics with electronic transitions. J. Chem. Phys. 1990, 93, 1061–1071. [Google Scholar]
- Ibele, L.M.; Curchod, B.F. A molecular perspective on Tully models for nonadiabatic dynamics. Phys. Chem. Chem. Phys. 2020, 22, 15183–15196. [Google Scholar] [CrossRef]
- Ibele, L.M.; Lassmann, Y.; Martínez, T.J.; Curchod, B.F. Comparing (stochastic-selection) ab initio multiple spawning with trajectory surface hopping for the photodynamics of cyclopropanone, fulvene, and dithiane. J. Chem. Phys. 2021, 154, 104110. [Google Scholar] [CrossRef] [PubMed]
- Vindel-Zandbergen, P.; Ibele, L.M.; Ha, J.K.; Min, S.K.; Curchod, B.F.; Maitra, N.T. Study of the decoherence correction derived from the exact factorization approach for nonadiabatic dynamics. J. Chem. Theory Comput. 2021, 17, 3852–3862. [Google Scholar] [CrossRef] [PubMed]
- Weight, B.M.; Mandal, A.; Huo, P. Ab initio symmetric quasi-classical approach to investigate molecular Tully models. J. Chem. Phys. 2021, 155, 084106. [Google Scholar] [CrossRef] [PubMed]
- Grohmann, T.; Deeb, O.; Leibscher, M. Quantum separation of para-and ortho-fulvene with coherent light: The influence of the conical intersection. Chem. Phys. 2007, 338, 252–258. [Google Scholar] [CrossRef]
- Alfalah, S.; Belz, S.; Deeb, O.; Leibscher, M.; Manz, J.; Zilberg, S. Photoinduced quantum dynamics of ortho-and para-fulvene: Hindered photoisomerization due to mode selective fast radiationless decay via a conical intersection. J. Chem. Phys. 2009, 130, 124318. [Google Scholar] [CrossRef]
- Mendive-Tapia, D.; Lasorne, B.; Worth, G.A.; Bearpark, M.J.; Robb, M.A. Controlling the mechanism of fulvene S 1/S 0 decay: Switching off the stepwise population transfer. Phys. Chem. Chem. Phys. 2010, 12, 15725–15733. [Google Scholar] [CrossRef]
- Mendive-Tapia, D.; Lasorne, B.; Worth, G.A.; Robb, M.A.; Bearpark, M.J. Towards converging non-adiabatic direct dynamics calculations using frozen-width variational Gaussian product basis functions. J. Chem. Phys. 2012, 137, 22A548. [Google Scholar] [CrossRef]
- Bearpark, M.J.; Bernardi, F.; Olivucci, M.; Robb, M.A.; Smith, B.R. Can fulvene S1 decay be controlled? A CASSCF study with MMVB dynamics. J. Am. Chem. Soc. 1996, 118, 5254–5260. [Google Scholar] [CrossRef]
- Toldo, J.M.; Mattos, R.S.; Pinheiro, M., Jr.; Mukherjee, S.; Barbatti, M. Recommendations for velocity adjustment in surface hopping. J. Chem. Theory Comput. 2024, 20, 614–624. [Google Scholar] [CrossRef]
- Cotton, S.J.; Miller, W.H. A new symmetrical quasi-classical model for electronically non-adiabatic processes: Application to the case of weak non-adiabatic coupling. J. Chem. Phys. 2016, 145, 144108. [Google Scholar] [CrossRef]
- Cotton, S.J.; Miller, W.H. A symmetrical quasi-classical windowing model for the molecular dynamics treatment of non-adiabatic processes involving many electronic states. J. Chem. Phys. 2019, 150, 104101. [Google Scholar]
- Liu, J. A unified theoretical framework for mapping models for the multi-state Hamiltonian. J. Chem. Phys. 2016, 145, 204105. [Google Scholar] [PubMed]
- Cheng, X.; He, X.; Liu, J. A novel class of phase space representations for the exact population dynamics of two-state quantum systems and the relation to triangle window functions. Chin. J. Chem. Phys. 2024, 37, 230–254. [Google Scholar]
- Gao, X.; Geva, E. Improving the accuracy of quasiclassical mapping Hamiltonian methods by treating the window function width as an adjustable parameter. J. Phys. Chem. A 2020, 124, 11006–11016. [Google Scholar] [CrossRef] [PubMed]
- Stock, G.; Müller, U. Flow of zero-point energy and exploration of phase space in classical simulations of quantum relaxation dynamics. J. Chem. Phys. 1999, 111, 65–76. [Google Scholar]
- Cotton, S.J.; Miller, W.H. Trajectory-adjusted electronic zero point energy in classical Meyer-Miller vibronic dynamics: Symmetrical quasiclassical application to photodissociation. J. Chem. Phys. 2019, 150, 194110. [Google Scholar] [CrossRef]
- He, X.; Gong, Z.; Wu, B.; Liu, J. Negative zero-point-energy parameter in the Meyer–Miller mapping model for nonadiabatic dynamics. J. Phys. Chem. Lett. 2021, 12, 2496–2501. [Google Scholar]
- He, X.; Wu, B.; Gong, Z.; Liu, J. Commutator matrix in phase space mapping models for nonadiabatic quantum dynamics. J. Phys. Chem. A 2021, 125, 6845–6863. [Google Scholar]
- Lax, M. The Franck-Condon principle and its application to crystals. J. Chem. Phys. 1952, 20, 1752–1760. [Google Scholar]
- Hillery, M.; O’Connel, R.F.; Scully, M.O.; Wigner, E.P. Distribution Functions in Physics: Fundamentals. Phys. Rep. 1984, 106, 121–167. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Werner, H.J.; Knowles, P.J.; Manby, F.R.; Black, J.A.; Doll, K.; Heßelmann, A.; Kats, D.; Köhn, A.; Korona, T.; Kreplin, D.A.; et al. The Molpro quantum chemistry package. J. Chem. Phys. 2020, 152, 144107. [Google Scholar]
- Du, L.; Lan, Z. An on-the-fly surface-hopping program jade for nonadiabatic molecular dynamics of polyatomic systems: Implementation and applications. J. Chem. Theory Comput. 2015, 11, 1360–1374. [Google Scholar] [PubMed]
- Farag, M.H.; Jansen, T.L.; Knoester, J. Probing the interstate coupling near a conical intersection by optical spectroscopy. J. Phys. Chem. Lett. 2016, 7, 3328–3334. [Google Scholar]
- Zhan, S.; Gelin, M.F.; Huang, X.; Sun, K. Ab initio simulation of peak evolutions and beating maps for electronic two-dimensional signals of a polyatomic chromophore. J. Chem. Phys. 2023, 158, 194106. [Google Scholar]
- Qiang, Y.; Sun, K.; Palacino-González, E.; Shen, K.; Rao, B.J.; Gelin, M.F.; Zhao, Y. Probing avoided crossings and conical intersections by two-pulse femtosecond stimulated Raman spectroscopy: Theoretical study. J. Chem. Phys. 2024, 160, 054107. [Google Scholar] [PubMed]
- Butkus, V.; Zigmantas, D.; Valkunas, L.; Abramavicius, D. Vibrational vs. Electronic coherences in 2D spectrum of molecular systems. Chem. Phys. Lett. 2012, 545, 40–43. [Google Scholar]
- Butkus, V.; Valkunas, L.; Abramavicius, D. Molecular vibrations-induced quantum beats in two-dimensional electronic spectroscopy. J. Chem. Phys. 2012, 137, 044513. [Google Scholar]
- Gómez, S.; Spinlove, E.; Worth, G. Benchmarking non-adiabatic quantum dynamics using the molecular Tully models. Phys. Chem. Chem. Phys. 2024, 26, 1829–1844. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Peng, J.; Zhu, Y.; Xu, C.; Gelin, M.F.; Gu, F.L.; Lan, Z. Transient-Absorption Pump-Probe Spectra as Information-Rich Observables: Case Study of Fulvene. Molecules 2025, 30, 1439. https://doi.org/10.3390/molecules30071439
Li Z, Peng J, Zhu Y, Xu C, Gelin MF, Gu FL, Lan Z. Transient-Absorption Pump-Probe Spectra as Information-Rich Observables: Case Study of Fulvene. Molecules. 2025; 30(7):1439. https://doi.org/10.3390/molecules30071439
Chicago/Turabian StyleLi, Zhaofa, Jiawei Peng, Yifei Zhu, Chao Xu, Maxim F. Gelin, Feng Long Gu, and Zhenggang Lan. 2025. "Transient-Absorption Pump-Probe Spectra as Information-Rich Observables: Case Study of Fulvene" Molecules 30, no. 7: 1439. https://doi.org/10.3390/molecules30071439
APA StyleLi, Z., Peng, J., Zhu, Y., Xu, C., Gelin, M. F., Gu, F. L., & Lan, Z. (2025). Transient-Absorption Pump-Probe Spectra as Information-Rich Observables: Case Study of Fulvene. Molecules, 30(7), 1439. https://doi.org/10.3390/molecules30071439






