Next Article in Journal
Detection of Retinoic Acid in Cosmetics Using Reactive Paper Spray Ionization Mass Spectrometry
Next Article in Special Issue
Power Frequency Breakdown Properties of LDPE-Doped Inorganic Nanoparticles
Previous Article in Journal
High-Temperature Layered Modification of Mn2In2Se5
Previous Article in Special Issue
Hydrogenation-Facilitated Spontaneous N-O Cleavage Mechanism for Effectively Boosting Nitrate Reduction Reaction on Fe2B2 MBene
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Molecules
Volume 30
Issue 9
10.3390/molecules30091905
molecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Insights into the Factors Controlling the Origin of Activation Barriers in the [2 + 2] Cycloaddition Reactions of Heavy Imine-like Molecules Featuring a Ge=Group 15 Double Bond with Heterocumulenes

by
Zheng-Feng Zhang
1 and
Ming-Der Su
1,2,*
1
Department of Applied Chemistry, National Chiayi University, Chiayi 60004, Taiwan
2
Department of Medicinal and Applied Chemistry, Kaohsiung Medical University, Kaohsiung 80708, Taiwan
*
Author to whom correspondence should be addressed.
Molecules 2025, 30(9), 1905; https://doi.org/10.3390/molecules30091905
Submission received: 24 March 2025 / Revised: 18 April 2025 / Accepted: 18 April 2025 / Published: 25 April 2025
(This article belongs to the Special Issue Inorganic Chemistry in Asia)
Browse Figures
Versions Notes

Abstract

:
The [2 + 2] cycloaddition reactions of the heterocumulene (N=C=N) with the heavy imine-like molecule Ge=G15-Rea (G15 = Group 15 element) were examined using density functional theory (M06-2X-D3/def2-TZVP). The theoretical findings indicate that the doubly bonded Ge=G15 moiety in Ge=G15-Rea (L1L2Ge=G15L3) is characterized by electron-sharing bonding between the triplet L1L2Ge and triplet G15–L3 fragments. All five Ge=G15-based heavy imine analogues readily undergo [2 + 2] cycloaddition reactions with N=C=N. Energy decomposition analysis (EDA–NOCV) suggests that the [2 + 2] cycloaddition reaction between Ge=G15-Rea and N=C=N involves a donor–acceptor (singlet–singlet) interaction instead of an electron-sharing (triplet–triplet) interaction. Frontier molecular orbital (FMO) theory and the energy decomposition analysis–natural orbitals for chemical valence (EDA–NOCV) findings emphasize that the key bonding interaction involves the occupied p-π orbital of Ge=G15-Rea and the vacant p-π* orbital of C=N=C. Based on the activation strain model results, the activation barrier of the [2 + 2] cycloaddition reaction is predominantly controlled by the deformation energies of Ge=G15-Rea and N=C=N.

1. Introduction

Historically, the creation of heavier element–element multiple bonds was regarded as unfeasible, resulting in the “double-bond rule” [1,2]. This rule highlights challenges like diminished p-orbital overlap and increased Pauli repulsion, which hinder synthetic efforts. The discovery of Si=Si [3] and P=P [4] double bonds in the 1980s spurred a new era of research into heavier diatomic multiple bonds, resulting in the isolation of heavier organic analogs [5,6,7,8,9,10,11,12,13,14,15,16,17,18]. Unlike their lighter counterparts, these analogs exhibit unique differences in stability, bonding behavior, and chemical properties, attributed to the minimal s/p hybridization seen in heavier elements. Their distinguishing features have propelled them into a pivotal position in synthetic chemistry, driving the development of unique compounds and the optimization of catalytic methodologies [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22].
Known for their bottle stability and widespread use, imines (R2C=NR′) are key organic compounds. Heavier analogs, on the other hand, exhibit significantly enhanced reactivity, as confirmed by experimental and theoretical studies [23,24,25,26,27,28,29,30]. This increased reactivity is a consequence of the greater polarity of their multiple bonds, resulting from weaker orbital overlap in heavier atoms [31,32,33,34,35]. Within this framework, germanimines featuring Ge=N double bonds have attracted considerable attention from researchers [36,37,38,39,40,41,42,43,44,45]. These compounds are considered heavier analogs of organic imines. The Ge=N bond, in contrast to the C=N bond, is significantly polarized due to poor p orbital overlap between germanium and nitrogen, resulting in high reactivity and synthetic difficulties [15,22]. Although challenging, the efforts of proficient synthetic chemists, along with the strategic use of bulky substituents, have made it possible to isolate and characterize heavier imine analogs containing a >Ge=N– skeleton [36,37,38,39,40,41,42,43,44,45]. Certain compounds additionally rely on stabilization by a Lewis acid or base [38,39,40,41]. While chemists have demonstrated significant success in synthesizing compounds containing >Ge=P– [6,8,46,47,48,49,50,51] and >Ge=As– [52,53] structures, it is surprising that >Ge=Sb– and >Ge=Bi– analogs, characterized by a tricoordinate germanium center and resembling organic imines (>C=N–), remain untouched in both experimental and computational research.
A novel germanimine, [(NONtBu)Ge=NMes] (1, NONtBu = O(SiMe2NtBu)2 and Mes = 2,4,6-Me3C6H2), was recently reported by Fulton and co-workers [42,43]. This compound demonstrates metalloid-like characteristics, showing reactivity akin to transition metal–imido complexes. It undergoes [2 + 2] cycloadditions with heterocumulenes and protic sources, as well as [4 + 2] cycloadditions (metallo–Diels–Alder reactions) with activated dienes [38]. For example, 1 reacts with dicyclohexylcarbodiimide and 4-nitro-phenyl isocyanate to form germanium–guanidinate 2 and germanium ureate 3, respectively. These compounds both feature germacycles with dianionic bidentate guanidinate and ureate ligands (Scheme 1) [42,43].
The fascinating experimental findings outlined above have sparked our interest and motivated us to delve deeper into this area of research. Although the reactions of germanimines, featuring a Ge=N double bond, with doubly bonded organic reagents have been extensively investigated by experimental chemists [54,55], their interactions with other doubly bonded species have been relatively overlooked, despite their potential importance in synthesizing and applying heavy analogues with a >Ge=G15– (G15 = Group 15 element) structure. Our objective is to examine how the replacement of the N atom in germanimines with other heavy Group 15 elements impacts the reactivity in [2 + 2] cycloaddition reactions. The primary focus of our inquiry is to understand the reactivity and the determinants of activation barriers in these reactions. Because they are limited by experimental constraints, theoretical computations now play a pivotal role in quickly predicting outcomes. We intend to apply density functional theory (DFT) and state-of-the-art methods to study the formation of [2 + 2] cycloaddition products between a heavy imine (>Ge=G15–) analog, composed of germanium and Group 15 element, and a heteroalkene, using the [2 + 2] reaction illustrated in Scheme 2 as a model. This effort seeks to facilitate the work of experimental chemists in optimizing synthesis and discovering novel applications.

2. Results and Discussion

2.1. The Nature of the Ge=G15 Bonding in Ge=G15-Rea

To understand the chemical bonding of the Ge=G15 double bond, valence bond theory suggests dividing the (L1L2)Ge=G15L3 molecule into two units: (L1L2)Ge and G15−L3 [56]. In terms of spin, two possible interaction pathways can merge the moieties to form a double-bonded (L1L2)Ge=G15L3 molecule in the singlet ground state. The first, the “singlet–singlet interaction” or “donor–acceptor interaction”, is [(L1L2)Ge:]1 + [:G15–L3]1 → [(L1L2)Ge=G15L3]1 (path A), and the second, the “triplet–triplet interaction” or “electron-sharing interaction”, is [(L1L2)Ge:]3 + [:G15–L3]3 → [(L1L2)Ge=G15L3]1 (path B). The valence bond orbital interactions are illustrated in Figure 1. As presented in Figure 1, our theoretical study indicates that the bond angle ∠Ge–G15–L3 in (L1L2)Ge=G15–L3 assumes a bent geometry, likely greater than 90° due to steric hindrance from the ligands. Fulton et al. [42,43] corroborate this with X-ray data, showing a bond angle of 126.66° for ∠Ge–N–MesC in Ge=N-Rea, which aligns with our theoretical findings.
Figure 1 illustrates that the pathway leading to the formation of (L1L2)Ge=G15–L3 is governed by the promotion energies of the units involved. Table S1 (Supporting Information) presents our M06-2X calculations, which establish that the (L1L2)Ge: ((L1L2) = NONtBu) component has a singlet ground state, whereas the :G15–L3 unit (L3 = Mes) adopt a triplet ground state. The computed singlet–triplet energy gap, ΔEST (=Etriplet − Esinglet), for the former is 42.7 kcal/mol, while for the latter (:G15–Mes; G15 = N, P, As, Sb, and Pb), it ranges from −31.0 to −28.6 kcal/mol.
The investigation continues with an in-depth analysis of the Ge=G15 bonding in doubly bonded, heavy imine-like Ge=G15-Rea molecules, employing EDA–NOCV [57,58,59,60,61,62,63,64,65,66]. As indicated in previous theoretical studies [67,68], ΔEOrb (orbital interaction energy) serves as the key indicator of bonding characteristics, capturing the total change in orbital interactions between fragments. Fragments with the smallest energy variation during bond formation provide the clearest insight into their electronic structure. Table 1 illustrates our M06-2X analysis, which suggests that the absolute |ΔEOrb| value for the “triplet–triplet interaction” (81.3–251.8 kcal/mol) is lower than that of the “singlet–singlet interaction” (163.8–334.4 kcal/mol). This suggests that the “triplet–triplet interaction” is essential in characterizing the bonding nature of the Ge=G15 bond in heavy imine-like Ge=G15-Rea molecules. In brief, our theoretical analysis provides clear evidence that the “electron-sharing interaction” between the triplet L1L2Ge and triplet G15–L3 moieties plays a predominant role in the characterization of the Ge=G15 double bond in heavy imine analogs (Ge=G15-Rea).

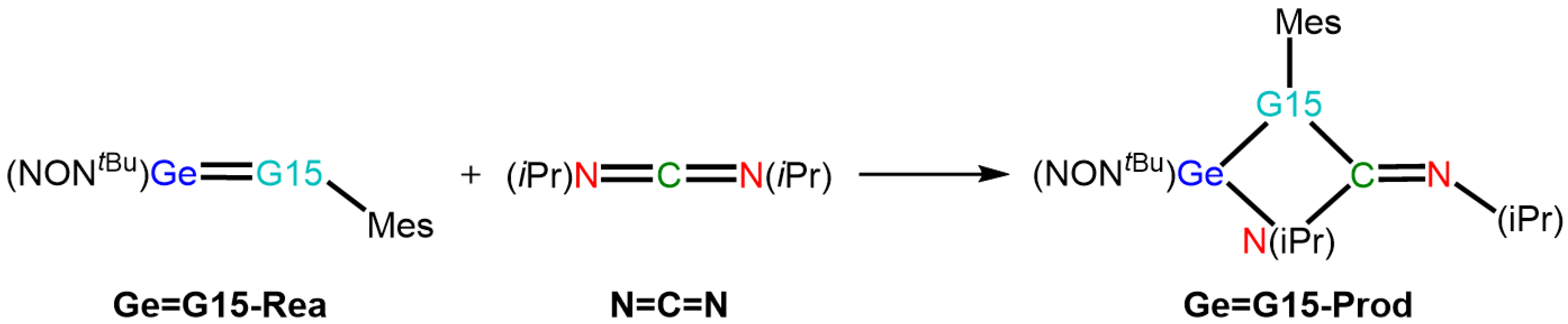
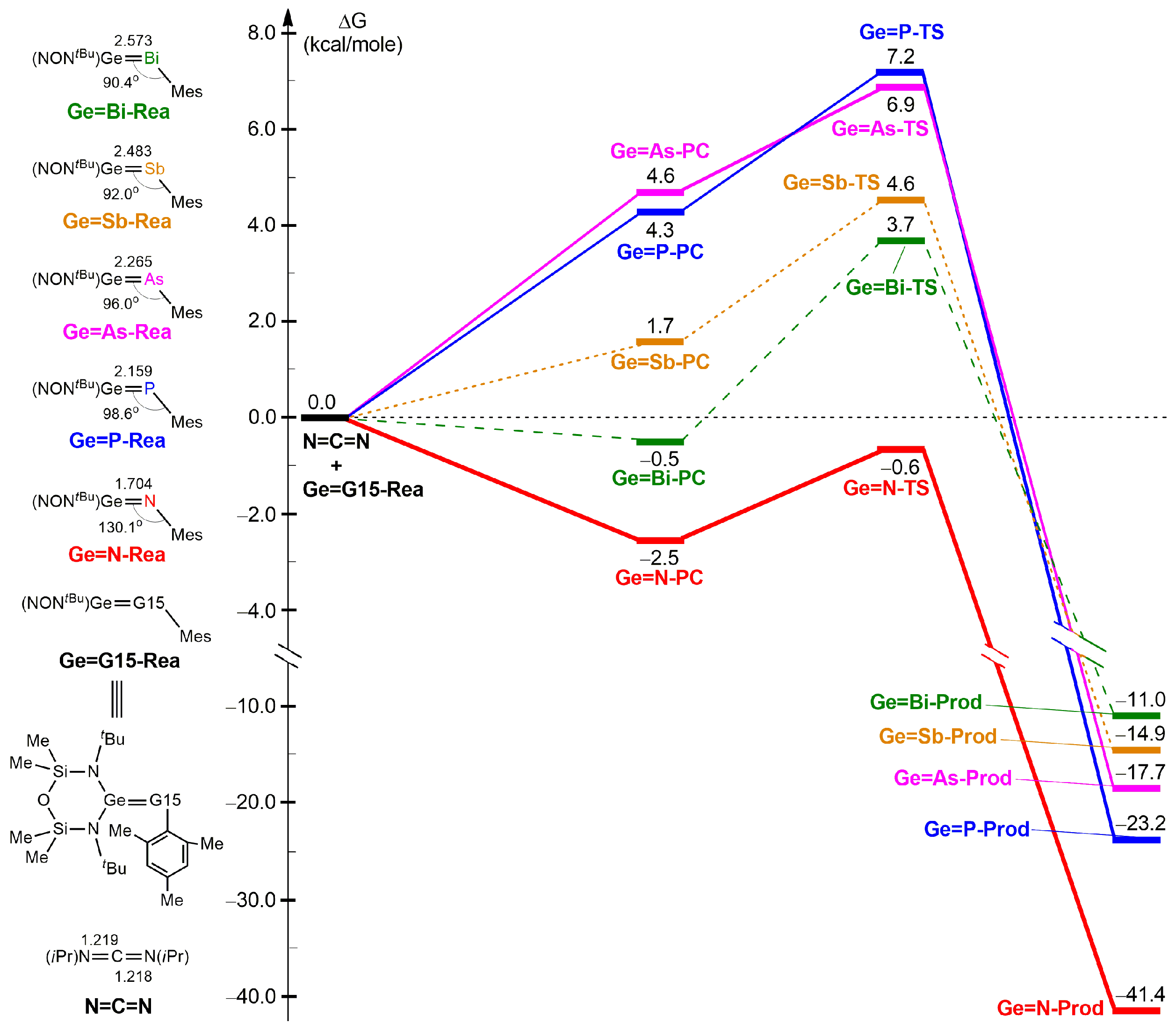
2.2. The [2 + 2] Cycloaddition Reactions of Ge=G15-Rea with N=C=N Outlined in Equation (1)

Figure 2 presents the free energy profiles for the [2 + 2] cycloaddition reactions of heavy imine-like Ge=G15-Rea molecules with N=C=N (Equation (1)), computed at the M06-2X-D3/def2-TZVP level. The calculated energy profile for the reaction sequence Ge=G15-Rea + N=C=N → Ge=G15-PC (precursor complex) → Ge=G15-TS → Ge=G15-Prod, is also illustrated in Figure 2. The geometrically optimized structures of Ge=G15-Rea, Ge=G15-TS, and Ge=G15-Prod can be found in Figure 3.
As predicted by the valence bonding model illustrated in Figure 1, steric interactions among the attached ligands should cause the bond angle ∠Ge–G15–L3 in Ge=G15-Rea to exceed 90°. Our M06-2X-D3 results in Figure 3 confirm that the bond angle ∠Ge–G15–Mes in Ge=G15-Rea is consistently above 90° (approximately 90.4–130.1°), which agrees well with our theoretical prediction. Additionally, the present DFT results shown in Figure 3 indicate that the bond angle ∠Ge–G15–Mes decreases in the following order: 130.1° (Ge=N-Rea) > 98.6° (Ge=P-Rea) > 96.0° (Ge=As-Rea) > 92.0° (Ge=Sb-Rea) > 90.4° (Ge=Bi-Rea). This trend aligns well with the variation in the Ge–G15 bond length (Å) in Ge=G15-Rea, which follows the sequence: 1.704 (Ge=N-Rea) < 2.159 (Ge=P-Rea) < 2.265 (Ge=As-Rea) < 2.483 (Ge=Sb-Rea) < 2.573 (Ge=Bi-Rea). In other words, as the Ge–G15 bond length increases in Ge=G15-Rea, the steric repulsion between the attached ligands decreases, ultimately resulting in a smaller bond angle ∠Ge–G15–Mes in Ge=G15-Rea. From Figure 2, our M06-2X-D3 calculations reveal that Ge=G15-PC precursor complexes lie at shallow energy levels (−2.5 to 4.6 kcal/mol) relative to their corresponding reactants, making their experimental detection unlikely.
As seen in Figure 2, the computed Gibbs free activation energies (ΔGACT) for heavy imine-like Ge=G15-Rea species are within −0.6–7.2 kcal/mol, suggesting relatively low barriers compared to the corresponding precursor complex, Ge=G15-PC. Meanwhile, their reaction free energies (ΔGRXN) remain negative (−41.4 to −11.0 kcal/mol), demonstrating a thermodynamically favorable process. More precisely, our M06-2X-D3 computations, presented in Figure 2, reveal that the Gibbs free activation barriers (ΔGACT, kcal/mol) increase relative to Ge=G15-PC in the order: Ge=N-TS (1.9) < Ge=P-TS (2.4) < Ge=As-TS (2.7) < Ge=Sb-TS (2.9) < Ge=Bi-TS (4.2). Additionally, the Gibbs free reaction energies (ΔGRXN, kcal/mol) for the [2 + 2] cycloaddition between N=C=N and Ge=G15-Rea exhibit an increasing trend: Ge=N-Prod (−41.4) < Ge=P-Prod (−23.2) < Ge=As-Prod (−17.7) < Ge=Sb-Prod (−14.9) < Ge=Bi-Prod (−11.0). Our computational findings indicate that the free activation and reaction energies exhibit a trend dictated by the atomic number of the Group 15 element. Specifically, in the Ge=G15-Rea system, a higher atomic number of G15 corresponds to an increased activation barrier, making the [2 + 2] cycloaddition reaction with N=C=N less exergonic. Until now, only one experimental study has supported our M06-2X prediction that the Ge=N-Rea molecule [42,43], possessing a Ge=N double bond and resembling a heavy imine, can undergo this reaction with ease (Scheme 1).

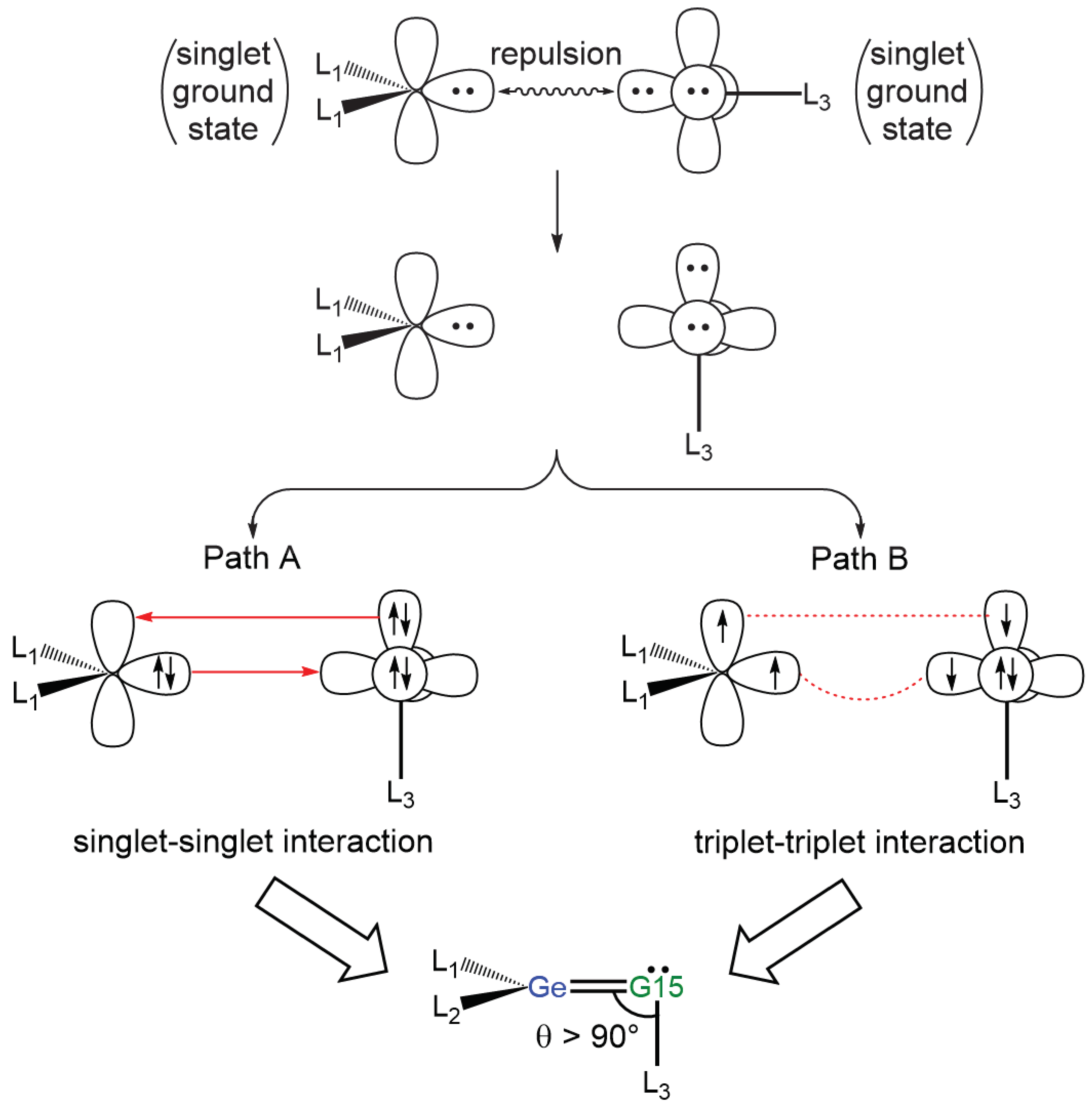
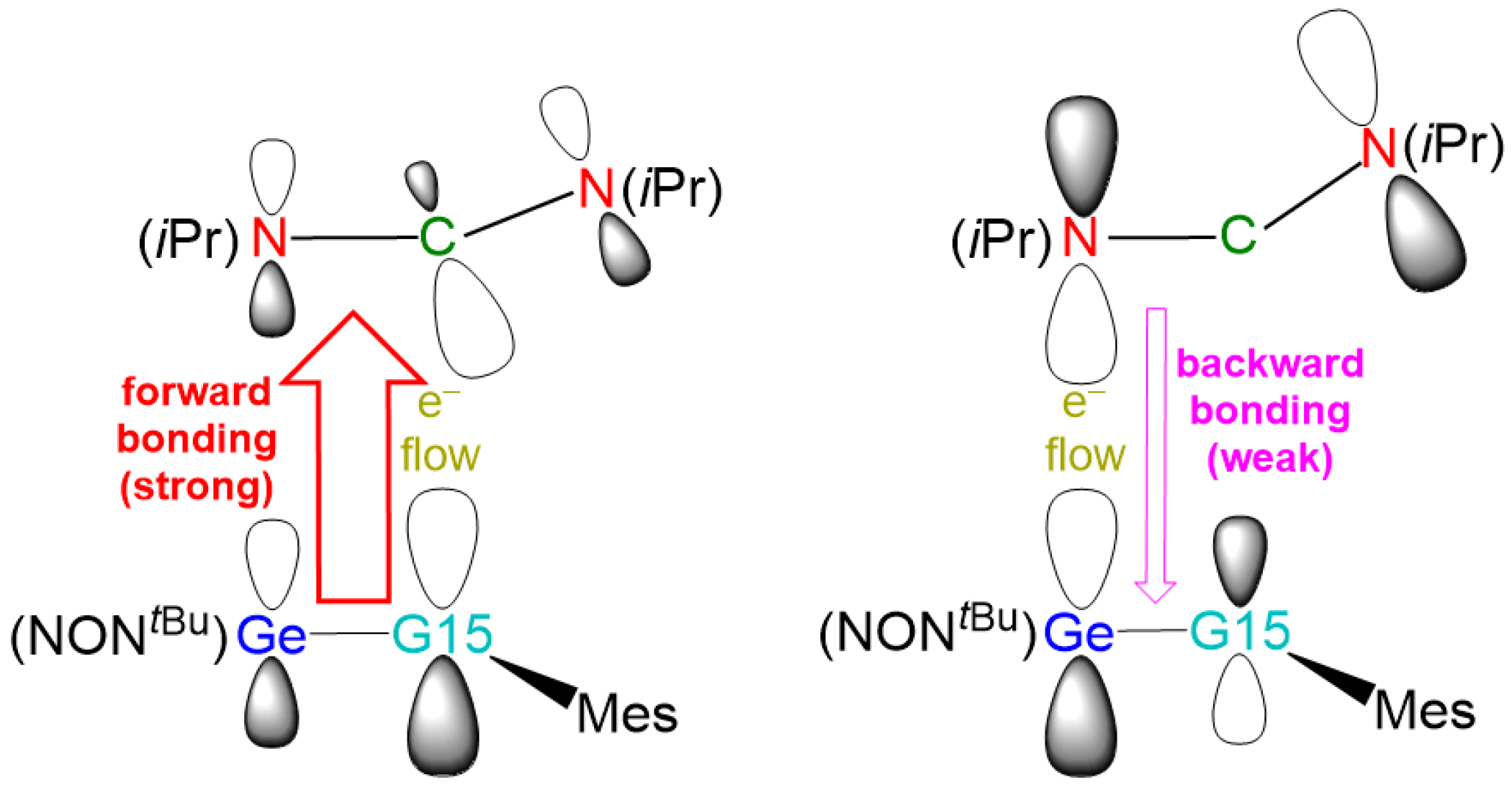
2.3. The Interaction Models

To better understand the bonding interactions in the [2 + 2] cycloaddition reaction between heavy imine-like Ge=N-Rea molecules and N=C=N, we introduce two bonding models, illustrated in Figure 4 and Figure 5, for analyzing the electronic interactions between Ge=G15-Rea and N=C=N. To analyze the transition state structure (Ge=G15-TS), we separate it into two fragments: Ge=G15-Rea and N=C=N. The interaction between their highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) leads to two bonding models: “singlet–singlet (S–S)” and “triplet–triplet (T–T)” interactions. These two bonding models, shown in Figure 4 and Figure 5, both contribute to the singlet reaction.
The “singlet–singlet interaction model” shown in Figure 4 is represented by [Ge=G15-Rea]1 + [N=C=N]1 → [Ge=G15-TS]1 and is also referred to as the “donor–acceptor bonding model.” Its stability is derived from two major interactions: (the filled p-π orbital of Ge=G15-Rea) → (the LUMO of N=C=N) and (the vacant p-π* orbital of Ge=G15-Rea) ← (the HOMO of N=C=N).
The “triplet–triplet interaction model” shown in Figure 5 describes the interaction of the p-π orbital of Ge=G15-Rea, containing one electron, with the singly occupied molecular orbital (SOMO) of N=C=N. Simultaneously, the SOMO of N=C=N interacts with the p-π* orbital of Ge=G15-Rea, which also contains one electron. This bonding interaction is called the “electron-sharing model” and is represented as [Ge=G15-Rea]3 + [N=C=N]3 → [Ge=G15-TS]1.

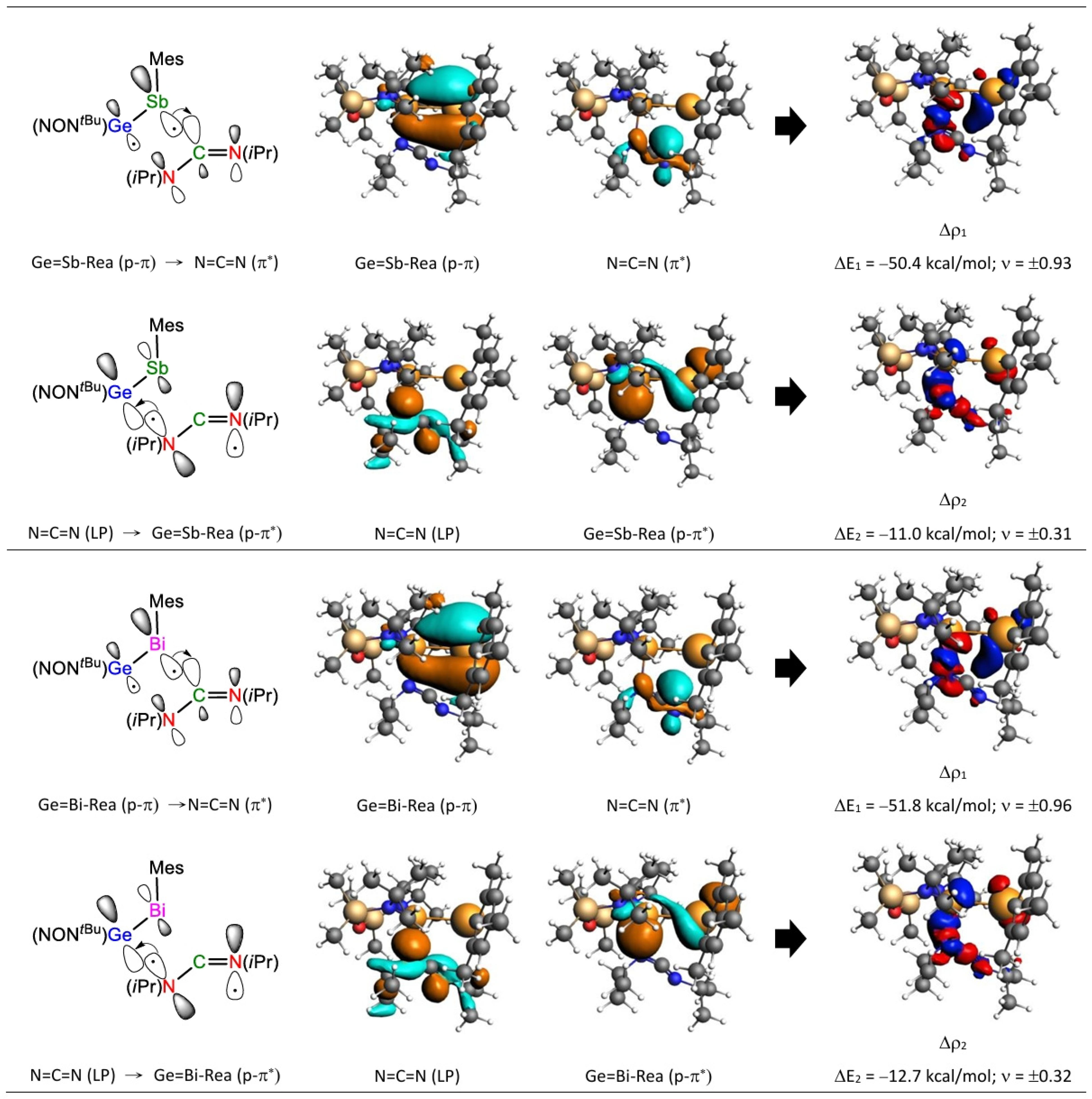
2.4. The FMO and EDA–NOCV Analyses

The critical frontier molecular orbitals of N=C=N and Ge=G15-Rea heavy imine analogues, including the filled p-π orbital and the empty p-π* orbital, along with their orbital energies, are collected in Figure 6. In Ge=G15-Rea, the p-π molecular orbital is largely localized on the more electronegative G15 atom, while the p-π* orbital is mainly centered on the less electronegative Ge element. According to Fukui’s frontier molecular orbital (FMO) theory [69], the reactivity of a chemical reaction is determined by the energy gap between the interacting molecular orbitals. As shown in Table 2, the energy gaps (in eV) between the p-π orbital of Ge=G15-Rea and the LUMO of N=C=N range from 7.356 to 8.039, which are narrower than the gaps between the HOMO-1 of N=C=N and the p-π* orbital of Ge=G15-Rea, which span 7.566 to 8.685. Consequently, our theoretical findings show that in the [2 + 2] cycloaddition reaction of Ge=G15-Rea with N=C=N, the electron transfer from the filled p-π orbital of Ge=G15-Rea to the LUMO of N=C=N (p-π (Ge=G15-Rea) → LUMO (N=C=N)) is more dominant than the electron transfer from the HOMO-1 of N=C=N to the vacant p-π* orbital of Ge=G15-Rea (p-π* (Ge=G15-Rea) ← HOMO-1 (N=C=N)). The aforementioned finding will be further substantiated using more advanced methods, which will be discussed later, with the supporting theoretical evidence presented in Table 3 and Figure 7.
To validate the FMO observations shown in Table 2, we also incorporate the EDA–NOCV results, considering the transition states, Ge=G15-TS, as two distinct parts: Ge=G15-Rea and N=C=N. As previously mentioned, two interaction models (S–S and T–T interaction models) were applied to explore the electronic structures of these Ge=G15-TS stationary points. The EDA–NOCV numerical results for the five Ge=G15-TS species, based on two different fragmentation schemes (Figure 4 and Figure 5), are provided in Table 3. As noted earlier [68,69], the fragmentation scheme that shows the least variation in ΔEOrb during bond formation best represents the electronic structure of a transition state. The absolute values of ΔEOrb (in kcal/mol) for the five Ge=G15-TS species in the “S–S interaction” model, as shown in Table 3, range from 80.5 to 95.4, which are significantly smaller than the absolute values in the “T–T interaction” model, where the range is from 208.8 to 291.1. Therefore, the analysis in Table 3 supports the idea that the “S–S interaction” (“donor–acceptor interaction”) model more closely represents the bonding interactions in the five Ge=G15-TS transition states compared to the “T–T interaction” (“electron-sharing interaction”) model. From now on, we will exclusively adopt the “S–S interaction” model rather than the “T–T interaction” model.
As displayed in Table 3, the orbital interaction energy decomposition (∆EOrb) in Ge=G15-TS, employing the “S–S interaction” model, reveals that ∆EOrb(1) and ∆EOrb(2) together constitute about 67.1% to 77.3% of the ∆EOrb. The EDA analysis given in Table 3 further dissects this energy into contributions from electron density deformation (Δρ), elucidating the nature of each interaction. The deformation density distributions of ∆ρ1 and ∆ρ2, mapped within the “S–S interaction” model and associated with ∆EOrb(1) and ∆EOrb(2), are shown in Figure 7. The red-to-blue color progression illustrates charge transfer directionality. The dominant interaction takes place as the filled p-π orbital of Ge=G15-Rea donates electron density to the vacant LUMO of N=C=N, with ∆EOrb(1) representing approximately 59.1–62.1% of the ∆EOrb term. In contrast, the ∆EOrb(2) interaction, where the HOMO-1 of N=C=N transfers electrons to the unoccupied p-π* orbital of Ge=G15-Rea, accounts for about 6.9–15.2%. The findings provide strong support that the bonding framework of the Ge=G15-TS transition state is predominantly influenced by the interaction between the filled p-π orbital of Ge=G15-Rea and the LUMO of N=C=N, labeled as p-π (Ge=G15-Rea) → LUMO (N=C=N). Notably, this theoretical insight, drawn from EDA–NOCV analysis in Table 3 and Figure 7, corresponds with the FMO-based results in Table 2.

2.5. The ASM Analyses

To determine the critical factor influencing the barrier heights of [2 + 2] cycloaddition reactions involving Ge=G15-Rea molecules and N=C=N, this study conducts an ASM analysis. Table 4 indicates that ΔEACT consists of two deformation energy contributions (ΔEDEF,N=C=N + ΔEDEF,Ge=G15-Rea), along with an interaction energy (ΔEINT) between the deformed reactants. Figure 8 demonstrates that ΔEINT remains nearly constant, irrespective of the G15 element present in Ge=G15-TS. Importantly, the deformation energies of both Ge=G15-Rea (ΔEDEF,Ge=G15-Rea) and N=C=N (ΔEDEF,N=C=N) fragments are the primary factors influencing the activation barrier (ΔEACT). The reasoning behind this phenomenon is straightforward. In the [2 + 2] cycloaddition between N=C=N and Ge=G15-Rea, the N=C bond of the former interacts with the Ge=G15 bond of the latter to form a four-membered heterocyclic ring (Ge=G15-Prod). Consequently, both N=C=N and Ge=G15-Rea experience structural distortions, making their deformation energies key factors in determining the activation energy of the [2 + 2] cycloaddition reaction. However, achieving maximum orbital overlap demands substantial geometric adjustments. As the atomic radius of the G15 element increases, the necessary distortions become more severe, leading to higher deformation energies and activation barriers, as depicted in Figure 8.
Moreover, based on the calculated structural parameters summarized in Figure 3, the ∠Ge–G15–C bond angle in the Ge=G15-TS transition state expands in the order 8.9% (Ge=N-TS) < 11.4% (Ge=P-TS) < 11.6% (Ge=As-TS) < 11.7% (Ge=Sb-TS) < 11.8% (Ge=Bi-TS), relative to its initial value in the heavy imine analog (Ge=G15-Rea). Similarly, the ∠N–C–N bond angle in the N=C=N unit of Ge=G15-TS follows an increasing trend: 10.4% (Ge=N-TS) < 10.9% (Ge=P-TS) ≈ 10.9% (Ge=As-TS) < 11.3% (Ge=Sb-TS). Besides, our DFT calculations, as summarized in Figure 3, indicate a systematic decrease in the ∠N–C–N bond angle within the N=C=N moiety of Ge=G15-Prod, following the order: Ge=N-Prod (22.5%) > Ge=P-Prod (22.3%) > Ge=As-Prod (22.2%) > Ge=Sb-Prod (22.1%) > Ge=Bi-Prod (21.4%), compared to its corresponding G13=P-TS stationary point. These computational results strongly indicate that Ge=N-TS is reactant-like, whereas Ge=Bi-TS is product-like. In other words, the theoretical findings indicate that the heavy imine-like Ge=N-Rea molecule, characterized by a Ge=N double bond, undergoes a [2 + 2] cycloaddition reaction with N=C=N via an earlier transition state, exhibiting the lowest activation barrier and the highest exergonicity. In contrast, the Ge=Bi-Rea molecule, which contains a Ge=Bi double bond, follows a reaction pathway with a later transition state, the highest activation barrier, and the lowest exergonicity. The consistency of these findings with the Hammond postulate [70] is confirmed by our M06-2X-D3 calculations, as shown in Figure 2 and Figure 3.

3. Methodology

The molecular geometry optimizations were carried out with the Gaussian 16 program [71] at the M06-2X [72]-D3 [71,72,73,74,75]/def2-TZVP [76] theoretical level, omitting any symmetry constraints. Subsequent frequency calculations ensured that the stationary points correspond to true energy minima on the potential energy surface.
Energy decomposition analyses (EDAs) [57,58,59,60,61,62] were carried out at the M06-2X-D3 level using the ADF 2023.104 program [77]. The analyses featured uncontracted Slater-type orbitals with two polarization functions, a triple-ζ-quality basis set, and a frozen-core approximation for the core electrons (TZ2P) [78]. Relativistic effects were incorporated into the single-point calculations using the zero-order regular approximation (ZORA) [79,80]. The EDA analyses relied on geometries optimized at the M06-2X-D3/def2-TZVP level. This computational approach is referred to as ZORA-M06-2X-D3/TZ2P//M06-2X-D3/def2-TZVP.
The EDA method was used to perform a quantitative analysis of the bonding interactions between the heavy imine-like fragment (Ge=G15-Rea) and dicyclohexylcarbodiimide (N=C=N, Scheme 2). The interaction energy (∆EINT) was further broken down into several physically relevant contributions.
ΔEINT = ΔEElstat + ΔEPauli + ΔEOrb + ΔEDisper
In Equation (1), ΔEElstat denotes the electrostatic interaction energy between the charge density distributions of Ge=G15-Rea and N=C=N (Scheme 2) in their transition state geometry, Ge=G15-TS. Furthermore, this term involves the doubly bonded segment of Ge=G15-Rea. ΔEPauli, the second term, describes the repulsive interaction between the Ge=G15-Rea and N=C=N fragments, driven by the Pauli exclusion principle, which restricts electrons with identical spins from sharing the same spatial region. The third term in Equation (1), ΔEOrb, represents the stabilization due to orbital interactions, assessed in the last phase of the EDA following the optimization of the Kohn–Sham orbitals. This term can also be broken down into contributions from orbitals associated with different irreducible representations in the interacting system. ΔEDisper, the fourth term, accounts for the dispersion interaction between the Ge=G15-Rea and N=C=N fragments.
Furthermore, natural orbitals for chemical valence (NOCV) [63,64,65,66] analysis enables visual inspection of the deformation density (Δρ), allowing researchers to attribute the ΔEOrb term to distinct bond types. This process illustrates the extent of charge deformation and provides a visual representation of the charge redistribution associated with pairwise orbital interactions. This allows the EDA–NOCV method to deliver both quantitative measurements and qualitative insights into the strength of orbital interactions in chemical bonds.
Additionally, to fully understand the factors affecting N=C=N capture reactions involving heavy imines, the research emphasized the energies required to distort the reactant fragments into the transition state geometry (ΔEDEF) and the energies arising from the interactions between these distorted reactants at that state (ΔEINT). The activation strain model (ASM) [81,82,83,84,85], an analytical framework, extends the distortion/interaction method first developed by Ess and Houk [86,87,88] and has proven effective in a variety of chemical systems.

4. Conclusions

By employing FMO, EDA–NOCV, and ASM approaches, this research investigates the reactivity patterns of [2 + 2] cycloaddition reactions involving the heavy imine-like molecule (Ge=G15-Rea) and the heterocumulene (N=C=N). Several noteworthy conclusions emerge from this research.
(1) Both EDA theoretical analysis and the valence-electron bonding model reveal that the Ge=G15 moiety in heavy imine-like Ge=G15-Rea molecules exhibits an “electron-sharing bonding interaction”.
(2) Our valence bond theory analysis suggests that steric effects between attached ligands cause the bond angle (∠Ge–G15–ligand) in heavy imine-like Ge=G15-Rea molecules to exceed 90°, a prediction that agrees with both experimental [42,43] and the present theoretical findings.
(3) Our M06-2X-D3 computations reveal that all heavy imine-like Ge=G15-Rea molecules studied here are capable of undergoing [2 + 2] cycloaddition reactions with the N=C=N molecule, yielding four-membered heterocyclic structures (Scheme 3). These findings are corroborated by kinetic and thermodynamic evaluations and are consistent with experimental reports on Ge=N-based imine-like molecules [42,43].
(4) Our EDA results demonstrate that the bonding interaction between N=C=N and the heavy imine-like molecule Ge=G15-Rea in Ge=G15-TS follows a “donor–acceptor bonding model” (“singlet–singlet bonding”) rather than an “electron-sharing bonding model” (“triplet–triplet bonding”).
(5) Both FMO and EDA–NOCV calculations indicate that the bonding in Ge=G15-TS is primarily characterized by electron transfer from the filled p-π orbital of Ge=G15-Rea to the vacant p-π* orbital of N=C=N, representing the dominant bonding interaction. A smaller contribution involves electron transfer from the filled p-π orbital of N=C=N to the empty p-π* orbital of Ge=G15-Rea, which is less significant (Scheme 4).
(6) The ASM analysis clearly shows that the activation barrier of the [2 + 2] cycloaddition reaction between the N=C=N molecule and the heavy imine-like molecule Ge=G15-Rea is greatly influenced by the deformation energies of both fragments.
It is hoped that our theoretical insights will inspire experimental chemists to develop more efficient and groundbreaking results.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/molecules30091905/s1. The optimized geometries calculated for all stationary points (Ge=G15-Rea, Ge=G15-TS, Ge=G15-Prod) using the M06-2X-D3/def2-TZVP level of theory are collected in the Supporting Information.

Author Contributions

Z.-F.Z. performed the theoretical calculations; Z.-F.Z. and M.-D.S. analyzed the data; M.-D.S. wrote the paper. All authors have read and agreed to the published version of the manuscript.

Funding

The authors thank the National Science and Technology Council of Taiwan for financial support.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data is contained within the article and Supplementary Materials.

Acknowledgments

The authors are grateful to the National Center for High-Performance Computing of Taiwan for providing huge computing resources to facilitate this research.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Kutzelnigg, W. Chemical Bonding in Higher Main Group Elements. Angew. Chem. Int. Ed. Engl. 1984, 23, 272–295. [Google Scholar] [CrossRef]
  2. Jacobsen, H.; Ziegler, T. Nonclassical double bonds in ethylene analogs: Influence of Pauli repulsion on trans bending and pi-bond strength. A density functional study. J. Am. Chem. Soc. 1994, 116, 3667–3679. [Google Scholar] [CrossRef]
  3. West, R.; Fink, M.J.; Michl, J. Tetramesityldisilene, a Stable Compound Containing a Silicon-Silicon Double Bond. Science 1981, 214, 1343–1344. [Google Scholar] [CrossRef]
  4. Yoshifuji, M.; Shima, I.; Inamoto, N.; Hirotsu, K.; Higuchi, T. Synthesis and structure of bis(2,4,6-tri-tert-butylphenyl)diphosphene: Isolation of a true phosphobenzene. J. Am. Chem. Soc. 1981, 103, 4587–4589. [Google Scholar] [CrossRef]
  5. Barrau, J.; Escudié, J.; Satgé, J. Multiply bonded germanium species. Recent developments. Chem. Rev. 1990, 90, 283–319. [Google Scholar] [CrossRef]
  6. Power, P.P. π-Bonding and the Lone Pair Effect in Multiple Bonds between Heavier Main Group Elements. Chem. Rev. 1999, 99, 3463–3504. [Google Scholar] [CrossRef] [PubMed]
  7. Sasamori, T.; Tokitoh, N. Doubly bonded systems between heavier Group 15 elements. Dalton Trans. 2008, 11, 1395–1408. [Google Scholar] [CrossRef]
  8. Fischer, R.C.; Power, P.P. π-Bonding and the Lone Pair Effect in Multiple Bonds Involving Heavier Main Group Elements: Developments in the New Millennium. Chem. Rev. 2010, 110, 3877–3923. [Google Scholar] [CrossRef] [PubMed]
  9. Lee, V.Y.; Sekiguchi, A. Organometallic Compounds of Low-Coordinate Si, Ge, Sn and Pb: From Phantom Species to Stable Compounds; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
  10. Power, P.P. Main-Group Elements as Transition Metals. Nature 2010, 463, 171–177. [Google Scholar] [CrossRef]
  11. Präsang, C.; Scheschkewitz, D. Reactivity in the periphery of functionalised multiple bonds of heavier group 14 elements. Chem. Soc. Rev. 2016, 45, 900–921. [Google Scholar] [CrossRef]
  12. Nesterov, V.; Breit, N.C.; Inoue, S. Advances in Phosphasilene Chemistry. Chem.-Eur. J. 2017, 23, 12014–12039. [Google Scholar] [CrossRef] [PubMed]
  13. Bag, P.; Weetman, C.; Inoue, S. Experimental Realisation of Elusive Multiple-Bonded Aluminium Compounds: A New Horizon in Aluminium Chemistry. Angew. Chem. Int. Ed. 2018, 57, 14394–14413. [Google Scholar] [CrossRef]
  14. Chu, T.; Nikonov, G.I. Oxidative Addition and Reductive Elimination at Main-Group Element Centers. Chem. Rev. 2018, 118, 3608–3680. [Google Scholar] [CrossRef]
  15. Nesterov, V.; Reiter, D.; Bag, P.; Frisch, P.; Holzner, R.; Porzelt, A.; Inoue, S. NHCs in Main Group Chemistry. Chem. Rev. 2018, 118, 9678–9842. [Google Scholar] [CrossRef] [PubMed]
  16. Guo, J.-D.; Sasamori, T. Activation of Small Molecules by Compounds that Contain Triple Bonds Between Heavier Group-14 Elements. Chem. Asia. J. 2018, 13, 3800–3817. [Google Scholar] [CrossRef]
  17. Melen, R.L. Frontiers in molecular p-block chemistry: From structure to reactivity. Science 2019, 363, 479–484. [Google Scholar] [CrossRef] [PubMed]
  18. Zhao, L.; Pan, S.; Holzmann, N.; Schwerdtfeger, P.; Frenking, G. Chemical Bonding and Bonding Models of Main-Group Compounds. Chem. Rev. 2019, 119, 8781–8845. [Google Scholar] [CrossRef]
  19. Power, P.P. An Update on Multiple Bonding Between Heavier Main Group Elements: The Importance of Pauli Repulsion, Charge- Shift Character, and London Dispersion Force Effects. Organometallics 2020, 39, 4127–4138. [Google Scholar] [CrossRef]
  20. Hanusch, F.; Groll, L.; Inoue, S. Recent advances of group 14 dimetallenes and dimetallynes in bond activation and catalysis. Chem. Sci. 2021, 12, 2001–2015. [Google Scholar] [CrossRef]
  21. Weetman, C. Main Group Multiple Bonds for Bond Activations and Catalysis. Chem.-Eur. J. 2021, 27, 1941–1954. [Google Scholar] [CrossRef]
  22. Dankert, F.; Hering-Junghans, C. Heavier group 13/15 multiple bond systems: Synthesis, structure and chemical bond activation. Chem. Commun. 2022, 58, 1242–1262. [Google Scholar] [CrossRef] [PubMed]
  23. Niesmann, J.; Klingebiel, U.; Rudolph, S.; Herbst-Inner, R.; Noltemeyer, M. [2 + 2]-Cycloadditionen Eines Iminosilans-Synthese Viergliedriger Heterocyclen. J. Organomet. Chem. 1996, 15, 43–49. [Google Scholar] [CrossRef]
  24. Xiong, Y.; Yao, S.; Driess, M. Chemical Tricks to Stabilize Silanones and Their Heavier Homologues with E=O Bonds (E=Si–Pb): From Elusive Species to Isolable Building Blocks. Angew Chem. Int. Ed. 2013, 52, 4302–4311. [Google Scholar] [CrossRef] [PubMed]
  25. Muck, F.M.; Baus, J.A.; Ulmer, A.; Burschka, C.; Tacke, R. Reactivity of the Donor-Stabilized Guanidinatosilylene [ArNC(NMe2)NAr]Si[N(SiMe3)2] (Ar = 2,6-Diisopropylphenyl). Eur. J. Inorg. Chem. 2016, 2016, 1660–1670. [Google Scholar] [CrossRef]
  26. Hadlington, T.J.; Szilvásib, T.; Driess, M. Metal Nitrene-Like Reactivity of A SiQN Bond Towards CO2. Chem. Commun. 2018, 54, 9352–9355. [Google Scholar] [CrossRef] [PubMed]
  27. Yuvaraj, K.; Jones, C. Synthesis and Reactivity of Boryl Substituted Silaimines. Dalton Trans. 2019, 48, 11961–11965. [Google Scholar] [CrossRef]
  28. Wright, R.J.; Phillips, A.D.; Hardman, N.J.; Power, P.P. The “Diindene” ArInInAr (Ar = C6H3-2,6-Dipp2, Dipp = C6H3-2,6-Pri2). Dimeric Versus Monomeric In(I) Aryls:  para-Substituent Effects in Terphenyl Ligands. J. Am. Chem. Soc. 2002, 124, 8538–8539. [Google Scholar] [CrossRef]
  29. Wright, R.J.; Phillips, A.D.; Hino, S.; Power, P.P. Synthesis and Reactivity of Dimeric Ar′TlTlAr′ and Trimeric (Ar′′Tl)3(Ar′, Ar′′ = Bulky Terphenyl Group) Thallium(I) Derivatives:  Tl(I)−Tl(I) Bonding in Species Ligated by Monodentate Ligands. J. Am. Chem. Soc. 2005, 127, 4794–4799. [Google Scholar] [CrossRef]
  30. Rivieṙe-Baudet, M.; Rivieṙe, P.; Satgé, J. Germa-2azetidines: Precurseurs Des Premieres Germaimines. J. Organomet. Chem. 1978, 154, C23–C27. [Google Scholar] [CrossRef]
  31. Lai, C.-H.; Su, M.-D.; Chu, S.-Y. Effects of First-Row Substituents on Silicon−Phosphorus Triple Bonds. Inorg. Chem. 2002, 41, 1320–1322. [Google Scholar] [CrossRef]
  32. Lai, C.-H.; Su, M.-D.; Chu, S.-Y. Relative stability of multiple bonds between germanium and arsenic. A theoretical study. Polyhedron 2002, 21, 579. [Google Scholar] [CrossRef]
  33. Hu, Y.-H.; Su, M.-D. Substituent Effect on Relative Stabilities of the Phosphorus and Tin Multiple Bonds. Chem. Phys. Lett. 2003, 378, 289–298. [Google Scholar] [CrossRef]
  34. Chen, C.H.; Su, M.D. Theoretical Design of Silicon−Phosphorus Triple Bonds: A Density Functional Study. Eur. J. Inorg. Chem. 2008, 2008, 1241–1247. [Google Scholar] [CrossRef]
  35. Wen, X.-T.; Li, Y.-C.; Su, M.-D. Substituent Effects on the Geometries and Energies of the Antimony–Silicon Multiple Bond. Bull. Chem. Soc. Jpn. 2014, 87, 816–818. [Google Scholar] [CrossRef]
  36. Meller, A.; Ossig, G.; Maringgele, W.; Stalke, D.; Herbst-Irmer, R.; Freitag, S.; Sheldrick, G.M. Synthesis and X-ray crystal structure of germaimines. J. Chem. Soc. Chem. Commun. 1991, 16, 1123–1124. [Google Scholar] [CrossRef]
  37. Ando, W.; Ohtaki, T.; Kabe, Y. Synthesis, Structure, and Photoreaction of Bis(germanimines). Organometallics 1994, 13, 434–435. [Google Scholar] [CrossRef]
  38. Veith, M.; Rammo, A. Synthese Von Cyclischen, Chiralen Verbindungen Mit Ge-El-Doppelbindungen (El = N, S, (O)) Und Deren Dynamisches Verhalten in Lösung. Z. Anorg. Allg. Chem. 1997, 623, 861–872. [Google Scholar] [CrossRef]
  39. Rit, A.; Tirfoin, R.; Aldridge, S. Exploiting Electrostatics To Generate Unsaturation: Oxidative Ge=E Bond Formation Using a Non π-Donor Stabilized [R(L)Ge:]+ Cation. Angew. Chem. Int. Ed. 2016, 55, 378–382. [Google Scholar] [CrossRef]
  40. Schneider, J.; Krebs, K.M.; Freitag, S.; Eichele, K.; Schubert, H.; Wesemann, L. Intramolecular Tetrylene Lewis Adducts: Synthesis and Reactivity. Chem.-Eur. J. 2016, 22, 9812–9826. [Google Scholar] [CrossRef]
  41. Sharma, M.K.; Sinhababu, S.; Mahawar, P.; Mukherjee, G.; Pandey, B.; Rajaraman, G.; Nagendran, S. Donor-Acceptor-Stabilised Germanium Analogues of Acid Chloride, Ester, and Acyl Pyrrole Compounds: Synthesis and Reactivity. Chem. Sci. 2019, 10, 4402–4411. [Google Scholar] [CrossRef]
  42. Evans, M.J.; Anker, M.D.; Mouchfiq, A.; Lein, M.; Fulton, J.R. The “Metallo”-Diels-Alder Reactions: Examining the Metalloid Behavior of Germani- mines. Chem.-Eur. J. 2020, 26, 2606–2609. [Google Scholar] [CrossRef] [PubMed]
  43. Evans, M.J.; Burke, F.M.; Chapple, P.M.; Fulton, J.R. Synthesis and Reactivity of Acyclic Germanimines: Silyl Rearrangement and Cycloadditions. Inorg. Chem. 2021, 60, 8293–8303. [Google Scholar] [CrossRef]
  44. Guthardt, R.; Oetzel, L.; Lang, T.; Bruhn, C.; Siemeling, U. Reactions of Mesityl Azide with Ferrocene-Based N-Heterocyclic Germylenes, Stannylenes and Plumbylenes, Including PPh2-Functionalised Congeners. Chem.-Eur. J. 2022, 28, e202200996. [Google Scholar] [CrossRef] [PubMed]
  45. Li, T.; Zhang, L.; He, Y.; Chen, Y.; Wang, D.; Liu, J.; Tan, G. A Germanimidoyl Chloride: Synthesis, Characterization and Reactivity. Chem. Commun. 2023, 59, 1533–1536. [Google Scholar] [CrossRef] [PubMed]
  46. Chen, H.; Chen, Y.; Li, T.; Wang, D.; Xu, L.; Tan, G. Synthesis and Reactivity of N-Heterocyclic Carbene Coordinated Formal Germanimidoyl-Phosphinidenes. Inorg. Chem. 2023, 62, 20906–20912. [Google Scholar] [CrossRef]
  47. Escudié, J.; Couret, C.; Satgé, J.; Andrianarison, M.; Andriamizaka, J.D. 2,2-Dimesityl-1-(2,4,6-tri-tert-butylphenyl)-germaphosphene: The first stable compound with a germanium- phosphorus double bond. J. Am. Chem. Soc. 1985, 107, 3378–3379. [Google Scholar] [CrossRef]
  48. Escudlé, J.; Couret, C.; Andrianarison, M.; Raharinirina, A.; Satgé, J. New Aspects of the Reactivity of the First Stable Germa-and Stannaphosphenes. Phosphorus Sulfur Rel. Elem. 1987, 30, 377–380. [Google Scholar] [CrossRef]
  49. Draeger, M.; Escudié, J.; Couret, C.; Ranaivonjatovo, H.; Satgé, J. Structure of the stable germaphosphene Mes2Ge=Par: A Ge=P connection with the geometry of a true double bond. Organometallics 1988, 7, 1010–1013. [Google Scholar] [CrossRef]
  50. Ranaivonjatovo, H.; Escudié, J.; Couret, C.; Satgé, J. A new stable germaphosphene and some of its chemical properties. J. Organomet. Chem. 1991, 415, 327–333. [Google Scholar] [CrossRef]
  51. Lee, V.Y.; Kawai, M.; Sekiguchi, A.; Ranaivonjatovo, H.; Escudié, J. A “Push-Pull” Phosphasilene and Phosphagermene and Their Anion-Radicals. Organometallics 2009, 28, 4262–4265. [Google Scholar] [CrossRef]
  52. Ballestero-Martınez, E.; Hadlington, T.J.; Tibor Szilvasi, T.; Yao, S.; Driess, M. From zinco(II) arsaketenes to silylene-stabilised zinco arsinidene complexes. Chem. Commun. 2018, 54, 6124–6127. [Google Scholar] [CrossRef] [PubMed]
  53. Lee, V.Y.; Manami Kawai, M.; Gapurenko, O.A.; Minkin, V.I.; Gornitzka, H.; Sekiguchi, A. Arsagermene, a compound with an –As=Ge< double bond. Chem. Commun. 2018, 54, 10947–10949. [Google Scholar]
  54. Lee, V.Y.; Sekiguchi, A. Heavy Analogs of Alkenes, 1,3-Dienes, Allenes and Alkynes: Multiply Bonded Derivatives of Si, Ge, Sn and Pb. In Organometallic Compounds of Low-Coordinate Si, Ge, Sn and Pb: From Phantom Species to Stable Compounds; Wiley: Chichester, UK, 2010; Chapter 5. [Google Scholar]
  55. Baceiredo, A.; Kato, T. Organosilicon Compounds (Volume 1: Theory and Experiment Synthesis); Lee, V.Y., Ed.; Elsevier: Amsterdam, The Netherlands, 2017; Chapter 9. [Google Scholar]
  56. Chen, J.-Y.; Su, M.-D. Diboration of the E=E Double Bond by [2]Metallocenophanes (E = N, P, As, Sb, and Bi): A Theoretical Study. Organometallics 2010, 29, 5812–5820. [Google Scholar] [CrossRef]
  57. Morokuma, K. Molecular Orbital Studies of Hydrogen Bonds. III. C=O···H–O Hydrogen Bond in H2CO···H2O and H2CO···2H2O. J. Chem. Phys. 1971, 55, 1236–1244. [Google Scholar] [CrossRef]
  58. Ziegler, T.; Rauk, A. On the Calculation of Bonding Energies by the Hartree Fock Slater Method. Theor. Chim. Acta 1977, 46, 1–10. [Google Scholar] [CrossRef]
  59. Ziegler, T.; Rauk, A. A Theoretical Study of the Ethylene-Metal Bond in Complexes Between Copper(1+), Silver(1+), Gold(1+), Platinum(0) or Platinum(2+) and Ethylene, Based on the Hartree-Fock-Slater Transition-State Method. Inorg. Chem. 1979, 18, 1558–1565. [Google Scholar] [CrossRef]
  60. Bickelhaupt, F.M.; Ziegler, T. Oxidative insertion as front-side SN2 substitution: A theoretical study of the model reaction system Pd + CH3Cl. Organometallics 1995, 14, 2288–2296. [Google Scholar] [CrossRef]
  61. Bickelhaupt, F.M. Understanding reactivity with Kohn-Sham molecular orbital theory: E2-SN2 mechanistic spectrum and other concepts. J. Comput. Chem. 1999, 20, 114–128. [Google Scholar] [CrossRef]
  62. Bickelhaupt, F.M.; Baerends, E.J. Kohn-Sham Density Functional Theory: Predicting and Understanding Chemistry. Rev. Comput. Chem. 2000, 15, 1–86. [Google Scholar]
  63. Mitoraj, M.; Michalak, A. Natural Orbitals for Chemical Valence as Descriptors of Chemical Bonding in Transition Metal Complexes. J. Mol. Model. 2007, 13, 347–355. [Google Scholar] [CrossRef]
  64. Mitoraj, M.; Michalak, A. Donor-acceptor properties of ligands from the natural orbitals for chemical valence. Organometallics 2007, 26, 6576–6580. [Google Scholar] [CrossRef]
  65. Michalak, A.; Mitoraj, M.; Ziegler, T. Bond orbitals from chemical valence theory. J. Phys. Chem. A 2008, 112, 1933–1939. [Google Scholar] [CrossRef] [PubMed]
  66. Mitoraj, M.; Michalak, A.; Ziegler, T. A Combined Charge and Energy Decomposition Scheme for Bond Analysis. J. Chem. Theory Comput. 2009, 5, 962–975. [Google Scholar] [CrossRef] [PubMed]
  67. Tonner, R.; Frenking, G. Divalent Carbon(0) Chemistry, Part 1: Parent compounds. Chem. Eur. J. 2008, 14, 3260–3272. [Google Scholar] [CrossRef]
  68. Gimferrer, M.; Danés, S.; Vos, E.; Corral, I.; Jana, A.; Salvador, P.; Andrada, D.M. Reply to the Comment on “The oxidation state in low-valent beryllium and magnesium compounds” by S. Pan and G. Frenking, Chem. Sci. 2022, 13, 6583. Chem. Sci. 2023, 14, 384–392. [Google Scholar] [CrossRef]
  69. Fukui, K. Recognition of Stereochemical Paths by Orbital Interaction. Acc. Chem. Res. 1971, 2, 57–64. [Google Scholar] [CrossRef]
  70. Hammond, G.S. A Correlation of Reaction Rates. J. Am. Chem. Soc. 1955, 77, 334–338. [Google Scholar] [CrossRef]
  71. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
  72. Zhao, Y.; Truhlar, D.G. Exploring the Limit of Accuracy of the Global Hybrid Meta Density Functional for Main-Group Thermochemistry, Kinetics, and Noncovalent Interactions. J. Chem. Theory Comput. 2008, 4, 1849–1868. [Google Scholar] [CrossRef]
  73. Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104–154122. [Google Scholar] [CrossRef]
  74. Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
  75. Smith, D.G.A.; Burns, L.A.; Patkowski, K.; Sherrill, C.D. Revised Damping Parameters for the D3 Dispersion Correction to Density Functional Theory. J. Phys. Chem. Lett. 2016, 7, 2197–2203. [Google Scholar] [CrossRef] [PubMed]
  76. Weigend, F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef]
  77. Computer Code ADF2023, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands. Available online: http://www.scm.com (accessed on 17 April 2025).
  78. van Lenthe, E.; Baerends, E.J. Optimized Slater-type basis sets for the elements 1–118. J. Comput. Chem. 2003, 24, 1142–1156. [Google Scholar] [CrossRef]
  79. Chang, C.; Pelissier, M.; Durand, P. Regular Two-Component Pauli-Like Effective Hamiltonians in Dirac Theory. Phys. Scr. 1986, 34, 394–404. [Google Scholar] [CrossRef]
  80. Heullyt, J.-L.; Lindgrent, I.; Lindrothi, E.; Lundqvist, S.; Pendrill, A.-M. Diagonalisation of the Dirac Hamiltonian as a basis for a relativistic many-body procedure. J. Phys. B 1986, 19, 2799–2815. [Google Scholar] [CrossRef]
  81. van Zeist, W.-J.; Bickelhaupt, F.M. The Activation Strain Model of Chemical Reactivity. Org. Biomol. Chem. 2010, 8, 3118–3127. [Google Scholar] [CrossRef] [PubMed]
  82. Fernańdez, I.; Bickelhaupt, F.M. The activation strain model and molecular orbital theory: Understanding and designing chemical reactions. Chem. Soc. Rev. 2014, 43, 4953–4967. [Google Scholar] [CrossRef]
  83. Fernańdez, I. Combined activation strain model and energy decomposition analysis methods: A new way to understand pericyclic reactions. Phys. Chem. Chem. Phys. 2014, 16, 7662–7671. [Google Scholar] [CrossRef]
  84. Wolters, L.P.; Bickelhaupt, F.M. The activation strain model and molecular orbital theory. WIREs Comput. Mol. Sci. 2015, 5, 324–343. [Google Scholar] [CrossRef]
  85. Fernańdez, I. Discoveringthe Future of Molecular Sciences; Pignataro, B., Ed.; Wiley-VCH: Weinheim, Germany, 2014; pp. 165–187. [Google Scholar]
  86. Ess, D.H.; Houk, K.N. Distortion/Interaction Energy Control of 1,3-Dipolar Cycloaddition Reactivity. J. Am. Chem. Soc. 2007, 129, 10646–10647. [Google Scholar] [CrossRef]
  87. Ess, D.H.; Houk, K.N. Theory of 1,3-Dipolar Cycloadditions: Distortion/Interaction and Frontier Molecular Orbital Models. J. Am. Chem. Soc. 2008, 130, 10187–10198. [Google Scholar] [CrossRef] [PubMed]
  88. Ess, D.H.; Jones, G.O.; Houk, K.N. Transition States of Strain-Promoted Metal-Free Click Chemistry: 1,3-Dipolar Cycloadditions of Phenyl Azide and Cyclooctynes. Org. Lett. 2008, 10, 1633–1636. [Google Scholar] [CrossRef] [PubMed]
Molecules 30 01905 sch001
Scheme 1. The [2 + 2] cycloaddition of heterocumulenes (2 and 3) with [(NONtBu)Ge=N–Mes] (1, NONtBu = O(SiMe2NtBu)2 and Mes = 2,4,6-Me3C6H2). See references [42,43].
Scheme 1. The [2 + 2] cycloaddition of heterocumulenes (2 and 3) with [(NONtBu)Ge=N–Mes] (1, NONtBu = O(SiMe2NtBu)2 and Mes = 2,4,6-Me3C6H2). See references [42,43].
Molecules 30 01905 sch001
Molecules 30 01905 sch002
Scheme 2. The [2 + 2] cycloaddition reaction model features ((NONtBu)Ge=G15–Mes) (Ge=G15-Rea, NONtBu = O(SiMe2NtBu)2) reacting with the doubly bonded heterocumulene N=C=N, also known as dicyclohexylcarbodiimide. Rea = reactant and Prod = product.
Scheme 2. The [2 + 2] cycloaddition reaction model features ((NONtBu)Ge=G15–Mes) (Ge=G15-Rea, NONtBu = O(SiMe2NtBu)2) reacting with the doubly bonded heterocumulene N=C=N, also known as dicyclohexylcarbodiimide. Rea = reactant and Prod = product.
Molecules 30 01905 sch002
Molecules 30 01905 g001
Figure 1. The valence bond bonding paths, path A and path B, for the doubly bonded Ge=G15-Rea ((NONtBu)Ge=G15–Mes) molecule. Valence bond theory predicts that the bond angle ∠Ge–G15–L3 (θ) in Ge=G15-Rea should be greater than 90° due to steric interactions between the attached ligands. The arrows stand for donor-acceptor interaction.
Figure 1. The valence bond bonding paths, path A and path B, for the doubly bonded Ge=G15-Rea ((NONtBu)Ge=G15–Mes) molecule. Valence bond theory predicts that the bond angle ∠Ge–G15–L3 (θ) in Ge=G15-Rea should be greater than 90° due to steric interactions between the attached ligands. The arrows stand for donor-acceptor interaction.
Molecules 30 01905 g001
Molecules 30 01905 g002
Figure 2. Using the M06-2X-D3/def2-TZVP method, the computed free energy profile was examined to uncover the mechanism of the [2 + 2] cycloaddition reaction between Ge=G15-Rea and N=C=N. Bond lengths are expressed in angstroms, and bond angles in degrees, with some hydrogen atoms omitted for clarity.
Figure 2. Using the M06-2X-D3/def2-TZVP method, the computed free energy profile was examined to uncover the mechanism of the [2 + 2] cycloaddition reaction between Ge=G15-Rea and N=C=N. Bond lengths are expressed in angstroms, and bond angles in degrees, with some hydrogen atoms omitted for clarity.
Molecules 30 01905 g002
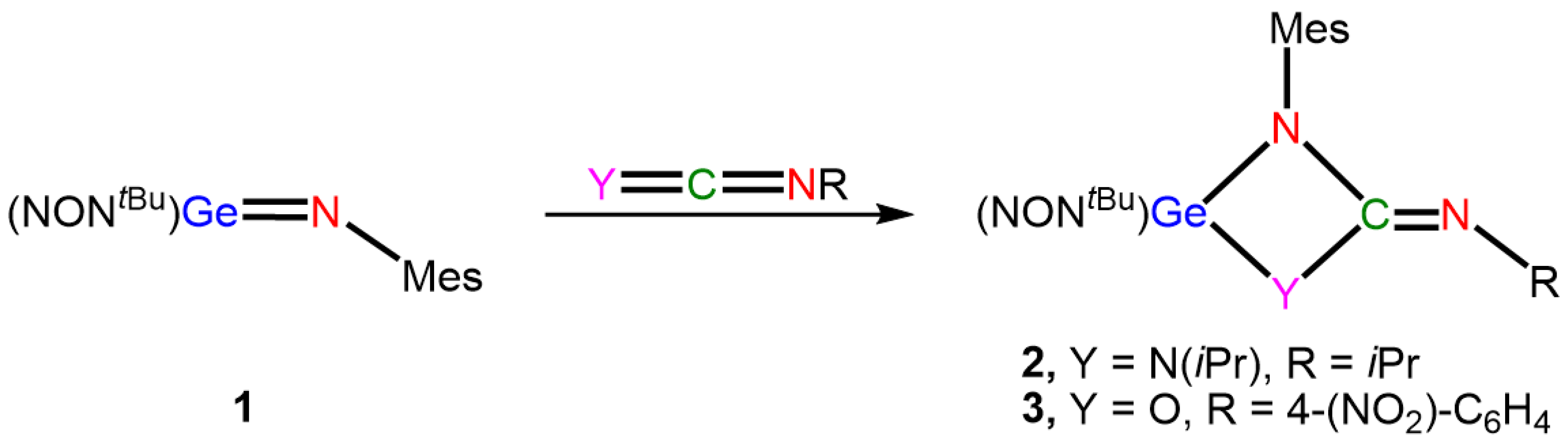
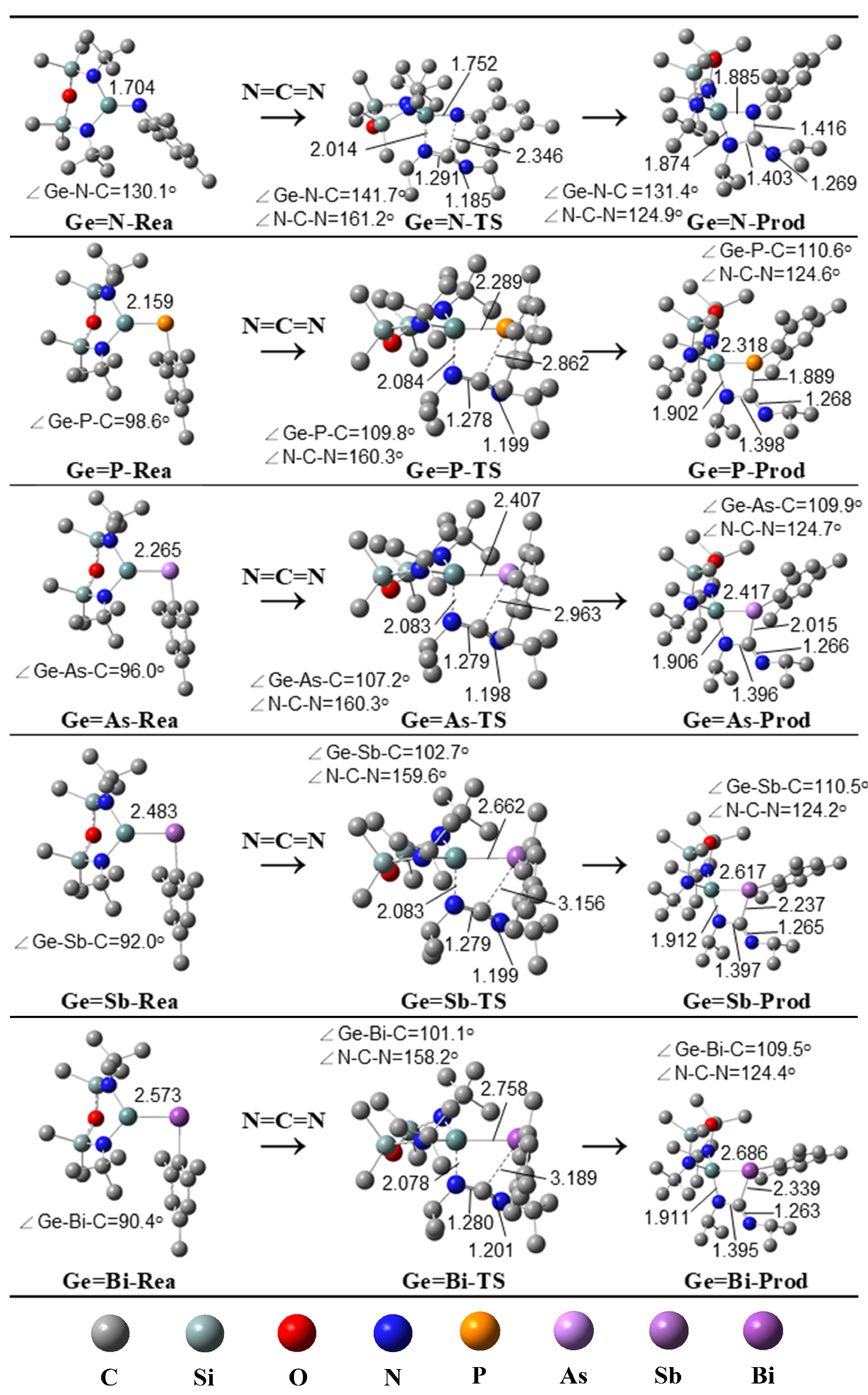
Molecules 30 01905 g003
Figure 3. The structures of the reactants (Ge=G15-Rea), transition states (Ge=G15-TS), and products (Ge=G15-Prod) in the gas phase for the cycloaddition reactions with N=C=N were optimized using the M06-2X-D3/def2-TZVP method. Bond lengths and bond angles are expressed in angstroms (Å) and degrees (°), respectively.
Figure 3. The structures of the reactants (Ge=G15-Rea), transition states (Ge=G15-TS), and products (Ge=G15-Prod) in the gas phase for the cycloaddition reactions with N=C=N were optimized using the M06-2X-D3/def2-TZVP method. Bond lengths and bond angles are expressed in angstroms (Å) and degrees (°), respectively.
Molecules 30 01905 g003
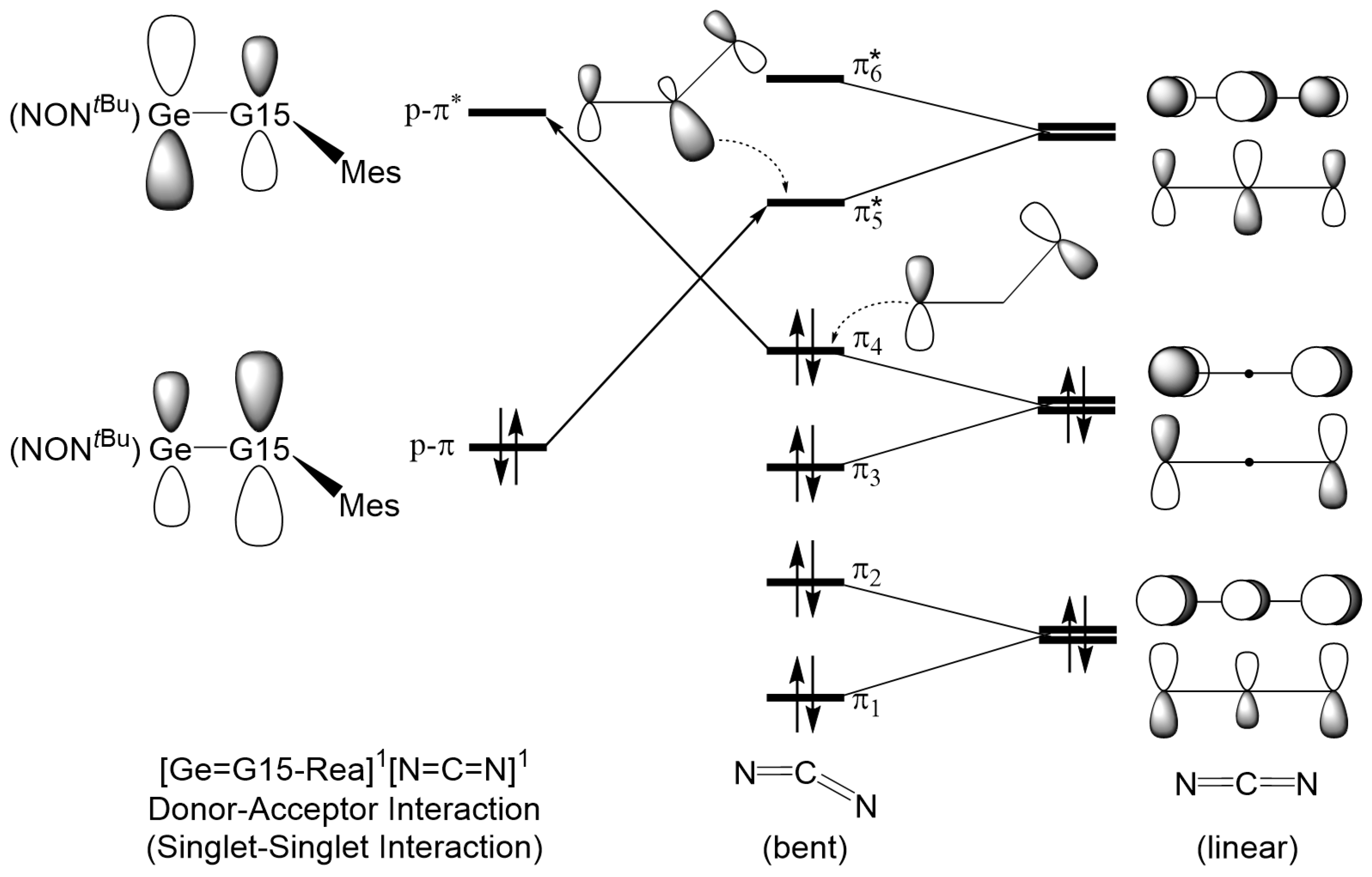
Molecules 30 01905 g004
Figure 4. The “donor–acceptor bonding model”, also known as the “singlet–singlet interaction model”, can be represented by the reaction: [Ge=G15-Rea]1 + [N=C=N]1 → [Ge=G15-TS]1. * means anti-bonding.
Figure 4. The “donor–acceptor bonding model”, also known as the “singlet–singlet interaction model”, can be represented by the reaction: [Ge=G15-Rea]1 + [N=C=N]1 → [Ge=G15-TS]1. * means anti-bonding.
Molecules 30 01905 g004
Molecules 30 01905 g005
Figure 5. The “electron-sharing bonding model”, also known as the “triplet–triplet interaction model”, can be represented by the reaction: [Ge=G15-Rea]3 + [N=C=N]3 → [Ge=G15-TS]1. * means anti-bonding.
Figure 5. The “electron-sharing bonding model”, also known as the “triplet–triplet interaction model”, can be represented by the reaction: [Ge=G15-Rea]3 + [N=C=N]3 → [Ge=G15-TS]1. * means anti-bonding.
Molecules 30 01905 g005
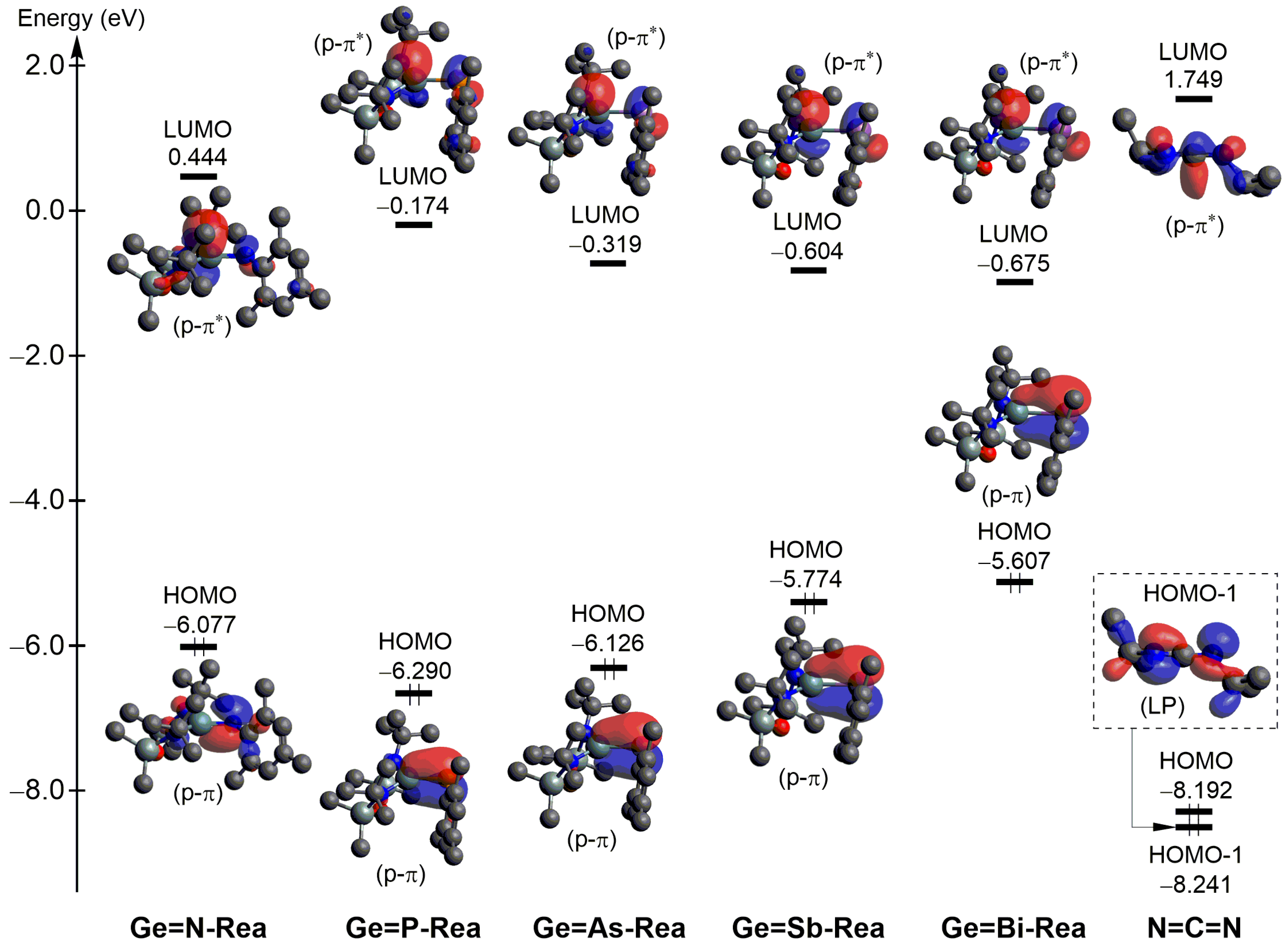
Molecules 30 01905 g006
Figure 6. A schematic representation of the essential frontier molecular orbitals and their orbital energies (in eV) is provided for five heavy imine analogues, Ge=G15-Rea and N=C=N, with hydrogen atoms excluded for clarity. * means anti-bonding.
Figure 6. A schematic representation of the essential frontier molecular orbitals and their orbital energies (in eV) is provided for five heavy imine analogues, Ge=G15-Rea and N=C=N, with hydrogen atoms excluded for clarity. * means anti-bonding.
Molecules 30 01905 g006
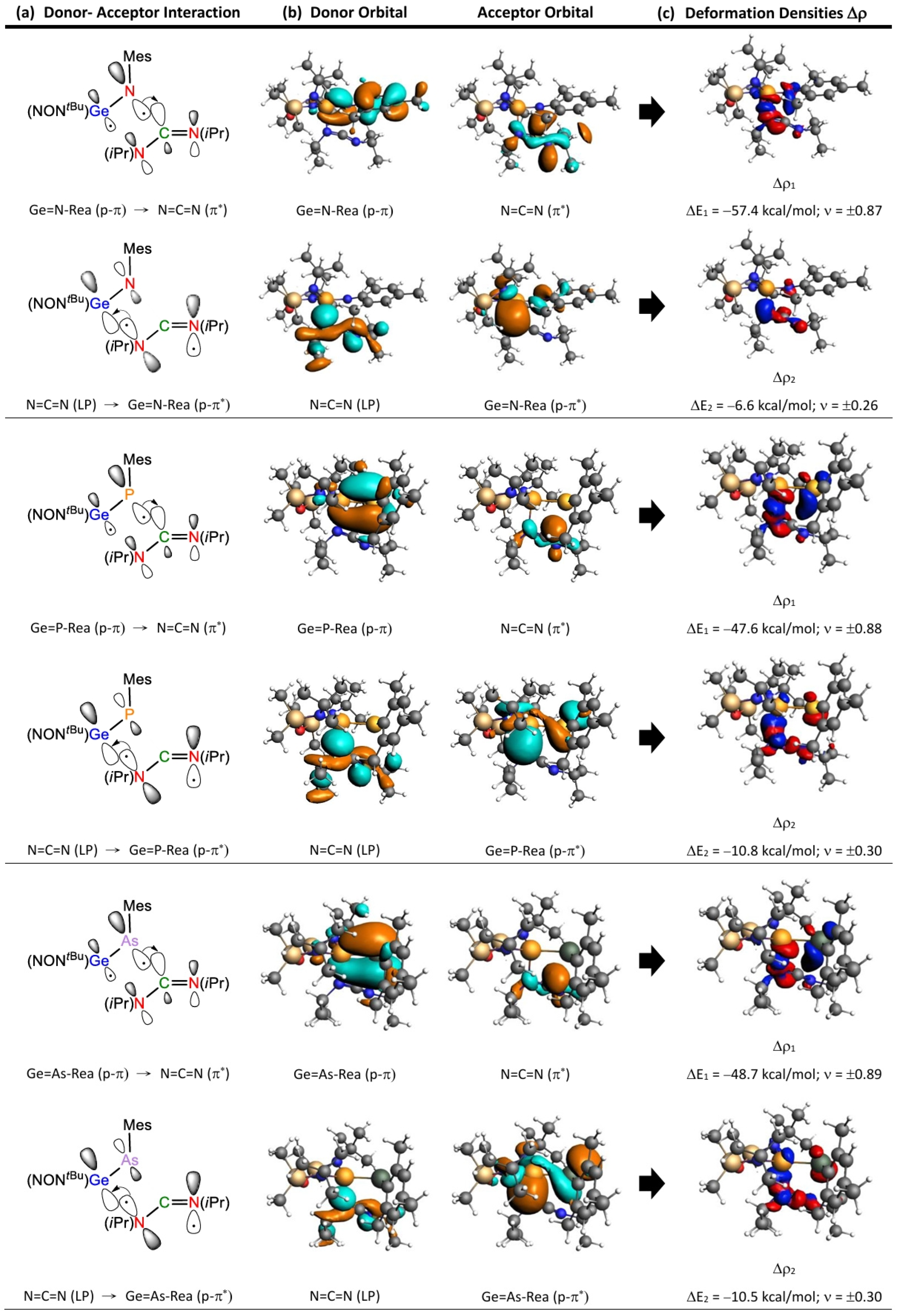
Molecules 30 01905 g007aMolecules 30 01905 g007b
Figure 7. The transition states (Ge=G15-TS) are shown with plots of (a) donor–acceptor interaction, (b) donor orbitals and acceptors, and (c) electron density deformations. These plots illustrate Δρ1 and Δρ2 corresponding to ∆EOrb(1) and ∆EOrb(2) for both S–S and T–T models. Each subplot features red and blue contours indicating negative and positive density deformations. Hydrogen atoms are excluded for clarity, and the contour value is set at |Δρ| = 0.002 a.u. across all transition states. Computational results were obtained with the ZORA-M06-2X-D3/TZ2P//M06-2X-D3/def2-TZVP method. * means anti-bonding.
Figure 7. The transition states (Ge=G15-TS) are shown with plots of (a) donor–acceptor interaction, (b) donor orbitals and acceptors, and (c) electron density deformations. These plots illustrate Δρ1 and Δρ2 corresponding to ∆EOrb(1) and ∆EOrb(2) for both S–S and T–T models. Each subplot features red and blue contours indicating negative and positive density deformations. Hydrogen atoms are excluded for clarity, and the contour value is set at |Δρ| = 0.002 a.u. across all transition states. Computational results were obtained with the ZORA-M06-2X-D3/TZ2P//M06-2X-D3/def2-TZVP method. * means anti-bonding.
Molecules 30 01905 g007aMolecules 30 01905 g007b
Molecules 30 01905 g008
Figure 8. The activation energy (ΔEACT) decomposition for the transition states (Ge=G15-TS) in the [2 + 2] cycloaddition reactions between Ge=G15-Rea and N=C=N, with data extracted from Table 4.
Figure 8. The activation energy (ΔEACT) decomposition for the transition states (Ge=G15-TS) in the [2 + 2] cycloaddition reactions between Ge=G15-Rea and N=C=N, with data extracted from Table 4.
Molecules 30 01905 g008
Molecules 30 01905 sch003
Scheme 3. Theoretical predictions of the [2 + 2] cycloaddition reaction between Ge=G15-Rea and the N=C=N molecule.
Scheme 3. Theoretical predictions of the [2 + 2] cycloaddition reaction between Ge=G15-Rea and the N=C=N molecule.
Molecules 30 01905 sch003
Molecules 30 01905 sch004
Scheme 4. Donor–acceptor bonding interactions between the heavy imine-like molecule Ge=G15-Rea and the N=C=N molecule.
Scheme 4. Donor–acceptor bonding interactions between the heavy imine-like molecule Ge=G15-Rea and the N=C=N molecule.
Molecules 30 01905 sch004
Table 1. The chemical bonding between (NONtBu)Ge: and :G15–Mes (with G15 representing a Group 15 element) in the reactant Ge=G15-Rea ((NONtBu)Ge=G15–Mes) was examined using EDA–NOCV at the ZORA-M06-2X-D3/TZ2P//M06-2X-D3/def2-TZVP level. The EDA–NOCV analysis takes into account both singlet (S) and triplet (T) spin states. All energy values are reported in kcal/mol.
Table 1. The chemical bonding between (NONtBu)Ge: and :G15–Mes (with G15 representing a Group 15 element) in the reactant Ge=G15-Rea ((NONtBu)Ge=G15–Mes) was examined using EDA–NOCV at the ZORA-M06-2X-D3/TZ2P//M06-2X-D3/def2-TZVP level. The EDA–NOCV analysis takes into account both singlet (S) and triplet (T) spin states. All energy values are reported in kcal/mol.
FragmentsGe=N-ReaGe=P-ReaGe=As-ReaGe=Sb-ReaGe=Bi-Rea
(NONtBu)Ge: (S)
+
:N–Mes (S)		(NONtBu)Ge: (T)
+
:N–Mes (T)		(NONtBu)Ge: (S)
+
:P–Mes (S)		(NONtBu)Ge: (T)
+
:P–Mes (T)		(NONtBu)Ge: (S)
+
:As–Mes (S)		(NONtBu)Ge: (T)
+
:As–Mes (T)		(NONtBu)Ge: (S)
+
:Sb–Mes (S)		(NONtBu)Ge: (T)
+
:Sb–Mes (T)		(NONtBu)Ge: (S)
+
:Bi–Mes (S)		(NONtBu)Ge: (T)
+
:Bi–Mes (T)
ΔEINT (a)−96.0−111.9−83.0−96.7−72.9−84.6−58.0−70.0−50.3−61.9
ΔEPauli490.1346.2445.9195.3422.8176.6323.6145.7295.7130.1
ΔEElstat (b)−249.8 (42.6%)−204.4 (44.6%)−241.5 (45.7%)−140.8 (48.2%)−236.2 (47.6%)−133.9 (51.3%)−192.7 (50.5%)−117.4 (54.4%)−180.4 (52.1%)−108.9 (56.7%)
ΔEOrb (b)−334.4 (57.1%)−251.8 (55.0%)−285.5 (54.0%)−149.3 (51.1%)−257.7 (52.0%)−125.4 (48.0%)−187.0 (49.0%)−96.5 (44.7%)−163.8 (47.4%)−81.3 (42.3%)
(a) ΔEINT = ΔEElstat + ΔEPauli + ΔEOrb. (b) The values in parentheses offer the percentage contribution to the total attractive interactions (ΔEElstat + ΔEOrb).
Table 2. Energy differences (in eV) between the critical molecular orbitals of Ge=G15-Rea and N=C=N in the [2 + 2] cycloaddition reaction, computed at the M06-2X-D3/def2-TZVP level, are shown. The data are taken from Figure 6.
Table 2. Energy differences (in eV) between the critical molecular orbitals of Ge=G15-Rea and N=C=N in the [2 + 2] cycloaddition reaction, computed at the M06-2X-D3/def2-TZVP level, are shown. The data are taken from Figure 6.
SystemEnergy Difference
N=C=N (LUMO)—Ge=G15-Rea (HOMO)		Energy Difference
Ge=G15-Rea (LUMO)—N=C=N (HOMO-1)
Ge=N-Rea + N=C=N7.8268.685
Ge=P-Rea + N=C=N8.0398.067
Ge=As-Rea + N=C=N7.8757.922
Ge=Sb-Rea + N=C=N7.5237.637
Ge=Bi-Rea + N=C=N7.3567.566
Table 3. The transition state (Ge=G15-TS) bonding between Ge=G15-Rea (G15 = Group 15 element) and N=C=N is explored using EDA–NOCV results at the ZORA-M06-2X-D3/TZ2P//M06-2X-D3/def2-TZVP level, with both singlet and triplet spin states considered. Energy values are given in kcal/mol.
Table 3. The transition state (Ge=G15-TS) bonding between Ge=G15-Rea (G15 = Group 15 element) and N=C=N is explored using EDA–NOCV results at the ZORA-M06-2X-D3/TZ2P//M06-2X-D3/def2-TZVP level, with both singlet and triplet spin states considered. Energy values are given in kcal/mol.
FragmentsGe=N-TSGe=P-TSGe=As-TSGe=Sb-TSGe=Bi-TS
Ge=N-Rea (S)
+
N=C=N (S)		Ge=N-Rea (T)
+
N=C=N (T)		Ge=P-Rea (S)
+
N=C=N (S)		Ge=P-Rea (T)
+
N=C=N (T)		Ge=As-Rea (S)
+
N=C=N (S)		Ge=As-Rea (T)
+
N=C=N (T)		Ge=Sb-Rea (S)
+
N=C=N (S)		Ge=Sb-Rea (T)
+
N=C=N (T)		Ge=Bi-Rea (S)
+
N=C=N (S)		Ge=Bi-Rea (T)
+
N=C=N (T)
ΔEINT (a)−30.1−172.8−29.7−155.0−31.1−148.1−30.8−139.4−30.3−131.1
ΔEPauli207.0291.4175.0236.6173.7232.6175.2223.1178.5219.0
ΔEElstat (b)−138.7 (58.5%)−170.2 (36.7%)−121.4 (59.3%)−144.0 (36.8%)−121.1 (59.1%)−142.6 (37.4%)−121.2 (58.9%)−139.1 (38.4%)−122.8 (58.8%)−138.6 (39.6%)
ΔEOrb (b)−95.4 (40.2%)−291.1 (62.7%)−80.5 (39.3%)−244.8 (62.5%)−81.0 (39.5%)−235.4 (61.8%)−82.1 (39.8%)−220.6 (60.9%)−83.4 (39.9%)−208.8 (59.6%)
ΔEOrb(1) (c)−57.4 (60.2%)−234.1 (80.4%)−47.6 (59.1%)−199.6 (81.6%)−48.7 (60.1%)−195.7 (83.1%)−50.4 (61.4%)−182.9 (82.9%)−51.8 (62.1%)−170.2 (81.5%)
ΔEOrb(2) (c)−6.6 (6.9%)−27.2 (9.4%)−10.8 (13.4%)−24.6 (10.1%)−10.5 (12.9%)−23.8 (10.1%)−11.0 (13.4%)−24.5 (11.1%)−12.7 (15.2%)−26.8 (12.8%)
ΔERest (c)−31.4 (32.9%)−29.7 (10.2%)−22.1 (27.5%)−20.5 (8.4%)−21.8 (27.0%)−15.9 (6.7%)−20.7 (25.2%)−13.3 (6.0%)−18.9 (22.7%)−11.8 (5.7%)
ΔEDisper (b)−3.0 (1.3%)−3.0 (0.6%)−2.8 (1.4%)−2.8 (0.7%)−2.8 (1.3%)−2.8 (0.7%)−2.7 (1.3%)−2.7 (0.7%)−2.7 (1.3%)−2.7 (0.8%)
(a) ΔEINT = ΔEElstat + ΔEPauli + ΔEOrb + ΔEDisper. (b) The percentages shown in parentheses indicate the contribution to the total attractive interactions, ΔEElstat + ΔEOrb + ΔEDisper. (c) The percentages shown in parentheses indicate the contribution to the total orbital interactions, ΔEOrb.
Table 4. The [2 + 2] cycloaddition reactions between Ge=G15-Rea and N=C=N were analyzed using energy decomposition analysis, with optimization at the ZORA-M06-2X-D3/TZ2P//M06-2X-D3/def2-TZVP level of theory.
Table 4. The [2 + 2] cycloaddition reactions between Ge=G15-Rea and N=C=N were analyzed using energy decomposition analysis, with optimization at the ZORA-M06-2X-D3/TZ2P//M06-2X-D3/def2-TZVP level of theory.
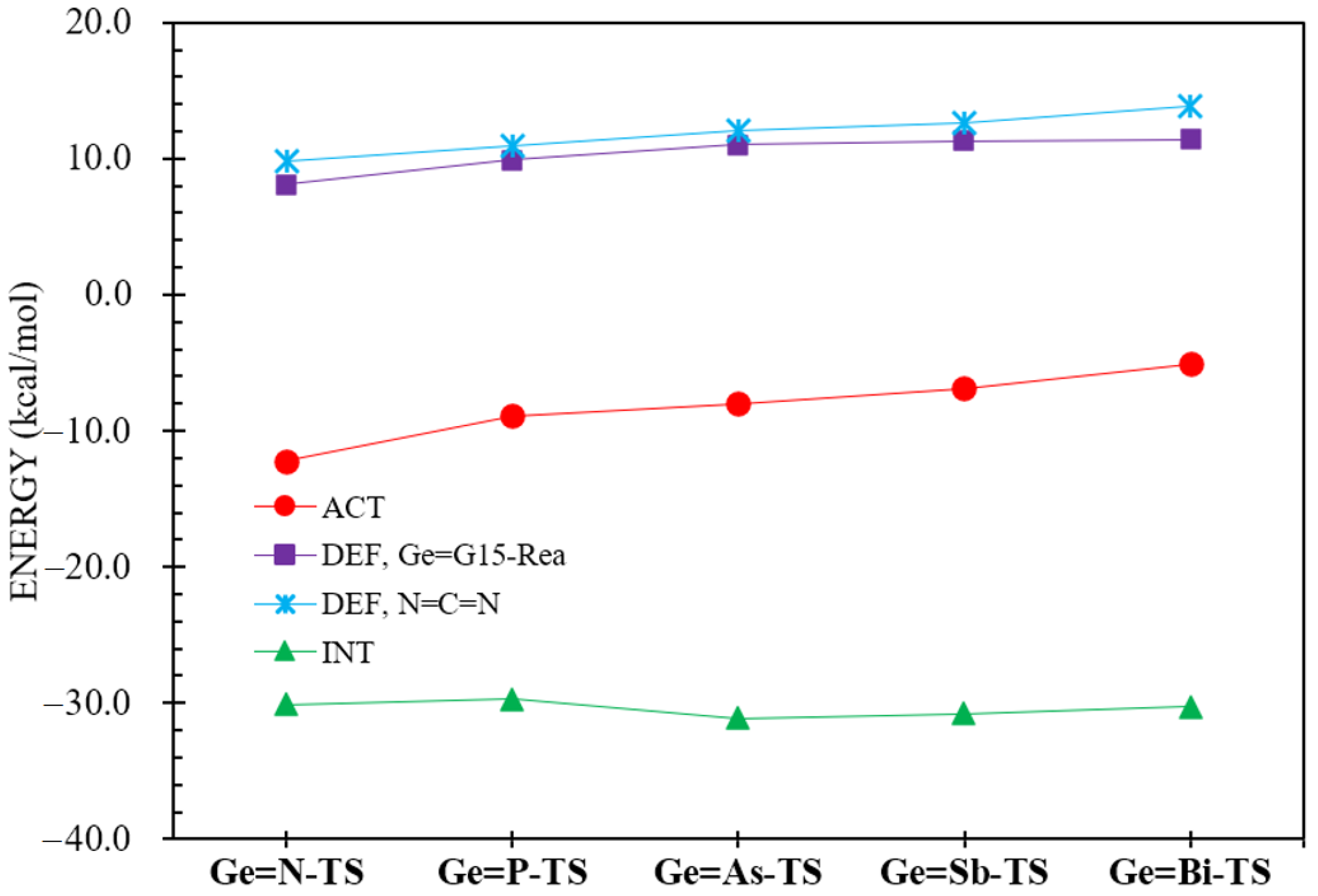
EntryGe=N-TSGe=P-TSGe=As-TSGe=Sb-TSGe=Bi-TS
ΔEACT (a,b)−12.2−8.9−8.0−6.9−5.1
ΔEDEF,N=C=N9.810.912.112.613.8
ΔEDEF,Ge=G15-Rea8.19.911.011.311.4
ΔEINT−30.1−29.7−31.1−30.8−30.3
(a) ΔEACT = ΔEDEF,N=C=N + ΔEDEF,Ge=G15-Rea + ΔEINT. (b) All in kcal mol−1.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Zhang, Z.-F.; Su, M.-D. Insights into the Factors Controlling the Origin of Activation Barriers in the [2 + 2] Cycloaddition Reactions of Heavy Imine-like Molecules Featuring a Ge=Group 15 Double Bond with Heterocumulenes. Molecules 2025, 30, 1905. https://doi.org/10.3390/molecules30091905

AMA Style

Zhang Z-F, Su M-D. Insights into the Factors Controlling the Origin of Activation Barriers in the [2 + 2] Cycloaddition Reactions of Heavy Imine-like Molecules Featuring a Ge=Group 15 Double Bond with Heterocumulenes. Molecules. 2025; 30(9):1905. https://doi.org/10.3390/molecules30091905

Chicago/Turabian Style

Zhang, Zheng-Feng, and Ming-Der Su. 2025. "Insights into the Factors Controlling the Origin of Activation Barriers in the [2 + 2] Cycloaddition Reactions of Heavy Imine-like Molecules Featuring a Ge=Group 15 Double Bond with Heterocumulenes" Molecules 30, no. 9: 1905. https://doi.org/10.3390/molecules30091905

APA Style

Zhang, Z.-F., & Su, M.-D. (2025). Insights into the Factors Controlling the Origin of Activation Barriers in the [2 + 2] Cycloaddition Reactions of Heavy Imine-like Molecules Featuring a Ge=Group 15 Double Bond with Heterocumulenes. Molecules, 30(9), 1905. https://doi.org/10.3390/molecules30091905

Article Metrics

Back to TopTop