Path Integrals for Electronic Densities, Reactivity Indices, and Localization Functions in Quantum Systems
Abstract
:1. Introduction
2. From Density Matrix to Path Integral
2.1. On Mono-, Many-, and Reduced- Electronic Density Matrices
- ○ Normalization
- ○ Recursion
- ○ First order Löwdin reduction
- ○ The idempotency
- ○ The normal additivity, see Equations (33)
- ○ Kernel multiplicity
- ○ Many-body normalization
2.2. Canonical Density, Bloch Equation, and the Need of Path Integral
- ○ It identifies the evolution operatoron the ground of Wick equivalence relationship of Equation (10), which allows the transformation of the Schrödinger into Heisenberg or Interaction pictures for appropriately describing the quantum interactions [53];
- ○ It produces the so called Bloch equation [21] by taking its β derivativethat identifies with the Schrödinger equation for genuine density operatorthrough the same Wick transformation given by Equation (10), thus providing the quantum-mechanically to quantum-statistical equivalence;
- ○ Fulfills the (short times, higher temperature) so called Markovian limiting condition
3. Feynman’s Path Integral of Evolution Amplitude
3.1. Construction of the General Path Integral
- ○ Attractive conceptual representation of dynamical quantum processes without operatorial excursion;
- ○ Allows for quantum fluctuation description in analogy with thermic description, through changing the temporal intervals with the thermodynamical temperature by means of Wick transformation (10), i.e., transforming quantum mechanical (QM) into quantum statistical (QS) propagators
3.2. Schrödinger Equation from Path Integral
3.2.1. Propagator’s Equation
3.2.2. Wave Function’s Equation
3.3. Calculation of Path Integrals. Basic Applications
3.3.1. Path Integrals’ Properties
- Firstly, one may combine the two above Schrödinger type bits of information about path integrals: the fact that propagator itself (xb, tb; xa, ta) obeys the Schrödinger equation, see Equation (127), thus behaving like a sort of wave-function, and the fact that Schrödinger equation of the wave-function is recovered by the quantum Huygens principle of wave-packet propagation, see Equation (131). Thus it makes sense to rewrite Equation (131) with the propagator instead of wave-function obtaining the so called group property for propagatorswhich, nevertheless, may be recursively applied until covering the entire time slicing of the interval [ta, tb] as given in (90)while remarking the absence of time intermediate integration.
- Secondly, from the Huygens principle (131) there is abstracted also the limiting delta Dirac-function for a propagator connecting two space events simultaneouslythat is immediately proofed outThis property is often used as the analytical check once a path integral propagator is calculated for a given system.
- Thirdly, and perhaps most practically, one would like to be able to solve the path integrals, say with canonical Lagrangean form (121a), in more direct way than to consider all multiple integrals involved by the measure (117).
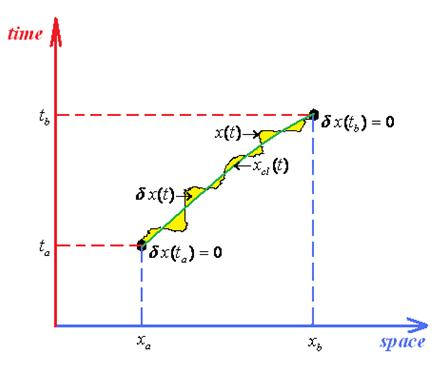
- ○ The classical action goes outside of the path integration by simply becoming the multiplication factor exp[(i / ħ)Scl];
- ○ Since the remaining contribution since depends only on quantum fluctuation δx(t) it allows the changing of the integration measureIn these circumstances the path integral propagator factorizes as
- ○ It is clear that the quantum fluctuation term does not depend on ending space coordinates but only on their time coordinates, so that in the end will depend only on the time difference (tb –ta) since by means of energy conservation all the quantum fluctuation is a time-translation invariant, see for instance the Hamilton-Jacobi Equation (126); therefore it may be further resumed under the fluctuation factor
- ○ Looking at the terms appearing in the whole Lagrangean (146) and to those present on the factor (150) it seems that once the last is known for a given Lagrangean, say L, then the same is characterizing also the modified one with the terms that are not present in the forms (150), namely
- ○ The resulting working path integral of the propagator now simply readsand gives intuitive inside of what path integral formalism of quantum mechanics really does: corrects the classical paths by the quantum fluctuations resumed as the amplitude of the (semi) classical wave.
- ○ the procedure is valid only when the quantity (158), here rewritten in the spirit of (161b) as ∂Scl (xb, tb; xa, ta)/∂xa, performed respecting one end-point coordinate remains linear in the other space (end-point) coordinate xb, so that the identity (159) holds; this is true for the quadratic Lagrangeans of type (146) but not when higher orders are involved, when the previously stipulated Fourier analysis has to be undertaken (one such case will be in foregoing sections presented).
- ○ In the case the formula (161b) is applicable, i.e., when previous condition are fulfilled, the obtained result has to be still verified in recovering the delta-Dirac function by the limitin accordance with the implemented recipe, see Equation (153); usually this step is providing additional phase correction to the solution (161b).
3.3.2. Path Integral for Free Particle
3.3.3. Path Integral for Harmonic Oscillator
- ○ The reliable application of the density computation upon the partition function algorithm, see Equations (128) and (129), prescribes the transformation of the obtained quantum result to the quantum statistical counterpart by means of Wick transformation (10), while supplemented by the functions (188) conversions;
- ○ In computation of the path integral propagator the workable Van Vleck-Pauli-Morette formula looks likewith the complex factor “i” included, as confirmed by both the free and harmonic oscillator quantum motions; it may be used for linear classical actions in one of the end-point space coordinates upon derivation respecting the other one; yet the formula (195) should be always checked for fulfilling the limiting (162) delta-Dirac function for simultaneous events for any applied potential.
4. Semiclassical Path Integral of Evolution Amplitude
4.1. Semiclassical Expansion
- ○ The real time dependency is “rotated” into the imaginary timeor in finite differences asaccording with the Wick transformation (10).
- ○ The quantum paths of (145a) are re-parameterized aswhere the classical path of (145a) is replaced by the fixed (non time-dependent) averagewhile the fluctuation path η(τ) remains to carry the whole path integral information, yet being departed at the end of integration frontier from previously Dirichlet boundary conditions (145c), where it vanished at the domain frontiers, to the actual different endpoint valuesin terms of the length of the “traveled” space
4.2. Connected Correlation Functions
4.3. Classical Fluctuation Path and Connected Green Function
- Solving the associate real time harmonic problem;
- Rotating the solution into imaginary time picture;
- Taking the “free harmonic limit”ω → 0.
4.3.1. Calculation of Classical Fluctuation Path
4.3.2. Calculation of the Connected Green Function
4.4. Second Order Semiclassical Propagator, Partition Function and Density
- At coincident timesor re-written aswithin the thermodynamical environment given by Equation (239).
- At different timeswith its quantum thermodynamical counterpart
4.5. Fourth Order Semiclassical Electronegativity and Chemical Hardness
- ▪ we retain the positive values of electronegativity (263) since EN is evaluated as a stability measure of such nuclear-electronic system;
- ▪ the sign is in accordance with the electric field orientation that drives the sense of the electronic conditional probability of the imaginary evolution amplitude evaluated from the center of atom (ra = 0) to the current valence shell radius (rb).
- the atoms N, O, F, Ne, and He have the highest electronegativities among the main groups;
- the electronegativity of N is by far greater than that of Cl - a situation that is not met in the finite-difference approach;
- the Silicium rule demanding that most metals to have EN values less than or equal to that of Si, is as well widely satisfied;
- the metalloid band (B, Si, Ge, As, Sb, Te) clearly separates the metals by nonmetals’ EN values;
- along periods the highest EN values belong to the noble elements – a rule not fulfilled by the couples (Cl, Ar), (Br, Kr), and (I, Xe) within the finite difference representation, see Table 1;
- the recorded electronegativity values of the chalcogens (O, S, Se, Te) reveal great distinction between the chemistry of oxygen and the rest elements of VIA group;
5. Effective Classical Path Integral of Evolution Amplitude
5.1. Effective Classical Partition Function
5.2. Periodic Path Integrals
5.2.1. Matsubara Frequencies and the Quantum Periodic Paths
5.2.2. Matsubara Harmonic Partition Function
5.2.3. The Generalized Riemann’ Series
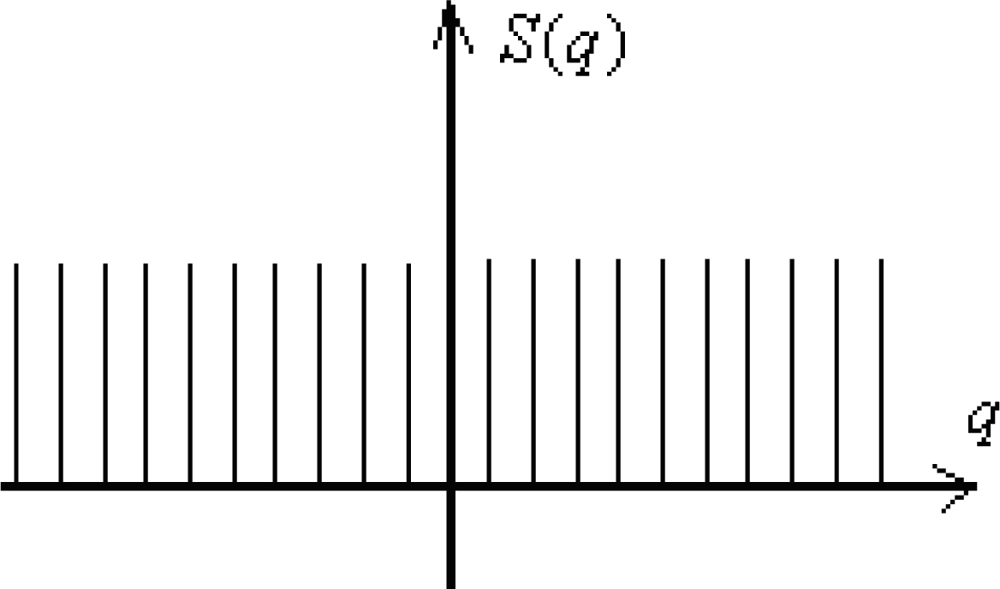
- ○ Writing it under the formin terms of the extended series
- ○ Applying the Poisson formula, see Appendix (A8), on series (298b)
- ○ Computing the integral under the sum of (299) by the complex integration, according with the contours of integration identified in Figure 5 around the poles q = ±iα throughout applying the residues’ theoremwhile summing upon the convergent casesarisen from the observation thatNote that the contour (I) is considered completed with trigonometric positive direction, while for the (II) contour the anti-trigonometric sense results, as being equivalent with the minus sign in front of its integral, which, explicitly giveswhile the other contour integration leads with similar result.
- ○ Insertion of these integration results in the expression (299) is done by attributing to each contour and integration the (series) summing range according with the constraints of (301a) to successively yield○ With expression (303) the Riemann series (298a) finally reads as
- ○ The cross-check with the usual Riemann series is performed by means of turning the harmonic to free motion picture, as the already consecrated free to harmonic motion interplay; That is to evaluate the limitwithin the hyperbolic cotangent function approximationto give the identityleaving with the classical Riemann series limit
5.2.4. Periodic Path Integral Measure
- ○ Computing the function (295) by inserting the above Riemann generalized series (304):
- ○ Evaluating the function (294) by the aid of (297) rule through considering the variable change z = ħβΩ/ 2 in (309)
- ○ Obtaining the function (293a) with the help of (293b) and (310)
- ○ Releasing the Matsubara partition function for the harmonic motion by replacing function (311) into expression (292)
- ○ Comparing the form (312) with the consecrated results (192) or (288b), thus getting the condition
- ○ Choosing for the Feynman centroid normalization factor the inverse of the thermal length (280)
- ○ Plugging expression (314) in (313) to yield the constantand then by considering it into the relation (291) to get the Matsubara constants
- ○ Replacing the constants (314) and (315b) in (287) to provide the normalized measure of the periodic integrals in terms of the Matsubara quantum frequencies (283)
5.3. Feynman-Kleinert Variational Formalism
5.3.1. Feynman-Kleinert Partition Function
5.3.2. Feynman-Kleinert Optimum Potential
5.3.3. Quantum Smeared Effects and the Stability of Matter
5.3.4. Ground State (β→∞, T→0K) Case
5.3.5. Excited State (β→0, T→∞) Case. Wigner Expansion
5.4. Path Integral Connection with Density Functional Theory
5.4.1. Feynman-Kleinert Electronic Density. Analogy with Levy’s Search Mechanism
- ○ The variational approach for effective-classical potential partition function provides the energy approximation for the ground state, leaving with the Feynman-Kleinert potential, see Equations (328) and (337);
- ○ The optimization of the Feynman-Kleinert potential respecting the trial harmonic frequency to achieving the thermodynamical equilibrium of the ground state, see Equations (338) & (341).
5.4.2. Mulliken Density Functional Electronegativity
5.4.3. Atomic Electronegativity by Feynman Centroid Path Integral
- ○ The first one considers only the pseudo-potentials into the path integral formalism that gives the electronic density in the quantum statistical manner as it was described in the previous Section 5.4.1. This way, a strong physical meaning is assured because all the information about the electronic density and electronegativity are comprised (and dictated) only by the pseudopotential. Yet, the problem that arises in this approach is that the electronic density depends on the β parameter. This parameter will be fixed so that the electronic density to fulfill the path integral normalization condition. Additionally, the search of the β parameter must be done in the semiclassical (high temperature) limit (β → 0) for which the path integral formalism corresponds to the excited (valence) states of atoms.
- ○ The second approach takes beyond to the pseudopotential data also the valence basis and the electronic densities are then computed in the accustomed quantum manner. At this point we need to consider the working orbital type for the atomic systems and we will chose the s-basis set because its spherical symmetry.
6. Non-equilibrium Path Integral of Evolution Amplitude
6.1. Levels of Non-equilibrium Dynamics
6.2. Non-equilibrium Lagrangean
6.3. Harmonic Markovian Density Matrix
6.4. Anharmonic Markovian Density Matrix


6.5. Path Integral Connection with Electronic Localization Functions (ELFs)
6.5.1. From Thom’s Catastrophe Concepts to Chemical Bond Topology
6.5.2. Fokker-Planck Approach of Electron Localization
- Solving the path integral of Equation (473) for the non-linear potential (476) the time-dependent (spin) conditioned probability is provided;
- The ω-limit (tb→∞) is performed on the previous (i) result leaving with the stationary (spin) conditioned probability
- The result from (ii) is employed upon the specific integration rule [3]providing the “renormalization” of the stationary spin conditioned probability (478) into the so called exchange (parallel spins) conditional probability: . Note that this “unusual” normalization condition makes in fact the proper link with the Fermi hole, in close relation with Pauli exchange repulsion, telling that the αα and ββ exchanged holes contain exactly minus one electron [135].
- Identification of the actual exchange probability with the previous general one given by Equation (472) delivers the polynomial equations that can be treated either as the gradient or Laplacian equations (466) and (467), respectively, towards identifying one of the universal unfolded catastrophes given in Table 6. In any case, either as a gradient or Laplacian equation, the companion equation results immediately assuring therefore the necessary number of equations from which the critical solution xb as well as the bifurcation parameter Aσσ are evaluated in terms of g and h.
- Finally, throughout the correspondences (475) the Markovian ELF is found. The next section is dedicated to applying the Markovian ELF algorithm for the anharmonic potential of (chemical) binding.
6.5.3. The Forms of General Markovian ELFs
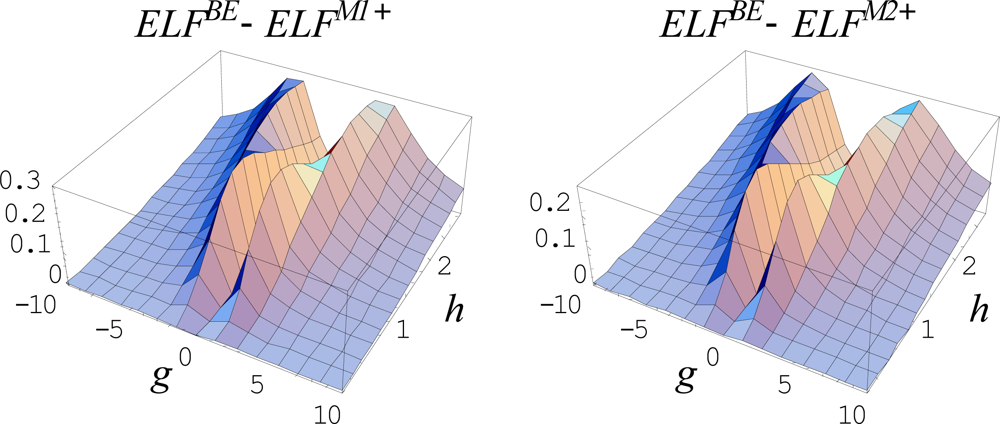
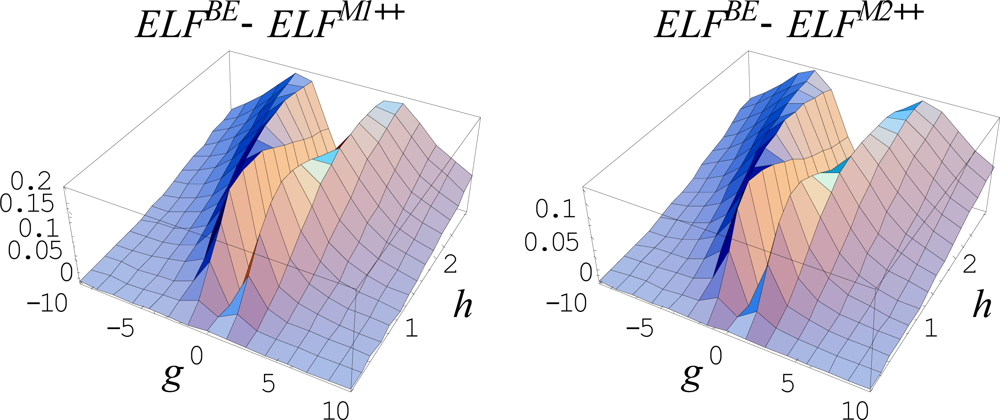
6.5.4. Working Markovian ELFs
7. Conclusions
- ○ ħ → 0: the quantum semiclassical limit;
- ○ ħβ → 0: the quantum statistical short-time limit;
- ○ T → ∞: the high-temperature limit;
- ○ ω → 0: the flat potential, or the quasi-homogeneous (Thomas-Fermi) limit; yet, this may be easier visualized by noting the discrete-to-quasi continuum transformation of eigen-levels intervals in the exited zones of quantum systems (atoms, molecules), i.e., where the approximation ωħβ = ωħ/(kBT) ≪1 holds; moreover, this limit nicely overlaps with the “free harmonic approximation” used in this work, when the interplay between the free and harmonic motion helped in elucidating and solving (by integrating out) the quantum fluctuations along the classical paths;
- ○ N → ∞ or Z → ∞: the bosonic limit due to the scaled equivalence T ~ N1/ 3 or T ~ Z1/ 3 when the system is thermally expanded, being it related with the Thomas-Fermi theory, here not exposed.
Acknowledgments
Appendix: Poisson Formula for Series
References
- Hohenberg, P; Kohn, W. Inhomogeneous electronic gas. Phys. Rev 1964, 136, 864–871. [Google Scholar]
- Kohn, W; Sham, LJ. Self-consistent equations including exchange and correlation effects. Phys. Rev 1965, 140, 1133–1138. [Google Scholar]
- Parr, RG; Yang, W. Density Functional Theory of Atoms and Molecules; Oxford University Press: New York, NY, USA, 1989. [Google Scholar]
- Dreizler, RM; Gross, EKU. Density Functional Theory; Springer Verlag: Heidelberg, Germany, 1990. [Google Scholar]
- Kohn, W; Becke, AD; Parr, RG. Density functional theory of electronic structure. J. Phys. Chem 1996, 100, 12974–12980. [Google Scholar]
- Parr, RG; Donnelly, RA; Levy, M; Palke, WE. Electronegativity: The density functional viewpoint. J. Chem. Phys 1978, 68, 3801–3807. [Google Scholar]
- Putz, MV. Contributions within Density Functional Theory with Applications in Chemical Reactivity Theory and Electronegativity. Dissertation.com, Parkland, FL, USA, 2003. [Google Scholar]
- Putz, MV; Chiriac, A. Quantum perspectives on the nature of the chemical bond. Advances in Quantum Chemical Bonding Structures, Putz, MV, Ed.; Transworld Research Network: Kerala, India, 2008; 1–43. [Google Scholar]
- Putz, MV. Absolute and Chemical Electronegativity and Hardness; Nova Science Publishers Inc: New York, NY, USA, 2008. [Google Scholar]
- Putz, MV. Density functionals of chemical bonding. Int. J. Mol. Sci 2008, 9, 1050–1095. [Google Scholar]
- Putz, MV. Electronegativity: quantum observable. Int. J. Quantum Chem 2009, 109, 733–738. [Google Scholar]
- Ayers, PW; Parr, RG. Variational principles for describing chemical reactions: Reactivity indices based on the external potential. J. Am. Chem. Soc 2001, 123, 2007–2017. [Google Scholar]
- Parr, RG. The Quantum Theory of Molecular Electronic Structure; Benjamin: New York, NY, USA, 1964. [Google Scholar]
- t’ Hooft, G. How does god throw dice? In Fluctuating Paths and Fields – Dedicated to Hagen Kleinert on the Occasion of his 60th Birthday; Janke, W, Pelster, A, Schmidt, H-J, Bachmann, M, Eds.; World Scientific: Singapore, 2001. [Google Scholar]
- Marañón, J; Pousa, JL. Path integral, collective coordinates, and molecular-orbital theory. Phys. Rev. A 1987, 36, 5530–5542. [Google Scholar]
- Grosche, C; Steiner, F. Path integrals on curved manifolds. Z. Phys. C 1987, 36, 699–714. [Google Scholar]
- Abolhasani, M; Golsgani, M. The path integral approach in the frame work of causal interpretation. Ann. Fond. L.de Broglie 2003, 28, 1–8. [Google Scholar]
- Putz, MV. Levels of a unified theory of chemical interaction. Int. J. Chem. Model 2009, 1, 141–147. [Google Scholar]
- Chen, J; Makri, N. Forward-backward semiclassical dynamics with single-bead coherent state density. Mol. Phys 2008, 106, 443–453. [Google Scholar]
- Putz, MV. Chemical action and chemical bonding. J. Mol. Structure: THEOCHEM 2009, 900, 64–70. [Google Scholar]
- Bloch, F. Theorie des Austauschproblems und der Remanenzerscheinung der Ferromagnetika. Z. Phys 1932, 74, 295–335. [Google Scholar]
- Löwdin, PO. Quantum theory of many-particle systems. I. Physical interpretations by means of density matrices, natural spin-orbitals, and convergence problems in the method of configurational interaction. Phys. Rev 1955, 97, 1474–1489. [Google Scholar]
- Fano, U. Description of states in quantum mechanics by density matrix and operator techniques. Rev. Mod. Phys 1957, 29, 74–93. [Google Scholar]
- McWeeny, R. The density matrix in many-electron quantum mechanics. I. Generalized product functions. Factorization and physical interpretation of the density matrices. R. Proc. Royal Soc A 1959, 253, 242–259. [Google Scholar]
- ter Haar, D. Theory and applications of the density matrix. Rep. Prog. Phys 1961, 24, 304–362. [Google Scholar]
- Carlson, BC; Keller, JM. Eigenvalues of density matrices. Phys. Rev 1961, 121, 659–661. [Google Scholar]
- Blum, K. Density Matrix Theory and Applications; Plenum Press: New York, NY, USA, 1981. [Google Scholar]
- Eberly, JH; Singh, LPS. Time operators, partial stationarity, and the energy-time uncertainty relation. Phys. Rev. D 1973, 7, 359–362. [Google Scholar]
- Donnely, RA; Parr, RG. Elementary properties of an energy functional of the first-order reduced density matrix. J. Chem. Phys 1978, 69, 4431–4438. [Google Scholar]
- Morell, MM; Parr, RG; Levy, M. Calculation of ionization potentials from density matrices and natural functions, and the long-range behavior of natural orbitals and electron density. J. Chem. Phys 1975, 62, 549–554. [Google Scholar]
- Belinfante, F. Density matrix formulation of quantum theory and its physical interpretation. Int. J. Quantum Chem 1980, 17, 1–24. [Google Scholar]
- Messiah, A. Quantum Mechanics; Volume 1 and 2, North-Holland: Amsterdam, The Netherlands, 1961. [Google Scholar]
- Kubo, R. Statistical Mechanics; North-Holland: Amsterdam, The Netherlands, 1965. [Google Scholar]
- Feynman, RP. Statistical Mechanics; Benjamin: Reading, PA, USA, 1972. [Google Scholar]
- Thouless, DJ. The Quantum Mechanics of Many-body Systems; Academic Press: New York, NY, USA, 1972. [Google Scholar]
- Isihara, A. Statistical Physics; Academic Press: New York, NY, USA, 1980. [Google Scholar]
- Dirac, PAM. The Lagrangian in quantum mechanics. Phys. Z. Sowjetunion 1933, 3, 64–72. [Google Scholar]
- Makri, N. Path integral methods. In The Encyclopedia of Computational Chemistry; Schleyer, PVR, Allinger, NL, Clark, T, Gasteiger, J, Kollman, PA, Schaefer, HF, III, Schreiner, PR, Eds.; John Wiley & Sons: Chichester, UK, 1998; pp. 2021–2029. [Google Scholar]
- Kleinert, H. Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets, 3rd ed; World Scientific: Singapore, 2004. [Google Scholar]
- Feynman, RP. Space-time approach to non-relativistic quantum mechanics. Rev. Mod. Phys 1948, 20, 367–387. [Google Scholar]
- Feynman, RP; Hibbs, AR. Quantum Mechanics and Path Integrals; McGraw Hill: New York, NY, USA, 1965. [Google Scholar]
- Kac, M. Probability and Related Topics in Physical Science; Interscience: New York, NY, USA, 1959; Chapter 4. [Google Scholar]
- Zin-Justin, J. Large order estimates in perturbation theory. Phys. Rep 1979, 49, 205–213. [Google Scholar]
- Kleinert, H. Systematic corrections to the variational calculation of the effective classical potential. Phys. Lett. A 1993, 173, 332–342. [Google Scholar]
- Janke, W; Kleinert, H. Scaling property of variational perturbation expansion for a general anharmonic oscillator with xp-potential. Phys. Lett. A 1995, 199, 287–290. [Google Scholar]
- Krzyweck, J. Variational perturbation theory for the quantum-statistical density matrix. Phys. Rev. A 1997, 56, 4410–4419. [Google Scholar]
- Kleinert, H; Mustapic, I. Decay rates of metastable states in cubic potential by variational perturbation theory. Int. J. Mod. Phys. A 1996, 11, 4383–4399. [Google Scholar]
- Kleinert, H; Pelster, A; Putz, MV. Variational perturbation theory for Markov processes. Phys Rev E 2002, 65, 066128:1–066128:7. [Google Scholar]
- Becke, AD; Edgecombe, KE. A simple measure of electron localization in atomic and molecular systems. J. Chem Phys 1990, 92, 5397–5403. [Google Scholar]
- Putz, MV. Markovian approach of the electron localization functions. Int. J. Quantum Chem 2005, 105, 1–11. [Google Scholar]
- Park, JL; Band, W; Yourgrau, W. Simultaneous measurement, phase-space distributions, and quantum state determination. Ann Phys 1980, 492, 189–199. [Google Scholar]
- Blanchard, CH. Density matrix and energy–time uncertainty. Am. J. Phys 1982, 50, 642–645. [Google Scholar]
- Snygg, J. The Heisenberg picture and the density operator. Am. J. Phys 1982, 50, 906–909. [Google Scholar]
- Wiener, N. Differential space. J. Math. Phys 1923, 2, 131–174. [Google Scholar]
- Infeld, L; Hull, TE. The factorization method. Rev. Mod. Phys 1951, 23, 21–68. [Google Scholar]
- Schulmann, LS. A Path integral for spin. Phys. Rev 1968, 176, 1558–1569. [Google Scholar]
- Rzewuski, J. Field Theory, Hafner: New York, NY, USA, 1969.
- Abarbanel, HDI; Itzykson, C. Relativistic eikonal expansion. Phys. Rev. Lett 1969, 23, 53–56. [Google Scholar]
- Campbell, WB; Finkler, P; Jones, CE; Misheloff, MN. Path-integral formulation of scattering theory. Phys. Rev.D 1975, 12, 2363–2369. [Google Scholar]
- Laidlaw, MGG; DeWitt-Morette, C. Feynman functional integrals for systems of indistinguishable particles. Phys. Rev.D 1971, 3, 1375–1378. [Google Scholar]
- Peak, D; Inomata, A. Summation over Feynman histories in polar coordinates. J. Math. Phys 1969, 10, 1422–1428. [Google Scholar]
- Gerry, CC; Singh, VA. Feynman path-integral approach to the Aharonov-Bohm effect. Phys. Rev. D 1979, 20, 2550–2554. [Google Scholar]
- Kleinert, H. Path collapse in Feynman formula. Stable path integral formula from local time reparametrization invariant amplitude. Phys. Lett. B 1989, 224, 313–318. [Google Scholar]
- Greiner, W; Reinhardt, J. Quantum Electrodynamics; Springer: Berlin, Germany, 1994. [Google Scholar]
- Dittrich, W; Reuter, M. Classical and Quantum Dynamics: From Classical Paths to Path Integrals; Springer: Berlin, Germany, 1994. [Google Scholar]
- Kleinert, H. Path integral for second-derivative Lagrangian L = (κ/2)χ̄2+(m/2)ẋ2+(k/2)x2–j(τ)x(τ). J. Math. Phys 1986, 27, 3003–3013. [Google Scholar]
- Putz, MV. First Principles of Quantum Chemistry Vol I Quantum Theory and Observability; Nova Science Publishers Inc: New York, USA, unpublished work.
- Dachen, R; Hasslacher, B; Neveu, A. Nonperturbative methods and extended-hadron models in field theory. I. Semiclassical functional methods. Phys. Rev. D 1974, 10, 4114–4129. [Google Scholar]
- Grosche, C. Path integration via summation of perturbation expansions and applications to totally reflecting boundaries, and potential steps. Phys. Rev. Lett 1993, 71, 1–4. [Google Scholar]
- Manning, RS; Ezra, GS. Regularized semiclassical radial propagator for the Coulomb potential. Phys. Rev. A 1994, 50, 954–966. [Google Scholar]
- Putz, MV; Pelster, A; Kleinert, H. Atomic radii scale by higher order semiclassical path integral of density matrix, unpublished work.
- Putz, MV. Semiclassical electronegativity and chemical hardness. J. Theor. Comput. Chem 2007, 6, 33–47. [Google Scholar]
- Parr, RG; Pearson, RG. Absolute hardness: Companion parameter to absolute electronegativity. J. Am. Chem. Soc 1983, 105, 7512–7516. [Google Scholar]
- Robles, J; Bartolotti, LJ. Electronegativities, electron affinities, ionization potentials, and hardnesses of the elements within spin polarized density functional theory. J. Am. Chem. Soc 1984, 106, 3723–3727. [Google Scholar]
- Gázquez, LJ; Ortiz, E. Electronegativities and hardnesses of open shell atoms. J. Chem. Phys 1984, 81, 2741–2748. [Google Scholar]
- Sen, KD (Ed.) Chemical Hardness; Springer Verlag: Berlin, Germany, 1993.
- Pearson, RG. Chemical Hardness; Wiley-VCH: Weinheim, Germany, 1997. [Google Scholar]
- Putz, MV; Russo, N; Sicilia, E. On the application of the HSAB principle through the use of improved computational schemes for chemical hardness evaluation. J. Comput. Chem 2004, 25, 994–1003. [Google Scholar]
- Slater, JC. Atomic shielding constants. Phys. Rev 1930, 36, 57–64. [Google Scholar]
- Bohr, N. Abhandlungen über Atombau aus des Jaren 1913–1916, Vieweg & Son: Braunschweig, Germany, 1921.
- Hassani, S. Foundation of Mathematical Physics; Prentice-Hall: Englewood Cliffs, NJ, USA, 1991. [Google Scholar]
- Lackner, KS; Zweig, G. Introduction to the chemistry of fractionally charged atoms: Electronegativity. Phys. Rev. D 1983, 28, 1671–1691. [Google Scholar]
- Murphy, LR; Meek, TL; Allred, AL; Allen, LC. Evaluation and test of pauling's electronegativity scale. J. Phys. Chem. A 2000, 104, 5867–5871. [Google Scholar]
- Bader, RFW. Atoms in Molecules: A Quantum Theory; Oxford Univerisity Press: Oxford, UK, 1990. [Google Scholar]
- Feynman, RP; Kleinert, H. Effective classical partition function. Phys. Rev. A 1986, 34, 5080–5084. [Google Scholar]
- Kleinert, H. Effective potentials from effective classical potentials. Phys. Lett. B 1986, 181, 324–326. [Google Scholar]
- Giachetti, R; Tognetti, V; Vaia, R. Quantum corrections to the thermodynamics of nonlinear systems. Phys. Rev. B 1986, 33, 7647–7658. [Google Scholar]
- Janke, W; Cheng, BK. Statistical properties of a harmonic plus a delta-potential. Phys. Lett. B 1988, 129, 140–144. [Google Scholar]
- Voth, GA. Calculation of equilibrium averages with Feynman-Hibbs effective classical potentials and similar variational approximations. Phys. Rev. A 1991, 44, 5302–5305. [Google Scholar]
- Cuccoli, A; Macchi, A; Neumann, M; Tognetti, V; Vaia, R. Quantum thermodynamics of solids by means of an effective potential. Phys. Rev. B 1992, 45, 2088–2096. [Google Scholar]
- Schulman, LS. Techniques and Applications of Path Integration; Wiley: New York, NY, USA, 1981. [Google Scholar]
- Wiegel, FW. Introduction to Path-Integral Methods in Physics and Polymer Science; World Scientific: Singapore, 1986. [Google Scholar]
- Dirac, PAM. The Principles of Quantum Mechanics; Oxford University Press: Oxford, UK, 1944. [Google Scholar]
- Duru, IH; Kleinert, H. Solution of the path integral for the H-atom. Phys. Lett. B 1979, 84, 185–188. [Google Scholar]
- Duru, IH; Kleinert, H. Quantum mechanics of H-atom from path integrals. Fortschr. Physik 1982, 30, 401–435. [Google Scholar]
- Blinder, SM. Analytic form for the nonrelativistic Coulomb propagator. Phys. Rev. A 1993, 43, 13–16. [Google Scholar]
- Kleinert, H. Path integral for a relativistic spinless Coulomb system. Phys. Lett. A 1996, 212, 15–21. [Google Scholar]
- Hillary, M; O’Connell, RF; Scully, MO; Wigner, EP. Distribution functions in physics: Fundamentals. Phys. Rep 1984, 106, 121–167. [Google Scholar]
- Levy, M. Universal variational functionals of electron densities, first order density matrices, and natural spin-orbitals and solution of the v-representability problem. Proc. Natl. Acad. Sci. USA 1979, 76, 6062–6065. [Google Scholar]
- Putz, MV; Russo, N. Electronegativity scale from path integral formulation. 2003.
- Putz, MV; Russo, N; Sicilia, E. About the Mulliken electronegativity in DFT. Theor. Chem. Acc 2005, 114, 38–45. [Google Scholar]
- Putz, MV. Systematic formulation for electronegativity and hardness and their atomic scales within density functional softness theory. Int. J. Quantum Chem 2006, 106, 361–386. [Google Scholar]
- Parr, RG; Donnelly, RA; Levy, M; Palke, WE. Electronegativity: The density functional viewpoint. J. Chem. Phys 1978, 68, 3801–3807. [Google Scholar]
- Garza, J; Robles, J. Density-functional-theory softness kernel. Phys. Rev. A 1993, 47, 2680–2685. [Google Scholar]
- Yang, W. Ab initio approach for many-electron systems without invoking orbitals: An integral formulation of the density functional theory. Phys. Rev. A 1988, 38, 5494–5503. [Google Scholar]
- Yang, W. Thermal properties of many-electron systems: An integral formulation of the density functional theory. Phys. Rev. A 1988, 38, 5504–5511. [Google Scholar]
- Szasz, L. Pseudopotential Theory of Atoms and Molecules; John Wiley: New York, NY, USA, 1985. [Google Scholar]
- Preuss, H. Quantenchemie fuer Chemiker; Verlag Chemie: Weinheim, Germany, 1969. [Google Scholar]
- Tables of Pseudopotential Data.
- Mulliken, RS. A New electroaffinity scale; together with data on valence states and on valence ionization potentials and electron affinities. J. Chem. Phys 1934, 2, 782–793. [Google Scholar]
- Hinze, J; Jaffé, HH. Electronegativity. I. Orbital electronegativity of neutral atoms. J. Am. Chem. Soc 1962, 84, 540–546. [Google Scholar]
- Huheey, JE. Inorganic Chemistry Principles of Structure and Reactivity, 2nd ed; Harper and Row: New York, USA, 1978. [Google Scholar]
- .
- Bartolotti, LJ; Gadre, SR; Parr, RG. Electronegativities of the elements from simple Xα theory. J. Am. Chem. Soc 1980, 102, 2945–2948. [Google Scholar]
- Sen, KD. Isoelectronic changes in energy, electronegativity and hardness in atoms via the calculations of <r–1>. Struct. Bond 1993, 80, 87–114. [Google Scholar]
- Putz, MV. Fulfilling the Dirac’s promise on quantum chemical bond. In Quantum Frontiers of Atoms and Molecules; Putz, MV, Ed.; NOVA Publishers, Inc: New York, NY, USA; in press.
- Matthews, PM; Saphiro, II; Falkoff, DL. Stochastic equations for non-equilibrium processes. Phys. Rev 1960, 120, 1–16. [Google Scholar]
- Haken, H. Synergetics; Springer: Berlin, Germany, 1978; Series in Synergetics, Vol. 1. [Google Scholar]
- van Kampen, NG. Stochastic Processes in Physics and Chemistry; North-Holland: Amsterdam, The Netherlands, 1981. [Google Scholar]
- Garddiner, CV. Handbook of Stochastic Methods; Springer: Berlin, Germany, 1983; Series in Synergetics, Vol. 13. [Google Scholar]
- Risken, H. The Fokker-Planck Equation; Springer: Berlin, Germany, 1983; Series in Synergetics, Vol. 18. [Google Scholar]
- Pawula, RF. Approximation of the linear Boltzmann equation by the Fokker-Planck equation. Phys Rev 1967, 162, 186–188. [Google Scholar]
- Einstein, A. Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Ann. Phys. (Leipzig) 1905, 322, 549–560. [Google Scholar]
- Nyquist, H. Thermal agitation of electric charge in conductors. Phys. Rev 1928, 32, 110–113. [Google Scholar]
- Callen, HB; Welton, TA. Irreversibility and generalized noise. Phys. Rev 1951, 83, 34–40. [Google Scholar]
- Adelman, SA. Quantum generalized Langevin equation approach to gas/solid collisions. Chem. Phys. Lett 1976, 40, 495–499. [Google Scholar]
- Ford, GW; Lewis, JT; O’Connell, RF. Quantum Langevin equation. Phys. Rev. A 1988, 37, 4419–4428. [Google Scholar]
- Schwinger, J. Brownian motion of a quantum oscillator. J. Math. Phys 1961, 2, 407–432. [Google Scholar]
- Thom, R. Stabilitè Structurelle et Morphogènése; Benjamin-Addison-Wesley: New York, NY, USA, 1973. [Google Scholar]
- Mezey, PG. Potential Energy Hypersurfaces; Elsevier: Amsterdam, The Netherlands, 1987. [Google Scholar]
- Gillespie, RJ. Molecular Geometry; Van Nostrand Reinhold: London, UK, 1972. [Google Scholar]
- Bader, RFW; Gillespie, RJ; McDougall, PJ. A physical basis for the VSEPR model of molecular geometry. J. Am. Chem. Soc 1988, 110, 7329–7336. [Google Scholar]
- Silvi, B; Savin, A. Classification of chemical bonds based on topological analysis of electron localization functions. Nature 1994, 371, 683–686. [Google Scholar]
- Savin, A; Jepsen, J; Andersen, OK; Preuss, H; von Schnering, HG. Electron localization in the solid-state structures of the elements: The diamond structure. Angew. Chem., Int. Ed. Engl 1992, 31, 187–188. [Google Scholar]
- Becke, AD. Correlation energy of an inhomogeneous electron gas: A coordinate-space model. J. Chem. Phys 1988, 88, 1053–1062. [Google Scholar]
- Frisch, HL; Wasserman, E. Chemical topology. J. Am. Chem. Soc 1961, 83, 3789–3795. [Google Scholar]
- Fuller, FB. The Writhing number of a space curve. Proc. Nat. Acad. Sci. USA 1971, 68, 815–819. [Google Scholar]
- Crick, FHC. Linking numbers and nucleosomes. Proc. Nat. Acad. Sci. USA 1976, 73, 2639–2643. [Google Scholar]
- Hänggi, P; Talkner, P; Borkovec, M. Reaction-rate theory: Fifty years after Kramers. Rev. Mod. Phys 1990, 62, 251–341. [Google Scholar]
- Weiss, U. Quantum Dissipative Systems; World Scientific: Singapore, 1993. [Google Scholar]











| H | He | Legend: Simbol of element | |||||||||||||||
| 1 | 1 | Valence principal quantum number: n | |||||||||||||||
| 1 | 1.7 | Slater effective charge: Zeff | |||||||||||||||
| 7.18 | 12.27 | Finite difference electronegativity:χFD * | |||||||||||||||
| 6.45 | 12.48 | Finite difference chemical hardness: ηFD * | |||||||||||||||
| Li | Be | B | C | N | O | F | Ne | ||||||||||
| 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | ||||||||||
| 1.30 | 1.95 | 2.60 | 3.25 | 3.90 | 4.55 | 5.2 | 5.85 | ||||||||||
| 3.02 | 3.43 | 4.26 | 6.24 | 6.97 | 7.59 | 10.4 | 10.71 | ||||||||||
| 4.39 | 5.93 | 4.06 | 4.99 | 7.59 | 6.14 | 7.07 | 10.92 | ||||||||||
| Na | Mg | Al | Si | P | S | Cl | Ar | ||||||||||
| 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | ||||||||||
| 2.20 | 2.85 | 3.50 | 4.15 | 4.80 | 5.45 | 6.10 | 6.75 | ||||||||||
| 2.80 | 2.6 | 3.22 | 4.68 | 5.62 | 6.24 | 8.32 | 7.7 | ||||||||||
| 2.89 | 4.99 | 2.81 | 3.43 | 4.89 | 4.16 | 4.68 | 8.11 | ||||||||||
| K | Ca | Sc | Ti | V | Cr | Mn | Fe | Co | Ni | Cu | Zn | Ga | Ge | As | Se | Br | Kr |
| 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 2.20 | 2.85 | 3.00 | 3.15 | 3.30 | 3.45 | 3.60 | 3.75 | 3.90 | 4.05 | 4.20 | 4.35 | 5.00 | 5.65 | 6.30 | 6.95 | 7.60 | 8.25 |
| 2.39 | 2.29 | 3.43 | 3.64 | 3.85 | 3.74 | 3.85 | 4.26 | 4.37 | 4.37 | 4.47 | 4.26 | 3.22 | 4.58 | 5.3 | 5.93 | 7.59 | 6.86 |
| 1.98 | 3.85 | 3.22 | 3.22 | 2.91 | 3.12 | 3.64 | 3.64 | 3.43 | 3.22 | 3.22 | 5.2 | 2.81 | 3.33 | 4.47 | 3.85 | 4.26 | 7.28 |
| Rb | Sr | Y | Zr | Nb | Mo | Tc | Ru | Rh | Pd | Ag | Cd | In | Sn | Sb | Te | I | Xe |
| 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 2.20 | 2.85 | 3.00 | 3.15 | 3.30 | 3.45 | 3.60 | 3.75 | 3.90 | 4.05 | 4.20 | 4.35 | 5.00 | 5.65 | 6.30 | 6.95 | 7.60 | 8.25 |
| 2.29 | 1.98 | 3.43 | 3.85 | 4.06 | 4.06 | 3.64 | 4.06 | 4.26 | 4.78 | 4.47 | 4.16 | 3.12 | 4.26 | 4.89 | 5.51 | 6.76 | 5.82 |
| 1.87 | 3.74 | 2.91 | 3.02 | 2.91 | 3.12 | 3.64 | 3.43 | 3.22 | 3.64 | 3.12 | 4.78 | 2.70 | 3.02 | 3.85 | 3.54 | 3.74 | 6.34 |
| Atom | Atom | ||||
|---|---|---|---|---|---|
| H | 7.18 | 6.45 | Ni | 0.99·10−4 | 2.6·10−5 |
| He | 15.52 | 5.91 | Cu | 1.1·10−4 | 2.68·10−5 |
| Li | 1.12·10−1 | 0.91·10−1 | Zn | 1.13·10−4 | 2.77·10−5 |
| Be | 2.43·10−1 | 1.28·10−1 | Ga | 1.48·10−4 | 3.15·10−5 |
| B | 4.15·10−1 | 1.6·10−1 | Ge | 1.88·10−4 | 3.51·10−5 |
| C | 6.2·10−1 | 1.86·10−1 | As | 2.32·10−4 | 3.86·10−5 |
| N | 8.54·10−1 | 2.07·10−1 | Se | 2.79·10−4 | 4.2·10−5 |
| O | 11.08·10−1 | 2.22·10−1 | Br | 3.31·10−4 | 4.54·10−5 |
| F | 13.77·10−1 | 2.31·10−1 | Kr | 3.88·10−4 | 4.86·10−5 |
| Ne | 16.54·10−1 | 2.35·10−1 | Rb | 0.32·10−6 | 1.59·10−7 |
| Na | 0.3·10−2 | 1.4·10−3 | Sr | 0.54·10−6 | 2.04·10−7 |
| Mg | 0.48·10−2 | 1.8·10−3 | Y | 0.59·10−6 | 2.15·10−7 |
| Al | 0.71·10−2 | 2.1·10−3 | Zr | 0.65·10−6 | 2.25·10−7 |
| Si | 0.99·10−2 | 2.5·10−3 | Nb | 0.72·10−6 | 2.35·10−7 |
| P | 1.3·10−2 | 2.8·10−3 | Mo | 0.78·10−6 | 2.45·10−7 |
| S | 1.64·10−2 | 3.06·10−3 | Tc | 0.85·10−6 | 2.56·10−7 |
| Cl | 2.02·10−2 | 3.33·10−3 | Ru | 0.92·10−6 | 2.66·10−7 |
| Ar | 2.4·10−2 | 3.58·10−3 | Rh | 1.·10−6 | 2.76·10−7 |
| K | 0.3·10−4 | 1.46·10−5 | Pd | 1.07·10−6 | 2.86·10−7 |
| Ca | 0.5·10−4 | 1.87·10−5 | Ag | 1.15·10−6 | 2.96·10−7 |
| Sc | 0.55·10−4 | 1.96·10−5 | Cd | 1.24·10−6 | 3.06·10−7 |
| Ti | 0.6·10−4 | 2.05·10−5 | In | 1.63·10−6 | 3.5·10−7 |
| V | 0.66·10−4 | 2.15·10−5 | Sn | 2.07·10−6 | 3.92·10−7 |
| Cr | 0.72·10−4 | 2.23·10−5 | Sb | 2.56·10−6 | 4.34·10−7 |
| Mn | 0.78·10−4 | 2.33·10−5 | Te | 3.1·10−6 | 4.75·10−7 |
| Fe | 0.85·10−4 | 2.42·10−5 | I | 3.68·10−6 | 5.16·10−7 |
| Co | 0.92·10−4 | 2.51·10−5 | Xe | 4.32·10−6 | 5.56·10−7 |
| Li | Be | B | C | N | O | F | Ne | ||||||||||
| 4.77 | 6.05 | 6.77 | 8.69 | 9.73 | 10.93 | 11.84 | 10.90 | ||||||||||
| 3.50 | 3.93 | 6.07 | 8.44 | 8.95 | 10.72 | 17.80 | 17.60 | ||||||||||
| Na | Mg | Al | Si | P | S | Cl | Ar | ||||||||||
| 4.09 | 5.18 | 8.73 | 5.95 | 8.38 | 9.48 | 9.94 | 9.25 | ||||||||||
| 3.02 | 3.08 | 6.20 | 6.71 | 7.72 | 10.32 | 12.07 | 13.36 | ||||||||||
| K | Ca | Sc | Ti | V | Cr | Mn | Fe | Co | Ni | Cu | Zn | Ga | Ge | As | Se | Br | Kr |
| 3.28 | 4.41 | 2.66 | 3.19 | 3.78 | 4.71 | 5.41 | 5.35 | 5.39 | 5.49 | 5.83 | 4.54 | 3.24 | 5.12 | 4.53 | 9.09 | 9.11 | 7.93 |
| 2.91 | 2.47 | 1.76 | 2.46 | 3.11 | 4.58 | 5.46 | 6.01 | 6.49 | 8.62 | 7.01 | 9.10 | 3.24 | 3.58 | 3.89 | 3.65 | 5.22 | 5.97 |
| Rb | Sr | Y | Zr | Nb | Mo | Tc | Ru | Rh | Pd | Ag | Cd | In | Sn | Sb | Te | I | Xe |
| 1.63 | 2.92 | 3.04 | 3.57 | 4.34 | 5.08 | 5.06 | 5.36 | 5.65 | 5.86 | 5.86 | 4.76 | 5.10 | 5.37 | 5.05 | 7.53 | 8.42 | 7.37 |
| 1.18 | 1.79 | 1.38 | 1.17 | 1.12 | 1.37 | 1.30 | 1.23 | 1.10 | 1.27 | 1.39 | 1.52 | 2.29 | 2.24 | 4.55 | 3.60 | 4.56 | 5.40 |
| Z | Element | Mulliken-Jaffe, Ref. [112, 113] | Experiment, Ref. [73, 77] | Xα, Ref. [114] | Density Functional of Equation (400) | |
|---|---|---|---|---|---|---|
| Path Integral | s-Basis Set | |||||
| 3 | Li | 1.8 | 3.01 | 2.58 | 4.11 | 3.02 |
| 4 | Be | 4.8 | 4.9 | 3.80 | 5.64 | 3.40 |
| 5 | B | 5.99 | 4.29 | 3.40 | 5.72 | 5.66 |
| 6 | C | 8.59 | 6.27 | 5.13 | 8.56 | 8.58 |
| 7 | N | 11.21 | 7.27 | 6.97 | 10.13 | 9.77 |
| 8 | O | 14.39 | 7.53 | 8.92 | 11.87 | 12.41 |
| 9 | F | 12.18 | 10.41 | 11.0 | 13.13 | 15.60 |
| 10 | Ne | 13.29 | - | 10.31 | 13.39 | 13.37 |
| 11 | Na | 1.6 | 2.85 | 2.32 | 3.16 | 2.64 |
| 12 | Mg | 4.09 | 3.75 | 3.04 | 4.52 | 3.93 |
| 13 | Al | 5.47 | 3.21 | 2.25 | 5.80 | 5.89 |
| 14 | Si | 7.30 | 4.76 | 3.60 | 6.56 | 6.80 |
| 15 | P | 8.90 | 5.62 | 5.01 | 9.04 | 8.33 |
| 16 | S | 10.14 | 6.22 | 6.52 | 10.09 | 11.88 |
| 17 | Cl | 9.38 | 8.30 | 8.11 | 10.64 | 14.59 |
| 18 | Ar | 9.87 | - | 7.11 | 10.12 | 12.55 |
| 19 | K | 2.90 | 2.42 | 1.92 | 3.15 | 2.48 |
| 20 | Ca | 3.30 | 2.2 | 1.86 | 4.21 | 2.19 |
| 21 | Sc | 4.66 | 3.34 | 2.52 | 2.93 | 1.83 |
| 22 | Ti | 5.2 | 3.45 | 3.05 | 3.52 | 2.28 |
| 23 | V | 5.47 | 3.6 | 3.33 | 4.19 | 2.42 |
| 24 | Cr | 5.56 | 3.72 | 3.45 | 5.23 | 2.72 |
| 25 | Mn | 5.23 | 3.72 | 4.33 | 6.02 | 2.01 |
| 26 | Fe | 6.06 | 4.06 | 4.71 | 5.96 | 3.90 |
| 27 | Co | 6.21 | 4.3 | 3.76 | 6.01 | 3.03 |
| 28 | Ni | 6.30 | 4.40 | 3.86 | 6.12 | 3.48 |
| 29 | Cu | 6.27 | 4.48 | 3.95 | 6.35 | 2.91 |
| 30 | Zn | 5.53 | 4.45 | 3.66 | 5.07 | 3.13 |
| 31 | Ga | 6.02 | 3.2 | 2.11 | 3.49 | 3.30 |
| 32 | Ge | 6.4 | 4.6 | 3.37 | 5.45 | 4.24 |
| 33 | As | 6.63 | 5.3 | 4.63 | 4.87 | 4.94 |
| 34 | Se | 7.39 | 5.89 | 5.91 | 7.71 | 4.82 |
| 35 | Br | 8.40 | 7.59 | 7.24 | 7.75 | 7.35 |
| 36 | Kr | 8.86 | - | 6.18 | 8.65 | 9.59 |
| 37 | Rb | 2.09 | 2.34 | 1.79 | 1.56 | 1.05 |
| 38 | Sr | 3.14 | 2.0 | 1.75 | 2.87 | 1.63 |
| 39 | Y | 4.25 | 3.19 | 2.25 | 3.33 | 1.76 |
| 40 | Zr | 4.57 | 3.64 | 3.01 | 3.92 | 1.73 |
| 41 | Nb | 5.38 | 4.0 | 3.26 | 4.77 | 1.68 |
| 42 | Mo | 7.04 | 3.9 | 3.34 | 5.59 | 2.07 |
| 43 | Tc | 6.27 | - | 4.58 | 5.57 | 1.96 |
| 44 | Ru | 7.16 | 4.5 | 3.45 | 5.91 | 1.93 |
| 45 | Rh | 7.4 | 4.3 | 3.49 | 6.23 | 1.72 |
| 46 | Pd | 7.16 | 4.45 | 3.52 | 6.46 | 1.98 |
| 47 | Ag | 6.36 | 4.44 | 3.55 | 6.47 | 2.18 |
| 48 | Cd | 5.64 | 4.43 | 3.35 | 5.26 | 2.36 |
| 49 | In | 5.22 | 3.1 | 2.09 | 5.38 | 2.48 |
| 50 | Sn | 6.96 | 4.30 | 3.20 | 5.75 | 2.74 |
| 51 | Sb | 7.36 | 4.85 | - | 5.44 | 6.29 |
| 52 | Te | 7.67 | 5.49 | 5.35 | 6.35 | 4.98 |
| 53 | I | 8.10 | 6.76 | 6.45 | 7.12 | 6.70 |
| 54 | Xe | 7.76 | - | 5.36 | 7.80 | 6.27 |
| Orbital (Hybrid) | s | p | sp | sp2 | sp3 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Element | Chemical Information | Basis Set | Path Integral | Basis Set | Path Integral | Basis Set | Path Integral | Basis Set | Path Integral | Basis Set | Path Integral |
| C | Mulliken-Jaffe’s Electronegativity | 8.59 | 5.80 | 10.39 | 8.79 | 7.98 | |||||
| Electronegativity Chemical Action | 8.58 8.44 | 8.56 8.69 | 3.11 3.11 | 4.04 4.1 | 10.73 11.43 | 9.89 10.04 | 7.53 7.74 | 6.99 7.1 | 5.77 5.83 | 5.71 5.71 | |
| N | Mulliken-Jaffe’s Electronegativity | 11.21 | 7.39 | 15.68 | 12.87 | 11.54 | |||||
| Electronegativity Chemical Action | 9.77 8.95 | 10.13 9.73 | 5.09 4.80 | 6.14 5.9 | 16.97 17.99 | 17.54 16.86 | 11.88 12.34 | 12.40 11.92 | 9.21 9.35 | 10.13 9.73 | |
| O | Mulliken-Jaffe’s Electronegativity | 14.39 | 9.65 | 27.25 | 17.07 | 15.25 | |||||
| Electronegativity Chemical Action | 12.41 10.72 | 11.87 10.93 | 8.06 7.35 | 8.39 7.73 | 27.06 28.07 | 27.40 25.23 | 18.54 19.48 | 19.38 17.84 | 14.48 14.84 | 15.82 14.57 | |
| Name | Co-dimension | Co-rank | Universal unfolding |
|---|---|---|---|
| Fold | 1 | 1 | x3 + ux |
| Cusp | 2 | 1 | x4 + ux2 + vx |
| Swallow tail | 3 | 1 | x5 + ux3 + vx2 + wx |
| Hyperbolic umbilic | 3 | 2 | x3 + y3 + uxy + vx + wy |
| Elliptic umbilic | 3 | 2 | x3 − xy2 + u(x2 + y2) + vx + wy |
| Butterfly | 4 | 1 | x6 + ux4 + vx3 + wx2 + tx |
| Parabolic umbilic | 4 | 2 | x2 y + y4 + ux2 + vy2 + wx + ty |
| QM | QS | FP |
|---|---|---|
| m | m | |
| ω | ω | γ |
| ħβ | tb – ta | |
| cosh(ωħβ) |
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Putz, M.V. Path Integrals for Electronic Densities, Reactivity Indices, and Localization Functions in Quantum Systems. Int. J. Mol. Sci. 2009, 10, 4816-4940. https://doi.org/10.3390/ijms10114816
Putz MV. Path Integrals for Electronic Densities, Reactivity Indices, and Localization Functions in Quantum Systems. International Journal of Molecular Sciences. 2009; 10(11):4816-4940. https://doi.org/10.3390/ijms10114816
Chicago/Turabian StylePutz, Mihai V. 2009. "Path Integrals for Electronic Densities, Reactivity Indices, and Localization Functions in Quantum Systems" International Journal of Molecular Sciences 10, no. 11: 4816-4940. https://doi.org/10.3390/ijms10114816
APA StylePutz, M. V. (2009). Path Integrals for Electronic Densities, Reactivity Indices, and Localization Functions in Quantum Systems. International Journal of Molecular Sciences, 10(11), 4816-4940. https://doi.org/10.3390/ijms10114816