Rise-Time of FRET-Acceptor Fluorescence Tracks Protein Folding
Abstract
:1. Introduction
2. Results and Discussion
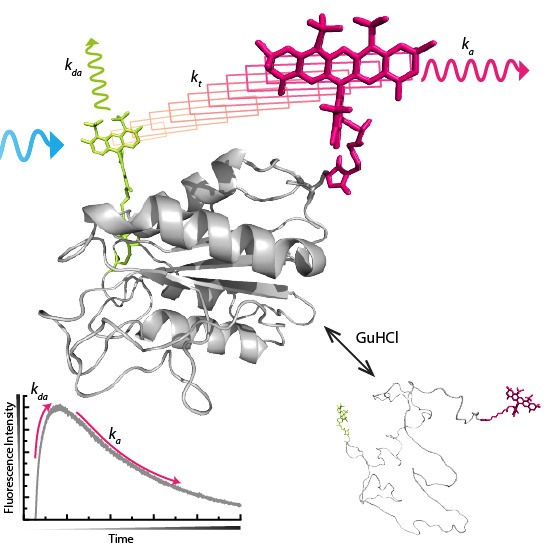
2.1. Acceptor Rise and Decay Times and Their Corresponding Amplitudes Track (Un)folding of Apoflavodoxin


2.2. FRET Rates Derived from Acceptor Rise Times Reveal Conformational Changes during Protein (Un)folding


3. Experimental Section
3.1. Theoretical and Practical Considerations of Time-Dependent Increase of Acceptor Fluorescence
3.2. Preparation of Double-Labeled Apoflavodoxin
3.3. Denaturant Dependent Equilibrium (Un)folding
3.4. Acquisition and Fitting of Time-Resolved Fluorescence Data
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Stryer, L.; Haugland, R.P. Energy transfer: A spectroscopic ruler. Proc. Natl. Acad. Sci. USA 1967, 58, 719–726. [Google Scholar] [PubMed]
- Stryer, L. Fluorescence energy-transfer as a spectroscopic ruler. Annu. Rev. Biochem. 1978, 47, 819–846. [Google Scholar] [CrossRef] [PubMed]
- Clegg, R.M. Fluorescence resonance energy-transfer and nucleic-acids. Methods Enzymol. 1992, 211, 353–388. [Google Scholar] [PubMed]
- Borst, J.W.; Visser, A.J.W.G. Fluorescence lifetime imaging microscopy in life sciences. Meas. Sci. Technol. 2010, 21, 102002. [Google Scholar] [CrossRef]
- Lakowicz, J.R. Principles of Fluorescence Spectroscopy, 3rd ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Valeur, B.; Berberan-Santos, M.N. Molecular Fluorescence: Principles and Applications, 2nd ed.; Wiley-VCH: Weinheim, Germany, 2012. [Google Scholar]
- Panchuk-Voloshina, N.; Haugland, R.P.; Bishop-Stewart, J.; Bhalgat, M.K.; Millard, P.J.; Mao, F.; Leung, W.Y.; Haugland, R.P. Alexa dyes, a series of new fluorescent dyes that yield exceptionally bright, photostable conjugates. J. Histochem. Cytochem. 1999, 47, 1179–1188. [Google Scholar] [CrossRef] [PubMed]
- Lindhoud, S.; Westphal, A.H.; Visser, A.J.; Borst, J.W.; van Mierlo, C.P. Fluorescence of Alexa fluor dye tracks protein folding. PLoS One 2012, 7, e46838. [Google Scholar] [CrossRef] [PubMed]
- Orevi, T.; Lerner, E.; Rahamim, G.; Amir, D.; Haas, E. Ensemble and single-molecule detected time-resolved FRET methods in studies of protein conformations and dynamics. Methods Mol. Biol. 2014, 1076, 113–169. [Google Scholar] [PubMed]
- Roy, R.; Hohng, S.; Ha, T. A practical guide to single-molecule FRET. Nat. Methods 2008, 5, 507–516. [Google Scholar] [CrossRef] [PubMed]
- Berney, C.; Danuser, G. FRET or no FRET: A quantitative comparison. Biophys. J. 2003, 84, 3992–4010. [Google Scholar] [CrossRef] [PubMed]
- Visser, N.V.; Borst, J.W.; Hink, M.A.; van Hoek, A.; Visser, A.J. Direct observation of resonance tryptophan-to-chromophore energy transfer in visible fluorescent proteins. Biophys. Chem. 2005, 116, 207–212. [Google Scholar] [CrossRef] [PubMed]
- Lu, P.Y.; Yu, Z.X.; Alfano, R.R.; Gersten, J.I. Picosecond studies of energy-transfer of donor and acceptor dye molecules in solution: II. A concentration-dependence. Phys. Rev. A 1983, 27, 2100–2109. [Google Scholar] [CrossRef]
- Laptenok, S.P.; Borst, J.W.; Mullen, K.M.; van Stokkum, I.H.; Visser, A.J.; van Amerongen, H. Global analysis of Förster resonance energy transfer in live cells measured by fluorescence lifetime imaging microscopy exploiting the rise time of acceptor fluorescence. Phys. Chem. Chem. Phys. 2010, 12, 7593–7602. [Google Scholar] [CrossRef] [PubMed]
- Kulinski, T.; Visser, A.J.; OʼKane, D.J.; Lee, J. Spectroscopic investigations of the single tryptophan residue and of riboflavin and 7-oxolumazine bound to lumazine apoprotein from Photobacterium leiognathi. Biochemistry 1987, 26, 540–549. [Google Scholar] [CrossRef] [PubMed]
- Borst, J.W.; Laptenok, S.P.; Westphal, A.H.; Kühnemuth, R.; Hornen, H.; Visser, N.V.; Kalinin, S.; Aker, J.; van Hoek, A.; Seidel, C.A.; Visser, A.J.W.G. Structural changes of yellow Cameleon domains observed by quantitative FRET analysis and polarized fluorescence correlation spectroscopy. Biophys. J. 2008, 95, 5399–5411. [Google Scholar] [CrossRef] [PubMed]
- Schuler, B.; Lipman, E.A.; Steinbach, P.J.; Kumke, M.; Eaton, W.A. Polyproline and the “spectroscopic ruler” revisited with single-molecule fluorescence. Proc. Natl. Acad. Sci. USA 2005, 102, 2754–2759. [Google Scholar] [CrossRef] [PubMed]
- Deniz, A.A.; Laurence, T.A.; Beligere, G.S.; Dahan, M.; Martin, A.B.; Chemla, D.S.; Dawson, P.E.; Schultz, P.G.; Weiss, S. Single-molecule protein folding: Diffusion fluorescence resonance energy transfer studies of the denaturation of chymotrypsin inhibitor 2. Proc. Natl. Acad. Sci. USA 2000, 97, 5179–5184. [Google Scholar] [CrossRef] [PubMed]
- Schuler, B.; Lipman, E.A.; Eaton, W.A. Probing the free-energy surface for protein folding with single-molecule fluorescence spectroscopy. Nature 2002, 419, 743–747. [Google Scholar] [CrossRef] [PubMed]
- Rhoades, E.; Gussakovsky, E.; Haran, G. Watching proteins fold one molecule at a time. Proc. Natl. Acad. Sci. USA 2003, 100, 7418–7418. [Google Scholar] [CrossRef]
- Rhoades, E.; Cohen, M.; Schuler, B.; Haran, G. Two-state folding observed in individual protein molecules. J. Am. Chem. Soc. 2004, 126, 14686–14687. [Google Scholar] [CrossRef] [PubMed]
- Lindhoud, S.; Westphal, A.H.; Borst, J.W.; van Mierlo, C.P. Illuminating the off-pathway nature of the molten globule folding intermediate of an α–β parallel protein. PLoS One 2012, 7, e45746. [Google Scholar] [CrossRef] [PubMed]
- Westphal, A.H.; Matorin, A.; Hink, M.A.; Borst, J.W.; van Berkel, W.J.; Visser, A.J. Real-time enzyme dynamics illustrated with fluorescence spectroscopy of p-hydroxybenzoate hydroxylase. J. Biol. Chem. 2006, 281, 11074–11081. [Google Scholar] [CrossRef] [PubMed]
- Bollen, Y.J.; Sanchez, I.E.; van Mierlo, C.P. Formation of on- and off-pathway intermediates in the folding kinetics of Azotobacter vinelandii apoflavodoxin. Biochemistry 2004, 43, 10475–10489. [Google Scholar] [CrossRef] [PubMed]
- Engel, R.; Westphal, A.H.; Huberts, D.H.; Nabuurs, S.M.; Lindhoud, S.; Visser, A.J.; van Mierlo, C.P. Macromolecular crowding compacts unfolded apoflavodoxin and causes severe aggregation of the off-pathway intermediate during apoflavodoxin folding. J. Biol. Chem. 2008, 283, 27383–27394. [Google Scholar] [CrossRef] [PubMed]
- Nabuurs, S.M.; Westphal, A.H.; aan den Toorn, M.; Lindhoud, S.; van Mierlo, C.P. Topological switching between an α–β parallel protein and a remarkably helical molten globule. J. Am. Chem. Soc. 2009, 131, 8290–8295. [Google Scholar] [CrossRef] [PubMed]
- Nabuurs, S.M.; Westphal, A.H.; van Mierlo, C.P. Extensive formation of off-pathway species during folding of an alpha-beta parallel protein is due to docking of (non)native structure elements in unfolded molecules. J. Am. Chem. Soc. 2008, 130, 16914–16920. [Google Scholar] [CrossRef] [PubMed]
- Nabuurs, S.M.; Westphal, A.H.; van Mierlo, C.P. Noncooperative Formation of the off-pathway molten globule during folding of the alpha-beta parallel protein apoflavodoxin. J. Am. Chem. Soc. 2009, 131, 2739–2746. [Google Scholar] [CrossRef] [PubMed]
- Zaragoza-Galan, G.; Fowler, M.A.; Duhamel, J.; Rein, R.; Solladie, N.; Rivera, E. Synthesis and characterization of novel pyrene-dendronized porphyrins exhibiting efficient fluorescence resonance energy transfer: optical and photophysical properties. Langmuir 2012, 28, 11195–11205. [Google Scholar] [CrossRef] [PubMed]
- Zaragoza-Galán, G.; Fowler, M.; Rein, R.; Solladié, N.; Duhamel, J.; Rivera, E. Fluorescence resonance energy transfer in partially and fully labeled pyrene dendronized prophyrins studied with model free analysis. J. Phys. Chem. C 2014, 118, 8280–8294. [Google Scholar] [CrossRef]
- Steensma, E.; Heering, H.A.; Hagen, W.R.; van Mierlo, C.P. Redox properties of wild-type, Cys69Ala, and Cys69Ser Azotobacter vinelandii flavodoxin II as measured by cyclic voltammetry and EPR spectroscopy. Eur. J. Biochem. 1996, 235, 167–172. [Google Scholar] [CrossRef] [PubMed]
- Lindhoud, S.; van den Berg, W.A.; van den Heuvel, R.H.; Heck, A.J.; van Mierlo, C.P.; van Berkel, W.J. Cofactor binding protects flavodoxin against oxidative stress. PLoS One 2012, 7, e41363. [Google Scholar] [CrossRef] [PubMed]
- Borst, J.W.; Hink, M.A.; van Hoek, A.; Visser, A.J. Effects of refractive index and viscosity on fluorescence and anisotropy decays of enhanced cyan and yellow fluorescent proteins. J. Fluoresc. 2005, 15, 153–160. [Google Scholar] [CrossRef] [PubMed]
- Boens, N.; Qin, W.; Basaric, N.; Hofkens, J.; Ameloot, M.; Pouget, J.; Lefevre, J.P.; Valeur, B.; Gratton, E.; van de Ven, M.; et al. Fluorescence lifetime standards for time and frequency domain fluorescence spectroscopy. Anal. Chem. 2007, 79, 2137–2149. [Google Scholar] [CrossRef] [PubMed]
- Vos, K.; van Hoek, A.; Visser, A.J. Application of a reference convolution method to tryptophan fluorescence in proteins: A refined description of rotational dynamics. Eur. J. Biochem. 1987, 165, 55–63. [Google Scholar] [CrossRef] [PubMed]
- Bastiaens, P.I.; van Hoek, A.; van Berkel, W.J.; de Kok, A.; Visser, A.J. Molecular relaxation spectroscopy of flavin adenine dinucleotide in wild type and mutant lipoamide dehydrogenase from Azotobacter vinelandii. Biochemistry 1992, 31, 7061–7068. [Google Scholar] [CrossRef] [PubMed]
- Toptygin, D.; Savtchenko, R.S.; Meadow, N.D.; Roseman, S.; Brand, L. Effect of the solvent refractive index on the excited-state lifetime of a single tryptophan residue in a protein. J. Phys. Chem. B 2002, 106, 3724–3734. [Google Scholar] [CrossRef]
- Knox, R.S.; van Amerongen, H. Refractive index dependence of the Förster resonance excitation transfer rate. J. Phys. Chem. B 2002, 106, 5289–5293. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lindhoud, S.; Westphal, A.H.; Van Mierlo, C.P.M.; Visser, A.J.W.G.; Borst, J.W. Rise-Time of FRET-Acceptor Fluorescence Tracks Protein Folding. Int. J. Mol. Sci. 2014, 15, 23836-23850. https://doi.org/10.3390/ijms151223836
Lindhoud S, Westphal AH, Van Mierlo CPM, Visser AJWG, Borst JW. Rise-Time of FRET-Acceptor Fluorescence Tracks Protein Folding. International Journal of Molecular Sciences. 2014; 15(12):23836-23850. https://doi.org/10.3390/ijms151223836
Chicago/Turabian StyleLindhoud, Simon, Adrie H. Westphal, Carlo P. M. Van Mierlo, Antonie J. W. G. Visser, and Jan Willem Borst. 2014. "Rise-Time of FRET-Acceptor Fluorescence Tracks Protein Folding" International Journal of Molecular Sciences 15, no. 12: 23836-23850. https://doi.org/10.3390/ijms151223836
APA StyleLindhoud, S., Westphal, A. H., Van Mierlo, C. P. M., Visser, A. J. W. G., & Borst, J. W. (2014). Rise-Time of FRET-Acceptor Fluorescence Tracks Protein Folding. International Journal of Molecular Sciences, 15(12), 23836-23850. https://doi.org/10.3390/ijms151223836