Classifying Incomplete Gene-Expression Data: Ensemble Learning with Non-Pre-Imputation Feature Filtering and Best-First Search Technique
Abstract
:1. Introduction
2. Results
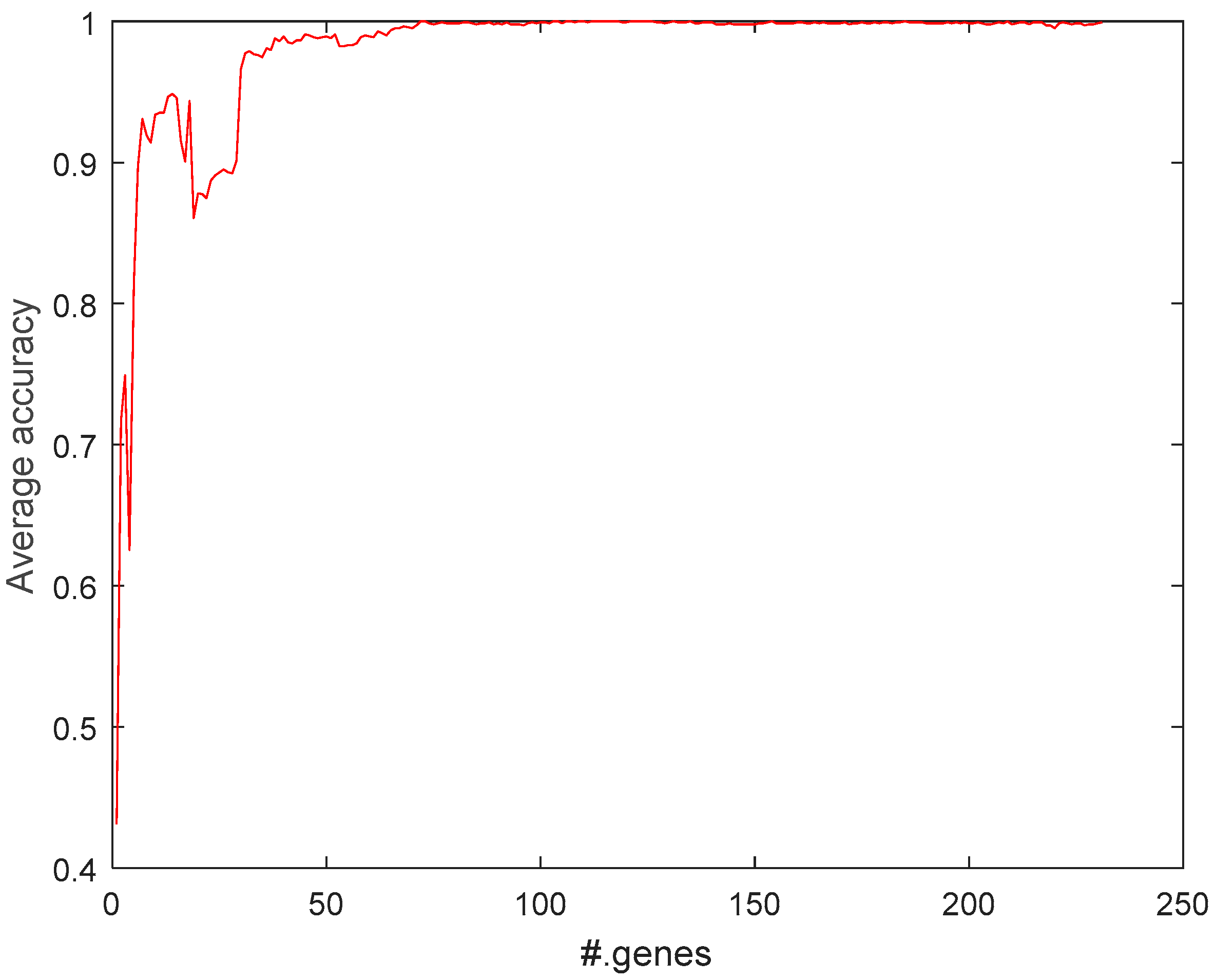
2.1. Feature-Selection Threshold for MCFS
2.2. MCFS with or without Preimputation
2.3. Comparison of Algorithm Stability under Three Imputation Methods
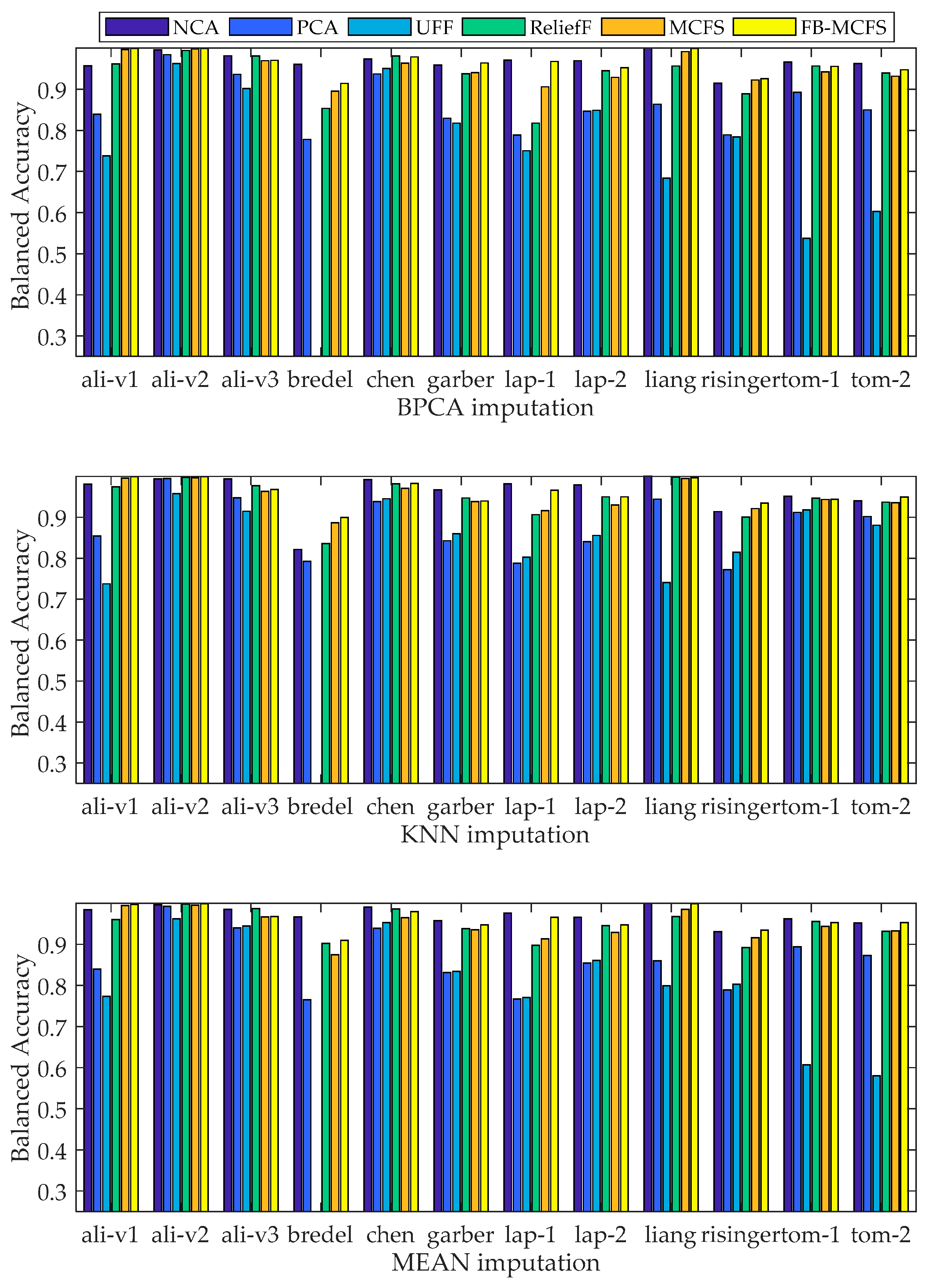
2.4. Comparison of Gene-Classification Analyses by MCFS and Other Methods
2.5. Gene and Pathway Analyses for the SRBCT Dataset by MCFS
2.5.1. Selecting Most Relevant Genes with MCFS
2.5.2. Function Analysis of the Selected Genes
3. Materials and Methods
3.1. Datasets
3.2. Design and Analytical Flowchart
3.3. Extreme Learning Machine (ELM)
3.4. MCFS for Incomplete Data
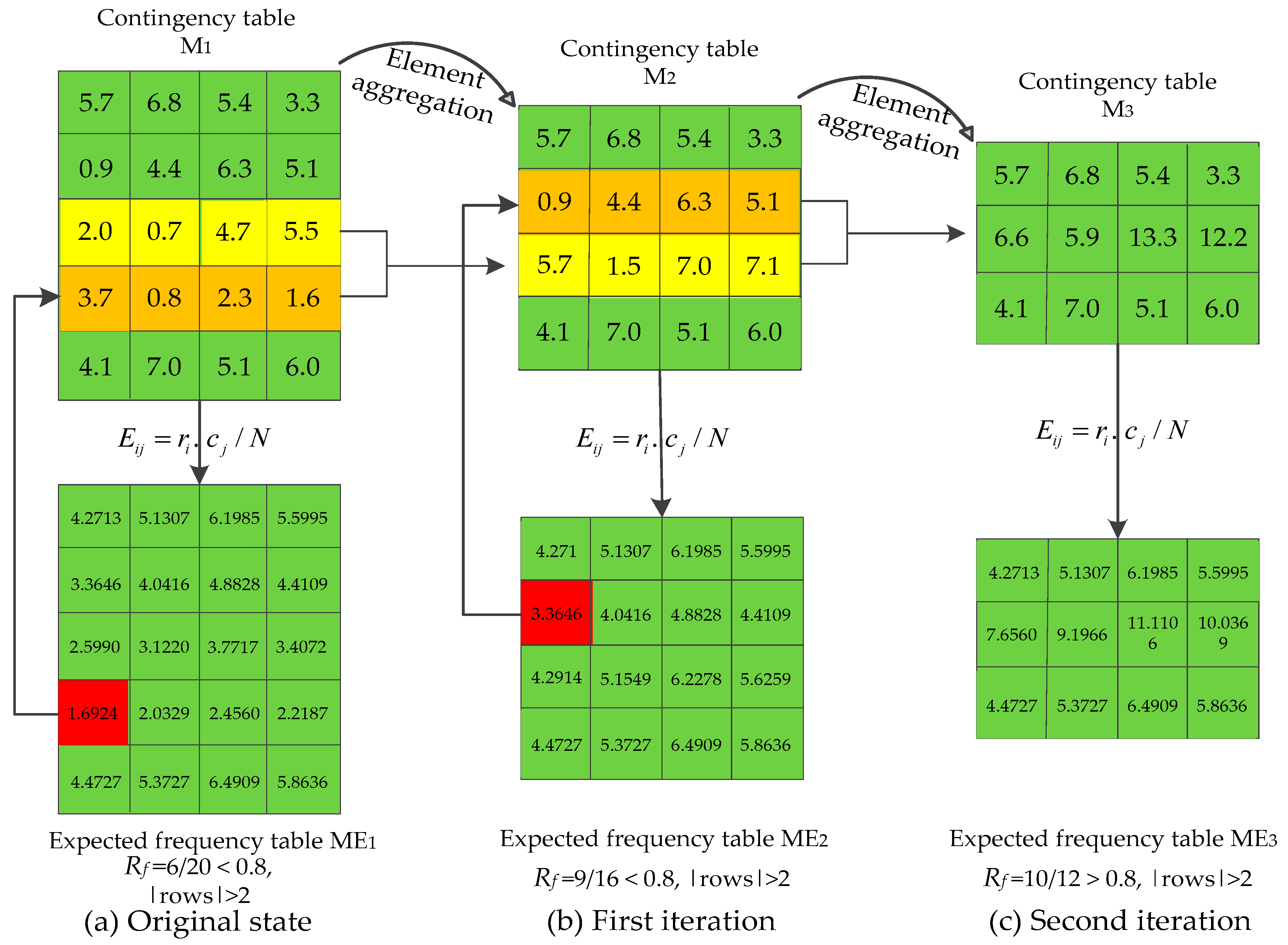
3.5. Recursive-Element Aggregation
| Algorithm 1. Recursive element aggregation for small sample size. |
| Input: Contingency table M. Output: Optimized contingency table M’. 1 Obtain corresponding expected frequency table ME; 2 Calculate ratio (Rf) of expected frequencies bigger than 5 in ME; 3 While ((Rf < 80%) && (rows of M > 2)) { 4 Find the smallest element of ME (eg: fij); 5 Merge the ith row of M with its adjacent row which has more elements smaller than 5; 6 Update M, ME; } 7 M’M. 8 return M’. |
3.6. Forward Best First Search on the MCFS Feature Subset
3.7. Comparison Settings
4. Discussion
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Quackenbush, J. Computational analysis of microarray data. Nat. Rev. Genet. 2001, 2, 418–427. [Google Scholar] [CrossRef] [PubMed]
- Oh, S.; Kang, D.D.; Brock, G.N.; Tseng, G.C. Biological impact of missing-value imputation on downstream analyses of gene expression profiles. Bioinformatics 2011, 27, 78–86. [Google Scholar] [CrossRef] [PubMed]
- Hossain, A.; Chattopadhyay, M.; Chattopadhyay, S.; Bose, S.; Das, C. A Bicluster-Based Sequential Interpolation Imputation Method for Estimation of Missing Values in Microarray Gene Expression Data. Curr. Bioinf. 2017, 12, 118–130. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, Z.; Song, D. Missing value imputation for microRNA expression data by using a GO-based similarity measure. BMC Bioinf. 2016, 17, S10. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.S.; Jhou, M.J. MVIAeval: A web tool for comprehensively evaluating the performance of a new missing value imputation algorithm. BMC Bioinf. 2017, 18, 31. [Google Scholar] [CrossRef] [PubMed]
- Stekhoven, D.J.; Bühlmann, P. MissForest--non-parametric missing value imputation for mixed-type data. Bioinformatics 2012, 28, 112–118. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Wang, Y.; Chang, Q. Feature Selection Methods for Big Data Bioinformatics: A Survey from the Search Perspective. Methods 2016, 111, 21–31. [Google Scholar] [CrossRef] [PubMed]
- Saeys, Y.; Inza, I.; Larrañaga, P. A review of feature selection techniques in bioinformatics. Bioinformatics 2007, 23, 2507–2517. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bø, T.H.; Dysvik, B.; Jonassen, I. LSimpute: Accurate estimation of missing values in microarray data with least squares methods. Nucleic Acids Res. 2004, 32, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Golub, G.H.; Park, H. Missing value estimation for DNA microarray gene expression data: Local least squares imputation. Bioinformatics 2005, 21, 187–198. [Google Scholar] [CrossRef] [PubMed]
- Oba, S.; Sato, M.; Takemasa, I.; Monden, M.; Matsubara, K.; Ishii, S. A Bayesian missing value estimation method for gene expression profile data. Bioinformatics 2003, 19, 2088–2096. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Troyanskaya, O.; Cantor, M.; Sherlock, G.; Brown, P.; Hastie, T.; Tibshirani, R.; Botstein, D.; Altman, R.B. Missing value estimation methods for DNA microarrays. Bioinformatics 2001, 17, 520–525. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nguyen, D.V.; Wang, N.; Carroll, R.J. Evaluation of Missing Value Estimation for Microarray Data. J. Data Sci. 2004, 2, 347–370. [Google Scholar]
- Sun, Y.; Braga-Neto, U.; Dougherty, E.R. Impact of missing value imputation on classification for DNA microarray gene expression data—A model-based study. EURASIP J. Bioinf. Syst. Biol. 2010, 2009, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Celton, M.; Malpertuy, A.; Lelandais, G.; Brevern, A.G. Comparative analysis of missing value imputation methods to improve clustering and interpretation of microarray experiments. BMC Genom. 2010, 11, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Lv, Y.; Guo, Z.; Li, X.; Li, Y.H.; Zhu, J.; Yang, D.; Xu, J.Z.; Wang, C.G.; Rao, S.Q.; et al. Effects of replacing the unreliable cDNA microarray measurements on the disease classification based on gene expression profiles and functional modules. Bioinformatics 2006, 22, 2883–2889. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guy, N.B.; John, R.S.; Richard, E.B.; Meredith, J.L.; George, C.T. Which missing value imputation method to use in expression profiles: A comparative study and two selection schemes. BMC Bioinf. 2008, 9, 1–12. [Google Scholar]
- Liew, A.W.C.; Law, N.F.; Yan, H. Missing value imputation for gene expression data: Computational techniques to recover missing data from available information. Briefings Bioinf. 2011, 12, 498–513. [Google Scholar] [CrossRef] [PubMed]
- Chiu, C.C.; Chan, S.Y.; Wang, C.C.; Wu, W.S. Missing value imputation for microarray data: A comprehensive comparison study and a web tool. BMC Syst. Biol. 2013, 7, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Aittokallio, T. Dealing with missing values in large-scale studies: Microarray data imputation and beyond. Briefings Bioinf. 2010, 11, 253–264. [Google Scholar] [CrossRef] [PubMed]
- Souto, M.C.D.; Jaskowiak, P.A.; Costa, I.G. Impact of missing data imputation methods on gene expression clustering and classification. BMC Bioinf. 2015, 16, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Bonilla-Huerta, E.; Hernandez-Montiel, A.; Morales-Caporal, R.; Arjona-López, M. Hybrid framework using multiple-filters and an embedded approach for an efficient selection and classification of microarray data. IEEE/ACM Trans. Comput. Biol. Bioinf. 2016, 13, 12–26. [Google Scholar]
- Wang, D.; Nie, F.; Huang, H. Feature selection via global redundancy minimization. IEEE Trans. Knowl. Data Eng. 2015, 27, 2743–2755. [Google Scholar] [CrossRef]
- Baldi, P.; Long, A.D. A Bayesian framework for the analysis of microarray expression data: Regularized t-test and statistical inferences of gene changes. Bioinformatics 2001, 17, 509–519. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.G.; Deng, H.W. Gene selection for classification of microarray data based on the Bayes error. BMC Bioinf. 2007, 8, 370. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.X.; Xu, Y.; Zheng, C.H.; Lai, Z.H. RPCA-based tumor classification using gene expression data. IEEE/ACM Trans. Comput. Biol. Bioinf. 2015, 12, 964–970. [Google Scholar]
- Yu, L.; Han, Y.; Berens, M.E. Stable gene selection from microarray data via sample weighting. IEEE/ACM Trans. Comput. Biol. Bioinf. 2012, 9, 262–272. [Google Scholar]
- Duan, K.B.; Rajapakse, J.C.; Wang, H.Y.; Azuaje, F. Multiple SVM-RFE for gene selection in cancer classification with expression data. IEEE Trans. Nanobiosci. 2005, 4, 228–234. [Google Scholar] [CrossRef]
- Lin, H.C.; Su, C.T. A selective Bayes classifier with meta-heuristics for incomplete data. Neurocomputing 2013, 106, 95–102. [Google Scholar] [CrossRef]
- Model, F.; Adorjan, P.; Olek, A.; Piepenbrock, C. Feature selection for DNA methylation based cancer classification. Bioinformatics 2001, 17, S157–S164. [Google Scholar] [CrossRef] [PubMed]
- Lazar, C.; Taminau, J.; Meganck, S.; Steenhoff, D.; Coletta, A.; Molter, C.; Schaetzen, V.; Duque, R.; Bersini, H.; Nowe, A. A survey on filter techniques for feature selection in gene expression microarray analysis. IEEE/ACM Trans. Comput. Biol. Bioinf. 2012, 9, 1106–1119. [Google Scholar] [CrossRef] [PubMed]
- Little, R.J.A.; Rubin, D.B. Statistical Analysis with Missing Data; John Wiley & Sons: New York, NY, USA, 2002; ISBN 0471183865. [Google Scholar]
- Chen, J.; Huang, H.; Tian, F.; Tian, S. A selective Bayes Classifier for classifying incomplete data based on gain ratio. Knowl. Based Syst. 2008, 21, 530–534. [Google Scholar] [CrossRef]
- Demšar, J. Statistical comparisons of classifiers over multiple data sets. J. Mach. Learn. Res. 2006, 7, 1–30. [Google Scholar]
- Wu, B. Differential gene expression detection and sample classification using penalized linear regression models. Bioinformatics 2005, 22, 472–476. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Varshavsky, R.; Gottlieb, A.; Horn, D.; Linial, M. Unsupervised feature selection under perturbations: Meeting the challenges of biological data. Bioinformatics 2007, 23, 3343–3349. [Google Scholar] [CrossRef] [PubMed]
- Khan, J.; Wei, J.S.; Ringnér, M.; Saal, L.H.; Ladanyi, M.; Westermann, F.; Berthold, F.; Schwab, M.; Antonescu, C.R.; Peterson, C.; Meltzer, P.S. Classification and diagnostic prediction of cancers using gene expression profiling and artificial neural networks. Nat. Med. 2001, 7, 673–679. [Google Scholar] [CrossRef] [PubMed]
- Szklarczyk, D.; Franceschini, A.; Wyder, S.; Forslund, K.; Heller, D.; Huerta-Cepas, J.; Simonovic, M.; Roth, A.; Santos, A.; Tsafou, K.P.; et al. STRING v10: Protein–protein interaction networks, integrated over the tree of life. Nucleic Acids Res. 2014, 43, D447–D452. [Google Scholar] [CrossRef] [PubMed]
- National Center for Biotechnology Information. Available online: https://www.ncbi.nlm.nih.gov/ (accessed on 23 September 2017).
- Alizadeh, A.A.; Eisen, M.B.; Davis, R.E.; Ma, C.; Lossos, I.S.; Rosenwald, A.; Boldrick, J.C.; Sabet, H.; Tran, T.; Yu, X.; et al. Distinct types of diffuse large B-cell lymphoma identified by gene expression profiling. Nature 2000, 403, 503–511. [Google Scholar] [CrossRef] [PubMed]
- Bredel, M.; Bredel, C.; Juric, D.; Harsh, G.R.; Vogel, H.; Recht, L.D.; Sikic, B.I. Functional network analysis reveals extended gliomagenesis pathway maps and three novel MYC-interacting genes in human gliomas. Cancer Res. 2005, 65, 8679–8689. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Cheung, S.T.; So, S.; Fan, S.T.; Barry, C.; Higgins, J.; Lai, K.M.; Ji, J.F.; Dudoit, S.; Ng, I.O.L.; et al. Gene expression patterns in human liver cancers. Mol. Biol. Cell 2002, 13, 1929–1939. [Google Scholar] [CrossRef] [PubMed]
- Garber, M.E.; Troyanskaya, O.G.; Schluens, K.; Petersen, S.; Thaesler, Z.; Pacyna-Gengelbach, M.; Rijn, M.; Rosen, G.D.; Perou, C.M.; Whyte, R.I.; et al. Diversity of gene expression in adenocarcinoma of the lung. Proc. Natl. Acad. Sci. USA 2001, 98, 13784–13789. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lapointe, J.; Li, C.; Higgins, J.P.; Rijn, M.; Bair, E.; Montgomery, K.; Ferrari, M.; Egevad, L.; Rayford, W.; Bergerheim, U.; et al. Gene expression profiling identifies clinically relevant subtypes of prostate cancer. Proc. Natl. Acad. Sci. USA 2004, 101, 811–816. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liang, Y.; Diehn, M.; Watson, N.; Bollen, A.W.; Aldape, K.D.; Nicholas, M.K.; Lamborn, K.R.; Berger, M.S.; Botstein, D.; Brown, P.O.; et al. Gene expression profiling reveals molecularly and clinically distinct subtypes of glioblastoma multiforme. Proc. Natl. Acad. Sci. USA 2005, 102, 5814–5819. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Risinger, J.I.; Maxwell, G.L.; Chandramouli, G.V.; Jazaeri, A.; Aprelikova, O.; Patterson, T.; Berchuck, A.; Barrett, J.C. Microarray analysis reveals distinct gene expression profiles among different histologic types of endometrial cancer. Cancer Res. 2003, 63, 6–11. [Google Scholar] [PubMed]
- Tomlins, S.A.; Mehra, R.; Rhodes, D.R.; Wang, L.; Dhanasekaran, S.M.; Kalyana-Sundaram, S.; Wei, J.T.; Rubin, M.A.; Pienta, K.J.; Shah, R.B.; et al. Integrative molecular concept modeling of prostate cancer progression. Nature Genet. 2007, 39, 41–51. [Google Scholar] [CrossRef] [PubMed]
- Serre, D. Matrices: Theory and Applications, 2nd ed.; Springer: New York, NY, USA, 2002; ISBN 1441976825. [Google Scholar]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef] [Green Version]
- Huang, G.B.; Chen, L.; Siew, C.K. Universal approximation using incremental constructive feedforward networks with random hidden nodes. IEEE Trans. Neural Netw. 2006, 17, 879–892. [Google Scholar] [CrossRef] [PubMed]
- Cao, J.; Lin, Z.; Huang, G.B.; Liu, N. Voting based extreme learning machine. Inf. Sci. 2012, 185, 66–77. [Google Scholar] [CrossRef]
- Pearson, K.X. On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling. Lond. Edinb. Dubl. Phil. Mag. J. Sci. 1900, 50, 157–175. [Google Scholar] [CrossRef]
- Viswanathan, K.V.; Bagchi, A. Best-first search methods for constrained two-dimensional cutting stock problems. Oper. Res. 1993, 41, 768–776. [Google Scholar] [CrossRef]
- Kourou, K.; Exarchos, T.P.; Exarchos, K.P.; Karamouzis, M.V.; Fotiadis, D.I. Machine learning applications in cancer prognosis and prediction. Comput. Struct. Biotechnol. J. 2015, 13, 8–17. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cogill, S.; Wang, L. Support vector machine model of developmental brain gene expression data for prioritization of Autism risk gene candidates. Bioinformatics 2016, 32, 3611–3618. [Google Scholar] [CrossRef] [PubMed]
- Goldberger, J.; Roweis, S.; Hinton, G.; Salakhutdinov, R. Neighbourhood components analysis. In Proceedings of the International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 13–18 December 2004; pp. 513–520. [Google Scholar]
- Yang, W.; Wang, K.; Zuo, W. Neighborhood Component Feature Selection for High-Dimensional Data. J. Comput. 2012, 7, 161–168. [Google Scholar] [CrossRef]
- Robnik-Šikonja, M.; Kononenko, I. Theoretical and empirical analysis of ReliefF and RReliefF. Mach. Learn. 2003, 53, 23–69. [Google Scholar] [CrossRef]
- Ilin, A.; Raiko, T. Practical approaches to principal component analysis in the presence of missing values. J. Mach. Learn. Res. 2010, 11, 1957–2000. [Google Scholar]
- Velez, D.R.; White, B.C.; Motsinger, A.A.; Bush, W.S.; Ritchie, M.D.; Williams, S.M.; Moore, J.H. A balanced accuracy function for epistasis modeling in imbalanced datasets using multifactor dimensionality reduction. Genet. Epidemiol. 2007, 31, 306–315. [Google Scholar] [CrossRef] [PubMed]
- Jiang, K.; Lu, J.; Xia, K. A novel algorithm for imbalance data classification based on genetic algorithm improved SMOTE. Arab. J. Sci. Eng. 2016, 41, 3255–3266. [Google Scholar] [CrossRef]






| Dataset | 0.01 | 0.005 | 0.001 | 0.0005 | 0.0001 | 0.00001 |
|---|---|---|---|---|---|---|
| alizadeh-v1 | 215 | 151 | 72 | 48 | 23 | 7 |
| alizadeh-v2 | 1811 | 1534 | 1077 | 924 | 589 | 306 |
| alizadeh-v3 | 1771 | 1535 | 1049 | 891 | 560 | 262 |
| bredel | 2904 | 2324 | 809 | 551 | 215 | 63 |
| chen | 5759 | 5007 | 3714 | 3276 | 2499 | 1700 |
| garber | 2125 | 1494 | 705 | 512 | 231 | 75 |
| lapointe-v1 | 3834 | 2875 | 1238 | 875 | 349 | 85 |
| lapointe-v2 | 7615 | 6113 | 3696 | 3012 | 1895 | 957 |
| liang | 2349 | 1302 | 717 | 623 | 17 | 3 |
| risinger | 681 | 419 | 114 | 61 | 16 | 1 |
| tomlins-v1 | 4699 | 3874 | 2460 | 1976 | 1284 | 570 |
| tomlins-v2 | 2650 | 2874 | 1678 | 1320 | 745 | 335 |
| Dataset | 0.01 | 0.005 | 0.001 | 0.0005 | 0.0001 |
|---|---|---|---|---|---|
| alizadeh-v1 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| alizadeh-v2 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| alizadeh-v3 | 0.9379 | 0.9390 | 0.9445 | 0.9455 | 0.9491 |
| bredel | 0.8653 | 0.8650 | 0.8690 | 0.8739 | 0.8782 |
| chen | 0.9578 | 0.9606 | 0.9638 | 0.9751 | 0.9751 |
| garber | 0.9009 | 0.9014 | 0.9024 | 0.9060 | 0.9035 |
| lapointe-v1 | 0.8732 | 0.8767 | 0.8827 | 0.8887 | 0.9211 |
| lapointe-v2 | 0.8679 | 0.8685 | 0.8670 | 0.8699 | 0.8709 |
| liang | 0.9751 | 0.9760 | 0.9822 | 0.9830 | 0.9575 |
| risinger | 0.8577 | 0.8627 | 0.8672 | 0.8852 | 0.8242 |
| tomlins-v1 | 0.8855 | 0.8895 | 0.8960 | 0.9048 | 0.9135 |
| tomlins-v2 | 0.8866 | 0.8874 | 0.8914 | 0.8944 | 0.9105 |
| Datasets | BPCA | KNN | MEAN | |||
|---|---|---|---|---|---|---|
| MCFS1 | MCFS2 | MCFS1 | MCFS2 | MCFS1 | MCFS2 | |
| alizadeh-v1 | 1.0000 | 0.9928 | 1.0000 | 0.9956 | 1.0000 | 0.9944 |
| alizadeh-v2 | 0.9967 | 0.9981 | 1.0000 | 1.0000 | 0.9971 | 0.9949 |
| alizadeh-v3 | 0.9565 | 0.9461 | 0.9503 | 0.9486 | 0.9449 | 0.9432 |
| bredel | 0.8638 | 0.8579 | 0.8706 | 0.8481 | 0.8719 | 0.8644 |
| chen | 0.9701 | 0.9597 | 0.9679 | 0.9641 | 0.9677 | 0.9581 |
| garber | 0.9074 | 0.9011 | 0.8889 | 0.8986 | 0.9054 | 0.9071 |
| lapointe-1 | 0.8523 | 0.8524 | 0.8533 | 0.8549 | 0.8492 | 0.8516 |
| lapointe-2 | 0.8621 | 0.8470 | 0.8583 | 0.8565 | 0.8506 | 0.8511 |
| liang | 0.9923 | 0.9863 | 0.9860 | 0.9863 | 0.9820 | 0.9856 |
| risinger | 0.8643 | 0.8659 | 0.8575 | 0.8589 | 0.8656 | 0.8663 |
| tomlins-v1 | 0.8879 | 0.8809 | 0.8892 | 0.8792 | 0.8965 | 0.8847 |
| tomlins-v2 | 0.8850 | 0.8678 | 0.8943 | 0.8637 | 0.8839 | 0.8776 |
| Average | 0.9199 | 0.9130 | 0.9180 | 0.9129 | 0.9179 | 0.9149 |
| Datasets | NCA | PCA | UFF | ReliefF | MCFS | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BPCA | KNN | MEAN | BPCA | KNN | MEAN | BPCA | KNN | MEAN | BPCA | KNN | MEAN | BPCA | KNN | MEAN | |
| ali1 | 0.9400 | 0.9870 | 0.9820 | 0.8550 | 0.8390 | 0.8270 | 0.8390 | 0.7770 | 0.7840 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| ali2 | 1.0000 | 1.0000 | 1.0000 | 0.9748 | 0.9933 | 0.9818 | 0.9023 | 0.9023 | 0.8860 | 1.0000 | 1.0000 | 1.0000 | 0.9967 | 1.0000 | 0.9971 |
| ali3 | 0.9625 | 0.9892 | 0.9672 | 0.8893 | 0.8952 | 0.8882 | 0.8138 | 0.8209 | 0.8156 | 0.9722 | 0.9746 | 0.9686 | 0.9565 | 0.9503 | 0.9449 |
| bredel | 0.9369 | 0.7689 | 0.9601 | 0.7840 | 0.7994 | 0.7931 | / | / | / | 0.8605 | 0.8432 | 0.8303 | 0.8638 | 0.8706 | 0.8719 |
| chen | 0.9833 | 0.9925 | 0.9946 | 0.9379 | 0.9316 | 0.9374 | 0.9448 | 0.9422 | 0.9475 | 0.9877 | 0.9865 | 0.9835 | 0.9701 | 0.9679 | 0.9677 |
| garber | 0.9327 | 0.9496 | 0.9242 | 0.7837 | 0.7985 | 0.7860 | 0.7944 | 0.7680 | 0.7734 | 0.8896 | 0.8965 | 0.9036 | 0.9074 | 0.8889 | 0.9054 |
| lap1 | 0.9416 | 0.9722 | 0.9466 | 0.7176 | 0.7352 | 0.7202 | 0.7048 | 0.7052 | 0.7110 | 0.8464 | 0.8570 | 0.8833 | 0.8523 | 0.8533 | 0.8492 |
| lap2 | 0.9353 | 0.9431 | 0.9401 | 0.7270 | 0.7324 | 0.7135 | 0.7169 | 0.7355 | 0.7285 | 0.9011 | 0.8948 | 0.9060 | 0.8621 | 0.8583 | 0.8506 |
| liang | 1.0000 | 1.0000 | 1.0000 | 0.9423 | 0.9553 | 0.9223 | 0.8813 | 0.9097 | 0.9143 | 1.0000 | 1.0000 | 1.0000 | 0.9923 | 0.9860 | 0.9820 |
| risinger | 0.8693 | 0.8679 | 0.8829 | 0.7067 | 0.6833 | 0.6910 | 0.7102 | 0.7180 | 0.6849 | 0.8267 | 0.8323 | 0.8427 | 0.8643 | 0.8575 | 0.8656 |
| tom1 | 0.9259 | 0.9010 | 0.9172 | 0.7833 | 0.8381 | 0.7956 | 0.2812 | 0.8305 | 0.4093 | 0.9191 | 0.9202 | 0.8984 | 0.8879 | 0.8892 | 0.8965 |
| tom2 | 0.9304 | 0.8937 | 0.9122 | 0.7389 | 0.8144 | 0.7435 | 0.4499 | 0.8168 | 0.4364 | 0.8859 | 0.8997 | 0.8794 | 0.8850 | 0.8943 | 0.8839 |
| BPCA | KNN | MEAN | |
|---|---|---|---|
| NCA | 1 | 0.5271 | 0.5236 |
| PCA | 0.0016 | 0.0044 | 0.0014 |
| UFF | 1.478 × 10−4 | 5.0422 × 10−4 | 4.5173 × 10−4 |
| ReliefF | 0.0578 | 0.0578 | 0.0557 |
| MCFS | 0.0016 | 0.0044 | 0.0041 |
| MCFS Ranking | Gene Name | Ref [37]’s Ranking | UFF Ranking |
|---|---|---|---|
| 1 | ‘growth arrest-specific 1’ | 4 | 33 |
| 2 | ‘selenium binding protein 1’ | 63 | / |
| 3 | ‘cyclin D1 (PRAD1: parathyroid adenomatosis 1)’ | 3 | 11 |
| 4 | ‘olfactomedin related ER (endoplasmic reticulum) localized protein’ | 19 | 23 |
| 5 | ‘recoverin’ | 29 | / |
| 6 | ‘thioredoxin’ | / | / |
| 7 | ‘quinone oxidoreductase homolog’ | 61 | / |
| 8 | ‘glycogen synthase 1 (muscle)’ | / | / |
| 9 | ‘amyloid precursor-like protein 1’ | 32 | / |
| 10 | ‘ESTs (EST: expressed sequence tag), Moderately similar to skeletal muscle LIM-protein (named for ‘LIN11, ISL1, and MEC3,’) FHL3 (FHL: four-and-a-half lim domains 3) (H.sapiens)’ | / | / |
| 11 | ‘type II integral membrane protein’ | / | / |
| 12 | ‘GLI (glioma-associated oncogene homolog)-Kruppel family member GLI3 (Greig cephalopolysyndactyly syndrome)’ | / | / |
| 13 | ‘transducin-like enhancer of split 2, homolog of Drosophila E(sp1)’ | 35 | / |
| 14 | ‘interferon-inducible’ | 44 | 78 |
| 15 | ‘calponin 3, acidic’ | 5 | 83 |
| 16 | ‘Fc (fragment, crystallizable) fragment of IgG (immunoglobulin G), receptor, transporter, alpha’ | 6 | 50 |
| 17 | ‘protein tyrosine phosphatase, non-receptor type 12’ | / | / |
| 18 | ‘cold shock domain protein A’ | / | / |
| 19 | ‘antigen identified by monoclonal antibodies 12E7, F21 and O13’ | 73 | 44 |
| 20 | ‘lectin, galactoside-binding, soluble, 3 binding protein (galectin 6 binding protein)’ | 20 | / |
| 21 | ‘Cbp/p300-interacting transactivator, with Glu/Asp-rich carboxy-terminal domain, 2’ | / | / |
| 22 | ‘dihydropyrimidinase-like 2’ | 60 | / |
| 23 | ‘suppression of tumorigenicity 5’ | / | / |
| 24 | ‘complement component 1 inhibitor (angioedema, hereditary)’ | 51 | 48 |
| 25 | ‘caveolin 1, caveolae protein, 22kD’ | 18 | 18 |
| 26 | ‘homeo box B7’ | / | / |
| 27 | ‘guanine nucleotide exchange factor; 115-kD; mouse Lsc homolog’ | / | / |
| 28 | ‘EphB4 (ephrin type-B receptor 4)’ | / | / |
| 29 | ‘death-associated protein kinase 1’ | 82 | / |
| 30 | ‘insulin-like growth factor 2 (somatomedin A)’ | 1 | 2 |
| Dataset | Array Type | Tissue | Dimensionality | Samples per Class | Classes |
|---|---|---|---|---|---|
| alizadeh-v1 | Double Channel | Blood | 4026 | 21,21 | DLBCL1, DLBCL2 |
| alizadeh-v2 | Double Channel | Blood | 4026 | 42, 9, 11 | DLBCL, FL, CLL |
| alizadeh-v3 | Double Channel | Blood | 4026 | 21, 21, 9, 11 | DLBCL1, DLBCL2, FL, CLL |
| bredel | Double Channel | Brain | 41472 | 31, 14, 5 | GBM, OG, A |
| chen | Double Channel | Liver | 24192 | 104, 75 | HCC, liver |
| garber | Double Channel | Lung | 24192 | 17, 40, 4, 5 | SCC, AC, LCLC, SCLC |
| lapointe-v1 | Double Channel | Prostate | 42640 | 11, 39, 19 | PT1, PT2, PT3 |
| lapointe-v2 | Double Channel | Prostate | 42640 | 11, 39, 19, 41 | PT1, PT2, PT3, Normal |
| liang | Double Channel | Brain | 24192 | 28, 6, 3 | GBM, ODG, Normal |
| risinger | Double Channel | Endometrium | 8872 | 13, 3, 19, 7 | PS, CC, E, N |
| tomlins-v1 | Double Channel | Prostate | 20000 | 27, 20, 32, 13, 12 | EPI, MET, PCA, PIN, STROMA |
| tomlins-v2 | Double Channel | Prostate | 20000 | 27, 20, 32, 13 | EPI, MET, PCA, PIN |
| A | d | ||
| d1 | … | dl | |
| a1 | f11 | … | f1l |
| … | … | … | … |
| am | fm1 | … | fml |
| Sample | Wind (a1) | Humidity (a2) | Temperature (a3) | Trip (d) |
|---|---|---|---|---|
| u1 | low | low | high | yes |
| u2 | medium | medium | medium | yes |
| u3 | high | high | ? | yes |
| u4 | low | medium | high | no |
| u5 | ? | ? | high | no |
| u6 | medium | high | low | yes |
| u7 | ? | low | low | yes |
| u8 | high | high | high | no |
| a1(wind) | d(trip) | ||
|---|---|---|---|
| Yes | No | ? | |
| low | 1 | 1 | 0 |
| medium | 2 | 0 | 0 |
| high | 1 | 1 | 0 |
| ? | 1 | 1 | 0 |
| a1 | d (trip) | |
|---|---|---|
| yes | no | |
| low | 4/3 | 4/3 |
| medium | 7/3 | 1/3 |
| high | 4/3 | 4/3 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Y.; Dai, T.; Yang, M.; Du, X.; Zhang, Y.; Zhang, Y. Classifying Incomplete Gene-Expression Data: Ensemble Learning with Non-Pre-Imputation Feature Filtering and Best-First Search Technique. Int. J. Mol. Sci. 2018, 19, 3398. https://doi.org/10.3390/ijms19113398
Yan Y, Dai T, Yang M, Du X, Zhang Y, Zhang Y. Classifying Incomplete Gene-Expression Data: Ensemble Learning with Non-Pre-Imputation Feature Filtering and Best-First Search Technique. International Journal of Molecular Sciences. 2018; 19(11):3398. https://doi.org/10.3390/ijms19113398
Chicago/Turabian StyleYan, Yuanting, Tao Dai, Meili Yang, Xiuquan Du, Yiwen Zhang, and Yanping Zhang. 2018. "Classifying Incomplete Gene-Expression Data: Ensemble Learning with Non-Pre-Imputation Feature Filtering and Best-First Search Technique" International Journal of Molecular Sciences 19, no. 11: 3398. https://doi.org/10.3390/ijms19113398
APA StyleYan, Y., Dai, T., Yang, M., Du, X., Zhang, Y., & Zhang, Y. (2018). Classifying Incomplete Gene-Expression Data: Ensemble Learning with Non-Pre-Imputation Feature Filtering and Best-First Search Technique. International Journal of Molecular Sciences, 19(11), 3398. https://doi.org/10.3390/ijms19113398





