Can Alkaline Hydrolysis of γ-HCH Serve as a Model Reaction to Study Its Aerobic Enzymatic Dehydrochlorination by LinA?
Abstract
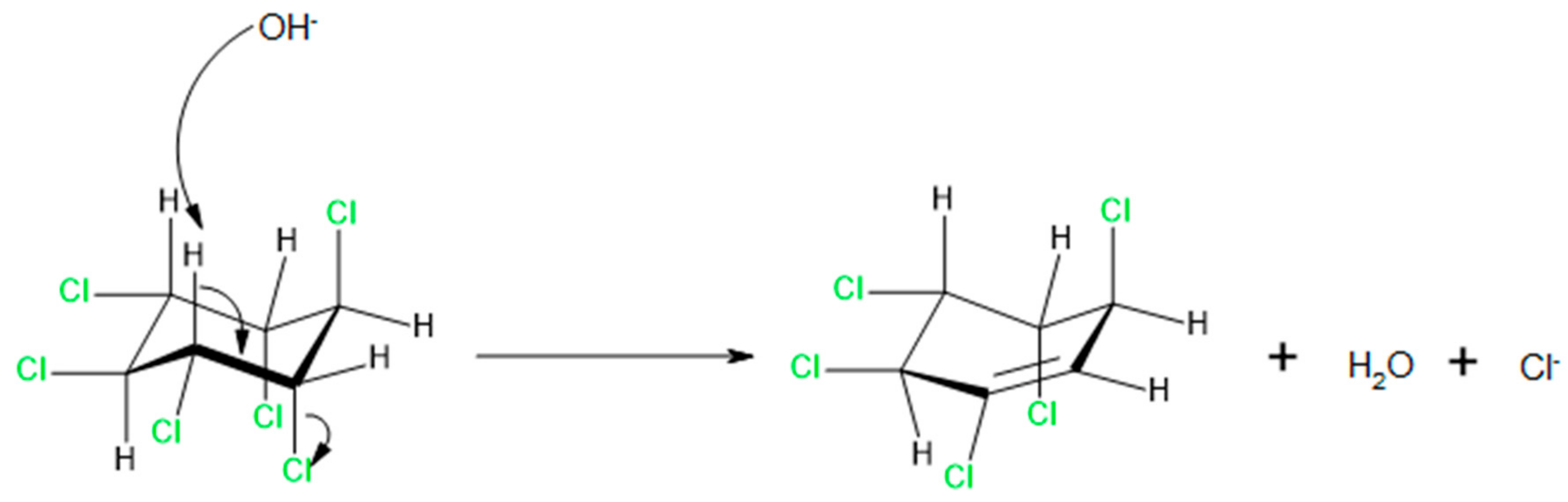
1. Introduction
2. Results and Discussion
3. Materials and Methods
3.1. Free Energy Surfaces for the QM Microsolvation Models
3.2. PI-FEP/UM
3.3. Determination of the Experimental Isotope Enrichment Factors of γ-HCH
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| KIE | Kinetic isotope effect |
| PI | Path integral |
| PI-FEP/UM | Path integral combined with free energy perturbation and umbrella sampling |
| QM | Quantum mechanical |
| QM/MM | Quantum mechanics/molecular mechanics |
| HCH | Hexachlorocyclohexane |
| PMF | Potential of Mean Force |
| CSIA | Compound-specific isotope analysis |
| PCM | Polarizable continuum model |
| MD | Molecular dynamics |
References
- Agency for Toxic Substances and Disease Registry, U.S. Toxicologic Profile for α-, β-, γ- and δ-Hexachlorocyclohenxane; U.S. Department of Health and Human Services: Atlanta, GA, USA, 2005.
- Draft Risk Management Evaluation for Lindane; Persistent Organic Pollutant Review Committee (POPRC): Geneva, Switzerland, 2007.
- Alvarez-Pedrerol, M.; Ribas-Fitó, N.; Torrent, M.; Carrizo, D.; Garcia-Esteban, R.; Grimalt, J.O.; Sunyer, J. Thyroid disruption at birth due to prenatal exposure to beta-hexachlorocyclohexane. Environ. Int. 2008, 34, 737–740. [Google Scholar] [CrossRef] [PubMed]
- Loomis, D.; Guyton, K.; Grosse, Y.; El Ghissasi, F.; Bouvard, V.; Benbrahim-Tallaa, L.; Guha, N.; Mattock, H.; Straif, K. Carcinogenicity of lindane, DDT, and 2,4-dichlorophenoxyacetic acid. Lancet Oncol. 2015, 16, 891–982. [Google Scholar] [CrossRef]
- United Nations Organization. Stockholm Convention on Persistent Organic Pollutants. Adoption of Amendments to Annexes A, B and C. 2009. Available online: http://www.pops.int/TheConvention/ThePOPs/TheNewPOPs/tabid/2511/Default.aspx (accessed on 17 February 2013).
- Vijgen, J. The Legacy of Lindane HCH Isomer Production. A Global Overview of Residue Management, Formulation and Disposal; International HCH & Pesticides Association (IHPA): Copenhagen, Denmark, 2006. [Google Scholar]
- Bashir, S.; Hitzfeld, K.L.; Gehre, M.; Richnow, H.H.; Fischer, A. Evaluating degradation of hexachlorcyclohexane (HCH) isomers within a contaminated aquifer using compound-specific stable carbon isotope analysis (CSIA). Water Res. 2015, 71, 187–196. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Bashir, S.; Stollberg, R.; Trabitzsch, R.; Weiß, H.; Paschke, H.; Nijenhuis, I.; Richnow, H.H. Compound Specific and Enantioselective Stable Isotope Analysis as tools to monitor transformation of hexachlorocyclohexane (HCH) in a complex aquifer system. Environ. Sci. Technol. 2017, 51, 8909–8916. [Google Scholar] [CrossRef]
- Wu, L.; Moses, S.; Liu, Y.; Renpenning, J.; Richnow, H.H. A concept for studying the transformation reaction of hexachlorocyclohexanes in food webs using multi-element compound-specific isotope analysis. Anal. Chim. Acta 2019, 1046, 56–64. [Google Scholar] [CrossRef]
- Wu, L.; Liu, Y.; Liu, X.; Bajaj, A.; Sharma, M.; Lal, R.; Richnow, H.H. Isotope fractionation approach to characterize the reactive transport processes governing the fate of hexachlorocyclohexanes at a contaminated site in India. Environ. Int. 2019, 132, 105036. [Google Scholar] [CrossRef]
- Nijenhuis, I.; Richnow, H.H. Stable isotope fractionation concepts for characterizing biotransformation of organohalides. Curr. Opin. Biotechnol. 2016, 41, 108–113. [Google Scholar] [CrossRef]
- Elsner, M.; Zwank, L.; Hunkeler, D.; Schwarzenbach, R.P. A new concept linking observable stable isotope fractionation to transformation pathways of organic pollutants. Environ. Sci. Technol. 2005, 39, 6896–6916. [Google Scholar] [CrossRef]
- Hofstetter, T.B.; Schwarzenbach, R.P.; Bernasconi, S.M. Assessing transformation processes of organic compounds using stable isotope fractionation. Environ. Sci. Technol. 2008, 42, 7737–7743. [Google Scholar] [CrossRef]
- Schilling, I.E.; Hess, R.; Bolotin, J.; Lal, R.; Hofstetter, T.B.; Kohler, H.-P.E. Kinetic Isotope Effects of the Enzymatic Transformation of γ-Hexachlorocyclohexane by the Lindane Dehydrochlorinase Variants Lin A1 and Lin A2. Environ. Sci. Technol. 2019, 53, 2353–2363. [Google Scholar] [CrossRef]
- Manna, R.N.; Zinovjev, K.; Tuñón, I.; Dybala-Defratyka, A. Dehydrochlorination of Hexachlorocyclohexanes Catalyzed by the LinA Dehydrohalogenase. A QM/MM Study. J. Phys. Chem. B 2015, 119, 15100–15109. [Google Scholar] [CrossRef] [PubMed]
- Manna, R.N. Theoretical Study on Aerobic Degradation Processes of Hexachlorocyclohexane Isomers Catalyzed by the Haloalkane Dehalogenases LinA and LinB. Ph.D. Thesis, Lodz University of Technology, Lodz, Poland, 2015. [Google Scholar]
- Szatkowski, L.; Manna, R.N.; Grzybkowska, A.; Kaminski, R.; Dybala-Defratyka, A.; Paneth, P. Measurement and Prediction of Chlorine Kinetic Isotope Effects in Enzymatic Systems in Measurement and Analysis of Kinetic Isotope Effects. Methods Enzymol. 2017, 596, 179–215. [Google Scholar] [PubMed]
- Manna, R.N.; Dybala-Defratyka, A. Insights into the elimination mechanisms employed for the degradation of different hexachlorocyclohexane isomers using kinetic isotope effects and docking studies. J. Phys. Org. Chem. 2013, 26, 797–804. [Google Scholar] [CrossRef]
- Ren, M.; Peng, P.; Huang, W.; Liu, X. Kinetics of Base-Catalyzed Dehydrochlorination of Hexachlorocyclohexanes: I. Homogeneous Systems. J. Environ. Qual. 2006, 35, 880–888. [Google Scholar] [CrossRef] [PubMed]
- Ngabe, B.; Bidleman, T.F.; Falconer, R.L. Base Hydrolysis of α- and γ-Hexachlorcyclohexanes. Environ. Sci. Technol. 1993, 27, 1930–1933. [Google Scholar] [CrossRef]
- Marx, D.; Chandra, A.; Tuckerman, M.E. Aqueous Basic Solutions: Hydroxide Solvation, Structural Diffusion, and Comparison to the Hydrated Proton. Chem. Rev. 2010, 110, 2174–2216. [Google Scholar] [CrossRef]
- Lev, B.; Roux, B.; Noskov, S.Y. Relative Free Energies for Hydration of Monovalent Ions from QM and QM/MM Simulations. J. Chem. Theory Comput. 2013, 9, 4165–4175. [Google Scholar] [CrossRef]
- Bergstrom, P.A.; Lindgren, J.; Kristiansson, O. An IR Study of the Hydration of ClO4-, NO3-, I-, Br-, Cl-, and SO42- Anions in Aqueous Solution. J. Phys. Chem. 1991, 95, 8575–8580. [Google Scholar] [CrossRef]
- Singh, U.C.; Kollman, P.A. An approach to computing electrostatic charges for molecules. J. Comp. Chem. 1984, 5, 129–145. [Google Scholar] [CrossRef]
- Besler, B.H.; Merz, K.M., Jr.; Kollman, P.A. Atomic charges derived from semiempirical methods. J. Comp. Chem. 1990, 11, 431–439. [Google Scholar] [CrossRef]
- Zinovjev, K.; Tuñón, I. Adaptive Finite Temperature String Method in Collective Variables. J. Phys. Chem. A 2017, 121, 9764–9772. [Google Scholar] [CrossRef] [PubMed]
- Tang, X.; Zhang, R.; Zhang, Q.; Wang, W. Dehydrochlorination mechanism of g-hexachlorocyclohexane degraded by dehydrochlorinase LinA from Sphingomonas paucimobilis UT26. RSC Adv. 2016, 6, 4183–4192. [Google Scholar] [CrossRef]
- Chai, J.-D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [PubMed]
- Hariharan, P.C.; Pople, J.A. The influence of polarization functions on molecular orbital hydrogenation energies. Theor. Chim. Acta 1973, 28, 213–222. [Google Scholar] [CrossRef]
- Ditchfield, R.; Hehre, W.J.; Pople, J.A. Self-consistent molecular orbital methods. IX. An extended Gaussian-type basis for molecular-orbital studies of organic molecules. J. Chem. Phys. 1971, 54, 724–728. [Google Scholar] [CrossRef]
- Francl, M.M.; Pietro, W.J.; Hehre, W.J.; Binkley, J.S.; Gordon, M.S.; DeGrees, D.J.; Pople, J.A. Self-consistent molecular orbital methods. XXIII. A polarization-type basis set for second-row elements. J. Chem. Phys. 1982, 77, 3654–3665. [Google Scholar] [CrossRef]
- Clark, T.; Chandrasekhar, J.; Spitznagel, G.W.; Von Ragué Schleyer, P. Efficient diffuse function-augmented basis sets for anion calculations. III. The 3-21+G basis set for first row elements, lithium to fluoride. J. Comp. Chem. 1983, 4, 294–301. [Google Scholar] [CrossRef]
- Frisch, M.J.; Pople, J.A.; Binkley, J.S. Self-consistent molecular orbital methods. XXV. Supplementary functions for Gaussian basis sets. J. Chem. Phys. 1984, 80, 3265–3269. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 09, Revision, A.02; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Miertus, S.; Scrocco, E.; Tomasi, J. Electrostatic interaction of the solute with a continuum. A direct utilization of the ab initio molecular potentials for the prevision of solvent effects. Chem. Phys. 1981, 55, 117–129. [Google Scholar] [CrossRef]
- Peng, C.; Ayala, P.Y.; Schlegel, H.B.; Frisch, M.J. Using redundant internal coordinates to optimize equilibrium geometries and transition states. J. Comp. Chem. 1996, 17, 49–56. [Google Scholar] [CrossRef]
- Reed, A.E.; Weinhold, F. Natural bond orbital analysis of near-Hartree-Fock water dimer. J. Chem. Phys. 1983, 78, 4066–4073. [Google Scholar] [CrossRef]
- Fukui, K. Formulation of the reaction coordinate. J. Phys. Chem. 1972, 74, 4161–4163. [Google Scholar] [CrossRef]
- Bigeleisen, J. Statistical mechanics of isotope systems with small quantum corrections. General considerations and the rule of the geometric mean. J. Chem. Phys. 1955, 23, 2264–2267. [Google Scholar] [CrossRef]
- Bigeleisen, J. The relative reaction velocities of isotopic molecules. J. Chem. Phys. 1949, 17, 675–678. [Google Scholar] [CrossRef]
- Anisimov, V.; Paneth, P. ISOEFF98. A program for studies of isotope effects using Hessian modifications. J. Math. Chem. 1999, 26, 75–86. [Google Scholar] [CrossRef]
- Major, D.T.; Garcia-Viloca, M.; Gao, J. Path Integral Simulations of Proton Transfer Reactions in Aqueous Solution Using Combined QM/MM Potentials. J. Chem. Theory Comput. 2006, 2, 236–245. [Google Scholar] [CrossRef]
- Brooks, B.R.; Bruccoleri, R.E.; Olafson, B.D.; States, D.J.; Swaminathan, S.; Karplus, M. CHARMM: A program for macromolecular energy minimization and dynamics calculations. J. Comput. Chem. 1983, 4, 187–217. [Google Scholar] [CrossRef]
- Torrie, G.M.; Valleau, J.P. Monte Carlo free energy esti-mates using non-Boltzmann sampling: Application tothe sub-critical Lennard-Jones fluid. Chem. Phys. Lett. 1974, 28, 578–581. [Google Scholar] [CrossRef]
- Torrie, G.M.; Valleau, J.P. Nonphysical sampling distribu-tions in Monte Carlo free-energy estimation: Umbrellasampling. J. Comput. Phys. 1977, 23, 187–199. [Google Scholar] [CrossRef]
- Stewart, J.P.P. Optimization of parameters for semiempirical methods I. Method. J. Comp. Chem. 1989, 10, 209–220. [Google Scholar] [CrossRef]
- Stewart, J.P.P. Optimization of parameters for semiempirical methods II. Applications. J. Comp. Chem. 1989, 10, 221–264. [Google Scholar] [CrossRef]
- Dewar, M.J.S.; Zoebisch, E.G.; Healy, E.F.; Stewart, J.J.P. Development and use of quantum mechanical molecular models. 76. AM1: A new general purpose quantum mechanical molecular model. J. Am. Chem. Soc. 1985, 10713, 3902–3909. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Ferrenberg, A.M.; Swendsen, R.H. Optimized Monte Carlo data analysis. Phys. Rev. Lett. 1989, 63, 1195–1198. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Bouzida, D.; Swendsen, R.H.; Kollman, P.A.; Rosenberg, J.M. The weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J. Comp. Chem. 1992, 13, 1011–1021. [Google Scholar] [CrossRef]
- Sprik, M.; Klein, M.L.; Chandler, D. Staging: A sampling technique for the Monte Carlo evaluation of path integrals. Phys. Rev. B Condens. Matter 1985, 31, 4234–4244. [Google Scholar] [CrossRef]
- Major, D.T.; Gao, J. Implementation of the Bisection Sampling Method in Path Integral Simulations. J. Mol. Graph. Model. 2005, 24, 121–127. [Google Scholar] [CrossRef]
- Hwang, J.K.; Chu, Z.T.; Yadav, A.; Warshel, A. Simulations of quantum mechanical corrections for rate constants of hydride-transfer reactions in enzymes and solutions. J. Phys. Chem. 1991, 95, 8445–8448. [Google Scholar] [CrossRef]
- Hwang, J.K.; Warshel, A. A quantized classical path approach for calculations of quantum mechanical rate constants. J. Phys. Chem. 1993, 97, 10053–10058. [Google Scholar] [CrossRef]
- Hwang, J.K.; Warshel, A. How Important Are Quantum Mechanical Nuclear Motions in Enzyme Catalysis? J. Am. Chem. Soc. 1996, 118, 11745–11751. [Google Scholar] [CrossRef]
- Maragliano, L.; Fischer, A.; Vanden-Eijnden, E. String method in collective variables: Minimum free energy paths and isocommittor surfaces. J. Chem. Phys. 2006, 125, 024106. [Google Scholar] [CrossRef] [PubMed]
- Case, D.A.; Ben-Shalom, I.Y.; Brozell, S.R.; Cerutti, D.S.; Cheatham, T.E., III; Cruzeiro, V.W.D.; Darden, T.A.; Duke, R.E.; Ghoreishi, D.; Gilson, M.K.; et al. AMBER 2018; University of California: San Francisco, CA, USA, 2018. [Google Scholar]


| Model | εC | εCl | εH |
|---|---|---|---|
| exp a | −7.0 ± 0.5 | −2.0 ± 0.2 | −162 ± 26 |
| H2O_2W b | −6.5 | −1.5 | −526 |
| 3W_OH | −5.7 | −0.8 | −692 |
| 4W_OH−4W_Cl | −6.0 | −0.9 | −680 |
| QM(AM1)/MM c | −7.5 (−6.7) | −1.4 (−1.2) | −481 (−463) |
| QM(PM3)/MM c | −3.6 (−2.8) | −1.0 (−0.8) | −756 (−738) |
| Model | C1 KIE | C2 KIE | Cl KIE | H1 KIE |
|---|---|---|---|---|
| H2O_2W a | 1.0182 | 1.0190 | 1.0081 | 4.0 |
| Bare model | 1.0113 | 1.0068 | 1.0018 | 5.1 |
| 3W_OH | 1.0178 | 1.0113 | 1.0029 | 5.1 |
| 4W_OH-4W_Cl | 1.0190 | 1.0144 | 1.0036 | 5.0 |
| QM(AM1)/MM | 1.0197 ± 0.0039 | 1.0204 ± 0.0010 | 1.0063 ± 0.0006 | 3.8 ± 0.2 |
| QM(PM3)/MM | 1.0083 ± 0.0019 | 1.0086 ± 0.0082 | 1.0037 ± 0.0020 | 5.5 ± 0.4 |
| Reaction | εC | εCl | εH |
|---|---|---|---|
| [14]a | −8.1 ± 0.3 (−8.3 ± 0.2) | n/d | −122 ± 6 (−160 ± 6) |
| This study | −5.3 ± 0.8 | −1.8 ± 0.4 | −119 ± 18 |
| [16,17] b | −5.0 | −0.7 | −633 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kannath, S.; Adamczyk, P.; Wu, L.; Richnow, H.H.; Dybala-Defratyka, A. Can Alkaline Hydrolysis of γ-HCH Serve as a Model Reaction to Study Its Aerobic Enzymatic Dehydrochlorination by LinA? Int. J. Mol. Sci. 2019, 20, 5955. https://doi.org/10.3390/ijms20235955
Kannath S, Adamczyk P, Wu L, Richnow HH, Dybala-Defratyka A. Can Alkaline Hydrolysis of γ-HCH Serve as a Model Reaction to Study Its Aerobic Enzymatic Dehydrochlorination by LinA? International Journal of Molecular Sciences. 2019; 20(23):5955. https://doi.org/10.3390/ijms20235955
Chicago/Turabian StyleKannath, Suraj, Paweł Adamczyk, Langping Wu, Hans H. Richnow, and Agnieszka Dybala-Defratyka. 2019. "Can Alkaline Hydrolysis of γ-HCH Serve as a Model Reaction to Study Its Aerobic Enzymatic Dehydrochlorination by LinA?" International Journal of Molecular Sciences 20, no. 23: 5955. https://doi.org/10.3390/ijms20235955
APA StyleKannath, S., Adamczyk, P., Wu, L., Richnow, H. H., & Dybala-Defratyka, A. (2019). Can Alkaline Hydrolysis of γ-HCH Serve as a Model Reaction to Study Its Aerobic Enzymatic Dehydrochlorination by LinA? International Journal of Molecular Sciences, 20(23), 5955. https://doi.org/10.3390/ijms20235955





