Cell-Fate Determination from Embryo to Cancer Development: Genomic Mechanism Elucidated
Abstract
1. Introduction
- -
- Is there any underlying principle that self-regulates the time evolution of whole-genome expression?
- -
- Can we identify a peculiar genome region that guides the super-critical genome and determines the cell-fate change?
- -
- Can we delineate a universal mechanism to understand the processes of the cell-fate change, and to further comprehend when and how it occurs?
2. Results
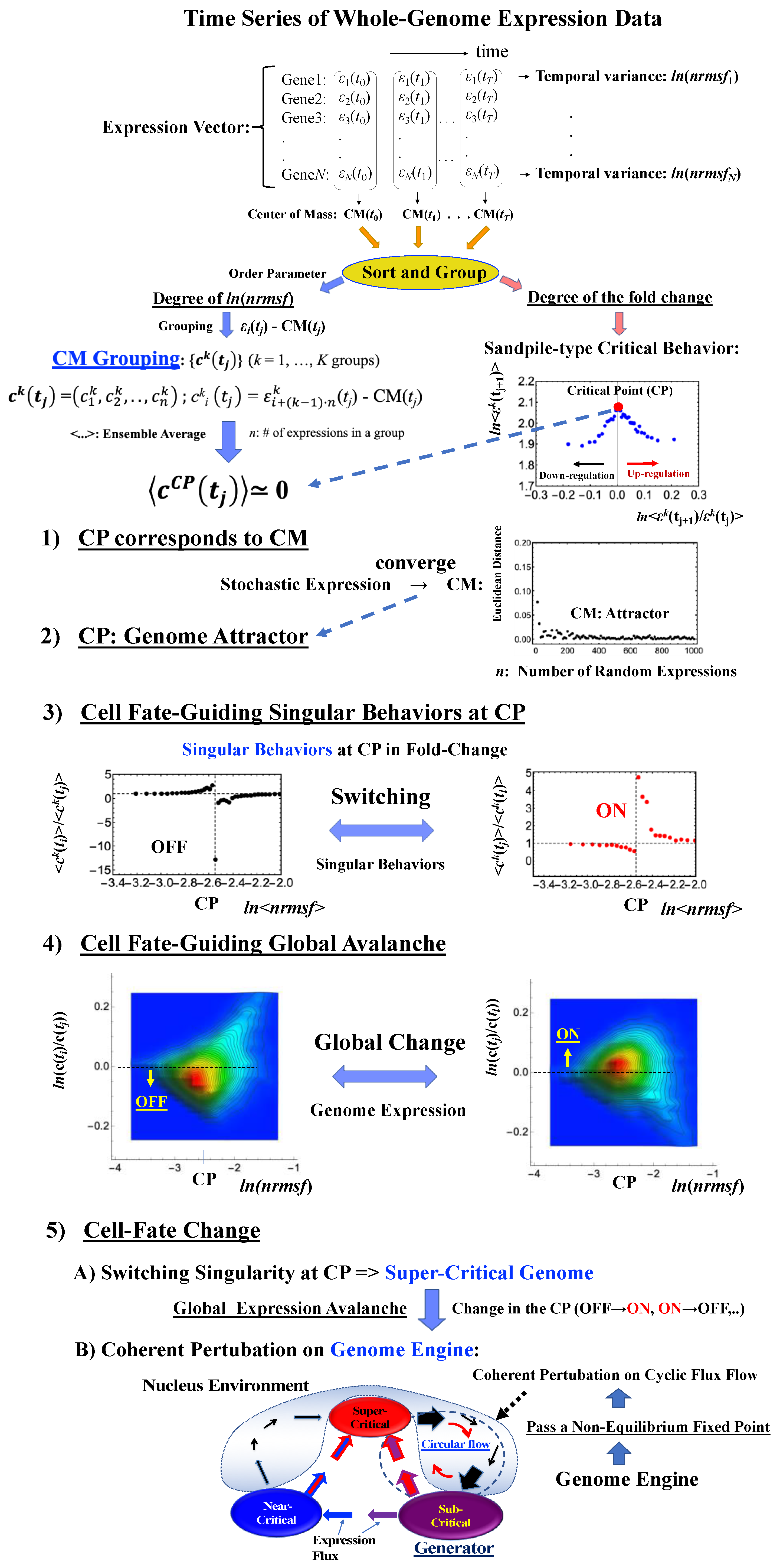
2.1. Fixed Critical Point: A Specific Group of Genes Corresponding to the Center of Mass of Whole-Genome Expression
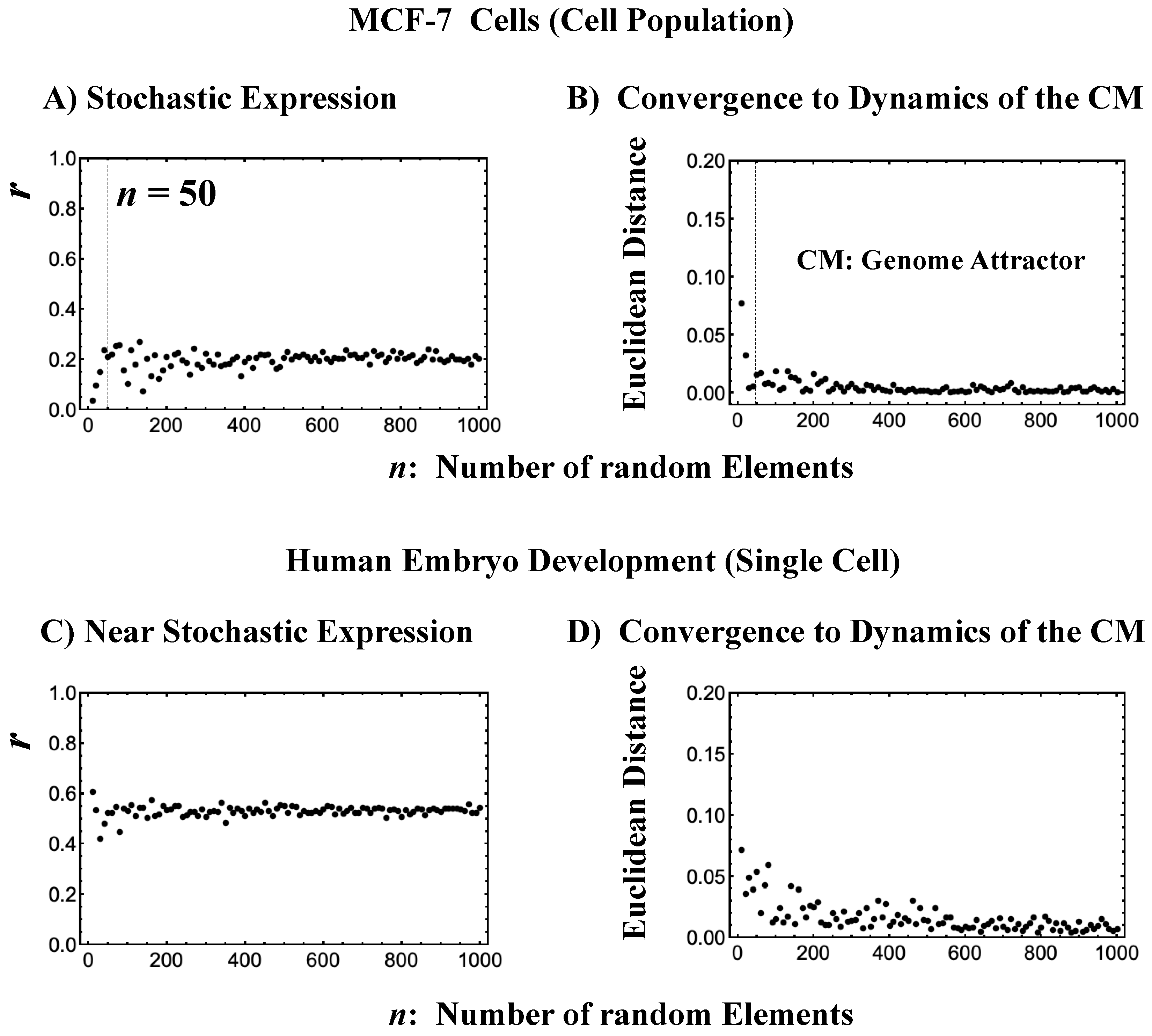
2.2. Critical Point Acting as the Genome Attractor: Mechanism for Genome-Wide Avalanche
- (1)
- The stochastic behavior of gene expression shows (relatively low) correlation convergence for randomly selected gene ensembles as the number of elements (n) is increased (Figure 3A).
- (2)
- The CM of randomly selected gene ensembles (with hundreds of repetitions for the gene ensembles) must dynamically converge to that of whole-genome expression as the number of elements (n) is increased (Figure 3B).
2.3. ON/OFF State of the CP: Cell Fate-Guiding and Global Avalanches
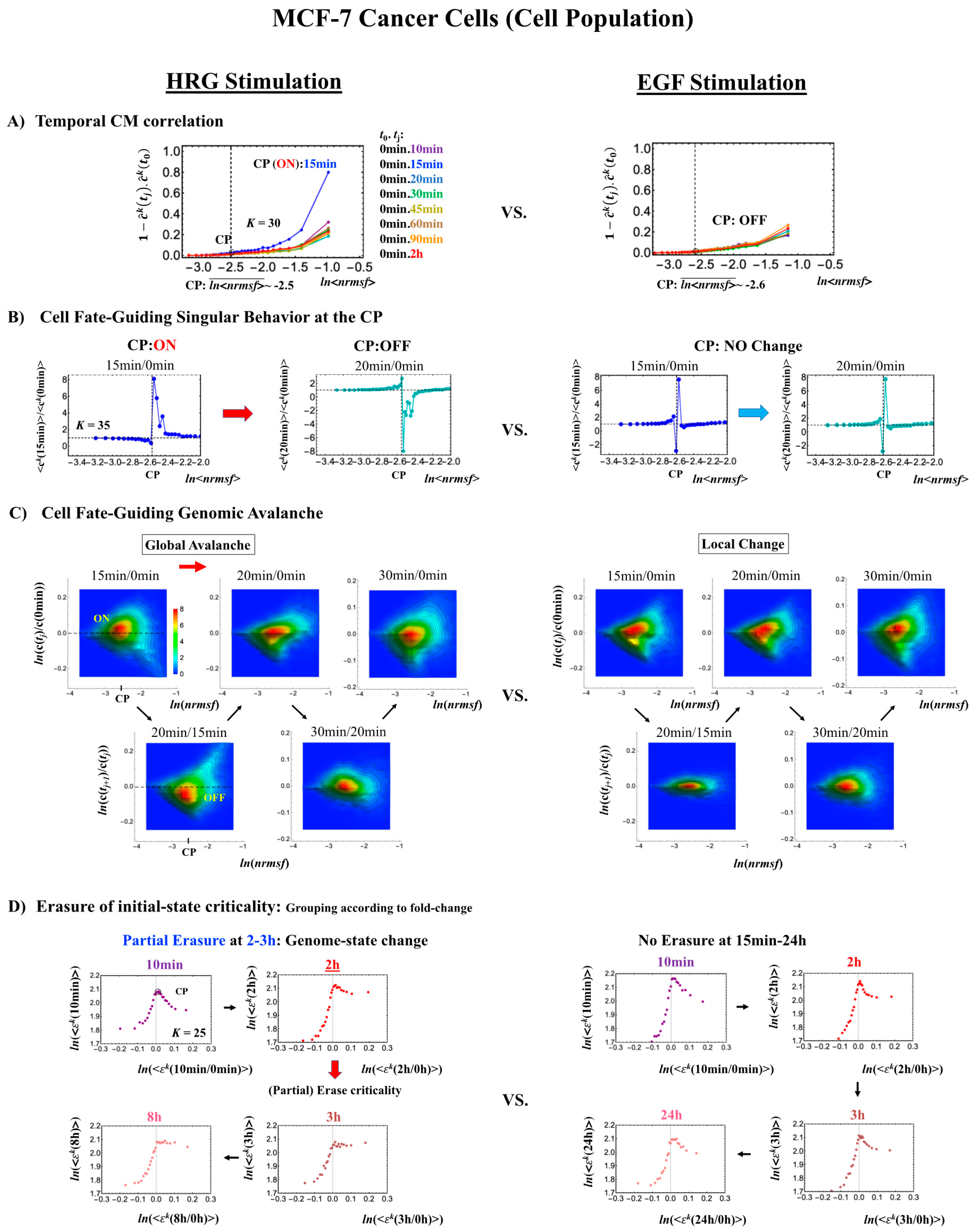
2.3.1. MCF-7 Breast Cancer Development (Cell-Population Level): ON–OFF State of the CP Revealed
- (1)
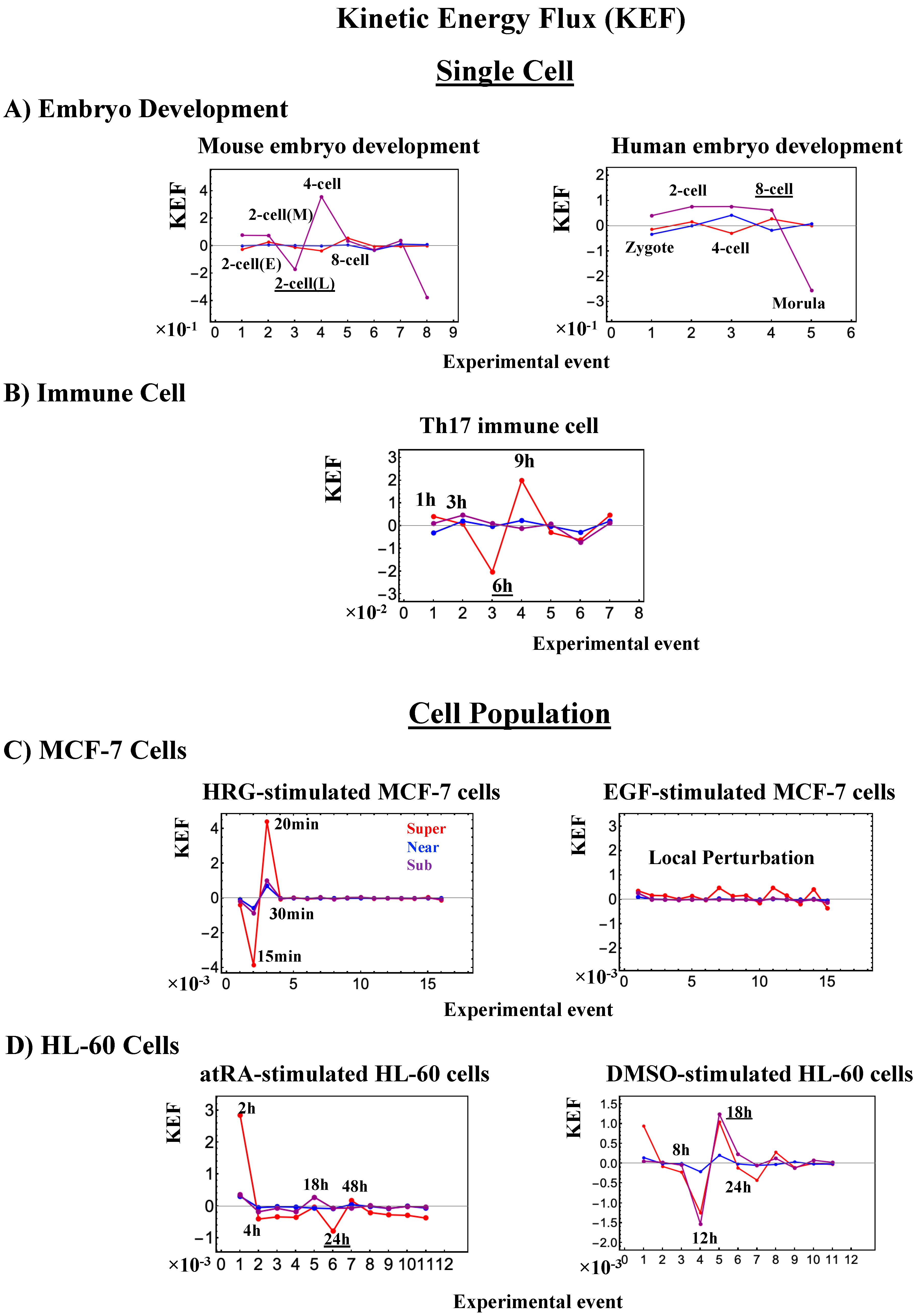
- In Figure 4B, for HRG stimulation, the switching of singular behaviors at 15–20 min occurs at the CP. At the boundary of the CP (ln<nrmsf> ~ −2.5), the singular behavior exhibits bimodal behavior in the fold-change on the CM grouping. At 15 min, a dominant positive (i.e., fold-change greater than one) singular behavior (ln<nrmsf> > −2.5) suggests that the swollen coil state of DNA occurs at the CP, while a negative singular behavior (ln<nrmsf> < −2.5) suggests the compact coil state of DNA. At 20 min, this bimodal behavior switches to a dominant negative singular behavior (> −2.5) with a positive singular behavior (< −2.5). With regard to EGF stimulation, such a switching transition does not occur during the early time points. Note: A negative fold-change occurs given that the reference point is the CM of whole-genome expression. Subtraction of the CM(tj) from each gene expression gives negative expression.
- (2)
- In Figure 4C, the probability density function (PDF) of whole- genome expression [27] shows that at 15 min, around the CP region, the maximum probability density occurs in a positive area, whereas it becomes negative at 15–20 min. This validates that the CP is in the ON state at 15 min and in the OFF state at 20 min. The PDF clearly shows that ON–OFF switching of the CP induces a global avalanche in whole- genome expression.
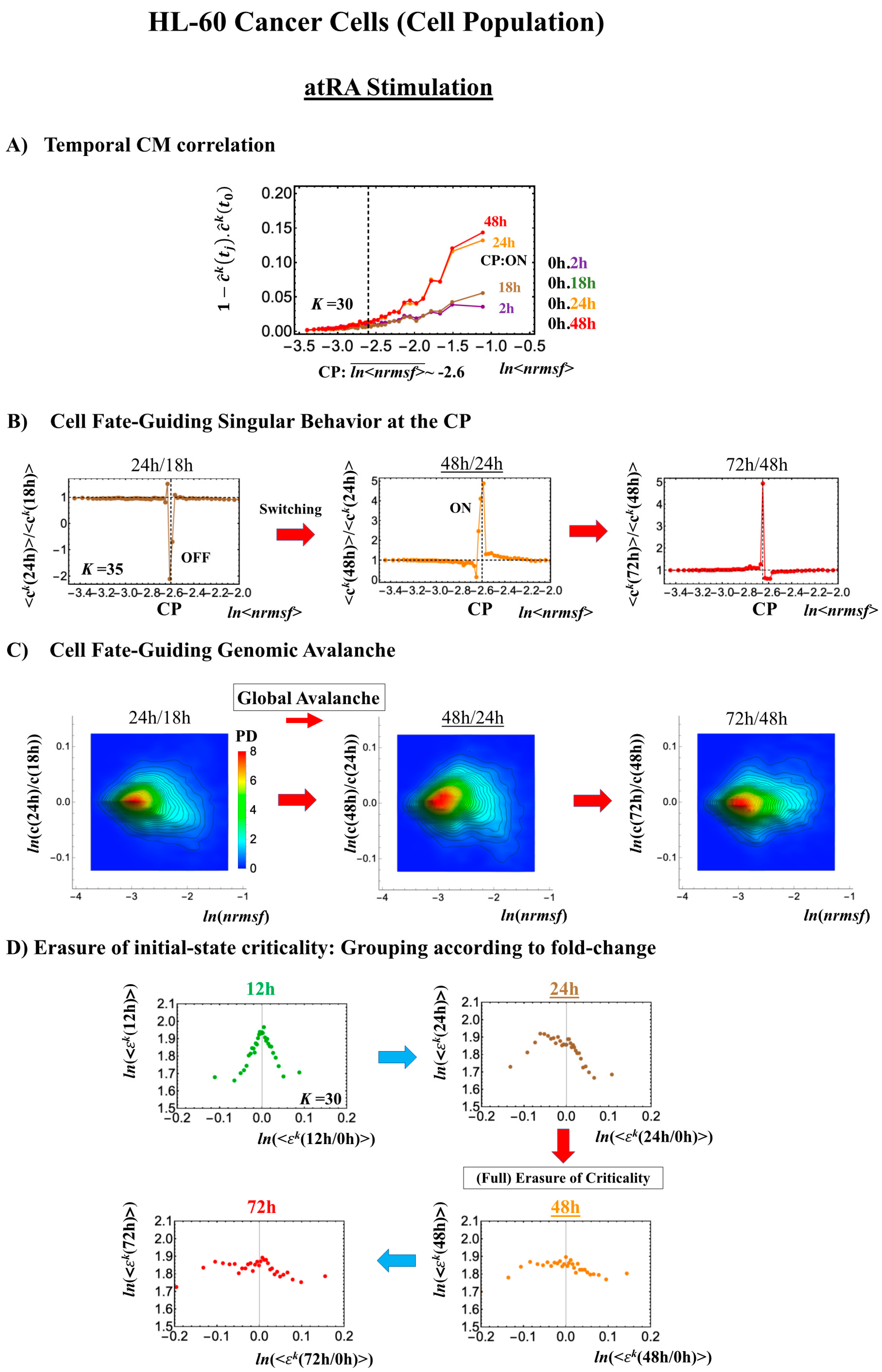
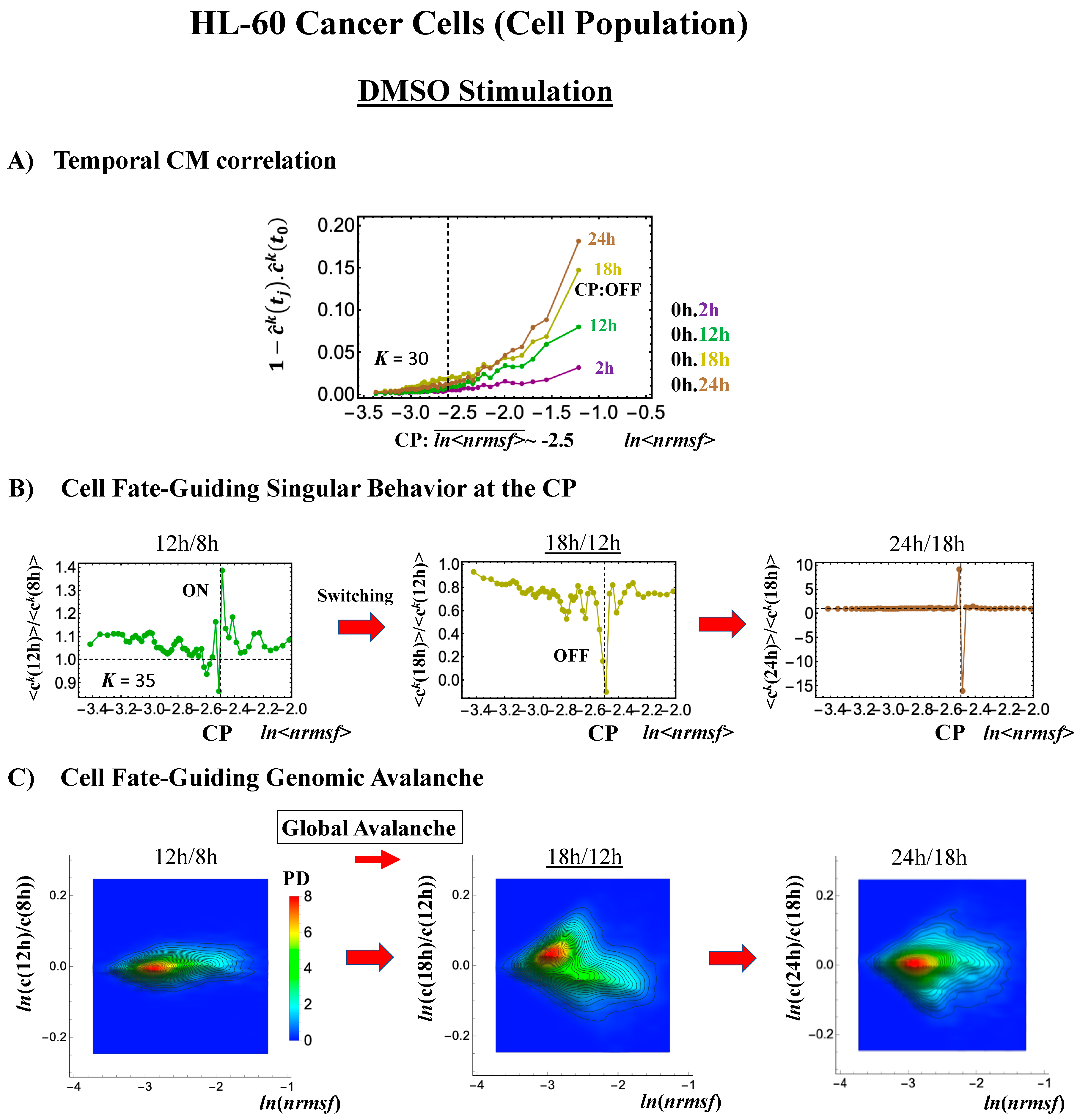
2.3.2. HL-60 Breast Cancer Cell Development (Cell-Population Level): Timing of Cell-Fate Change
- (1)
- Under atRA stimulation (Figure 5B), the dominant negative fold-change (compact globule state) indicates the OFF state of the CP at 18–24 h, while the dominant positive fold-change (swollen coil state) indicates the ON state at 24–48 h: the change from OFF to ON occurs at the CP. The global avalanche is shown by swelling of the probability density from 18–24 h to 24–48 h and contraction at 48–72 h (Figure 5C).
- (2)
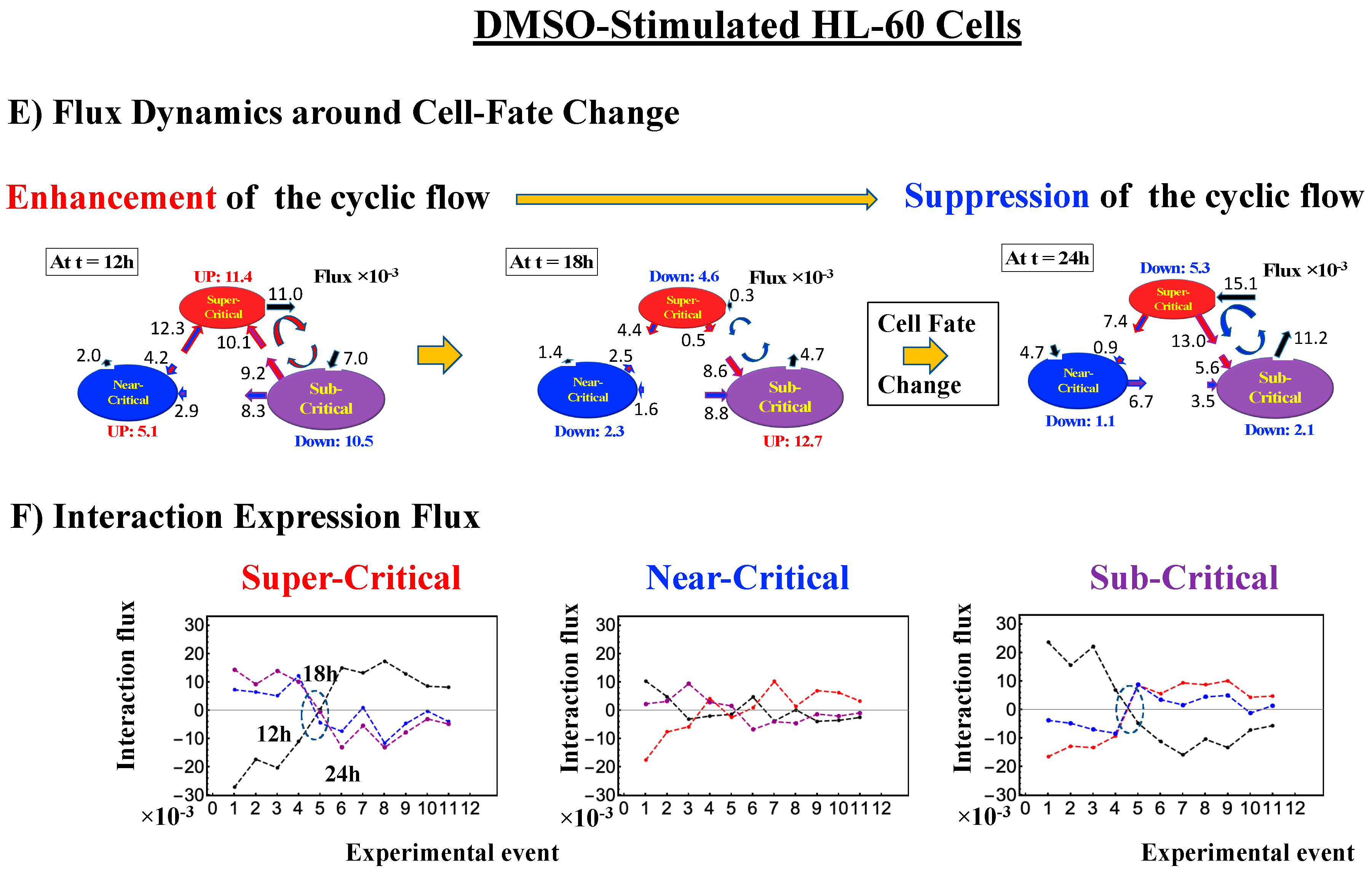
- Under DMSO stimulation (Figure 6B), the dominant positive-to-negative fold-change (the opposite of the case with atRA stimulation) occurs from 8–12 h to 12–18 h, i.e., the change from OFF to ON occurs at the CP. At 18–24 h, the CP is neither ON nor OFF. These points are confirmed by the temporal change in the PDF profile (Figure 6C) around the CP: the fold-change (ln<nrmsf> ~ −2.5) goes from positive to negative to neutral.
2.4. Cell-Fate Change in Single-Cell Dynamics
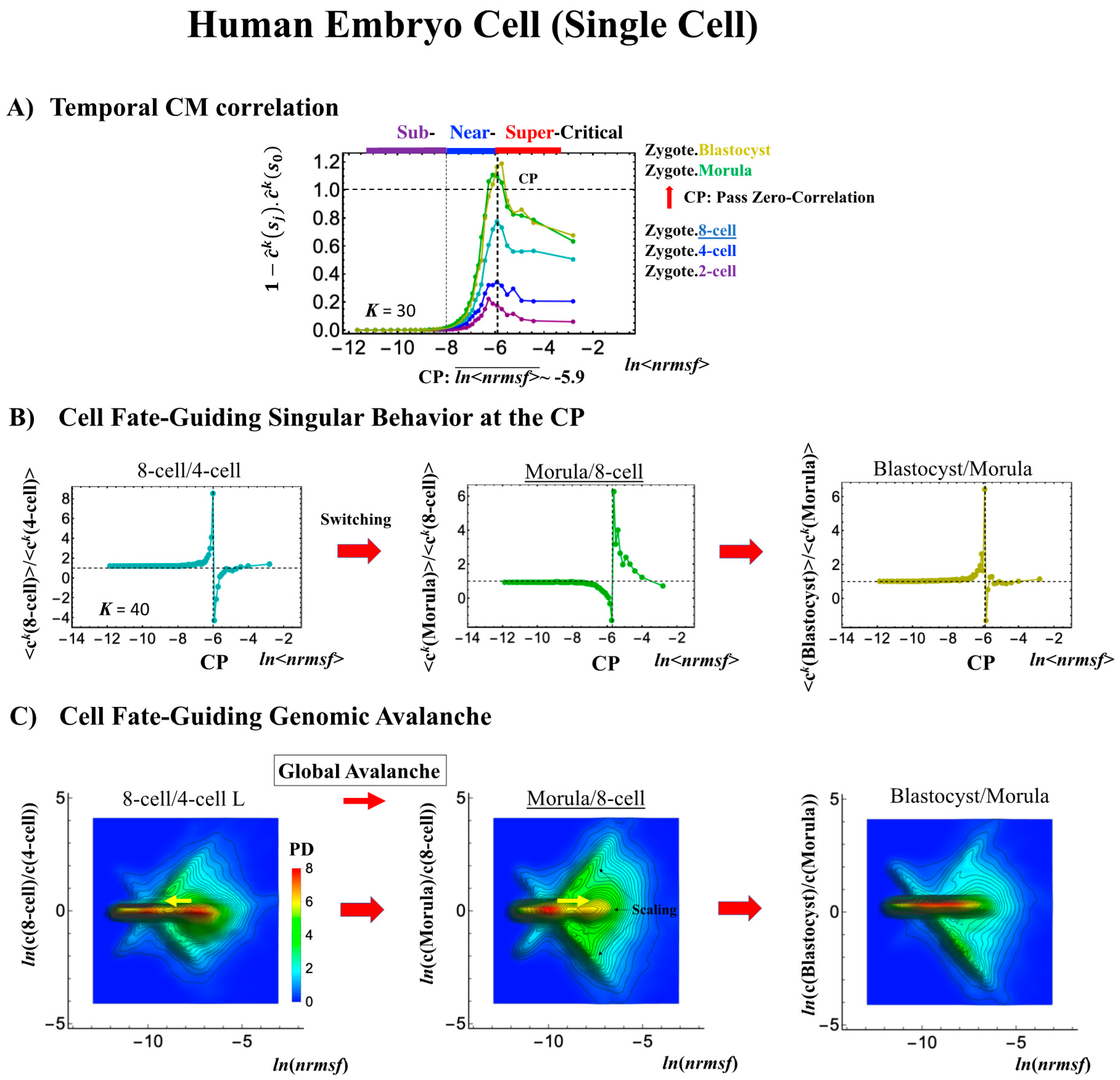
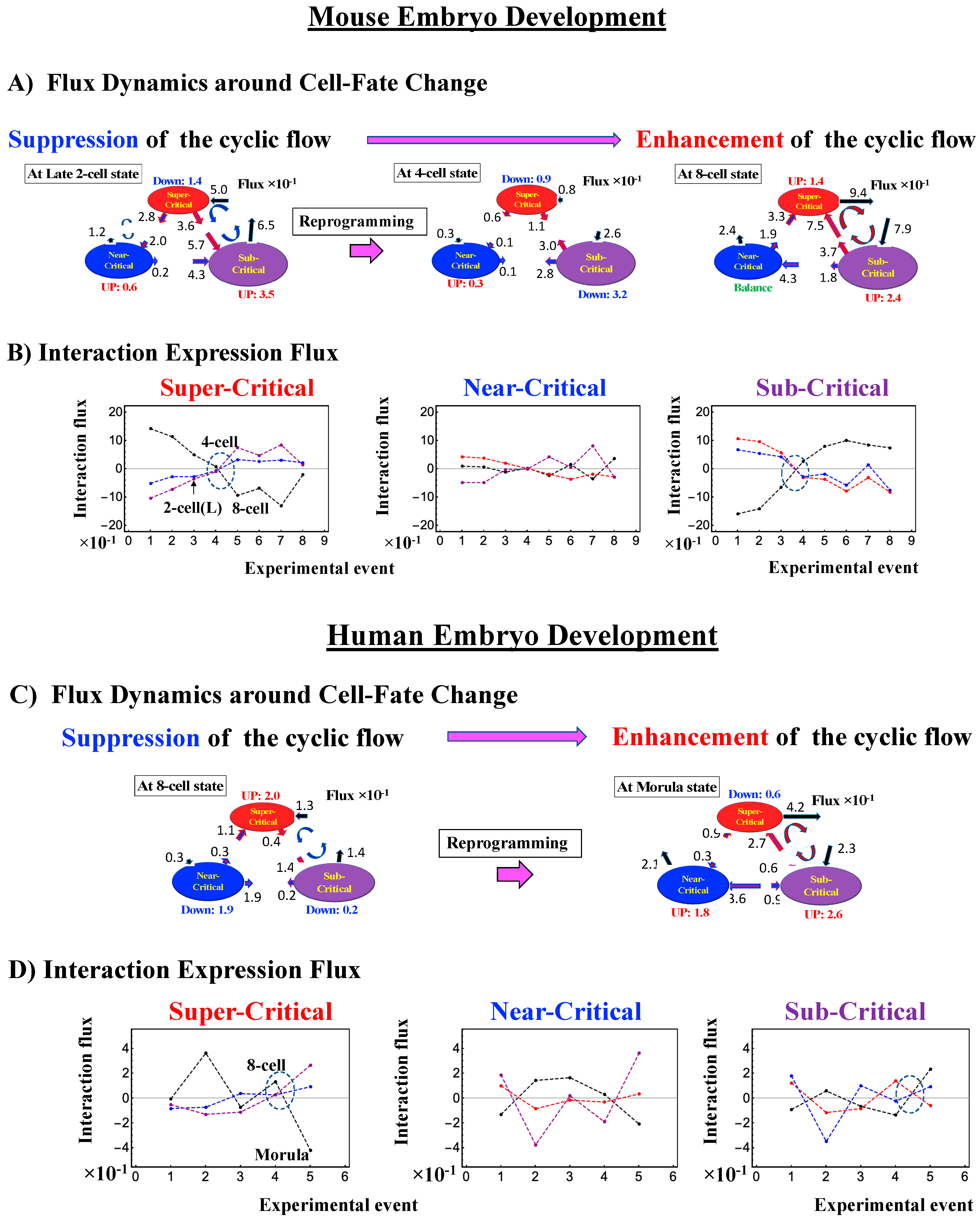
2.4.1. Human Embryo Development: Genome Avalanche Along Low-Expressed Genes
2.4.2. Mouse Embryo Development: Switching Scaling Behaviors in the Cell-Fate Change
- (1)
- (2)
- This is confirmed by a temporal change in the PDF (Figure 8C): during cell development from the middle 2-cell to 4-cell states through the late 2-cell state (2-cell L), the whole density profile reflects along the axis of zero-fold change. This clearly manifests as the ON state of the CP at the middle 2-cell – late 2-cell state, and as the OFF state at the late 2-cell – 8-cell state. There are also three distinct scaling behaviors, as in human embryo development. Notably, during the middle 2-cell to 4-cell state through the late 2-cell state, whole-genome expression shifts from up- to downregulation, i.e., marking the occurrence of a global avalanche, and furthermore, there is a reflection of the scaling behavior in the local sub-critical state (ln(nrmsf) < −11) along the zero-fold change axis (y = 0). This reflection illustrates that a coherent switching of folding and unfolding chromatin dynamics occurs, which supports the important role in the local sub-critical state in early embryo development [8].
- (3)
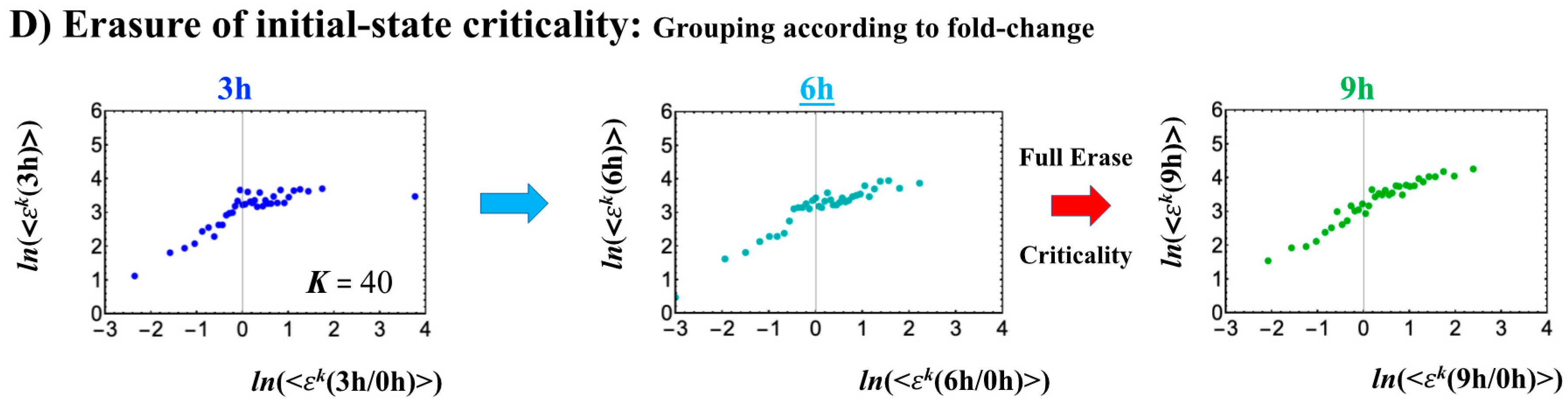
- The timing of the cell-fate change is further confirmed by the erasure of zygote sandpile criticality after the late 2-cell state.
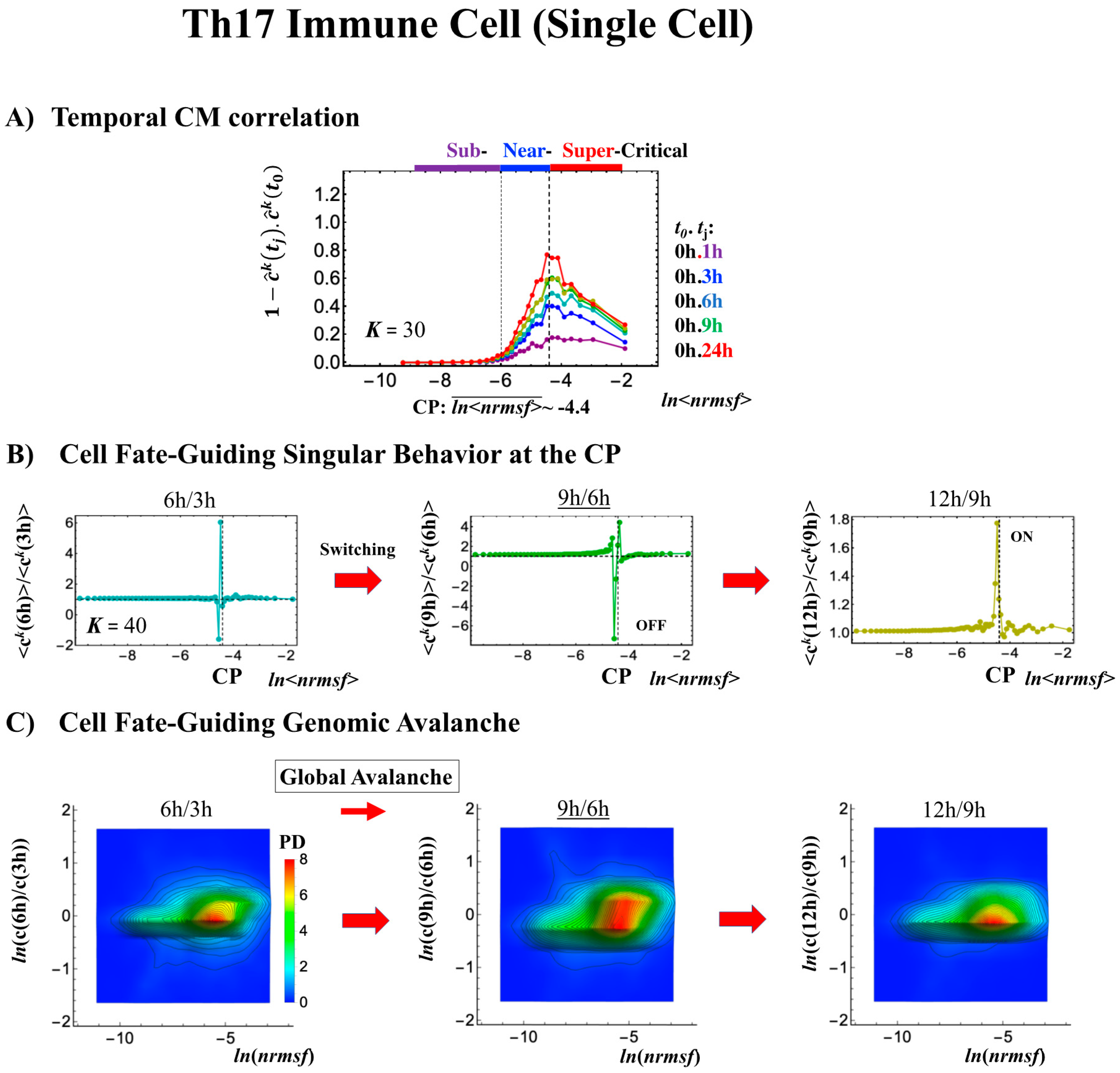
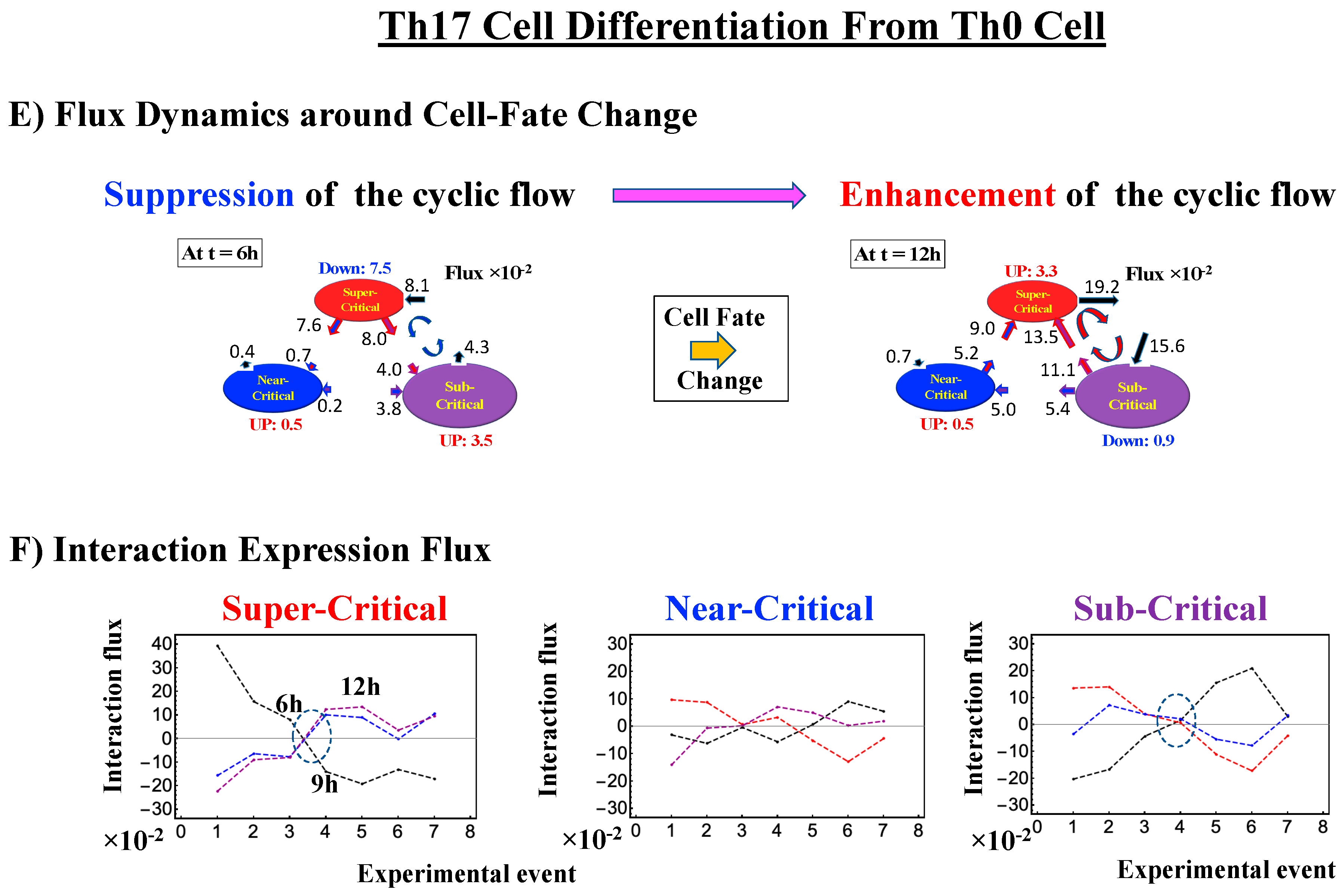
2.4.3. Differentiation of Th17 Immune Cells from Th0 Cells: Partial Avalanche Guides the Cell-Fate Change
- (1)
- The CP does not pass over zero temporal correlation with the initial state (t = 0 h; Figure 9A), although the correlation response increases in time, which indicates that cell differentiation induces a partial-scale (specific set) change in whole-genome expression (vs. whole genome-scale change in embryonic reprogramming).
- (2)
- The switching singular transition at the CP (genome attractor) occurs sequentially from 3 h to 12 h (Figure 9B). This manifests as the OFF state of the CP at 6–9 h and as the ON state at 9–12 h. Figure 9C illustrates that the change in expression for switching is still on a large scale, which is confirmed by the temporal change in the PDF of whole-genome expression. However, there is no distinct scaling behavior as in embryo development.
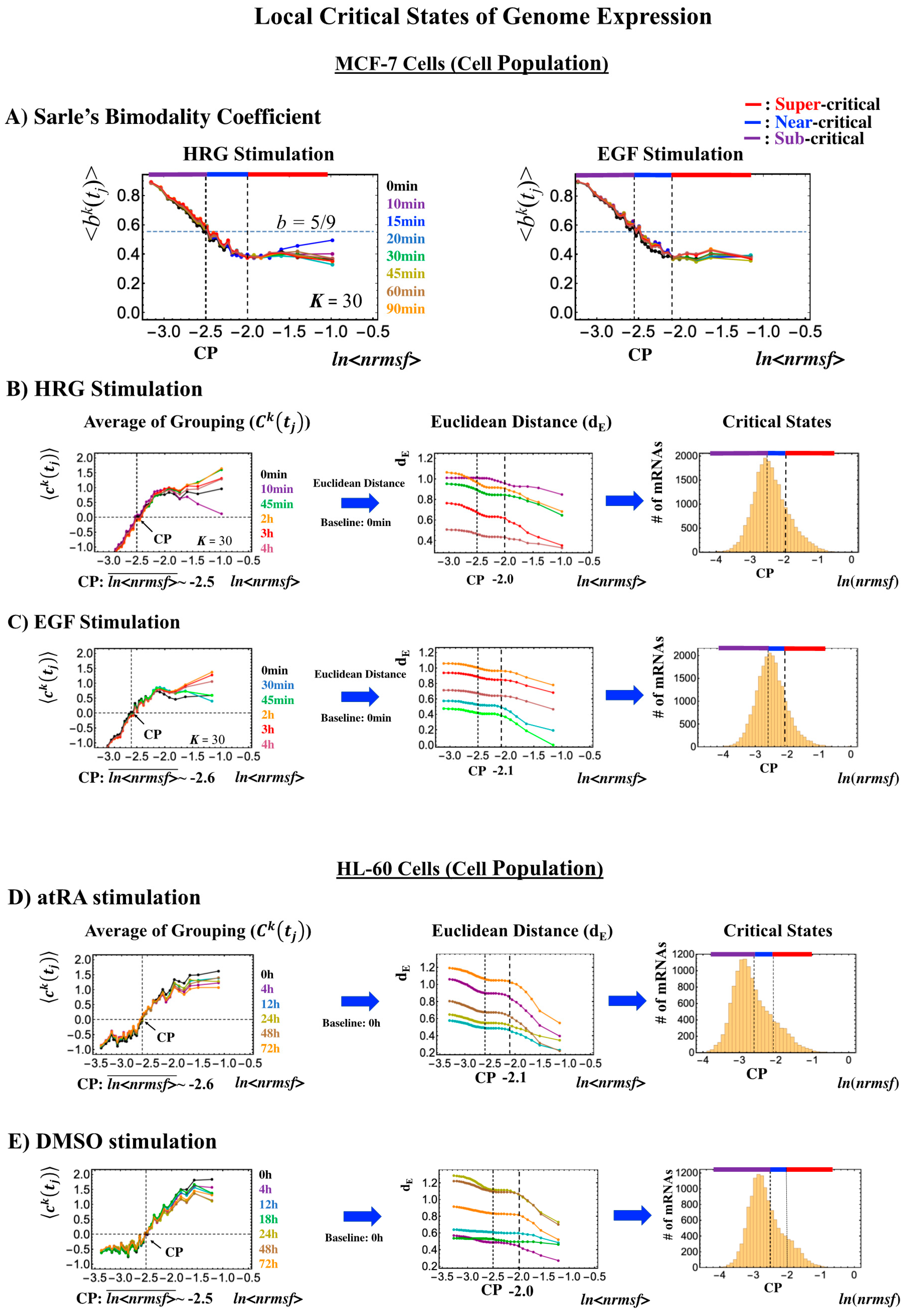
2.5. Systematic Determination of Local Critical States in Genome Expression
- (1)
- Single-cell level: Temporal CM correlation (Figure 7A, Figure 8A and Figure 9A) manifests distinct response domains according to nrmsf: low-variance expression (sub-critical state) for the region of flattened correlation, intermediate variance for the near-critical state from the edge of flattened correlation to the CP, and high-variance expression for the super-critical state above the CP (Table 1).
- (2)
- Cell-population level: the Euclidean distance (from the highest nrmsf group) between the temporal responses of CM grouping (Figure 2: t = 0 vs. other experimental time points) reveals critical states (Figure 10; summary: Table 2), where the CP exists at the boundary between near-and sub-critical states (vs. between super-and sub-critical states in a single cell). This occurs for both MCF-7 and HL-60 cancer cell populations. In our previous studies on microarray data (cell-population level), critical states were determined by a change in expression profile by means of Sarle’s bimodality coefficient (Figure 10A; see Figure 9 for MCF-7 and HL-60 cells in [7]). This was accomplished by adding evidence of distinct response domains (super-, near- and sub-critical domains according to nrmsf).
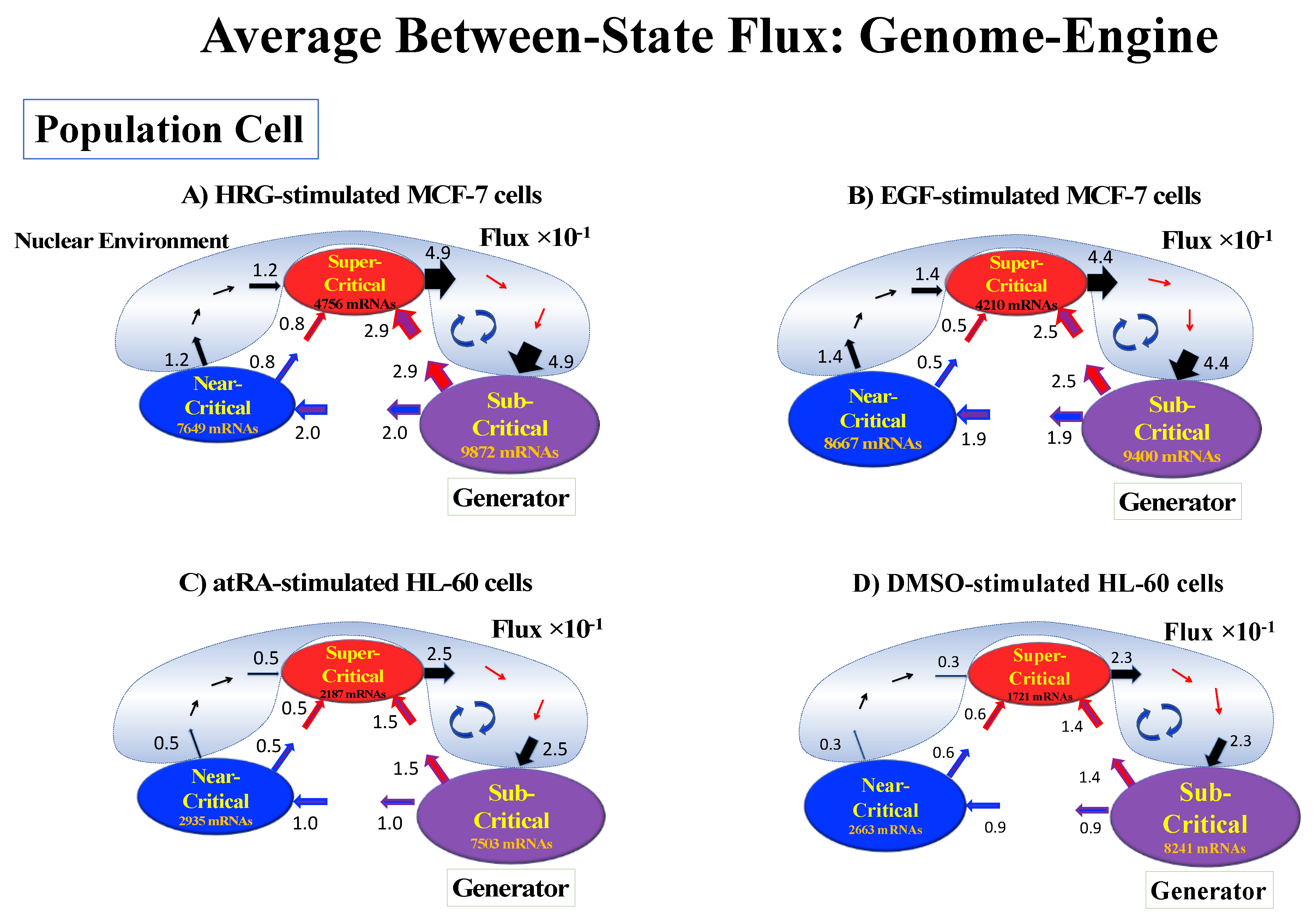
2.6. Genome Engine Mechanism for SOC-Control of Genome Expression: Heteroclinic Critical-State Attractor System
3. Discussion and Conclusion
3.1. Genomic Dynamics Determining the Cell-Fate Change from Embryo to Cancer: Cell-Fate Change Passing through a Non-Equilibrium Fixed Point
3.2. Synergetic Behaviors of Mega Base Pair-Size DNAs Through a Phase Transition
3.3. CP Potentially Acting as the Center of Genome Computing
3.4. Biological Meaning of the CP
3.5. Final Remarks
- (1)
- The critical point (CP) acts as the center of the cell fate.
- (2)
- How the cell-fate change occurs: Before the cell-fate change, the genomic system passes over the stable point (non-equilibrium fixed point) of the thermodynamically open system. The genome engine, an emergent dynamic property of an autonomous interaction flux between local critical states (distinct expression domains in whole-genome expression), is enhanced or suppressed to induce coherent perturbation of the dominant cyclic flux between local super- and sub-critical states.
- (3)
- When the cell-fate change occurs: The change occurs at the timing of the erasure of the initial-state sandpile CP. At this time, a global genome avalanche occurs, except in HRG-stimulated MCF-7 cell differentiation, with a time lag between the genome avalanche and the cell-fate change (for further details of this mechanism, see [10]).
4. Materials and Methods
4.1. Biological Data Sets
4.1.1. Cell population:
4.1.2. Single-cell:
4.2. Methods
4.2.1. Normalized Root Mean Square Fluctuation (nrmsf)
4.2.2. CM Correlation Analysis
4.2.3. Probability Density Function (PDF)
4.2.4. Expression Flux Analysis: Expression Flux Between Critical-State Attractors
Order of averaging: vs.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| atRA CM | All-trans retinoic acid Center of mass |
| CP | Critical point |
| CSB | Coherent-stochastic behavior |
| EGF | Epidermal growth factor |
| KEF | Kinetic energy flux |
| DMSO | Dimethyl sulfoxide |
| HRG | Heregulin |
| iPS cell | Induced pluripotent stem cell |
| Nrmsf | Normalized root mean square fluctuation |
| PC1, PC2 | The first principal component, the second principal component |
| Probability density function | |
| SOC | Self-organized criticality |
| Th0 | Naïve T helper |
| Th17 | T helper 17 |
References
- Takahashi, K.; Yamanaka, S. A decade of transcription factor-mediated reprogramming to pluripotency. Nat. Rev. Mol. Cell Biol. 2016, 17, 183–193. [Google Scholar] [CrossRef] [PubMed]
- MacArthur, B.D.; Ma’ayan, A.; Lemischka, I.R. Systems biology of stem the cell-fate and cellular reprogramming. Nat. Rev. Mol. Cell Biol. 2009, 10, 672–681. [Google Scholar] [CrossRef]
- Raser, J.M.; O’Shea, E.K. Noise in gene expression: Origins, consequences, and control. Science 2005, 309, 2010–2013. [Google Scholar] [CrossRef]
- Yoshikawa, K. Field hypothesis on the self-regulation of gene expression. J. Biol. Phys. 2002, 28, 701–712. [Google Scholar] [CrossRef] [PubMed]
- Tsuchiya, M.; Hashimoto, M.; Takenaka, Y.; Motoike, I.N.; Yoshikawa, K. Global genetic response in a cancer cell: Self-organized coherent expression dynamics. PLoS ONE 2014, 9, e97411. [Google Scholar] [CrossRef] [PubMed]
- Tsuchiya, M.; Giuliani, A.; Hashimoto, M.; Erenpreisa, J.; Yoshikawa, K. Emergent Self-Organized Criticality in gene expression dynamics: Temporal development of global phase transition revealed in a cancer cell line. PLoS ONE 2015, 11, e0128565. [Google Scholar] [CrossRef] [PubMed]
- Tsuchiya, M.; Giuliani, A.; Hashimoto, M.; Erenpreisa, J.; Yoshikawa, K. Self-organizing global gene expression regulated through criticality: Mechanism of the cell-fate change. PLoS ONE 2016, 11, e0167912. [Google Scholar] [CrossRef]
- Tsuchiya, M.; Giuliani, A.; Yoshikawa, K. Single-Cell Reprogramming in Mouse Embryo Development through a Critical Transition State. Entropy 2017, 19, 584. [Google Scholar] [CrossRef]
- Giuliani, A.; Tsuchiya, M.; Yoshikawa, K. Self-Organization of Genome Expression from Embryo to Terminal The cell-fate: Single-Cell Statistical Mechanics of Biological Regulation. Entropy 2018, 20, 13. [Google Scholar] [CrossRef]
- Zimatore, G.; Tsuchiya, M.; Hashimoto, M.; Kasperski, A.; Giuliani, A. Self-Organization of Whole Gene Expression through Coordinated Chromatin Structural Transition: Validation of Self-Organized Critical Control of Genome Expression. bioRxiv 2019. [Google Scholar] [CrossRef]
- Bak, P.; Tang, C.; Wiesenfeld, K. Self-organized criticality: An explanation of the 1/f noise. Phys. Rev. Lett. 1987, 59, 381–384. [Google Scholar] [CrossRef] [PubMed]
- Langton, C.G. Computation at the edge of chaos-phase transitions and emergent computation. Physica D 1990, 42, 12–37. [Google Scholar] [CrossRef]
- Kauffman, S.A. The Origins of Order: Self-Organization and Selection in Evolution; Oxford University Press: New York, NY, USA, 1993. [Google Scholar] [CrossRef]
- Jensen, H.J. Self-Organized Criticality; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Marković, D.; Gros, C. Power laws and self-organized criticality in theory and nature. Phys. Rep. 2014, 536, 41–74. [Google Scholar] [CrossRef]
- Muñoz, M.A. Colloquium: Criticality and dynamical scaling in living systems. Rev. Mod. Phys. 2018, 90, 31001–31030. [Google Scholar] [CrossRef]
- Wagner, J.R.; Lee, C.T.; Durrant, J.D.; Malmstrom, R.D.; Feher, V.A.; Amaro, R.E. Emerging Computational Methods for the Rational Discovery of Allosteric Drugs. Chem. Rev. 2016, 116, 6370–6390. [Google Scholar] [CrossRef]
- Halley, J.D.; Burden, F.R.; Winkler, D.A. Summary of stem cell decision making and critical-like exploratory networks. Stem Cell Res. 2009, 2, 165–177. [Google Scholar] [CrossRef]
- Nagashima, T.; Shimodaira, H.; Ide, K.; Nakakuki, T.; Tani, Y.; Takahashi, K.; Yumoto, N.; Hatakeyama, M. Quantitative transcriptional control of ErbB receptor signaling undergoes graded to biphasic response for cell differentiation. J. Biol. Chem. 2007, 282, 4045–4056. [Google Scholar] [CrossRef]
- Nakakuki, T.; Birtwistle, M.R.; Saeki, Y.; Yumoto, N.; Ide, K.; Nagashima, T.; Brusch, L.; Ogunnaike, B.A.; Okada-Hatakeyama, M.; Kholodenko, B.N. Ligand-specific c-Fos expression emerges from the spatiotemporal control of ErbB network dynamics. Cell 2010, 141, 884–896. [Google Scholar] [CrossRef]
- Huang, S.; Eichier, G.; Bar-Yam, Y.; Ingber, D.E. The cell-fates as high-dimensional attractor states of a complex gene regulatory network. Phys. Rev. Lett. 2005, 94, 128701–128705. [Google Scholar] [CrossRef]
- Ciofani, M.; Madar, A.; Galan, C.; Sellars, M.; Mace, K.; Pauli, F.; Agarwal, A.; Huang, W.; Parkhurst, C.N.; Muratet, M.; et al. A validated regulatory network for Th17 cell specification. Cell 2012, 151, 289–303. [Google Scholar] [CrossRef] [PubMed]
- Deng, Q.; Ramsköld, D.; Reinius, B.; Sandberg, R. Single-cell RNA-seq reveals dynamic, random monoallelic gene expression in mammalian cells. Science 2014, 343, 193–196. [Google Scholar] [CrossRef] [PubMed]
- Yan, L.; Yang, M.; Guo, H.; Yang, L.; Wu, J.; Li, R.; Liu, P.; Lian, Y.; Zheng, X.; Yan, J.; et al. Single-cell RNA-Seq profiling of human preimplantation embryos and embryonic stem cells. Nat. Struct. Mol. Biol. 2013, 20, 1131–1139. [Google Scholar] [CrossRef] [PubMed]
- Censi, F.; Giuliani, A.; Bartolini, P.; Calcagnini, G. A Multiscale Graph Theoretical Approach to Gene Regulation Networks: A Case Study in Atrial Fibrillation. IEEE Trans. Biomed. Eng. 2011, 99, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Tsuchiya, M.; Wong, S.T.; Yeo, Z.X.; Colosimo, A.; Palumbo, M.C.; Crescenzi, M.; Mazzola, A.; Negri, R.; Bianchi, M.M.; Selvarajoo, K.; et al. Gene expression waves: Cell cycle independent collective dynamics in cultured cells. FEBS J. 2007, 274, 2874–2886. [Google Scholar] [CrossRef]
- Shu, G.; Zeng, B.; Chen, Y.P.; Smith, O.H. Performance assessment of kernel density clustering for gene expression profile data. Comp. Funct. Genomics 2003, 4, 287–299. [Google Scholar] [CrossRef]
- Tsuchiya, M.; Giuliani, A.; Yoshikawa, K. A Quantitative Evaluation of Symmetry Breaking in Nonlinear-Oscillatory System—Based on Flux Dynamics (Effective force) View Point. 2018. Available online: https://www.researchgate.net/publication/323365534_A_Quantitative_Evaluation_of_Symmetry_Breaking_In_Nonlinear-Oscillatory_System_-_Based_on_Flux_Dynamics_Effective_force_View_Point (accessed on 31 March 2020).
- Saeki, Y.; Endo, T.; Ide, K.; Nagashima, T.; Yumoto, N.; Toyoda, T.; Suzuki, H.; Hayashizaki, Y.; Sakaki, Y.; Okada-Hatakeyama, M. Ligand-specific sequential regulation of transcription factors for differentiation of MCF-7 cells. BMC Genom. 2009, 10, 545. [Google Scholar] [CrossRef]
- Flory, P. Principles of Polymer Chemistry; Cornell University Press: Ithaca, NY, USA, 1953. [Google Scholar]
- De Gennes, P.G. Scaling Concepts in Polymer Physics; Cornell University Press: Ithaca, NY, USA, 1979. [Google Scholar]
- Yoshikawa, K.; Takahashi, M.; Vasilevskaya, V.V.; Khokhlov, A.R. Large Discrete Transition in a Single DNA Molecule Appears Continuous in the Ensemble. Phys. Rev. Lett. 1996, 76, 3029–3031. [Google Scholar] [CrossRef]
- Yoshikawa, K.; Yoshikawa, Y. Compaction and Condensation of DNA, in Pharmaceutical Perspective of Nucleic Acid-Base Therapy; Taylor & Francis: Abingdon, UK, 2002; pp. 137–163. [Google Scholar]
- Zinchenko, A.; Pyshkina, O.; Lezov, A.; Sergeyev, V.; Yoshikawa, K. Single DNA molecules: Compaction and Decompaction (chapter 3). In DNA interactions with Polymers and Surfactants; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2008; pp. 59–88. [Google Scholar] [CrossRef]
- Sakaue, T.; Yoshikawa, K. On the formation of rings-on-a-string conformations in a single polyelectrolyte chain: A possible scenario. J. Chem. Phys. 2006, 125, 074904. [Google Scholar] [CrossRef]
- Shew, C.Y.; Yoshikawa, K. Mean field theory for the intermolecular and intramolecular conformational transitions of a single flexible polyelectrolyte chain. J. Chem. Phys. 2007, 126, 144913. [Google Scholar] [CrossRef]
- Schiessel, H. The physics of chromatin. J. Phys. Condes. Matter 2003, 15, R699–R774. [Google Scholar] [CrossRef]
- Nakai, T.; Hizume, K.; Yoshimura, S.H.; Takeyasu, K.; Yoshikawa, K. Phase transition in reconstituted chromatin. Europhys. Lett. 2005, 69, 1024–1030. [Google Scholar] [CrossRef]
- Suzuki, Y.; Yoshikawa, Y.; Yoshimura, S.H.; Yoshikawa, K.; Takeyasu, K. Unraveling DNA dynamics using atomic force microscopy. Wiley Interdiscip. Rev. Nanomed. Nanobiotechnol. 2011, 3, 574–588. [Google Scholar] [CrossRef] [PubMed]
- Krigerts, J.; Salmina, K.; Freivalds, T.; Rumnieks, F.; Inashkina, I.; Zayakin, P.; Hausmann, M.; Erenpreisa, J. Early Critical Phase Transitions of Pericentromere-Associated Domains in MCF-7 Breast Cancer Cells Committed to Differentiation by Heregulin. Preprints 2020. [Google Scholar] [CrossRef]
- Wachsmuth, M.; Knoch, T.A.; Rippe, K. Dynamic properties of independent chromatin domains measured by correlation spectroscopy in living cells. Epigenetics Chromatin 2016, 9, 57. [Google Scholar] [CrossRef] [PubMed]
- Takagi, S.; Yoshikawa, K. Stepwise collapse of polyelectrolyte chains entrapped in a finite space as predicted by theoretical considerations. Langmuir 1999, 15, 4143–4146. [Google Scholar] [CrossRef]
- Yoshikawa, K.; Noguchi, H. A working hypothesis on the mechanism of molecular machinery. Chem. Phys. Lett. 1999, 303, 10–14. [Google Scholar] [CrossRef]
- Ginzburg, V.L.; Landau, L.D. On the theory of superconductors. Zh. Eksp. Teor. Fiz. 1965, 20, 1064–1082. [Google Scholar]
- Daniels, B.C.; Kim, H.; Moore, D.; Zhou, S.; Smith, H.B.; Karas, B.; Kauffman, S.A.; Walker, S.I. Criticality distinguishes the ensemble of biological regulatory networks. Phys. Rev. Lett. 2018, 121, 138102. [Google Scholar] [CrossRef]
- Maeshima, K.; Ide, S.; Hibino, K.; Sasai, M. Liquid-like behavior of chromatin. Curr. Opin. Genet. Dev. 2016, 37, 36–45. [Google Scholar] [CrossRef]
- Bolstad, B.M.; Irizarry, R.A.; Astrand, M.; Speed, T.P. A comparison of normalization methods for high density oligonucleotide array data based on variance and bias. Bioinformatics 2003, 19, 185–193. [Google Scholar] [CrossRef]
- Irizarry, R.A.; Hobbs, B.; Collin, F.; Beazer-Barclay, Y.D.; Antonellis, K.J.; Scherf, U.; Speed, T.P. Exploration, normalization, and summaries of high density oligonucleotide array probe level data. Biostatistics 2003, 4, 249–264. [Google Scholar] [CrossRef] [PubMed]
- McClintick, J.N.; Edenberg, H.J. Effects of filtering by present call on analysis of microarray experiments. BMC Bioinform. 2006, 7, 49. [Google Scholar] [CrossRef] [PubMed]





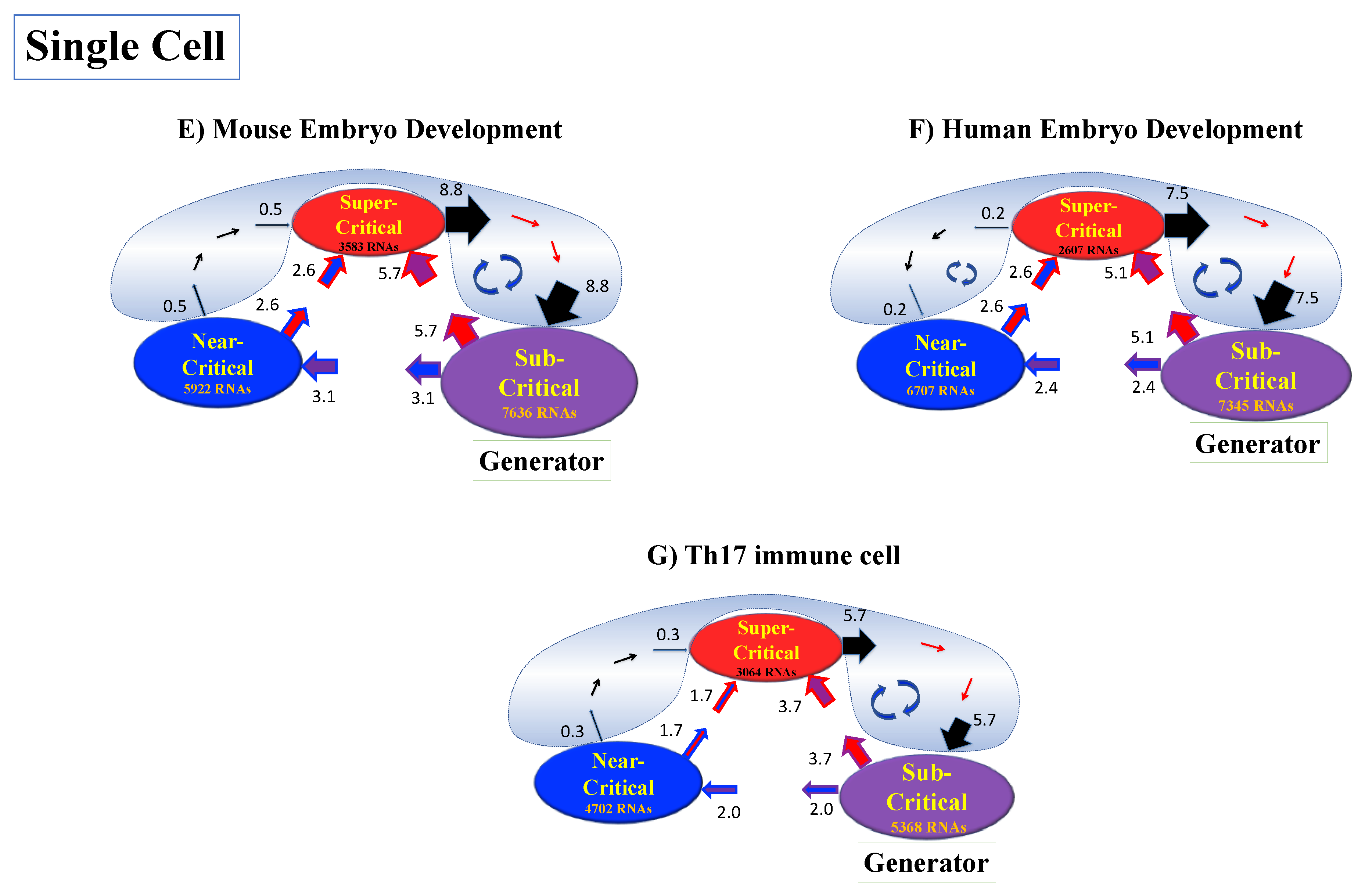


| Mouse Embryo Development | Human Embryo Development | Th17 Cell Differentiation |
|---|---|---|
| Critical States: | Critical States: | Critical States: |
| Super-critical: 3583 RNAs −5.6 * <ln<nrmsf> | Super-critical: 2607 RNAs −5.9 * <ln<nrmsf> | Super-critical: 3064 RNAs −4.4 * <ln<nrmsf> |
| Near-critical: 5922 RNAs −7.5< ln<nrmsf> < −5.6 | Near-critical: 6707 RNAs −8.0 < ln<nrmsf> < −5.9 | Near-critical: 4702 RNAs −6.0< ln<nrmsf> < −4.4 |
| Sub-critical: 7636 RNAs ln<nrmsf> < −7.5 | Sub-critical: 7345 RNAs ln<nrmsf> < −8.0 | Sub-critical: 5368 RNAs ln<nrmsf> < −6.0 |
| HRG-MCF-7 Cells | EGF-MCF-7 Cells | atRA-HL-60 Cells | DMSO-HL-60 Cells |
|---|---|---|---|
| Critical States: | Critical States: | Critical States: | Critical States: |
| Super-critical: 4756 RNAs −2.0 <ln<nrmsf> | Super-critical: 4210 RNAs −2.1 <ln<nrmsf> | Super-critical: 2187 RNAs −2.1 <ln<nrmsf> | Super-critical: 1721 RNAs −2.0 <ln<nrmsf> |
| Near-critical: 7649 RNAs −2.5 * < ln<nrmsf> <−2.0 | Near-critical: 8667 RNAs −2.6 * < ln<nrmsf> < −2.1 | Near-critical: 2935 RNAs −2.6 * < ln<nrmsf> < −2.1 | Near-critical: 2663 RNAs −2.5 * < ln<nrmsf> <−2.0 |
| Sub-critical: 9872 RNAs ln<nrmsf> < −2.5 | Sub-critical: 9400 RNAs ln<nrmsf> < −2.6 | Sub-critical: 7503 RNAs ln<nrmsf> < −2.6 | Sub-critical: 8241 RNAs ln<nrmsf> < −2.5 |
| Biological Regulation | Location of the CP | State Change * in the CP | Coherent Perturbation of Genome Engine | Reprogramming **/Cell-Fate Cange |
|---|---|---|---|---|
| Mouse Embryo Development | ln<nrmsf>CP ~ −5.6 | ON → OFF: At late 2-cell - 4-cell | Suppression- Enhancement | After late 2-cell ** |
| Human Embryo Development | ln<nrmsf>CP ~ −5.9 | Singular Switching: At 8-cell -Morula | Suppression- Enhancement | After 8-cell ** |
| Th17 Cell Immune Differentiation | ln<nrmsf>CP ~ −4.4 | OFF → ON: At 6–9 h | Suppression- Enhancement | After 6 h |
| Biological Regulation | Location of the CP | State Change * in the CP | Coherent Perturbation of Genome Engine | Cell-Fate Change |
|---|---|---|---|---|
| Cell Proliferation: EFG-Stimulated MCF-7 Cells | ln<nrmsf>CP ~ −2.6 | OFF State | Local Perturbation | NO |
| Cell Differentiation: HRG-Stimulated MCF-7 Cells | ln<nrmsf>CP ~ −2.5 | OFF → ON: At 15–20 min | Suppression- Enhancement | After 2 h ** |
| Cell Differentiation: atRA-Stimulated HL-60 Cells | ln<nrmsf>CP ~ −2.6 | OFF → ON: At 24–48 h | Enhancement- Suppression | After 24 h |
| Cell Differentiation: DMSO-Stimulated HL-60 Cells | ln<nrmsf>CP ~ −2.5 | ON → OFF: At 12–18 h | Enhancement- Suppression | After 18 h |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsuchiya, M.; Giuliani, A.; Yoshikawa, K. Cell-Fate Determination from Embryo to Cancer Development: Genomic Mechanism Elucidated. Int. J. Mol. Sci. 2020, 21, 4581. https://doi.org/10.3390/ijms21134581
Tsuchiya M, Giuliani A, Yoshikawa K. Cell-Fate Determination from Embryo to Cancer Development: Genomic Mechanism Elucidated. International Journal of Molecular Sciences. 2020; 21(13):4581. https://doi.org/10.3390/ijms21134581
Chicago/Turabian StyleTsuchiya, Masa, Alessandro Giuliani, and Kenichi Yoshikawa. 2020. "Cell-Fate Determination from Embryo to Cancer Development: Genomic Mechanism Elucidated" International Journal of Molecular Sciences 21, no. 13: 4581. https://doi.org/10.3390/ijms21134581
APA StyleTsuchiya, M., Giuliani, A., & Yoshikawa, K. (2020). Cell-Fate Determination from Embryo to Cancer Development: Genomic Mechanism Elucidated. International Journal of Molecular Sciences, 21(13), 4581. https://doi.org/10.3390/ijms21134581







