Fock-Space Coupled Cluster Theory: Systematic Study of Partial Fourth Order Triples Schemes for Ionization Potential and Comparison with Bondonic Formalism
Abstract
1. Introduction
2. Conceptual Method
2.1. FS-CC Theory
2.2. Perturbative Triples
2.3. Comparison with the Bondonic Diagrammatic Formalism of Many-Body Perturbation Theory
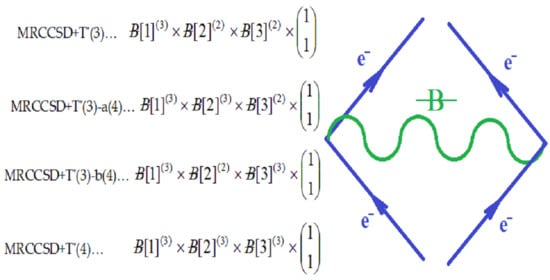
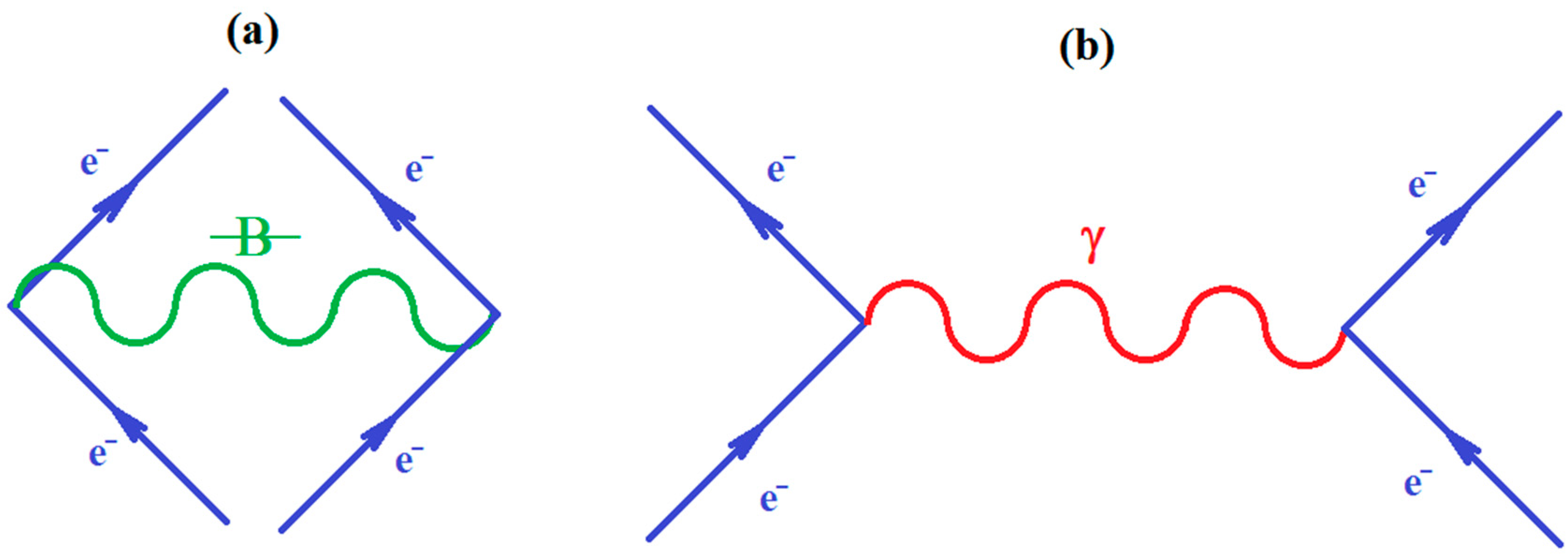
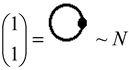 , along the higher interaction with active particles (), as the effective formalisms usually prescribe; ii) it features the “superposition” multiplied with the recalling the undiscernible particle statistics; iii) it is a particle size dependent as so “recuperating” in a bosonic way (viz. the bondons as “gluing” the fermions in chemical bonding) the “condensation ordering parameter”, and being in the same time suitable for chemical bonding dynamics – since chemical reactivity usually conveys with energy variation (e.g. by the chemical hardness dependency, etc.), see Ref. [51]. Moreover, worth mentioning that earlier study of applying bondonic theory to elemental chemical bonding in hydrogen molecule revealed that, indeed, the presence of order parameter in the master quantum equation (of Hartree–Fock–Bogoliubov type) development; while, when combining with fermionic superposition in a Heitler–London formalism leaves with the shifts of both nominator and denominators of resulted variational energies of bonding, see Ref. [52]; this is in phenomenological agreement with the many-body perturbation theory which, through infinite summation of interacting orders yields with geometrical series solved with such energetic corrections in both effective potential and in referential energies alike. Of course, much work should be done in order to establish one-to-one correspondence between the present bondonic formalism as diagrammatic results and the standard perturbative theory of N-states. Yet, the present endeavors like to open such a way. All-in-all, as a corollary for the theoretical purpose of the actual paper, the bondonic diagrammatic framework of the present partial fourth order triples scheme looks like the composed diagram:
, along the higher interaction with active particles (), as the effective formalisms usually prescribe; ii) it features the “superposition” multiplied with the recalling the undiscernible particle statistics; iii) it is a particle size dependent as so “recuperating” in a bosonic way (viz. the bondons as “gluing” the fermions in chemical bonding) the “condensation ordering parameter”, and being in the same time suitable for chemical bonding dynamics – since chemical reactivity usually conveys with energy variation (e.g. by the chemical hardness dependency, etc.), see Ref. [51]. Moreover, worth mentioning that earlier study of applying bondonic theory to elemental chemical bonding in hydrogen molecule revealed that, indeed, the presence of order parameter in the master quantum equation (of Hartree–Fock–Bogoliubov type) development; while, when combining with fermionic superposition in a Heitler–London formalism leaves with the shifts of both nominator and denominators of resulted variational energies of bonding, see Ref. [52]; this is in phenomenological agreement with the many-body perturbation theory which, through infinite summation of interacting orders yields with geometrical series solved with such energetic corrections in both effective potential and in referential energies alike. Of course, much work should be done in order to establish one-to-one correspondence between the present bondonic formalism as diagrammatic results and the standard perturbative theory of N-states. Yet, the present endeavors like to open such a way. All-in-all, as a corollary for the theoretical purpose of the actual paper, the bondonic diagrammatic framework of the present partial fourth order triples scheme looks like the composed diagram:2.4. Computational Details
3. Results and Discussions
4. Conclusions and Perspectives
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Berkowitz, J. Photoabsorption, Photoionization, and Photoelectron Spectroscopy; Academic Press: Cambridge, MA, USA, 1979. [Google Scholar]
- Cederbaum, S.L.; Schirmer, J.; Domcke, W.; von Niessen, W. Complete breakdown of the quasiparticle picture for inner valence electrons. J. Phys. B 1977, 10, L549. [Google Scholar] [CrossRef]
- Ponzi, A.; Quadri, N.; Angeli, C.; Decleva, P. Electron correlation effects in the photoionization of CO and isoelectronic diatomic molecules. Phys. Chem. Chem. Phys. 2019, 21, 1937–1951. [Google Scholar] [CrossRef]
- Evangelista, A.F.; Chan, C.K.G.; Scuseria, E.G. Exact parameterization of fermionic wave functions via unitary coupled cluster theory. J. Chem. Phys. 2019, 151, 244112. [Google Scholar] [CrossRef] [PubMed]
- Crawford, D.T.; Schaefer, F.H. An introduction to coupled cluster theory for computational chemists. Rev. Comput. Chem. 1999, 14, 33–136. [Google Scholar]
- Putz, M.V. The Bondons: The Quantum Particles of the Chemical Bond. Int. J. Mol. Sci. 2010, 11, 4227–4256. [Google Scholar] [CrossRef] [PubMed]
- Putz, M.V. Bondonic Theory. In New Frontiers in Nanochemistry: Concepts, Theories, and Trends, Volume 1: Structural Nanochemistry; Mihai, V.P., Ed.; Apple Academic Press: Palm Bay, FL, USA, 2020; pp. 49–58. [Google Scholar]
- Bartlett, J.R. Modern Electronic Structure Theory; Yarkony, D.R., Ed.; World Scientific: Singapore, 1995; Volume 2, pp. 1047–1131. [Google Scholar]
- Cizek, J. On the Correlation Problem in Atomic and Molecular Systems. Calculation of Wavefunction Components in Ursell-Type Expansion Using Quantum-Field Theoretical Methods. J. Chem. Phys. 1966, 45, 4256. [Google Scholar] [CrossRef]
- Paldus, J.; Ciziek, J.; Shavitt, I. Correlation Problems in Atomic and Molecular Systems. IV. Extended Coupled-Pair Many-Electron Theory and Its Application to the BH3 Molecule. Phys. Rev. A 1972, 5, 50. [Google Scholar] [CrossRef]
- Bartlett, J.R.; Purvis, D.G. Many-body perturbation theory, coupled-pair many-electron theory, and the importance of quadruple excitations for the correlation problem. Int. J. Quantum Chem. 1978, 14, 561–581. [Google Scholar] [CrossRef]
- Bartlett, J.R. Many-body perturbation theory and Coupled-cluster theory for electron correlation in molecule. Annu. Rev. Phys. Chem. 1981, 32, 359–401. [Google Scholar] [CrossRef]
- Bartlett, R.J. Coupled-cluster approach to molecular structure and spectra: A step toward predictive quantum chemistry. J. Phys. Chem. 1989, 93, 1697–1708. [Google Scholar] [CrossRef]
- Lee, S.Y.; Kucharski, A.S.; Bartlett, J.R. A coupled cluster approach with triple excitations. J. Chem. Phys. 1984, 81, 5906–5912. [Google Scholar] [CrossRef]
- Urban, M.; Noga, J.; Cole, J.S.; Bartlett, J.R. Towards a full CCSDT model for electron correlation. J. Chem. Phys. 1985, 83, 4041–4046. [Google Scholar] [CrossRef]
- Piecuch, P.; Li, X.; Paldus, X. An ab initio determination of 1A1-3B1 energy gap in CH2 using orthogonally spin-adapted state-universal and state-specific coupled-cluster methods. J. Chem. Phys. Lett. 1994, 230, 377–386. [Google Scholar] [CrossRef]
- Hoffmann, R.M.; Simons, J. A unitary multiconfigurational coupled-cluster method: Theory and applications. J. Chem. Phys. 1988, 88, 993. [Google Scholar] [CrossRef]
- Malrieu, P.J.; Ph Durand, P.; Daudey, P.J. Intermediate Hamiltonians as a new class of effective Hamiltonians. J. Phys. A. 1985, 18, 809. [Google Scholar] [CrossRef]
- Mukherjee, D.; Pal, S. Use of Cluster expansion methods in the open shell correlation problem, Advances in Quantum Chemistry. Adv. Quantum Chem. 1989, 20, 291–373. [Google Scholar]
- Jeziorski, B.; Monkhorst, J.H. Coupled-cluster method for multideterminantal reference states. Phys. Rev. A 1981, 24, 1668. [Google Scholar] [CrossRef]
- Balkova, A.; Kucharski, A.S.; Meissner, L.; Bartlett, J.R. The multireference coupled-cluster method in Hilbert space: An incomplete model space application to the LiH molecule. J. Chem. Phys. 1991, 95, 4311–4316. [Google Scholar] [CrossRef]
- Mukherjee, D. The linked-cluster theorem in the open-shell coupled-cluster theory for incomplete model spaces. Chem. Phys. Lett. 1986, 125, 207–212. [Google Scholar] [CrossRef]
- Mukherjee, D. On the hierarchy equations of the wave-operator for open-shell systems. Pramana 1979, 12, 203–225. [Google Scholar] [CrossRef]
- Pal, S. Fock space multi-reference coupled cluster method for energies and energy derivatives. Mol. Phys. 2010, 108, 3033–3042. [Google Scholar] [CrossRef]
- Pal, S. Multireference coupled cluster response approach for the calculation of static properties. Phys. Rev. A 1989, 39, 39–42. [Google Scholar] [CrossRef] [PubMed]
- Pal, S. An open shell coupled cluster response approach for static properties. Int. J. Quantum Chem. 1992, 41, 443–452. [Google Scholar] [CrossRef]
- Kutzelnigg, W. Quantum chemistry in Fock space. III. Particle-hole formalism. J. Chem. Phys. 1984, 80, 822. [Google Scholar] [CrossRef]
- Sinha, D.; Mukhopadhyay, D.; Mukhejee, D. A note on the direct calculation of excitation energies by quasi-degenerate MBPT and coupled-cluster theory. Chem. Phys. Lett. 1986, 129, 369–374. [Google Scholar] [CrossRef]
- Pal, S.; Rittby, M.; Bartlett, J.R. Multi reference coupled cluster methods for ionization potentials with partial inclusion of triple excitations. Chem. Phys. Lett. 1989, 160, 212–218. [Google Scholar] [CrossRef]
- Pal, S.; Rittby, M.; Bartlett, J.R.; Sinha, D.; Mukherjee, D. Multireference coupled-cluster methods using an incomplete model space: Application to ionization potentials and excitation energies of formaldehyde. Chem. Phys. Lett. 1987, 137, 273–278. [Google Scholar] [CrossRef]
- Pal, S.; Rittby, M.; Bartlett, J.R.; Sinha, D.; Mukherjee, D. Molecular applications of multireference coupled-cluster methods using an Incomplete model space. J. Chem. Phys. 1988, 88, 4357–4365. [Google Scholar] [CrossRef]
- Rittby, M.; Pal, S.; Bartlett, J.R. Multi reference coupled cluster method: Ionization potentials and excitation energies of ketene and Diazomethane. J. Chem. Phys. 1989, 90, 3214–3220. [Google Scholar] [CrossRef]
- Mattie, R.; Rittby, M.; Pal, S.; Bartlett, J.R. Applications of Multi Reference Coupled Cluster Theory, Lect. Notes in Chemistry; Springer: Berlin/Heidelberg, Germany, 1989; Volume 50, pp. 143–153. [Google Scholar]
- Haque, A.; Kaldor, U. Open-shell coupled-cluster theory applied to atomic and molecular systems. Chem. Phys. Lett. 1985, 117, 347–351. [Google Scholar] [CrossRef]
- Haque, A.; Kaldor, U. Direct calculation of excitation energies by the coupled-cluster method: Mg and Ar atoms. Int. J. Quantum Chem. 1986, 20, 445–453. [Google Scholar]
- Bartlett, J.R.; Watts, D.J.; Kucharski, A.S.; Noga, J. Non-iterative fifth-order triple and quadruple excitation energy Corrections in correlated methods. Chem. Phys. Lett. 1990, 165, 513–522. [Google Scholar] [CrossRef]
- Vaval, N.; Pal, S. Molecular property calculation for excited states using a multireference coupled cluster approach. Chem. Phys. Lett. 1999, 300, 125. [Google Scholar] [CrossRef]
- Vaval, N.; Ghose, B.K.; Pal, S.; Mukherjee, D. Fock-space multireference coupled-cluster theory. fourth-order corrections to the ionization potential. Chem. Phys. Lett. 1993, 209, 292–298. [Google Scholar] [CrossRef]
- Vaval, N.; Pal, S.; Mukherjee, D. Fock space multi reference coupled cluster theory: Noniterative inclusion oftriples for excitation energies. Theor. Chem. Acc. 1998, 99, 100–105. [Google Scholar] [CrossRef]
- Lindgren, L.; Mukherjee, D. On the connectivity criteria in the open-shell coupled-cluster theory for general model spaces. Phys. Rep. 1987, 151, 93–127. [Google Scholar] [CrossRef]
- Manohar, U.P.; Vaval, N.; Pal, S. First- and Second-order electrical properties computed at the FSMRCCSD level for excited states of closed-shell molecules using the constrained-variational approach. J. Chem. Phys. 2009, 131, 024102. [Google Scholar]
- Bhattacharyya, D.; Vaval, N.; Pal, S. Electronic transition dipole moments and dipole oscillator strengths within Fock-space multi-reference coupled cluster framework—An efficient and novel approach. J. Chem. Phys. 2013, 138, 094108. [Google Scholar] [CrossRef]
- Stanton, J.; Gauss, J. Analytic energy derivatives for ionized states described by the equation-of-motion coupled cluster method. J. Chem. Phys. 1994, 101, 8938. [Google Scholar] [CrossRef]
- Bartlett, J.R.; Stanton, F.J. Reviews in Computational Chemistry; Lipkowitz, K.B., Boyd, D.B., Eds.; Vancouver Coastal Health: Vancouver, BC, Canada, 1994; Volume 5, p. 65. [Google Scholar]
- Nooijen, M.; Bartlett, J.R. Similarity transformed equation-of-motion coupled-cluster theory: Details, examples, and comparisons. J. Chem. Phys. 1997, 107, 6812–6830. [Google Scholar] [CrossRef]
- Krylov, I.A. Size-consistent wave functions for bond-breaking: The equation-of-motion spin-flip model. Chem. Phys. Lett. 2001, 338, 375. [Google Scholar] [CrossRef]
- Nooijen, M. Many-body similarity transformations generated by normal ordered exponential excitation operators. J. Chem. Phys. 1996, 104, 2638. [Google Scholar] [CrossRef]
- Nooijen, M.; Bartlett, J.R. Similarity transformed equation-of-motion coupled-cluster study of ionized, electron attached, and excited states of free base porphin. J. Chem. Phys. 1997, 106, 6449–6455. [Google Scholar] [CrossRef]
- Haque, A.; Mukhejee, D. Application of cluster expansion techniques to open shells: Calculation of difference energies. J. Chem. Phys. 1984, 80, 5058. [Google Scholar] [CrossRef]
- Szabo, A.; Ostlund, N.S. Modern Quantum Chemistry. In Introducing to Advanced Electronic Structure Theory; McGraw-Hill Publishing Company: New York, NY, USA, 1996; Reprinted in Dover Publications, Inc.: Mineola, NY, USA, 2020. [Google Scholar]
- Parr, R.G.; Yang, W. Density Functional Theory of Atoms and Molecules; Oxford University Press: Oxford, NY, USA, 1989. [Google Scholar]
- Putz, M.V. Density Functional Theory of Bose-Einstein Condensation: Road to Chemical Bonding Quantum Condensate. In Applications of Density Functional Theory to Chemical Reactivity, in Structure and Bonding Series; Putz, M.V., Mingos, D.M.P., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 149, pp. 1–50. [Google Scholar]
- Wetmore, R.W.; Boyd, R.K.; Leroy, R.J. A theoretical investigation of the CH2+ di-cation. Chem. Phys. 1984, 89, 329. [Google Scholar] [CrossRef]
- Ghose, K.B.; Pal, S. Multi-reference coupled-cluster calculations on CH2+. J. Chem. Phys. 1992, 97, 3863. [Google Scholar]
- Trickl, T.; Cromwell, E.F.; Lee, Y.T.; Kung, A.H. State-selective ionization of nitrogen in the X2 = 0 and v = 1 states by two-color (1 + 1) photon excitation near threshold. J. Chem. Phys. 1989, 91, 6006. [Google Scholar] [CrossRef]
- Rachlew-Kallne, E.; Stromholm, C.; Larsson, J.; Persson, A.; Zerne, R. Direct determination of the ionization potential of CO by resonantly enhanced multiphoton ionization mass spectrometry. Chem. Phys. Lett. 1993, 215, 173. [Google Scholar]
- Herzberg, G. Molecular Spectra and Molecular Structure, Vol I—Spectra of Diatomic Molecule; Erman, P., Karawajczyk, A., Eds.; Kreiger: Malabar, FL, USA, 1989. [Google Scholar]

| METHODS | Orbital | RESULTS (eV) | |
|---|---|---|---|
| Basis-A (5s4p2d1f) | Basis-B (aug-cc-pVDZ) | ||
| MRCCSD | 3 | 15.645 | 15.443 |
| 17.262 | 17.129 | ||
| MRCCSD+ | 3 | 15.637 | 15.486 |
| 16.966 | 16.890 | ||
| MRCCSD+ | 3 | 15.280 | 15.189 |
| 16.750 | 16.685 | ||
| MRCCSD+ | 3 | 15.639 | 15.525 |
| 17.000 | 16.908 | ||
| MRCCSD+ | 3 | 15.541 | 15.424 |
| 16.907 | 16.810 | ||
| Experimental Ref. [55] | 3 | 15.581 ± 0.008 | |
| 16.8 | |||
| METHODS | Orbital | RESULTS (eV) | ||
|---|---|---|---|---|
| Basis-A (cc-pVDZ) | Basis-B (cc-pVTZ) | Basis-C (aug-cc-pVDZ) | ||
| MRCCSD | 5 | 13.827 | 14.149 | 13.995 |
| 16.746 | 17.048 | 16.915 | ||
| 4 | 19.487 | 19.759 | 19.678 | |
| MRCCSD+ | 5 | 13.616 | 13.967 | 13.837 |
| 16.847 | 17.137 | 17.092 | ||
| 4 | 20.030 | 20.274 | 20.293 | |
| MRCCSD+ | 5 | 13.458 | 13.763 | 13.642 |
| 16.559 | 16.773 | 16.769 | ||
| 4 | 19.170 | 19.357 | 19.498 | |
| MRCCSD+ | 5 | 13.663 | 13.988 | 13.865 |
| 16.766 | 17.026 | 16.995 | ||
| 4 | 19.424 | 19.653 | 19.769 | |
| MRCCSD+ | 5 | 13.575 | 13.903 | 13.773 |
| 16.716 | 16.968 | 16.936 | ||
| 4 | 19.336 | 19.554 | 19.671 | |
| Experimental Ref. [56] | 5 | 14.0142 ± 0.0003 | ||
| 16.5 | ||||
| 4 | 19.7 | |||
| METHODS | Orbital | RESULTS (eV) | ||
|---|---|---|---|---|
| Basis-A (cc-pVDZ) | Basis-B (aug-cc-pVDZ) | Basis-C (cc-pVTZ) | ||
| MRCCSD | 9.786 | 9.927 | 9.921 | |
| 4 | 10.816 | 11.005 | 10.962 | |
| MRCCSD+ | 10.358 | 10.529 | 10.429 | |
| 4 | 11.681 | 11.879 | 11.744 | |
| MRCCSD+ | 9.646 | 9.648 | 9.649 | |
| 4 | 10.539 | 10.556 | 10.540 | |
| MRCCSD+ | 9.888 | 9.909 | 9.934 | |
| 4 | 10.810 | 10.853 | 10.859 | |
| MRCCSD+ | 9.760 | 9.800 | 9.934 | |
| 4 | 10.607 | 10.684 | 10.663 | |
| Experimental Ref. [57] | 10.10 | |||
| 4 | 10.40 | |||
| IP (eV) | Methods | ||||
|---|---|---|---|---|---|
| Bond Distance (a.u.) | MRCCSD | ||||
| 1.8 | 28.580 | 28.363 | 28.040 | 28.042 | 27.865 |
| 1.9 | 28.267 | 28.057 | 27.657 | 27.650 | 27.470 |
| 2.0 | 27.396 | 27.734 | 27.256 | 27.240 | 27.058 |
| IP (eV) | Methods | |||||
|---|---|---|---|---|---|---|
| Bond Distance (a.u.) | MRCCSD | Full CI (FCI) | ||||
| 1.8 | 24.594 | 24.581 | 24.550 | 24.575 | 24.549 | 24.528 |
| 1.9 | 24.424 | 24.409 | 24.377 | 24.403 | 24.376 | 24.354 |
| 2.0 | 24.245 | 24.230 | 24.195 | 24.224 | 24.196 | 24.189 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Basumallick, S.; Pal, S.; Putz, M.V. Fock-Space Coupled Cluster Theory: Systematic Study of Partial Fourth Order Triples Schemes for Ionization Potential and Comparison with Bondonic Formalism. Int. J. Mol. Sci. 2020, 21, 6199. https://doi.org/10.3390/ijms21176199
Basumallick S, Pal S, Putz MV. Fock-Space Coupled Cluster Theory: Systematic Study of Partial Fourth Order Triples Schemes for Ionization Potential and Comparison with Bondonic Formalism. International Journal of Molecular Sciences. 2020; 21(17):6199. https://doi.org/10.3390/ijms21176199
Chicago/Turabian StyleBasumallick, Suhita, Sourav Pal, and Mihai V. Putz. 2020. "Fock-Space Coupled Cluster Theory: Systematic Study of Partial Fourth Order Triples Schemes for Ionization Potential and Comparison with Bondonic Formalism" International Journal of Molecular Sciences 21, no. 17: 6199. https://doi.org/10.3390/ijms21176199
APA StyleBasumallick, S., Pal, S., & Putz, M. V. (2020). Fock-Space Coupled Cluster Theory: Systematic Study of Partial Fourth Order Triples Schemes for Ionization Potential and Comparison with Bondonic Formalism. International Journal of Molecular Sciences, 21(17), 6199. https://doi.org/10.3390/ijms21176199