Computational Modeling of Claudin Structure and Function
Abstract
:1. Introduction to Tight Junctions
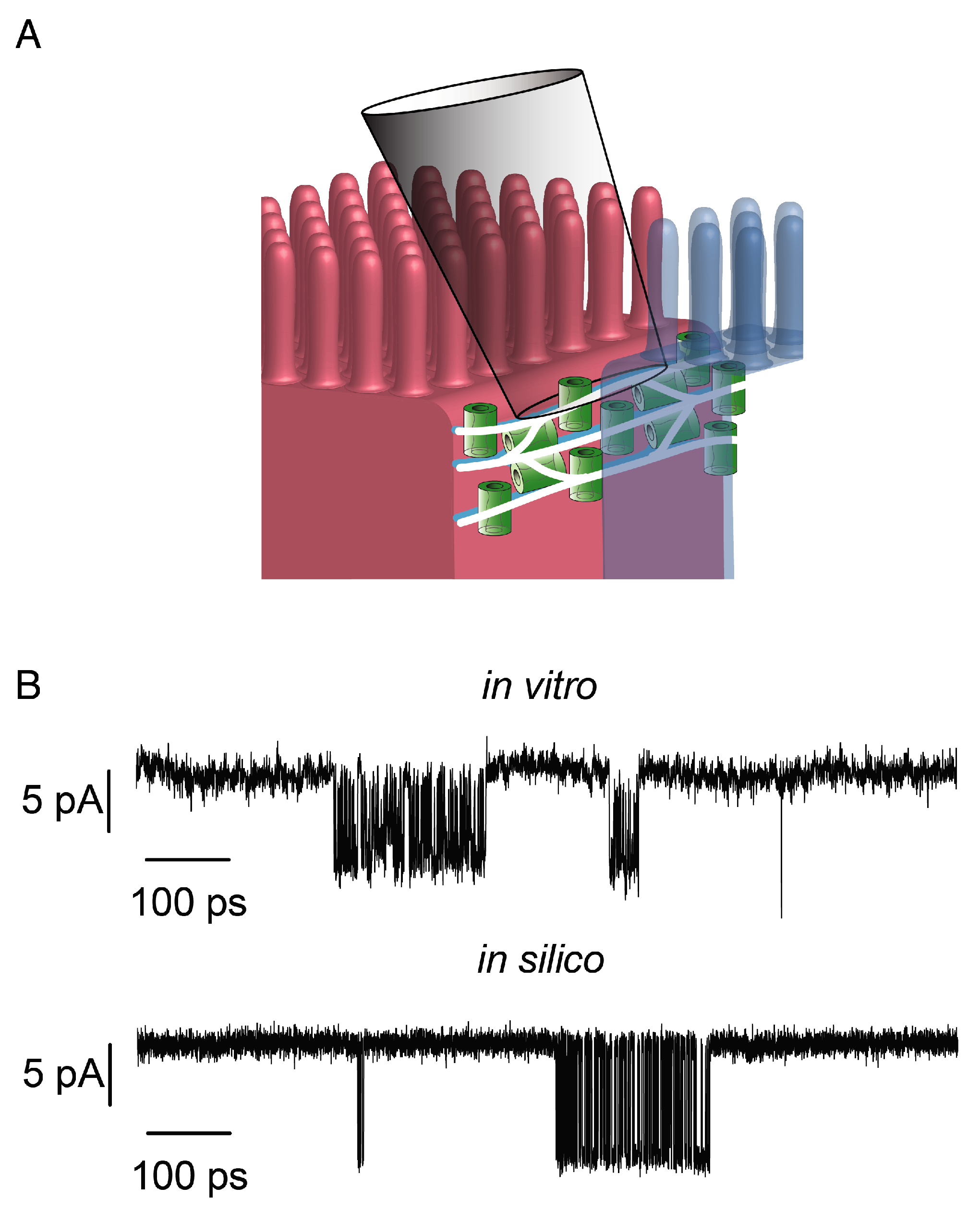
2. Resistive Models of Paracellular Flux through the Tight Junctions
3. Dynamic Models of Claudin Function
4. A Structural Model of Claudin Pores
5. Ion Transport Simulations
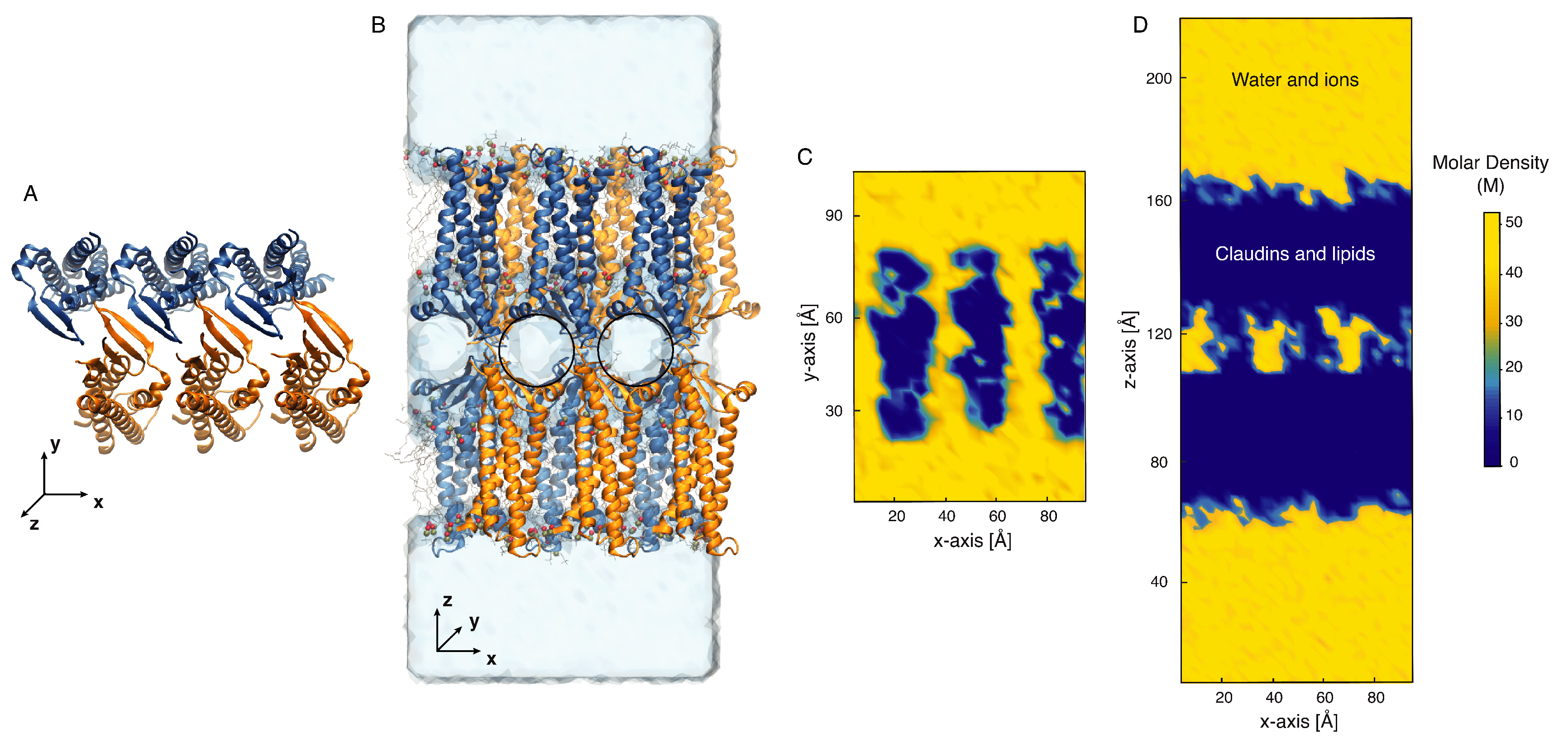
6. Claudin Polymerization in Lipid Bilayers
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| MD | Molecular Dynamics |
| CG | Coarse-grained |
| PMF | Potential of Mean Force |
| TER | Transepithelial Electrical Resistance |
| TJ | Tight Junction |
| TM | Transmembrane |
| ECS | Extracellular Segment |
| ECH | Extracellular Helix |
| FFEM | Freeze Fracture Electron Microscopy |
References
- Farquhar, M.G.; Palade, G.E. Junctional complexes in various epithelia. J. Cell Biol. 1963, 17, 375–412. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Staehelin, L.A.; Mukherjee, T.; Williams, A.W. Freeze-etch appearance of the tight junctions in the epithelium of small and large intestine of mice. Protoplasma 1969, 67, 165–184. [Google Scholar] [CrossRef] [PubMed]
- Claude, P.; Goodenough, D.A. Fracture faces of zonulae occludentes from “tight” and “leaky” epithelia. J. Cell Biol. 1973, 58, 390–400. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Claude, P. Morphological factors influencing transepithelial permeability: A model for the resistance of theZonula Occludens. J. Membr. Biol. 1978, 39, 219–232. [Google Scholar] [CrossRef]
- Weber, C.R.; Raleigh, D.R.; Su, L.; Shen, L.; Sullivan, E.A.; Wang, Y.; Turner, J.R. Epithelial myosin light chain kinase activation induces mucosal interleukin-13 expression to alter tight junction ion selectivity. J. Biol. Chem. 2010, 285, 12037–12046. [Google Scholar] [CrossRef] [Green Version]
- Furuse, M.; Furuse, K.; Sasaki, H.; Tsukita, S. Conversion of zonulae occludentes from tight to leaky strand type by introducing claudin-2 into Madin-Darby canine kidney I cells. J. Cell Biol. 2001, 153, 263–272. [Google Scholar] [CrossRef]
- Van Itallie, C.M.; Rogan, S.; Yu, A.S.; Vidal, L.S.; Holmes, J.; Anderson, J.M. Two splice variants of claudin-10 in the kidney create paracellular pores with different ion selectivities. Am. J. Physiol.-Ren. Physiol. 2006, 291, F1288–F1299. [Google Scholar] [CrossRef]
- Van Itallie, C.M.; Holmes, J.; Bridges, A.; Gookin, J.L.; Coccaro, M.R.; Proctor, W.; Colegio, O.R.; Anderson, J.M. The density of small tight junction pores varies among cell types and is increased by expression of claudin-2. J. Cell Sci. 2008, 121, 298–305. [Google Scholar] [CrossRef] [Green Version]
- Yu, A.S.; Cheng, M.H.; Angelow, S.; Günzel, D.; Kanzawa, S.A.; Schneeberger, E.E.; Fromm, M.; Coalson, R.D. Molecular basis for cation selectivity in claudin-2–based paracellular pores: Identification of an electrostatic interaction site. J. Gen. Physiol. 2009, 133, 111–127. [Google Scholar] [CrossRef] [Green Version]
- Watson, C.; Rowland, M.; Warhurst, G. Functional modeling of tight junctions in intestinal cell monolayers using polyethylene glycol oligomers. Am. J. Physiol.-Cell Physiol. 2001, 281, C388–C397. [Google Scholar] [CrossRef]
- Krug, S.M.; Günzel, D.; Conrad, M.P.; Lee, I.F.M.; Amasheh, S.; Fromm, M.; Yu, A.S. Charge-selective claudin channels. Ann. N. Y. Acad. Sci. 2012, 1257, 20–28. [Google Scholar] [CrossRef] [PubMed]
- Weber, C.R.; Liang, G.H.; Wang, Y.; Das, S.; Shen, L.; Yu, A.S.; Nelson, D.J.; Turner, J.R. Claudin-2-dependent paracellular channels are dynamically gated. Elife 2015, 4, e09906. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Angelow, S.; Linge, A.; Zhuo, M.; Yu, A.S. Claudin-2 pore function requires an intramolecular disulfide bond between two conserved extracellular cysteines. Am. J. Physiol.-Cell Physiol. 2013, 305, C190–C196. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Weber, C.R.; Turner, J.R. Dynamic modeling of the tight junction pore pathway. Ann. N. Y. Acad. Sci. 2017, 1397, 209. [Google Scholar] [CrossRef]
- Tervonen, A.; Ihalainen, T.O.; Nymark, S.; Hyttinen, J. Structural dynamics of tight junctions modulate the properties of the epithelial barrier. PLoS ONE 2019, 14, e0214876. [Google Scholar] [CrossRef]
- Buschmann, M.M.; Shen, L.; Rajapakse, H.; Raleigh, D.R.; Wang, Y.; Wang, Y.; Lingaraju, A.; Zha, J.; Abbott, E.; McAuley, E.M.; et al. Occludin OCEL-domain interactions are required for maintenance and regulation of the tight junction barrier to macromolecular flux. Mol. Biol. Cell 2013, 24, 3056–3068. [Google Scholar] [CrossRef]
- Krug, S.M.; Amasheh, S.; Richter, J.F.; Milatz, S.; Günzel, D.; Westphal, J.K.; Huber, O.; Schulzke, J.D.; Fromm, M. Tricellulin forms a barrier to macromolecules in tricellular tight junctions without affecting ion permeability. Mol. Biol. Cell 2009, 20, 3713–3724. [Google Scholar] [CrossRef] [Green Version]
- Marcial, M.; Madara, J. Analysis of absorptive cell occluding junction structure-function relationships in a state of enhanced junctional permeability. Lab. Investig. A J. Tech. Methods Pathol. 1987, 56, 424–434. [Google Scholar]
- Suzuki, H.; Nishizawa, T.; Tani, K.; Yamazaki, Y.; Tamura, A.; Ishitani, R.; Dohmae, N.; Tsukita, S.; Nureki, O.; Fujiyoshi, Y. Crystal structure of a claudin provides insight into the architecture of tight junctions. Science 2014, 344, 304–307. [Google Scholar] [CrossRef]
- Suzuki, H.; Tani, K.; Tamura, A.; Tsukita, S.; Fujiyoshi, Y. Model for the architecture of claudin-based paracellular ion channels through tight junctions. J. Mol. Biol. 2015, 427, 291–297. [Google Scholar] [CrossRef] [Green Version]
- Angelow, S.; Yu, A.S. Structure-function studies of claudin extracellular domains by cysteine-scanning mutagenesis. J. Biol. Chem. 2009, 284, 29205–29217. [Google Scholar] [CrossRef] [Green Version]
- Krause, G.; Protze, J.; Piontek, J. Assembly and function of claudins: Structure–function relationships based on homology models and crystal structures. Semin. Cell Dev. Biol. 2015, 42, 3–12. [Google Scholar] [CrossRef]
- Alberini, G.; Benfenati, F.; Maragniano, L. A refined model of claudin-15 tight junction paracellular architecture by molecular dynamics simulations. PLoS ONE 2017, 12, e0184190. [Google Scholar] [CrossRef] [Green Version]
- Zhao, J.; Krystofiak, E.S.; Ballesteros, A.; Cui, R.; Van Itallie, C.M.; Anderson, J.M.; Fenollar-Ferrer, C.; Kachar, B. Multiple claudin–claudin cis interfaces are required for tight junction strand formation and inherent flexibility. Commun. Biol. 2018, 1, 50. [Google Scholar] [CrossRef]
- Samanta, P.; Wang, Y.; Fuladi, S.; Zou, J.; Li, Y.; Shen, L.; Weber, C.; Khalili-Araghi, F. Molecular determination of claudin-15 organization and channel selectivity. J. Gen. Physiol. 2018, 150, 949–968. [Google Scholar] [CrossRef] [Green Version]
- Rosenthal, R.; Günzel, D.; Piontek, J.; Krug, S.M.; Ayala-Torres, C.; Hempel, C.; Theune, D.; Fromm, M. Claudin-15 forms a water channel through the tight junction with distinct function compared to claudin-2. Acta Physiol. 2019, e13334. [Google Scholar] [CrossRef]
- Rosenthal, R.; Günzel, D.; Krug, S.M.; Schulzke, J.D.; Fromm, M.; Yu, A.S. Claudin-2-mediated cation and water transport share a common pore. Acta Physiol. 2017, 219, 521–536. [Google Scholar] [CrossRef] [Green Version]
- Song, X.; Jensen, M.; Jogini, V.; Stein, R.A.; Lee, C.H.; Mchaourab, H.S.; Shaw, D.E.; Gouaux, E. Mechanism of NMDA receptor channel block by MK-801 and memantine. Nature 2018, 556, 515. [Google Scholar] [CrossRef]
- Jensen, M.; Jogini, V.; Borhani, D.W.; Leffler, A.E.; Dror, R.O.; Shaw, D.E. Mechanism of voltage gating in potassium channels. Science 2012, 336, 229–233. [Google Scholar] [CrossRef]
- Ostmeyer, J.; Chakrapani, S.; Pan, A.C.; Perozo, E.; Roux, B. Recovery from slow inactivation in K+ channels is controlled by water molecules. Nature 2013, 501, 121. [Google Scholar] [CrossRef]
- Li, Q.; Wanderling, S.; Paduch, M.; Medovoy, D.; Singharoy, A.; McGreevy, R.; Villalba-Galea, C.A.; Hulse, R.E.; Roux, B.; Schulten, K.; et al. Structural mechanism of voltage-dependent gating in an isolated voltage-sensing domain. Nat. Struct. Mol. Biol. 2014, 21, 244. [Google Scholar] [CrossRef]
- Gumbart, J.; Khalili-Araghi, F.; Sotomayor, M.; Roux, B. Constant electric field simulations of the membrane potential illustrated with simple systems. Biochim. Biophys. Acta (BBA)-Biomembr. 2012, 1818, 294–302. [Google Scholar] [CrossRef] [Green Version]
- Alberini, G.; Benfenati, F.; Maragniano, L. Molecular dynamics simulations of ion selectivity in a claudin-15 paracellular channel. J. Phys. Chem. B 2018, 122, 10783–10792. [Google Scholar] [CrossRef]
- Torrie, G.M.; Valleau, J.P. Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling. J. Comput. Phys. 1977, 23, 187–199. [Google Scholar] [CrossRef]
- Maragliano, L.; Vanden-Eijnden, E.; Roux, B. Free energy and kinetics of conformational transitions from Voronoi tessellated milestoning with restraining potentials. J. Chem. Theory Comput. 2009, 5, 2589–2594. [Google Scholar] [CrossRef]
- Faradjian, A.K.; Elber, R. Computing time scales from reaction coordinates by milestoning. J. Chem. Phys. 2004, 120, 10880–10889. [Google Scholar] [CrossRef]
- Conrad, M.P.; Piontek, J.; Günzel, D.; Fromm, M.; Krug, S.M. Molecular basis of claudin-17 anion selectivity. Cell. Mol. Life Sci. 2016, 73, 185–200. [Google Scholar] [CrossRef]
- Van Itallie, C.M.; Mitic, L.L.; Anderson, J.M. Claudin-2 forms homodimers and is a component of a high molecular weight protein complex. J. Biol. Chem. 2011, 286, 3442–3450. [Google Scholar] [CrossRef] [Green Version]
- Rossa, J.; Ploeger, C.; Vorreiter, F.; Saleh, T.; Protze, J.; Günzel, D.; Wolburg, H.; Krause, G.; Piontek, J. Claudin-3 and claudin-5 protein folding and assembly into the tight junction are controlled by non-conserved residues in the transmembrane 3 (TM3) and extracellular loop 2 (ECL2) segments. J. Biol. Chem. 2014, 289, 7641–7653. [Google Scholar] [CrossRef] [Green Version]
- Milatz, S.; Piontek, J.; Hempel, C.; Meoli, L.; Grohe, C.; Fromm, A.; Lee, I.F.M.; El-Athman, R.; Günzel, D. Tight junction strand formation by claudin-10 isoforms and claudin-10a/-10b chimeras. Ann. N. Y. Acad. Sci. 2017, 1405, 102–115. [Google Scholar] [CrossRef]
- Gong, Y.; Renigunta, V.; Zhou, Y.; Sunq, A.; Wang, J.; Yang, J.; Renigunta, A.; Baker, L.A.; Hou, J. Biochemical and biophysical analyses of tight junction permeability made of claudin-16 and claudin-19 dimerization. Mol. Biol. Cell 2015, 26, 4333–4346. [Google Scholar] [CrossRef]
- Piontek, A.; Rossa, J.; Protze, J.; Wolburg, H.; Hempel, C.; Günzel, D.; Krause, G.; Piontek, J. Polar and charged extracellular residues conserved among barrier-forming claudins contribute to tight junction strand formation. Ann. N. Y. Acad. Sci. 2017, 1397, 143–156. [Google Scholar] [CrossRef]
- Irudayanathan, F.J.; Wang, N.; Wang, X.; Nangia, S. Architecture of the paracellular channels formed by claudins of the blood–brain barrier tight junctions. Ann. N. Y. Acad. Sci. 2017, 1405, 131–146. [Google Scholar] [CrossRef]
- Ingólfsson, H.I.; Melo, M.N.; Van Eerden, F.J.; Arnarez, C.; Lopez, C.A.; Wassenaar, T.A.; Periole, X.; De Vries, A.H.; Tieleman, D.P.; Marrink, S.J. Lipid organization of the plasma membrane. J. Am. Chem. Soc. 2014, 136, 14554–14559. [Google Scholar] [CrossRef]
- Zhao, G.; Perilla, J.R.; Yufenyuy, E.L.; Meng, X.; Chen, B.; Ning, J.; Ahn, J.; Gronenborn, A.M.; Schulten, K.; Aiken, C.; et al. Mature HIV-1 capsid structure by cryo-electron microscopy and all-atom molecular dynamics. Nature 2013, 497, 643. [Google Scholar] [CrossRef]
- Grime, J.M.; Dama, J.F.; Ganser-Pornillos, B.K.; Woodward, C.L.; Jensen, G.J.; Yeager, M.; Voth, G.A. Coarse-grained simulation reveals key features of HIV-1 capsid self-assembly. Nat. Commun. 2016, 7, 11568. [Google Scholar] [CrossRef]
- Yu, H.; Schulten, K. Membrane sculpting by F-BAR domains studied by molecular dynamics simulations. PLoS Comput. Biol. 2013, 9, e1002892. [Google Scholar] [CrossRef]
- Koldsø, H.; Sansom, M.S. Organization and dynamics of receptor proteins in a plasma membrane. J. Am. Chem. Soc. 2015, 137, 14694–14704. [Google Scholar] [CrossRef] [Green Version]
- Simunovic, M.; Evergren, E.; Golushko, I.; Prévost, C.; Renard, H.F.; Johannes, L.; McMahon, H.T.; Lorman, V.; Voth, G.A.; Bassereau, P. How curvature-generating proteins build scaffolds on membrane nanotubes. Proc. Natl. Acad. Sci. USA 2016, 113, 11226–11231. [Google Scholar] [CrossRef] [Green Version]
- Rajagopal, N.; Irudayanathan, F.J.; Nangia, S. Computational Nanoscopy of Tight Junctions at the Blood–Brain Barrier Interface. Int. J. Mol. Sci. 2019, 20, 5583. [Google Scholar] [CrossRef] [Green Version]
- Marrink, S.J.; Risselada, H.J.; Yefimov, S.; Tieleman, D.P.; De Vries, A.H. The MARTINI force field: Coarse grained model for biomolecular simulations. J. Phys. Chem. B 2007, 111, 7812–7824. [Google Scholar] [CrossRef] [Green Version]
- Irudayanathan, F.J.; Trasatti, J.P.; Karande, P.; Nangia, S. Molecular architecture of the blood brain barrier tight junction proteins—A synergistic computational and in vitro approach. J. Phys. Chem. B 2015, 120, 77–88. [Google Scholar] [CrossRef]
- Milatz, S.; Piontek, J.; Schulzke, J.D.; Blasig, I.E.; Fromm, M.; Günzel, D. Probing the cis-arrangement of prototype tight junction proteins claudin-1 and claudin-3. Biochem. J. 2015, 468, 449–458. [Google Scholar] [CrossRef]
- Irudayanathan, F.J.; Wang, X.; Wang, N.; Willsey, S.R.; Seddon, I.A.; Nangia, S. Self-Assembly Simulations of Classic Claudins—Insights into the Pore Structure, Selectivity, and Higher Order Complexes. J. Phys. Chem. B 2018, 122, 7463–7474. [Google Scholar] [CrossRef]
- Gumbart, J.C.; Roux, B.; Chipot, C. Standard binding free energies from computer simulations: What is the best strategy? J. Chem. Theory Comput. 2012, 9, 794–802. [Google Scholar] [CrossRef]
- Gumbart, J.C.; Roux, B.; Chipot, C. Efficient determination of protein–protein standard binding free energies from first principles. J. Chem. Theory Comput. 2013, 9, 3789–3798. [Google Scholar] [CrossRef] [Green Version]
- Woo, H.J.; Roux, B. Calculation of absolute protein—ligand binding free energy from computer simulations. Proc. Natl. Acad. Sci. USA 2005, 102, 6825–6830. [Google Scholar] [CrossRef] [Green Version]
- Periole, X.; Knepp, A.M.; Sakmar, T.P.; Marrink, S.J.; Huber, T. Structural determinants of the supramolecular organization of G protein-coupled receptors in bilayers. J. Am. Chem. Soc. 2012, 134, 10959–10965. [Google Scholar] [CrossRef] [Green Version]
- Provasi, D.; Johnston, J.M.; Filizola, M. Lessons from free energy simulations of δ-opioid receptor homodimers involving the fourth transmembrane helix. Biochemistry 2010, 49, 6771–6776. [Google Scholar] [CrossRef]
- Johnston, J.M.; Filizola, M. Differential stability of the crystallographic interfaces of mu-and kappa-opioid receptors. PLoS ONE 2014, 9, e90694. [Google Scholar] [CrossRef]
- Castillo, N.; Monticelli, L.; Barnoud, J.; Tieleman, D.P. Free energy of WALP23 dimer association in DMPC, DPPC, and DOPC bilayers. Chem. Phys. Lipids 2013, 169, 95–105. [Google Scholar] [CrossRef] [Green Version]
- Baaden, M.; Marrink, S.J. Coarse-grain modelling of protein–protein interactions. Curr. Opin. Struct. Biol. 2013, 23, 878–886. [Google Scholar] [CrossRef] [Green Version]
- Periole, X. Interplay of G protein-coupled receptors with the membrane: Insights from supra-atomic coarse grain molecular dynamics simulations. Chem. Rev. 2016, 117, 156–185. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nakamura, S.; Irie, K.; Tanaka, H.; Nishikawa, K.; Suzuki, H.; Saitoh, Y.; Tamura, A.; Tsukita, S.; Fujiyoshi, Y. Morphologic determinant of tight junctions revealed by claudin-3 structures. Nat. Commun. 2019, 10, 816. [Google Scholar] [CrossRef]
- Piontek, J.; Winkler, L.; Wolburg, H.; Muller, S.L.; Zuleger, N.; Piehl, C.; Wiesner, B.; Krause, G.; Blasig, I.E. Formation of tight junction: Determinants of homophilic interaction between classic claudins. FASEB J. 2008, 22, 146–158. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Q.; Zhang, Q.; Wang, M.; Zhao, S.; Ma, J.; Luo, N.; Li, N.; Li, Y.; Xu, G.; Li, J. Interferon-γ and tumor necrosis factor-α disrupt epithelial barrier function by altering lipid composition in membrane microdomains of tight junction. Clin. Immunol. 2008, 126, 67–80. [Google Scholar] [CrossRef]
- Chen-Quay, S.C.; Eiting, K.T.; Li, A.W.A.; Lamharzi, N.; Quay, S.C. Identification of tight junction modulating lipids. J. Pharm. Sci. 2009, 98, 606–619. [Google Scholar] [CrossRef]
- Lambert, D.; O’NEILL, C.A.; Padfield, P.J. Depletion of Caco-2 cell cholesterol disrupts barrier function by altering the detergent solubility and distribution of specific tight-junction proteins. Biochem. J. 2005, 387, 553–560. [Google Scholar] [CrossRef] [Green Version]
- Nusrat, A.; Parkos, C.; Verkade, P.; Foley, C.; Liang, T.; Innis-Whitehouse, W.; Eastburn, K.; Madara, J. Tight junctions are membrane microdomains. J. Cell Sci. 2000, 113, 1771–1781. [Google Scholar]
- Rajagopal, N.; Irudayanathan, F.J.; Nangia, S. Palmitoylation of Claudin-5 Proteins Influences Their Lipid Domain Affinity and Tight Junction Assembly at the Blood–Brain Barrier Interface. J. Phys. Chem. B 2019, 123, 983–993. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fuladi, S.; Jannat, R.-W.; Shen, L.; Weber, C.R.; Khalili-Araghi, F. Computational Modeling of Claudin Structure and Function. Int. J. Mol. Sci. 2020, 21, 742. https://doi.org/10.3390/ijms21030742
Fuladi S, Jannat R-W, Shen L, Weber CR, Khalili-Araghi F. Computational Modeling of Claudin Structure and Function. International Journal of Molecular Sciences. 2020; 21(3):742. https://doi.org/10.3390/ijms21030742
Chicago/Turabian StyleFuladi, Shadi, Ridaka-Wal Jannat, Le Shen, Christopher R. Weber, and Fatemeh Khalili-Araghi. 2020. "Computational Modeling of Claudin Structure and Function" International Journal of Molecular Sciences 21, no. 3: 742. https://doi.org/10.3390/ijms21030742
APA StyleFuladi, S., Jannat, R.-W., Shen, L., Weber, C. R., & Khalili-Araghi, F. (2020). Computational Modeling of Claudin Structure and Function. International Journal of Molecular Sciences, 21(3), 742. https://doi.org/10.3390/ijms21030742




