Next Article in Journal
Blue Cone Monochromatism with Foveal Hypoplasia Caused by the Concomitant Effect of Variants in OPN1LW/OPN1MW and GPR143 Genes
Next Article in Special Issue
Viral Induced Protein Aggregation: A Mechanism of Immune Evasion
Previous Article in Journal
The Underlying Nature of Epigenetic Variation: Origin, Establishment, and Regulatory Function of Plant Epialleles
Previous Article in Special Issue
Biflavonoid-Induced Disruption of Hydrogen Bonds Leads to Amyloid-β Disaggregation
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
IJMS
Volume 22
Issue 16
10.3390/ijms22168619
ijms-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Identification of Two Early Folding Stage Prion Non-Local Contacts Suggested to Serve as Key Steps in Directing the Final Fold to Be Either Native or Pathogenic

by
Fernando Bergasa-Caceres
* and
Herschel A. Rabitz
Department of Chemistry, Princeton University, Princeton, NJ 08544, USA
*
Author to whom correspondence should be addressed.
Int. J. Mol. Sci. 2021, 22(16), 8619; https://doi.org/10.3390/ijms22168619
Submission received: 28 June 2021 / Revised: 30 July 2021 / Accepted: 4 August 2021 / Published: 10 August 2021
(This article belongs to the Special Issue Regulation of Functional Protein Aggregation: From Amyloids to Biomaterials)
Browse Figures
Versions Notes

Abstract

:
The initial steps of the folding pathway of the C-terminal domain of the murine prion protein mPrP(90–231) are predicted based on the sequential collapse model (SCM). A non-local dominant contact is found to form between the connecting region between helix 1 and β-sheet 1 and the C-terminal region of helix 3. This non-local contact nucleates the most populated molten globule-like intermediate along the folding pathway. A less stable early non-local contact between segments 120–124 and 179–183, located in the middle of helix 2, promotes the formation of a less populated molten globule-like intermediate. The formation of the dominant non-local contact constitutes an example of the postulated Nature’s Shortcut to the prion protein collapse into the native structure. The possible role of the less populated molten globule-like intermediate is explored as the potential initiation point for the folding for three pathogenic mutants (T182A, I214V, and Q211P in mouse prion numbering) of the prion protein.

1. Introduction

A direct link between the misfolding of the prion protein and several severe neurodegenerative conditions such as Creutzfeldt–Jakob and Kuru disease in humans, mad cow disease in cattle, and scrapie in sheep has been firmly established [1,2]. Specifically, the onset and development of the diseases was observed to be directly related to the accumulation in the brain of aggregates of a misfolded isoform of the native prion protein PrPc, called PrPSc [1,2]. The pathogenic isoform PrPSc has the same amino acid sequence as the native fold prion, but it bears considerably more ß-sheet secondary structure [3] and aggregates into oligomers and fibrils resistant to denaturation [4,5]. Thus, the elucidation of the mechanism by which the prion protein misfolds into its pathogenic isoform has become a prime issue. The importance of understanding the mechanisms underlying disease-related protein misfolding, aggregation, and fibrillization has become even more pressing as other neurodegenerative diseases such as Alzheimer’s [6] and Parkinson’s disease as well as Lewy dementia [7,8] have also been shown to display similar molecular mechanisms. Recently, it has also been suggested that the prion-like aggregation of the misfolded protein P53 might contribute to the onset and spreading of certain cancers [9,10].
This paper will consider the folding pathway of the prion protein into its native structure, while also giving a particular emphasis to issues associated with the pathogenic transition of the T182A, I214V, and Q211P mutants. A significant body of experimental evidence has shown that the prion pathogenic transformation is favored by mildly denaturing conditions, suggesting the involvement of molten globule-like states [11,12,13,14]. Direct experimental evidence indicates that: (a) the amyloid transition of the prion protein might be related to the presence of molten globule-like states that are prone to aggregation under pathogenic conditions [15,16,17,18,19], and (b) the branching point for the pathogenic transition is likely to be an on-pathway intermediate state [19]. Support for this hypothesis is also available from other protein systems such as β-microglobulin that display structural correlations between the molten globule state and the misfolded state [20,21]. However, the structure of such molten globule-like intermediate states of the prion protein remains unclear despite considerable efforts to elucidate them [22,23,24]. Thus, a topic of prime importance is the development of theoretical models to investigate the possible existence and structure of any intermediates along the folding pathway of the prion protein and consideration of their involvement in the pathogenic transition.
In this paper, we will apply the sequential collapse model (SCM) [25,26] to predict the earliest structure-forming events along the folding pathway of the murine prion protein mPrP(90–231). In the SCM, the multi-state folding process of proteins with a length of ~100–150 amino acids is initiated by the formation of a specific non-local contact between two distinct locations along the protein sequence called the primary contact [25,26]. The establishment of the primary contact that nucleates the folding process is hypothesized to considerably simplify the stochastic search leading to the native structure, by constraining the configurational options into smaller sets of potential dynamical trajectories. The primary contact would then constitute a set of emergent natural physical constraints that sidestep Levinthal’s paradox [26,27]. The SCM has been applied to investigate some general properties of the folding dynamics of pathogenic proteins in several contexts [28,29,30,31,32]. The main features of the SCM folding pathway for proteins ~100–150 amino acids long are explained in the Methods section.
The results presented in this paper include: (a) The prediction of two possible and competitive primary contacts nucleating the earliest stages of the folding pathway of the murine prion protein mPrP(90–231). The early populations of the non-local contacts are then explained to (b) produce a molten globule ensemble for mPrP(90–231) composed mostly of two different species, corresponding to the superposition of the molten globule-like intermediate states (MGLIS). The results are then applied to (c) explore the possible role in the pathogenesis of a change in the relative populations of MGLIS for three pathogenic mutations that are known to exist on the predicted primary contacts (T182A, I214V, Q211P) [33]. Additionally, (d) it is explained that the results suggest that the early non-local contact formation dynamics underlie the route to the prion pathogenic transition. Finally, (e) the model is shown to analytically provide for a quantitative estimate of the entropic barrier to the folding of the native prion protein, which is consistent with experimental observations.
Finally, it is important to point out that the investigation presented here deals only with the possible presence of a branching point towards the pathogenic structure along the folding pathway of the prion. It is not a study of possible interconversion mechanisms of the folded native structure as contemplated in many theoretical and experimental studies [34]. The possible existence of such an early branching mechanism from the molten globule does not necessarily imply that the same pathogenic structure could not be attained from the native fold. As the pathogenic isoform is a stable folded state of the prion, it is possible that it might be attained through more than one mechanism.

2. Results

2.1. The Murine Prion Protein mPrP

The murine prion protein PrPC is a glycoprotein of 209 amino acids, (numbered 23–231 for human PrP) attached to the cell membrane by a glycosylphosphatidyl inositol (GPI) anchor at ser231 [35,36]. Its three-dimensional structure, shown in Figure 1, includes an autonomously folding C-terminal domain involving residues 121–231, mPrP(121–231) [12]. The structure of the C-terminal domain of PrPC bears three α-helices (helix 1: D143-N153, helix 2: Q171-T192, and helix 3: E199-S226) and a short two-stranded antiparallel β-sheet [35].
The folding pathway of the C-terminal domain mPrP(121–231) has been explored employing a mutant F175W in order to have a fluorescence probe [37]. The folding reaction is very fast, with a half-time of τ ~170 μs at 4 °C. The reaction proceeds in almost two-state fashion, being one of the fastest naturally occurring protein folding reactions known to date. Experimental evidence on the human prion protein huPrP(90–231) shows that there are intermediates along the folding pathway of prion proteins [16,38,39,40,41]. However, the experimental evidence is limited, and the structure of the intermediates is unclear. There is evidence for a very early intermediate in mPrP(121–231) [19]. This intermediate appears to be only marginally stable and involves few native-like contacts, with most of the chain folding in a two-state collapse-like mode [19,37].
The prion protein is very flexible, with regions of the protein chain apparently disordered in the native state [35,36]. Consistent with this flexibility, its sequence contains a larger percentage of relatively small amino acids including glycine (i.e., compared to most globular proteins) and less hydrophobic side chains as compared to compact globular proteins. In this sense, the prion sequence represents an intermediate stage between those of compact globular proteins and the vastly more flexible intrinsically disordered proteins (IDP) [42,43].

2.2. Primary Contacts for mPrP(90–231)

Following the methodology employed in the SCM before [25,26], our calculations searched for the most stable possible hydrophobic contacts between pairs of 5-amino acid segments i and j, located at a distance nij along the sequence such that 57 ≲ nij  ≲ 100 amino acids. For this purpose, the hydrophobicity hi of each segment was estimated and is shown in Figure 1 (see Section 4.3 in Methods for a complete explanation along with citations giving further details). Our results predict that there are two possible primary contacts (i.e., the earliest contacts along the folding pathway) as initiation points for the folding of mPrP(90–231) as shown in Table 1:
As shown in the table: (1) The best primary contact, PC1, in mPrP(90–231) is established between the two segments comprising residues 136PMIHF140, centered at I138, and 211QMCVT215, centered at C213. The 136–140 segment is located in the connecting region between strand 1 of the β-sheet and helix 1, and the 211–215 segment is included in the C-terminal region of helix 3. Contact PC1 has a stability of ΔGcont ≈ −4.2 kT. (2) The second-best possible contact, PC2, appears between segment 120VVGLG124, centered at G122, a segment not included in the major secondary structure elements, and 179VNITI183, centered at I181. Segment 179–183 is included in the middle section of helix 2 in the native structure. Contact PC2 has a stability of ΔGcont ≈ −2.1 kT. All other possible contacts have stabilities < kT and will not be considered in this analysis, as their populations are one order of magnitude, or more, smaller than those of the two most stable contacts. Based on the calculated stabilities, the populations of both contacts in the earliest stage of the folding pathway of mPrP(90–231) are then ~89% for PC1 and ~11% for PC2.
The segments included in the two predicted primary contacts are highlighted on the native structure of mutant N173T (PDB: 1Y15 in mouse prion numbering) [36] in Figure 1. The two segments defining the dominant contact PC1 are close in the tertiary structure. The primary contact is relatively unstructured, enabling it to undergo further interactions in later folding phases. Thus, the segments involved in the primary contact are not necessarily precisely in coincidence in the native structure. However, they are generally close, with side chains within the Van der Waals interaction range, as they nucleate further structure attainment. The second-best contact (122–181) is not fully represented in the available NMR structure for mPrP(121–231) (PDB: 1AG2) [35], as it only includes residues V121-G124. It can be readily seen, however, on the structure of the mutant N173T [36] that the second-best contact, PC2, is not as close as the dominant one in the native structure, but still native-like.

2.3. Molten Globule State for mPrP(90–231)

Within the SCM model, the formation of a primary contact nucleates a molten globule-like intermediate state [25,26], as explained in the Methods section of the paper. The molten globule ensemble is then defined by the superposition of the MGLIS associated with each possible primary contact. Based on the predictions made above for the possible primary contacts, the molten globule ensemble of mPrP(90–231) is expected to include contributions from the MGLISs associated with each of the two predicted primary contacts. The expected composition of the molten globule ensemble is depicted in Figure 2.
Because of the difference in population of the two possible primary contacts, the molten globule ensemble is heavily dominated by the native-like contribution of the MGLIS1 associated with PC1. Upon being nucleated by the primary contact PC1, the MGLIS1 could include the primary contact and several additional structural elements located within the segments 121–136 and 218–231 outside of this primary contact. Thus, the potentially folded region of MGLIS1 could include the C-terminal region of helix 3 in the native structure. While the formation of a well-defined molten globule, with considerable native-like structure is observed in other proteins, it is not evident experimentally for the prion protein [18].
The less populated PC2 nucleates a different MGLIS2, which, besides the primary contact, could include structure in the region 90–119. Region 90–119 is generally expected to be disordered in the native state. Structure could also form in the region 184–231, which includes helix 3 and helix 2 from its middle up to the C-terminal section in the folded structure. Because the population of MGLIS1 is predicted to be higher than that of MGLIS2, the population of native-like helix 3 should also be higher relative to that of helix 2.
The predicted molten globule ensemble correlates well with the limited experimental information that is available about the structure of the folding intermediates of mPrP(90–231). A molten globule state of mPrP(90–231) obtained through acid denaturation was observed to retain structure in the helix 2-helix3 region, while lacking any in the strand 1-helix 1-strand 2 segment [46]. The folding kinetics of human prion protein huPrP(91–231), with a sequence very closely related to that of the murine protein, have been probed by temperature jump [47], and the folding nucleus was observed to contain elements of helices 2 and 3, which are both involved in the primary contacts predicted here. Additionally, hydrogen exchange of human PrP shows that a few residues clustered around region 179–214, which includes segments of both predicted primary contacts, have exchange rates sufficiently low to imply protection in the unfolded state [48]. Hydrogen exchange data of an on-pathway intermediate of the W145H/Y218W mutant of mPrP(90–231) are available [19]. For this mutant, the predicted native primary contact changes slightly from the one predicted here for the native sequence; the N-terminal segment remains the same, but the C-terminal segment becomes C214 to W218, centered at T216. This minor shift does not substantially affect the consideration of the molten globule above. The experiment yielded an intermediate with severe NMR line broadening in the helix 2-helix 3 region and with native-like elements, including amino acids at both ends of helix 3. The line broadening in the helix 2-helix 3 was expected to reflect the presence of the fluctuating folded-unfolded structure on the millisecond time scale. There was little protection elsewhere, including the N-terminal region where the P137-F141 segment is located, but protection of this segment is also low in the native state, so no definitive conclusions regarding its involvement in forming an early contact can be reliably reached. Consistent with the predictions made here, NMR chemical shifts in strand 1 of the β-sheet show significant displacement from negative values in the native state to values close to zero in the intermediate [19]. Helices 2 and 3 are also found to be critical in molecular dynamics studies of the prion interconversion due to the observed propensity of residues in helices 2 and 3 to interact to form β-sheet structures [49].

2.4. Is the Less Populated MGLIS the Branching Point for the Pathogenic Transition from the Molten Globule?

Several researchers have focused on the instabilities of helices 2 and 3 in the native state [50,51,52,53] and the significant number of pathogenic mutations that they can bear to propose that the transition from the native state is likely to be initiated from helices 2 and 3. Helices 2 and 3 remain partially folded in denatured states of the prion, while helix 1 is largely absent from such states [19]. This observation, combined with the additional stability of helix 1 as compared to helices 2 and 3 [54], has led some researchers to propose that the pathogenic transition from the native structure of the prion involves the destabilization of helix 1 [54], and conversely, that the stability of helix 1 constitutes a barrier to the pathogenic transition from the native state [55].
The presence in our predictions of a MGLIS defined by a significantly less populated primary contact in the earliest folding stages of the prion protein makes it important to investigate the possibility that the less populated MGLIS might constitute a pathway branching point leading to the pathogenic transition to PrPSc. Consistent with this hypothesis, experiments carried out with deletion mutants of the human prion protein, showed that the region encompassing helix 2 is involved in the nucleation of amyloid fibrils [56]. Helix 2 peptides have also been shown to seed the formation of fibrils of full length mPrP with the same kinetics as full length mPrPSc [57], a property not shared by helix 3 seed peptides. In order to investigate this possibility, we will focus here on the three pathogenic mutations of mPrP that directly involve the segments defining the primary contacts that nucleate the MGLISs leading to the molten globule: T182A, I214V, and Q211P [33,58,59,60,61,62,63].
An atomic-level detailed analysis of the effects of these mutations on the stability of the two MGLIS states of the prion protein predicted here would require sophisticated molecular dynamics, which is beyond the scope of this paper. However, a similar approximation to the one made to calculate the stability of the primary contact can be made to estimate the effect of the mutations on the stability ΔΔGMGLIS of the MGLISs. We will do so by employing empirically determined scales to estimate the combined effects of the mutation on the hydrophobic stabilization of the contact and the effect on the stability of helices 2 and 3 arising from the mutations. The approach is explained in the Methods section. The effect of the three mutations on the stability of the MGLISs is shown in Table 2.
An inspection of Table 2 shows that the effect of the three mutations is to increase the population of MGLIS2 with respect to that of MGLIS1. Mutation T182A does so by directly increasing the stability of MGLIS2, while mutations I214V and Q211P destabilize MGLIS1. The absolute value of the energy shift due to the change in secondary structure propensity is stronger than that calculated from hydrophobic stabilities alone for mutations T182A and Q211P. The T182A mutant suffers a considerable reduction both in secondary and tertiary native structure as compared to the native state [59,60], but not in the segment 182–196 corresponding to the primary contact [59]. Mutation I214V (I215V in human prion numbering) appeared in patients affected not only by Creutzfeldt–Jacob disease (CJD) but also in one case of Alzheimer’s disease, leading to the suggestion that it might be a marker for more general dementia conditions than just CJD [62]. Mutation Q211P (Q212P in human prion numbering) is remarkable because it induces significant adjustments in the prion structure, including partial disruption of helix 3, and an altered ability to bind copper, thus probably leading to alterations in copper homeostasis and redox activity in the affected cells [63].
The results presented here provide support for the hypothesis that mutations T182A, I214V, and Q211P become pathogenic by increasing the relative population of MGLIS2 with respect to MGLIS1. Contact PC2 for this mutation would become a gateway towards the pathogenic structure. In contrast, contact PC1 would constitute an example of what has been called in the context of the SCM “Nature’s Shortcut” to the native structure of the prion [26]. This result suggests that helix 2 might be critical to the interconversion process, as it appears partially folded in MGLIS2 but not in MGLIS1. This result is consistent with existing Φ-analysis of the aggregation process which suggests that α → β interconversion of helix 2 is an essential step in the formation of oligomers and fibrils [56]. Additionally, peptides mimicking helix 2 suffice to seed the short-time lag oligomerization of the native prion protein, while the same phenomenon was not observed when helix 3 mimicking peptides were employed [57].

2.5. Kinetics of the Two-State Collapse of the Prion Protein

In the SCM, the MGLIS collapses through two-state kinetics into the native topology [64]. The kinetics of the two-state collapse are described by the following equation:
ln κf ≈ ln g − RCO ΔGconf
where κf is the rate of two-state collapse, g is the characteristic diffusional frequency, RCO is the relative contact order (i.e., the average loop size of the final topology), and ΔGconf is the entropic free energy cost of folding.
Equation (1) provides an analytical procedure to determine the size of the configurational barrier to the two-state collapse ΔGconf from the observed two-state rate [28], such that
ΔGconf ≈ (16.1 − ln κf)/RCO
The observed apparent two-state rate of collapse of mPrP(121–231) has a value of ln κf ≈ 8.65 [37]. Then, the application of Equation (1), employing the value of RCO = 0.104 obtained for mPrP(121–231) (PDB file 1AG2) [65], yields the configurational entropic free energy change of ΔGconf ≈ 42.6 Kcal/mole, which compares very well with the experimental value of ΔGconf = ΔGint + ΔGnat ≈ 42.5 Kcal/mole [66] for the full native mPrP. This result is in excellent agreement with two-state folding and experimental data, and it confirms that the C-terminal domain mostly participates in the folding process, with the N-terminal domain remaining significantly disordered.
The complete native-like predicted folding pathway of the prion protein is shown in Figure 3.
Several pathogenic prion mutations exist whose effect on the overall stability of the prion protein is only ~1–3 Kcal/mole [67]. This result is somewhat puzzling as, on the basis of simple transition-state theory, the kinetic separation between PrPc and PrPSc is estimated to be ΔΔGconf (PrPc → PrPSc) ~36–39 Kcal/mole in order for the relative populations to be consistent with the clinical evidence (1). Thus, based on simple transition-state theory we expect ΔGconf(PrPSc) ~1.9·ΔGconf(PrPc), corresponding to a rate of folding difference such that κf(PrPSc)/κf(PrPc) ~0.15. As explained above, within the SCM, the activation barrier to folding contains two distinct physical elements: (a) the configurational cost of burying a significant fraction of the amino acids into attractive interactions, and (b) the configurational activation barrier emerging from the complexity of the correct chain topology from the unfolded state, where higher complexity is understood as reflected in the higher fraction of long-range contacts in the native structure (i.e., higher contact order). Thus, it is possible within the SCM that ΔGconf(PrPSc) ≈ ΔGconf(PrPc) and that the difference in folding rates between the pathogenic and the native forms is explained by the topological factor b) alone. Then, the contact order of PrPSc must be around RCO(PrPSc) ≈ 1.9 RCO(PrPc) ≈ 0.2. This value compares well with naturally occurring proteins ranging between 0.1 and slightly larger than 0.2. Moreover, it is well established that the pathogenic PrPSc has a much larger β-sheet content (42%) than native PrPc (3%) [68,69], and contact order values of β-sheet rich proteins tend to be higher than those of helical proteins [70]. Thus, a natural conclusion of the present analysis is that topology is the key kinetic protective factor that prevents most prion proteins from folding into the pathogenic PrPSc form. Finally, because the pathogenic transition in the current model requires the conformational search for the pathogenic topology described above, it is reasonable to expect that the proposed branching transition from MGLIS2 to the pathogenic structure takes place relatively late along the overall folding process as suggested by experimental data [19]. Figure 4 presents a schematic illustration of the pathogenic mechanism suggested by our results.

3. Discussion

The hypothesis that there is a pathogenic pathway to PrPSc through a molten globule-like state is broadly supported by a number of experimental observations. Thus, it is important to investigate the structure of such a molten globule state in order to understand the nature of the pathogenic transition. The current work predicts that two different molten globule-like states coexist within the molten globule for the murine prion protein mPrP(90–231). One of the two possible MGLISs is nucleated by a native-like contact and has the highest predicted population. The second possible MGLIS is also native-like but much less populated. The kinetics of formation of the dominant MGLIS and its progression towards the native structure were then investigated and shown to provide a strong consistency test for the model. Finally, it was also explained that the pathogenic mutations T182A, I214V, and Q211P stabilize the non-native MGLIS, suggesting a possible involvement of such a state in the pathogenic pathway associated with this mutation. The investigation of the pathogenic mutations required the consideration of the effects of secondary structure propensity in promoting the formation of primary contacts, which represents a significant predictive enrichment of the SCM model.
The results presented here strongly suggest that the pathogenic effects of mutations T182A, Q211P, and I214V arise due to a shift in the relative population of native and non-native early non-local (i.e., primary) contacts. This hypothesis could be confirmed experimentally, for example, by altering the relative primary contact populations through directed mutation. It is important to bear in mind that the etiology of prion diseases is complex and multi-factorial [1,2,71]. This is clear from observation of the different progression of prion misfolding-related disease in several animal species [71]. Thus, while the results presented here aim to provide a significant additional perspective towards understanding the underlying molecular mechanisms at play, they should be viewed as a piece in a complex physiological puzzle.
If proven correct, the results presented here could provide a new avenue for the development of therapeutic drugs. For example, a specific molecule could be sought that attaches to the segments that define PC2, thereby aiming to interdict in the formation of MGLIS2 and re-establish the native equilibrium between MGLIS1 and MGLIS2 within the molten globule. Such a folding interdiction of the target region (FITR) concept was proposed before within the SCM model for SARS-CoV-2 [72]. In particular, since the model predicts the specific segments that define PC2, it provides for natural templates to start the search for such an inhibitor of its formation, consisting of the peptides VVGLG or VNITI, corresponding to the protein segments that define PC2. There are many factors that go into the discovery of an effective therapeutic drug, and this natural suggestion or those possibly derived from it would also need to meet the host of criteria involved. The search for therapeutic drugs for prion diseases is an active field [60,73,74], including molecules aimed against the late stages of the folding process [75].
Furthermore, if our hypothesis is confirmed, it possibly could reveal a similarity of the pathogenic transition of the prion protein and that of the Parkinson’s disease-related protein α-synuclein. Although α-synuclein appears generally disordered both in vitro and in vivo, it is well established that there exist non-local contacts within the disordered state that are neuroprotective [76,77,78]. The relative populations of non-local contacts for α-synuclein were studied in previous work [32], and it was found that there is a dominant non-local contact and smaller populations of less stable ones. The results obtained here for mPrP(9.231) suggest that it could also be that a shift in the relative populations of the early non-local contacts of the prion protein similarly triggers agglomeration and pathogenesis. Recent experimental evidence indicates that the pathogenic transition of α-synuclein is dependent on the release of non-local interactions involving the N-terminal region [79]. The hypothesis that a common mechanism might underlie the pathogenic transition of the prion and α-synuclein could be investigated experimentally by altering the relative population of the non-local contacts of both proteins through directed mutation. If the hypothesis is confirmed, such equivalent mechanisms for the pathogenic transition of the prion protein and that of α-synuclein would point to the existence of a common intramolecular origin for at least some prion diseases and synucleinopathies. This, as yet, conjectured result would provide support for the commonality in the onset and development of several devastating neural diseases that has been suggested on the basis of broad biomedical considerations [80].
Further work will strive to investigate the effect of other pathogenic mutations in the folding pathway of the prion protein, thereby aiming to elucidate whether a common set of similar mechanisms underlies the pathogenic transition into PrPSc. Finally, the identification of early non-local contacts that are critical to drive the folding of the prion protein into native or pathogenic structures could also provide insight into the search for potential inhibitors of misfolding by suggesting target regions along the sequence that are critical to reduce the population of misfolded proteins.

4. Methods

The physical basis of the SCM and its most up-to-date formulation have been recently explained in full detail [26,32]. Here, only a brief summary of the main concepts that are relevant to the issues investigated in the present paper is presented.

4.1. The Multi-State Folding Pathway of Small Proteins in the SCM

The SCM considers early non-local contacts based on the entropy of formation of the resultant protein loops and the hydrophobic stabilization energy of the protein segments that define the contacts. The SCM has successfully predicted many of the observed features of protein folding pathways at low resolution [26]. Within the SCM, the folding of proteins with a length of ~100–150 amino acids such as mPrP(90–231) is nucleated by the formation of specific early non-local contacts, called primary contacts, that define the earliest folding phase. Primary contacts form at an optimal distance that, following previous work [32], we calculated for mPrP(90–231) to be n ≥ nop ≈ 57 along the sequence of amino acids determined from excluded volume considerations and polymer statistics [81]. The same kind of analysis showed that each primary contact in a long protein tends to define an autonomous folding region [82]. For a given protein sequence, there might be several possible stable primary contacts accordingly nucleating multiple parallel folding pathways [83]. Within the SCM, only those primary contacts that are native-like in the 3D structure lead to native-like folding pathways [26,82]. Because, at most, two simultaneous primary contacts can be established in proteins of a length of ~100–150 amino acids, most of the tertiary structure contacts will still be defined by contacts at a shorter range established in later folding phases. The nucleation by an early primary contact has been referred to within the model as “Nature’s shortcut to protein folding” [26].
It is important to bear in mind that the SCM is concerned with the optimal sizes of loops in the fluctuating unfolded chain rather than with the loops connecting secondary elements in the fully folded protein. Finally, because proteins longer than ~100 amino acids do not generally undergo complete two-state collapse 26but rather fold through multi-step pathways, consistent simple physical reasoning implies that there is an upper limit to the size of the primary loop that can successfully lead to the native SCM folding pathway of ~100 amino acids.
The concept of folding nucleated by non-local contacts is not exclusive of the SCM, having arisen earlier in the context of the diffusion-collision model [84], the loop hypothesis [85], and the energy landscape picture [86]. It also has appeared in simulations of the transition state of two-state folding proteins [87]. Additionally, protein topology has been considered an essential element of the folding mechanisms in a number of theoretical efforts [88,89,90,91,92]. The particular feature in the SCM is that the early non-local contacts are highly specific as in the loop hypothesis [85], and the SCM provides the means to determine their location from primary sequence information [25,26].

4.2. The Molten Globule

In the SCM, formation of a primary contact (i.e., a non-local early hydrophobic cluster) in a protein of ~100–150 amino acids nucleates the MGLIS. The MGLIS includes: (1) structured elements of the regions close to the segments defining the primary contact [25], located mostly within the N- and C-terminal ends of the protein, and (2) an open and fluctuating loop encompassing the regions of the sequence comprising the two segments defining the primary contact. The properties of the MGLIS listed below are close to those experimentally observed for the molten globule state [93]:
(a)
The MGLIS has a primary loop in a fluctuating but generally open conformation due to the need to minimize ∆Gloop in the early folding stages.
(b)
The MGLIS shows structural fluctuations on a larger scale compared to the native state because of the unfolded primary loop.
(c)
The overall dimensions of the MGLIS are larger than those of the native protein because of the open primary loop.
(d)
The extra volume of the MGLIS with respect to the native state is mostly water due to the open conformation of the loop.
(e)
Side chains in the primary loop of the MGLIS retain much of their torsional freedom, because the loop is not a fully folded structure.
If several primary contacts arise, the set of possible MGLISs will appear experimentally superimposed in the molten globule ensemble.

4.3. Determining the Primary Contact

Based on the model presented in the previous sections, whether there is a non-local contact in an otherwise unfolded state is dependent upon the stability of the potential contact candidates at loop lengths of n ≥ nop amino acids. In the SCM, the stability of a contact formed by the number ncont of amino acids, ΔGcontact(ncont, nloop), can be written as
ΔGcontact(ncont, nloop) ≈ ΔGint,H(ncont) + ΔGloop(nloop) + ΔGcont,S(ncont)
Here, ΔGloop represents the entropic free energy cost of the loop as discussed in Section 4.1. The term ∆Gint,H denotes all the enthalpic interactions that help stabilize the contact, possibly including hydrophobic interactions, van der Waals interactions, hydrogen bonds, disulfide bonds, and salt bridges [94], and its value satisfies ∆Gint < 0. The term ΔGcont,S > 0 represents the entropic cost of constraining the side chains of the amino acids defining the contact such that the contact is stable, and it opposes contact formation. A segment-specific determination of the value ΔGcont,S(ncont) for a given contact would require detailed MD techniques. However, a heuristic estimate can be made from earlier work within the SCM which showed that the average entropic cost of folding per amino acid for a sample of thirteen proteins was ΔGfolding/residue,S ≈ 0.85 kT/residue [28], and the maximum was ΔGfolding/residue,S ≈ 1.09 kT/residue. As these are estimates for the entropic cost for folding per residue of complete proteins that include highly buried as well as flexible exposed regions, it is then reasonable to expect that the entropic cost of a contact-forming region must be closer to the highest calculated values for ΔGfolding/residue,S. Here, we will assume that ΔGcontact,S(ncontact) for a contact including ncont amino acids is approximately ΔGfolding/residue,S determined by the number of residues defining the contact, such that ΔGcont,S(ncont) ≈ 1.09 ncont. This result is clearly an approximation but suffices for establishing a cut-off in the number of possible contacts that is consistent with the available experimental data.
Hydrophobic interactions are well understood to constitute the main driving force of the folding process [95]. Additionally, it is widely expected that secondary structure formation can contribute to the stability of early contacts [96]. Other interactions such as disulfide bonds and salt bridges are also understood to form later along the folding pathway [94]. Thus, for an early contact forming from the unfolded state, we can take ∆Gint(nop) ≈ ∆Ghyd(nop) + ∆Ghelix(nop), where ∆Ghyd(nop) represents the stabilizing effect of hydrophobicity in the early contacts, and Equation (3) can be written as
ΔGcontact(ncont, nloop) ≈ ΔGhyd(ncont) + ∆Ghelix(ncont) + ΔGloop(nloop) + ΔGcontact,S(ncontact)
There are no highly stable secondary elements in the intermediate states of the prion protein, so Equation (4) can be written as:
ΔGcontact(ncont, nloop) ≈ ΔGhyd(ncont) + ΔGloop(nloop) + ΔGcont,S(ncont)
Since the hydrophobic stabilization energy of the contact ΔGhyd is determined by the hydrophobicity of the segments involved, the hydrophobicity values hk are obtained from the Fauchere–Pliska scale [97] and assigned to each residue in accordance with previous calculations within the SCM.
Because the amino acid side chains are significantly larger than the typical peptide bond length, early contacts between two hydrophobic amino acids will inherently involve segments including several amino acids adjacent to the initial contact. The stability of this early hydrophobic contact will determine where the folding process is initiated. This picture is not unlike the zapping model of Dill et al. [98]. Here, the typical early contact segment size will be taken to be ~5 amino acids in line with previous calculations within the SCM [25]. Also, a value of zero is assigned to the hydrophobicity of the end residues. Then, the hydrophobicity hk of each residue is added over a segment contact window of five amino acids centered at residue i, resulting in a segment hydrophobicity hi,5 (a value of ~0.45 is equivalent to a change in energy of kT, and the margin of error is ~0.1 kT [96]).
In order to determine the best contact, the hi,5 values of a segment centered at residue i are added to the hj values of a segment centered at residue j, located at a distance nij at least nop amino acids apart along the sequence, no longer than the maximum loop length of ~100 amino acids, to give a contact propensity of ΔGcont(ncont, nloop) ≈ kT {−(1/0.45)(hi,5 + hj,5) + [3/2 ln nij] + 10.9}, where the term [3/2 ln nij] is the classical Jacobson–Stockmeyer approximation to the entropic cost of loop closure [99]. We consider any two segments centered at less than 5 amino acids to represent the same contact-forming region, as there must be some flexibility as to the precise location of relatively loose hydrophobic contacts.

4.4. Calculating the Effect of Mutations of the Primary Contact on the Stability of the MGLIS

The effect on the stability of the MGLIS, ΔGMGLIS, of any point mutation M is difficult to calculate precisely in the absence of detailed structural information. In any case, precisely obtaining such an estimate would require sophisticated molecular dynamics [44] that are outside the scope of this paper. However, in order to estimate whether the effect on the stability of the MGLIS of a mutation in the primary contact, a simpler heuristic approach in line with the methodology explained above can be applied. Such a heuristic approach is consistent with the SCM’s main contention that the earliest folding steps can be determined through coarse-grained thermodynamic analysis and do not depend critically on the atomic detailed nature of the interactions involved [25]. We will consider two main effects of the mutation: a) the change in hydrophobicity, and b) the effect on formation of secondary structure, that is, helices 2 and 3. Then, the overall change in stability, ΔΔGMGLIS, upon mutation can be written as
ΔΔGMGLIS ≈ ΔΔGMGLIS,hyd + ΔΔGMGLIS,α
where ΔΔGMGLIS,hyd is the hydrophobic change in free energy upon mutation of the primary contact, and ΔΔGMGLIS,α is the change in free energy produced by the change in helical propensity of the primary contact upon mutation.
With respect to the hydrophobic change in free energy, ΔΔGMGLIS,hyd, for mutations located on the primary contact, we closely follow the methodology described in Section 4.3. Then, the change in hydrophobic stability becomes ΔΔGMGLIS,hyd ≈ ΔΔhi,5(M), that is, the result of calculating the difference between the hydrophobicity for the native primary contact and that for the same contact bearing mutation M.
An approximation to ΔΔGMGLIS,α will be made here in the same semi-empirical spirit as applied in estimating the hydrophobic stability of the primary contacts by employing the O’Neil–DeGrado scale [100] for the helix-forming tendencies αi of the amino acids involved in close interactions. The scale is based on the stabilization energies of contacts between highly helical segments in dimers. This circumstance is an idealized physical situation unlikely to exactly resemble most primary contacts. At the level of resolution sought here, it is useful to provide a heuristic estimate of the mutation’s effect. Then, for a mutation M that replaces amino acid i for amino acid j, we can write ΔΔGMGLIS,α (M) ≈ αiI − αj, where the αiI coefficients are the O’Neil–DeGrado values for the free energy change upon replacement of glycine by amino acid i in a helical contact [100].

Author Contributions

Conceptualization, F.B.-C.; methodology, F.B.-C.; formal analysis, F.B.-C.; investigation, F.B.-C.; data curation, F.B.-C.; writing F.B.-C. and H.A.R.; project administration, F.B.-C. and H.A.R.; funding acquisition, F.B.-C. and H.A.R. Both authors have read and agreed to the published version of the manuscript.

Funding

This research was partially funded by NSF grant CHE-1763198.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The authors acknowledge support from NSF grant CHE-1763198.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

mPrP(90–231)Murine prion protein (90–231)
SCMSequential collapse model
MGLISMolten globule-like state

References

  1. Prusiner, S.B. (Ed.) Prion Biology and Diseases; Cold Spring Harbor Laboratory Press: Cold Spring Harbor, NY, USA, 2014. [Google Scholar]
  2. Ramirez-Alvarado, M.; Kelly, J.W.; Dobson, C.M. Protein Misfolding Diseases, Current and Emerging Principles and Therapies; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
  3. Ji, H.-F.; Zhang, H.-Y. ß-Sheet Constitution of Prion Proteins. Trends Biochem. Sci. 2010, 35, 129–134. [Google Scholar] [CrossRef]
  4. Yamaguchi, K.-I.; Kuwata, K. Formation and Properties of Amyloid Fibrils of Prion Protein. Biophys. Rev. 2018, 10, 517–525. [Google Scholar] [CrossRef] [Green Version]
  5. Cescatti, M.; Saverioni, D.; Capellani, S.; Tagliavini, F.; Kitamoto, T.; Ironside, J.; Giese, A.; Parchi, P. Abalysis of Conformational Stability of Abnormal Protein Aggregates Across the Spectrum of Creutzfeldt-Jakob Disease Prions. J. Virol. 2016, 90, 6244–6254. [Google Scholar] [CrossRef] [Green Version]
  6. Kondo, J.; Ihara, Y.; Sairoh, T. Molecular Cloning of cDNA Encoding an Unrecognized Component of Amyloid in Alzheimer Disease. Proc. Natl. Acad. Sci. USA 1993, 90, 11282–11287. [Google Scholar]
  7. Uversky, V.N. α-Synuclein Misfolding and Neurodegenerative Diseases. Curr. Protein Pept. Sci. 2009, 9, 507–540. [Google Scholar] [CrossRef] [Green Version]
  8. Spillantini, M.G.; Schmidt, M.L.; Lee, V.M.; Trojanowski, J.Q.; Jakes, R.; Goedert, M. α-Synuclein in Lewy Bodies. Nature 1997, 388, 839–840. [Google Scholar] [CrossRef]
  9. Navalkar, A.; Ghosh, S.; Pandey, S.; Paul, A.; Datta, D.; Maji, S.K. Prion-like p53 Amyloids in Cancer. Biochemistry 2020, 59, 146–155. [Google Scholar] [CrossRef] [PubMed]
  10. Silva, J.L.; Rangel, L.P.; Costa, D.C.F.; Cordeiro, Y.; De Moura Gallo, C.V. Expanding the prion concept to cancer biology: Dominant-negative effect of aggregates of mutant p53 tumor suppressor. Biosci. Rep. 2013, 33, e00054. [Google Scholar] [CrossRef] [PubMed]
  11. Kelly, J.W. The Environmental Dependency of Protein Folding Best Explains Prion and Amyloid Diseases. Proc. Natl. Acad. Sci. USA 1998, 95, 930–932. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  12. Alonso, D.O.V.; DeArmond, S.J.; Cohen, F.E.; Daggett, V. Mapping the Early Steps in the pH-Induced Conformational Conversion of the Prion Protein. Proc. Natl. Acad. Sci. USA 2001, 98, 2985–2989. [Google Scholar] [CrossRef] [Green Version]
  13. Nielsen, L.; Khurana, R.; Coats, A.; Frokjaer, S.; Brange, J.; Vyas, S.; Uversky, V.N.; Fink, A.L. Effect of Environmental Factors on the Kinetics of Insulin Fibril Formation: Elucidation of the Molecular Mechanism. Biochemistry 2001, 40, 6036–6046. [Google Scholar] [CrossRef]
  14. Hamada, D.; Dobson, C.M. A Kinetic Study of β-Lactoglobulin Amyloid Fibril Formation Promoted by Urea. Protein Sci. 2002, 11, 2417–2426. [Google Scholar] [CrossRef]
  15. Safar, J.; Roller, P.P.; Gajdusek, D.C.; Gibbs, C.J. Scrapie Amyloid (Prion) Protein has the Conformational Characteristics of an Aggregated Molten Globule Folding Intermediate. Biochemistry 1994, 33, 8375–8383. [Google Scholar] [CrossRef]
  16. Apetri, A.C.; Maki, K.; Roder, H.; Surewicz, W.K. Early Intermediate in Human Prion Protein as Evidenced by Ultrarapid Mixing Experiments. J. Am. Chem. Soc. 2006, 128, 11673–11678. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  17. Apetri, A.C.; Surewicz, K.; Surewicz, W.K. The Effect of Disease-Associated Mutations on the Folding Pathway of Human Prion Protein. J. Biol. Chem. 2004, 279, 18008–18014. [Google Scholar] [CrossRef] [Green Version]
  18. Jenkins, D.C.; Sylvester, I.D.; Pinheiro, T.J.T. The Elusive Intermediate on the Folding Pathway of the Prion Protein. FEBS J. 2008, 275, 1323–1335. [Google Scholar] [CrossRef] [PubMed]
  19. Honda, R.P.; Xu, M.; Yamaguchi, K.; Roder, H.; Kuwata, K. A Native-like Intermediate Serves as a Branching Point between the Folding and Aggregation Pathways of the Mouse Prion Protein. Structure 2015, 23, 1735–1742. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  20. Jahn, T.R.; Parker, M.J.; Homans, S.W.; Radford, S.E. Amyloid Formation Under Physiological Conditions Proceeds Via a Native-like Folding Intermediate. Nat. Struct. Mol. Biol. 2006, 13, 195–201. [Google Scholar] [CrossRef] [PubMed]
  21. Mukaiyama, A.; Nakamura, T.; Makabe, K.; Maki, K.; Goto, Y.; Kuwajima, K. The Molten Globule of β(2)-Microglobulin Accumulated at pH 4 and its Role in Protein Folding. J. Mol. Biol. 2013, 425, 273–291. [Google Scholar] [CrossRef]
  22. Gerber, R.; Tahiri-Alaoui, A.; Hore, P.J.; James, W. Oligomerization of the Human Prion Protein Proceeds via a Molten Globule Intermediate. J. Biol. Chem. 2007, 282, 6300–6307. [Google Scholar] [CrossRef] [Green Version]
  23. Moulick, R.; Das, R.; Udgaonkar, J.B. Partially Unfolded Forms of the Prion Protein Populated Under Misfolding-promoting Conditions: Characterization by Hydrogen Exchange Mass Spectroscopy and NMR. J. Biol. Chem. 2015, 290, 25227–25240. [Google Scholar] [CrossRef] [Green Version]
  24. Hosszu, L.L.P.; Wells, M.A.; Jackson, G.S.; Jonse, S.; Batchelor, M.; Clarke, A.R.; Craven, C.J.; Waltho, J.P.; Collinge, J. Definable Equilibrium States in the Folding of Human Prion Protein. Biochemistry 2005, 44, 16649–16657. [Google Scholar] [CrossRef]
  25. Bergasa-Caceres, F.; Ronneberg, T.A.; Rabitz, H.A. Sequential Collapse Model for Protein Folding Pathways. J. Phys. Chem. B 1999, 103, 9749–9758. [Google Scholar] [CrossRef]
  26. Bergasa-Caceres, F.; Haas, E.; Rabitz, H.A. Nature’s Shortcut to Protein Folding. J. Phys. Chem. B 2019, 123, 4463–4476. [Google Scholar] [CrossRef] [PubMed]
  27. Stepney, S. The neglected pillar of material computation. Phys. D 2008, 237, 1157–1164. [Google Scholar] [CrossRef]
  28. Bergasa-Caceres, F.; Rabitz, H.A. Low Entropic Barrier to the Hydrophobic Collapse of the Prion Protein: Effects of Intermediate States and Conformational Flexibility. J. Phys. Chem. A 2010, 114, 6978–6982. [Google Scholar] [CrossRef]
  29. Bergasa-Caceres, F.; Rabitz, H.A. A Simple Quantitative Model of Macromolecular Crowding Effects on Protein Folding: Application to the Murine Prion Protein (121–231). Chem. Phys. Lett. 2013, 574, 112–115. [Google Scholar] [CrossRef]
  30. Bergasa-Caceres, F.; Rabitz, H.A. Flexibility Damps Macromolecular Crowding Effects on Protein Folding Dynamics: Application to the Murine Prion Protein (121–231). Chem. Phys. Lett. 2014, 591, 207–211. [Google Scholar] [CrossRef]
  31. Bergasa-Caceres, F.; Rabitz, H.A. Macromolecular Crowding Facilitates the Conformational Transition of Molten Globule States of the Prion Protein. J. Phys. Chem. B 2016, 120, 11093–11101. [Google Scholar] [CrossRef] [PubMed]
  32. Bergasa-Caceres, F.; Rabitz, H. Predicting the location of the non-local contacts in alpha-synuclein Biochimica et Biophysica Acta Proteins and Proteomics. Biochim. Biophys. Acta Proteins Proteom. 2018, 1201–1208. [Google Scholar] [CrossRef] [PubMed]
  33. Bernardi, L.; Bruni, A.C. Mutations in Prion Protein Gene: Pathogenic Mechanisms in C-Terminal vs. N-Terminal Domain, a Review. Int. J. Mol. Sci. 2019, 20, 3606. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  34. Singh, J.; Udgaonkar, J.B. Molecular Mechanism of the Misfolding and Oligomerization of the Prion Protein: Current Understanding and Its Implication. J. Phys. Chem. B 2015, 54, 4431–4442. [Google Scholar] [CrossRef]
  35. Riek, R.; Hornemann, S.; Wider, G.; Billeter, M.; Glockshuber, R.; Wüthrich, K. NMR Structure of the Mouse Prion Protein Domain PrP(121-231). Nature 1996, 382, 180–182. [Google Scholar] [CrossRef]
  36. Gossert, A.D.; Bonjour, S.; Lysek, D.A.; Fiorito, F.; Wüthrich, K. Prion Protein NMR Structures of Elk and of Mouse/Elk Hybrids. Proc. Natl. Acad. Sci. USA 2005, 102, 646–650. [Google Scholar] [CrossRef] [Green Version]
  37. Wildegger, G.; Glockshuber, R. Extremely Rapid Folding of the C-Terminal Domain of the Prion Protein Without Kinetic Intermediates. Nat. Struct. Biol. 1999, 6, 550–553. [Google Scholar]
  38. Kachel, N.; Kremer, W.; Zahn, R.; Kalbitzer, H.R. Observation of intermediate states of the human prion protein by high pressure NMR spectroscopy. BMC Struct. Biol. 2006, 6, 16. [Google Scholar] [CrossRef] [Green Version]
  39. O’Sullivan, D.B.D.; Jones, C.E.; Abdelraheim, S.R.; Thompsett, A.R.; Brazier, M.W.; Toms, H.; Brown, D.R.; Viles, J.H. NMR characterization of the pH 4 β-intermediate of the prion protein: The N-terminal half of the protein remains unstructured and retains a high degree of flexibility. Biochem. J. 2007, 401, 533–540. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  40. Hingant, E.; Fontes, P.; Alvarez-Martinez, M.T.; Arnaud, J.-D.; Liautard, J.-P.; Pujo-Menjouet, L. A Micellar On-Pathway Intermediate Step Explains the Kinetics of Prion Amyloid Formation. PLoS Comput. Biol. 2014, 10, e1003735. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  41. Monad, B.; Reddy, G. A Transient Intermediate Populated in Prion Folding Leads to Domain Swapping. Biochemistry 2020, 59, 114–124. [Google Scholar]
  42. Dunker, A.K.; Garner, E.; Guilliot, S.; Romero, P.; Albrecht, K.; Hart, J.; Obradovic, Z.; Kissinger, C.; Villafranca, J.E. Protein disorder and the evolution of molecular recognition: Theory, predictions and observations. Pac. Symp. Biocomput. 1998, 3, 473–484. [Google Scholar]
  43. Dunker, A.K.; Lawson, J.D.; Brown, C.J.; Williams, R.M.; Romero, P.; Oh, J.S.; Oldfield, C.J.; Campen, A.M.; Ratliff, C.M.; Hipps, K.W.; et al. Intrinsically disordered protein. J. Mol. Graph. Model. 2001, 19, 26–59. [Google Scholar] [CrossRef] [Green Version]
  44. Piana, S.; Klepeis, J.L.; Shaw, D.E. Assessing the accuracy of physical models used in protein-folding simulations: Quantitative evidence from long molecular dynamics simulations. Curr. Opin. Struct. Biol. 2014, 24, 98–105. [Google Scholar] [CrossRef] [Green Version]
  45. Moreland, J.L.; Gramada, A.; Buzko, O.V.; Zhang, Q.; Bourne, P.E. The Molecular Biology Toolkit (MBT): A Modular Platform for Developing Molecular Visualization Applications. BMC Bioinform. 2005, 6, 21. [Google Scholar] [CrossRef] [Green Version]
  46. Honda, R.P.; Yamaguchi, K.; Kuwata, K. Acid-Induced Molten Globule of a Prion Protein: Crucial Role of Strand 1-Helix 1-Strand 2 Segment. J. Biol. Chem. 2014, 289, 30355–30363. [Google Scholar] [CrossRef] [Green Version]
  47. Hart, T.; Hosszu, L.L.P.; Trevitt, C.R.; Jackson, G.S.; Waltho, J.P.; Collinge, J.; Clarke, A.R. Folding kinetics of the human prion protein probed by temperature jump. Proc. Natl. Acad. Sci. USA 2009, 106, 5651–5656. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  48. Liemann, S.; Glockshuber, R. Influence of amino acid substitutions related to inherited human prion diseases on the thermodynamic stability of the cellular prion protein. Biochemistry 1999, 38, 3258–3267. [Google Scholar] [CrossRef] [PubMed]
  49. Chakroun, N.; Fornili, A.; Prigent, S.; Kleinjung, J.; Dreiss, C.A.; Rezaei, H.; Fraternali, F. Decrypting Prion Protein Conversion into a β-Rich Conformer by Molecular Dynamics. J. Chem. Theor. Comp. 2012, 9, 2455–2465. [Google Scholar] [CrossRef] [PubMed]
  50. Dima, R.I.; Thirumalai, D. Probing the Instabilities in the Dynamics of Helical Fragments from Mouse PrPC. Proc. Natl. Acad. Sci. USA 2004, 101, 15335–15340. [Google Scholar] [CrossRef] [Green Version]
  51. Chen, J.; Thirumalai, D. Helices 2 and 3 Are the Initiation Sites in the PrP(C) → PrP(SC) Transition. Biochemistry 2013, 52, 310–331. [Google Scholar] [CrossRef] [Green Version]
  52. Bae, S.-H.; Legname, G.; Serban, A.; Prusiner, S.B.; Wright, P.E.; Dyson, H.J. Prion Proteins with Pathogenic and Protective Mutations Show Similar Structure and Dynamics. Biochemistry 2009, 48, 8120–8128. [Google Scholar] [CrossRef] [Green Version]
  53. Yamamoto, N. Hot Spot of Structural Ambivalence in Prion Protein Revealed by Secondary Structure Principal Component Analysis. J. Phys. Chem. B 2014, 118, 9826–9833. [Google Scholar] [CrossRef]
  54. Liu, A.; Riek, P.; Zahn, R.; Hornemann, S.; Glockshuber, R.; Wuthrich, K. Peptides and Proteins in Neurodegenerative Disease: Helix Propensity of a Polypeptide Containing Helix 1 of the Mouse Prion Protein Studied by NMR and CD Spectroscopy. Biopolymers 1999, 51, 145–152. [Google Scholar] [CrossRef]
  55. Ziegler, J.; Sticht, H.; Marx, U.; Muller, W.; Rosch, P.; Schwarzinger, S. CD and NMR Studies of Prion Protein (PrP) Helix 1. J. Biol. Chem. 2003, 278, 50175–50181. [Google Scholar] [CrossRef] [Green Version]
  56. Honda, R.; Kuwata, K. Evidence for a central role of PrP helix 2 in the nucleation of amyloid fibrils. FASEB J. 2018, 32, 3641–3652. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  57. Kei-Ichi, Y.; Matsumoto, T.; Kuwata, K. Critical Region for Amyloid Fibril Formation of Mouse Prion Protein: Unusual Amyloidogenic Properties of the Helix 2 Peptide. Biochemistry 2008, 47, 13242–13251. [Google Scholar]
  58. Bagyinszky, E.; Van Giau, V.; Youn, Y.C.; An, S.S.A.; Kim, S. Characterization of mutations in PRNP (prion) gene and their possible roles in neurodegenerative diseases. Neuropsychiatr. Dis. Treat. 2018, 14, 2067–2085. [Google Scholar] [CrossRef] [Green Version]
  59. Singh, J.; Udgaonkar, J.B. The Pathogenic Mutation T182A Converts the Prion Protein into a Molten Globule-like Conformation Whose Misfolding to Oligomers but Not to Fibrils is Drastically Accelerated. J. Phys. Chem. B 2015, 55, 459–469. [Google Scholar] [CrossRef]
  60. Hernández, M.S.; Barritt, J.D.; Sobek, J.; Hornermann, S.; Aguzzi, A.; De Simone, A. Mechanism of Misfolding of the Human Prion Protein Revealed by a Pathological Mutation. Proc. Natl. Acad. Sci. USA 2021, 118, e2019631118. [Google Scholar] [CrossRef]
  61. Grasbon-Frodl, E.; Lorenz, H.; Mann, U.; Nitsch, R.M.; Windl, O.; Kretzschmar, H.A. Loss of glycosylation associated with the T183A mutation in human prion disease. Acta Neuropathol. 2004, 476–484. [Google Scholar] [CrossRef]
  62. Muñoz-Nieto, M.; Ramonet, N.; López-Gastón, J.I.; Cuadrado-Corrales, N.; Calero, O.; Díaz-Hurtado, M.; Ipiens, J.R.; Ramón y Cajal, S.; De Pedro-Cuesta, J.; Calero, M. A Novel Mutation I215V in the PRNP Gene Associated with Creutzfeldt-Jakob and Alzheimer’s Diseases in Three Patients with Divergent Clinical Phenotypes. J. Neurol. 2013, 260, 77–84. [Google Scholar] [CrossRef] [PubMed]
  63. D’Angelo, P.; Della Longa, S.; Arcovito, A.; Mancini, G.; Zitolo, A.; Chillemi, G.; Giachin, G.; Legname, G.; Benetti, F. Effects of the Pathological Q212P Mutation on Human Prion Protein Non-Octarepeat Copper-Binding Site. Biochemistry 2012, 51, 6068–6079. [Google Scholar] [CrossRef]
  64. Bergasa-Caceres, F.; Rabitz, H. Relating contact order to the rate of cooperative collapse in the sequential collapse model for protein folding pathways. Chem. Phys. Lett. 2003, 376, 612–617. [Google Scholar] [CrossRef]
  65. Plaxco, K.W.; University of California, Santa Barbara, CA, USA; Lawrence, C.; University of California, Santa Barbara, CA, USA. Personal Communication of Internal Computational Result for RCO in 1AG2, 2010.
  66. Moulick, R.; Udgaonkar, J.B. Thermodynamic Characterization of the Unfolding of the Prion Protein. Biophys J. 2014, 106, 410–420. [Google Scholar] [CrossRef] [Green Version]
  67. Sabareesan, A.T.; Udgaonkar, J.B. The G126V Mutation of the Mouse Prion Protein Hinders Nucleation-Dependent Fibril Formation by Slowing Initial Fibril Growth and by Increasing the Critical Concentration. Biochemistry 2017, 56, 5931–5942. [Google Scholar] [CrossRef]
  68. Pan, K.M.; Baldwin, M.; Nguyen, J.; Gasset, M.; Serban, A.N.A.; Groth, D.; Mehlhorn, I.; Huang, Z.; Fletterick, R.J.; Cohen, F.E. Conversion of α-helices into β-sheets features in the formation of the scrapie prion proteins. Proc. Natl. Acad. Sci. USA 1993, 90, 10962–10966. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  69. Nelson, R.; Sawaya, M.R.; Balbirnie, M.; Madsen, A.O.; Riekel, C.; Grothe, R.; Eisenberg, D. Structure of the cross-β spine of amyloid-like fibrils. Nature 2005, 435, 773–777. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  70. Makarov, D.E.; Keller, C.A.; Plaxo, K.W.; Metiu, H. How the folding rate constant of simple, single-domain proteins depends on the number of native contacts. Proc. Natl. Acad. Sci. USA 2002, 99, 3535–3539. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  71. Brandner, S.; Jaunmukiane, Z. Prion Disease: Experimental Models and Reality. Acta Neuropathol. 2017, 133, 197–222. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  72. Bergasa-Caceres, F.; Rabitz, H.A. Interdiction of Protein Folding for Therapeutic Drug Development in SARS-CoV-2. J. Phys. Chem. B 2020, 124, 8201–8208. [Google Scholar] [CrossRef]
  73. Mustazza, C.; Sbriccoli, M.; Minosi, P.; Raggi, C. Small Molecules with Anti-Prion Activity. Curr. Med. Chem. 2020, 27, 5446–5479. [Google Scholar] [CrossRef] [PubMed]
  74. Baral, P.K.; Wieland, B.; Swayampakula, M.; Polymenidou, M.; Rahman, M.H.; Kv, N.N.V.; Aguzzi, A.; James, M.N.G. Structural studies of the folded domain of the prion protein bound to the Fab fragment of the antibody POM1. Acta Crystallogr. D Biol. Crystallogr. 2012, 68, 1501–1512. [Google Scholar] [CrossRef]
  75. Spagnolli, G.; Massignan, T.; Astolfi, A.; Biggi, S.; Rigoli, M.; Brunelli, P.; Libergoli, M.; Ianeselli, A.; Orioli, S.; Boldrini, A. Pharmacological Inactivation of the Prion Protein by Targeting a Folding Intermediate. Nat. Comm. Biol. 2021, 4, 62. [Google Scholar] [CrossRef] [PubMed]
  76. Bertoncini, C.W.; Jung, Y.S.; Fernandez, C.O.; Hoyer, W.; Griesinger, C.; Jovin, T.M.; Zwecktetter, M. Release of Long-Range Interactions Potentiates Aggregation of Natively Unstructured Alpha-Synuclein. Proc. Natl. Acad. Sci. USA 2005, 102, 1430–1435. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  77. Lee, J.C.; Lai, B.T.; Kozak, J.J.; Gray, H.B.; Winkler, J.R. Alpha-Synuclein Tertiary Contact Dynamics. J. Phys. Chem. B 2007, 111, 2107–2112. [Google Scholar] [CrossRef] [Green Version]
  78. Dedmon, M.M.; Lindorff-Larsen, K.; Christodolou, J.; Vendruscolo, M.; Dobson, C.M. Mapping Non-local Interactions in α-Synuclein using Spin-Label NMR and Ensemble Molecular Dynamics Simulations. J. Am. Chem. Soc. 2005, 127, 476–477. [Google Scholar] [CrossRef]
  79. Ranjan, P.; Kumar, A. Perturbation in Long-Range Contacts Modulates the Kinetics of amyloid Formation in α-Synuclein Familial Mutants. ACS Chem. Neurol. 2017, 8, 2235–2246. [Google Scholar] [CrossRef] [PubMed]
  80. Angot, E.; Steiner, J.A.; Hansen, C.; Li, J.-Y.; Brundin, P. Are synucleinopathies prion-like diseases? Lancet Neurol. 2010, 9, 1128–1138. [Google Scholar] [CrossRef]
  81. Bergasa-Caceres, F.; Rabitz, H. Sequential Collapse Folding Pathway of Staphylococcal Nuclease: Entropic Activation Barriers to Hydrophobic Collapse of the Protein Core. J. Phys. Chem. B 2004, 108, 8023–8030. [Google Scholar] [CrossRef]
  82. Bergasa-Caceres, F.; Rabitz, H. Role of Topology in the Cooperative Collapse of the Protein Core in the Sequential Collapse Model. Folding Pathway of r-Lactalbumin and Hen Lysozyme. J. Phys.Chem.B 2001, 105, 2874–2880. [Google Scholar] [CrossRef]
  83. Bergasa-Caceres, F.; Rabitz, H.A. Sequential Collapse Folding Pathway of β-Lactoglobulin: Parallel Pathways and Non-Native Secondary Structure. J. Phys. Chem. B 2003, 107, 3606–3612. [Google Scholar] [CrossRef]
  84. Karplus, M.; Weaver, D.L. Diffusion–collision model for protein folding. Biopolymers 1979, 18, 1421–1437. [Google Scholar] [CrossRef]
  85. Ittah, V.; Haas, E. Nonlocal interactions stabilize long range loops in the initial folding intermediates of reduced bovine pancreatic trypsin inhibitor. Biochemistry 1995, 34, 4493–4506. [Google Scholar] [CrossRef]
  86. Sali, A.; Shakhnovich, E.; Karplus, M. How does a protein fold? Nature 1994, 369, 248–251. [Google Scholar] [PubMed]
  87. Vendruscolo, M.; Paci, E.; Dobson, C.M.; Karplus, M. Three key residues form a critical contact network in a protein folding transition state. Nature 2001, 409, 641–645. [Google Scholar] [CrossRef] [PubMed]
  88. Berezovsky, I.N.; Trifonov, E.N. Loop fold structure of proteins: Resolution of Levinthal’s paradox. J. Biomol. Struct. Dyn. 2002, 20, 5–6. [Google Scholar] [CrossRef] [PubMed]
  89. Berezovsky, I.N.; Guarnera, E.; Zheng, Z. Basic units of protein structure, folding, and function. Prog. Byophys. Mol. Biol. 2016, 128, 85–99. [Google Scholar] [CrossRef] [PubMed]
  90. Alm, E.; Baker, D. Prediction of Protein-Folding Mechanisms from Free-energy Landscapes Derived from Native Structures. Proc. Natl. Acad. Sci. USA 1999, 96, 11305–11310. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  91. Munoz, V.; Eaton, W.A. A Simple Model for Calculating the Kinetics of Protein Folding from Three-dimensional Structures. Proc. Natl. Acad. Sci. USA 1999, 96, 11311–11316. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  92. Makarov, D.E.; Plaxco, K.W. The Topomer Search Model: A Simple, Quantitative Theory of Two-State Protein Folding Kinetics. Protein Sci 2003, 12, 17–26. [Google Scholar] [CrossRef] [Green Version]
  93. Kuwajima, K. The molten globule state as a clue for understanding the folding and cooperativity of globular-protein structure. Proteins Struct. Funct. Genet. 1989, 6, 87–103. [Google Scholar] [CrossRef] [PubMed]
  94. Dill, K.A. Dominant Forces in Protein Folding. Biochemistry 1990, 29, 7133–7155. [Google Scholar] [CrossRef]
  95. Baldwin, R.L.; Rose, G.D. How the Hydrophobic Effect Drives Protein Folding. Proc. Natl. Acad. Sci. USA 2016, 113, 12462–12466. [Google Scholar] [CrossRef] [Green Version]
  96. Shiraki, K.; Nishikawa, K.; Goto, Y. Trifluoroethanol-induced Stabilization of the α-Helical Structure of β-Lactoglobulin: Implication for Non-hierarchical Protein Folding. J. Mol. Biol. 1995, 245, 180–194. [Google Scholar] [CrossRef] [PubMed]
  97. Ozkan, S.B.; Wu, G.A.; Chodera, J.D.; Dill, K.A. Protein Folding by Zipping and Assembly. Proc. Natl. Acad. Sci. USA 2007, 104, 11987–11992. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  98. Fauchere, J.L.; Pliska, V. Hydrophobic Parameters II of Amino-Acid Side Chains from the Partitioning of N-Acetyl-Amino-Acid Amides. Eur. J. Med. Chem. 1983, 18, 369–375. [Google Scholar]
  99. Jacobson, H.; Stockmeyer, W.H. Intramolecular Reactions in Polycondensations. I. The Theory of Linear Systems. J. Chem. Phys. 1950, 18, 1600–1607. [Google Scholar] [CrossRef]
  100. O’Neil, K.T.; DeGrado, W.F. A Thermodynamic Scale for the Helix-Forming Tendencies of the Commonly Occurring Amino. Acids Sci. 1990, 250, 646–651. [Google Scholar] [CrossRef] [PubMed]
Ijms 22 08619 g001 550
Figure 1. The location on the native structure [36,44] of mPrP(121–231) of the two possible primary contacts: (a) contact (138–213), and (b) contact (122–181) [45]; (c) the hydrophobicity coefficients hi calculated employing a rolling 5-amino acid window (see Section 4.2 in Methods).
Figure 1. The location on the native structure [36,44] of mPrP(121–231) of the two possible primary contacts: (a) contact (138–213), and (b) contact (122–181) [45]; (c) the hydrophobicity coefficients hi calculated employing a rolling 5-amino acid window (see Section 4.2 in Methods).
Ijms 22 08619 g001
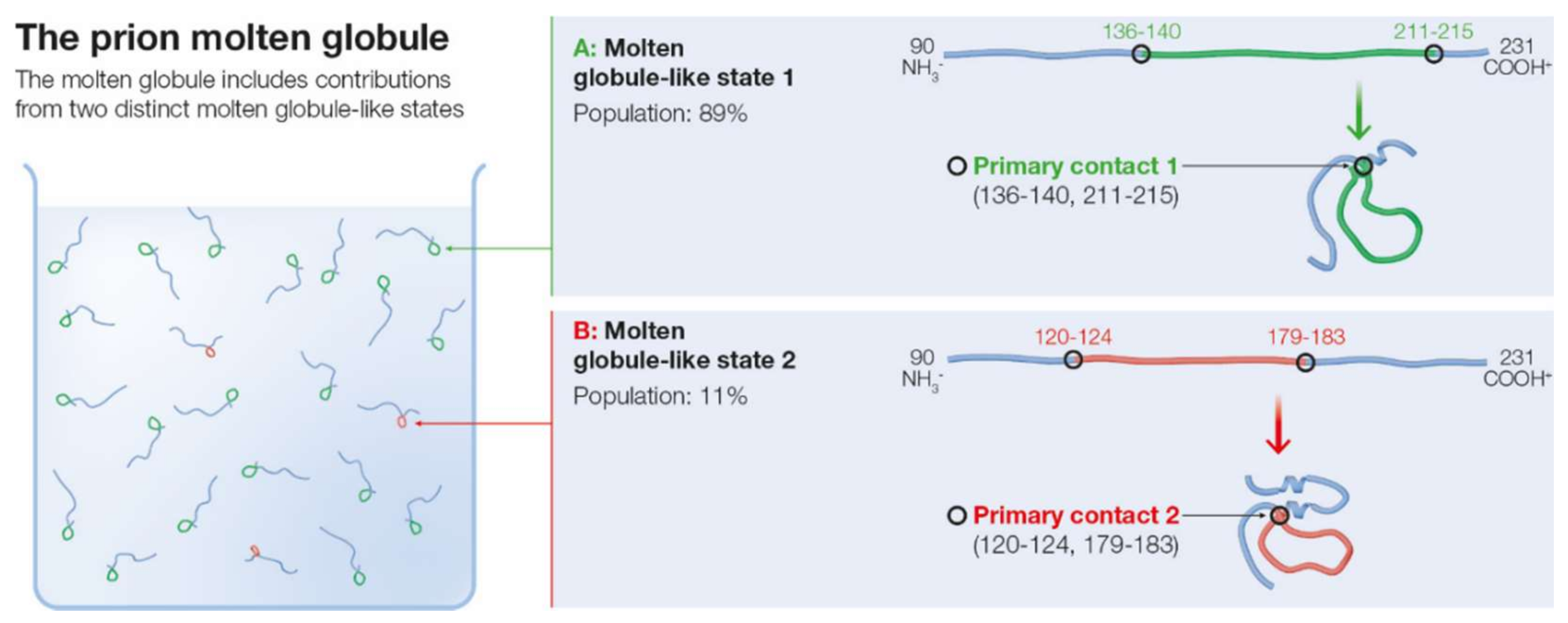
Ijms 22 08619 g002 550
Figure 2. The molten globule of mPrP(90–231) includes contributions from two distinct MGLISs arising from the two primary contacts: (A) the MGLIS arising from the dominant primary contact, including helix 3; (B) the MGLIS arising from the second-best primary contact including helix 2 and, possibly, also helix 3.
Figure 2. The molten globule of mPrP(90–231) includes contributions from two distinct MGLISs arising from the two primary contacts: (A) the MGLIS arising from the dominant primary contact, including helix 3; (B) the MGLIS arising from the second-best primary contact including helix 2 and, possibly, also helix 3.
Ijms 22 08619 g002
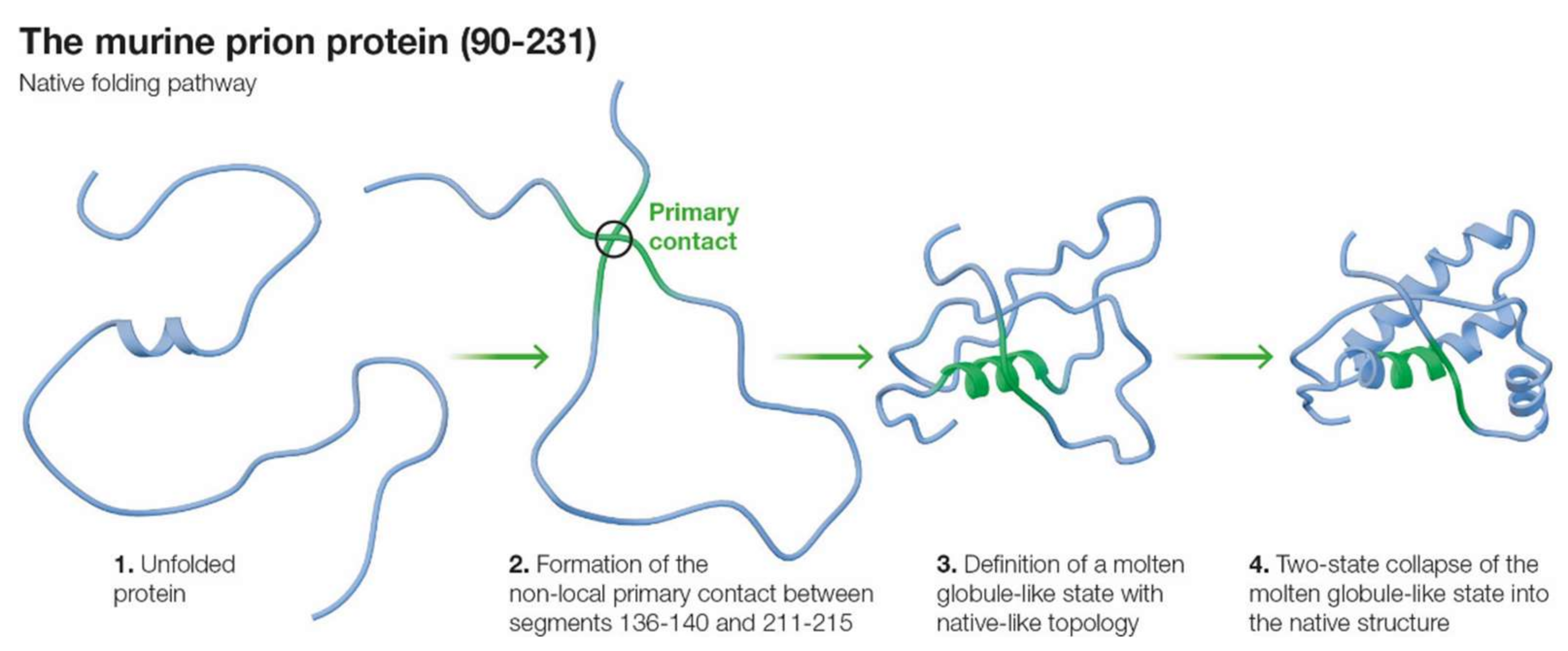
Ijms 22 08619 g003 550
Figure 3. The native folding pathway of mPrP(90–231) predicted by the SCM. Helix 3 appears structured in MGLIS1 due to its participation in the primary contact. Stochastic search for the native topology is the rate limiting factor between the MGLIS (step 3) and the final native structure (step 4).
Figure 3. The native folding pathway of mPrP(90–231) predicted by the SCM. Helix 3 appears structured in MGLIS1 due to its participation in the primary contact. Stochastic search for the native topology is the rate limiting factor between the MGLIS (step 3) and the final native structure (step 4).
Ijms 22 08619 g003
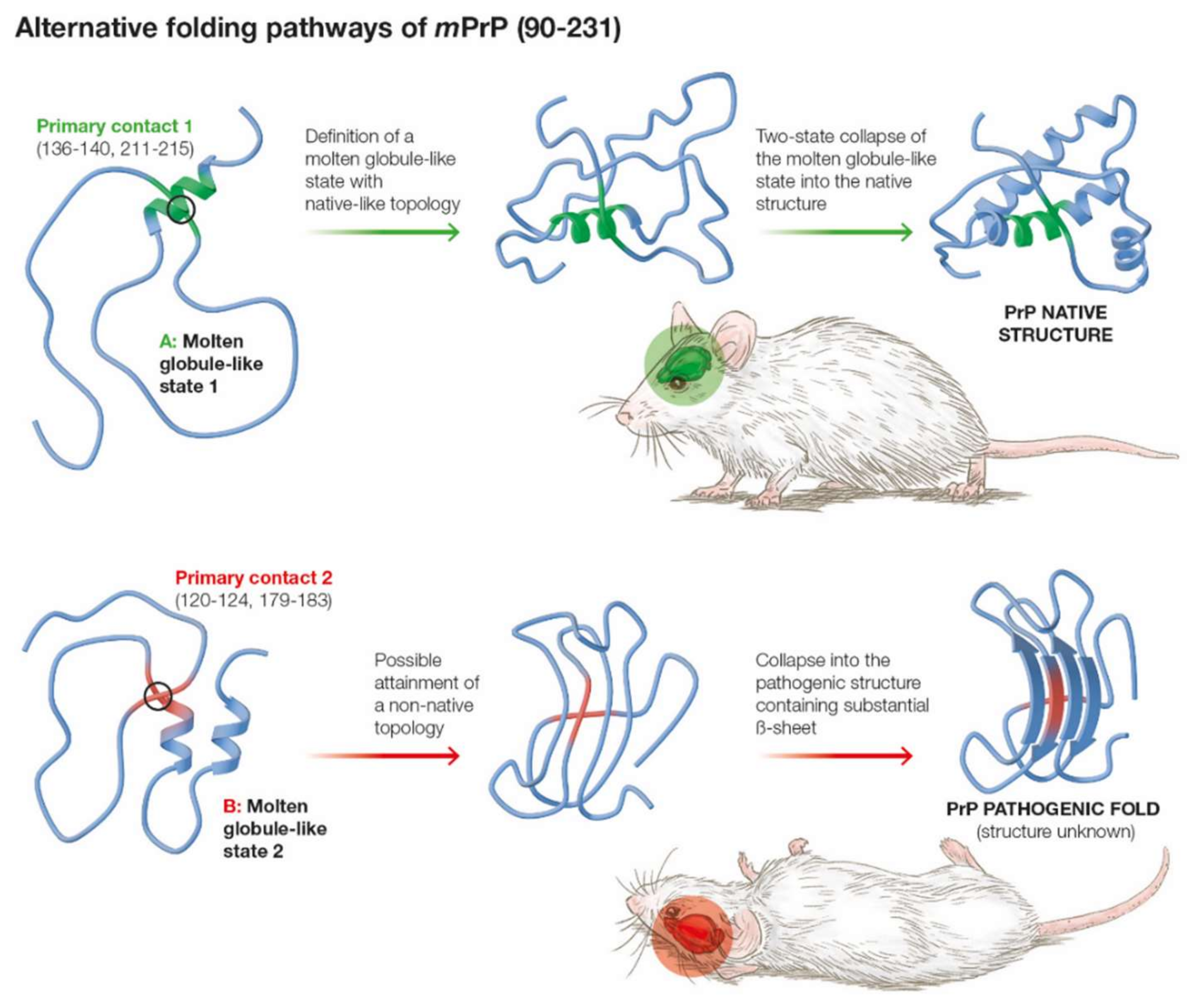
Ijms 22 08619 g004 550
Figure 4. The alternative folding pathways with the less populated one possibly leading to pathogenesis. The schematic representation of the pathogenic topology and final fold is illustrative.
Figure 4. The alternative folding pathways with the less populated one possibly leading to pathogenesis. The schematic representation of the pathogenic topology and final fold is illustrative.
Ijms 22 08619 g004
Table
Table 1. Predicted primary contacts for mPrP(90–231) (in kT).
Table 1. Predicted primary contacts for mPrP(90–231) (in kT).
Primary ContactStabilityNative-like
PC1 (138 on 213)−4.2Yes
PC2 (122 on 181)−2.1Yes
Table
Table 2. Estimated change in stability (in kT) of the corresponding MGLIS for mutations T182A, I214V, and Q211P, located in the two predicted primary contacts of the prion protein. Mutation T182A increases the stability of MGLIS2, while mutations I214V and Q211P reduce the stability of MGLIS1.
Table 2. Estimated change in stability (in kT) of the corresponding MGLIS for mutations T182A, I214V, and Q211P, located in the two predicted primary contacts of the prion protein. Mutation T182A increases the stability of MGLIS2, while mutations I214V and Q211P reduce the stability of MGLIS1.
MutantMGLISΔΔGMGLIS,hydΔΔGMGLIS,αΔΔGMGLIS
T182A MGLIS2−0.1−1.1−1.2
I214VMGLIS10.60.20.8
Q211PMGLIS1−0.94.53.6
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Bergasa-Caceres, F.; Rabitz, H.A. Identification of Two Early Folding Stage Prion Non-Local Contacts Suggested to Serve as Key Steps in Directing the Final Fold to Be Either Native or Pathogenic. Int. J. Mol. Sci. 2021, 22, 8619. https://doi.org/10.3390/ijms22168619

AMA Style

Bergasa-Caceres F, Rabitz HA. Identification of Two Early Folding Stage Prion Non-Local Contacts Suggested to Serve as Key Steps in Directing the Final Fold to Be Either Native or Pathogenic. International Journal of Molecular Sciences. 2021; 22(16):8619. https://doi.org/10.3390/ijms22168619

Chicago/Turabian Style

Bergasa-Caceres, Fernando, and Herschel A. Rabitz. 2021. "Identification of Two Early Folding Stage Prion Non-Local Contacts Suggested to Serve as Key Steps in Directing the Final Fold to Be Either Native or Pathogenic" International Journal of Molecular Sciences 22, no. 16: 8619. https://doi.org/10.3390/ijms22168619

APA Style

Bergasa-Caceres, F., & Rabitz, H. A. (2021). Identification of Two Early Folding Stage Prion Non-Local Contacts Suggested to Serve as Key Steps in Directing the Final Fold to Be Either Native or Pathogenic. International Journal of Molecular Sciences, 22(16), 8619. https://doi.org/10.3390/ijms22168619

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop